SPECULATIVE PROPULSION SYSTEMS
As far as we know, nothing travels faster than light. Aside from energy issues, it takes a long time to get anywhere interesting. The nearest star apart from the Sun is the triple-star system Alpha Centauri, located 4.3 light-years away. There are about 32 star systems within 15 light-years of the Sun, and roughly 600 within 100 light-years. This means it will take years to get to the nearest stars even traveling at speeds close to light. There is one saving grace: because of relativity, the trip won’t seem as long to the voyagers. However, to get to these speeds, even the Orion drive is insufficient.
11.1 MORE SPECULATIVE PROPULSION SYSTEMS
11.1.1 Fusion Reactors
Fusion reactions generate energy from building up heavier nuclei from lighter ones. Again, there is net energy produced in the reaction because the reaction products are lighter than the reactants. This is the energy source inside the Sun. The reaction there is the proton-proton cycle,
![]()
This reaction needs high densities and is relatively slow, making it unusable for Earth-based fusion applications. Most researchers concentrate on the deuterium-deuterium reaction:
![]()
or the deuterium-tritium reaction:
![]()
The latter process has (in principle) an energy density of 3×1014 J/kg of total fuel, or one to two orders of magnitude greater than fission processes [246]. If you used the reaction products as ejection mass for the spacecraft, you would have an exhaust velocity of about 2×107 m/s, or 20,000 km/s, roughly 7% of the speed of light. In principle, half a kilogram of this fuel could send a 1,000 kg spacecraft to the Moon. The proton-proton cycle has a higher exhaust velocity of approximately 12% of the speed of light. One tricky part is that while deuterium is pretty common, tritium is not: it is an unstable isotope with a half-life of 12 years. Even given this issue, a 1974 study of how to build a spacecraft capable of interstellar flight, Project Daedalus, fixed on a deuterium-tritium fusion reactor as the only feasible means of powering the spacecraft.
Fusion energy can only be generated at temperatures of millions of degrees and high densities, which is why it is difficult to generate it controllably; however, if one could harness it, it would supply an essentially limitless source of power. This is why the development of controllable fusion has been something of a holy grail for physicists for the past fifty years; commercial fusion power plants would essentially solve the world’s energy problems. However, it is a holy grail in many senses: no one really has any idea how to do it, although much work has been done on the problem. As the joke goes, fusion power is always 20 years away. Needless to say, no one knows how to build a fusion-powered rocket either, although there have been suggestions on that issue as well.
So fusion rockets are a good way to go, if we had any idea how to make them. The first study I know of on making an interstellar probe using a fusion engine was Project Daedalus in 1975. This was a serious study undertaken by a number of scientists and engineers to put together a “proof-of-principle” design for a probe capable of a flyby mission to Barnard’s star, six light-years from Earth. The speed chosen was 15% of light-speed, making it an approximately 40-year journey. There are definitely some science-fictiony aspects of the project; for example, it called for mining Jupiter for tritium for the fuel supply. This seems to be on the borderline of possible, but exactly which side is anyone’s guess.
However, the implication of an interstellar probe like this one is that we possess an extremely energy-rich society. The cost of Project Daedalus was estimated at $10 trillion. Using the rule of thumb that prices for everything double every 20 years, the estimate comes in at about $40 trillion today, dwarfing the U.S. GDP. This amount of money is about equal to the GDP of the entire world. Energetics tell us why this is so: the total energy contained in the payload is about 10% of the total world energy usage for one year. This is too expensive for any current world civilization to undertake, and it may well be too expensive for any civilization to undertake under any circumstances.
11.1.2 The Bussard Ramjet
The nearest star apart from our sun, Alpha Centauri, is about 4.3 light-years away, At an average speed of 10% of the speed of light, it would take 43 years for a spacecraft to get there and the same to return, if we want it to return. This speed is possible for a fusion-powered craft; assuming the exhaust speed is as stated above, 2×107 m/s, the mass ratio isn’t too prohibitive. The spacecraft needs about 3.5 kg of fuel for every kilogram of payload if we don’t decelerate. If we do decelerate, then we need this quantity squared, or about 12 for a fuel/payload ratio; if we want it to return, then the quantity is raised to the fourth power (about 144). However, the round trip is clearly longer than any human life, and even relativistic time dilation will not help us much. Unfortunately, going much faster gets very difficult. At this point, for speeds near the speed of light, our original formula for the rocket equation doesn’t work any more, so we need to use a version that is corrected to take the special theory of relativity into account. This was first derived by Ackeret in a 1946 paper; you can find a derivation of the same formula in English in the paper “Relativistic Rocket Theory” by Bade in The American Journal of Physics [17][29]:

The variables are:
• u: exhaust velocity (assumed to be 2×107 m/s);
• v: final velocity reached by the spacecraft;
• mi: initial (payload + fuel) mass of the spacecraft;
• mf: final (payload) mass of the spacecraft;
• c: speed of light (3×108 m/s).
I’ll going to define three new variables, to make life easy on us:
• R: mass ratio mi/mf;
• α: ratio of exhaust speed to speed of light (= u/c);
• β: ratio of final speed to speed of light (= v/c).
We can then solve for the mass ratio needed to get to any fraction of the speed of light:

The issue is that nothing can go faster than the speed of light. The nonrelativistic rocket equation doesn’t take this into account; basically, as you go faster and faster, the mass ratio increases more and more, to the point that going at the speed of light would require an infinite mass ratio. Simply to get to 90% of the speed of light with the exhaust velocity given above, we would need a mass ratio of 3.9 billion.
This clearly won’t work. So what are we to do? In 1960 the physicist Robert Bussard had an ingenious idea: “empty” space isn’t really empty. There is very thinly spread matter in interstellar space, mostly hydrogen. On average, there is about one atom per cubic centimeter in interstellar space (or about 106/m3), although in dense molecular clouds, there can be as much as 109/m3, or even much more [130, pp. 435–438]. So: en route, scoop up the material between the stars and use it as fuel [44].
Bussard envisioned a large “scoop” or funnel of some kind extending for hundreds or even thousands of kilometers ahead of the ship, gathering and compressing the hydrogen to the point that it underwent fusion, serving as fuel for the spacecraft. Figure 16 shows a schematic of a Bussard ramjet. This idea has proved incredibly popular in the science fiction literature as it seems to be the only plausible way, apart from matter-antimatter reactions, to get a spacecraft to travel at an appreciable fraction of the speed of light. The idea has been used by a large number of science fiction writers (including Poul Anderson in his novel Tau Zero), but it was certainly used most extensively and popularized enormously by the writer Larry Niven in his Known Space stories. Indeed, it is almost easier to list his stories that don’t use this concept. A sampling:
• In the novel Protector, Phssthpok the Pak uses a ramjet to get from the center of the galaxy to Earth (over the course of 30,000 years). Later in the novel, the Brennan-monster and the Pak scouts use ramjets to fight their extended interstellar skirmishes [179].
• In A Gift From Earth (and other novels and stories), it is mentioned that unmanned Bussard ramjets explore interstellar space for inhabitable planets (or, as mentioned in the novel, “inhabitable points”), which are later settled by “slowboats” carrying human settlers.
• In the story “The Ethics of Madness,” a paranoid steals a spacecraft and kills a friend’s family using it, and is then literally chased to the ends of the universe by the other in a second ramjet.
• In the non-Known Space novel A World out of Time, the world government known as “The State” uses revived “corpsicles” to pilot ramjets to seed potentially Earth-like planets with bacterial life in the hopes of terraforming them for settlement.1
And this is just a sampling.
I’m going to present a nonrelativistic analysis of the Bussard ramjet: for a fully relativistic one, see Bussard’s original paper or any of the references below.
At first glance, because the ramjet picks up its fuel en route, it appears that we can keep accelerating forever, not subject to the limitations imposed by the rocket equation. Let’s make some assumptions:
1. The ramjet, of total mass M, is under way and traveling at some speed v relative to the Earth.
2. It has a funnel of some sort that scoops matter into the fusion engines. The funnel has area A.
3. Fusion uses a fraction f of the hydrogen for fuel, which yields energy with an efficiency α and ejects the rest to the rear at speed u (which depends on both f and α).
4. The interstellar hydrogen has a mass density ρ.
The thrust of the spacecraft is proportional to two things, the fuel speed, u, and the rate at which mass is being fed to the engine, dm/dt, which can be shown to be equal to ρAv. This makes sense: the faster a ship moves forward, the more hydrogen it scoops up; the large the funnel area, the more hydrogen it scoops up; and the higher the density, the more it scoops up:
![]()
The thrust increases with increasing speed, all other things being equal [44]. If we want the acceleration to be constant (meaning that the thrust is constant), we need to control the fraction f of the fuel undergoing fusion. If we intake a certain amount of hydrogen equal to m into the ramjet, the exhaust speed of the fuel can be found (in the nonrelativistic limit):
![]()
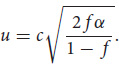
This means that we can write the equation for the acceleration (=T/M) in the form
![]()
If we want the acceleration to be constant (say, 1 g for the entire flight) then we must make f, the fraction of hydrogen used as fuel used by the ramjet, depend on v. To calculate f we must solve the quadratic equation

If we want a certain value of acceleration, there will be a minimum speed below which this is impossible to do. The reason is simple: at low speeds, the amount of mass going into the ramscoop will not provide enough thrust.
There is another force acting on the ship. By analogy with motion through fluids on Earth, there will be a “drag force” exerted on the ship. This drag force will have the general form
![]()
where β is a dimensionless coefficient of order 1; its exact value will depend on the design of the ramscoop. This implies a maximum velocity for the ship: as the speed gets higher, the drag force increases until it exactly balances the thrust. At this point,
![]()
The maximum value of f (1 − f) occurs at f = 1/2, so the maximum speed of the ship is

At best, α = 7×10−3 for the proton-proton cycle, so the maximum speed is going to be around 6% of the speed of light. This depends on β, of course, so there might be some way of “streamlining” the ramscoop to minimize this problem.
There are a number of problems with the idea, which probably make it untenable, apart from the speed limitation mentioned above:
• Unknown in 1960, when Bussard first published his paper, is that the Solar System is in the middle of a high-temperature “bubble” of interstellar gas about 650 light-years across whose density is relatively low, about .006 molecules per cm3, or about 6,000 /m3 [130, p. 435]. This density is about two orders of magnitude lower than Bussard’s estimates [44].
• Most of the matter in interstellar space is hydrogen; however, as noted above, fusing hydrogen is difficult because of the slowness of the reaction.
• Fusion of deuterium is easier, but deuterium is many thousands of times less common in interstellar space than hydrogen.
• Because the ramjet will work only if the ratio of the funnel area to the mass is very large, most papers concentrate on using magnetic fields as funnels.
These work only with charged particles; some have suggested using either lasers to ionize the interstellar medium or using strong magnetic fields. Materials limitations on our ability to produce large magnetic fields reduce the acceleration of the ramjet significantly once it reaches relativistic speeds, even if we ignore drag [158]. The scoop diameter also needs to be about 107 km at low speeds for it to work [159].
• Losses due to radiation from the conversion of matter into energy will limit the ship to speeds significantly less than the speed of light [215].
• When charged particles are accelerated they lose energy. These Bremsstrahlung losses may exceed energy gained by fusion of the interstellar medium by a factor of 109 [123].2
• Finally, a point I don’t think anyone else has ever brought up: an influx of charged particles at high speeds entering the ramscoop magnetic field will distort its shape in the same way that the solar wind distorts the Earth’s and Jupiter’s magnetic fields [130, p. 275]. It will compress the field in the direction of the ship’s motion and drag it behind the ship, making it less effective as a funnel.
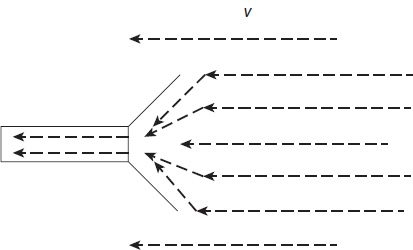
Figure 11.1. Particles funneled into the ramscoop.
More problems with the idea are discussed in detail in John Mauldin’s book, Prospects for Interstellar Travel [160, pp. 110–116, 326]. If the ramship idea can be made to work, the issues associated with it will probably limit its speed to a small fraction, probably less than 10%, of the speed of light.
Most science fiction writers ignore this and assume that the ramjet can accelerate indefinitely. However, this speed limit puts the kibosh on novels like Tau Zero and A World out of Time. While this speed is pretty good, if we really want to get to the stars within a human lifetime, we need to go faster—much faster. How do we do that?
11.1.3 Matter-Antimatter Drives
Popular culture once again comes to our aid. As everyone knows, the Starship Enterprise, serial number NCC-1701 (or 1701A, or 1701D, etc., depending on which movie or show you watch), is powered by the reaction of matter and antimatter. It is in fact unclear from the show whether the ship is powered by these reactions or whether the ship is propelled by them when using its impulse engines. (I’m typing this in the realization that some diehard fan is going to email me, quoting chapter and verse, exactly how it is used.) Maybe we can use antimatter for spacecraft propulsion, just as the Federation of Planets does.
What is antimatter, anyway? It’s a long story. Back in the 1930s, one of the major challenges facing physics was how to marry the two newly discovered theories of special relativity and quantum mechanics. An English physicist, Paul Dirac, proposed an equation that described the relativistic quantum behavior of the electron. When the equation was solved it predicted there should be a companion particle to the electron, one with identical mass and other properties but with opposite electrical charge. Because the electron has negative charge, this new particle was dubbed the positron. The Caltech physicist Carl David Anderson detected the positron in cloud chamber experiments in 1932. It quickly became apparent to physicists that all elementary particles must have antiparticles associated with them, and the antiproton and antineutron were discovered within the next few decades.
There’s a tendency for nonphysicists to somehow think that antimatter is exotic, or a theory that hasn’t been proved yet. All these notions are untrue: antimatter particles by the trillions are produced in accelerator experiments all over the world. This is not to say that much has been produced: in 2001 CERN, a European consortium running the largest particle accelerators in the world, estimated that antimatter production is less than one-billionth of a gram per year at an equivalent cost of several trillion dollars per gram [2].
Why so expensive? Because antimatter doesn’t exist in nature, at least to any appreciable amount. Most matter is “ordinary”; antiparticles are produced naturally only in radioactive decays or in processes that have temperatures equivalent to the center of the Sun or higher. It all hinges on E = Mc2. To produce a kilogram of antimatter, you have to supply the energy equivalent to it, or roughly 9×1016 J. Put differently all of the energy used by the United States in the course of one year (1.4 × 1020 J) is equivalent to the energy produced by the annihilation of about 750 kg of matter with 750 kg of antimatter. If antimatter existed in large quantities, it could be used to fuel civilization; because it doesn’t, the tables are turned. It takes enormous amounts of energy to produce it.
This doesn’t mean that it has to be as exquisitely expensive to produce as it currently is. If the energy costs were the only issue involved in producing it, the cost would be less than one-millionth of the current costs: gasoline, for example, has an energy density of about 108 J per gallon, meaning that we’d have to burn 900 million gallons of gas to give us the energy equivalent to 1 kg of antimatter. This would cost about $2.25 billion at 2009 U.S. prices of $2.50 per gallon. There have been several serious proposals for large antimatter creation facilities, mostly authored by the late Robert L. Forward, which would bring the cost of antimatter production low enough to make it a viable starship fuel [87].
On to the question of how to use antimatter in propulsion systems. One issue is that we have to get rid of the notion that the “annihilation” of a particle with its antiparticle somehow produces “pure” energy. Such a statement is meaningless. What really happens is that the interaction of a particle with its antiparticle produces different reactant products, similar to what happens in a chemical reaction. The amount of energy available for use in a propulsion system is determined by what the reactants are. The simplest thing to consider is an electron-positron reaction occurring in which the two particles are at rest with respect to each other. The reaction here is
![]()
This is shorthand notation for the reaction of an electron and a positron to create 2 gamma rays, that is, two very high-energy photons. If the electron and positron are at rest, the total energy of the gammas will be equal to the equivalent rest-mass energy of the electron and positron, that is, about 1 MeV or 1.6×10−13 J. “MeV” is the abbrevation for the unit mega-electron volt, the electron volt being a unit of energy equal to 1.6×10−19 J. Most particle masses are quoted in units of MeV or GeV (= 1,000 MeV) for the sake of convenience. Physicists learn to quickly convert from these units into more standard units of energy when needed. Because the electron is one of the lightest particles that have mass (only the neutrinos have less mass), an electron-antielectron annihilating at rest can produce only photons. This is good, because in principle, 100% of the rest mass of the electrons can be used as energy for propulsion.
One method of driving the spacecraft forward is to use the momentum of the photons created to propel it. A light beam shining on your hand carries a force, though a very weak one under normal circumstances. If we shine a light beam on a mirror, there will be a force acting to push the mirror forward equal to
![]()
where P is the power of the light beam (i.e., the energy per unit time hitting the mirror) and c is the speed of light. Under most circumstances, this force is weak: for example, if we shine a 1 W flashlight on the mirror, the net force is only 3×10−9 N. However, if we took 1 kg of matter and reacted it with 1 kg of antimatter to produce a beam of gamma rays directed against the mirror, and did it in a time of 1 second, the net force would be 6×108 N. Even if the mirror had a mass of 10,000 kg (10 tons), it would end up moving at a speed of 60,000 m/s!
11.2 MASS RATIOS FOR MATTER-ANTIMATTER PROPULSION SYSTEMS
Proponents of such a technology, including Forward and Robert Frisbee at the Jet Propulsion Laboratory (JPL), have put together elaborate studies of propulsion systems based on matter-antimatter reactions. There are a lot of nitty-gritty details that we won’t go into here; in particular, Frisbee’s studies seem to indicate that proton-antiproton reactions are better than electron-positron reactions for spaceship drives, even though less of the initial “mass-energy” of the reactants is available for propulsion [88]. For the sake of simplicity I will consider only cases in which the reactants are transformed into high-energy gamma rays and bounced against some sort of mirror to propel the spacecraft.
Using equation (11.5) with u = c, we find

where c is the speed of light, R is the mass ratio (mi/mf), and v is the final speed reached by the spaceship (assuming that it starts from rest). For v ≪ c, this is approximately v/c ≈ R − 1. Since c = 3×105 km/s, to get a 1,000 kg payload to Earth’s escape speed of 11 km/s takes a mass of 18 grams of normal matter reacted with 18 grams of antimatter.
Table 11.1
Final Velocity of an Antimatter Rocket as a Function of Mass Ratio
Ratio (R) | v/c | v(m/s) |
1.01 | 0.01 | 3.00×106 |
1.05 | 0.05 | 1.50×107 |
1.1 | 0.1 | 3.00×107 |
1.2 | 0.18 | 5.40×107 |
1.3 | 0.26 | 7.80×107 |
1.5 | 0.38 | 1.14×108 |
2 | 0.6 | 1.80×108 |
5 | 0.92 | 2.76×108 |
10 | 0.98 | 2.94×108 |
20 | 0.995 | About 3×108 |
100 | 0.9998 | About 3×108 |
Table 11.1 shows the real advantages of using a matter-antimatter propulsion system. A mass ratio of 10 gets you to 98% of the speed of light. Unfortunately, this means that for every kilogram of payload mass you need 5 kg of antimatter to react with 5 kg of normal matter, but 5 kg of antimatter exceeds the world’s supply by a factor of about a trillion.
There are no naturally occurring sources of antimatter handy. As far as we can tell, the universe is overwhelmingly made of normal matter. This means that any antimatter will have to be created. This is possible; antimatter is created in particle accelerators all over the world, but in very small quantities. Typical generation rates for antimatter are of the order 1010–1012 particles per second, or (assuming the particles are antiprotons) 10−17–10−15 kg/s. Generously, generating 1 kg of antimatter using current accelerators will take about 1015 s, or 30,000,000 years.
However, we’re not trying to produce antimatter for spacecraft propulsion right now. Without going into details, essentially the question is one of energy. If we have access to enough energy, we can create antimatter. The questions are how much can we create, and how much will it cost?
11.2.1 The Cost and Time of Producing Antimatter
From the relation E = Mc2, we can’t generate more mass than E / c2 given energy E. So let’s make the following assumptions:
1. We have a power plant that supplies energy at a rate of P J/s to supply us with energy.
2. The energy costs us s cents per kilowatt-hour (= 3.6×106 J).
3. We can convert the energy into mass with efficiency f < 1.
4. We want to generate 1 kg of antimatter (which is equivalent to 9×1016 J).
The twin questions we want to ask are: How long will it take as a function of P and f. How much will it cost?
In time t, the power plant will generate a total energy Pt joules, or a mass of P ft/c2 kg of antimatter. Therefore, the time to generate 1 kg is
![]()
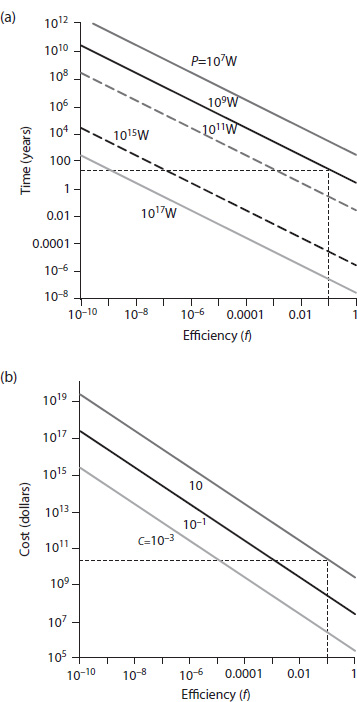
using the fact that a year is 3.16 × 107 s. Figure 11.2 shows the time it takes given power plants with energy generation rates running from 107 W to 1017 W. Two points to note: 1013 W is about the total power the world currently produces, and 1017 W is about the total power the Earth receives from the Sun.
The total cost (in dollars) can be worked out as well in terms of the energy cost s:
![]()
where M stands for “money.” Figure 21.8 shows the total cost for three different values of s: 10−3 cents/kW-hr, 10−1, and 10 (which is about the current cost of electricity production in the United States). It should be noted that both figures are on logarithmic scales, as I want to show this as a function of widely differing values of efficiencies, costs, and total power allocated to the task. Also, f ≤ 0.5 because for every particle of antimatter created, one particle of normal matter is created because of the conservation laws of physics.
What are realistic values for f given today’s technology? Robert Forward looked into this problem in detail. In a 1984 Air Force technical report he estimated that by using specially designed linear accelerators, one might achieve an overall energy efficiency of f = 2.5×10−4 [87, p. 3].3 To the best of my knowledge, such specially dedicated linear accelerators have never been built. However, a recent paper in Physical Review Letters demonstrated anti-electron production using high-energy-density laser pulses with an overall efficiency of 1011 electrons per kilojoule, which corresponds to an efficiency of f = 8×10−6 [104]. This was a tabletop experiment, so it’s not that difficult to imagine that if it were properly scaled up, one could gain a few orders of magnitude in efficiency, to maybe f = 10−4. I don’t believe any specific physics limits overall efficiency, merely engineering details, but I could be very wrong. This is ignoring the other vexing issue of how we contain all of the antimatter we produce.
The figures make it clear: under almost any reasonable conditions, this is an expensive and lengthy task. I’ve marked a point on each using dashed lines: assuming that we put all of the power of a 1 GW power plant toward this task (which is just barely possible today) and figured out a way to do this at 10% efficiency (i.e., f = 0.1) (which is probably impossible), it would take about 30 years and cost $25 billion.
Using a more reasonable efficiency of 10−4 we could produce 1 gram of antimatter in the same time at the same cost, which is more or less the goal Forward was hoping to achieve in his report. Forward’s estimates of costs are similar to mine: he calculated that with f = 10−4, the cost would be 107 $/mg [87, p. 150].
The only novel I have read that deals with this issue honestly is Building Harlequin’s Moon by Larry Niven and Brenda Cooper [185]. In this book the starship John Glenn is fleeing an Earth ruined by nanotechnology. The ship is powered using a matter-antimatter drive, but it has a problem with it and so must stop en route in another star system to generate enough antimatter to be able to proceed onward. The process of generating the antimatter takes literally hundreds of years. Antimatter generation is power-limited: the rate at which you can create it is limited by the available energy you have on hand. Under most circumstances, this will be pretty slow.
Edward Purcell, the Nobel laureate physicist, pointed out in 1963 that even apart from expenses, there are some real problems with trying to get anywhere really fast [46, pp. 121–143]. Those problems have to do with exposure to radiation, both to our astronauts and (if we’re not careful) to the entire Earth as well.
Let’s say we have collected our antimatter and we want to send a group of explorers out to explore the cosmos. Let’s say we want them to travel there and back at 99.5% of the speed of light, and maintain an acceleration of 1 g the whole time. This implies a mass ratio of 20 from table 11.1. But that’s only for the journey out. To decelerate to a stop, we need another ratio of 20; to accelerate back toward Earth, another ratio of 20; and to decelerate to a stop again, another ratio of 20. The rocket equation is merciless: the overall mass ratio must be
R = 204 = 160,000.
In words, for every kilogram of mass on the spacecraft we need 160,000 kg of fuel, which is to say 80,000 kg of antimatter and 80,000 kg of normal matter. For our canonical 10,000 kg payload spacecraft (which, if manned, will probably need to be bigger), we need a whopping 1.6×1019 kg of fuel with a stored energy of 1.44×1026 J, or about as much energy as our current world civilization will use in about half a million years.
Be that as it may: the power the spacecraft will use on “takeoff” can be found from the fact that the power of a “photon rocket” such as this one is intimately related to the force the rocket exerts: if the force is F and the power P, then
F = 2P/c.
Since the rocket is accelerating at 1 g, and g ∼ 10 m/s2, the net force needed is 1.6×1010 N and the power required is 2.4×1018 W. This is an energy usage rate more than 100,000 times greater than our current civilization’s. The total power the Earth receives from the Sun is about an order of magnitude less than this; if we launch from anywhere near Earth’s orbit, we will likely destroy Earth’s ecology, especially if we consider that (unlike the Sun) all of the energy is being delivered in the form of high-energy gamma rays [46, p. 138]. A starship like this one clearly cannot be launched from anywhere near Earth. Purcell also pointed out that at relativistic speeds like this, the hydrogen atoms that the ship intercepts essentially have the same energy as high-energy cosmic rays, meaning that extensive shielding would be needed to protect the crew from radiation exposure.
Purcell ended with this comment:
Well, this is preposterous, you are saying. That is exactly my point. It is preposterous. And remember, our conclusions are forced upon us by the elementary laws of mechanics. All those people who have been talking about lebensraum in space and so on, simply haven’t made this calculation and until they do, what they say is nonsense. [46, p. 138]
I am not sure it is nonsense, but it is clearly beyond anything our human civilization can do, and perhaps beyond what any civilization can do. Or perhaps not: in chapter 21, “A Googol Years,” I’ll discuss the issue of really advanced civilizations. In the meanwhile, however, we’ve talked about relativity a lot but haven’t gotten to the good part: the issues of time dilation. Even though the universe is huge, given access to enough energy one could explore it within one human lifetime because of the theory of relativity.
NOTES
1. “Corpsicles” are people placed in cryogenic suspension just before death and revived, in different bodies, by the state hundreds of years later. This sort of cryonics is popular in science fiction. Perhaps the most widely seen use of it is in the TV show Futurama.
2. The author of this paper has suggested that because of Bremsstrahlung losses, using a ramscoop might be a good way of decelerating a ship traveling at a large fraction of the speed of light.
3. One must take care when reading this report to distinguish between two types of efficiency: overall energy efficiency, which is relatively low, versus the efficiency of a high-energy proton striking a target in producing antiprotons, which is relatively high.