Chapter 1
Introduction
We consider a physical system where variables and parameters interact in a domain of interest. Variables are physical quantities that are observable or measurable, and their values change with position and time to form signals. We may express system structures and properties as parameters, which may also change with position and time. For a given system, we understand its dynamics based on underlying physical principles describing the interactions among the variables and parameters. We adopt mathematical tools to express the interactions in a manageable way.
A physical excitation to the system is an input and its response is an output. The response is always accompanied by some form of energy transfer. The input can be applied to the system externally or internally. For the internal input, we may also use the term “source”. Observations or measurements can be done at the outside, on the boundary and also on the inside of the system. For the simplicity of descriptions, we will consider boundary measurements as external measurements. Using the concept of the generalized system, we will introduce the forward and inverse problems of a physical system.
1.1 Forward Problem
The generalized system H in Figure 1.1 has a system parameter p, input x and output y. We first need to understand how they are entangled in the system by understanding underlying physical principles. A mathematical representation of the system dynamics is the forward problem formulation. We formulate a forward problem of the system in Figure 1.1 as
where H is a nonlinear or linear function of p and x. We should note that the expression in (1.1) may not be feasible in some cases where the relation between the input and output can only be described implicitly.
Figure 1.1 Forward problem for a system with parameter p, input x and output y

To treat the problem in a computationally manageable way, we should choose core variables and parameters of most useful and meaningful information to quantify their interrelations. The expression in (1.1), therefore, could be an approximation of complicated interactions among variables and parameters. In practice, we may not be able to control the input precisely because of technical limitations, and the measured output will always be contaminated by noise. Solving a forward problem is to find the output from a given input and system parameter. Evaluation of (1.1) suffices for its solution.
A simple example is a sound recording and reproduction system including a microphone, amplifier and speaker. An input sound wave enters the system through the microphone, goes through the amplifier and exits the system as an output sound wave through the speaker. The system characteristics are determined by the electrical and mechanical properties of the system components, including the gain or amplitude amplification factor, phase change, frequency bandwidth, power and so on.
1.2 ![]()
![]()
![]()
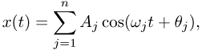
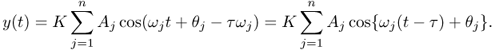
In most physical systems, inputs are mixed within the system to produce outputs. The mixing process is accompanied by smearing of information embedded in the inputs. Distinct features of the inputs may disappear in the outputs, and the effects of the system parameters may spread out in the observed outputs.
1.2 Inverse Problem
For a given forward problem, we may consider two types of related inverse problems as in Figure 1.2. The first type is to find the input from a measured output and identified system parameter. The second is to find the system parameter from a designed input and measured output. We symbolically express these two cases as follows:
1.5 ![]()
and
1.6 ![]()
where ![]() and
and ![]() are nonlinear or linear functions. We may need to design multiple inputs carefully to get multiple input–output pairs with enough information to solve the inverse problems.
are nonlinear or linear functions. We may need to design multiple inputs carefully to get multiple input–output pairs with enough information to solve the inverse problems.
Figure 1.2 Two different inverse problems for a system with parameter p, input x and output y
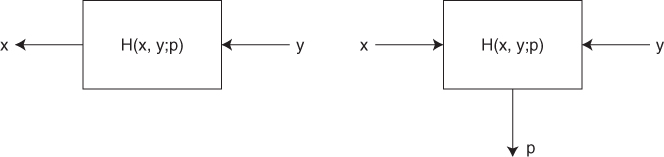
1.7 ![]()
1.8 ![]()
1.9 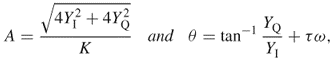
In general, most inverse problems are complicated, since the dynamics among inputs, outputs and system parameters are attributed to complex, possibly nonlinear, physical phenomena. Within a given measurement condition, multiple inputs may result in the same output for given system parameters. Similarly, different system parameters may produce the same input–output relation. The inversion process, therefore, suffers from the uncertainty that originates from the mixing process of the corresponding forward problem.
To seek a solution of an inverse problem, we first need to understand how those factors are entangled in the system by understanding the underlying physical principles. Extracting core variables of most useful information, we should properly formulate a forward problem to quantify their interrelations. This is the reason why we should investigate the associated forward problem before trying to solve the inverse problem.
1.3 Issues in Inverse Problem Solving
In solving an inverse problem, we should consider several factors. First, we have to make sure that there exists at least one solution. This is the issue of the existence of a solution, which must be checked in the formulation of the inverse problem. In practice, it may not be a serious question, since the existence is obvious as long as the system deals with physically existing or observable quantities. Second is the uniqueness of a solution. This is a more serious issue in both theoretical and practical aspects, and finding a unique solution of an inverse problem requires careful analyses of the corresponding forward and inverse problems. If a solution is not unique, we must check its optimality in terms of its physical meaning and practical usefulness.
To formulate a manageable problem dealing with key information, we often go through a simplification process and sacrifice some physical details. Mathematical formulations of the forward and inverse problems, therefore, suffer from modeling errors. In practice, measured data always include noise and artifacts. To acquire a quantitative numerical solution of the inverse problem, we deal with discretized versions of the forward and inverse problems. The discretization process may add noise and artifacts. We must carefully investigate the effects of these practical restrictions in the context of the existence and uniqueness of a solution.
We introduce the concept of well-posedness as proposed by Hadamard (1902). When we construct a mathematical model of a system to transform the associated physical phenomena into a collection of mathematical expressions and data, we should consider the following three properties.
In the sense of Hadamard, a problem is well-posed when it meets the above requirements of existence, uniqueness and continuity. If these requirements are not met, the problem is ill-posed.
If we can properly formulate the forward problem of a physical system and also its inverse problem, we can safely assume that a solution exists. Non-uniqueness often becomes a practically important issue, since it is closely related with the inherent mixing process of the forward problem. Once the inputs are mixed, uniquely sorting out some inputs and system parameters may not be feasible. The mixing process may also cause sensitivity problems. When the sensitivity of a certain output to the inputs and/or system parameters is low, small changes in the inputs or system parameters may result in small and possibly discontinuous changes in the output, with measurement errors. The inversion process in general includes a step where the measured output values are divided by sensitivity factors. If we divide small measured values, including errors, by a small sensitivity factor, we may amplify the errors in the results. The effects of the amplified errors may easily dominate the inversion process and result in useless solutions, which do not comply with the continuity requirement.
Considering that mixing processes are embedded in most forward problems and that the related inverse problems are ill-posed in many cases, we need to devise effective methods to deal with such difficulties. One may incorporate as much a priori information as possible in the inversion process. Preprocessing methods such as denoising and feature extraction can be employed. One may also need to implement some regularization techniques to find a compromise between the robustness of an inversion method and the accuracy or sharpness of its solution.
1.4 Linear, Nonlinear and Linearized Problems
Linearity is one of the most desirable features in solving an inverse problem. We should carefully check whether the forward and inverse problems are linear or not. If not, we may try to approximately linearize the problems in some cases. We first define the linearity of the forward problem in Figure 1.1 as follows.
For a linear system, we can, therefore, apply the following principle of superposition: if y1 = H(x1) and y2 = H(x2), then
1.10 ![]()
for any constants K1 and K2.
For the inverse problems in Figure 1.2, we may similarly define the linearity for two functions ![]() and
and ![]() . Note that we should separately check the linearity of the three functions H,
. Note that we should separately check the linearity of the three functions H, ![]() and
and ![]() . Any problem, either forward or inverse, is nonlinear if it does not satisfy both of the homogeneity and additivity requirements.
. Any problem, either forward or inverse, is nonlinear if it does not satisfy both of the homogeneity and additivity requirements.
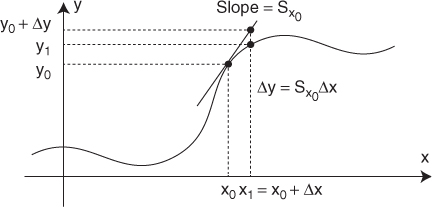
For a nonlinear problem y = H(x), we may fix x = x0 and consider a small change Δx around x0. As illustrated in Figure 1.3, we can approximate the corresponding change Δy as
where ![]() is the sensitivity of Δy to Δx at x = x0, which can be found from the analysis of the problem. The approximation in (1.11) is called the linearization to find y1 = H(x0 + Δx) ≈ y0 + Δy where y0 = H(x0). The approximation is accurate only for a small Δx.
is the sensitivity of Δy to Δx at x = x0, which can be found from the analysis of the problem. The approximation in (1.11) is called the linearization to find y1 = H(x0 + Δx) ≈ y0 + Δy where y0 = H(x0). The approximation is accurate only for a small Δx.
Figure 1.3 Illustration of a linearization process
Problems either forward or inverse can be linear or nonlinear depending on the underlying physical principles. Proper formulations of forward and inverse problems using mathematical tools are essential steps before any attempt to seek solution methods. In the early chapters of the book, we study mathematical backgrounds to deal with linear and nonlinear problems. In the later chapters, we will introduce several imaging modalities.
Reference
Hadamard J 1902 Sur les problèmes aux dérivées partielles et leur signification physique. Bull. Univ. Princeton, 13, 49–52.
