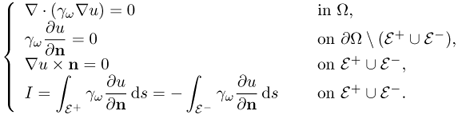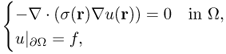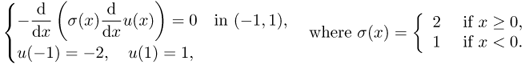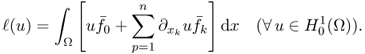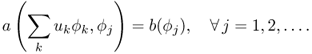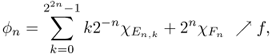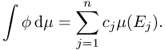Chapter 4
Analysis for Inverse Problem
Inverse problems are ill-posed when measurable data are either insufficient for uniqueness or insensitive to perturbations of parameters to be imaged. To solve an inverse problem in a robust way, we should adopt a reasonably well-posed modified model at the expense of a reduced spatial resolution and/or add additional a priori information. Finding a well-posed model subject to practical constraints of measurable quantities requires deep knowledge about various mathematical theories in partial differential equations (PDEs) and functional analysis, including uniqueness, regularity, stability, layer potential techniques, micro-local analysis, regularization, spectral theory and others. In this chapter, we present various mathematical techniques that are frequently used for rigorous analysis and investigation of quantitative properties in forward and inverse problems.
4.1 Examples of Inverse Problems in Medical Imaging
Most inverse problems in imaging are to reconstruct cross-sectional images of a material property P from knowledge of input data X and output data Y. We express its forward problem in an abstract form as
where F is a nonlinear or linear function of P and X. To treat the problem in a computationally manageable way, we need to figure out its sensitivity, explaining how a perturbation P + ΔP influences the output data Y + ΔY. In this section, we briefly introduce some examples of forward problem formulations in imaging electrical and mechanical material properties of an imaging object such as the human body.
4.1.1 Electrical Property Imaging
We assume that an imaging object occupies a domain Ω in the three-dimensional space ![]() . When the object is a human body, we are interested in visualizing electrical properties of biological tissues inside the body. We denote the admittivity of a biological tissue at a position r and angular frequency ω as
. When the object is a human body, we are interested in visualizing electrical properties of biological tissues inside the body. We denote the admittivity of a biological tissue at a position r and angular frequency ω as ![]() , where σω(r) and
, where σω(r) and ![]() are the conductivity and permittivity, respectively. Most biological tissues are resistive at low frequencies but capacitive terms may not be negligible at 10 kHz or above. Electrical property imaging aims to image the internal admittivity distribution P = γω(r), which depends on r = (x, y, z) and ω. To measure the passive material property, we must employ a probing method, which excites the object by externally applying a form of energy and measures its response affected by the admittivity.
are the conductivity and permittivity, respectively. Most biological tissues are resistive at low frequencies but capacitive terms may not be negligible at 10 kHz or above. Electrical property imaging aims to image the internal admittivity distribution P = γω(r), which depends on r = (x, y, z) and ω. To measure the passive material property, we must employ a probing method, which excites the object by externally applying a form of energy and measures its response affected by the admittivity.
As a probing method, we inject a sinusoidal current of Isin(ωt) mA through a pair of electrodes that are attached on the surface Ω. This sinusoidally time-varying current produces sinusoidal variations of electric and magnetic fields at every point r with the same angular frequency ω. For these sinusoidal fields, it is convenient to use the phasor notation. We denote the sinusoidally time-varying electric and magnetic fields by ![]() and
and ![]() , respectively. We express them using vector field phasors of E(r) and H(r) as
, respectively. We express them using vector field phasors of E(r) and H(r) as
![]()
Each component of E(r) or H(r) is a complex-valued function (independent of time) that contains amplitude and phase information. Table 4.1 summarizes important variables and parameters in the steady-state or time-harmonic electromagnetic field analysis.
Table 4.1 Time-varying and time-harmonic electromagnetic fields in Maxwell's equations
| Name | Time-varying field | Time-harmonic field |
| Gauss's law | ||
| Gauss's law for magnetism | ∇ · B = 0 | |
| Faraday's law of induction | ∇ × E = − iωB | |
| Ampère's circuit law | ∇ × H = σE + iωD |
For the admittivity imaging, it is imperative to produce a current density J inside Ω to sense the admittivity by Ohm's law ![]() , where E is the electric field intensity. To create J(r) and E(r) inside the body Ω, we can use a pair of electrodes (attached on the surface of the body) to inject sinusoidal current. This produces J, E, B inside Ω, where B is the magnetic flux density. Alternatively, we may use an external coil to produce eddy currents inside the body Ω. In both cases, we should measure some quantities that enable us to estimate J and E (directly or iteratively). Here, we use Maxwell's equations to establish relations among J, E, input data and measured data.
, where E is the electric field intensity. To create J(r) and E(r) inside the body Ω, we can use a pair of electrodes (attached on the surface of the body) to inject sinusoidal current. This produces J, E, B inside Ω, where B is the magnetic flux density. Alternatively, we may use an external coil to produce eddy currents inside the body Ω. In both cases, we should measure some quantities that enable us to estimate J and E (directly or iteratively). Here, we use Maxwell's equations to establish relations among J, E, input data and measured data.
We inject current of Isin(ωt) mA with 0 ≤ ω/2π ≤ 100 kHz through a pair of surface electrodes ![]() and
and ![]() on ∂Ω. The diameter of the imaging object is less than 1 m. Since the Faraday induction is negligibly small in this case, E, J and H approximately satisfy
on ∂Ω. The diameter of the imaging object is less than 1 m. Since the Faraday induction is negligibly small in this case, E, J and H approximately satisfy
4.2 ![]()
4.3 ![]()
with the boundary conditions
4.6 ![]()
where n is the outward unit normal vector on ∂Ω and dS is the area element on ∂Ω. The first boundary condition (4.4) comes from J = γωE = 0 in the air, where γω ≈ 0. The boundary condition (4.5) means that the vector J on each electrode is parallel or antiparallel to n since the electrodes are highly conductive. One may adopt the Robin boundary condition to include effects of the electrode–skin contact impedance.
Since ∇ × E ≈ 0, there exists a scalar potential u such that
![]()
Since 0 = ∇ · (∇ × H) = ∇ · J = − ∇ · (γω∇u), the potential u is a solution of the following boundary value problem:
![]()
![]()
4.8 ![]()
4.9 ![]()
4.10 ![]()
4.1.2 Mechanical Property Imaging
Elasticity is a mechanical property of an elastic object describing how the deformed object, subject to an external force, returns to its original state after the force is removed. Elastography measures the propagation of transverse strain waves in an object. Tissue stiffness is closely related to the velocity of the wave, and the shear modulus (or modulus of rigidity) varies over a wide range, differentiating various pathological states of tissues. Hence, the speed of the harmonic elastic wave provides quantitative information for describing malignant tissues, which typically are known to be much stiffer than normal tissues.
In imaging a mechanical property, we should use Hooke's law, which links the stress and strain tensors:
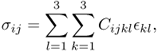
where (Cijkl) is the stiffness tensor, (σij) is the strain tensor and ![]() is the stress tensor. We need to apply a mechanical vibration or stress to create a displacement in Ω and measure some quantity that enables us to estimate the displacement inside Ω. Then, we use an elasticity equation to connect the stress tensor, strain tensor, displacement, input data and measured data.
is the stress tensor. We need to apply a mechanical vibration or stress to create a displacement in Ω and measure some quantity that enables us to estimate the displacement inside Ω. Then, we use an elasticity equation to connect the stress tensor, strain tensor, displacement, input data and measured data.
Assuming that we are trying to image a shear modulus distribution in a linearly elastic and isotropic material, the time-harmonic elastic displacement field denoted by u = (u1, u2, u3) is dictated by the following PDE:
where we use the following notation: ρ is the density of the material,
![]()
is the shear modulus,
![]()
is the Lamé coefficient, E is Young's modulus and σ is Poisson's ratio.
4.1.3 Image Restoration
The image restoration problem is to recover an original image P = u from a degraded measured (or observed) image Y = f that are related by
4.12 ![]()
where η represents noise and H is a linear operator including blurring and shifting. One may often use a priori knowledge about the structure of the true image that can be investigated by looking at geometric structure by level curves.
A typical way of denoising (or image restoration) is to find the best function by minimizing the functional
4.13 ![]()
where the first fidelity term ![]() forces the residual Hu − f to be small, the second regularization term
forces the residual Hu − f to be small, the second regularization term ![]() enforces the regularity of u and the regularization parameter λ controls the tradeoff between the residual norm and the regularity.
enforces the regularity of u and the regularization parameter λ controls the tradeoff between the residual norm and the regularity.
4.2 Basic Analysis
To deal with an imaging object with an inhomogeneous material property, we consider the following PDE:
where σ is differentiable and u is twice differentiable in Ω for ∇ · (σ(r)∇u(r)) = 0 to make sense with the classical derivatives.
In practice, the material property σ may change abruptly. For example, we may consider a conductivity distribution σ inside the human body Ω. Then, σ may have a jump along the boundary of two different organs. Along such a boundary, the electrical field E = − ∇u, induced by an injection current through a pair of surface electrodes attached on ∂Ω, may not be continuous due to interface conditions of the electric field (like the refractive condition of Snell's law). In this case, there exists no solution u ∈ C2(Ω) in the classical sense and we should seek a practically meaningful solution u ∉ C2(Ω). Hence, we need to expand the admissible set of solutions of (4.14), which must include all practically meaningful solutions.
This motivates the concept of the generalized derivative called the weak derivative, which is a natural extension of the classical derivative. With the use of the weak derivative (reflecting the refractive condition of Snell's law), we can manage the equation ∇ · (σ∇u) = 0 for a discontinuous σ. For a quick understanding of the weaker derivative, we consider the following one-dimensional Dirichlet problem:
Hence, u satisfies
![]()
We should note that u is different from the solution v of
![]()
This is because v is linear whereas the potential u is piecewise-linear satisfying the following transmission condition (the refractive condition) at x = 0 where σ is discontinuous:
Indeed, the practical solution of (4.15) is
![]()
Note that the classical derivative u′ does not exist at x = 0:
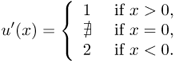
The difficulty regarding the refraction contained in the PDE
![]()
can be removed by the use of the variational framework:
We need to take account of the set of physically meaningful solutions of the variational problem (4.17). A practically meaningful solution u, which is a voltage, should have a finite energy, that is,
![]()
We solve (4.15) by finding u in the admissible set ![]() Indeed, the solution u of (4.15) is a minimizer of Φ(v) within the set
Indeed, the solution u of (4.15) is a minimizer of Φ(v) within the set ![]() :
:
4.18 ![]()
This will be explained in section 4.3.
We return to the three-dimensional problem of (4.14), where u(r) represents an electrical potential at r in an electrically conducting domain Ω. The physically meaningful solution u must have a finite energy:
![]()
Hence, the solution of (4.14) should be contained in the set ![]() . Assuming
. Assuming ![]() , the set
, the set ![]() is the same as the following Hilbert space:
is the same as the following Hilbert space:
![]()
where

Indeed, the solution is the minimizer of Φ(u) within the set {v ∈ H1(Ω):v|∂Ω = f}. As we mentioned before, the PDE − ∇ · (σ(r)∇u(r)) = 0 should be understood in the variational framework as
4.19 ![]()
4.2.1 Sobolev Space
To explain the solution of a PDE in the variational framework, it is convenient to introduce the Sobolev space. Let Ω be a bounded smooth domain in ![]() with its smooth boundary ∂Ω and let x = (x1, …, xn) represent a position. We introduce a Sobolev space H1(Ω), which is the closure of the set
with its smooth boundary ∂Ω and let x = (x1, …, xn) represent a position. We introduce a Sobolev space H1(Ω), which is the closure of the set ![]() equipped with the norm
equipped with the norm
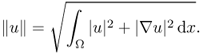
The finite element method (FEM) for computing an approximate numerical solution and its error analysis can be easily accomplished within the variational framework with the Hilbert space. This Hilbert space H1(Ω) is the most widely used Sobolev space in PDE theory.
The generalized derivative can be explained by means of the integration-by-parts formula:
![]()
In general,
![]()
where the notions ∂α and |α| are understood in the following way:
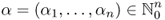 ,
,  and
and 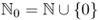 ;
; , for example,
, for example, 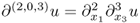 ;
;- |α| = ∑k=1nαk.
A function vi satisfying the following equality behaves like the classical derivative ![]() :
:
![]()
![]()
We will assume that Ω is an open subdomain of ![]() with its Ck, α boundary ∂Ω, where k + α ≥ 1. We are now ready to introduce the Sobolev spaces Wk, p(Ω) and
with its Ck, α boundary ∂Ω, where k + α ≥ 1. We are now ready to introduce the Sobolev spaces Wk, p(Ω) and ![]() , where Ω is a domain in
, where Ω is a domain in ![]() with its boundary ∂Ω and
with its boundary ∂Ω and ![]() :
:
- W1, p(Ω) and
 are the completion (or closure) of
are the completion (or closure) of 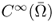 and
and 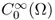 , respectively, with respect to the norm
, respectively, with respect to the norm
![]()
![]()
- W2, p(Ω) and
 are the completion (or closure) of
are the completion (or closure) of 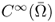 and
and 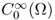 , respectively, with respect to the norm
, respectively, with respect to the norm
![]()
- We denote
 and
and 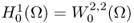 .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.2.2 Some Important Estimates
We begin by explaining simplified versions of two important inequalities, the Poincaré and trace inequalities.
- A simplified version of the Poincaré inequality is
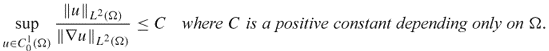
- A simplified version of the trace inequality is
![]()
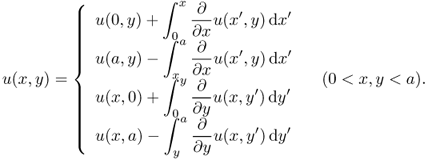
![]()
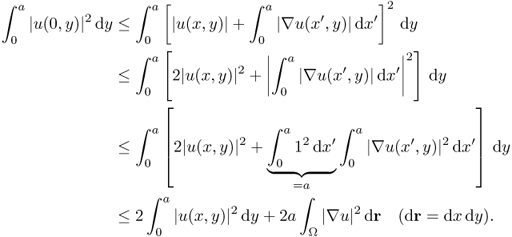

![]()
![]()
![]()
![]()
![]()
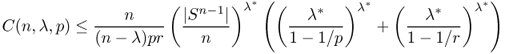
For the proof, see Theorem 4.3 in the book by Lieb and Loss (2001).
- For n ≥ 3,
4.21 ![]()
![]()
- If
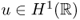 (one dimension), then
(one dimension), then
4.22 ![]()
- If
 (two dimensions), then, for each
(two dimensions), then, for each  ,
,
4.23 ![]()

- Let Ω be a C0, 1 domain and 1 ≤ p ≤ q, m ≥ 1 and k ≤ m. Then,
4.24 ![]()
4.25 ![]()
For the proof, see Theorem 8.8 in the book by Lieb and Loss (2001).
4.26 ![]()

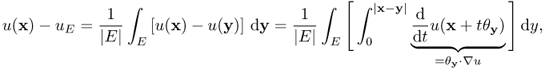


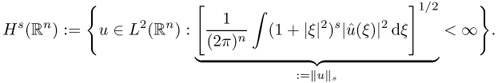
This definition is consistent with the previous definition of Hk(Ω) for ![]() . For the example of
. For the example of ![]() , it follows from the Plancherel theorem that
, it follows from the Plancherel theorem that
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()
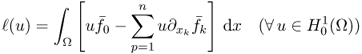
![]()
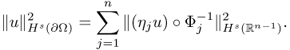
![]()
![]()
![]()
![]()
![]()
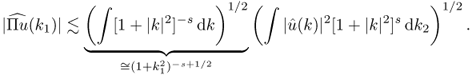
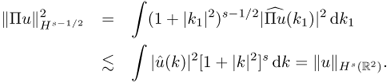
4.2.3 Helmholtz Decomposition
The Helmholtz decomposition states that any smooth vector field F in a smooth bounded domain Ω can be resolved into the sum of a divergence-free (solenoidal) vector field and a curl-free (irrotational) vector field.
4.29 ![]()
4.30 ![]()
4.31 ![]()
![]()
![]()
![]()
![]()
4.33 ![]()
![]()
4.3 Variational Problems
4.3.1 Lax–Milgram Theorem
Let Ω be a bounded domain in ![]() with smooth boundary ∂Ω. In this section, we discuss the existence, uniqueness and stability of the boundary value problem (BVP):
with smooth boundary ∂Ω. In this section, we discuss the existence, uniqueness and stability of the boundary value problem (BVP):
where c0 and c1 are positive constants. In the case when σ is discontinuous, the fundamental mathematical theories of solutions such as existence, uniqueness and stability can be established within the framework of the Hilbert space H1(Ω), which is a norm closure of ![]() with the norm
with the norm ![]() .
.
This problem (4.34) is equivalent to the following variational problem:
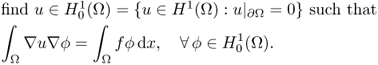
Define the map ![]() by
by
4.35 ![]()
and define ![]() by
by
4.36 ![]()
Hence, the solvability problem of (4.34) is equivalent to the uniqueness and existence question of finding ![]() satisfying
satisfying
Note that the map ![]() satisfies the following:
satisfies the following:
- both
 and
and 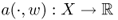 are linear for all u, w ∈ X;
are linear for all u, w ∈ X; - |a(u, v)| < c1||u|| ||v|| and c0||u||2 ≤ a(u, u).
Here, the norm ||u|| is ![]() . The estimate |a(u, v)| < c1||u|| ||v|| can be obtained using the Schwarz inequality and the Poincaré inequality gives the estimate c0||u||2 ≤ a(u, u).
. The estimate |a(u, v)| < c1||u|| ||v|| can be obtained using the Schwarz inequality and the Poincaré inequality gives the estimate c0||u||2 ≤ a(u, u).
Assuming that the Hilbert space ![]() has a basis {ϕk:k = 1, 2, …}, the variational problem (4.37) is to determine the coefficient {uk:k = 1, 2, …} of u = ∑ukϕk satisfying
has a basis {ϕk:k = 1, 2, …}, the variational problem (4.37) is to determine the coefficient {uk:k = 1, 2, …} of u = ∑ukϕk satisfying
Taking advantage of the linearity of a( ·, · ) and b( · ), the problem (4.38) is equivalent to solving
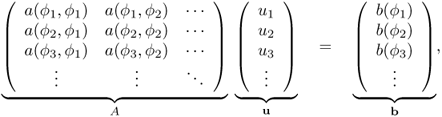
where A can be viewed as an ![]() matrix with coefficients akj = a(ϕk, ϕj). From the fact that
matrix with coefficients akj = a(ϕk, ϕj). From the fact that ![]() , A is positive definite and invertible. Therefore, for given data b, there exists a unique u satisfying Au = b.
, A is positive definite and invertible. Therefore, for given data b, there exists a unique u satisfying Au = b.
Now, we will prove the uniqueness and existence in ![]() in a general setting. Let X be a Hilbert space over
in a general setting. Let X be a Hilbert space over ![]() with a norm || · ||. The map
with a norm || · ||. The map ![]() is called a bounded bilinear map on the Hilbert space X if
is called a bounded bilinear map on the Hilbert space X if
- both
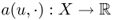 and
and 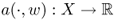 are linear for all u, w ∈ X, and
are linear for all u, w ∈ X, and - there exist M so that |a(u, v)| < M||u|| ||v||.
The solvability of the problem (4.34) can be obtained from the following theorem.
4.41 ![]()
Before proving Theorem 4.3.1, we gain its key idea by simple examples.
![]()
![]()
![]()
![]()
-
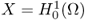 is a Hilbert space with the norm
is a Hilbert space with the norm 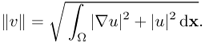
 is bounded bilinear on X.
is bounded bilinear on X. is bounded linear on X when f ∈ L2(Ω).
is bounded linear on X when f ∈ L2(Ω).- a( ·, · ) is coercive (which will be proved in the next section):

- From Theorem 4.3.1, there exists a unique solution
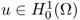 of the above minimization problem.
of the above minimization problem. - This minimizer u satisfies the variational problem:
![]()
- This solution u is a solution of the corresponding Euler–Lagrange equation:
4.42 ![]()
4.43 ![]()
![]()
![]()
4.45 ![]()
4.46 ![]()
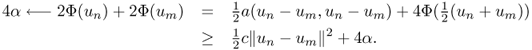
![]()
![]()
![]()
![]()
![]()
4.3.2 Ritz Approach
Taking account of the finite element method, we continue to study Hilbert space techniques. As before, we assume the following:
- X is a real Hilbert space with norm || · ||;
- {Xn} is a sequence of a finite-dimensional subspaces of X such that Xn ⊂ Xn+1 and

 is a basis of Xn;
is a basis of Xn;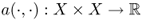 is a bounded, symmetric, strongly positive, bilinear map and
is a bounded, symmetric, strongly positive, bilinear map and
![]()
- b ∈ X* where X* is the set of linear functionals on X.
As before, we consider the minimization problem:
The variational problem is as follows:
According to the Lax–Milgram theorem, we know the solvability of (4.47) and (4.48). We try to give a rather different analysis by using the new inner product a(u, v). Since ||u||2 ≈ a(u, u), ![]() can be viewed as a norm of the Hilbert space X.
can be viewed as a norm of the Hilbert space X.
4.49 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.52 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
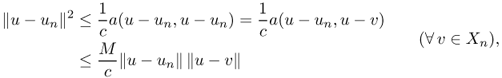
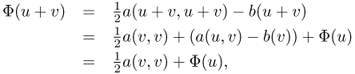
![]()
![]()
![]()
![]()
![]()
![]()
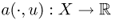 is linear for each u ∈ X;
is linear for each u ∈ X;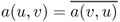 for all u, w ∈ X;
for all u, w ∈ X;- there exists M so that |a(u, v)| < M||u|| ||v||;
- there exists c so that
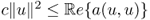 for all u.
for all u.
![]()
![]()
4.3.3 Euler–Lagrange Equations
We now study how to compute the gradient of Φ(u) on a subset X of the Hilbert space H1(Ω) using several important examples.

![]()
![]()
![]()
![]()
![]()

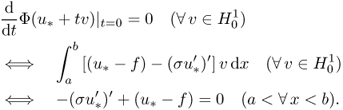

![]()
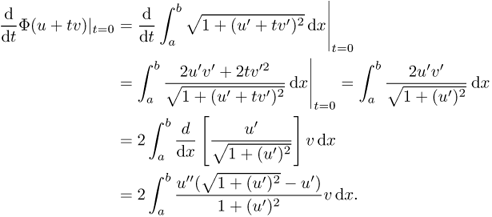
![]()
![]()
![]()

![]()
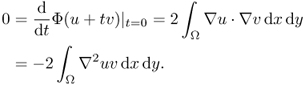
![]()
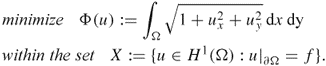
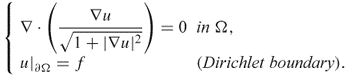

Since this holds for all ![]() , we have
, we have
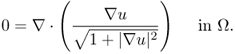
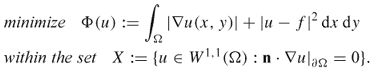
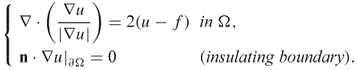
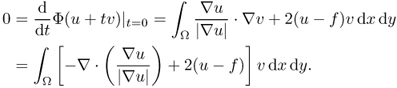
![]()
4.3.4 Regularity Theory and Asymptotic Analysis
We briefly discuss the regularity theory for the elliptic PDE. We know that a solution of the Laplace equation has the mean value property and therefore it is analytic (“having the ability to analyze”): if we have knowledge of all derivatives of a harmonic function at one fixed point, we can get full knowledge of the solution in its neighborhood. This mean value type property can be applied in some sense to solutions of elliptic equations. Basically, Harnack's inequality comes from a weighted mean value property. For details, please refer to the book by Gilbarg and Trudinger (2001).
Let Ω be a bounded smooth domain in ![]() . Consider the following divergence-form elliptic operator:
. Consider the following divergence-form elliptic operator:
4.53 ![]()
where ![]() and
and

is symmetric, bounded and positive definite. Assume that there exist positive constants c1 and c2 such that
The bounded linear form ![]() associated with a divergence-form elliptic operator L is
associated with a divergence-form elliptic operator L is
4.55 ![]()
4.58 ![]()
4.60 ![]()
4.62 ![]()
Now, we will estimate ![]() . From now on, we shall use the notation x = (x1, x2, x3) = r = (x, y, z) just for simple expressions. For the estimate of
. From now on, we shall use the notation x = (x1, x2, x3) = r = (x, y, z) just for simple expressions. For the estimate of ![]() , substitute
, substitute ![]() into (4.56), where
into (4.56), where ![]() denotes the difference quotient
denotes the difference quotient
![]()
where h is very small and ![]() . Then,
. Then,
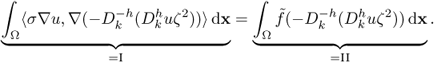
We write I as
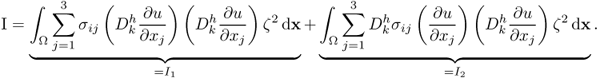
From the assumption of ellipticity,
![]()
Using the Hölder inequality and Poincaré inequality,
![]()
where ![]() can be chosen arbitrarily small,
can be chosen arbitrarily small, ![]() depends on
depends on ![]() ,
, ![]() and
and ![]() .
.
Then, we have the estimate
![]()
Since this is true for arbitrarily small h, we have the estimate
![]()
Here, we may use a convergence theorem in real analysis. Combining this estimate into (4.59) with an appropriate choice of ![]() leads to (4.57).
leads to (4.57).
Next, we study some important techniques for asymptotic analysis. We will use a nice simple model in the book by Chipot (2009) describing asymptotic analysis for problems in a large cylinder.
For a given f(y) ∈ C([ − a, a]), let uL and ![]() , respectively, be solutions of
, respectively, be solutions of
4.63 ![]()
and
4.64 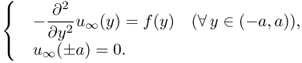
Then, we have the following estimates.
![]()
4.67 ![]()
4.68 ![]()
![]()
4.75 ![]()
![]()
![]()
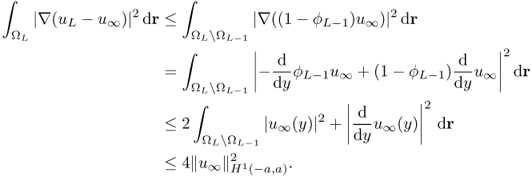
We can generalize this simple asymptotic analysis (4.76) to an elliptic PDE:
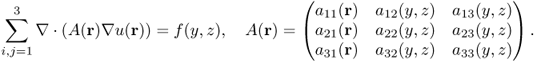
For details, please see section 6.3 in the book by Chipot (2009).
4.4 Tikhonov Regularization and Spectral Analysis
In this section, we briefly present a functional analytic approach for the Tikhonov regularization method, which is probably the most commonly used method when the problem ![]() is ill-posed. Regularization is an important tool to deal with an ill-posed problem by imposing a priori information on the solution. We discuss the regularization techniques for solving T*Tx = T*y, where T*T is an n × n matrix having a large condition number. For more detailed aspects, the reader may refer to the book by Engl et al. (1996).
is ill-posed. Regularization is an important tool to deal with an ill-posed problem by imposing a priori information on the solution. We discuss the regularization techniques for solving T*Tx = T*y, where T*T is an n × n matrix having a large condition number. For more detailed aspects, the reader may refer to the book by Engl et al. (1996).
Let X and Y be Hilbert spaces. We denote by ![]() the set of linear operators T:X → Y. For each
the set of linear operators T:X → Y. For each ![]() , the Hilbert spaces X and Y, respectively, can be decomposed into
, the Hilbert spaces X and Y, respectively, can be decomposed into
![]()
where
- N(T): = {x ∈ X:Tx = 0} is the kernel of T,
- R(T): = {Tx:x ∈ X} is the range of T,
- N(T)⊥: = {x ∈ X:〈x, z 〉 = 0 for all z ∈ N(T)} is the orthogonal space of N(T),
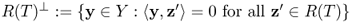 is the orthogonal space of R(T).
is the orthogonal space of R(T).
- D(T†) = R(T) ⊕ R(T)⊥,
- T†:D(T†) → N(T)⊥ is a linear operator such that N(T†) = R(T)⊥ and
![]()
![]()
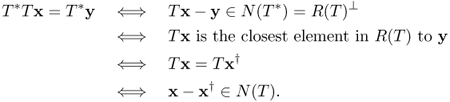
4.4.1 Overview of Tikhonov Regularization
This section is based on a lecture by Bastian von Harrach. To get insight into Tikhonov regularization, we consider the simplest operator ![]() , which is an m × n matrix. Assume that the problem
, which is an m × n matrix. Assume that the problem ![]() is ill-posed. For ease of explanation, we assume that
is ill-posed. For ease of explanation, we assume that ![]() satisfies the following:
satisfies the following:
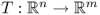 is injective and bounded,
is injective and bounded,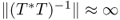 (very large),
(very large),
where T* is the transpose of T. Consider the ill-posed problem:
![]()
or the corresponding least-squares problem
![]()
In practice, the data b are always contaminated by noise; hence we may consider the following problem:
![]()
where bδ are the noisy data. Here, the norm || · || is the standard Euclidean distance.
From the assumption that ![]() , unregularized solutions (T*T)−1T*bdelta are prone to magnify noise in the data btrue, where btrue are the true data. Hence, (T*T)−1T*bdelta may be very different from the true solution xtrue: = (T*T)−1T*btrue even if δ ≈ 0. Hence, the goal is to find a good operator Gδ:X → X so that Gδ ≈ (T*T)−1 and GδT*bδ is a reasonably good approximation of xtrue when bδ ≈ btrue.
, unregularized solutions (T*T)−1T*bdelta are prone to magnify noise in the data btrue, where btrue are the true data. Hence, (T*T)−1T*bdelta may be very different from the true solution xtrue: = (T*T)−1T*btrue even if δ ≈ 0. Hence, the goal is to find a good operator Gδ:X → X so that Gδ ≈ (T*T)−1 and GδT*bδ is a reasonably good approximation of xtrue when bδ ≈ btrue.
The motivation of Tikhonov regularization is to minimize not only ||Tx − bδ|| but also ||x||. By adding a regularization parameter, α, we consider the following minimization problem:
4.78 ![]()
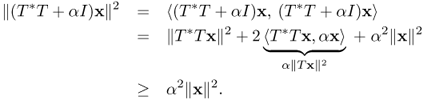
Hence T*T + αI is injective. We can prove that T*T + αI is surjective by the Riesz lemma or Lax–Milgram theorem. Therefore T*T + αI is invertible and
![]()
Next, we will prove (4.79). Using the fact that
![]()
(see Exercise 4.4.5), we have

This proves (4.79). Here, the last inequality in the above estimate comes from
![]()
(see Exercise 4.4.5) and the following estimate:
![]()
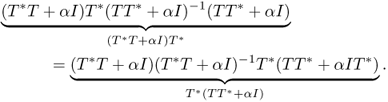
![]()
![]()
![]()
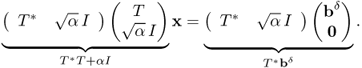
To maximize the effect of the regularization, it is important to choose an appropriate regularization parameter α. The strategy is to choose an appropriate parameter α = α(δ), which can be viewed as a function of δ, such that
![]()
Hence, we must have α(δ) → 0 as δ → 0 because xtrue = (T*T)−1T*btrue. We need to make an appropriate choice of α(δ) so that it provides a “stable” convergence xα = (T*T + αI)−1T*bδ → xtrue as δ → 0.
![]()
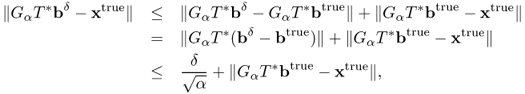
In the proof of the previous theorem for a fixed δ, note the estimate
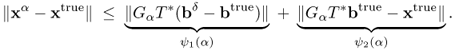
The term ψ1(α): = ||GαT*(bδ − btrue)|| indicates the amplified measurement error related to the difference between the exact data and the measurement data, and the term ψ2(α): = ||GαT*btrue − xtrue||, called the regularization error, illustrates how well GαT* approximates T−1. Roughly speaking, the optimal α would be a quantity near the intersecting point of ψ1(α) = ψ2(α) as shown in Figure 4.1.
Figure 4.1 Error estimation

4.4.2 Bounded Linear Operators in Banach Space
The following are important examples of Banach spaces in PDE theory:
 for
for 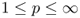 ;
;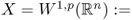 the closure of
the closure of 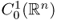 with norm
with norm 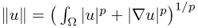 ;
;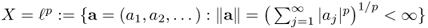 .
.
Note that the vector space ![]() equipped with the Lp-norm is a normed space but not a Banach space.
equipped with the Lp-norm is a normed space but not a Banach space.
![]()
![]()
![]()
![]()
![]()
We should note that, in order to apply the closed graph theorem, the domain of T should be a Banach space. To see this, consider the Hilbert space X = L2([0, 1]) equipped with L2-norm. We know that C2([0, 1]) is a dense subset of the Hilbert space X = L2([0, 1]). It is easy to see that the Laplace operator T:C2([0, 1]) → X defined by
![]()
is unbounded because
![]()
Defining ![]() , we can extend the unbounded operator T to V by defining the extension operator
, we can extend the unbounded operator T to V by defining the extension operator ![]() :V → X in such a way that
:V → X in such a way that ![]() whenever it makes sense. Clearly
whenever it makes sense. Clearly ![]() is a closed operator. However,
is a closed operator. However, ![]() is an unbounded operator, but it does not contract to the closed graph theorem because V is not complete (not a Banach space). At this point, we should note that V is a dense subset in L2([0, 1]) since
is an unbounded operator, but it does not contract to the closed graph theorem because V is not complete (not a Banach space). At this point, we should note that V is a dense subset in L2([0, 1]) since ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The proof is left as an exercise for the reader.
4.4.3 Regularization in Hilbert Space or Banach Space
Regularization is an important tool to deal with an ill-posed problem by approximating it as a well-posed problem using a priori information on solutions. We discuss regularization techniques for solving K*Kx = K*y, where K*K is an n × n matrix having a large condition number.
- The map K:X → Y is said to be a compact operator if
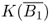 is compact, where B1 is the unit ball in X. Equivalently, K is compact if, for any bounded sequence {xn} in X, {Kxn} has a convergent subsequence.
is compact, where B1 is the unit ball in X. Equivalently, K is compact if, for any bounded sequence {xn} in X, {Kxn} has a convergent subsequence. - The operator norm of K is
 .
. - For an eigenvalue
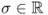 , Xσ: = {x ∈ X:K*Kx = σx} is called a σ-eigenspace of K*K.
, Xσ: = {x ∈ X:K*Kx = σx} is called a σ-eigenspace of K*K.
Throughout this section, we assume that ![]() is a compact operator. Note that K*K maps from X to X and KK* maps from Y to Y. Both K*K and KK* are compact operators and self-adjoint, that is, 〈K*Kx, x′ 〉 = 〈x, K*Kx′ 〉 for all x, x′ ∈ X.
is a compact operator. Note that K*K maps from X to X and KK* maps from Y to Y. Both K*K and KK* are compact operators and self-adjoint, that is, 〈K*Kx, x′ 〉 = 〈x, K*Kx′ 〉 for all x, x′ ∈ X.
![]()
- There exist eigenvalues σ1 ≥ σ2 ≥ ··· ≥ 0 and the corresponding orthonormal eigenfunctions {vn:n = 1, 2, …} of K*K such that
![]()
- For each σn > 0,
 and
and
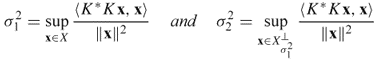
- If K*K has infinitely many different eigenvalues, then
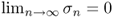 .
. 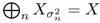 .
.- Writing un = Kvn/||vn||, we have
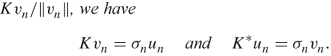
![]()
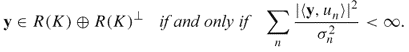
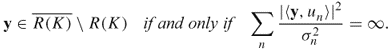
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For a compact operator K, the following are equivalent:
- K† is unbounded;
- R(K) is not closed, that is,
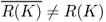 ;
; 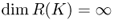 ;
;- if
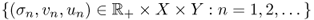 is a singular system for K such that
is a singular system for K such that 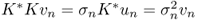 , then there are infinitely many σn > 0 such that σn → 0 as
, then there are infinitely many σn > 0 such that σn → 0 as  .
.
Hence, if K† is unbounded and K is compact, the problem Kx = y is ill-posed, that is, a small error in the data y may result in a large error in the solution x = K†y. Recall that K† = (K*K)†K*. Numerous regularization techniques have been used to deal with this ill-posedness.
We now introduce the Tikhonov regularization method. Let ![]() be a compact operator. To explain the regularization method, it will be convenient to express the compact operator K*K in the form
be a compact operator. To explain the regularization method, it will be convenient to express the compact operator K*K in the form
![]()
where Pλ is the projection map from X to the set ![]() . Note that
. Note that ![]() . Hence, if x ∈ D(K*K), then
. Hence, if x ∈ D(K*K), then
![]()
Using the above property, we can show that
![]()
where ![]() is defined by
is defined by
![]()
For y ∈ D(K†), the solution x† = K†y can be expressed as
4.80 ![]()
If ![]() is compact and R(K) is not closed, then the operator K† is unbounded and the problem Kx = y is ill-posed. If
is compact and R(K) is not closed, then the operator K† is unbounded and the problem Kx = y is ill-posed. If ![]() , then
, then
![]()
On the other hand,
![]()
This reconstruction method is called Tikhonov regularization. The solution
![]()
can also be interpreted as a minimizer of the energy functional:
Denoting ![]() , the regularization
, the regularization ![]() can be viewed as an approximation of K† in the sense that
can be viewed as an approximation of K† in the sense that
![]()
Here, we should note that N(K*) = R(K)⊥. The most widely used iteration method for solving y = Kx is based on the identity x = x + αK*(y − Kx) for some α > 0. This method is called the Landweber iteration, which expects xk → x by setting
![]()
With this Landweber iteration, y ∈ D(K†) if and only if xk converges. Indeed,
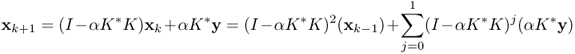
which leads to
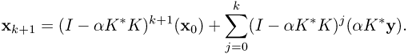
Regularization is to replace the ill-conditioned problem Kx = y by its neighboring well-posed problem in which we impose a constraint on desired solution properties. The problem of choosing the regularization parameter α in (4.81) is critical. In MR-based medical imaging, we often need to deal with the tradeoff between spatial resolution and temporal resolution. Accelerating the MR imaging speed requires the phase encoding lines in k-space to be skipped, and results in insufficient k-space data for MR image reconstruction via inverse Fourier transformation. To deal with the missing data, one may use the minimization problem (4.81), which consists of the fidelity term (ensuring that the k-space data y are consistent with the image x) and the regularization term (which incorporates the desired solution properties). Nowadays many research areas use regularization techniques.
4.5 Basics of Real Analysis
We now briefly review the real analysis techniques that are used in this chapter. For more details, we refer to the books by Lieb and Loss (2001), Marsden (1974), Rudin (1970) and Wheeden and Zygmund (1977). Throughout this section, we assume that Ω is a bounded domain in ![]() (n = 1, 2 or 3) and
(n = 1, 2 or 3) and ![]() is a function.
is a function.
4.5.1 Riemann Integrability
For a quick overview of the Riemann integral, we will explain its concept only in two-dimensional space. Let ![]() be a bounded domain and let
be a bounded domain and let ![]() be a bounded function. We enclose Ω in a rectangle and extend f to the whole rectangle B = [a1, b1] × [a2, b2] by defining it to be zero outside Ω. Let
be a bounded function. We enclose Ω in a rectangle and extend f to the whole rectangle B = [a1, b1] × [a2, b2] by defining it to be zero outside Ω. Let ![]() be a partition of B obtained by dividing a1 = x0 < x1 < ··· < xn = b1 and a2 = y0 < y1 < ··· < ym = b2:
be a partition of B obtained by dividing a1 = x0 < x1 < ··· < xn = b1 and a2 = y0 < y1 < ··· < ym = b2:
![]()
- Define the upper sum of f by
![]()
![]()
- Define the upper integral of f on Ω by
![]()
![]()
We say that f is Riemann integrable or integrable if
![]()
If f is integrable on Ω, we denote
![]()
4.5.2 Measure Space
For a domain E in ![]() , we will denote the area of the domain E by μ(E). We can measure the area μ(E) based on the area of rectangles. If Q = (a, b) × (c, d) and Qj for j = 1, 2, … is a sequence of rectangles with
, we will denote the area of the domain E by μ(E). We can measure the area μ(E) based on the area of rectangles. If Q = (a, b) × (c, d) and Qj for j = 1, 2, … is a sequence of rectangles with ![]() for j ≠ k, then we measure them in the following ways:
for j ≠ k, then we measure them in the following ways:
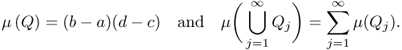
It seems that any open domain E is measurable since any open set can be expressed as a countable union of rectangles. Then, can we measure any subset in ![]() ? For example, consider the set
? For example, consider the set ![]() , where
, where ![]() is the set of rational numbers. What is its area μ(E)? It is a bit complicated. Measure theory provides a systematic way to assign to each suitable subset E a positive quantity μ(E) representing its area.
is the set of rational numbers. What is its area μ(E)? It is a bit complicated. Measure theory provides a systematic way to assign to each suitable subset E a positive quantity μ(E) representing its area.
The triple ![]() is said to be a measure space if the following are true:
is said to be a measure space if the following are true:
If the σ-algebra ![]() includes all null sets (a null set is a set N such that μ(N) = 0), then μ is said to be complete. Let
includes all null sets (a null set is a set N such that μ(N) = 0), then μ is said to be complete. Let ![]() denote the collection of all subsets of X.
denote the collection of all subsets of X.
With the use of the outer measure, we can describe a general constructive procedure for obtaining the complete measure. Let ![]() be an algebra of sets and
be an algebra of sets and ![]() a set-valued function such that μpre(∅) = 0. For A ⊂ X, we define
a set-valued function such that μpre(∅) = 0. For A ⊂ X, we define
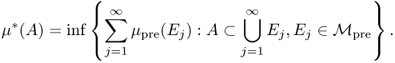
Then, μ* is an outer measure.
![]()
![]()
The following Caratheodory definition provides a method of constructing a complete measure space ![]() .
.
![]()
The Lebesgue measure on ![]() is an extension of the pre-measure defined by μpre((a, b]) = b − a.
is an extension of the pre-measure defined by μpre((a, b]) = b − a.
4.5.3 Lebesgue-Measurable Function
Throughout this section, we restrict ourselves to the standard Lebesgue measure μ in X (![]() or
or ![]() ) that is generated by the outer measure,
) that is generated by the outer measure,
![]()
where μpre is a pre-measure defined on open sets in X. For example, in ![]() , μpre(U) is the volume of U.
, μpre(U) is the volume of U.
A function ![]() is said to be measurable if f−1(U) is measurable for every open set U.
is said to be measurable if f−1(U) is measurable for every open set U.
![]()
From now on, we assume that E, Ej are measurable sets. The characteristic function of E, denoted by χE, is the function defined by
![]()
Let ![]() be the set of all simple functions, a finite linear combination of characteristic functions:
be the set of all simple functions, a finite linear combination of characteristic functions:
4.82 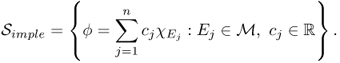
Let ![]() be the set of measurable functions and let
be the set of measurable functions and let
![]()
For given ![]() , we say that f = 0 holds almost everywhere (abbreviated a.e.) if μ({x:f(x) ≠ 0}) = 0.
, we say that f = 0 holds almost everywhere (abbreviated a.e.) if μ({x:f(x) ≠ 0}) = 0.
![]()
The proof is straightforward by drawing a diagram of ϕn. From the above theorem, we can prove that, for any measurable function f, there is a sequence of simple functions ϕn such that ϕn → f on any set on which f is bounded. The reason is that f can be decomposed into f = f+ − f−, where f = max{f, 0} and f− = max{ − f, 0}.
Now, we are ready to give the definition of the Lebesgue integral using the integral of a measurable simple function ![]() , which is defined as
, which is defined as
We use the convention that ![]() . Let
. Let ![]() be a vector space of measurable simple functions. Then the integral
be a vector space of measurable simple functions. Then the integral ![]() (as a function of
(as a function of ![]() ) can be viewed as a linear functional on
) can be viewed as a linear functional on ![]() , that is, the operator
, that is, the operator ![]() is linear.
is linear.
4.85 ![]()
![]()
Using the definition (4.84) of the integral of a measurable simple function, we can define the integral of a measurable function f ≥ 0.
4.86 ![]()
From the definition, we obtain that f ≤ g implies ∫f dμ ≤ ∫g dμ.
![]()
![]()
![]()
![]()
![]()
![]()
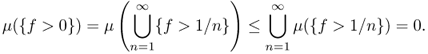
![]()
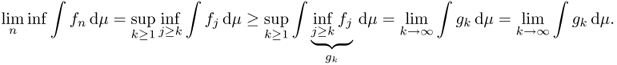
![]()
It is easy to see that L1(X, dμ) is a vector space equipped with the norm ||f|| = ∫|f| dμ satisfying the following:
Now, we will prove that L1(X, dμ) is a complete normed space (or Banach space). To prove this, we need to study several convergence theorems.
![]()
![]()
![]()
![]()
![]()
The above exercise explains the reason why the LDCT requires the assumption that {fn} is dominated by a fixed L1 function g.
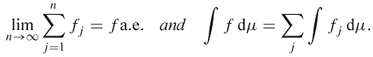
From (4.83), for any function f ∈ L1, there exists a sequence ![]() such that
such that
![]()
From the LDCT, ||ϕn − f|| = ∫|ϕn − f| dμ → 0. Hence, ![]() is dense in L1, that is, every element in L1 is an L1-limit of a sequence of elements in
is dense in L1, that is, every element in L1 is an L1-limit of a sequence of elements in ![]() .
.
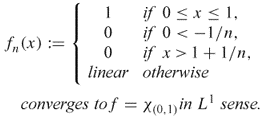
![]()
![]()
![]()
4.5.4 Pointwise, Uniform, Norm Convergence and Convergence in Measure
Let Ω be a subdomain in ![]() . The sequence of functions fk ∈ C(Ω) is said to converge pointwise to f if, for each
. The sequence of functions fk ∈ C(Ω) is said to converge pointwise to f if, for each ![]() , fk(r) → f(r). We say that the sequence of functions fk ∈ C(Ω) converges uniformly to f if
, fk(r) → f(r). We say that the sequence of functions fk ∈ C(Ω) converges uniformly to f if ![]() .
.
![]()
![]()
![]()
![]()
For example, the sequences ϕn = (1/n)χ(0, n), χ(0, 1/n) and ![]() converge to 0 in measure, but the sequence ϕn = χ(n, n+1) does not converge to 0 in measure.
converge to 0 in measure, but the sequence ϕn = χ(n, n+1) does not converge to 0 in measure.
- there exists
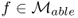 such that fn → f in measure,
such that fn → f in measure, - there exists
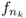 such that
such that 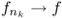 a.e.,
a.e., - f is uniquely determined a.e.
![]()
![]()
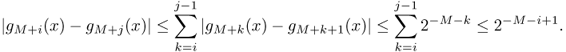
![]()
The statement [ fn → f in L1 ] implies [ fn → f in measure ] since
![]()
From the proof of the previous theorem, if [ fn → f in L1 ], then we can choose a subsequence nk such that ![]() ,
,
![]()
Hence, according to Theorem 4.5.20, [ fn → f in L1 ] implies the statement [![]() gk → f a.e. ].
gk → f a.e. ].
Proof. Since fn → f a.e., there exists Z ⊂ E so that μ(Z) = 0 and fn(x) → f(x) for ![]() . Hence, it suffices to prove the theorem for the case when Z = ∅.
. Hence, it suffices to prove the theorem for the case when Z = ∅.
Let ![]() . Then,
. Then, ![]() for n = 1, 2, … . Hence, there exists mn such that
for n = 1, 2, … . Hence, there exists mn such that ![]() . Let
. Let ![]() . Then,
. Then, ![]() . Moreover, if j > mn, then
. Moreover, if j > mn, then ![]() Hence, fn → f uniformly on F.
Hence, fn → f uniformly on F.
4.5.5 Differentiation Theory
Throughout this section, we consider a bounded function ![]() . We will study a necessary and sufficient condition that f′ exists almost everywhere and
. We will study a necessary and sufficient condition that f′ exists almost everywhere and
![]()
Recall that the derivative of f at x exists if all four of the following numbers have the same finite value:
![]()
According to Lebesgue's theorem, every monotonic function ![]() is differentiable almost everywhere.
is differentiable almost everywhere.
![]()
To understand why ![]() for a Cantor function f, we need to understand the concept of absolute continuity.
for a Cantor function f, we need to understand the concept of absolute continuity.
![]()
![]()
![]()
![]()
From this theorem, the Cantor function is not absolutely continuous.
Every continuous and non-decreasing function f can be decomposed into the sum of an absolutely continuous function and a singular function, both monotone:
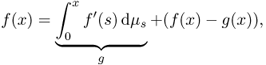
where g is an absolutely continuous function.
![]()
References
Akoka S, Franconi F, Seguin F and le Pape A 2009 Radiofrequency map of an NMR coil by imaging. Magn. Reson. Imag. 11, 437–441.
Chipot M 2009 Elliptic Equations: An Introductory Course. Birkhäuser Advanced Texts. Birkhäuser, Basel.
Engl HW, Hanke M and Neubauer A 1996 Regularization of Inverse Problems. Mathematics and Its Applications. Kluwer Academic, Dordrecht.
Feldman J and Uhlmann G 2003 Inverse Problems. Lecture Note. See http://www.math.ubc.ca/∼feldman/ibook/.
Gilbarg D and Trudinger N 2001 Elliptic Partial Differential Equations of Second Order. Springer, Berlin.
Lieb EH and Loss M 2001 Analysis, 2nd edn. Graduate Studies in Mathematics, no. 14. American Mathematical Society, Providence, RI.
Marsden JE 1974 Elementary Classical Analysis. W. H. Freeman, San Francisco.
Rudin W 1970 Real and Complex Analysis. McGraw-Hill, New York.
Stollberger R and Wach P 1996 Imaging of the active B1 field in vivo. Magn. Reson. Med. 35, 246–251.
Wheeden RL and Zygmund A 1977 Measure and Integral: An Introduction to Real Analysis. Monographs and Textbooks in Pure and Applied Mathematics, vol. 43. Marcel Dekker, New York.
Further Reading
Evans LC 2010 Partial Differential Equations. Graduate Studies in Mathematics, no. 19. American Mathematical Society, Providence, RI.
Folland G 1976 Introduction to Partial Differential Equations. Princeton University Press, Princeton, NJ.
Giaquinta M 1983 Multiple Integrals in the Calculus of Variations and Non-linear Elliptic Systems. Princeton University Press, Princeton, NJ.
Grisvard P 1985 Elliptic Problems in Nonsmooth Domains. Monographs and Studies in Mathematics, no. 24. Pitman, Boston, MA.
John F 1982 Partial Differential Equations. Applied Mathematical Sciences, vol. 1. Springer, New York.
Kellogg OD 1953 Foundations of Potential Theory. Dover, New York.
Reed M and Simon B 1980 Functional Analysis. Methods of Modern Mathematical Physics, vol. I. Academic Press, San Diego, CA.
Rudin W 1970 Functional Analysis. McGraw-Hill, New York.
Zeidler E 1989 Nonlinear Functional Analysis and Its Applications. Springer, New York.