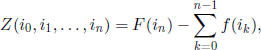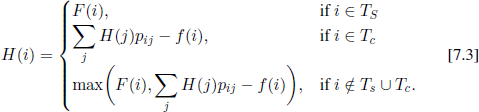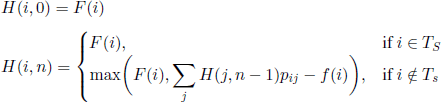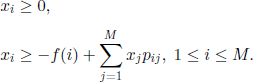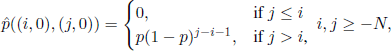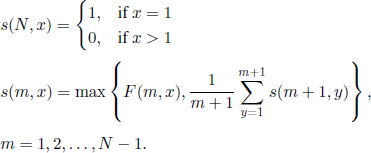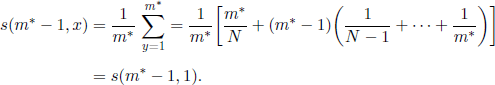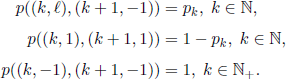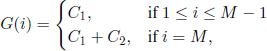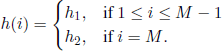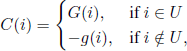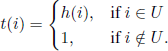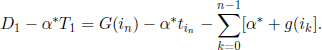Chapter 7
Optimal Stopping Models
Some optimal stopping problems, such as, for instance, the secretary problem, have a long history. The optimal stopping theory started to form a specific branch of the stochastic processes theory during the 40s. In the period between the publication of A. Wald’s monograph (1947) and that of A. N. Shiryaev (1978), we witness an increasing interest in solving certain specific problems as well as in building up an ever more comprising general theory.
In this chapter we will describe the general issues of this theory as well as some classic models.
7.1. The classic optimal stopping problem
7.1.1. Formulation of the problem
First of all we will give some examples.
EXAMPLE 7.1.– Let us consider a repeated coin tossing, with the convention that player A earns one unit if tails occurs, whereas player B gets one unit if heads occur. If Sn is the gain of A after n rounds, then
where 
is a sequence of i.i.d. r.v. with 
.1 We have described up to now the probabilistic structure of the experiment and now we will specify the structure of the decision. We first assume that the amount of money that the two players have at their disposal is unlimited. What they both have to do is to decide when to end the game so that they ensure a maximum gain. After each round, each player must decide either to continue playing or to stop and take the gain he earned. One thing about this experiment: there is no participation cost, that is players do not have to pay in order to toss the coin again.
The rule is “we stop when we have an advantage”; according to this rule, the first player stops at the first moment n when Sn > 0.
If the first player has an initial amount of money S, then when Sn = S he is forced to stop playing.
EXAMPLE 7.2.– This example will show us the advantage of setting a stopping rule different from that where we decide beforehand the number of steps before ending the game. Let 
bea sequence of i.i.d. r.v. with 
, and let us define the gain at time n by Sn/n.
Obviously, 
(Sn/n) = 1/2, so the end of the game at a moment n decided beforehand will yield an average gain of 1/2 units. Now we will set a stopping rule which will lead to a greater average gain. Here is the rule: if ξ1 = 1, the game is stopped after the first round, if not, it will be after two rounds. The gain will be 1 if ξ1 = 1; 0 if ξ1 = 0 and ξ2 = 0; 1/2 if ξ1 =0 and ξ2 = 1. Thus, in this case the average gain is 1 · 1/2 + 0 · 1/4 +1/2 · 1/4 = 5/8 > 1/2.
For other theoretical developments related to optimal stopping rules in this context, see [CHO 75].
EXAMPLE 7.3.– (The secretary problem) We set out to recruit a secretary from among N applicants. The applicants are interviewed one after the other. After each interview, there exists the possibility either to recruit the candidate or to reject her/his application. At each moment the profile of the applicant can be compared to that of the previous applicants, but never to the next candidates. If a candidate is rejected, there is no possible way to change this decision afterward. The problem is that we need to find a stopping rule which should ensure, with a maximum probability, the selection of the best secretary.
This problem, also called the best choice problem, can be presented from a mathematical point of view as follows. Let a1, a2, …, aN be a permutation of the integers 1, 2, …, N. We assume that 1 corresponds to the best “object” and that the qualities of the object decrease as the rank increases, such that the object N is the worst one. Additionally, we assume that the N! permutations are equally likely to occur.
The first results on this problem can be found in [ARR 49, WAL 48]; for modifications and extensions see [PRE 83].
EXAMPLE 7.4.– (The problem of buying (selling) a house) This problem is related to that presented in example 7.3 and could be formulated as follows: we make repeated and independent choices from a population of known distribution; to be more specific, let Xn, n ∈ 
, represent the supply at time n, with 
(Xn = i)= pi, i ∈ . When the process stops at time n there is an associated cost (gain) given by min(X1, …, Xn) (max(X1, …, Xn)), which is the best supply up to time n. The process of these successive choices is conditioned, at each step, by a cost (for instance the cost of a new advert being published in a newspaper).
There are some issues which differ in this example from the secretary problem: the choice is made out of an infinite population; there exists the possibility of choosing the best offer from among all the offers available up to the stopping time; if the decision to continue is made, then a cost is incurred.
This problem was described for the first time in [CHO 61].
EXAMPLE 7.5.– (The car parking problem) We wish to park a car as close as possible to a given point, denoted by 0. We approach the destination driving along a negative axis and we suppose that the nth parking space, n = −N, − N + 1, …, −1, 0, 1, …, is free with the probability p, independently of the situation of the other parking spaces. Obviously, if the parking space is taken, we are forced to drive ahead; when we see a free parking space, we can either park the car or go on, hoping that we would find a place even closer to our destination point. The choice of the parking space n, n = −N, −N + 1, …, −1, 0, 1, …, implies a “loss” proportional to |n| = the distance left for us to walk to the destination.
These examples show that an optimal model has the following structure:
1) A mechanism that randomly evolves in time from one state to another; in various cases, we know completely or partially the law that governs this evolution. In other cases, we do not have such information.
2) A decision system that, at any time, associates a set of possible decisions with the state of the mechanism.
3) A gain (reward) rule that specifies the reward received if the decision to stop is made, and also specifies the cost associated with the decision to continue.
A well defined stopping rule must specify the stopping time for every state sequence (trajectory) of the considered mechanism. Assuming that such a rule exists, a state sequence i0, i1, …, in is called a stopping sequence if we decide to stop the mechanism when it is in state in, but not before. Consequently, a stopping rule represents a list of all stopping sequences subject to the following constraints. First of all, if i0,i1, …, in is a stopping sequence, no sequence that has on the first n + 1 positions these states in the same order is a stopping sequence. Practical considerations (see Examples 7.1 and 7.5) lead us to define two important subspaces of the state space: Tc = the subset of all the states where we are obliged to continue and Ts = the subset of all the states where we are forced to stop the experiment. It is clear that in a stopping sequence io, h, …,in, only in can belong to Ts and, obviously, in ∉ Tc. For a reasonable stopping rule, we also need the following condition to be satisfied
where the sum is over all the stopping sequences of the rule at stake. Thus we are sure that, for any trajectory of the mechanism, the stopping occurs in a finite time.
On the other hand, the set of stopping sequences is fully characterized by a function r defined on the set of the trajectories of the process, with values in 
; this function associates to each trajectory the rank of the last term of the stopping sequence that we encounter along the trajectory. The r.v. τ is called a stopping time for the process studied.
The reward can be specified by considering a real function Z, defined on the set of stopping sequences, called reward (gain) function. For a given stopping sequence i0 ,i1,…,in, we assume that the reward function has the expression
where F(i) is the amount received if we stop in state % and f (j) is the continuation cost when the mechanism is in state j. It is clear that a rule providing large gains for stopping sequences with small probabilities of occurrence and small gains for stopping sequences with large probabilities of occurrence cannot be well evaluated. Consequently, it is reasonable to take the mean value of the gain function 
Z as the evaluation criterion of a stopping rule. A rule for which Z is maximum, if this maximum does exist, is called an optimal stopping rule.
7.1.2. Optimal stopping for a Markov structure
In the general case, it is very difficult to make an exhaustive list of stopping sequences and to compute the probabilities that appear in Formula [7.1]. The computation of these probabilities is essentially simplified if we assume a Markovian evolution of the mechanism. Moreover, this hypothesis of Markovian evolution yields an important simplification of the list of stopping rules. More precisely, under this hypothesis, if there exists an optimal stopping rule, then any optimal stopping sequence is completely determined by its last state; consequently, an optimal stopping rule will be completely specified by a subset T of the state space with the following properties: on every trajectory we stop as soon as we encounter a state from T, Ts ⊂ T, Tc ⊂ Tc,2 and the probability that the mechanism never arrives in a state of T is 1. In other words, an optimal stopping rule is completely specified if we know the stopping time τ given by the first hitting time of set T. Consequently, T* is an optimal stopping rule if, for any other rule T, we have 
The rigorous proof of this fact can be found in ([DER 53], pp. 103–117). The proof uses complex mathematical tools, although the underlying idea is intuitive. If the mechanism is in state i after a certain number of transitions, we are affected by the “history” through the participation costs we paid, but once paid they are no longer a burden! In fact, the decision to continue or not depends on the comparison between the reward F(i) obtained if we stop and the possible reward expected if we continue; besides, note that the Markovian evolution of the mechanism implies that this reward depends only on the present state.
In the rest of this section we will show that the examples presented above are characterized by a Markovian evolution of the mechanism and that the gain structure is given by [7.2].
In Example 7.1 with infinite initial fortunes, (Sn, n ∈ ) is a Markov chain with state space 
and transition probabilities
with initial state 0. The amount received if we stop in state i is F(i) = i and, since there is no participation cost, f (i) = 0 for all i ∈ . Not that Tc and Ts are empty sets.
If the first gambler has an initial fortune S, then the state space of the Markov chain is the same as before, the set Tc is empty, and Ts = {i | i ≤ −S}.
If in Example 7.2 we consider the Markov chain with state space N and transition probabilities defined for Example 7.1, then we encounter the following difficulty. If at time n the process is in state i, the amount received if we stop is i/n; this depends on n, so the reward is not given anymore by Formula [7.2]. We can overcome this difficulty by a procedure frequently used in Markov process theory, namely by considering the state space × and taking as initial state the pair (0, 0). In the pair (i, n), the first component i represents the value taken by Sn, whereas the second component n represents the time. If the new process is in state (i,n), then the only transitions are to states (i + 1, n + 1) and (i, n + 1); more precisely, we have
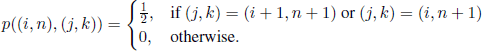
For this new process, we have F(i,n) = i/n (which depends only on the current state of the process), f (i,n) = 0 for all (i,n) ∈ 
, and Tc and Ts are empty sets.
In Example 7.4, the r.v. Yn = max (X1, …, Xn), n ∈ 
, form a Markov chain with state space and transition probabilities
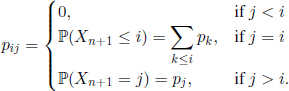
It is clear that F(i)= i and f (i)= constant for all 
. The sets Tc and Ts are empty.
For Example 7.5 we will proceed as we did for Example 7.2. The state space of the Markov chain describing the random mechanism is {−N, −N + 1, … } × {0,1}. In the pair (i, k), the first component represents the number of the parking space, while the second component represents its state: 0 for a free place, 1 for an occupied place. The transition probabilities are
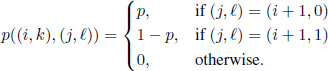
Contrary to the other examples, the set Tc for this Example is not empty anymore, but we have Tc = {(i, 1) | i ≥ −N}. For this reason, the function F has to be defined only for pairs of the form (i, 0), with i ≥ −N. Taking into account the hypotheses we made, we obtain F(i,0)= −α|i|, where α is a positive constant; without loss of generality, we can take α = 1. On the other hand, f (i, k)= 0 for all i ≥ −N, k = 0,1.
Concerning the secretary problem, we will prove that “the criterion of maximal probability” can be in fact reduced to the criterion of mean value.
Let Ω = {ω | ω = (α1, …, αN)} be the set of permutations of the integers 1, …, N; obviously, 
(ω) = 1/N!. Let us define the sequence of r.v. X1, X2, …, Xn as follows: Xk(ω) = the number of terms from a1, …,ak that are less than or equal to ak. We can prove that the r.v. X1, X2, …, Xn are independent and that (Xk = i)= 1/k, 1 ≤ i ≤ k. The secretary problem is equivalent to the problem of finding the stopping time τ* for which
We can associate with this problem a Markov chain (Yn, 1 ≤ n ≤ N) defined by Yn = (n, Xn), 1 ≤ n ≤ N. In this case, if we take f (y)= 0 and
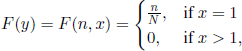
a simple computation yields
where the mean value is computed with respect to the initial distribution concentrated at state (1,1). Thus, the secretary problem is reduced to a problem that uses the mean value criterion. Nonetheless, this problem is essentially different from those presented before, due to the fact that, if we make the decision to stop before time N, we have to stop in any state visited by the chain. Such a problem, where the decision has to be made before a time fixed in advance, is called a. finite-horizon control problem.
We end this section with a simple example that illustrates the fact that an optimal stopping time does not always exist.
As we did in Example 7.1, let us consider the sequence of i.i.d. r.v. (ξn, n ∈ 
), with (ξk = −1) = (ξk = 1) =1/2. The sequence of r.v. (Yn,n ∈ 
) given by
is a Markov chain with state space I = {0, 2, 4, …, 2n, …} and transition probabilities
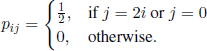
Let F(i)= i, f (i)= 0 for all i ∈ I;Ts = {0} and Tc = Ø. This is the mathematical model for the game we win double or lose all. The structure of this Markov chain implies that a set T of stopping states can have only one element. (In order to get to state 2n the chain has to pass through all the states 2k, 1 ≤ k ≤ n − 1.) We consider that T = {k} and, applying the mean value criterion, we obtain
Consequently, any stopping rule is optimal.
Let us slightly modify this example by introducing a sequence of r.v. (Zn, n ∈ 
) defined by
which is obviously a Markov chain too. The coefficient (2n) /(n + 1), that is increasing with n, has the meaning of an encouraging coefficient for continuing the game. Like in Example 7.2, we place ourselves in the general context that we presented by considering F(Zn,n)= Zn. The above statements on stopping rules still hold here; thus, considering T = {k} and using the mean value criterion, we obtain
Obviously, supT T Z = 2, but this supremum is never reached for any T; consequently, there does not exist an optimal stopping rule.
If, in this example, we forget about the mean value criterion and we use instead the mean value criterion conditioned by the reward at a given time, we obtain
On the one hand, following this criterion, each time we win we have to continue the game. On the other hand, since 0 is an absorbing state of the chain, such a strategy leads, with probability 1, to the loss of the entire initial fortune. We can conclude that a strategy that is good at each step could eventually end being unfavorable.
7.1.3. The functional equation
There are several methods for solving an optimal stopping problem. The first one, that we will present right now, is that of the functional equation, similar to the methods used by R. Bellman [BEL 57] in dynamic programming.
We are only interested here in problems for which there exists an optimal stopping rule. In fact, any problem that arises in practical situations has a solution, even unique, provided that it is well formulated.
If we denote by H(i) the mean value of the reward function in the case where the process starts from state i and is stopped according to an optimal stopping rule, we can prove that function H(i) satisfies the functional equation
A rigorous proof of this statement can be found in [DER 53], p. 54, but we prefer here to give only an intuitive justification. First, it is clear that, if i ∈ Ts, we are obliged to stop, so h(i)= F(i). Second, if i ∈ Tc, then the participation cost f(i) is incurred and the mechanism moves to an arbitrary state j with probability pij; since the stopping rule is optimal, the mean value of the reward function is Σj H(J)Pij − f (i). Finally, if i ∉ TS ∪ TC, it is natural to make a decision and then to compare the previous two reward functions.
Let us define
If we know the solution of equation [7.3], then it is easy to construct the set T*. Using the definition of this set we see that, if the mechanism is in a state i ∈ T* at a certain moment, then the maximum mean reward H(i) is equal to F(i), so the best decision is to stop. In order for T* to be an optimal stopping rule we additionally need the mechanism to arrive with probability 1 in a state of T*, independently of its initial state.
For a finite-horizon control problem, for instance for the secretary problem, such that Tc = Ø, the functional equation [7.3] is not satisfied. Nevertheless, denoting by H(i, n) the reward obtained by using an optimal rule in a finite-horizon control problem (note that this reward depends on n), given that the chain starts from state i, we obtain that the values H(i, n) satisfy equation
for 1 ≤ n ≤ N.
There are no general methods for solving equation [7.3]; a usual method for approximating its solution is the well known method of successive approximations. For instance, in the particular case where Tc = Ø, the sequence of successive approximations is given by H(0)(i)= F(i) and
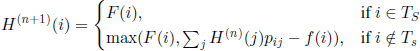
for all 
. It is easy to see that (H(n) (i), n ∈ ) is a decreasing sequence for any i.
The natural question here is: under what conditions, the limit of this sequence is H(i) ? A sufficient condition for this convergence is that the stopping rule is stable. A stopping rule is said to be stable if
where T(n) is the rule T truncated at time n, i.e. the list of all stopping sequences for T(n) contains all the stopping sequences of T of a length shorter than n and, additionally, all the sequences of length n.
In Example 7.1, let T be the rule that imposes to the first player to stop as soon as his reward is greater than a given number α > 0. Obviously, TZ ≥ α but we can easily prove that 
for all n ∈ Consequently, this rule T is not stable.
We want to stress that there is another difficulty even in the case of stable stopping rules. In fact, even if (H(n) (i),n ∈ ) is convergent to H(i), this does not mean that we can determine T* if we know the iterative sets
Nonetheless, this difficulty could be overcome by the procedure of stopping rule improvement, which, in a finite number of steps, provides the optimal stopping rule ([DER 53], pp. 56–57).
7.1.4. Reduction to linear programming
Another method for solving an optimal stopping problem under the hypothesis of Markovian evolution consists of transforming the initial problem in a linear programming problem. In this way, it is possible to use specific softwares that provide solutions for such problems.
For this purpose, we need to replace the optimal stopping problem with an equivalent one that has the following properties:
1) The set Tc is empty.
2) The set 
of non-stopping states is finite; we will denote it by {1, 2, …, M}.
3) The function F is identically zero.
Assuming that these conditions are satisfied, we will consider the following standard linear programming problem. Let x1, …, xm be r.v. subject to the constraints
We consider the linear programming problem
where ai, = δ (i, i0), 1 ≤ i ≤ M, and i0 is the initial state of the Markov chain.
The relation between the two problems is given in the next result.
THEOREM 7.6.− Let 
be a solution of the linear programming problem and
Then, the set T* = T ∪ TS is the solution of the optimal stopping problem and, moreover, we have
A rigorous proof in a more general context can be found in ([DER 53], pp. 57–58,113–114).
What is left to determine are the classes of optimal stopping problems that satisfy properties 1–3 given above.
Basically, any optimal stopping problem that has a solution can be modified such that condition 1 is fulfilled. Let us assume that the initial state of the chain, denoted by i0, does not belong to Tc. We can accept this assumption because our aim is to stop the mechanism unless it is in a state of (Tc)c; but the chain arrives in (Tc)c a.s., due to the existence of the solution of the problem. Note that for any state i ∈ Tc with the property
we certainly have as well
Indeed, in the opposite case, we would have a positive probability that, starting from i0, the chain always remains in Tc, which is in contradiction with the existence of the solution of the problem. In the modified problem, the random mechanism has the state space (Tc)c and the transition probabilities
Clearly,
where
In the reward structure, we restrict the function F to the set (Tc)c and we replace the function f with the function 
, where
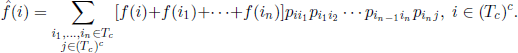
Intuitively, the modified problem derives from the initial one by considering only the moments when the chain is in states of (Tc)c; the participation costs are now mean values of participations paid between two successive passages through states where the stopping is not possible.
We will illustrate these results for Example 7.5. Note that in this case we have
The transition probabilities in the modified problem are
and 
, since f (i)= 0 for all i.
Note that any optimal stopping problem can be modified such that it satisfies property 3. Indeed, it suffices to replace the function f of the initial problem by a function 
given by
and the function F by 
. We can prove that, if T is a stopping rule for the initial problem, then it is also a stopping rule for the modified problem and, additionally, if T is a stable rule, then
where 
is the reward structure of the modified problem and i0 is the initial state of the chain. Consequently, if both problems have stable optimal solutions, then the above equality shows that any optimal stopping rule for one of the problems is also optimal for the other one.
In Example 7.1, since f = 0 and F(i)= i, we have
Thus, for any stable optimal stopping rule T we have 
. Consequently, within the class of stable optimal stopping rules, all the rules are equally good.
Concerning property 2, in some particular cases it is possible, as a first approximation, to have this condition fulfilled by a modification of the state space. More precisely, if (Ts)c is not a finite set, but there exists a state subset T0 ⊂ (Ts)c where f takes values so large that it is reasonable to stop the chain when it is in T0, we consider the set 
is finite, then the modified problem satisfies property 2.
7.1.5. Solving an optimal stopping problem in some special cases
In this section we take into account only problems that satisfy property 3. An arbitrary problem can be reduced to this case using formula [7.8] for defining the function 
; consequently, we no longer consider this function as a participation cost, because it can also have negative values.
A state i will be called favorable if 
. Clearly, if we are in a favorable state, say i, then we make the decision to continue because the reward −
is associated with this decision. The question of stopping is raised only in unfavorable states; it is not compulsory that the best rule imposes stopping when we are in such a state. In fact, it is possible that some unfavorable states lead, with a large probability, to favorable states.
This discussion highlights a particular class of optimal stopping problems with immediate solutions. An optimal stopping problem is called absolutely monotone if
where T* is the set of unfavorable states. If T* satisfies the conditions of a stopping rule (see section 7.1.1), then T* is a solution of the problem.
We will show in the following that the optimal stopping problems described in Examples 7.4 and 7.5 can be reduced to equivalent absolutely monotone problems, for which we will find the solutions.
From Example 7.4 we have
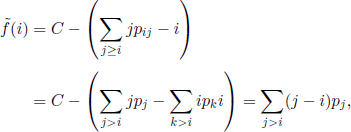
which implies
Consequently, 
and, moreover, pij = 0 for j < i; thus we have an absolutely monotone problem whose solution is
where
The problem of Example 7.5 was modified in section 7.1.4 in order to satisfy property 1. Starting from this formulation and taking into account [7.7], we define
For i ≥ 0 we have
an analogous computation shows that, for i < 0, we have
Consequently, also in this case we obtain 
and pij = 0 for j < i. Finally, we get the solution
where
Another class of optimal stopping problems whose solution is of the form [7.9] is the class of monotone problems, where condition [7.9] is strengthened and we impose an additional condition. More precisely, an optimal stopping problem is called monotone if f (i + 1) ≥ f (i) and the transition probabilities are such that for any non-decreasing function h defined on the state space, the function Σj h(j)pij is also non-decreasing. For such a problem we can prove that T* is given by [7.10], where
and H is the mean value of the reward function in the case of an optimal policy.
Finally, for the problem of Example 7.3 (the secretary problem) we can note that (see section 7.1.4), denoting H((n, x), N − n) by s (n, x), equations [7.1.3] become
If we denote by m* = m* (N) the natural number that satisfies the inequalities
then from [7.11] we easily obtain
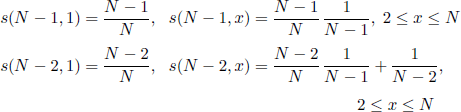
and, in general, for all m ≥ m*,
For m = m* − 1 we have
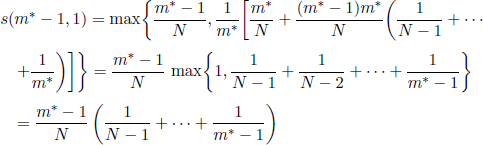
and, for 2 ≤ x ≤ N,
Using [7.11] we infer
We have already seen in section 7.1.2 that an optimal stopping rule imposes the stopping at time m in state y if s(m, y)= F(m, y).Since s(m, y)> 0 for all y = 1, 2, …, m and F(m, y) = 0 for all y > 1, we obtain that the optimal stopping time τ* must be chosen as the smallest m such that Xm = 1 and 
. From [7.12] we see that, for all m < m*, we have s(m, 1) > m/N, so
Additionally,
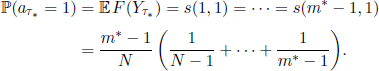
From the definition of m* we note that
which yields
7.2. Renewal with binary decision
7.2.1. Formulation of the problem
We shall start with several examples.
EXAMPLE 7.7.– The probability that a component of a plant will fail between moments n and n + 1 (the time is measured from the moment when the component started to work) is pn, 
;. At any moment 
, there is the possibility to replace this component by a new one. Assume that at time n the component is in a working state. Then, we have to choose between two possible choices. The first one is to replace the component with a new one that will function at time n + 1; this replacement supposes a cost C1. The second decision is to let the component work. If it fails during the time interval (n,n + 1), we are obliged to replace it with a cost C1 + C2 In this case, the new component will be working at time n + 2. So, in both situations,the replacement time is one unit. As this process evolves indefinitely, our problem is to find a replacement policy that leads to a minimum cost per unit of time.
This problem, called the default and replacement problem, was introduced in [DER60].
EXAMPLE 7.8.– The states 1,2, …,M of a plant are arranged in the decreasing order of their functioning capacity. With this notation, state 1 is the perfectly working state, whereas M is the failure state. At any time a check is done in the plant and provides the state i, 1 ≤ i ≤ M, in which the plant is. We assume that state changes are Markovian with known transition probabilities. If at time n the plant is in state j, j ≠ M, we can make the decision to repair it, with a cost C1. In this case, at time n + h1, the plant will be again in state 1. If at time n, the plant breaks down (obviously, it failed during the time interval (n − 1, n)), then its repairing costs C1 + C2 and it will be in state 1 at time n + h2.
Our goal is to find a repairing policy such that the cost per unit of time is minimum.
EXAMPLE 7.9.– We make the assumption that the maintenance cost for a plant of age i (measured in years, for instance) is an r.v. Mi, with a known distribution. At any time n ∈ we can choose between the following two decisions: either we replace the plant by a new one (immediately available), with a cost C, or we keep the plant during the period (n, n + 1), accepting the corresponding cost over that period.
Our goal is the same as in the previous examples.
We can say that a renewal problem with binary decision is characterized by the following:
1) A random mechanism with Markovian evolution, with known transition probabilities, and a state i0, called origin, wherefrom the mechanism starts.
2) A (binary) decision structure and a cost structure specified as follows. We consider three real functions G, g, and h, defined on the state space of the Markov chain, with h taking values only in taking values only in . We assume that, . We assume that, if at time n ∈ the mechanism is in state i, then we can make one of the following two decisions:
(a) Pay the amount G(i), which makes the mechanism come back to origin at time n + h(i). This operation is called renewal, and G(i) and h(i) are called renewal cost and return time to origin, respectively. We assume that the mechanism does not work during the time interval (n, n + h(i)).
(b) Receive the amount g(i) and let the mechanism work.
Like for optimal stopping problems, there are states where we can take only one decision. Let Ur be the state set where the only decision is that of renewal and Uc be the state set where we continue.
The essential difference between a stopping and a renewal problem with binary decision is that, in the latter case, the mechanism works indefinitely, coming back to origin at various time moments. In other words, the stopping is replaced with a renewal. Consequently, we need to choose other optimality criteria than in the classic stopping problem.
In Example 7.7, the state space consists of pairs 
, and (k, −1), where state (k, 1) means that the component is working at time k, whereas state (k, −1) means that it failed at time k. The origin i0 is the state 
. The transition probabilities are
The functions G,g,h are given by g = 0, h = 1, and
In Example 7.8, the state space is {1,2, …, M}, the origin is 1, Uc = Ø, and Ur = {M}. The transition probabilities can be specified from case to case. The functions G,g,h are given by g ≡ 0,
In Example 7.9, the state space is N, the origin is 0, and Uc = Ur = Ø. In fact, the Markov chain is deterministic, the only possible transitions being k → k + 1, k ∈ , where k is the age of our plant. If we put (Mi = r)= pr(i), r ∈ , then
Consequently, −g(k) is the mean maintenance cost over the interval (k,k +1). Note also that h ≡ 0 and G ≡ C.
A renewal policy should specify the states for which we take a renewal decision. In other words, a renewal policy is a state set U that satisfies the conditions: Ur ⊂ U, Uc ⊂ Uc, and
In order to state the optimality criterion, we need to introduce the functions
We obtain that for a state sequence i0, i1, …, in the total cost is C(i0) + C(i1) + · · · + C(in) and the total time in which the mechanism goes through this sequence is t(i0) + t(i1) + · · · + t(in). Consequently, the mean cost per unit of time for this sequence is
If the Markov chain that governs the evolution of the mechanism satisfies rather general conditions, then there exists
and, moreover, this limit is a.s. independent of the trajectory used for its computation and depends only on the considered renewal policy U.
As a consequence, the limit WU will be the optimality criterion. So, we can call an optimal renewal policy a policy U* such that
for any policy U.
7.2.2. Reduction to an optimal stopping problem
The definition of a renewal policy implies that, with probability 1, state i0 occurs an infinitely often. We call cycle of order k the state sequence containing the states between the kth occurrence of i0 and the state just before the (k + l)th occurrence of i0- If Dk is the cost associated with the cycle of order k and Tk is the return time to origin along this cycle, we obtain that for m cycles the mean cost per unit of time is
Since state i0 is recurrent for any policy U, this yields that, with probability 1, 
are sequences of i.i.d. r.v. Applying the strong law of large numbers we get
so
We see that the problem has been reduced to the minimization of an expression involving only quantities related to the evolution of the mechanism during the first cycle. If T1 were not an r.v., then this would be just an optimal stopping problem, with F(i)= −G(i), f (i)=−g(i), and Z = −D1. Anyway, we will show that we can still reduce this problem to an optimal stopping problem.
Let α* = minU WU; we have
with equality for U = U*. This relationship can be written as
Assuming that the first cycle is i0,i1, … ,in,in ∈ U, we get
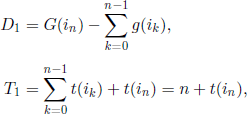
so
Taking into account [7.25] and [7.26], the optimality criterion can be written as
We can note the equivalence between the renewal problem with binary decision written under this form and an optimal stopping problem, if we make the following identifications:
However, obtaining the solution is not straightforward, because we do not know the value of the parameter α*. Thus, we have to introduce a family of optimal stopping problems specified by [7.30], where α* is replaced by a parameter α ∈ 
. For a given value of the parameter , we put β(α)= maxTTZ(α). From equation [7.29], α* is the solution of equation β(α)= 0. For the value α* of parameter α, the solution of the optimal stopping problem parameterized
is also the solution of the renewal problem with binary decision and WU* = a*.
The difficulty of solving this problem obviously consists of determining the number α*.
The above results allow us to solve the problems presented in section 7.2.1.
From Example 7.7 we have
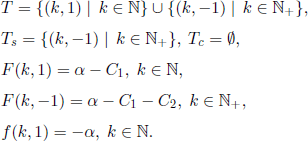
In this case, Formula [7.8] becomes
Under the natural hypothesis Pk+i ≥ Pk, k ∈ , we infer that 
; consequently, we are in the absolutely monotone case and we get
The number α* is determined from equation
where
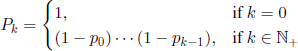
is the probability that the component is still working at time k ∈ .
From Example 7.8 we have
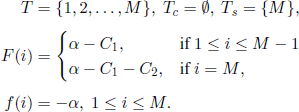
In this case, Formula [7.8] becomes
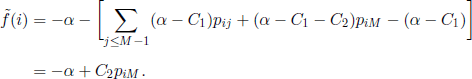
Under the natural hypothesis PiM ≥ Pi+1,M, 1 ≤ i ≤ M − 1, pij = 0 if j < i, 2 ≤ i ≤ M − 1, we get 
and the chain does not make a transition from an unfavorable state to a favorable one; so, we are in the absolutely monotone case and we get
Finally, from Example 7.9 we have
Formula [7.8] becomes
Under the natural hypothesis 
, we are in the absolutely monotone case and we obtain
The number α* is obtained from equation
1. In fact, (Sn , n ∈ ) is a random walk (see section 2.2).
2. We denote by Ac the complement of set A, i.e. Ac = 
A.