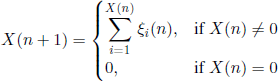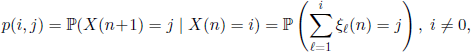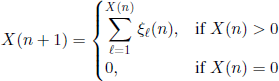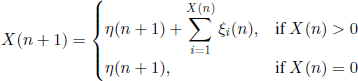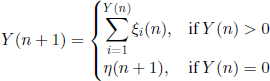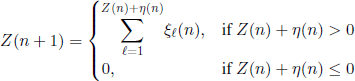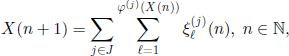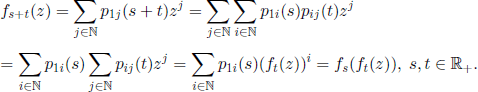Chapter 6
Branching Models
The theory of branching processes focuses on the study of mathematical models related to the increase or decrease of populations of individuals who procreate and replace one another throughout generations, according to rules where chance plays a major role. At the beginning of this theory, the objects under study were married men and the aim was to see how fast surnames disappeared. In recent applications, the study objects are heterozygous subjects carrying a mutant gene, clients in a queueing system, or neutrons in a nuclear reactor, to cite just three main examples. We can also find other examples throughout this chapter.
6.1. The Bienaymé-Galton-Watson model
6.1.1. Historical considerations
The history of the branching process theory represents one of the most exciting pages of probability theory. Just some time ago, we thought we should date back this theory to 1873 when the British biometrician, Francis Galton (1822–1911), who had been for some time been interested in measuring the decline of aristocratic families (in terms of their decrease and extinction), published the famous Problem 4001 in the London newspaper The Educational Times on the 1st of April 1873:
“A large nation, of whom we will only concern ourselves with adult males, N in number, and who each bear separate surnames colonize a district. Their law of population is such that, in each generation, a0 per cent of the adult males have no male children who reach adult life; a1 have one such male child; a2 have two; and so on up to a5 who have five. Find (1) what proportion of their surnames will have become extinct after r generations; and (2) how many instances there will be of the surname being held by m persons.”
Letting pk = ak/100 and removing the restriction k ≤ 5, Galton’s problem can be rewritten as follows.
Let ξi(n), i ∈ ![]() , n ∈
, n ∈ ![]() + be independent r.v. with the same distribution and generating function
+ be independent r.v. with the same distribution and generating function
![]()
Define the r.v. X(N)(n) = X(n), n ∈ N, with the relations X(0) = N and
for all n ∈ ![]() . Find: (1) P(X(r) = 0), r ∈
. Find: (1) P(X(r) = 0), r ∈ ![]() +; (2) the asymptotic behavior of the probabilities P(X(1)(n) = m), m ∈
+; (2) the asymptotic behavior of the probabilities P(X(1)(n) = m), m ∈ ![]() , as n →∞.1
, as n →∞.1
Four months later, the clergyman Henry William Watson (1827–1903) dwelled on this very topic in the same journal (from August 1st, 1873), using generating functions. If we define
![]()
where f0 (z) = z, it is easy to prove by induction that the generating function of X(n) is [fn(z)]N, n ∈ ![]() . Consequently,
. Consequently, ![]() (X(r) = n) = the coefficient of zn in [fn(z)]N , n ∈
(X(r) = n) = the coefficient of zn in [fn(z)]N , n ∈ ![]() . In particular, the probability P(X(r) = 0) of population extinction at the rth generation is equal to [fr(0)]N, r ∈
. In particular, the probability P(X(r) = 0) of population extinction at the rth generation is equal to [fr(0)]N, r ∈ ![]() +. The extinction probability of the population in an arbitrary generation, non-specified, is the limit
+. The extinction probability of the population in an arbitrary generation, non-specified, is the limit
![]()
where q satisfies equation q = f(q).2 This fact is easy to justify: we have qr+i = fr+1(0) = fr(f(0)) ≥ fr(0) := qr, so the sequence (qr, r ∈ ![]() +) is increasing and qr+1 = fr + 1(0) = f(fr(0)) = f{qr); we just have to let r tend to ∞.
+) is increasing and qr+1 = fr + 1(0) = f(fr(0)) = f{qr); we just have to let r tend to ∞.
As equation q = f(q) has always the solution q = 1, Watson was wrong when he concluded that the male line becomes extinct. The correct solution to this problem of surname disappearance was given by the Danish mathematician G. F. Steffensen in 1930; extinction is almost sure for subcritical populations where the mean number ![]() of sons per male adult is strictly less than 1, and also for critical populations, where m = 1; there exists a positive probability 1 − qN of survival for supercritical populations, for which m > 1, where q is the unique solution of the equation q = f(q) in the open interval (0,1). The British geneticist J. B. S. Haldane proposed a similar formulation of this result in 1927, though he provided an incomplete proof of it. For all these historical details and many others, see Kendall’s article [KEN 66]. See also [GUT 95].
of sons per male adult is strictly less than 1, and also for critical populations, where m = 1; there exists a positive probability 1 − qN of survival for supercritical populations, for which m > 1, where q is the unique solution of the equation q = f(q) in the open interval (0,1). The British geneticist J. B. S. Haldane proposed a similar formulation of this result in 1927, though he provided an incomplete proof of it. For all these historical details and many others, see Kendall’s article [KEN 66]. See also [GUT 95].
The above mentioned result was called the critical theorem of Galton-Watson-Haldane-Steffensen.
Thus, it took almost 60 years to obtain the correct solution to the problem of family extinction. This is why it was even more surprising when the Australian mathematicians C. C. Heyde and E. Seneta ([HEY 72b]) discovered a note by I.J. Bienaymé (1796–1878) titled De la loi de multiplication et de la durée des familles, which had been sent to the Société Philomatique of Paris on the 29th of March 1845. (This article is included in [KEN 75a].)
In his article, Bienaymé shows that he knows the correct formulation of the critical theorem: “Si le rapport d’une génération à l’autre, ou la moyenne du nombre des enfants mâles qui remplaceront le nombre des mâles de la génération précédente, était strictement plus petite que l’unité, on concevrait sans peine que les familles s’éteignissent par la disparition des membres qui les composent. Mais l’analyse montre de plus que quand cette moyenne est égale à l’unité, les familles tendent à disparaître, quoique moins rapidement. Ainsi, par exemple, s’il y avait des chances égales pour que tout homme eût deux garçons ou n’en eût pas (ce qui donnerait un garçon reproduit pour un homme venu au monde, un peu plus de deux garçons ou de quatre enfants par mariage), de cent familles il n’en subsisterait probablement que cinq à la 35e génération, soit, au bout de 11 à 12 siècles, en comptant comme Hérodote trois générations par siècle. A la longue toutes les familles s’éteindraient, très probablement du moins.”3
This analysis implies that the mean mentioned above should be greater than unity, since there have been about 200 generations along the historical time. But, as more than just one people disappeared from the earth, and various races become extinct every day, and at the same time it is highly improbable for our planet to be more populated than in previous times, we must draw the following remarkable conclusion: the ratio of generations cannot have the same value, so it would sometimes go beyond unity and sometimes it would fall below it. Thus, one population cannot remain in the same steady state that the first authors of mortality tables took for granted in their computations. This proves once again that those computations cannot possibly be exact, and that this inevitable inexactness has pervaded all the subsequent ideas related to lifetimes ever prompted by these calculations. It is also a new example of a mean value at which a large number of observations cannot provide any stability. At this point, Bienaymé recalls that he showed that Poisson had not actually proved what he thought to be a law governing the large numbers.
“L’analyse montre aussi clairement que le rapport moyen étant supérieur à l’unité, la probabilité de destruction des familles ne peut plus se changer en certitude avec l’aide du temps. Elle ne fait que s’approcher d’une limite finie, assez facile à calculer, et qui offre ce caractère singulier d’être donnée par celle des racines de l’équation (où l’on fait infini le nombre des générations), qui ne convient pas à la question quand le rapport moyen est inférieur à l’unité.”4
It is clear that the last phrase concerns the equation f(qr) = qr+1 (see above). However, Bienaymé gives no proof and his reasoning allows nothing but suppositions on our part. His communication ends with the promise that a continuation would be eventually published: “M. Bienaymé développe diverses autres considérations que les éléments de la question lui ont suggérées, et qu’il se propose de publier bientôt dans un mémoire spécial.”5 In the already mentioned article of Kendall ([KEN 75a]), the author tried to reproduce the possible line of reasoning of Bienaymé and thought that the latter might have published his solution in a French journal of the time and that, consequently, we could very well find this publication one day.
However, the outcome of this enigma seems to be quite different. Losing hope of ever finding the “special issue”, Bernard Bru [BRU 91] had the idea of tracing possible formulations of Bienaymé’s and perhaps the proof of his theorem in the works of his contemporaries. It turned out indeed that both the formulation of the problem and the proof are reproduced in a less known work by A. A. Cournot (1801–1877) titled De l’origine et des limites de la correspondance entre l’algèbre et la géométrie, published in 1847 by Hachette, Paris, and reedited by Vrin, Paris, in 1999 (see pages 83–86). It looks credible that the proof given by Cournot is that of Bienaymé, though this is not explicitly mentioned; it coincides, even in terms of notations, with that proposed by Kendall ([KEN 75a], p. 233).
At this point, it is worth dwelling a little on the personality and the work of Irénée-Jules Bienaymé. Thanks to the book I. J. Bienaymé: Statistical Theory Anticipated, Springer, New York, 1977, by C. C. Heyde and E. Seneta, Bienaymé appears to have been ahead of his time due to his profound ideas. Overshadowed by his great contemporaries, Laplace, Gauss, Poisson, Cauchy, Bertrand and disadvantaged by the style of his works, which are too wordy, but at the same time too concise in terms of mathematics, Bienaymé is little known today and his own contributions are sometimes wrongly attributed to more recent authors. In addition to the correct formulation of the critical theorem, we owe to him the following: (a) a test for checking the random character of a sequence of observations; (b) the Bienaymé-Tchébycheff inequality, based on a simple reasoning, which continues to be used today; (c) a first formulation of the notion of sufficient statistics and the emphasis placed on its importance; (d) the chi-square distribution; (e) a first description of the properties of the cumulants and of their use in probability theory. For more detailed information, see [BRU 91, BRU 92, GUT 95, SEN 98].
To conclude, we should mention that a Galton problem for a two-sex population was studied by Hull [HUL 98].
6.1.2. Some elementary results
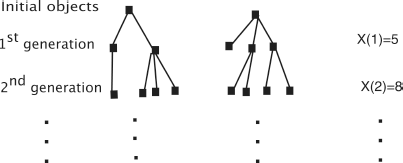
It is clear that the sequence of r.v. X(N) = (X(n), n ∈ ![]() ) defined in the preceding section can be seen as describing the evolution of the size of a population of objects (organisms, bacteria, elementary atomic particles, etc.) that multiply after the following rules (see Figure 6.1): each of the N initial objects multiplies independently of each other and, at the end of their lives
) defined in the preceding section can be seen as describing the evolution of the size of a population of objects (organisms, bacteria, elementary atomic particles, etc.) that multiply after the following rules (see Figure 6.1): each of the N initial objects multiplies independently of each other and, at the end of their lives
(considered to be, for the sake of simplicity, of fixed duration equal to one unit of time), they produce a random number of descendants, according to a given probability distribution (pk, k ∈ ![]() ), i.e. the probability of producing k descendants is pk, k ∈
), i.e. the probability of producing k descendants is pk, k ∈ ![]() . The offspring of the initial objects form the first generation. The objects of this generation act exactly as the initial objects and give birth to the second generation, etc. At any moment, the number of the descendants of an object does not depend either on the other existing objects or on the history of the process.
. The offspring of the initial objects form the first generation. The objects of this generation act exactly as the initial objects and give birth to the second generation, etc. At any moment, the number of the descendants of an object does not depend either on the other existing objects or on the history of the process.
From relations [6.1] we see that X(N) = (X(n), n ∈ ![]() ) is a homogenous Markov chain with state space included in
) is a homogenous Markov chain with state space included in ![]() , initial distribution concentrated at state N, and transition probabilities
, initial distribution concentrated at state N, and transition probabilities
and p(0, 0) = 1. This last relation shows that, if X(n) = 0, then X(n + k) = 0 for all k ∈ N. Consequently, 0 is an absorbing state and the population extinction means the absorption into 0.
By the Bienaymé-Galton-Watson model (from now on B-G-W model) we mean relations [6.1] together with the Markov chain X(N) = (X(n), n ∈ ![]() ). We initiate the study of this model by investigating more precisely several issues discussed in the previous section.
). We initiate the study of this model by investigating more precisely several issues discussed in the previous section.
PROPOSITION 6.1.– (H. Watson) The generating function of X(n) is [fn(z)]N.
PROOF.– This fact is obviously true for n = 0. Let f(n) be the generating function of X(n), n ∈ ![]() . From [6.1] we obtain that the generating function of X(n + 1) conditioned on (X(n) = k) is [f(z)]k. Thus
. From [6.1] we obtain that the generating function of X(n + 1) conditioned on (X(n) = k) is [f(z)]k. Thus
![]()
Since f(0)(z) = zN = [f(0)]N , we obtain by induction that f(n)(z) = [f(n)(z)]N , n ∈ ![]() .
.
COROLLARY 6.2.– The n-step transition probabilities of the Markov chain (X(n),n ∈ ![]() ) are given by the following relationships
) are given by the following relationships
![]()
COROLLARY 6.3.– (Additive property) The chain X(N) that starts from state X(0) = N and has the transition probabilities [6.2] is the sum of N copies of the chain X(1) that starts from state X(0) = 1 and has the same transition probabilities [6.2].
So, without loss of generality, we can study only the case N = 1. For this reason, unless otherwise stated, we assume in the following that N = 1.
Corollary 6.4.– Let us introduce ![]()
![]()
![]() (here and in the following, f′(l), f″(l), etc. are left derivatives of the generating function f at point 1). Then
(here and in the following, f′(l), f″(l), etc. are left derivatives of the generating function f at point 1). Then ![]() [X(n)] = mn and
[X(n)] = mn and
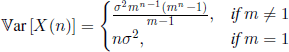
for all n ∈ ![]() .
.
PROOF.– We have
![]()
Differentiating two times relation ![]() , and taking into account that
, and taking into account that ![]() , we obtain
, we obtain
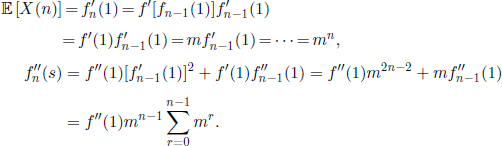
Consequently,

A B-G-W model will be called (see section 6.1.1) subcritical, critical, or supercritical according as m < 1, m = 1 or m > 1. From Corollary 6.4 we infer that, for a subcritical model the variance of X(n) tends to 0 as n → ∞, for a critical model the variance of X(n) is increasing proportionally to n, whereas for a supercritical model the variance of X(n) is exponentially increasing with n (see also the formulation of the critical theorem in section 6.1.1 and its proof in section 6.1.4).
6.1.3. A fundamental example
Basically, there exists only one case when the computation of the iterates fn(z) can be done explicitly. This is the homographic case, where
![]()
with
with
![]()
Noting
![]()
we immediately see that f(z0) = z0 and
Taking into account that
![]()
for any u and v, and letting u = z0 and v = 1, we obtain
![]()
and, iterating this relation, we get
![]()
From this relation, for m ≠ 1 (if m = 1, then z0 = 1) we obtain
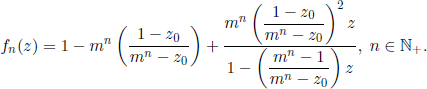
If m = 1, then b = (1 −c)2 and
![]()
We can easily check that in this case
6.1.4. Extinction probability: critical theorem
We will prove here the critical theorem formulated by Bienaymé (see section 6.1.1). Let us denote by q the extinction probability of the population, i.e.

Since X(u) = 0 implies X(v) = 0 for all v ≥ u, we have (X(1) = 0) U … U (X(n) = 0) = (X(n) = 0) for all n ∈ N+, so
![]()
We will exclude the trivial case where p1 = 1, i.e. f(z) = z. This means that either / is linear with /(0) > 0, or / is strictly convex on (0,1) (f″(x) > 0 for 0 < x < 1). In the case where f(z) = z, we have q = 0, since X(n) = 1 for all n ∈ class="equation">![]() .
.
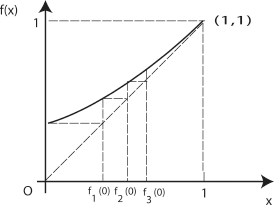
THEOREM 6.5.– (Bienaymé-Galton-Watson-Haldane-Steffensen) If m < 1, then q = 1. If m > 1, then the extinction probability q is the unique solution
in [0,1) of the equation x = f{x).
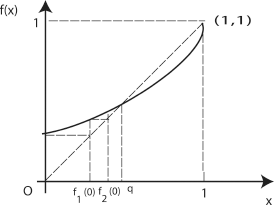
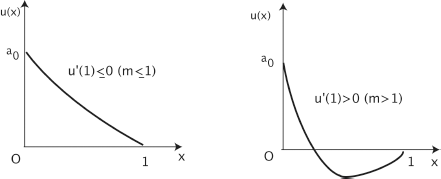
PROOF.– Figures 6.2 and 6.3 illustrate the following reasoning.
We have already seen that
Since fn+1(0) = f(fn(0)), we have q = f(q) and 0 ≤ q ≤ 1.
If m < 1, then /(0) > 0 and f′(x) ≤ f′(1) = m ≤ 1 for all x ∈ [0,1]. Then, the mean value theorem shows that f(x) > x for all x ∈ [0,1], so we must have q = 1.
If m > 1, then by the same theorem we obtain that f(x) < x for values of x close enough to 1. The strict convexity of / (in this case / cannot be linear) guarantees the uniqueness of the solution of equation f(x) = x in [0,1). It remains to show that q ≠ 1. If we had q = 1, then fn(0) would converge to 1 as n → ∞ and we would have fn+1 (0) = f(fn(0)) < fn(0) for large enough values of n. But this is in contradiction with [6.5], so we have q ≠ 1.
Remark. We can prove (Figures 6.2 and 6.3 are once again relevant!) that if x ∈ [0, g), then fn(z) ↑ q as n → ∞, whereas if x ∈ (q, 1), then fn (z) ↓ 1 as n → ∞. (It is clear that if x = q or x = 1 then fn (x) = x,n ∈ ![]() +.) In the first case, the convergence is uniform with respect to x because fn(0) ≤ fn(x) ≤ q. So, fn{x) → q as n → ∞ for all 0 ≤ x ≤ 1. Moreover, if z is a complex number with z < 1, then
+.) In the first case, the convergence is uniform with respect to x because fn(0) ≤ fn(x) ≤ q. So, fn{x) → q as n → ∞ for all 0 ≤ x ≤ 1. Moreover, if z is a complex number with z < 1, then
![]()
so fn(z) → q as n → ∞ for |z| < 1. This procedure of extending results which are valid for a real argument to a complex argument is common in the theory of branching processes.
From relation limn→∞ fn(x) = q, that is true for all x ∈ [0,1), we obtain6
In fact, we can prove a stronger result. We already know that P(limn→∞ X(n) = 0) = ![]() (X(n) = 0 for a value n ∈
(X(n) = 0 for a value n ∈ ![]() +) = q. The complement probability 1 − q can be interpreted as follows.
+) = q. The complement probability 1 − q can be interpreted as follows.
PROPOSITION 6.6.– If p1 ≠ 1, then ![]() (limn→∞ X(n) = ∞) = 1 − q.
(limn→∞ X(n) = ∞) = 1 − q.
PROOF.– If q = 1, there is nothing to prove.
If q ∈ (0,1), then the convexity of the function f(x) − x implies the inequality f′(q) < 1 (see once again, Figure 6.3). By induction we get ![]() , and we can write
, and we can write
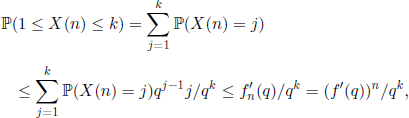
for all ![]() . The Borel-Cantelli theorem shows that, with probability 1, X(n) cannot take an infinity number of values in the interval [l,k], whatever the fixed positive integer k is. Consequently, if the sequence (X(n),n ∈
. The Borel-Cantelli theorem shows that, with probability 1, X(n) cannot take an infinity number of values in the interval [l,k], whatever the fixed positive integer k is. Consequently, if the sequence (X(n),n ∈ ![]() ) does not contain 0 (in the opposite case, we obviously have limn→∞ X(n) = 0), then this sequence converges to ∞, such that
) does not contain 0 (in the opposite case, we obviously have limn→∞ X(n) = 0), then this sequence converges to ∞, such that
![]()
If q = 0, then p0 = 0 and the sequence (X(n), n ∈ ![]() ) is increasing. Let X(∞) be the limit of this sequence. Note that the event (X(∞) = k) occurs if and only if the following event occurs
) is increasing. Let X(∞) be the limit of this sequence. Note that the event (X(∞) = k) occurs if and only if the following event occurs
![]()
However, from [6.6] we get
![]()
We conclude that X(∞) = ∞ with probability 1, i.e. P(limn→∞ X(n) = ∞) = 1 = 1 −q.
Harris ([HAR 63], ch. 1) considers that the instability revealed by relation [6.6] and Proposition 6.6 is in contradiction with the behavior of biological populations which tend to an equilibrium with respect to their environment (even if, obviously, there can be some fluctuations). He concludes that the B-G-W model does not describe in a satisfactory manner the evolution of most biological populations. Jagers ([JAG 75], p. 70) has a more nuanced position, namely he considers that the B-G-W model illustrates a fundamental property of the reproduction process of biological populations: in the absence of external influence, these populations either explode, or become extinct; stability is a result of the competition between species and of certain subtle influences of the environment. These considerations are at the origin of some generalization of B-G-W model that we will investigate further on.
6.1.5. Asymptotic formulas for the extinction probability
The following results that we present are concerned with the rate of convergence of fn(0) to q.
PROPOSITION 6.7.– (S. Karlin and J. McGregor) If m>1 and p0 > 0, or if m < 1 and Σk∈![]() Pk k log k < ∞, then there exists a sequence (ar, r ∈
Pk k log k < ∞, then there exists a sequence (ar, r ∈ ![]() +) with a1 > 0 that depends on the generating function f, such that, for values of n large enough,7 we have
+) with a1 > 0 that depends on the generating function f, such that, for values of n large enough,7 we have
![]()
If m <1 and ![]() k log k = ∞, then
k log k = ∞, then
![]()
PROPOSITION 6.8.– (A. N. Kolmogorov) If m = 1, then
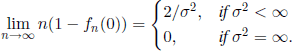
For the proofs of Propositions 6.7 and 6.8 we can see [ATH 72] (pp. 19–23 and 38–42). See also [SEN 74a].
In fact, Proposition 6.7 is a consequence of the properties (thoroughly studied by S. Karlin and J. McGregor) of the functions
![]()
where γ = f′(q) when m = f′(l) ≠ 1. We can prove that limn→∞ ϒ−n [fn (x) − q] = Q(x) exists for 0 ≤ x ≤ 1 and that Q(x) = 0 if and only if m < 1 and Σk∈N Pk k log k = ∞; otherwise, Q(x) ≠ 0, x ≠ q, Q(q) = 0, Q′(x) > 0 and limx→q Q′(x) = 1. Spataru [SPA 76] proved that the series Σn∈N|Q n (x) − Q(x)| is convergent if m > 1; when m < 1 and Σk∈N pk k log k < 1 the convergence of the series is equivalent to Σk∈N pk k(log k)2 < ∞. If m < 1 and Σk∈N pk k log k < 00, then Q is the unique solution of the functional equation Q(f(x)) = ϒQ(x), 0 < x < 1, that satisfies the conditions Q(q) = 0 and limx→q Q′(x) = 1. Iterating this functional equation we obtain Q{fn(x) = ϒnQ(x), so, denoting by P the inverse of Q, we get fn(x) = P(ϒnQ(x)), n ∈ ![]() +. This last relation explains the presence of powers of 7 in the text of Proposition 6.7.
+. This last relation explains the presence of powers of 7 in the text of Proposition 6.7.
Remark. Without excluding the case m < 1 and Σk∈![]() Pk k log k = ∞, Lambotte [LAM 78] showed that, if m ≠ 1 and q > 0 (inequality that is equivalent to p0 > 0), then for all X0 ∈ [0, q) the limit
Pk k log k = ∞, Lambotte [LAM 78] showed that, if m ≠ 1 and q > 0 (inequality that is equivalent to p0 > 0), then for all X0 ∈ [0, q) the limit
![]()
exists, is finite and non-identically zero. Except for the case m < 1 and ![]() , we have Q(x,x0) = Q(x)/Q(x0).
, we have Q(x,x0) = Q(x)/Q(x0).
In the case of a homographic generating function (see section 6.1.3) it is easy to verify Propositions 6.7 and 6.8.
First, if m > 1, we have zo = q, so
![]()
by Equality [6.4], so f′(q) = 1/m and we get
![]()
Second, for m < 1 we have
![]()
Note that in this case z0 > 1.
Finally, if m = 1, we have
![]()
so
![]()
We see immediately that in this last case we have σ2 = f″(l)+m−m2 = 2bc/ (1 − c)3 = 2c/(l − c), so 2/σ2 = (1 − c)/c.
The reader can easily check that the function Q(x) = lirrin^oo ϒ−n (fn (q) − q) is given by formulas
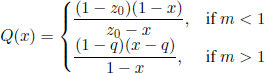
for 0 < x < 1.
6.1.6. Bounds for the extinction probability
For a supercritical B-G-W model the extinction probability q is < 1. Intuitively, it is very clear that, if m > 1 is close to 1, the same result has to hold for q. The results presented below specify this intuition.
For notational simplicity, let us put f″(1) = b, f′″(1) = c.
PROPOSITION 6.9.– (Quine [QUI 76b]) If b < ∞, then
where equality holds if and only if c = 0 (i.e. pk = 0 for k ≥ 3).
PROPOSITION 6.10.– (Daley and Narayan [DAL 80]) If b < ∞, then 1 − q ≥ m(m − l)/b.
We will assume in the following that b < ∞ and 0 < c ≤ ∞.
PROPOSITION 6.11.– (Daley and Narayan [DAL 80]) We have
If 8(m − 1)c < 3b2 (this condition implies that m ≤ 3,2), then
The proofs of Propositions 6.9 and 6.11 are based on the representation of the generating function f under the form
![]()
respectively
![]()
where b(z)/b and c(z)/c are probability generating functions.
The following theorem presents the best bounds for q in terms of the first three moments of the offspring distribution.
THEOREM 6.12.– The bounds of q defined below are the best possible.
(i) If m > 1, then 0 ≤ q < 1.
(ii) (Turnbull [TUR 73]) If m > 1 and b < ∞, then 0 ≤ q ≤ qmax ≤ qmax(m, b), where qmax is the root in (0,1) of equation qmax = fm,b{qmax) with fm,b(x) = 1 – Pj − Pj+1 + Pjxi + Pj+ 1xi+1, j =integralpart of 1 + b/m, pj = m − b/j, pj+i = (b − m(j − l))/(j + 1) (obviously, Pj+1 = 0 if b/m is integer).
(iii) (Narayan [NAR 81b]) If m > 1 and b,c < ∞, then qmin = qmin(m, b, c) ≤ q ≤ qmax(m, b), where, letting k = integral part 2+c/b, qmin = 0 when 1 − m + ((2k −1)b − c)/k(k + l) ≤ 0 and 0 < qmin = fm,b,c(qmin) < 1 in the opposite case, with 1 − P1 − Pk − Pk+1 + P1x + Pkxk + pk+1xk+1, p1 = m − 2b/k + c/k(k − 1), pk+1 = (c − (k − 2)b)/k(k + 1).
We see from Theorem 6.12 that the bounds [6.7], [6.8], and [6.9] cannot be improved. In fact, if j = 1, the bound [6.7] coincides with 1 − qmax; if j = 2, the bound in [6.8] also coincides with 1 − qmax; finally, if j = 3, the bound in [6.9] coincides with 1 − qmin.
Obviously, for particular classes of generating functions, there exist better bounds than those in [6.7], [6.8], or [6.9]. Thus, Brook [BRO 66] obtained the bound
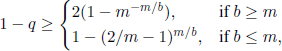
which is better than the bound in [6.7] if m < b (because 2(1 − m−m/b) > 2(m − l)/b when m < b). For instance, for the generating function em(z−l) of the Poisson distribution with m > 1, we have m < b = m2. Other examples can be found in [NAR 81a].
Choosing other parameters instead of the moments, the optimal bounds of q will be modified accordingly. Let us present an example.
THEOREM 6.13.– (Heyde and Schuh [HEY 78]) Let ![]() be a probability generating function satisfying the following conditions: po ≥ δ and 0 < m ≤ k(1 − δ)+ η, where 0 < δ < 1, 0 ≤ η < 1 − δ and k ∈
be a probability generating function satisfying the following conditions: po ≥ δ and 0 < m ≤ k(1 − δ)+ η, where 0 < δ < 1, 0 ≤ η < 1 − δ and k ∈ ![]() +. The best lower bound of q is qmin = qmin(k, δ, η), the root in [0,1) of the equation
+. The best lower bound of q is qmin = qmin(k, δ, η), the root in [0,1) of the equation
![]()
6.1.7. A decomposition of supercritical models
In the supercritical case m > 1, the extinction probability q is positive if and only if p0 = f(0) > 0. It is convenient sometimes to assume that q = 0. An artifice owed to T. E. Harris and B. A. Sevastyanov (see [SCH 82a]) ensures that there is no loss of generality due to this assumption. For /(0) > 0 let us define
![]()
It is clear that ![]() is a probability generating function with
is a probability generating function with ![]() (0) = 0 and
(0) = 0 and ![]() ′(l) = f′(1) = m. We can easily verify that the iterates of
′(l) = f′(1) = m. We can easily verify that the iterates of ![]() are
are
![]()
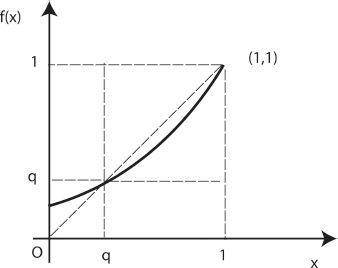
The graph of ![]() over [0,1] can be obtained from that of f (see Figure 6.4) by a homothety of center (1,1) and ratio 1/(1 − q). The square with opposed vertices (q, q) and (1,1) is then transformed into the unit square, while the graph of
over [0,1] can be obtained from that of f (see Figure 6.4) by a homothety of center (1,1) and ratio 1/(1 − q). The square with opposed vertices (q, q) and (1,1) is then transformed into the unit square, while the graph of ![]() over (q, 1) is transformed into the graph of f over [0,1].
over (q, 1) is transformed into the graph of f over [0,1].
Let X = (X(n),n ∈ ![]() ) and
) and ![]() = (
= (![]() (n),n ∈
(n),n ∈ ![]() ) be B-G-W models associated with the generating functions f and
) be B-G-W models associated with the generating functions f and ![]() , respectively. Since
, respectively. Since ![]() (0) = 0,
(0) = 0,
we have ![]() (= the extinction probability of
(= the extinction probability of ![]() ) = 0. Consequently, it is enough to prove properties of X only in the case q = 0, when these properties are also true for
) = 0. Consequently, it is enough to prove properties of X only in the case q = 0, when these properties are also true for ![]() , and conversely.
, and conversely.
What is the probabilistic interpretation of ![]() in relation with X? Let A = {ω | X(n,ω) → ∞ as n → ∞} and B = Ac = {ω | X(n,ω) = 0 for an n ∈
in relation with X? Let A = {ω | X(n,ω) → ∞ as n → ∞} and B = Ac = {ω | X(n,ω) = 0 for an n ∈ ![]() +}. We have P(A) = 1 − q and
+}. We have P(A) = 1 − q and ![]() (B) = q. Let us define X1 (n, ω) = 0 if ω ∈ B and X1 (n, ω) = the number of objects (≤ X(n, ω)) from the nth generation of X that have an infinite line of descendants, if ω ∈ A. We can prove that (see [ATH 72], pp. 48–50), under the conditional probability
(B) = q. Let us define X1 (n, ω) = 0 if ω ∈ B and X1 (n, ω) = the number of objects (≤ X(n, ω)) from the nth generation of X that have an infinite line of descendants, if ω ∈ A. We can prove that (see [ATH 72], pp. 48–50), under the conditional probability ![]() A(·) =
A(·) = ![]() (·)/
(·)/![]() (A), the sequence (X1(n),n ∈
(A), the sequence (X1(n),n ∈ ![]() ) is a B-G-W model with generating function
) is a B-G-W model with generating function ![]() . Concerning the sequence (X2(n),n ∈
. Concerning the sequence (X2(n),n ∈ ![]() ), where X2(n) = X(n) − X1(n), under the conditional probability
), where X2(n) = X(n) − X1(n), under the conditional probability ![]() B, this is a B-G-W model with generating function
B, this is a B-G-W model with generating function ![]() (z) = q−l f(qz), |z| ≤ 1. Note that
(z) = q−l f(qz), |z| ≤ 1. Note that ![]() ′(l) = f′(q) < 1, so this is a subcritical model (for which the extinction probability is 1). The graph of
′(l) = f′(q) < 1, so this is a subcritical model (for which the extinction probability is 1). The graph of ![]() over [0,1] can be obtained from that of f (see Figure 6.4) through a homothety of center (0, 0) and ratio 1/q. The square with opposed vertices (0, 0) and (q, q) is transformed into the unit square, while the graph of f over [0, q] is transformed into the graph of
over [0,1] can be obtained from that of f (see Figure 6.4) through a homothety of center (0, 0) and ratio 1/q. The square with opposed vertices (0, 0) and (q, q) is transformed into the unit square, while the graph of f over [0, q] is transformed into the graph of ![]() over [0,1).
over [0,1).
It is thus justified to speak about a true “decomposition” of the supercritical model with q > 0 into the sum of two models, a supercritical one with the extinction probability equal to 0, and a subcritical one with extinction probability equal to 1.
6.1.8. Extinction time
The extinction time v is defined as the absorption time into 0 for the Markov chain (X(n),n ∈ ![]() ), i.e. it is the smallest integer n ∈
), i.e. it is the smallest integer n ∈ ![]() + such that X(n) = 0. In other terms, we have v = k if and only if X(k − 1) > 0 and X(k) = 0. The extinction time is nothing but the number of generations up to population extinction. The distribution of v is given by the relations
+ such that X(n) = 0. In other terms, we have v = k if and only if X(k − 1) > 0 and X(k) = 0. The extinction time is nothing but the number of generations up to population extinction. The distribution of v is given by the relations
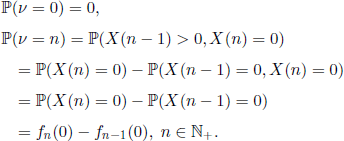
Letting v = ∞ in the case when the population does not disappear (so it explodes−see Proposition 6.6), we have
![]()
We have ![]() 0 in the supercritical case m > 1 only if, obviously, the moments of ν of any order are infinite. In the subcritical case m < 1, by Proposition 6.7, the tail of the distribution of ν, i.e.
0 in the supercritical case m > 1 only if, obviously, the moments of ν of any order are infinite. In the subcritical case m < 1, by Proposition 6.7, the tail of the distribution of ν, i.e. ![]() n ∈
n ∈ ![]() , converges to 0 at least exponentially. Consequently, since
, converges to 0 at least exponentially. Consequently, since
![]()
in this case the moments of v of any order are finite. The most difficult and the most interesting case is the critical one m = 1. A sufficient condition to have ![]() since, using Proposition 6.8, we have
since, using Proposition 6.8, we have ![]() (ν > n) ~ 2/(nσ2) as n → ∞. The general case is solved by the following result.
(ν > n) ~ 2/(nσ2) as n → ∞. The general case is solved by the following result.
THEOREM 6.14.– (H. Breny, G. E. H. Reuter, E. Seneta) In the case m = 1, the integral ![]() dx and the mean
dx and the mean ![]() v are simultaneously Jo finite or infinite.
v are simultaneously Jo finite or infinite.
The proof can be found in ([IOS 73], I, p. 98).
The total number τ of objects existing up to the extinction time has a certain interest. We have
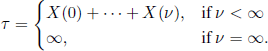
Let ![]() . We can prove the following result.
. We can prove the following result.
THEOREM 6.15.– (H. Hawkins, S. Ulam) If p0 > 0, then the generating function c is the unique solution of the functional equation
such that 0 < c(x) ≤ 1 for 0 < x ≤ 1. We have
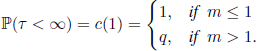
It is clear that, if p0 = 0, then q = 0 and ![]() .
.
It is possible to solve the functional equation [6.10] only in a small number of cases, for example if / is a second degree polynomial or a homographic function. However, we have to note that in fact, according torn ≤ 1 or m > 1, c(x) is the inverse function of x/f(x) or the product of q and the inverse function of qx/ f(qx), x ∈ (0,1] (see [JAG 75], p. 39). The functional equation satisfied by c allows to easily compute the mean and the variance of r. We immediately obtain that ![]() (τ) = 1/(1 − m) and Var (τ) = σ2/(l − m)3 if m < 1. It is clear that
(τ) = 1/(1 − m) and Var (τ) = σ2/(l − m)3 if m < 1. It is clear that ![]() (τ) = ∞ if m = 1.
(τ) = ∞ if m = 1.
Keeping in mind the previous remarks, the following result is even more surprising. Its proof can be found in ([JAG 75], p. 40).
THEOREM 6.16.– (M. Dwass) We have

More generally, the probabilities ![]() corresponding to the case X(0) = r are given by the relations
corresponding to the case X(0) = r are given by the relations
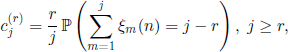
and ![]() . (Obviously, we have
. (Obviously, we have![]()
In particular,
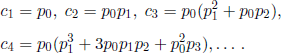
For the study of the behavior of the B-G-W model, conditioned on the event (τ = n) as n → ∞, we can look at [KEN 75b, KOL 78a].
The extinction time v is essentially used in one of the procedures aimed at eliminating the instability of the B-G-W model (see relation [6.2] and Proposition 6.6).
Basically, there are two procedures meant to eliminate this instability. The first one, that we will present below, is to condition on survival without explosion. The second procedure is the introduction of an “immigration” component (see section 6.2.3).
The probability generating function of X(n), conditioned on survival without explosion (obviously, we assume that q > 0), is
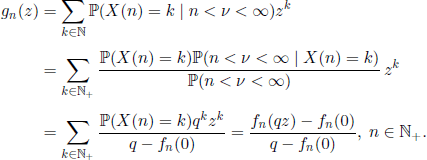
Note that in the above computations we used the fact that the probability P(n < v < ∞ | X(0) = k) coincides with ![]() , which is the extinction probability of a B-G-W model starting with k objects, i.e. qk.
, which is the extinction probability of a B-G-W model starting with k objects, i.e. qk.
Let us note that in the subcritical case m < 1 or in the critical case m = 1, we have {n < v < ∞} = {v > n} = {X(n) ≠ 0}, because the explosion, i.e. the event {v = ∞}, is impossible. In this case we have
![]()
THEOREM 6.17.– (i) (F. Papangelou, E. Seneta) If q > 0, then ![]() , exists. If m = 1, we have
, exists. If m = 1, we have ![]() , then b is a probability generating function. This is the unique probability generating function vanishing at 0 and satisfying the functional equation
, then b is a probability generating function. This is the unique probability generating function vanishing at 0 and satisfying the functional equation
with ![]() .
.
(ii) (J. P. Lambotte) If q>0 and m ≠ 1, then we have the relations
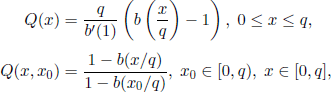
where the functions Q and Q( ., X0) were defined in section 6.1.5.
COROLLARY 6.18.– Let q > 0 and m ≠ 1.
(j) (E. Seneta, D. Vere-Jones) We have b′(l) = ∞ if and only if m < 1 and ![]() .
.
(jj) (K. B. Athreya, P. E. Ney) If m > 1, then b is analytic on the disk ![]() .
.
(jjj) (K. B. Athreya, P. E. Ney) If m > 1 or if m < 1 and ![]() , then the coefficient a1 from Proposition 6.7 is equal to l/b′ (1) = −Q(0)/q.
, then the coefficient a1 from Proposition 6.7 is equal to l/b′ (1) = −Q(0)/q.
(jv) (J. P. Lambotte) For all X0 ∈ [0, q] we have
For the proof, we can see ([ATH 72], I. 8 and I. 12) and [LAM 78].
Remarks. 1. The existence of the function b in the subcritical case m < 1 was first proved by A. M. Iaglom, assuming that σ2 < ∞. For this reason, the mean b′(1) of the probability distribution (bk,k ∈ ![]() +) was called the Iaglom constant. Evans [EVA 78] showed that b′(1) ≤ σ2/(m − m2) if m < 1 and a2 < ∞. This is a strict upper bound because it is reached only by the generating function f(z) = 1 − m + mz, |z| ≤ 1 and for no other.
+) was called the Iaglom constant. Evans [EVA 78] showed that b′(1) ≤ σ2/(m − m2) if m < 1 and a2 < ∞. This is a strict upper bound because it is reached only by the generating function f(z) = 1 − m + mz, |z| ≤ 1 and for no other.
2. In the subcritical case m < 1, the convergence of the series ![]() is equivalent to the existence of the finite mean
is equivalent to the existence of the finite mean ![]() for all α > 1. This result has to be compared to (jj) of Corollary 6.18. See also [BAG 82], where we can find other results associating the existence of certain characteristics of the distribution
for all α > 1. This result has to be compared to (jj) of Corollary 6.18. See also [BAG 82], where we can find other results associating the existence of certain characteristics of the distribution ![]() with the existence of the corresponding characteristics of the distribution
with the existence of the corresponding characteristics of the distribution ![]() .
.
3. The practical determination of function b is not generally possible, despite the apparent simplicity of the functional equation [6.11]. It is easy to check that for a homographic generating function f (see section 6.1.3) we have
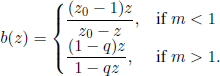
4. Combining (ii) of Theorem 6.17 with (jv) of Corollary 6.18, we infer that
It is easy to verify that [6.12] and [6.13] imply
![]()
respectively
![]()
In the critical case m = 1, Theorem 6.17 shows that gn(z) converges to 0 as n → ∞ for all z such that z < 1. In other words, the conditioning on survival leads to explosion. We can have an idea of the order of magnitude of this explosion by the following simple computation:
![]()
so
![]()
and, with Proposition 6.8, we obtain
![]()
Thus, the conditional mean increases linearly with n. This fact suggests the study of the random variable X(n)/n conditioned on survival (X(n) ≠ 0). We obtain the following result.
THEOREM 6.19.– (A. M. Iaglom) If m = 1 and p1 ≠ 1, then we have
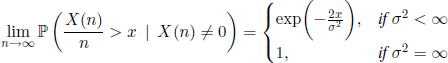
for all ![]() .
.
The proof of this theorem (proved by Iaglom under the superfluous hypothesis f′″(l) < ∞ can be found in ([ATH 72], p. 20).
Limit results in the critical case can be found in [EST 76, KHA81, MAK 80, POM 81, SZE 76].
6.1.9. Bounds for the distribution and the mean of the extinction time
It is easy to see that, if L and U are two generating functions such that
then
![]()
with the convention ![]() (see the previous section), this implies that
(see the previous section), this implies that
![]()
and, if m < 1, the mean ![]() of extinction time satisfies the double inequality
of extinction time satisfies the double inequality
![]()
Similarly, if m < 1 and ![]() , then the constant a1 from Proposition 6.7 satisfies the double inequality
, then the constant a1 from Proposition 6.7 satisfies the double inequality
![]()
As homographic generating functions of the form [6.3] represent in fact the only class of generating functions for which iterates of any order can be actually computed, it is natural to try to find the best generating functions L and U in [6.14] for a given generating function f.
Elementary computations lead to the following result.
THEOREM 6.20.– (Agresti [AGR 74], Hwang and Wang [HWA 79]) Let f be a probability generating function with m = f′(l) < ∞ and let f(x; m, c) = 1 − m(l − c) + m(l − c)2x/(l − cx), 0 < x < 1, such that the function f(x;m, ·) is increasing. If
![]()
(in particular, ifmf″(x) > f′(x)f″(l), 0 < x < 1) then:
(i) the minimum value of c for which f(x) ≤ f(x;m,c), 0 ≤ x ≤ 1, is C2 = (m + f(0) − l)/m;
(ii) the maximum value of c for which f(x;m,c) < f(x), 0 < x < 1, is C1 = f″(l)/(2m + f″(l)) (assuming that f″(l) < ∞.
Let us now give several particular cases for which the condition of Theorem 6.20 is satisfied.8
1. f(x) = eλ(x−1), λ > 0 (Poisson generating function), with
![]()
2. f(x) = (px + (1 − p))r, 0 < p ≤ 1, r ∈ ![]() + (binomial generating function), with
+ (binomial generating function), with
![]()
3. ![]() , with
, with
![]()
4. ![]() , with
, with
![]()
Agresti [AGR 74] obtained the best bounds for the generating function / in [6.14], consisting of function L of type 3 and a function U of type 4, such that ![]() , assuming that f″(l) < ∞.9 Using the best bounds of the functions L and U by homographic generating functions, as well as the inequalities obtained at the beginning of this section, we get the following results.
, assuming that f″(l) < ∞.9 Using the best bounds of the functions L and U by homographic generating functions, as well as the inequalities obtained at the beginning of this section, we get the following results.
THEOREM 6.21.– (Agresti [AGR 74]) Let f be a probability generating function with m < 1 and ![]() we hane
we hane
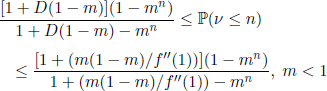
and
![]()
for all n ∈ ![]() . Similarly,
. Similarly,

and
![]()
The case m > 1 can be obtained from the case m < 1, using a result from section 6.1.7. For the generating function ![]() we have
we have ![]() so
so ![]() . By Theorem 6.21 we can thus obtain bounds for
. By Theorem 6.21 we can thus obtain bounds for ![]() , as well as for
, as well as for ![]() .
.
We can also prove that in certain situations we can get better bounds than those of Theorem 6.21. As a general rule, this is the case when the restrictive conditions of Theorem 6.20 are verified. In particular, we can obtain better bounds for Poisson or binomial generating functions (types 1 and 2 given above).
6.1.10. Asymptotic properties
Let us present now the most important asymptotic properties of the random variables X(n), n∈![]() . The proofs of these properties (and of many others) can be found in [ATH 72, JAG 75].
. The proofs of these properties (and of many others) can be found in [ATH 72, JAG 75].
From [6.1] we obtain that
![]()
and, letting Wn = X(n)/mn, we have
![]()
This last relation shows that (Wn, n ∈![]() ) is a martingale. This remark (that we owe to J. L. Doob) yields the following result.
) is a martingale. This remark (that we owe to J. L. Doob) yields the following result.
PROPOSITION 6.22.– There exists an r.v. W with mean < 1 such that X(n)/mn → W a.s. as n → ∞.
Obviously, W = 0 a.s. if m < 1. Consequently, Proposition 6.22 is not trivial only in the supercritical case.
THEOREM 6.23.– (H. Kesten, B. P. Stigum) Let m > 1. Then either ![]() (W) = 1 or W = 0 a.s., according as the series
(W) = 1 or W = 0 a.s., according as the series ![]() is convergent or divergent. In the first case, if pk < 1 for all k ∈
is convergent or divergent. In the first case, if pk < 1 for all k ∈ ![]() , then the distribution of W has a positive and continuous density on (0, ∞) and it also has a jump of magnitude q at the origin
, then the distribution of W has a positive and continuous density on (0, ∞) and it also has a jump of magnitude q at the origin ![]() .
.
Theorem 6.23 and Proposition 6.6 imply that, if ![]() then W(n) ~ Wmn when n → ∞, a.s. on the event (X(n) → ∞). This result is the probabilistic analog of the Malthusian law of geometric growth of population.
then W(n) ~ Wmn when n → ∞, a.s. on the event (X(n) → ∞). This result is the probabilistic analog of the Malthusian law of geometric growth of population.
In particular, condition ![]() is verified if
is verified if ![]() that is if σ2 < ∞. Thus we get the following result.
that is if σ2 < ∞. Thus we get the following result.
THEOREM 6.24.– (T. E. Harris) If m > 1 and σ2 < ∞, then X(n)/mn converges in quadratic mean to W. Moreover, ![]() σ2 /(m2 − m).
σ2 /(m2 − m).
It is not difficult to obtain the functional equation satisfied by the characteristic function ![]() . Let us denote by φn the characteristic function of Wn = X(n)/mn, i.e.
. Let us denote by φn the characteristic function of Wn = X(n)/mn, i.e.
![]()
From the definition of /„ we have
![]()
Since Wn converges a.s. to W as n → ∞, we get that φn(t) → φ(t), t ∈ ![]() , as n → ∞. Then, the continuity of f on the disk |z| ≤ 1 yields the functional equation
, as n → ∞. Then, the continuity of f on the disk |z| ≤ 1 yields the functional equation
It is obvious that this equation, obtained by assuming only the existence of the finite mean m, is useful only in the case when ![]() (W) = 1, that is when φ′(0) = i.
(W) = 1, that is when φ′(0) = i.
THEOREM 6.25.– (T. E. Harris, K. B. Athreya) If ![]() then there exists a unique characteristic function φ that satisfies the functional equation [6.15] with φ′(0) = i. For all
then there exists a unique characteristic function φ that satisfies the functional equation [6.15] with φ′(0) = i. For all ![]() if and only if
if and only if ![]()
It is interesting to illustrate the above results for homographic generating functions [6.3]. In this case we can easily verify that for m > 1 we have
![]()
This function satisfies the functional equation [6.15] and φ′(0) = i. The distribution function corresponding to φ is F(x) = qF0(x) + (1 − q)E1_q(x), where
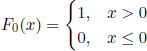
and
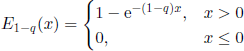
(the exponential distribution function of parameter 1 − q). We verify thus (Theorem 6.23) the existence of a jump of magnitude q at origin and of a continuous density on (0, ∞).
Conversely, it is not difficult to see that, if the distribution function of W has the expression obtained above, then its generating function is homographic.
Theorem 6.23 can be strengthened in order to provide a non-degenerated limit even if the series ![]() is divergent. This is given in the following result.
is divergent. This is given in the following result.
THEOREM 6.26.– Let m > 1.
(i) (E. Seneta, C. C. Heyde) There exists a sequence ![]() of constants with limn→∞ Cn = ∞ and limn→∞ Cn+1Cn = m, such that Wn = X(n)/Cn converges a.s. as n → ∞ to an r.v. W such that
of constants with limn→∞ Cn = ∞ and limn→∞ Cn+1Cn = m, such that Wn = X(n)/Cn converges a.s. as n → ∞ to an r.v. W such that ![]() (W > 0) = 1 − q. The characteristic function φ(t) =
(W > 0) = 1 − q. The characteristic function φ(t) = ![]() exp(itW) satisfies the functional equation [6.15]. Any other characteristic function that satisfies [6.15] is of the form ip(ct), for a certain
exp(itW) satisfies the functional equation [6.15]. Any other characteristic function that satisfies [6.15] is of the form ip(ct), for a certain ![]() .
.
(ii) (K. B. Athreya) The mean value ![]() (W) is finite if and only if
(W) is finite if and only if ![]() or, equivalently, if and only if Cn ~ const. x mn, n → ∞.
or, equivalently, if and only if Cn ~ const. x mn, n → ∞.
(iii) (K. B. Athreya, S. Dubuc) If pk < 1 for all k ∈ ![]() , then W has a continuous and positive density on (0, ∞) and a jump of magnitude q at origin
, then W has a continuous and positive density on (0, ∞) and a jump of magnitude q at origin ![]() .
.
(iv) (S. Dubuc) ![]() .
.
(v) (Bingham and Doney [BIN 75]) For β > 0 we have ![]() if and only if
if and only if ![]() . More generally, let L be a positive measurable function defined on (1, ∞), with slow variation at infinity, i.e. limx→∞ L(λx)/L(x) = 1 for all λ > 0. Then, for (3 > 1 we have
. More generally, let L be a positive measurable function defined on (1, ∞), with slow variation at infinity, i.e. limx→∞ L(λx)/L(x) = 1 for all λ > 0. Then, for (3 > 1 we have ![]() if and only if
if and only if ![]() .
.
Concerning the choice of the constants Cn in Theorem 6.26, there exist different possibilities. E. Seneta (see [ATH 72], p. 30) used the values
![]()
where y0 is a fixed arbitrary point in the open interval (0, − log q) and ![]() is the inverse of the generating function fn (which exists, since fn is an increasing and continuous function on [0,1]). Cohn [COH 82a, COH 83a] showed that, denoting by Fn the distribution function of the random variable X(n) and letting x0 be an arbitrary fixed point in (q, 1), we can define the constants Cn by the relations
is the inverse of the generating function fn (which exists, since fn is an increasing and continuous function on [0,1]). Cohn [COH 82a, COH 83a] showed that, denoting by Fn the distribution function of the random variable X(n) and letting x0 be an arbitrary fixed point in (q, 1), we can define the constants Cn by the relations
![]()
Assmussen and Hering ([ASM 83], p. 45) proved that, choosing Cn such that ![]() , we can take
, we can take
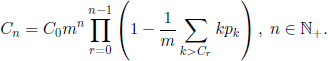
This choice is founded on purely analytical considerations concerning the generating functions fn or the distribution functions Fn. On the contrary, Grey [GRE 80] proposed a purely probabilistic method to determine the constants ![]() . He starts from the following result.
. He starts from the following result.
LEMMA 6.27.– (D. R. Grey) Let (X(n),n ∈ ![]() ) and (X*(n),n ∈
) and (X*(n),n ∈ ![]() ) be two independent B-G-W models with the same offspring distribution and arbitrary initial distributions (possibly distinct). Let
) be two independent B-G-W models with the same offspring distribution and arbitrary initial distributions (possibly distinct). Let ![]() be the σ-algebra generated by the r.v. X(0), … ,X(n),X*(0), … ,X*(n) and let Yn = X(n)/(X(n) + X*(n)), with the convention that if extinction occurs simultaneously in both models, Yn takes the last value well defined just prior to the extinction time and retains that value for all subsequent n. Under these conditions, (Yn, Fn), n ∈
be the σ-algebra generated by the r.v. X(0), … ,X(n),X*(0), … ,X*(n) and let Yn = X(n)/(X(n) + X*(n)), with the convention that if extinction occurs simultaneously in both models, Yn takes the last value well defined just prior to the extinction time and retains that value for all subsequent n. Under these conditions, (Yn, Fn), n ∈ ![]() , is a martingale with values in [0,1], that converges a.s. as n → ∞ to a limit r.v. with values in the same interval. Hence X(n)/X*(n) = 1/Yn − 1 converges a.s. as n → ∞ to an r.v. with values in the extended half-line [0, ∞].
, is a martingale with values in [0,1], that converges a.s. as n → ∞ to a limit r.v. with values in the same interval. Hence X(n)/X*(n) = 1/Yn − 1 converges a.s. as n → ∞ to an r.v. with values in the extended half-line [0, ∞].
Lemma 6.27 allows us to conclude that almost all trajectories of ![]() provide a sequence of constants Cn with the properties mentioned in Theorem 6.26 (i).
provide a sequence of constants Cn with the properties mentioned in Theorem 6.26 (i).
Theorem 6.26 closes the study of the asymptotic behavior of supercritical B-G-W models with finite mean m. Deep results were also obtained in the case m = ∞, where we can distinguish two types of models: regular and irregular. A regular model satisfies the inequality
![]()
for any sequence ![]() of real positive constants such that limn→∞ X(n)/Cn exists a.s. An irregular model satisfies the inequality
of real positive constants such that limn→∞ X(n)/Cn exists a.s. An irregular model satisfies the inequality
![]()
for one sequence ![]() of positive constants. For any model of infinite mean m, we can construct increasing functions U: [0, ∞) → [0, ∞) such that e−nU(X(n)) converges a.s. as n → ∞ to a r.v. V with
of positive constants. For any model of infinite mean m, we can construct increasing functions U: [0, ∞) → [0, ∞) such that e−nU(X(n)) converges a.s. as n → ∞ to a r.v. V with ![]() and
and ![]() . For a regular model, all these functions U are with slow variation at infinity. The distribution of V depends on U and it is possible that this distribution:
. For a regular model, all these functions U are with slow variation at infinity. The distribution of V depends on U and it is possible that this distribution:
(a) is absolutely continuous on [0, ∞);
(b) has atoms in (0, ∞);
(c) is continuous on (0, ∞) but not absolutely continuous;
(d) assigns probability 0 to some intervals from (0, ∞).
Fundamental references on the study of infinite mean models can be found in [COH 77a, SCH77]. See also [BAR 79b, DAV78, COH 82c, COH78, COH 80, GRE 79, HUD 77, SEN 74a, SEN 75].
We conclude this section with some results in the case when the initial number of objects N is not fixed (= 1, as it has been supposed here, see section 6.1.2), but tends to infinity through a sequence of integers (Nn, n ∈ ![]() +).
+).
THEOREM 6.28.– (J. Lamperti) (i) If m > 1 and σ2 < ∞, then
for all x ∈ R, provided that
(ii) If m ![]() , then
, then
![]()
where b is the generating function given in Theorem 6.17. If m < 1, σ2 < ∞, and limn→∞ mnNn = ∞, then we have relation [6.16] with an satisfying [6.17]. Without taking into account degenerated limit distributions and trivial changes of normalizing constants, these are the only possible distributions.
(iii) Let m = 1 and a2 < ∞. If limn→∞ Nn/n = a < ∞, then, for u > 0 we have
![]()
which in fact is the Laplace transform of a mixture of Poisson and gamma distributions. If limn→∞ Nn/n = ∞, then we have relation [6.16] with an ~ ![]() . Once again, these distributions are essentially unique.
. Once again, these distributions are essentially unique.
The proofs of these results can be found in ([JAG 75], p. 61–63). They are only consequences of certain theorems for independent r.v. For functional versions (invariance principle) see [LIN 72].
6.1.11. Local limit laws
Theorem 6.26 states that in the supercritical case m > 1 the ratio X(n)/Cn tends as n→∞ to an r.v. W having a density w, that is continuous and positive on (0, ∞). Consequently,
![]()
where w*i is the i-fold convolution of w. This relation is a “global” limit law that can be written in terms of the transition probabilities
![]()
under the form
![]()
where ![]() . The last equality suggests to study “local” laws concerning the asymptotic behavior of the transition probabilities p(n, i,j). We present here some results of this type, whose proofs can be found in [ATH 72, DUB 76].
. The last equality suggests to study “local” laws concerning the asymptotic behavior of the transition probabilities p(n, i,j). We present here some results of this type, whose proofs can be found in [ATH 72, DUB 76].
THEOREM 6.29.– (S. Dubuc) Let m > 1. If the greatest common divisor of the numbers k ∈ N for which pk > 0 is equal to 1 and if n→∞, j→∞ such that j/Cn → c > 0, then
![]()
THEOREM 6.30.– (H. Kesten, P. Ney, and F. Spitzer) Let m = 1. If the greatest common divisor of the numbers k ∈ N for which pk > 0 is equal to 1, if ![]() log k < ∞, and if n → ∞, j → ∞ such that j/n is bounded, then
log k < ∞, and if n → ∞, j → ∞ such that j/n is bounded, then
![]()
Note that in the above theorems n and j tend simultaneously to infinity. We also give a result where only n tends to infinity.
PROPOSITION 6.31.– If m ≠ 1 and ![]() when m < 1, then
when m < 1, then
![]()
where γ = f′(q) and qj, j ∈ ![]() , are the coefficients of the power series expansion around the origin of the function Q (see section 6.1.5).
, are the coefficients of the power series expansion around the origin of the function Q (see section 6.1.5).
For other results of local type see ([ATH 72], ch. II), [BÜH 75, HÖP 82].
6.1.12. Complete solution of Galton’s problem and a genetics problem
We are now able to present the complete solution of the famous Problem 4001 associated with the name of Galton and Watson (see section 6.1.1).
From Theorem 6.5 we see (see also footnote 2) that in the supercritical case m > 1, after a time interval large enough, about qN of the initial surnames will have disappeared, whereas the others (1 − q)N would last forever. Nevertheless, we have to mention (see Corollary 6.2 and relation [6.6], which is obviously true for any initial value X(0)) that ![]() the coefficient of zs in [fn(z)]N, which represents the probability that in the nth generation exactly s men bear the same surname, tends to 0 as n→∞ for any fixed s. Since the initial number of surnames N is fixed, the mean value of the number of surnames, each of them being held by exactly s men in the nth generation, i.e.
the coefficient of zs in [fn(z)]N, which represents the probability that in the nth generation exactly s men bear the same surname, tends to 0 as n→∞ for any fixed s. Since the initial number of surnames N is fixed, the mean value of the number of surnames, each of them being held by exactly s men in the nth generation, i.e. ![]() , tends also to 0 as n → ∞. But the sum of these means, which is the mean value of the number of surnames that do not disappear, tends to the positive limit (1 − q)N as n → ∞. Similarly, the mean value of the total number of men whose surnames appear exactly s times in the nth generation, i.e.
, tends also to 0 as n → ∞. But the sum of these means, which is the mean value of the number of surnames that do not disappear, tends to the positive limit (1 − q)N as n → ∞. Similarly, the mean value of the total number of men whose surnames appear exactly s times in the nth generation, i.e. ![]() , tends to 0 as n → ∞, but the sum of these mean values (which is the mean value of the total number of men in the nth generation) is equal to Nmn, which explodes geometrically as n → ∞.
, tends to 0 as n → ∞, but the sum of these mean values (which is the mean value of the total number of men in the nth generation) is equal to Nmn, which explodes geometrically as n → ∞.
Theorem 6.26 says that if we are interested in the surnames that survive by chance, then the number X(x) (n) of men that bear the surname x in the nth generation is of the form W(x)Cn + o(Cn) as n→∞, where Wx is a positive r.v. whose characteristic function is (φ(t) − q)/(1 − q) (obviously, if ![]() , then we can take Cn = mn). For different surnames x, the corresponding r.v. W(x) are independent.
, then we can take Cn = mn). For different surnames x, the corresponding r.v. W(x) are independent.
We want to emphasize that only the conclusions of Theorems 6.5 and 6.26 together provide what we can call the complete solution of Galton’s problem.
Bearing this remark in mind, we will be interested in the first serious attempt to apply the B-G-W model to the interpretation of empirical demographic data. We are talking about the works of A. J. Lotka from 1931 [see ([GAN 75], pp. 225–226), ([KEN 66], pp. 389–390), and ([KEN 75a], pp. 238–241)], whose computations are based on the recordings of the American census from 1920 concerning the fertility of s wives of white Americans. Lotka managed to determine the probabilities pk that a newborn male has k = 0,1,2, … sons at adult age, given by p0 = 0.4982; p1 = 0.2103; P2 = 0.1270; p3 = 0.0730; p4 = 0.0418; p5 = 0.0241; p6 = 0.0132; p7 = 0.0069; p8 = 0.0035; p9 = 0.0015; p10 = 0.0005; pk ≅ 0, k ≥ 11. For these values, we obtain with no difficulty that m = 1.145 > 1 and q = 0.8797. Then Lotka noted that the relations pk = bck−1, k ∈ ![]() ,
, ![]() with b = 0.2290 and c = 0.5586 provide very good approximations of the empirical data. As we know (see section 6.1.3), this leads to the generating function
with b = 0.2290 and c = 0.5586 provide very good approximations of the empirical data. As we know (see section 6.1.3), this leads to the generating function
which, as opposed to the empirical data, yields the values ![]() and
and ![]() . As an alternative, we can obtain the values of b and c in [6.3] that lead to the empirical values m = 1.145 and q = 0.8797. From relations m = b/(1 −c)2 and q = (1 −b − c)/c(1 −c) we get
. As an alternative, we can obtain the values of b and c in [6.3] that lead to the empirical values m = 1.145 and q = 0.8797. From relations m = b/(1 −c)2 and q = (1 −b − c)/c(1 −c) we get
![]()
that yield the generating function
The coefficients of the power series expansion of this generating function around z = 0 provide the empirical values pk, k ∈ ![]() , which are worse than Lotka’s approximations.
, which are worse than Lotka’s approximations.
We could ask ourselves, for example, admitting the immutability (obviously non-existent!) of the conditions of mortality, fertility, etc. what will be the situation of the 3rd generation of descendants of men born in 1920 (thus, this will mean the year 2010). We have
![]()
On the one hand, we see in this way that the total male population should increase on average by about 50% (62%). On the other hand, assuming that all the men of the generation 1920 had different surnames, we see that the number of surnames decreases about 3–4 times in the third generations. Similarly, in the 10th generation (year 2220) the extinction of all the disapearing names would be almost complete.
Note that for homographic generating functions like [6.18] and [6.18′], the variables Wx are exponentially distributed (see the remarks after Theorem 6.25). Kendall ([KEN 66], p. 390) says that it is not possible to verify this fact, because the available statistics have not been built in a form that is convenient for such a verification.
We mention that Hull reconsidered Lotka’s computations for a two-sex population [HUL 01].
Finally, let us note the long gestation period of the complete solution of Galton’s problem. This shows that, in certain cases, the developing of a mathematical model is the work of several generations of researchers.
For the B-G-W model we can solve a more general problem, that is the determination of the probability distribution of the number of relatives of an individual (referred to as “Ego”), randomly chosen from a population, for example children, grandchildren, great grandchildren, brothers, uncles, etc. The applications of such a problem are numerous: to social policy (number of necessary housings), to demography, to anthropology (where family relationships may affect the status of a person in a tribe), to sanitary policy (where an inquiry into the health of a cancer victim’s relatives depends on their number and degree of affinity). See [WAU 81] who obtains the probability generating function for an arbitrary number of generations preceding or succeeding “Ego.” The same problem was studied for other branching models. See Bellman-Harris (see section 6.3.2) and [JAG 82, JAG 84a, JAG 84b] for the Crump-Mode-Jagers-Ryan model (see section 6.3.3).
To conclude, let us quickly present a problem in genetics where the B-G-W model proves its usefulness. Here, this model places Galton’s problem in a genetic context, related to Darwin’s theory of natural selection. In a preliminary note published first in 1922, then in 1930 in his book The Genetical Theory of Natural Selection, 2nd edition, Dover, New York, 1958, R. A. Fisher treated the survival problem of a mutant gene in the context of the B-G-W model with Poisson P(l) generating function, that is f(z) = ez−1, |z| ≤ 1. If we have a population of fixed large size, we can assume that the probability that a mutant gene is present in k descendants of the next generation is e_1 /k!, k ∈ N. In the case where the gene confers a small selective advantage we would have a Poisson distribution P(l+∈), ∈ > 0, for the offspring still having this gene, i.e. a B-G-W model with generating function f(z) = e(1+ε)(z−1). In this last case, the extinction probability q, which is the root in [0,1) of equation x = e(1+∈)(z−1), has the approximative value q ~ exp[−2e/(l + ∈)] (which is an exact value if ∈ = 0). The computations of Fisher for ∈ = 0 and ∈ = 0, 01 (selective advantage 1%) shows, for example, that the extinction probability of the mutant gene in the 63rd generation is 0.9698, respectively 0.9591 (the approximative value of q for ∈ = 0.01 is 0.9804). For the 127th generation, these probabilities are 0.9847, respectively 0.9729. Fisher concluded that, in the absence of selection, the number of descendants from a single mutant cannot greatly exceed the number of generations produced since its occurrence. Subsequent researches showed that the majority of the mutant genes disappear during the next 10-20 generations, in a more or less random manner (see [IOS 73], II, p. 13).
6.1.13. Elements of statistical inference
In any real application of the B-G-W model it is necessary to estimate its parameters, that is the probabilities pk, k ∈ ![]() . Obviously, the estimation of an infinite number of parameters has no sense from a practical point of view. The problem can nevertheless be solved, either by assuming a certain parameterization of the probabilities Pk, k ∈
. Obviously, the estimation of an infinite number of parameters has no sense from a practical point of view. The problem can nevertheless be solved, either by assuming a certain parameterization of the probabilities Pk, k ∈ ![]() , as it is the case for instance for the homographic generating function [6.3] or by sticking to the estimation of some representative characteristics, as m, σ2 or q.
, as it is the case for instance for the homographic generating function [6.3] or by sticking to the estimation of some representative characteristics, as m, σ2 or q.
In the following we will present some important results of statistical inference for the B-G-W model. In order to have a complete picture of the topic, the interested reader is referred to [BAD 77, DIO 78, GUT 91, HEY 77a, LOC 82].
We will consider three cases: (a) increasing number of ancestors (N → ∞), which leads to the classic theory of i.i.d. r.v.; (b) increasing number of generations (n → ∞), which raises more difficult problems, whose solutions cannot be found in the classic theory; (c)=(a)∩(b), that is N → ∞ and n → ∞ simultaneously.
Concerning the data at our disposal, we will consider two cases: (A) we have observed values ![]() of the sizes of offspring of all the objects of the first n generations; (B) we only have the observed values of the sizes X(0), X(1), …, X(n) of the first n + 1 generations.
of the sizes of offspring of all the objects of the first n generations; (B) we only have the observed values of the sizes X(0), X(1), …, X(n) of the first n + 1 generations.
THEOREM 6.32.– (T. E. Harris) In the case (A) let
![]()
= the number of cases where the size of the offspring is equal to k during the first n generations. Then, the maximum likelihood estimator of pk is
![]()
COROLLARY 6.33.– In the case (A) the maximum likelihood estimator of m = ![]() is
is
![]()
i.e. the total of “children” divided by the total of “parents.”
THEOREM 6.34.– (T. E. Harris, J.-P. Dion) The statistics m is equally the maximum likelihood estimator in the case (B).
On the one hand, let us note that there do not exist results concerning the distributions of ![]() and
and ![]() , for small values of n and N. On the other hand, there exist asymptotic results.
, for small values of n and N. On the other hand, there exist asymptotic results.
THEOREM 6.35.– (Yanev [YAN 75]) For n fixed and X(0) = n → ∞,
(i) If m ≠ ∞, then ![]() → m a.s. and
→ m a.s. and ![]() → m;
→ m;
(ii) If0 < a2 < m, then the r.v.
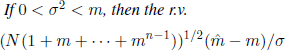
is asymptotically normal N(0,1).
Let A = {X(n)→∞} be the event consisting of the explosion of the population and let ![]() A ( •) be the conditional probability given A (see section 6.1.7).
A ( •) be the conditional probability given A (see section 6.1.7).
PROPOSITION 6.36.– ForX(0) = N fixed and n→∞, if 1 < m < ∞, then ![]() a.s. on A.
a.s. on A.
This result is a direct corollary of Theorem 6.26 (i), but it can also be directly obtained from the strong law of large numbers for i.i.d. r.v. ([DIO 78], p. 111).
Let ![]() , where the r.v. W was defined in section 6.1.10, and let S*N be the N-fold convolution of S.
, where the r.v. W was defined in section 6.1.10, and let S*N be the N-fold convolution of S.
THEOREM 6.37.– (J.-P. Dion, P. Jagers) Suppose m > 1 and 0 < σ2 < ∞. For fixed X(0) = N and n→∞, for any x ∈ ![]() :
:
(i) 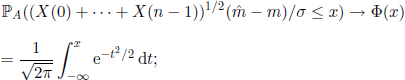
(ii)![]()
(iii) The results in (i) and (ii) still hold if the probability ![]() A is replaced by
A is replaced by ![]() ( • | X(n) ≠ 0).
( • | X(n) ≠ 0).
Note that (ii) above shows that the r.v. rh is not asymptotically normal if the standardization is done deterministically. As an exercise, we can check that for the homographic function [6.3], the distribution in (ii) is the Student distribution with 2N degrees of freedom.
Concerning (iii), we have to prove that we do not know the asymptotic distribution of m conditioned on (X(n) ≠ 0) in the critical case m = 1 and subcritical one m < 1. Results of this type for the estimators pk defined in Theorem 6.32 were obtained by Pakes [PAK75a]. Concerning the behavior of these estimators in the supercritical case (m > 1), there exists a result completely analogous to Theorem 6.37.
THEOREM 6.38.– (Dion [DIO 74]) Suppose that m > 1 and 0 < σ2 < ∞. For fixed X(0) = N and n→∞, for any k ∈ ![]() and x ∈
and x ∈ ![]() :
:
(i) 
(ii)
(iii) The results in (i) and (ii) still hold if the probability ![]() A is replaced by
A is replaced by ![]() .
.
We will conclude the study of the estimator ![]() some results in the case (c), when N and n tend simultaneously to infinity.
some results in the case (c), when N and n tend simultaneously to infinity.
THEOREM 6.39.– (Yanev [YAN 75]) Suppose 0 < σ2 < ∞. If X(0) = N → ∞ and n→∞, then:
(i) ![]() in probability and
in probability and ![]() E (m)→m;10
E (m)→m;10
(ii) If m <1, then the r.v.
![]()
is asymptotically normal N(0,1);
(iii) 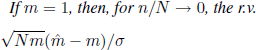
is asymptotically normal N(0, 1), whereas, for n/N2 → ∞, the asymptotic distribution of the r.v.
![]()
is a distribution whose Laplace transform is ![]() ;
;
(iv) ![]() then the r.v.
then the r.v.
![]()
is asymptotically normal N(0,1).
Another estimator of m was proposed by A. J. Lotka in 1939 and was first studied by Nagaev [NAG 67], then by Bühler [BÜH 69], Crump and Howe [CRU 72], and Dion [DIO 74]. This one is defined by the relation
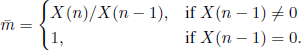
We have ![]() , and, if 1 < m < ∞, then
, and, if 1 < m < ∞, then ![]() a.s. as n → ∞ on A = {X(n) → ∞}. If, additionally, 0 < a2 < ∞, then
a.s. as n → ∞ on A = {X(n) → ∞}. If, additionally, 0 < a2 < ∞, then ![]() .
.
Heyde [HEY 75] pointed out the possibility of using ![]() as an estimator of m. By Theorem 6.23, if m > 1 and
as an estimator of m. By Theorem 6.23, if m > 1 and ![]() , then m* → m on A as n→∞. Under the same conditions, we can prove that n(m* − m) → m log W a.s. on A as n→∞. This rate of convergence to m is lower than the one of
, then m* → m on A as n→∞. Under the same conditions, we can prove that n(m* − m) → m log W a.s. on A as n→∞. This rate of convergence to m is lower than the one of ![]() which does not plead for the use of m*. For other considerations on m as well as on the r.v.
which does not plead for the use of m*. For other considerations on m as well as on the r.v. ![]() we can see [NAN 80].
we can see [NAN 80].
In order to obtain confidence intervals for m using the previous results, it is necessary to dispose of consistent estimators of the variance a2. Let
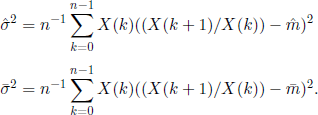
The asymptotic behavior of ![]() and
and ![]() was studied in the supercritical case m > 1 for p0 = 0, so q = 0 (see [DIO 75, HEY 74], ([DIO 78], pp. 115–116)). If
was studied in the supercritical case m > 1 for p0 = 0, so q = 0 (see [DIO 75, HEY 74], ([DIO 78], pp. 115–116)). If ![]() are consistent and asymptotically normal estimators of σ2.
are consistent and asymptotically normal estimators of σ2.
In the critical case m = 1, Nagaev [NAG 67] noted that the r.v.
![]()
can be used for estimating σ2, since ![]() and, if
and, if ![]() .
.
We will end this section with some results on the estimation of the extinction probability q.
In the case (A) (with n→∞) and (a) with n = 1, S. M. Stiegler (see [JAG 75], pp. 50–52) showed that the maximum likelihood estimator of q is
![]()
where ![]()
THEOREM 6.40.– (S. M. Stiegler) In the supercritical case m > 1, if p0 > 0, the r.v. (qN − q)/(l −f′(q))2 is asymptotically normal N(0, {f{q2) −q2)/{l − f′(q))2) as n→∞.
In the critical case m = 1, if 0<σ2 < ∞, then
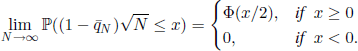
In the subcritical case m < 1, starting from a certain value of N we have ![]() , with probability 1.
, with probability 1.
Pakes [PAK 75a] extended these results to the case n > 1. There are no studies yet of the properties of an estimator of q that involves the estimators ![]() from Theorem 6.32 (with n > 1).
from Theorem 6.32 (with n > 1).
In the case (B), Srivastava and Potter ([SRI 79], pp. 469–470) proposed the variable ![]() as an estimator of q.
as an estimator of q.
6.2. Generalizations of the B-G-W model
6.2.1. The non-homogenous B-G-W model (in a varying environment)
A straightforward and natural generalization of the B-G-W model is obtained allowing the offspring distribution to vary from a generation to another. This variability can be associated with environmental change or to population evolution. We will try to see in the following whether this way of taking into account the environmental influence can ensure the stability of the population (see the final part of section 6.1.4).
Formally, we will place ourselves in the following context. Let ξi (n), i ∈ ![]() +, n ∈
+, n ∈ ![]() , be independent r.v. such that the generating function
, be independent r.v. such that the generating function ![]()
![]() of variables
of variables ![]() , is not anymore independent of the rank n of generations, as was the case in section 6.1.1. Let us define the r.v.
, is not anymore independent of the rank n of generations, as was the case in section 6.1.1. Let us define the r.v.![]() by the relations X(0) = N and
by the relations X(0) = N and
for n ∈ ![]() .
.
By non-homogenous B-G-W model (in varying environment) we mean the random sequence ![]() together with relations [6.19], in the context specified above.
together with relations [6.19], in the context specified above.
Let us define the generating functions fn,n ∈ ![]() , by the relations f0 (z) = z and
, by the relations f0 (z) = z and
![]()
and let

It is easy to see that [fn(z)]N is the generating function of ![]() , and that μn and mn have the following meaning:
, and that μn and mn have the following meaning:
![]()
As we saw in the homogenous case (see section 6.1.2), X(N) is a Markov chain with the state space included in N and the initial distribution concentrated at state N. This chain is not homogenous anymore, but it is not difficult to compute its transition probabilities. Here too the state 0 is absorbing, i.e. if X(N) (n) = 0, then X(N) (n+k) = 0 for all k ∈ ![]() . Finally, the chain X(N) is the sum of N independent versions of the chain X(1), which allows us, without loss of generality, to study only the case N = 1.
. Finally, the chain X(N) is the sum of N independent versions of the chain X(1), which allows us, without loss of generality, to study only the case N = 1.
As state 0 is absorbing, we obtain, as in the homogenous case (see section 6.1.4), that the extinction probability
![]()
is given by the relation
![]()
Defining the extinction moment v as we did in the homogenous case (see section 6.1.8), we have ![]() .
.
Several criteria for the almost sure extinction of the population (q = 1) are known. In order to avoid trivial situations, we will always assume in the following that pn0 < 1, n ∈![]() , or, equivalently, that μn > 0, n ∈
, or, equivalently, that μn > 0, n ∈ ![]() .
.
THEOREM 6.41.– (P. Jagers, M. Ji![]() ina) (i) Let lim infn→∞ mn < ∞ (in particular, this hap pens if the product
ina) (i) Let lim infn→∞ mn < ∞ (in particular, this hap pens if the product ![]() is finite, i.e. if the
is finite, i.e. if the ![]() exists and is finite). Then q = 1 if and only if
exists and is finite). Then q = 1 if and only if ![]() =∞, or, equivalently,
=∞, or, equivalently, ![]() .
.
(ii) If ![]() does not exist, which means there is no finite nor infinite
does not exist, which means there is no finite nor infinite ![]() .
.
For the proof we can see ![]()
Remarks. 1. The case ![]() remains undecided.
remains undecided.
2. The fact that q = 1 for homogenous subcritical or critical models is a direct consequence of Theorem 6.41 (i).
THEOREM 6.42.– ![]() In the particular case when all the generating functions φi, i ∈
In the particular case when all the generating functions φi, i ∈ ![]() , are polynomials of degree ≤ r =constant:
, are polynomials of degree ≤ r =constant:
(a) If ![]() , then
, then
is a necessary condition for q = 1.
(b)Without any further hypothesis, condition [6.20] is sufficient for q = 1.
(c)If ![]() then
then
is a necessary and sufficient condition for q = 1.
(d) If ![]() , then [6.21] is a sufficient condition for q = 1.
, then [6.21] is a sufficient condition for q = 1.
Remarks. 1. J![]() rina conjectures [JI
rina conjectures [JI![]() 76] that [6.21] is a sufficient condition for q = 1 for any non-homogenous B-G-W model.
76] that [6.21] is a sufficient condition for q = 1 for any non-homogenous B-G-W model.
2. For non-homogenous B-G-W models such that the finite or infinite limit limn→∞ exists, Fujimagari [FUJ 81] gives different conditions for q − 1 or q < 1, obtains asymptotic estimators of ![]() (ν ≤ n) when q = 1, and also an upper bound for 1 − q =
(ν ≤ n) when q = 1, and also an upper bound for 1 − q = ![]() (ν = ∞) when q < 1. Bounds for
(ν = ∞) when q < 1. Bounds for ![]() (ν ≤ n) analogous to those from Theorem 6.20 were obtained by Agresti [AGR 75]. These bounds lead to the conclusion that, for non-homogenous B-G-W models that satisfy
(ν ≤ n) analogous to those from Theorem 6.20 were obtained by Agresti [AGR 75]. These bounds lead to the conclusion that, for non-homogenous B-G-W models that satisfy
![]()
for an no ∈ ![]() , the divergence of the series
, the divergence of the series ![]() is a necessary and sufficient condition for q = 1.
is a necessary and sufficient condition for q = 1.
It appears that the non-homogenity introduced in the B-G-W models does not ensure the stability of the population. Indeed, we have the following results.
THEOREM 6.43.– (i) (J. D. Church and T. Lindvall) There exists an r.v. X(∞) with values in![]() to which X(n) converges a.s. as n → ∞.
to which X(n) converges a.s. as n → ∞.
(ii) (J. D. Church) We have ![]() if and only if
if and only if ![]() .
.
(iii) (J. D. Church) ![]() .
.
We refer to ([JAG 75], pp. 72–76) for the proofs of these results.
Point (ii) of Theorem 6.43 shows that an asymptotic behavior different from the one of the homogenous model can only occur if pn1 → 1 as n → ∞, with a convergence rate high enough in order to ensure the convergence of the series ![]() . In such a case, it could happen that the population is stabilized at constant (finite) levels with corresponding probabilities (see Theorem 6.46 further).
. In such a case, it could happen that the population is stabilized at constant (finite) levels with corresponding probabilities (see Theorem 6.46 further).
We will see now how results from section 6.1.10 can be generalized to the non-homogenous case. As in the homogenous case, it is easy to see that, letting Wn = X(n)/mn, the sequence (Wn,n ∈ ![]() ) is a positive martingale. Consequently, there exists a positive r.v. W of mean < 1, such that X(n)/mn → W a.s. as n → ∞.
) is a positive martingale. Consequently, there exists a positive r.v. W of mean < 1, such that X(n)/mn → W a.s. as n → ∞.
The following result is the analogous of Theorem 6.24.
THEOREM 6.44.– (D. H. Fearn) If there exists a non-zero limit (possibly infinite) limn→∞ mn = a, then Wn converges in quadratic mean to W as n → ∞ if and only if ![]() . We have
. We have ![]() (W) = 1 and
(W) = 1 and
![]()
with the convention (1 − ∞)/∞ = − 1.
See ([JAG 75], p. 77) for the proof.
Remarks. 1. If ![]() , Theorem 6.44 gives a version in quadratic mean of the results of Theorem 6.43 (i) (with X(∞) = aW).
, Theorem 6.44 gives a version in quadratic mean of the results of Theorem 6.43 (i) (with X(∞) = aW).
2. Theorem 6.44 suggests that for non-homogenous models the cases supercritical, critical, and subcritical would correspond, respectively, to the following cases:
(a)mn → ∞ with high rate of convergence, whereas ![]() rests bounded;
rests bounded;
(b) ![]() ;
;
(c)limn→∞ mn = 0.
However, in the following, in a way completely analogous to the homogenous case, a non-homogenous B-G-W model will be called supercritical if q = limn→∞ fn(0) < 1. This definition does not suppose at all the existence of the finite values ![]() .
.
Concerning the analoguous of Theorem 6.27, a partial result is the following.
THEOREM 6.45.– (Goettge [GOE75]) Let us consider a supercritical non-homogenous B-G-W model and let ![]() , where y0 is an arbitrary fixed point in the interval (0, − log q).
, where y0 is an arbitrary fixed point in the interval (0, − log q).
(i) Wn = X(n)/Cn converges a.s., as n → ∞, to an r.v. W, possibly degenerated.
(ii) If there exists no such that ![]() , and if μn < ∞,
, and if μn < ∞, ![]() . If, additionally,
. If, additionally, ![]() , then Cn ~ const. x m„, n ∈
, then Cn ~ const. x m„, n ∈ ![]() .
.
Remarks. 1. Goettge ([GOE75], p. 187) gives an example where the commutativity condition from (ii) is satisfied; the generating function
![]()
commutes with the generating functions
![]()
for all a > 1.
2. The properties of the r.v. W are studied in [COH 83b].
We will conclude this section with the important particular case when all the generating functions (φn are homographic (see [6.3]),
![]()
with ![]() . As in the homogenous case, here also we can explicitly compute the iterates fn(z)=
. As in the homogenous case, here also we can explicitly compute the iterates fn(z)=![]() see [AGR75]). On the one hand, letting
see [AGR75]). On the one hand, letting ![]() , it is easy to see that fn(z) = 1 −
, it is easy to see that fn(z) = 1 − ![]() . On the other hand, we have φn(z) = μnz/[1 + (φ″(n)z/
. On the other hand, we have φn(z) = μnz/[1 + (φ″(n)z/ ![]() , the values of μn and φ″(1) being
, the values of μn and φ″(1) being
![]()
such that the composition of these functions is well defined. We obtain thus
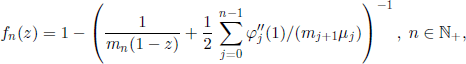
that immediately implies that
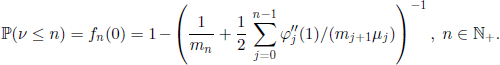
As (fn(0), n ∈ ![]() is an increasing sequence and its limit is the extinction probability q, the limit of
is an increasing sequence and its limit is the extinction probability q, the limit of
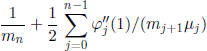
as n → ∞ exists (finite or infinite) and is equal to (1 − q)−1 (with the convention 0−1 = ∞).
Taking into account all these facts, we easily obtain [KEI75] the results that specify Theorems 6.43 and 6.44 to this particular case.
THEOREM 6.46.– For the non-homogenous B-G-W model with homographic generating functions, we have the following properties:
(i) If ![]() , then q < 1, mn → a, 1 − q < a < ∞, X(n) → X(∞) a.s. as n → ∞, with
, then q < 1, mn → a, 1 − q < a < ∞, X(n) → X(∞) a.s. as n → ∞, with ![]() (X(∞) < ∞) = 1. The generating function of X(∞) is
(X(∞) < ∞) = 1. The generating function of X(∞) is
![]()
The convergence ofX(n) to X(∞) also holds in quadratic mean and we have ![]() .
.
(ii) If ![]() , then:
, then:
(ii1) q = 1, so X(n) → 0, a.s.
or else
(ii2) ![]() ,
,![]() 11so
11so ![]() (X(n) → ∞) = 1 − q. The convergence of X(n)/mn to W is also in quadratic mean and we have
(X(n) → ∞) = 1 − q. The convergence of X(n)/mn to W is also in quadratic mean and we have ![]() (W) = 1 and
(W) = 1 and ![]() Var (W) = 2(1 − q)−1 − 1.
Var (W) = 2(1 − q)−1 − 1.
Remarks. 1. Theorem 6.46 (i) provides a concrete example of stabilization of the population size to constant levels, according to certain probability distribution.
2. The generating function of the r.v. X(n) conditioned on survival is (see section 6.1.8)
![]()
where dn = mn/(l − fn(0)) (obviously, dn > 1). Consequently, if ![]() bn < ∞ , then
bn < ∞ , then
![]()
where d = a/(1 −q), so

This result reminds us Theorem 6.17 (i) and Corollary 6.18 (jjj). For other results of this type and of the type of Theorem 6.19 in a general context, see ([JAG 75], p. 80).
The reader surely noted that, as opposed to the homogenous case, in the non-homogenous case we have not given any method for the computation of the extinction probability q when it is ≠ 1. This does not occur by chance, but because this problem has not a satisfactory solution yet [FEA 76a, FEA 76b, FEA 81].
For aspects of non-homogenous B-G-W models that have not been considered here, see [COH 82c, FOS 76a, GRE 78, HAR 78, KLE 82b, POM 81, SEN 75].
We conclude this section by noticing that, ideally, the model we presented should have taken into account not only the ranks of generations, but also their sizes. This is a difficult (and open) problem. Nonetheless, we studied a B-G-W model depending on the size of the population, where the reproduction distribution of an object depends on the size of the generation to which it belongs (but it does not depend on the rank of this generation). This model is somehow the dual of the non-homogenous model. The reader can see [HAC 05, KLE 83, KLE 84, LÉV 79].
6.2.2. The B-G-W model in a random environment
The B-G-W model studied in the previous section includes a variability of the environmental conditions that we can consider as deterministic (the environment changes from one generation to another, leading thus to the corresponding modification of the offspring distribution). In this section we consider the case of a more complex environmental change, having a random character.
Formally, let p(![]() ) be the set of all probability distributions p = (pk, k ∈ N) on N such that
) be the set of all probability distributions p = (pk, k ∈ N) on N such that ![]() Let us consider the usual cr-algebra of p(N), i.e. that generated by all the sets of the form {p ∈ p(
Let us consider the usual cr-algebra of p(N), i.e. that generated by all the sets of the form {p ∈ p(![]() ) : (p0,…,pk) ∈ A}, for all measurable subsets A ⊂
) : (p0,…,pk) ∈ A}, for all measurable subsets A ⊂ ![]() k +1, k ∈
k +1, k ∈ ![]() . Let (Ω,
. Let (Ω,![]() ) be a probability space rich enough in order to be able to define on it: (a) a sequence π = (πn, n ∈
) be a probability space rich enough in order to be able to define on it: (a) a sequence π = (πn, n ∈ ![]() ) of measurable applications from
) of measurable applications from ![]() to p(
to p(![]() ); (b) a system of
); (b) a system of ![]() , that, given π, are conditionally independent and the variables
, that, given π, are conditionally independent and the variables ![]() , have the common distribution πn, n ∈
, have the common distribution πn, n ∈ ![]() .
.
Let us define the r.v. X(N) (n) = X(n), n ∈ ![]() , by the relations X(0) = N and
, by the relations X(0) = N and
By B-G-W model in random environment we mean the sequence (X(N) >(n), n ∈ ![]() ) together with relations [6.22].12
) together with relations [6.22].12
It is clear that, conditioned on π, a B-G-W model in random environment is reduced to a non-homogenous B-G-W model (in varying environment). For this reason, under convenient hypotheses for π, the results obtained in the previous section can be transposed in the context of this section. Besides, special hypotheses on π allow to directly obtain some results which do not have an equivalent in the non-homogenous case. In conclusion, the B-G-W model in random environment deserves a separate study.
From [6.22] we immediately obtain that the generating function of X(N)(n) conditioned on π is ![]() , where
, where ![]()
![]() n ∈ N. Note that, in the present context, fn(z) and φn(z) are r.v., as well as the mean values
n ∈ N. Note that, in the present context, fn(z) and φn(z) are r.v., as well as the mean values ![]() . Even if X(N) is no longer a Markov chain, the Markovian character is restored when conditioning on π, and, like for homogenous and non-homogenous B-G-W models, the conditional chain is the sum of N independent copies of the chain X(1). Thus it always suffices to consider only the case N = 1. Letting B = {ω | Xn(ω) = 0 for a value
. Even if X(N) is no longer a Markov chain, the Markovian character is restored when conditioning on π, and, like for homogenous and non-homogenous B-G-W models, the conditional chain is the sum of N independent copies of the chain X(1). Thus it always suffices to consider only the case N = 1. Letting B = {ω | Xn(ω) = 0 for a value ![]() , we obviously
, we obviously ![]() . As the sequence ({ω | Xn(ω) = 0}, n ∈
. As the sequence ({ω | Xn(ω) = 0}, n ∈ ![]() ) is increasing to B, we can write
) is increasing to B, we can write
![]()
and we obtain the functional equation qπ = φ0(qTπ) a.s. Here T is the shift operator defined by the relation Tπ = (π1,π2,…). The last equation, which is the analogous of equation q = f(q) from section 6.1.1, allows us to conclude that the event {qπ = 1} is shift invariant, i.e. that the events {qπ = 1} and {qTπ = 1} coincide a.s. To exploit this invariance, it is natural to introduce the hypothesis that π is a strictly stationary ergodic sequence.13 (In particular, this hypothesis is true if π is a sequence of i.i.d. r.v.) Under this hypothesis, the following result holds:
![]()
The following theorem provides criteria to distinguish between these two possibilities.
THEOREM 6.47.– (Athreya and Karlin [ATH 71a]) Let us consider a strictly stationary ergodic B-G-W model in random environment π.
(i) If E (log μ0)+ < ∞, then:14
(i1) E (log/xo)+ ≤ E(log )- ≤ ∞ implies P(q7π = 1) = 1 whereas
(i2) E(log μ0)+ > E (log μ0)−and E [− log(l − π00)] < ∞ implies P(q7π = 1) = 0.
(ii) If E (log μ0+) = ∞, then E [− log(l − π00)] < ∞ implies P(qπ= 1) = 0.
Remarks. 1. Theorem 6.47 leaves undecided the following cases:
(a) ![]()
(b) ![]() .
.
2. We can find in [ATH 71a] results on the rate of convergence of fπn (0) to qπ, completely similar to those of Proposition 6.7.
3. For the effective computation of the distribution function P(qπ < u), u ∈ (0,1), in a particular case, see [KEI75].
Bounds of the probability P(ν ≤ u), where v is the extinction time (defined as in sections 6.1.8 and 6.2.1), were given in [AGR 75]. (Note that in our case we have ![]() In the last two cited works, the random environment π= (πn, n ∈ N) is a sequence of i.i.d. r.v.
In the last two cited works, the random environment π= (πn, n ∈ N) is a sequence of i.i.d. r.v.
A strictly stationary ergodic B-G-W model in random environment π will be called supercritical, critical, or subcritical accordingly whether E (log μ0) is > 0, = 0, or < 0, respectively. Theorem 6.47 shows that this terminology is compatible to that used for the classic model, that is obtained as a particular case, letting π1 = π2 = … = p = (pk,k ∈ N) (non-random probability distribution).
The strictly stationary ergodic B-G-W model in random environment π preserves a characteristic property of the classic B-G-W model, namely the alternative extinction-explosion a.s. Indeed, by eliminating the trivial case ![]() for an n ∈ N) = 1, where X(n) → 0 a.s. as n → ∞, Theorem 6.43 (ii) allows us to state that
for an n ∈ N) = 1, where X(n) → 0 a.s. as n → ∞, Theorem 6.43 (ii) allows us to state that ![]() ∞} | π) = 1 if and only if P(∑n∈N(l − πn1) < ∞ |π) = 1 a.s., which immediately yields P{limn→∞ X(n) = 0} ∪ {limn→∞ X(n) = ∞}) < 1 if and only if
∞} | π) = 1 if and only if P(∑n∈N(l − πn1) < ∞ |π) = 1 a.s., which immediately yields P{limn→∞ X(n) = 0} ∪ {limn→∞ X(n) = ∞}) < 1 if and only if ![]() . As the environment π is strictly stationary and ergodic, the series with positive terms ∑n∈N(1 −πn1) can converge a.s. only if E−π01 = 1, which implies π01 = 1 a.s., so πn1 = 1 a.s., n ∈ N, when X(n) = 1 a.s., n ∈ N. Consequently, except the trivial case πn1 = 1 a.s., n ∈ N, the alternative extinction-explosion has the associated probabilities q = E qπ and 1 − q, respectively. (In the supercritical case, if E [− log(l − π00)] < ∞, by Theorem 6.47 (i) we have P(qπ < 1) = 1, so q = E qπ < 1 and explosion takes place with a positive probability).
. As the environment π is strictly stationary and ergodic, the series with positive terms ∑n∈N(1 −πn1) can converge a.s. only if E−π01 = 1, which implies π01 = 1 a.s., so πn1 = 1 a.s., n ∈ N, when X(n) = 1 a.s., n ∈ N. Consequently, except the trivial case πn1 = 1 a.s., n ∈ N, the alternative extinction-explosion has the associated probabilities q = E qπ and 1 − q, respectively. (In the supercritical case, if E [− log(l − π00)] < ∞, by Theorem 6.47 (i) we have P(qπ < 1) = 1, so q = E qπ < 1 and explosion takes place with a positive probability).
Remark. In fact, for an arbitrary random environment π, Theorem 6.43 allows to conclude that there exists a r.v. X(∞) to which X(n) converges a.s. as n → ∞ and that a necessary and sufficient condition such that the only possible values of X(∞) are 0 and ∞ is
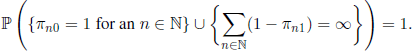
Similarly, ![]() , a.s. This implies that a necessary and sufficient condition for the mean value E X(∞) to be finite is
, a.s. This implies that a necessary and sufficient condition for the mean value E X(∞) to be finite is
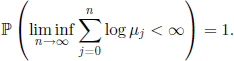
For more details we can see ([JAG 75], pp. 81–84).
The following result corresponds to Theorems 6.23 and 6.25.
THEOREM 6.48.– (Athreya and Karlin [ATH71b]) For a strictly stationary ergodic B-G-W model in random environment π that is supercritical and satisfies the condition E [− log(l − π00)] < ∞, the sequence
![]()
where ![]() the σ-algebra generated by π0…, πn, X(0), …, X(n), n ∈ N, is a positive martingale, whose limit limn→∞ Wn = W exists a.s. If, additionally,
the σ-algebra generated by π0…, πn, X(0), …, X(n), n ∈ N, is a positive martingale, whose limit limn→∞ Wn = W exists a.s. If, additionally,
![]()
then:
(i) The characteristic function E (exp(itW) | π) = ψπ, t ∈ R, is the unique solution of the functional equation ψπ(t) = φ0(ψTπ(t/μ0)) a. s. in the set of functions of the form ![]() , where Hπ is a distribution function on [0, ∞) with Hπ(0+) < 1 and
, where Hπ is a distribution function on [0, ∞) with Hπ(0+) < 1 and ![]()
(ii) ![]() (W | π) = 1 a.s.
(W | π) = 1 a.s.
(iii) ![]() (W = 0 | π) = q a.s.
(W = 0 | π) = q a.s.
There exists also an analogous of Theorem 6.26 that we state below.
THEOREM 6.49.– (Tanny [TAN 78]) For a strictly stationary ergodic B-G-W model in random environment π such that E | log μ0 | < ∞, there exists a sequence ![]() of r.v. (that depends on π only), with the following properties:
of r.v. (that depends on π only), with the following properties:
(j) ![]() converges in distribution to μ0 as n → ∞;
converges in distribution to μ0 as n → ∞;
(jj) ![]() converges a.s. as n → ∞ to a r.v. W with
converges a.s. as n → ∞ to a r.v. W with ![]() (W = 0 | π) = q and
(W = 0 | π) = q and ![]() (W < 0 | π) = 1 a.s.
(W < 0 | π) = 1 a.s.
For other aspects of B-G-W models in random environment we can see [BIR 05, BOU81, COF 84, COH81, DIO 79, EST 79, EZO 79, HAR78, KOZ 76, KUR 78, LEB 79a, LEB 79b, NAN 79, PAK 79a, RAF 73, TAN 78, TAN 81].
6.2.3. The B-G-W model with immigration
The B-G-W models already studied concern isolated populations that grow or decline purely according to their multiplication laws, without any contact with other populations.15 We have seen in sections 6.2.1 and 6.2.2 that, with the exception of the case of Theorem 6.42 (ii), taking into account a varying or random environment does not ensure the stability of the population. In this section we will examine a modification of the homogenous B-G-W model that consists of introducing an immigration component whose members multiply according to the laws of the original population. We will see that this procedure−that from the point of view of the applications in biology or ecology is not at all artificial−allows us to obtain the desired stability of the population.
The model thus modified will describe the evolution of the size of a population whose each member produces k ∈ N descendants with the probability pk at the end (or by the end) of his life, the time being measured in generations. A number j ∈ N of immigrants join the generation with probability aj and contribute to the following generation in the same way as the individuals born in the original population. We suppose that all the objects reproduce mutually independently and independently of the immigration process, and also that the immigration rates in successive generations are independent.
Formally, we will place ourselves in the following context. Let ξi(n), η(r),![]() , be independent r.v. with generating functions
, be independent r.v. with generating functions
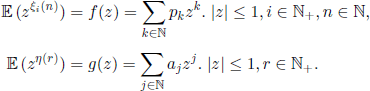
Let us define the r.v. X(N)(n) = X(n), n ∈ N, by the relations X(0) = N and
for n ∈ N. By B-G-W model with immigration we mean the random sequence X(N) = {X(N)(n),n ∈ ![]() ) together with relations [6.23]. Obviously, for a0 = 1 we get the classic model. Therefore, we will suppose in the following that a0 < 1.
) together with relations [6.23]. Obviously, for a0 = 1 we get the classic model. Therefore, we will suppose in the following that a0 < 1.
Like in the classic model, relations [6.23] show that X(N) is a homogenous Markov chain with state space N, initial distribution concentrated at state N, and transition probabilities
Note that for the B-G-W model with immigration, the state 0 is not absorbing anymore, hence we can no longer speak about population extinction and extinction probability (more precisely, this probability is equal to 0). Note that, if pk ≠ 1, k ∈ N, then the state space of the chain X(N) is in fact an infinite subset S of N, and the chain is irreducible and aperiodic; we have S = N if, for instance, a0 > 0, p0 > 0, p1 > 0.
Starting from relations [6.23] we immediately obtain, through a reasoning completely similar to the one used for proving Proposition 6.1, that the generating function h(N) of the r.v. Xn(N) is given by the relations

where, as in section 6.1.1, fj is the iterate of order j of f, j ∈ ![]() +. This implies that the n-step transition probabilities of the Markov chain X(N) are given by p(n, i, j) = the coefficient of zj in h(ni)(z), n, i, j ∈ N.
+. This implies that the n-step transition probabilities of the Markov chain X(N) are given by p(n, i, j) = the coefficient of zj in h(ni)(z), n, i, j ∈ N.
It also implies that, as opposed to the classic model, the chain X(N) does not satisfy the additive property. In the following we will suppose either that N has a fixed value (often 1) or that it is an r.v. with an arbitrary probability distribution. Obviously, the transition probabilities [6.24] are the same for all the chains X(N), n ∈ N+. Note that, if N is a r.v. with generating function g, then the generating function of X(n) is
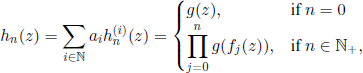
where f0(z) = z. (Obviously, in the case when N is random we have to consider a non-degenerated initial probability, which does not affect at all the transition probabilities [6.24].) If the generating functions h(ni)(z) satisfy the functional equations h(ni+) 1(z) = g(z)h(ni)(f(z)), n ∈ N+, then the generating functions hn(z) satisfy the functional equations hn+1(z) = g(z)hn(f(z)), n ∈ N. As the sequence (hn(z), n ∈ N) is decreasing, the limit h(z) = limn→∞ hn(z) exists and satisfies the functional equation
A B-G-W model with immigration will be called subcritical, critical, or supercritical according as m(=∑k∈N kpk) < 1, m = 1, or m > 1.
THEOREM 6.50.– (i) (C. R. Heathcote) In the supercritical case m > 1 or in the critical case m = 1 with f″(l) < ∞, for all k ∈ ![]() + we have
+ we have
(ii) (C.R. Heathcote, E. Seneta, M.P. Quine) In the subcritical case m < 1 the sequence X(n) converges in distribution, as n → ∞, to an r.v. X(∞) whose generating function π(z) = Πj∈Ng(fj(z)) = ∑k∈N πkzk is the unique solution of equation [6.25]. The r.v. X(∞) is non-degenerated (7r(l) = 1) if and only if
(iii) (Pakes [PAK 79b]) In the subcritical case, when [6.26] does not hold,16 we have:
(iii1) If limx→∞ x(1 −g(1 − e−x)) = 0, then the limit distribution function of the r.v. Λ(X(n))/Λ(m−n) as n → ∞ is
![]()
Where ![]() , and ζ = −1log m.
, and ζ = −1log m.
(iii2) If limx→∞ x(1 − g(1 − e−x)) = a > 0, then the limit distribution function of the r.v. (ζ/n) log (l + X(n)) as n → ∞ is
![]()
(iii3) If 1 − g(1 − e−x) = (xδ L(x))−l, x > 0, where L is a function with slow variation at infinity, and either 0<δ<1 or δ = l and limx→∞ L(x) = 0, then the limit distribution function of the r.v. an−1 log(l + X(n))as n→∞ is
![]()
where the constants an satisfy the relations 1 − g(1 − e−an)= (ζ/n, n ∈ ![]() +.
+.
(iii4) If 1 − g(l − e~x) = (L(x))−1, x ≥ 0, where L is a function with slow variation at infinity, then the limit distribution function of the r.v. n(1 − g (exp(−1/X(n))) as n → ∞ is
![]()
For the proof we can see ([JAG 75], (p. 55) and [PAK 82].
Remarks. 1. Theorem 6.50 (ii) shows that in the subcritical case the Markov chain X(N) is strictly positive recurrent, i.e. there exist the positive limits limn→∞ P(X(n) = k) = πk, k ∈ S, independently of N, if and only if condition [6.26] is verified. In [FOS 71b] it is proved that for m < 1 the chain X(N) is strictly positive recurrent if and only if
So, for m < 1, conditions [6.26] and [6.27] are equivalent. Hence, we see that the immigration ensures the stability of the population under conditions not too restrictive. It is natural to ask what happens if [6.26] does not hold. A partial answer was given by Pakes [PAK 75b]: for m < 1, if limn→∞ n(l − g(fn(0))) < 1(> 1), then the chain X(N) is null recurrent (non-recurrent).
2. We have to mention ([JAG 75], pp. 55–56) the parallel between “the classic model conditioned on survival” and “the subcritical model with immigration.” Equation [6.11] for m < 1, written as b(f(z)) = mb(z) + 1 − m, is a particular case of equation [6.25]. Indeed, if we put (1 − b(z))/(l − z) = h(z) and (1 − f(z))/m(l − z) = g(z), equation [6.11] is reduced to equation [6.25]. It is true that (1 − b(z))/(l − z) is not a generating function (except if b′(l) = 1). But, if b′(l) < 1, then we can take h(z) = (1 − b(z))/b′(1)(1 − z), which is a generating function.
In the supercritical case we expect the immigration to have a non-significative effect on the asymptotic behavior of the model.
THEOREM 6.51.– (i) (E. Seneta) In the supercritical case m > 1, there exists a sequence (Cn, n ∈ ![]() +) of constants (the same as in Theorem 6.26) satisfying the relations
+) of constants (the same as in Theorem 6.26) satisfying the relations
![]()
such that X(1)(n)/Cn converges a.s. as n → ∞ to an r.v. V. If [6.26] holds, then ![]() (V < ∞) = 1 and V has an absolutely continuous distribution on (0, ∞). If [6.26] does not hold, then
(V < ∞) = 1 and V has an absolutely continuous distribution on (0, ∞). If [6.26] does not hold, then ![]() (V = ∞) = 1.
(V = ∞) = 1.
(ii) (Jagers [JAG 75], pp. 58–59) If [6.26] holds, then the characteristic function of V is given by the infinite product ![]() and its mean is equal to
and its mean is equal to ![]() (W)g′(1)m/(m − 1), where W is the r.v. from Theorem 6.26 and φ is its characteristic function. If
(W)g′(1)m/(m − 1), where W is the r.v. from Theorem 6.26 and φ is its characteristic function. If ![]() , then we can take Cn = mn, n ∈
, then we can take Cn = mn, n ∈ ![]() +.
+.
(iii) (Pakes [PAK 74]) If [6.26] holds, we have:
(iii1) If −log(q)/ log m > 1, where q is the root in (0,1) of equation f(x) = x, then V has a continuous and bounded density;
(iii2) If g′(l) < ∞ and ![]() , then V has a continuous density;
, then V has a continuous density;
(iv) (Cohn [COH 77b]) If [6.26] does not hold, then there does not exist a sequence (Cn,n ∈ ![]() +) of constants that tends to infinity such that X(n)/Cn converges in distribution as n → ∞ to a proper r.v. non-degenerated at the origin.
+) of constants that tends to infinity such that X(n)/Cn converges in distribution as n → ∞ to a proper r.v. non-degenerated at the origin.
In [PAK 82] we can find results for the supercritical case that correspond to the conditions imposed to the function 1 − g(1 − e−x) in Theorem 6.50 (iii); we can also find a study of the asymptotic behavior of the transition probabilities of the chain X(N) with respect to n.
For results concerning B-G-W models with immigration when m = ∞, we can see [BAR 79a].
Finally, in the critical case m = 1 we can prove the following result, similar to Theorem 6.19.
THEOREM 6.52.– (J. Foster, E. Seneta) In the critical case m = 1, if f″(l) = σ2 < ∞ and 0 < λ = g′(l) < ∞, then 2X(1)(n)/nσ2 converges in distribution as n → ∞ to an r.v. of density
![]()
For the proof we can see [JAG 75], pp. 56–57.
Note that, if A = σ2/2, then p(x) = e−x. Recalling Theorem 6.19, we can therefore say that the impact of the conditioning of the limit distribution of X(n)/n on survival is identical to that of immigration of mean σ2/2.
All these results underline the importance of the parameters m and A. There are in-depth studies concerning their estimation ([DIO 78], pp. 117–119). Let us consider the chain X(1) and suppose that 0 < σ2 = Var [X(l)] < ∞, 0 < b2 = Var [η(l)] < ∞. In the supercritical case m > 1, the asymptotic properties of the Lotka-Nagaev estimator m of m or of the estimator σ2 of σ2 (see section 6.1.13) are robust, in the sense that they are still valid for the B-G-W model with immigration. In the subcritical case m < 1 we have to face a new situation. Thus we have the following result.
THEOREM 6.53.– (C. C. Heyde, E. Seneta, M. P. Quine) In the subcritical case m < 1, assuming that 0 < σ2, b2 < ∞, the variables
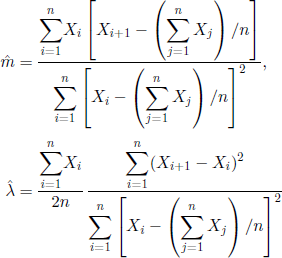
are strongly consistent estimators of m and A, respectively. Both of them are also asymptotically normal.
This theorem is obtained using well known properties of the countable Markov chains [QUI 76a].
For other researches concerning statistical inference in B-G-W models with immigration, we can see [BHA 81, VEN 82, YAN 80b, ZUR 77, ZUR 78].
Let us mention an interesting application of the B-G-W model with immigration to the problem of the fluctuation in the number of particles contained in a geometrically well-defined small element of volume, from a much larger volume of solution containing particles in random motion. This problem was studied by the Polish physicist Marjan von Smoluchowski starting from 1915, without any specific link to branching processes. As Heyde and Seneta show [HEY 72a], it was actually the B-G-W model with immigration that was used in that application, with f(z) = 1 − m + mz, m < 1, g(z) = exp[λ(l − z)], λ > 0, and the generating function of the limit distribution given by π(z) = exp[λ(l − z)/(l − m)]. For details we can see [HEY 72a] and ([IOS 73], II, pp. 44–46).
We will conclude this section by presenting three B-G-W models with immigration.
I. If the r.v. r)(r),r ∈ N+, do not have the same distribution anymore, so the generating function gr(z) of η(r) depends on r ∈ N+, we obtain the B-G-W model with varying immigration (dependent on generation). In this case, the sequence X(N) = (X(N)(n),n ∈ N) defined by [6.23] is a Markov chain, while the generating function of X(N)(n) is equal to zN, g1(z) fN(z), or ![]() according ton = 0, n = l,or n > 1.In the critical case m = 1 (see [FOS 76a]) if σ2 < ∞ we have limn→∞ P(X(n) = k) = 0, k ∈ N+, whatever the choice of the generating functions gr, r ∈ N+ is (compare to Theorem 6.50 (i)). This model did not interest the researchers (see [BAD 81, RAH 78, RAH 79, RAH 81a, RAH 81b]).
according ton = 0, n = l,or n > 1.In the critical case m = 1 (see [FOS 76a]) if σ2 < ∞ we have limn→∞ P(X(n) = k) = 0, k ∈ N+, whatever the choice of the generating functions gr, r ∈ N+ is (compare to Theorem 6.50 (i)). This model did not interest the researchers (see [BAD 81, RAH 78, RAH 79, RAH 81a, RAH 81b]).
II. It is clear that from an applied point of view, the introduction of an immigration component that depends on the size of the population is more realistic. In the general case this is a difficult problem (and still open). Nevertheless, a particular case was deeply studied. We mean the case where the immigration component is active only at the moments when the size of the population is reduced to 0. Formally, in the context we considered at the beginning of this section, we define the r.v. Y(N)(n) = Y(n), n ∈ N, by the relations Y (0) = N and
for n ∈ N. The random sequence Y (N) = (Y (N)(n), n ∈ N), which is a Markov chain (irreducible and aperiodic if 0 < p0, p0 + p1, a0 < 1, p1 > 0), together with relations [6.28] define the B-G-W model with immigration dependent on survival. For this model, the generating function fn(N)(z) of Y (N)(n) satisfies the recurrence relation
![]()
We obtain that
![]()
where f0 (z) = z. Concerning the asymptotic behavior, we have to mention the following result [FOS 71a]: if m = 1, f″(l) < ∞, Pk < 1, g′(l) < ∞, pk < 1, k ∈ N, a0 < 1 then limn→∞ (log Yn(N)(n)/log n < x) = x, 0 ≤ x ≤ 1. For other results we can see [KUL 83, LÉV 54, STE 76a, STE 76b].
A model Y(N) = (Y(n),n ∈ N) dual to the one presented above, where immigration is allowed only if the size of the population is > 0, defined by the relations Y(0) = N and
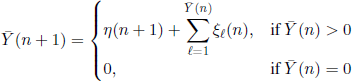
for n ∈ N, was studied in [SEN 83] (see also [VAT 74]).
III. Let us assume that the variables η(r), r ∈ N, take also a finite number of negative values, their common distribution being given by the relations P(η(r) = k) = ak, k ∈ N, P(η(r) = −u) = eu, 1 ≤ u ≤, with ![]() , and let us define the r.v. Z(N) (n) = Z(n),n ∈
, and let us define the r.v. Z(N) (n) = Z(n),n ∈ ![]() , by the relations Z(0) = N and
, by the relations Z(0) = N and
for n ∈ N. The random sequence Z(N) = (Z(N)(n),n ∈ N), which is a Markov chain (irreducible and aperiodic if po > 0), together with relations [6.29], defines the B-G-W model with immigration and emigration. Obviously, the emigration component is introduced by the negative values taken by the variables η(r), r ∈ N. For this model, studied in [HAN 80, NAG 80], the generating function ![]() of Z(N)(n) has not a simple form. It is not difficult to prove the recurrence relations
of Z(N)(n) has not a simple form. It is not difficult to prove the recurrence relations
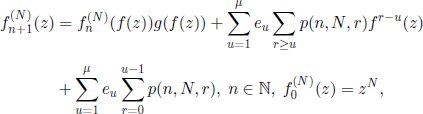
where g(z) ![]() . (In our case we have g(1) < 1.)
. (In our case we have g(1) < 1.)
The asymptotic behavior of the B-G-W model with immigration and emigration depends in a crucial way on the value ![]() , where A = g′(1) = ∑k∈N kak. Assuming that m = f′(l) < ∞, po,eμ > 0, δ < ∞, in [HAN 80] it is proved that:
, where A = g′(1) = ∑k∈N kak. Assuming that m = f′(l) < ∞, po,eμ > 0, δ < ∞, in [HAN 80] it is proved that:
(a)If m = 1, f″(l) < ∞ and δ > 0, then the asymptotic behavior of the r.v. Z(0) (n)/δn as n → ∞ is of the type presented in Theorem 6.52.
(b)If m = 1 and δ < 0, then the Markov chain Z(N) is positive recurrent (compare to Theorem 6.50 (ii)).
(c)If m > 1, then the asymptotic behavior of the r.v. Z(0) (n)/mn as n → ∞ is of the type that appears in Theorem 6.23.
In [NAG 80] it is proved that, if p0, eμ > 0, m = 1, f″(l) < ∞, and δ = 0, then
![]()
We have already seen that this behavior occurs for the B-G-W model with immigration dependent on survival.
If the emigration component does not exist (eu = 0, 1 ≤ u ≤ μ), the model we considered is reduced to a B-G-W model with immigration for which the generating function of the immigration component is g(f(z)). If the immigration component does not exist (ak = 0, k ∈ N), the model we considered is reduced to what we could call the B-G-W model with emigration. Such a model was studied in [VAT 77] under the hypothesis e1 = 1.
6.2.4. B-G-W models with controlled multiplication
In this section we present a generalization of the classic model that includes many extensions of the classic model that we have already presented.
The basic idea of this generalization [SEV 74b] is to consider that either only a part of the X(n) objects in the nth generation is able to multiply in order to form the (n + l)th generation, or the (n + l)th generation is formed by the multiplication of more than X(n) objects. This is achieved by introducing a function φ of control (of the multiplication) from N to N. If ξi, i ∈ N+, n ∈ N, are independent r.v. with the same generating function /, then the size X(N) = X(n) of the population at time n ∈ N is defined by the relations X(N) (0) = N and
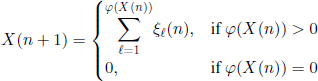
for n ∈ N. The random sequence X(N) = (X(n),n ∈ N), which is a homogenous Markov chain with state space included in N and initial distribution concentrated at N, is called a φ-controlled B-G-W model or, briefly, model (1,1); the meaning of this designation will be clarified in the following. Obviously, the classic model is obtained for φ(n) = n, n ∈ N. If φ(n) < n, this means that n − φ(n) objects do not multiply when the size of the population is n, whereas φ(n) > n means that a number of φ(n) − n objects join the population and they multiply there. Thus we see that the case φ(n) = max(0,n−1), n ∈ N, corresponds to the model studied in [VAT 77]− see the end of section 6.2.3.
Here is a result that highlights a certain robustness of the classic model.
THEOREM 6.54.– (Sevastyanov and Zubkov [SEV 74b]) Let us assume that the limit imn→∞ φ(n)/n = α exists. If α f′(1) < 1, φ(0) = 0, and p0 = /(0) > 0, then the extinction probability qN = limn→∞P(X(N)(n) = 0) is equal to 1.
We can render the model (1,1) more complicated with the introduction of random control functions [YAN 75]. Formally, we start with two independent families ξ = (ξi(n),i ∈ N+,n ∈ N) and φ = (φt(n),t,n ∈ N) of independent r.v. with non-negative integer values, such that the variables from ∈ are independent with the same generating function / and the sequences φt = (φt(n),n ∈ N), t ∈ N, are independent and have the same 1D distributions, i.e. P(φt(n) = k) = Pn(k) does not depend on t ∈ ![]() , for all k, n ∈
, for all k, n ∈ ![]() . Let us consider now the variables X(N) (n) = X(n), defined by the relations X(N) (0) = N and
. Let us consider now the variables X(N) (n) = X(n), defined by the relations X(N) (0) = N and
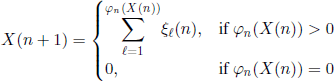
for n ∈ N. These variables form the φ-controlled B-G-W model with φ random. It is easy to see that the B-G-W model with immigration and emigration (see section 6.2.3) is a particular case of a (φ-controlled B-G-W model with pt(n) = n + η(t), t,n ∈ N, provided that we allow that the variables pt(n) take also a finite number of negative integer values. For the (φ-controlled B-G-W model with φ random we give the following interesting result (that asks no conditions for the family φ).
THEOREM 6.55.– (Bruss [BRU78, BRU80]) If for any t ∈ N we have Pt(n) = 0 if and only if n = 0, and if Pt(n) ≤ αtn, where (at,t ∈ N) is a sequence of positive random variables, then a sufficient condition for qN = limn→∞ P(X(N)(n) =0) = l is E (log f′(1)αt) ≤ ∈ < 0, t ∈ N.
A more complex (φ-controlled B-G-W model with φ random was considered in [YAN 77], where the model is placed in a random environment.
For details concerning the (1,1) model, the reader is referred to the works already cited and also to [SCH 76, ZUB 74, YAN 80a, YAN 83].
We will conclude this presentation of models with controlled multiplication by introducing a generalization of the (1,1) model, that will partially explain this designation; the complete explanation will result from section 6.2.6. Let![]() (at most countable set), i ∈ N+, n ∈ N, be independent r.v. and let φ(j), j ∈ J, be functions from N to N. The model (card J, 1) is formed by the variables X(N)(n) = X{n), n ∈ N, defined by the relations X(N)(0) = N and
(at most countable set), i ∈ N+, n ∈ N, be independent r.v. and let φ(j), j ∈ J, be functions from N to N. The model (card J, 1) is formed by the variables X(N)(n) = X{n), n ∈ N, defined by the relations X(N)(0) = N and
with the convention ![]() .
.
Here are some particular cases of the model (card J, 1) for J = {1,2}: if <φ(1)(n) = n and φ(2)(n) = 1 then we have the B-G-W model with immigration; if φ(1)(n) = n and φ(2)(n) = max(l − n, 0) then we have the B-G-W model with immigration depending on survival; if φ(1)(n) = n and φ(2) (n) = min(n, 1), then we have the model YN dual to the previous model (see section 6.2.3).
It is clear that the model (card J, 1) can be rendered more complicated by introducing random functions φ(j), j ∈ J, and/or a random environment.
It is worth mentioning that the results obtained for a model (card J, 1) are generally weaker than the results obtained for particular cases of this model. Like any generalization, the model (card J, 1) provides first of all a unifying framework.
6.2.5. B-G-W models with spatial spread
These models combine the multiplication phenomenon with spatial movements. For example, to a classic B-G-W model with generating function ∑k∈N Pkzk we can superpose a movement of the random walk type on the real line as follows. Suppose that an initial object is at point x0 ∈ R. At the end of his lifetime, with probability pk, k ∈ N+, it is replaced by k identical objects which are at points xq + ξ1, …, x0 + ξk, where (ξk, k ∈ N+) is a sequence of i.i.d. r.v. The objects of the next generation behave in the same manner, their movements being independent of those of their parents, etc. By multiplicative random walk we mean the family of r.v. {X(n, x | X0) = number of objects in the nth generation that are to the left side with respect to x : x ∈ R,n ∈ N}.
We do not discuss here the researches dedicated to this type of model. The interested reader can see [ASM 83, ATH 72, ATH 78, BIG 78, BIG 79a, BIG 80, BIG 81, BIG 79b, BRA 78, BRO 75, DUR75, DUR 79, DUR83, IVA 80a, IVA 80b, IVA 81a, IVA 81b, IVA 83, KAP 82, KLE 82a, LEN 84, OGU 83, PAS 78, SAW 76, SHI 77].
6.2.6. B-G-W model with r types of objects
The populations modeled by the different B-G-W models that we have presented up to here were formed by identical objects. We are interested now in the case of a population whose objects are of several types, say r ∈ ![]() +. This situation is in fact the most frequent in various physical or biological contexts. These types can represent different genotypes in an animal population, mutant alleles in a bacterium population, electrons, photons, neutrons, etc. in a cosmic ray shower, etc. The simplest model for the evolution of such a population, which is a straightforward generalization of the classic B-G-W model, was studied after World War II by M. S. Bartlett, N. A. Dmitriev, C. J. Everett, A. N. Kolmogorov, B. A. Sevastyanov, and S. Ulam.
+. This situation is in fact the most frequent in various physical or biological contexts. These types can represent different genotypes in an animal population, mutant alleles in a bacterium population, electrons, photons, neutrons, etc. in a cosmic ray shower, etc. The simplest model for the evolution of such a population, which is a straightforward generalization of the classic B-G-W model, was studied after World War II by M. S. Bartlett, N. A. Dmitriev, C. J. Everett, A. N. Kolmogorov, B. A. Sevastyanov, and S. Ulam.
Formally, we consider the following framework. Let ![]()
![]() be r-dimensional independent random (row) vectors such that the generating function of the vectors
be r-dimensional independent random (row) vectors such that the generating function of the vectors ![]() is
is
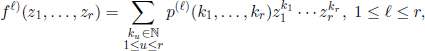
for |z1| ≤ 1,…, |zr| ≤ 1 (independent of % and n). Here, p(i) (k1, … ,kr) is the probability that an object of type ∈ has k1 descendants of type 1, … , kr descendants of type kr. Let us define the r-dimensional random vectors Xl(n) = (Xiu(n),1 ≤ u ≤ r), n ∈ ![]() , by the relations Xl(0) = el (r-dimensional vector whose components are equal to 0, except the one of rank
, by the relations Xl(0) = el (r-dimensional vector whose components are equal to 0, except the one of rank ![]() which is equal to 1) and
which is equal to 1) and
for n ∈ N, where 0 is the r-dimensional zero vector, with the usual convention ![]() . By an r-type B-G-W model with ancestor of type ∈ we mean the sequence of r.v. (Xl(n), n ∈ N) together with relations [6.31]. Note that (Xl (n) ,n ∈ N) is a homogenous Markov chain with state space included in Nr and absorbing state 0. It is very easy in the present context to see the interpretations corresponding to the classic case r = 1 (see section 6.1.2).
. By an r-type B-G-W model with ancestor of type ∈ we mean the sequence of r.v. (Xl(n), n ∈ N) together with relations [6.31]. Note that (Xl (n) ,n ∈ N) is a homogenous Markov chain with state space included in Nr and absorbing state 0. It is very easy in the present context to see the interpretations corresponding to the classic case r = 1 (see section 6.1.2).
For the sake of simplicity, let us introduce the following vector notations: z = (z1, …, zr), k = (k1, …, kr), z = (1, …, 1), zk ![]() (z) =
(z) = ![]() (z1, …, zr) =
(z1, …, zr) = ![]() (k)zk, 1 ≤
(k)zk, 1 ≤ ![]() ≤ r, f(z) =(f(1)(z), …, f(r)(z)),
≤ r, f(z) =(f(1)(z), …, f(r)(z)), ![]() =
= ![]() fn(z) =
fn(z) = ![]() , 1 ≤
, 1 ≤ ![]() ≤ r, n ∈
≤ r, n ∈ ![]() so f0(z) = z, f1(z) = f(z), muv =
so f0(z) = z, f1(z) = f(z), muv = ![]() Xuv(1) = (∂f(u) /∂zv)(1), 1 ≤ u, v ≤ r, m = (muv, 1 ≤ u, v ≤ r). With these notations, the iterative scheme of the classic model still holds here: f0(z) = z, fn+1(z) = fn(f(z)), n ∈
Xuv(1) = (∂f(u) /∂zv)(1), 1 ≤ u, v ≤ r, m = (muv, 1 ≤ u, v ≤ r). With these notations, the iterative scheme of the classic model still holds here: f0(z) = z, fn+1(z) = fn(f(z)), n ∈ ![]() +, and mn is the matrix whose entries are
+, and mn is the matrix whose entries are ![]() [Xuv (n)] ,1 ≤ u,v ≤ r,n ∈
[Xuv (n)] ,1 ≤ u,v ≤ r,n ∈ ![]() . Consequently,
. Consequently, ![]() Xu(n) = eumn and, more generally,
Xu(n) = eumn and, more generally, ![]() (X(n + n′) Xu(n′)) = Xu(n′)mn, n, n′ ∈
(X(n + n′) Xu(n′)) = Xu(n′)mn, n, n′ ∈ ![]() , 1 ≤ u ≤ r. If we let
, 1 ≤ u ≤ r. If we let ![]() 1 ≤ u, v ≤ r), n ∈
1 ≤ u, v ≤ r), n ∈ ![]() , then it is easy to prove the formula
, then it is easy to prove the formula
![]()
Here ′ stands for the matrix transpose, while (a)v means the entry of rank v, 1 ≤ v ≤ r, of the r-dimensional vector a.
It is also easy to see that the generating function of Xu (n+n′) conditioned on Xu(n′) is (fn(z)Xu(n′). This shows that, as in the classic model (r = 1), for the r-type B-G-W model we have the additive property: a model with X(0) = i = {i1,…, ir) is the sum of i1 +… + ir independent models, il of which are initiated by an ancestor of type l, 1 ≤ l ≤ r.
It is useless to recall once again the difficulty of explicitly computing the iterates of fn(z). In fact, the only case when this is possible is that of generating functions f(l) of the form ![]()
![]() (see [POL 74]).
(see [POL 74]).
This is not to say that all the theory in the case r > 1 can be reduced to the classic case written in matrix notation. As it is pointed out in ([JAG 75], p. 89), multi-type models are more complex than classic ones, because, besides the multiplicative structure, they also have a structure of Markovian movement between the different types. The extreme cases are r = 1 (the classic model), where there is only multiplication, and that of a Markov chain with r > 1 and transition matrix (pli, 1 ≤ l, j ≤ r), where there is no multiplication and ![]() . The latter model is called singular and can be seen as describing the passage of an object through the r possible types. The difficulty brought about by the second structure (several classes, periodicity) can be avoided if we limit our study to positive regular models, characterized by the existence of an n ∈ N+ such that the matrix m″ has only positive entries. The main tool in this case is the Perron-Frobenius theorem.17
. The latter model is called singular and can be seen as describing the passage of an object through the r possible types. The difficulty brought about by the second structure (several classes, periodicity) can be avoided if we limit our study to positive regular models, characterized by the existence of an n ∈ N+ such that the matrix m″ has only positive entries. The main tool in this case is the Perron-Frobenius theorem.17
We will state in the following several results for positive regular models. These results are completely similar to their analogue for classic models. For proofs and other developments the reader is referred to ([ATH 72], ch. V) and [MOD 71, SEV 74a]. The study of models that are not positive regular (also called decomposable) is far from being complete. On this topic, we can see [MOD 88, SEV 74a, HOP 75a, HOP 75b, FOS 76b, FOS 79, SUG 81].
Let us denote by ql the extinction probability of an r-type B-G-W model with ancestors of type ξ, i.e.
![]()
and let q = {q1,…, qr). The eigenvalue ρ plays a similar role as the one of the mean value m in the classic model (r = 1).
THEOREM 6.56.– (C. Everett, B.A. Sevastyanov, S. Ulam) For a positive regular non-singular model we have q = 1 if ρ < 1. If ρ > 1, then 0 < q < 1, i.e. 0 ≤ ql < 1, 1 ≤ ∈ ≤ r, and q is the unique solution ≠ 1 of equation q = f(q) in the r-dimensional unit cube. In either case, we have q = limn→∞ fn(q0) for any q0 ≠ 1 in this cube.
In all the statements below, we have vm = ρv, mu′ = ρu′, u1′ = vu′ = 1. Let
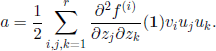
THEOREM 6.57.– (T. W. Mullikin, A. Joffe, F. Spitzer) If ρ = 1 and 0 < a < ∞, then
![]() for all 1 ≤ i ≤ r. The distribution of Xl(n)/n conditioned on Xl(n) ≠ 0 converges as n → ∞ to the distribution of αv, where a is an exponential r.v. of parameter a, for any 1 ≤ l ≤ r.
for all 1 ≤ i ≤ r. The distribution of Xl(n)/n conditioned on Xl(n) ≠ 0 converges as n → ∞ to the distribution of αv, where a is an exponential r.v. of parameter a, for any 1 ≤ l ≤ r.
THEOREM 6.58.– (M. J![]() rina, T. E. Harris, A. Joffe, F. Spitzer) If ρ < 1, then for any 1 ≤ l ≤ r the limit
rina, T. E. Harris, A. Joffe, F. Spitzer) If ρ < 1, then for any 1 ≤ l ≤ r the limit
![]()
exists, does not depend on ξ, and is positive if and only if
For any k = (k1,…, kr) ∈ Nr+ and 1 ≤ l ≤ r, the limit limn→∞ P(Xl(n) = k | Xl(n) ≠ 0) = bk exists, does not depend on ξ, and we have ∑k∈N bk = 1. If [6.32] holds, then ![]() . The generating function
. The generating function ![]() satisfies the functional equation g(f(z)) = g(z) + 1 − ρ, that uniquely determines it if and only if [6.32] holds.
satisfies the functional equation g(f(z)) = g(z) + 1 − ρ, that uniquely determines it if and only if [6.32] holds.
THEOREM 6.59.– (Pollak [POL 74]) If p > 1 and ql > 0, 1 < l < r, then there exist the positive limits ![]() , where ρ is the eigenvalue with maximum absolute value of the matrix m(q), whose components are
, where ρ is the eigenvalue with maximum absolute value of the matrix m(q), whose components are ![]() r) satisfies the relation
r) satisfies the relation ![]() .
.
THEOREM 6.60.– (H. Kesten, B. P. Stigum) If ρ > 1, then limn→∞ Xl(n)/ρn = Wlv, where Wl is an r.v., 1 ≤ l ≤ r. If [6.32] fails to hold, then Wl = 0 a.s., 1 ≤ l ≤ r. If [6.32] holds, then we have EWi = ul, P(Wl = 0) = ql, 1 ≤ l ≤ r, and the characteristic functions φl (t) = exp(it Wl), 1 ≤ l ≤ r, satisfy the equation
where va(t) = (φ1(t),… ,φr(t)). The r.v. Wl has a positive, continuous density on (0, ∞), 1 ≤ l ≤ r.
THEOREM 6.61.– (Hoppe [HOP 75a]) Suppose ρ > 1.
(i) There exists a sequence (Cn,n ∈ N+) of positive vectors and a sequence (γn,n ∈ N+) of positive numbers such that limn→∞ Cn [Xl(n)]′ = ![]() a.s.,exists with
a.s.,exists with ![]() a.s.,18
a.s.,18 ![]()
![]() . The characteristic functions φl(t) = exp(itWl), 1 < ∈ < r, satisfy equation [6.33]. Any other function that satisfies this equation is of the form φl(ct), 1 ≤ l ≤ r, with c ∈ R+.
. The characteristic functions φl(t) = exp(itWl), 1 < ∈ < r, satisfy equation [6.33]. Any other function that satisfies this equation is of the form φl(ct), 1 ≤ l ≤ r, with c ∈ R+.
(ii) The mean values E Wl, 1 ≤ ∈ ≤ r, are finite (in fact, if one of them is finite, then all of them are finite) if and only if a < ∞, or if and only if [6.32] holds.
(iii) The r.v. Wl, 1 ≤ l ≤ r, have non-negative continuous densities on (0, ∞).
(iv) We have ![]() , for any 0 ≤ α ≤ 1.
, for any 0 ≤ α ≤ 1.
COROLLARY 6.62.– Under the hypotheses of Theorem 6.60 or under those of Theorem 6.61, for any 1 ≤ i, l ≤ r we have
![]()
on the set where the model does not explode.
Remark. This corollary is particularly interesting, because it shows that the limit proportions of the types of objects are determined by the structure of the models and that chance plays no role.
The applications of the r-type B-G-W model are extremely numerous. We will only present three of them here.
(a)The dynamics of female population in Australia was studied by a B-G-W model with 60 types of objects corresponding to the age classes in the time interval 0–60 years. See, for example, ([IOS 73], II, pp. 97–110).
(b) The size of the nest of some species of birds, which according to Darwin’s theory of natural selection should ensure their survival, was analyzed by Heyde and Schuh [HEY 78] using a B-G-W model with several types of objects, corresponding to the number of eggs laid. For many species of birds, this number is either k (fixed) or of the form k or k + 1 for a certain k, 2 ≤ k ∈ N+. The authors concluded that under reasonable biological conditions, the birds’ behavior can correspond to the maximization of the survival probability of the species in any generation. We have thus an intuitive confirmation of the power of natural selection.
(c)Asymptotic theorems for the B-G-W model with two types of objects were used by Moore and Snell [MOO 79] for the study of Ising (-Lenz) model for magnetism. [For an interesting presentation of the origins and the developments of this model see S. Brush, History of Lenz-Ising model, Rev. Mod. Phys. 39, 883–893 (1967).]
We will conclude our short presentation of the theory of B-G-W models with several types of objects with two remarks.
There are numerous works that study different extensions of the models that we have presented to the multi-type case. In particular, we can define the model (cardJ, r) by considering that all the quantities that appear in equations [6.30] are random vectors and that the functions φ(j), j ∈ J, are from Nr to N. For J = {1} and r = 2, two interesting particular cases are: (a) φ(n1,n2) = n1 min(n2,l); (b) φ(n1,n2) = min(n1,n2), with d ∈ N+. These cases correspond to multiplication models in two-sex populations; they were considered by Daley [DAL 68] and studied in [KAP 73] and [HUL 84]. See also ([ASM 83], ch. XI).
Another direction is the study of those models where the state space is neither a subset of N (as in the classic model with r = 1) nor a subset of Nr (as in the case r > 1), but a subset of an euclidean space with an arbitrary number of dimensions, or, more generally, an abstract space with an additive structure. These models were introduced by M. Jirina in 1958. The fundamental references on this topic are [ASM 83, KAL 79, MAT 78].
6.3. Continuous-time models
An essential characteristic of the models studied in sections 6.1 and 6.2 was the hypothesis that the lifetime of all the objects of the populations was equal to one unit of time. In other words, the unit of time was the lifetime of a generation. Since in the most natural processes lifetime is random, the study of models whose objects have lifetimes that are discrete or continuous r.v. is of an undeniable interest. In this section we will successively investigate the case of exponentially distributed lifetime (the Markov model) and of arbitrarily distributed lifetime (the Bellman-Harris model). In both cases, the birth of descendants occurs at the end of the life of the objects, exactly like in the models previously presented. This restrictive hypothesis will be removed in the Crump-Mode-Jagers-Ryan model that we will present at the end of the section. We have to stress that if we set aside the exponential distribution for modeling the lifetimes, we lose the additive property that is a fundamental feature of the B-G-W model.
We want to warn the reader that, due to the well known complications of the theory of stochastic processes with continuous parameter, we can only present here some introductory notions. For further details and developments, the reader is referred to [ASM 83, ATH 72, HAR 63, JAG 75, MOD 71], as well as to the works cited in each section.
6.3.1. The Markov model
Let us consider a homogenous Markov process ![]() with state space
with state space ![]() (or a subset of
(or a subset of ![]() ), whose transition probabilities
), whose transition probabilities ![]() , i, j ∈
, i, j ∈ ![]() , satisfy the relations
, satisfy the relations
where ![]() . A Markov process with these properties will be called a branching Markov process. It is clear that this is the analogous in continuous time of the B-G-W model, relations [6.34] being the mathematical expression of the additive property of this model (see Corollary 6.2). Note also that using the Chapman-Kolmogorov equations
. A Markov process with these properties will be called a branching Markov process. It is clear that this is the analogous in continuous time of the B-G-W model, relations [6.34] being the mathematical expression of the additive property of this model (see Corollary 6.2). Note also that using the Chapman-Kolmogorov equations
![]()
and taking into account [6.34], we can write
Relations [6.35] are the analogous of relations fm+n(z) = fm(fn(z)), m, n ∈ N, that trivially holds for the B-G-W model. They allow to state that, modulo an equivalence, X(t) has a representation of the form
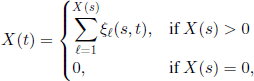
where ξl(s, t), l ∈ N+, for fixed 0 < s < t, are r.v. with generating function ft-s(z), conditionally independent given X(s). This representation is to be compared with relations [6.1].
The definition of a Markov model as given before does not say anything about how the model is actually built. A possible way to do this (see [HAR 63]) is to consider a positive number a and a probability distribution (ak, k ∈ N) on N with a1 = 0. Then, a branching Markov process is the minimal Markov process whose transition probabilities pij(t), t ∈ R+, i, j ∈ N, satisfy the Kolmogorov equations (see section 1.6.2)
with P(0) = I (identity matrix), where P(t) = (pij (t), i, j ∈ N), and Q = (qij , i, j ∈ N) (= dP/dt(0)) is defined by qii = -ai, i ∈ N, and
for i ≠ j, i, j ∈ N. The minimal Markov process can be described as follows. If the process is in state i ∈ N at a certain time (i.e. the size of the population is i), then the process stays in this state for a random duration that is exponentially distributed with parameter ia (so it stays indefinitely if i = 0); then it moves to a state j ≥ i − 1 with the probability aj−i+1 (we can see now the justification of the choice a1 = 0). Once the process is in state j, the process stays there for a random duration that is exponentially distributed with parameter ja, then it moves to a state k with probability ak−j+1, etc. A necessary and sufficient condition for P(t),t ∈ R+, to be stochastic matrices (which is equivalent to P(X(t) < ∞) = 1 for all t ∈ R+) is that for any ∈ > 0, the integral
![]()
is divergent, where a(x) = ∑k∈N akxk. (A simple probabilistic proof of this result owed to E. B. Dynkin is given in [SCH 82b].) In particular, this condition is satisfied if m = a′(l) < ∞, which will be assumed in the following.
Note that from equations [6.36] we can immediately obtain the equations satisfied by the generating functions ft(z),
with ![]()
As for the discrete parameter case, it is difficult to solve these equations. There exists a particular case where the generating functions ft, t ∈ ![]() +, can be explicitly obtained. We mean the linear birth and death process (the Feller-Arley process) for which a = λ + μ and a(z) = (μ + λz2)/(λ + μ), λ, μ > 0. (In this model, each object either disappears without any descendant or has two descendants.) The first equation [6.37] becomes
+, can be explicitly obtained. We mean the linear birth and death process (the Feller-Arley process) for which a = λ + μ and a(z) = (μ + λz2)/(λ + μ), λ, μ > 0. (In this model, each object either disappears without any descendant or has two descendants.) The first equation [6.37] becomes
![]()
with f0(z) = z. The solution is
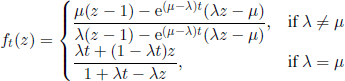
for t ∈ ![]() +, |z| ≤ 1 (compare to section 6.1.3). Taking μ = 0 and A > 0, we obtain the linear pure birth process (the Yule-Furry-McKendrick process).
+, |z| ≤ 1 (compare to section 6.1.3). Taking μ = 0 and A > 0, we obtain the linear pure birth process (the Yule-Furry-McKendrick process).
From the first equation [6.37], we can get the mean values m1(t) = E [X(t)] and m2(t) = E [X2(t)]. Differentiating with respect to z and letting z → 1 we obtain
![]()
with m1(0) = 1, so m1(t) = ea(m−1)t , t ∈ R+. In the same way, m2(t) satisfies the differential equation
![]()
with m2(0) = 1. The solution of this equation is
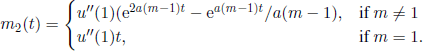
It is useful to compare these formulas with those obtained for the B.-G.-W model (see section 6.1.2).
A simple way of solving problems concerning a Markov model is to reduce them to the corresponding problems concerning the analogous of this model in discrete time, that is the B-G-W model. From equation [6.35] we see immediately that (X(nδ),n ∈ N) is a B-G-W model with generating function fs(z) for all 5 > 0. This remark allows to transfer results from one of the models to the other. To illustrate this fact, let us present the problem of population extinction in the Markov model. Defining this probability q by the relations
![]()
and noticing that the extinction for (X(t),t ∈ R+) is equivalent to the extinction for (X(n5), n ∈ N) for any δ > 0, we obtain that q satisfies the equation q = fs(q) for all 5 > 0. Consequently, ft{q) does not depend on t > 0; therefore, the first equation [6.37] yields u(q) = 0.
THEOREM 6.63.– (B. A. Sevastyanov) Let m = a′(l) < ∞. The probability q is the smallest positive root of equation u(x) = 0. We have q = 1 if and only if m ≤ 1.
PROOF.– We have already seen that q is a root of equation u(x) = a(a(x) − x) = 0. Since ![]() for x > 0 (in the trivial case a0= 1 the theorem is obviously true), the function u is strictly convex on [0,1) (see Figure 6.5).
for x > 0 (in the trivial case a0= 1 the theorem is obviously true), the function u is strictly convex on [0,1) (see Figure 6.5).
If m < 1, then there is no root of equation u(x) = 0 in [0,1), and u(q) = 0 implies that q = 1. If m > 1, then E [X(t)] = ea(m−1)t > 1, t ∈ ![]() +, which means that the B-G-W model (X(n5), n ∈ N) is supercritical and therefore we get that q, which is also the extinction probability of this model, is < 1. We conclude that in both cases q is the smallest positive root of equation u{x) = 0.
+, which means that the B-G-W model (X(n5), n ∈ N) is supercritical and therefore we get that q, which is also the extinction probability of this model, is < 1. We conclude that in both cases q is the smallest positive root of equation u{x) = 0.
For a linear birth and death process, equation u(x) = 0 is λx2 − (λ +μ)x +μ = 0 and m = 2λ/(λ + μ). So m < 1 if and only if A < μ, with q = 1. We have m > 1 if and only if λ > μ, with q = μ/λ.
The asymptotic behavior of X(t) as ∈ → ∞ is completely similar to that of the B-G-W model. For instance, X(t)/m1(t) = X{t)e−a(m−1)t converges a.s., as t → ∞, to a non-negative r.v. W. If m < 1 then W = 0 a.s.; if m > 1, then either P(W = 0) = 1 or E (W) = 1, where the last case occurs if and only if ∑k∈N akk log k < ∞, with P(W = 0) = q.
We end our study of branching Markov processes here. We have to mention that practically all the extensions discussed for B-G-W models have also been considered for branching Markov processes. In addition to the books already recommended, see also [DIO 78, HAC 05, KUR 78, COH 83b].
6.3.2. The Bellman-Harris model
The Bellman-Harris model generalizes the Markov model by assuming that the lifetime distribution of objects is no longer exponential, but it has an arbitrary distribution function G. In this model, an object born at time t = 0 with a lifetime To either dies without having any descendant with probability a0, or gives birth to k > 0 identical objects at the end of his life, with probability ak, k ∈ N+. These descendants have lifetimes τ11, τ12, …, τ1k and, at the end of their lives, they give birth to descendants according to the probability distribution (ak,k ∈ N), etc. This reproduction process continues as long as there exists at least one object. We assume that: the different variables τ are i.i.d. with distribution function G; the appearance of descendants does not depend, either on the state of the population at the corresponding moment, or on the past history of the process; the lifetimes and the production of descendants are independent. Let X(t) be the number of objects at time t ∈ R+. The process (X(t),t ∈ R+) is called the Bellman-Harris model (so called after the names of R. Bellman and T. E. Harris who introduced it in 1952) or the age-dependent branching model. This name is justified by the fact that the probability dG(r)/(l − G(t)) that an object that is alive at time τ will dye during the time interval (τ, τ + dτ) is a non-constant function of τ (except for the case where G(t) = 1 − eaτ, τ ∈ R+).19
Let ![]() . We will obtain (in a rather heuristic manner, with no pretensions of rigor) the integral equation satisfied by the generating functions ft. We have
. We will obtain (in a rather heuristic manner, with no pretensions of rigor) the integral equation satisfied by the generating functions ft. We have
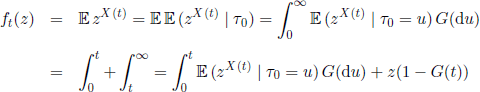
(the last term appears because, if τ0 ≥ t, then the initial object is always alive at time t, so X(t) = 1). If 0 < τ0 < t, then ![]() , where ξi(t − τ0) = number of descendants from object i, 1 < i < v = number of descendants from the initial object that were born at time τ0. Conditioned on τ0 the r.v. ξi(t − τ0) are independent and have the same distribution as X(t − τ0). Consequently,
, where ξi(t − τ0) = number of descendants from object i, 1 < i < v = number of descendants from the initial object that were born at time τ0. Conditioned on τ0 the r.v. ξi(t − τ0) are independent and have the same distribution as X(t − τ0). Consequently,
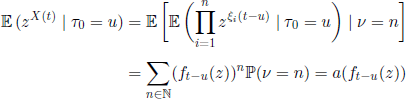
and we obtain the integral equation
This equation corresponds to the first equation [6.37], to which it is in fact reduced if G(t) = l − eat,t ∈ K+, a1 = 0. Equation [6.38] is the fundamental tool in the study of Bellman-Harris models (see [ATH 72], ch. IV).
For the Bellman-Harris model it is no longer true that the sequences (X(n5),n ∈ N), 5 > 0, are B-G-W models. Nevertheless, denoting by ζ(n) the number of objects of the nth generation, the sequence (ζ(n),n ∈ N) is a B-G-W model with generating function a(z). This remark allows us to state that the extinction probability q of the Bellman-Harris model, i.e.
![]()
is the smallest non-negative root of equation x = a(x). There are also other similarities with the Markov model. If G(0+) = 0 (i.e. there is 0 probability of instantaneous death) and m = a′(l) < ∞, then P(X(t) < ∞) = 1, t ∈ R+. Under these conditions, differentiating equation [6.38] with respect to t yields the integral equation satisfied by the mean value m(t) = E X(t)
![]()
which is a renewal equation (see Chapter 4). This equation determines m(t) as its unique solution that is bounded on finite intervals of values of t.
Concerning the asymptotic behavior of X(t) as t → ∞, this is essentially of the same type as that of B-G-W models. The differences consist of the more complicated character of some scaling parameters. An example will clarify this statement. Let us consider the supercritical case m = a′(l) > 1. It is obvious that equation
![]()
has a unique root α = α(m, G) > 0, that is called the Malthusian parameter associated with m and G. Let
![]()
Then we have limt→∞m(t)/c′eat = 1. We can prove that X(t)/c′eat converges a.s., as t → ∞, to a non-negative r.v. W that is equal to 0 a.s. if ![]() and satisfies the relations
and satisfies the relations ![]() q if
q if ![]() . In the first case, Cohn [COH 82b] showed that there exist some deterministic functions C(t), t > 0, such that X(t)/C(t) converges a.s. as t → ∞ to a non-negative and non-degenerated r.v.
. In the first case, Cohn [COH 82b] showed that there exist some deterministic functions C(t), t > 0, such that X(t)/C(t) converges a.s. as t → ∞ to a non-negative and non-degenerated r.v.
For recent references on Bellman-Harris see [ATH 76, HAC 05, HEY 95].
6.3.3. The Crump-mode-Jagers-Ryan model
We limit ourselves to giving only the description of the model. Let us consider a population descending from a unique common ancestor 0. An object of the population will be denoted by (i1,…, in), where the sequence i1,…, in will stand for the line of descent; for example, (2,3) is the 3rd descendant of the 2nd descendant of the initial object. This initial object represents the generation 0, while the objects of the form (i1,…, in) form the nth generation, ![]() . To any x ∈ I we associate a non-negative r.v. Ax, the lifetime of x, and a point process (see section 2.4) ξx on R+, the reproduction of x. We assume that (Ax,ξx), x ∈ I, are i.i.d. r.v. with common distribution Q, which is a probability on the product space R+ x N(R+) with the corresponding σ-algebra, where N(R+) is the class of the measures on B(R+) with values in N ∪ {∞}, that are finite on bounded Borel sets. The restriction L(u) = P(λX ≤ u), u ∈ R+, of Q to R+ is the lifetime distribution function and the restriction of Q to N(R+) is the reproduction distribution. In particular, we will write ξx(t) = ξx([0,t]), t ∈ R+, and ξx(∞) = ξx([0, ∞)), x ∈ I. It is usual to assume that P(ξx(λX, ∞) = 0) = 1, i.e. no descendant is born after the death of its parent.
. To any x ∈ I we associate a non-negative r.v. Ax, the lifetime of x, and a point process (see section 2.4) ξx on R+, the reproduction of x. We assume that (Ax,ξx), x ∈ I, are i.i.d. r.v. with common distribution Q, which is a probability on the product space R+ x N(R+) with the corresponding σ-algebra, where N(R+) is the class of the measures on B(R+) with values in N ∪ {∞}, that are finite on bounded Borel sets. The restriction L(u) = P(λX ≤ u), u ∈ R+, of Q to R+ is the lifetime distribution function and the restriction of Q to N(R+) is the reproduction distribution. In particular, we will write ξx(t) = ξx([0,t]), t ∈ R+, and ξx(∞) = ξx([0, ∞)), x ∈ I. It is usual to assume that P(ξx(λX, ∞) = 0) = 1, i.e. no descendant is born after the death of its parent.
The realization of objects is defined as follows: 0 (the initial object) is realized, (xk) is realized if x ∈ I is realized and ξx(∞) ≥ k. The realized object (xk) is born at time σxk, when its parent has the age τx(k) = inf{t | ξx ≥ k}. If x = (i1,… ,in) is realized, then σx = τ0(i1) + τ(i1,…,in_1)(in) and, by convention, we put σ0 = 0. The object x is alive at time t ∈ R+ if it is not dead, that is if σx ≤ t < σx + λx. Its age is t − σx, such that ![]() , defined for a, t ∈ R+ by the relations
, defined for a, t ∈ R+ by the relations
![]()
has the value 1 if and only if the object x is alive and its age is less than a at time t. Let
![]()
By the general branching model (Crump-Mode-Jagers-Ryan) we mean the stochastic process (X(a)(t), a, t ∈ R+). Note that if L(0) = 1 a.s. none of the objects is ever alive. For this reason, we assume that L(0) < 1.
Obviously, X(a)(t) does not depend on a if a > t. The common value X(t) = X(a)(t), a > t, is the size of the population at time t ∈ R+. If we put ζ(n) = number of objects realized within the nth generation, then it is easy to see that ζ(n),n ∈ N) is a B-G-W model with generating function f(z) = E [zξ(∞)]. Thus we inevitably go back to our starting point, which proves once again the fundamental importance of the classic model.
If P(ξx({λx}) = ξx(∞)) = 1, the general model is known as Sevastyanov’s model or the multiplication by division model. If, additionally, ξx and Ax are independent, then we have the Bellman-Harris model.
The fundamental reference for general branching models is the book of Jagers ([JAG 75], chapters 6–8). See also [ATH97, HAC 05]. For Sevastyanov’s model see [SEV 74a].
It is worth noticing that by calling the Crump-Mode-Jagers-Ryan model “general,” we mean that the character of the relation lifetime-reproduction in this model is general. There are other models that bring more generality concerning the interaction between objects. See, for instance, [HAC 05].
We will conclude this section by presenting an interesting particular case of the Crump-Mode-Jagers-Ryan model, namely the stochastic Fibonacci model.
It is well known that the Fibonacci sequence (un)n∈N defined by the relations u0 = u1 = 1, un = un−1 + un−2, n ≥ 2, is the most ancient population growth model. It was conceived by Leonardo of Pisa (son of Bonacci) who included it in his book Liber Abacci published in 1202. Leonardo’s model describes the evolution of an isolated population of rabbits that starts with a couple of newborn rabbits. Each month a couple of mature rabbits produce a new couple (rabbits reach maturity 2 months after their birth). It is obvious enough that the number of rabbit couples in the nth month is un, assuming that no rabbit dies in the meantime. Consequently, this model comprises an immaturity phase, during which the members of the population do not reproduce. We must say that this kind of behavior is actually very common in nature.
Heyde [HEY 81] proposed a stochastic Fibonacci model for the evolution of populations whose members undergo an immaturity phase. Let ξi (n), i ∈ N+, n ∈ N, be i.i.d. r.v. of generating function f(z) = ∑k∈N Pkzk , with 0 < m = f′(l) < ∞. Let also X(0) and X(l) be independent r.v. that are also independent of ξ. The stochastic Fibonacci model is defined by the relations
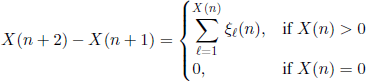
for n ∈ N. Obviously, the particular case ξi(n) = X(0) = X(1) = 1 a.s., i ∈ N+, n ∈ N, is nothing but the Fibonacci sequence (un)n∈N.
Note that, in fact, (X(t), t ∈ R+), with X(t) = X(n), n ≤ t < n + l,n ∈ N, is a Crump-Mode-Jagers-Ryan model whose objects have infinite lifetimes and give birth to ξi descendants at ages i = 2,3,…, where ξi, i ≥ 2, are i.i.d. r.v. with generating function /. Therefore, the reproduction law is
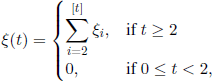
with [t] = integral part of t ∈ R+.
The asymptotic behavior of the variables X(n), n ∈ N, is similar to that encountered in the B-G-W model. See [HEY 81] for further details.
Let us note that the stochastic Fibonacci model can be seen as a B-G-W model with two types of objects, mature and immature. Each immature object gives birth to only one mature object, whereas any mature object gives birth to only one mature object (itself) + a random number (according to the generating function /) of immature objects.
Remarks on bibliographical references. There is a great number of research dedicated to branching models and this number is constantly increasing. The very dynamics of this process could be described as a branching model, but of a different type from those we presented; all we need to do is to think that a new work succeeds to a group of works. This explains the large number of works cited in this chapter. An almost complete bibliography up to 1983 can be obtained by going through the references of the following books [IOS 84, IOS 73, JAG 75, DIO 78, MOD 71]. For works after 1983 the reader is referred to the books [ATH 97, GUT 91, HEY 72b, HAC 05, TAI 92], as well as mainly to the journals published by the Applied Probability Trust, that is Advances in Applied Probability and Journal of Applied Probability, together with the references therein. Let us say that during the last 25 years we could find in these journals more than 180 articles dedicated to branching models and more than 1,200 references.
1. This seems to be the meaning of the second question of Problem 4001, which is not explicit enough.
2.In other words, within the rth generation we still have approximatively (1 − fr (0)) N from the N initial surnames, whereas the number of surnames that will last forever is approximatively (1 − q)N.
3. If the ratio between two successive generations, or the mean of the number of male children who replace the number of males of the preceding generation were less than unity, it would be easily realized that families are dying out due to the disappearance of the members of which they are composed. However, the analysis shows further that when this mean is equal to unity families tend to disappear, although less rapidly. Thus, for example, if there were equal chances for each man to have had two male children or none at all (which in the end means one male child per adult male, a little bit more than two male children or four children per family), then out of 100 families there would probably be only five left by the 35th generation, that is within 11 to 12 centuries, considering with Herodotus 3 generations in a century. In the long run, all families become extinct, or most probably so (translation taken partially from [HEY 77b], pp. 117–118).
4.The analysis also shows clearly that if the mean ratio is greater than unity, the probability of the extinction of families with the passing of time no longer reduces to certainty. It only approaches a finite limit, which is fairly simple to calculate and which has the singular characteristic of being given by one of the roots of the equation (in which the number of generations is made infinite) which is not relevant to the question when the mean ration is less than unity (translation from [HEY 77b], p. 118).
5. Bienaymé develops on other points inspired by this specific problem, and he intends to publish all these soon in a special issue.
6. We use here the following result ([FEL 66], vol. 1, third edition, p. 280). Let (pr (n), r ∈ ![]() +), n ∈
+), n ∈ ![]() +, be probability distributions (pr (n) ≥ 0, Σr∈pr (n) = 1, n ∈
+, be probability distributions (pr (n) ≥ 0, Σr∈pr (n) = 1, n ∈ ![]() +). In order to have limn→∞ pr (n) = pr, r ∈
+). In order to have limn→∞ pr (n) = pr, r ∈ ![]() , it is sufficient that the relation
, it is sufficient that the relation ![]() holds in the points z of a set contained into the disk | z | < 1 and which has there an accumulation point. Conversely, this relation holds for all z < 1 if limn→∞pr (n) = pr, r ∈
holds in the points z of a set contained into the disk | z | < 1 and which has there an accumulation point. Conversely, this relation holds for all z < 1 if limn→∞pr (n) = pr, r ∈ ![]() + .
+ .
7. We have already proved that 0 < f′(q) < 1 (see the proof of Proposition 6.6). In the subcritical case m < 1, we have q = 1 and f′(q) = f′(l) = m. Obviously, if p0 = 0, then q = 0 and fn(0) = 0, n ∈ ![]() .
.
8. There are probability generating functions that do not satisfy this condition. The negative binomial generating function f(z) = [(1 − pz)/(l − p)]−α, 0 < p < 1, α > 0, is such an example (see [ADÈ 82]).
9. See [BRA 75, NAG 76] for more general results.
10. In the critical case m = 1, this statement can be more specified in the sense that limN → ∞ ![]() = 1 in probability and
= 1 in probability and ![]() uniformly with respect to n.
uniformly with respect to n.
11. See the comments following Theorem 6.25.
12. A B-G-W model in random environment where the hypotheses of independence and common distribution of (b) is weakened is considered by [TUR 73].
13.A sequence π = ![]() is called strictly stationary if the common distribution of the 0 ≤ r ≤ n, does not depend on h ∈ N for any n ∈ P. The strict stationarity implies, in particular, the independence of the mean values
is called strictly stationary if the common distribution of the 0 ≤ r ≤ n, does not depend on h ∈ N for any n ∈ P. The strict stationarity implies, in particular, the independence of the mean values ![]() of n ∈ N, for all k ∈ N. A strictly stationary sequence π is called ergodic if (π ∈ E) = 0 or 1 for any E ⊂ (p(N))N that is T-invariant, i.e. TE = E. In particular, for an ergodic strictly stationary sequence π, the limit limn→∞P exists a.s. and it is equal to Eπ0k for all k ∈ N (see, for example, [KAR 75], p. 487).
of n ∈ N, for all k ∈ N. A strictly stationary sequence π is called ergodic if (π ∈ E) = 0 or 1 for any E ⊂ (p(N))N that is T-invariant, i.e. TE = E. In particular, for an ergodic strictly stationary sequence π, the limit limn→∞P exists a.s. and it is equal to Eπ0k for all k ∈ N (see, for example, [KAR 75], p. 487).
14.We note a+ = max(a, 0), a− = max(−a, 0).
15. This tradition has its origin in the formulation of Galton’s problem (see section 6.1.1).
16. The divergence of the series ∑k≥2 ak log k is equivalent to the divergence of the integral ![]() .
.
17. The Perron-Frobenius theorem can be stated as follows. Let A be a matrix of order r. If there exists an n e N+ such that all the entries of the matrix An are positive, then there exists a positive eigenvalue p of A that is the largest eigenvalue in absolute value among all the eigenvalues of the matrix. There exist row vectors u = (ui, 1 ≤ i ≤ r) and v = (vi, 1 ≤ i ≤ r) with positive components such that Au′ = pu′, vA = pv. If u and v are normalized such that u1′ = vu′ = 1, then An/ρn converges, as n → ∞, to the matrix B = (uivj, 1 ≤ i, j ≤ r).
18. For this relation, Hoppe [HOP 75a] proves only the convergence in probability. The proof of the a.s. convergence was given by H. Hering. For a simple proof see [COH 81].
19. There are some situations, for example in cell populations, where the birth of descendants does not depend on the age, but on the size of the parents. It is for such situations that size-dependent branching models were introduced.