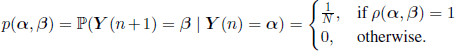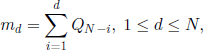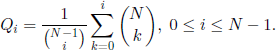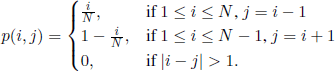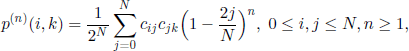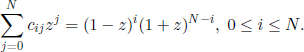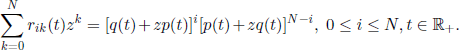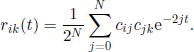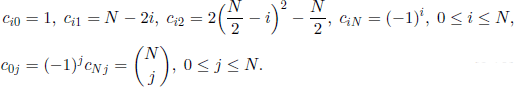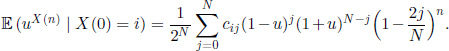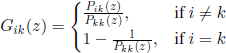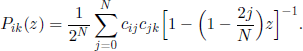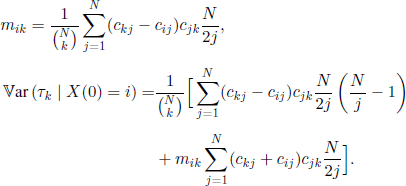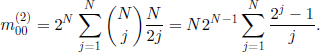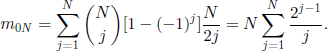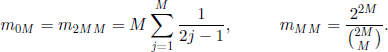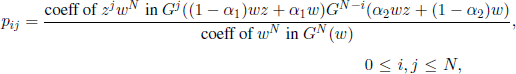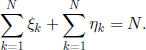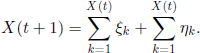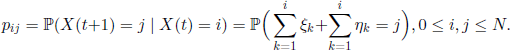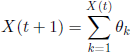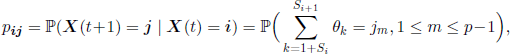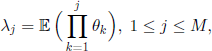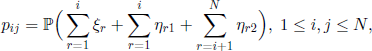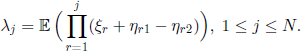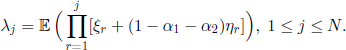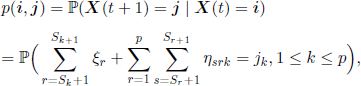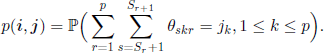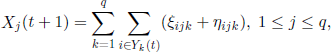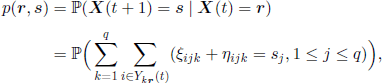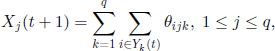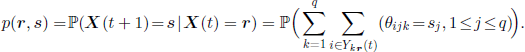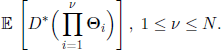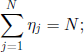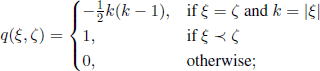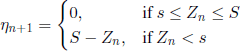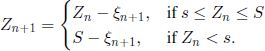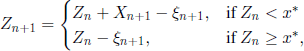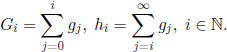Chapter 3

Elements of Markov Modeling

This chapter is devoted to the study of Markov models used in several problems of physics, biology, economy and engineering.

3.1. Markov models: ideas, history, applications

The concept of Markovian dependence that we owe to the Russian mathematician A. A. Markov (1856-1922) appeared for the first time in an explicit form in the article “Extension of the law of large numbers to quantities dependent on each other” (in Russian).¹ Later, Markov studied the properties of some sequences of dependent r.v. that nowadays are called Markov chains. He wanted to generalize classic properties of independent r.v. to sequences of r.v. for which the independence hypothesis is not satisfied. On the one hand, it is clear that if the concept of dependence had been too general, then the extension of the properties of independent r.v. would have been either impossible or restricted to a limited number of results. On the other hand, the notion of dependence that we consider needs to be “natural” in the sense that it has to really be encountered in a certain range of applications. The concept of Markovian dependence has the quality of complying with these criteria.

In the same period, the French mathematician H. Poincaré, studying the problem of shuffling playing cards, considered sequences of r.v. that are, using the current terminology, Markov chains with a doubly stochastic transition matrix. However, Poincaré did not carry out a systematic study of these sequences. Thus, A. A. Markov is legitimately considered the founder of the theory of the chains that now bear his name.

There is a vast number of papers and books on Markovian dependence. We only list here the names of B. Hostinsky, R. von Mises, M. Fréchet, S. N. Bernstein, V. I. Romanovski, W. Feller, J. G. Kemeny and J. L. Snell, K. L. Chung, E. Nummelin, S. Orey, S. P. Meyn and R. L. Tweendie, and A. N. Kolmogorov, whose books marked important steps in the history of Markov chains.

The first results on non-homogenous Markov chains were obtained by Markov himself; important contributions in this field were made later by S. N. Bernstein, W. Doeblin, J. V. Linnik, and R. L. Dobrusin.

We also mention that researches on the generalization of the Markovian dependence concept, started by the Romanian mathematicians O. Onicescu and Gh. Mihoc, led to the ideas ofmultiple Markovian dependence and random chains with complete connections.

In the beginning, Markov studied theoretical aspects of the dependence he had introduced, combating the idea, still widespread, that randomness is synonymous of independence. Nonetheless, later on he became interested in the applications of this new concept. For instance, taking into account the suggestion of V. I. Buniakovski that linguistics is a field where mathematics can be widely applied, Markov realized a statistical analysis of the novel Evgheni Oneghin by Puskin. He drew the conclusion that the succession of vowels and consonants in the novel can be seen as a two-state homogenous Markov chain. He obtained the same result when investigating Aksakov’s book Childhood Years of Bagrov’s Grandson.

Started by Markov, the use of the Markov dependence for the modeling of real phenomena has known, after the second world war, a quite amazing increase. This is true with respect to the huge number of papers and books published on Markov models, as well as with respect to the variety of application fields where these models have been used.

We will further address the best known applications of Markov models.

First of all, there are applications in engineering: quality statistical control for industrial products, reliability of complex systems, electronics, and communications.

The applications in exact sciences are very important: physics, quantum mechanics, thermodynamics, statistical mechanics, chemistry.

We remark a significant increase in the use of Markov models in human sciences: demography, theory of social mobility, sociology, education systems, ecology, environmental sciences, psychology, etc.

Note also that traditional application fields of Markov models are biology and medicine.

Today, financial mathematics and econometrics, fields where Markov models are largely used, have become important tools for the study of economic phenomena.

There are so many applications in decision theory, queueing theory, and storage reservoir theory that these directions tend to become separate fields of the modern theory of stochastic processes.

We have chosen three fields in order to illustrate in this chapter the use of Markov models. The next section is concerned with the Ehrenfest model in discrete time and with some generalizations; this model is used in thermodynamics. Some models for genetic drift of haploid populations are presented in section 3.3; we end that section with the presentation of a genealogy model for the same type of population. In section 3.4 we consider storage models, in particular the reservoir case and the risk in insurance. The last section is devoted to the very rich field of reliability, whose models are extensively used in engineering studies.

3.2. The discrete-time Ehrenfest model

3.2.1. The microscopic chain

In a well known paper published in the journal Physikalische Zeitung, 8, 311-314 (1907), Paul and Tatiana Ehrenfest introduced an urn model for explaining the apparent discrepancy between recurrence and irreversibility in the kinetic theory of gases developed by Boltzmann. This model describes the heat exchange between two isolated bodies of different temperatures, from the point of view of kinetic theory. Although it is presented as an urn model, it will be seen to be a Markov model; moreover, it can be successfully used for explaining some reversibility phenomena in statistical mechanics.

From a mathematical point of view, the Ehrenfest model can be described as follows. A number N of balls, numbered 1, 2, …, N, are distributed into two urns. We chose at random an integer between 1 and N and we move the ball whose number was drawn, from the urn in which it is to the other urn. We make the assumption that the N numbers are uniformly distributed. This procedure is indefinitely repeated.

We have the following physical interpretation of the model. The temperatures of the two bodies are determined by the number of balls in the first and in the second urn, respectively, and also by the heat exchange, which is a consequence of the balls (representation of the molecules) moving from one urn to another. This interpretation is in accordance to Boltzmann’s ideas detailed in his paper Vorlesungen iiber Gastheorie, published in Leipzig in 1896.

Looking at the physical interpretation of the model, it is clear that we are interested in the number of balls in each of the two urns, at any instant in time; besides, we would like to answer questions like “Given that the first urn is initially empty, what is the necessary mean time to equalize the number of balls in the two urns, provided that N is even?”. We shall prove that the number of balls in an urn evolves as a Markov chain.

Let us define the vectors Y (n) = (y₁ (n), y₂ (n),…,y_N (in)), n ∈ , where y_i(n) = 1, 1 ≤ i ≤ N, if the ball i is in the first urn at time n ∈ , whereas y_i(n) = 0 in the opposite case. Obviously, the vector Y(n) describes the composition of the first urn at time n, and implicitly the composition of the second one. From the hypotheses considered above, the sequence of random vectors (Y(n), n ∈ ) is a homogenous Markov chain with state space

and transition probabilities

[3.1]

In the above formula we have denoted ρ the distance between states α and β, i.e.

This Markov chain is called the microscopic chain associated with the Ehrenfest model and it has some remarkable properties that we will present in the following.

First of all, note that, with a positive probability, we can transition from one state to another in a finite number of steps; from a state α to itself we can arrive, with a positive probability, in an even number of steps; moreover, we can transition from α to α, with a positive probability, in two steps. Consequently, the microscopic chain is irreducible, recurrent, and periodic of period 2. Since a one-step transition from a state α to a state β is possible iff a one-step transition from β to α is possible, we obtain that the transition matrix of the Matrix chain is symmetric. Therefore, there exists a unique stationary (invariant) distribution which is uniform, charging each state with the probability 2^−N =1/card Δ. Note also that the chain is reversible.

The microscopic chain can be considered as a random walk from one node to another in the N -dimensional unit cube. Starting from an arbitrary node, we can reach in one step any node that is connected to the initial node by an arc. In this context, ρ(α, (β) is the minimum number of steps necessary for reaching α when starting from β.

Furthermore, the mean value of the first-passage time to state β, starting from α, depends only on the distance ρ(α, β) between these two states; let m_d be this mean value for the case ρ(α, β) = d, 1 ≤ d ≤ N. Note that ρ(α, β) = d means that the vectors α and β have exactly d different coordinates. After one step, there are d possibilities that the chain is one unit closer to β (in the sense of the distance ρ) and N − d possibilities for it to be one unit further from β; all these cases have the same probability of occurrence. All this discussion implies that the following relations hold

with the natural convention m₀ = m_N+1 = 0. These equations have a unique solution

[3.2]

where

[3.3]

We have considered above that N is a fixed number. If N is random, then m_d = m_d(N) is a function of N. We can show that, for N fixed, m_d(N) is an increasing function of d, which was actually predictable. Nevertheless, this increase is rather slow, as we can see in Table 3.1, where the values of the function m_d(N) for N =5, 6, 7, and 8 were recorded, with a 0.1 approximation.

The microscopic chain was used by Siegert (1949) and Hess (1954) for the study of Ehrenfest model. However, from a certain point of view, this chain contains too much information about the model; it keeps track not only of the number of balls in the first urn, but also of the precise balls that are in the first urn at successive times. As we are only interested in the number of balls in an urn (the body temperature), we will introduce in the next section a Markov chain which provides exactly this information.

3.2.2. The macroscopic chain

The chain we are going to define, called the macroscopic chain, will be obtained from the microscopic chain by the technique called aggregation.

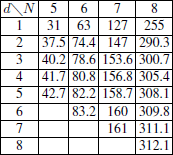
Let us consider the partition Δ = S₀ ∪ S₁ ∪ S₂ ∪ · · · ∪ S_N, where S_i is the set of the vectors A that have exactly i components equal to 1. Therefore, for any state of S_i, there are i balls in the first urn. Starting from any of the states of S_i, the microscopic chain can arrive in any of the states of S_i−1 or in any of the states of S_i+1. Taking into account [3.1], we obtain that the probability of arriving in S_i−1 is i/N, 1 ≤ i ≤ N, and that the probability of arriving in S_i+1 is 1 − i/N, 1 ≤ i ≤ N − 1, these probabilities being the same for all the states of S_i. Thus, the chain (Y_n,n ∈ ) can be aggregated with respect to the considered partition. Let (X_n, n ∈ ) be the aggregation chain (the macroscopic chain); its state space is {0,1,…, N} and its transition matrix is given by

[3.4]

Using the results of the previous subsection, we find that the chain (X_n, n ∈ ) is irreducible, is recurrent, and has B_i(N, 1/2) as its unique stationary distribution, i.e.

We have to mention that this Markov chain with the transition matrix [3.4] can be obtained using another urn model. Indeed, let us consider an urn containing N white and black balls. At every moment, we randomly draw a ball from the urn and we put in another of the opposite color. It is easy to see that the number of white balls in the urn has a Markovian evolution with the transition matrix [3.4].

The first problem that arises for the macroscopic chain is to compute the n-step transition probabilities, n ≥ 2. A way to achieve this could be to prove that the eigenvalues of the transition matrix are

[3.5]

then to find the left and the right eigenvectors, denoted by (u_r, 0 ≤ r ≤ N), respectively, by (v_r,0≤ r ≤ N), and to use the spectral representation of the transition matrix P in order to obtain that ([IOS 80], p. 161, pp. 205–208)

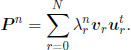
We will also present a different approach to this problem [TAK 79]. We will prove that

[3.6]

where c_ij, 0 ≤ i,j ≤ N, are determined using the generating functions

[3.7]

The proof uses the properties of a Poisson process. Let us suppose that N components work independently during the time interval [0, ∞). For each component, the working and failure periods are independent r.v., with the common distribution Exp(1).

If ξ(t) is the number of working components at time t, then (ξ(t),t ∈ ) is a homogenous Markov chain with state space E ={0, 1, …, N}; additionally, if r_ik(t) = (ξ(t) = k | ξ(0) = i) are the transition functions, then the intensities of the process, defined by

are given by

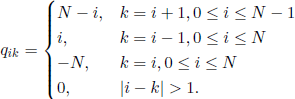
Let p(t) = (ξ(t) = ξ(0)) and q(t) = 1− p(t). Following the hypotheses we have (prove this!)

so

[3.8]

On the other hand, using the independence hypothesis we obtain

[3.9]

We note that the total number of changes in the functioning of the components during the time interval [0, t) has a Po(Nt) distribution (see section 2.4) and that the changes obey the same transition probabilities as in the Ehrenfest model; consequently, we obtain a simple relation between r_ik(t) and P_ik(t), that is,

[3.10]

From [3.8] and [3.9] we obtain

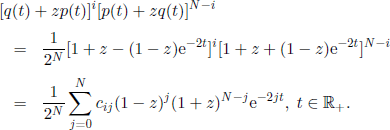
In the previous expression we calculated the coefficient of z^k, and using [3.10] we obtain

[3.11]

The comparison between [3.10] and [3.11] gives

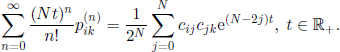
Finally, equalizing the coefficients of tⁿ of the left- and right-hand sides of this equality, we obtain [3.6].

For the coefficients c_ij, 0 ≤ i,j ≤ N, note that, using [3.7], we have

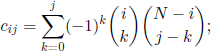
moreover, they satisfy the recurrence relations

which allows us to obtain their values. Some of them have a very simple expression. For instance, it is not difficult to prove that

[3.12]

Furthermore, if N = 2M is an even number, then

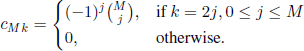
From [3.7] and [3.12] we obtain

[3.13]

for n large enough.

The n-step transition probabilities that we have just computed will allow us in the next section to derive some important characteristics of the Ehrenfest model.

3.2.3. Some characteristics of the Ehrenfest model

First of all, we compute the expected value and the variance of X(n), n ≥ 1, given that X(0) = i.

If we define the generating function

then we can prove the equality

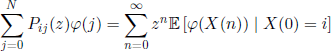
for any |z| < 1 and any arbitrary bounded function φ. Particularly,

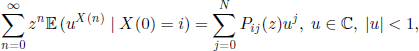
which, using [3.6], gives

[3.14]

By considering the coefficient of (u − l)^m in the series expansion of the right-hand side term of [3.14] in the neighborhood of u =1, we obtain

[3.15]

this formula being also valid for m > N, provided that c_ij = 0 for j > N. Taking m = 1 in [3.15] and taking into account [3.12], it follows that

[3.16]

Using the same formula with m = 2 we can prove that

[3.17]

It is worth noticing here that Newton’s law of cooling can be derived using the Ehrenfest model. Indeed, suppose that the chain (the heating exchange) has been observed during a time interval (0, t), that n state changes occurred during this period and, consequently, each of them happened during a time equal to Δ = t/n. Then, taking the limit as , and i − N = i₀ (constant), from [3.16] we obtain

which is exactly Newton’s law of cooling.

Let τ_k be the first-passage time to state k, 0 ≤ k ≤ N. If we let

then the generating function is given by

[3.18]

and, using [3.6], we obtain

[3.19]

For computing the mean values m_ij = (τ_j | X(0) = i), 0 ≤ i, j ≤ N, we are going to employ an easier method. Using the fact that, starting from state i + 1, the chain can reach state 0 if and only if it passes through i, we have

and, in a similar manner, we obtain

Taking into account that

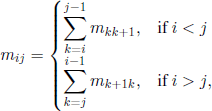
it follows that we only have to calculate m_i0 and m_iN, 0 ≤ i ≤ N. Now we should use the fact that the states 0 and N come from the microscopic states (0, 0, …, 0) and (1,1,…,1), respectively, and that the mean passage time from S_j to S_k, 0 ≤ j, k ≤ N, is the same for all the states in S_j. Hence, m_i0 = m_i, m_iN = m_N−i, where the quantities m_i„ i ≤ i ≤ N, were introduced and calculated in section 3.2.1. Thus we have

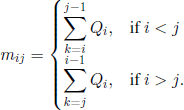
Let us denote by (α)β = α(α − 1) · · · (α − β + 1) the number of β-permutation of a; we will give now a method for calculating

On the one hand, J. H. B. Kemperman ([KEM 61], pp. 18-19, p. 26) proved that

[3.20]

On the other hand, from a series expansion in the neighborhood of z =1 of the right-hand side term of [3.19], we obtain

[3.21]

where

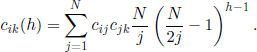
Formulas [3.18], [3.19], and [3.20] allow us to calculate the values of . In some particular cases, they have much easier expressions; for instance, if we note that , we have and

[3.22]

For the case i ≠ k, we obtain

[3.23]

Using [3.12], these formulas have even simpler expressions for the particular cases when i and k take one of the values 0, N, or N/2 (if N is even). For example, the equality

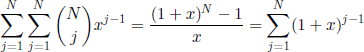
yields through integration

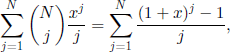
and from [3.21] we obtain

[3.24]

In a similar way, from formula [3.23] we obtain

[3.25]

Moreover, if N = 2M, then

[3.26]

The proof of these two formulas is given in [KEM 61], where we can also find the following more profound results.

First, if c ∈ and n = 2M, we have

[3.27]

Second, for N = 2M, the r.v. [τ_M − (l/2)M log(k²/M)]/M converges in distribution, if X(0) = M+k, as M → ∞, k → ∞ such that . The limit is an r.v. with the characteristic function .²

Finally, for N = 2M and for all σ ≥ 0, we have

[3.28]

We will end this section with several remarks on the validity of the Ehrenfest model for the explanation of heat exchange between two isolated bodies of unequal temperatures, from the viewpoint of kinetic theory.

First of all, let us note that we have to distinguish between the notion of reversibility of a Markov chain, on the one hand, and the reversibility of a thermodynamic process, on the other hand. The reversibility of a thermodynamic process means, according to the famous Wiederkehrsatz theorem of Poincare, that a closed dynamical system will return with probability 1, after a time long enough, to an arbitrarily small neighborhood of its initial state. So, from a mathematical viewpoint, the reversibility of a thermodynamic process is equivalent to the recurrence of the associated Markov chain.

A first problem that arises is the following: is it possible to reconcile the reversibility and the recurrence with the “observable” irreversible behavior? In other words, does a random “direction” exist of the system’s evolution like the one we can model as a consequence of the convergence to the stationary distribution? In fact, this was the objection made by J. Loschmidt to the Boltzmann’s theory, whose H-theorem seemed to suggest a “direction,” whereas all the mechanics laws are time reversible, i.e. invariant to the transformation t → −t. The Ehrenfest model gives an answer to the reversibility paradox. Obviously, if the process starts from state 0, it surely moves to state M (for N = 2M). But, if the process is observed after a long time period, that is starting from a moment when the system can be considered as being in equilibrium, then it is not obvious whether it is observed in the normal sense of time or vice- versa, due to its reversibility property. In other words, a physicist who performs a series of observations cannot tell if they are ordered in the positive or negative sense of time.

Zermelo’s objection to Boltzmann’s theory is of a different, deeper nature. He doubted the possibility of explaining the heat exchange by molecule movement, because classic thermodynamics postulates the irreversibility of the heat exchange process, whereas dynamical systems evolve according to the theorem of Poincaré, which assumes a continuous return to the initial state, so the reversibility of the process. Boltzmann himself had the intuition that this seeming contradiction comes from the fact that Poincaré cycles (state recurrence periods, in mathematical terms) are extremely large compared to the time intervals of ordinary experiences; consequently, classic thermodynamic models are a very good approximation of reality. Nevertheless, Boltzmann’s arguments are incomplete and we are indebted the Ehrenfests and to M. von Smoluchowski for a clear answer to Zermelo’s objection, based on the Ehrenfest model. In this context, the explanation is quite simple. The statistical analogous of a Poincaré cycle is the mean recurrence time of a state, say k. We have already seen that . If k and N − k differ considerably, then m_kk is indeed huge. For instance, for k =0 and N =20,000 we get m_kk =2^20,000 steps, which would mean about 10^6,000 years if a step lasts one second. Therefore, it makes no sense to wait for a return to the initial state 0 in a time interval of the size of a Poincaré cycle. However, if i and N−i are nearly equal, then m_ii is quite small. For instance, if i = N/2 = 10, 000, using Stirling’s formula we obtain steps. So the Markov chain returns quite fast to state i and the thermodynamic process is seen to be reversible after a short period.

3.2.4. The discrete-time Ehrenfest model: history, generalizations, similar models

As we have previously mentioned, in 1907 P. and T. Ehrenfest introduced the model that now bears their name, without calculating its characteristics.

However, some time before, the transition matrix whose entries are given in [3.3] enjoyed particular attention. In 1854, J. J. Sylvester published the paper Théorème sur les déterminants in Nouvelles Annates de Mathématiques, where he states without proof that the eigenvalues of this matrix are given by formula [3.5].

When analyzing the Stark effect in hydrogen, E. Schrödinger was brought to study in 1926 the matrix Φ(b), whose entries are

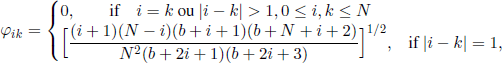
with b ∈ . He stated that the eigenvalues of this matrix are given by formula [3.5] too, adding that he did not know the proof of this result. The proof was given in 1928 by R. Schlapp.

If we note that the transition matrix P of the macroscopic chain satisfies

where B is a diagonal matrix with , then it is clear that the eigenvalues of the matrix P are given by [3.5]. This is the idea of the proof provided by M. Kac in 1947. So, it took almost a century to prove Sylvester’s statement, while interest in this matrix was revived due to its usefulness in understanding some physical phenomena.

Regarding the generalizations of the Ehrenfest model, we would like to mention first the chain associated with stimulus-sampling models. This is a stochastic model used in mathematical psychology, proposed by W. K. Estes in 1959. It leads to a Markov chain with the following transition matrix [IOS 80]:

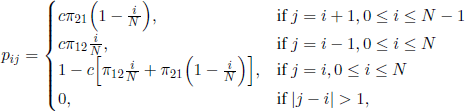
where 0 ≤ π₁₂, π₂₁ ≤ 1 and 0 < c ≤ 1 are constant. In the case π₁₂ = π₂₁ = c = 1, we obtain the Markov chain associated with the Ehrenfest model.

In 1964 I. Vincze [VIN 64] studied a Markov chain of transition matrix

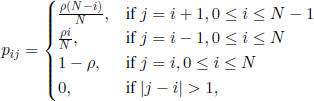
where 0 < ρ ≤ 1 is a constant. For ρ =1 we obtain the Ehrenfest model.

In 1982 E. Seneta [SEN 82] introduced the following urn model. Suppose that N balls are contained in two urns; a randomly drawn ball is placed in one of the two urns with equal probability. If Z(n) is the number of balls in the first urn at time n, (Z(n), n ∈ ) is a Markov chain with transition matrix

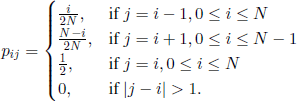
If we observe this chain only at the moments when it effectively switches from one state to another, we obtain the chain associated with the Ehrenfest model. Seneta considers that this chain (Z(n),n ∈ ) describes better the heating exchange between two isolated bodies, because it has all the useful properties of the chain (X(n),n ∈ ) associated with the Ehrenfest model, and, moreover, it has a limit distribution. Following Seneta, it is the tendency to equilibrium of any ball to be in any of the urns, with the same probability and independently of the other balls, which corresponds to the tendency of the system to have maximum entropy.

3.3. Markov models in genetics

3.3.1. Laws of heredity and mathematics

In order for genetics,³ the branch of biology which studies the phenomena of variation and heredity of all living organisms, to become the science that we all know today, cell theory had to be born first.

According to this theory, there is a common denominator for any one living organism, be it simple or complex: the cell. It is a constitutive unit of any organism, of microscopic size (between 10 μ and 100 μ), formed of the cytoplasm, that is enveloped in a membrane, and of the cell nucleus, which has its own membrane too.

The basic elements of hereditary transmission, for the majority of traits, are chromosomes, compact nucleoproteic structures which can be found in the cell nucleus. Chromosomes exist in a constant number in each species; they are the only units within the nucleus to divide into two identical copies through the two types of cell division (mitosis and meiosis), and they maintain their uniqueness throughout generations. Plants and developed animals normally have two copies of each type of chromosome, so the cell displays a set of chromosome pairs. These organisms are called diploids. Those having only one copy of each type of chromosome are called haploids.⁴ For instance, bacteria and some primitive plants are haploids.⁵ Polyploid cells also exist, especially in plants.

In living cells their ability to transmit their particular traits through heredity is most remarkable. By trait we mean a distinctive characteristic relative to shape, size, structure, color, etc., which actually differentiate human beings. According to G. Mendel, the various traits are dictated by pairs of genes, one from the paternal organism and one from the maternal organism. A gene, a part of the DNA molecule or viral RNA, which contains the whole information about a certain hereditary trait, occupies a very specific position on the chromosome, that is the locus. A gene from a pair or a series of alternative genes which can occupy the same locus and which dictates the various expressions of the same hereditary trait is called an allele. In the most simple case, that of a gene having two alleles A and a, in the locus we can find one of the pairs of the genes AA, Aa, and aa (we do not differentiate between Aa and a A). These are called genotypes. Individuals carrying the genotype AA or aa are called homozygous, and those with the genotype Aa are heterozygous or hybrids.

The genetic variation of a given population, expressed by the frequency of certain genes, represents the very essence of evolution and it is affected by random factors. The most well-known factors are mutation (recurrence), gene migration, natural selection, and genetic drift. Mutation transforms an allele into another allele through a repeated process and with a certain frequency, which alters some of the frequencies of various genes within the population, and then modifies its genetic balance. Selection causes different degrees of participation in offspring generation of the various types of genotypes in a population, due to the fact that these genotypes differ in terms of viability and/or fertility. Migration leads to changes in gene frequency inside a population due to the exchange with a different population whose gene frequency is not the same. Genetic drift is the random change in the gene frequency of certain genes around an equilibrium point (probably) because of the small size of the population, which causes the gamete combinations not to be equiprobable. Usually, species formed by a lot of individuals are divided into populations living physically separated, which means that these populations that are distant in space are inevitably of small size.

The current presentation deals briefly with only few of the notions of modern genetics.

The founder of genetics is the Austrian monk Gregor Mendel (1822-1884), who made public his results, obtained after having undertaken numerous experiments, in his work Versuche über Pflanzenhybriden published in 1866 in Verhandlungen der Naturforschenden Vereins in Bruenn, IV Band, Abhandlungen, 1865 (Experiments on Plant Hybridization, Harvard Univ. Press, Cambridge, 1946). Despite the fact that the accuracy and clearness of Mendel’s ideas were in stark contrast with the rather vague and confusing statements of his forerunners, his works have either been misunderstood, or fully ignored. This is the reason why the year 1900, when Mendel’s works⁶ were rediscovered, is rightfully considered as the beginning of genetics.

We could say that it was Mendel who used mathematics for the very first time in his genetic research, because, unlike his forerunners and contemporaries, he used statistical methods to precisely determine the frequency of different types present in the obtained hybrid generations.

The random trait of the hereditary process has of course always got the attention of mathematicians. This is why genetics became one of the fields most open to applications of probability theory. The age of mathematical genetics was initiated by the English statistician R. A. Fisher (1890-1962) in 1930 with the publication of The Genetical Theory of Natural Selection. The decade 1930-1940 is dominated by the essential contributions of R. A. Fisher, J. B. S. Haldane, and S. Wright. The ever increasing interest in mathematical genetics leads to the publication of various articles, journals and series of books.

Mathematical models proved that the evolution of genetic populations could be fully explained by Mendel’s laws and by natural selection. They have equally shown that certain paths of research taken by evolutionists are actually a dead end that lead nowhere. Mathematical models offered a logical framework within which genetics research data could be usefully exploited.

3.3.2. Haploid models

Within this section we will present some remarkable Markov models, used for the study of genetic composition of a haploid population of fixed size. We will focus on the problem of genetic drift, whose study means, from a mathematical point of view, finding the eigenvalues of the transition matrix of a Markov chain.

Multiplication processes are generally not appropriate models for the description of certain biological phenomena, taking into account the fact that the size of a population is determined by external causes (food availability, a necessary space for living, presence of rival populations), rather than by the independent sum of the descendants of successive generations. Consequently, the assumption that the size of the population is fixed seems to be a natural hypothesis for a first approach to biological reality.

Wright model. In 1931 S. W. Wright introduced a model for non-overlapping generations, with fixed size N of the population, whose organisms have two genotypes A and B. It is assumed that at each time t ∈ , the N individuals are replaced by N descendants. Let X(t) be the number of gametes of genotype A at time t. For independent mutations, (X(t), t ∈ ) is a homogenous Markov chain with state space {0, 1, …, N} and transition probabilities given by

[3.29]

with

where we denoted by α₁ the mutation rate of genotype A to genotype B and by α₂ the mutation rate of genotype B to A. Therefore, the process evolves as follows: each of the i gametes of genotype A produces a large number of gametes of genotype A and each of the N − i gametes of genotype B produces a large number of gametes of genotype B. Thus, the proportions of individuals of genotype A among all these newly obtained individuals are i/N; afterward, each individual is subject to independent mutation and N individuals are selected in order to form the new generation.

W. Feller proved in 1951 that the eigenvalues of the transition matrix of the chain are

where (N)_j = N(N − 1) · · · (N − j + 1).

If α₁ > 0, α₂ > 0, and α₁ + α₂ < 1, then these eigenvalues are all distinct and the chain is regular (see section 1.5.1), so the limits exist. Moreover, there also exists an A > 0 such that

which shows that the convergence rate to the state of equilibrium does not depend on the population size N.

If there is no mutation, which happens if α₁ = α₂ = 0, we have λ₀ = λ₁ = 1 and λ₂ = 1 − 1/N. In this case, the Markov chain (X(t), t ∈ ) has two absorbing states 0 and N, and the convergence of the matrix P^k of the chain to the limit matrix A (whose elements could be zero only on the first and last column) is at a rate given by the value λ₂ [IOS 80], according to Perron-Frobenius theorem; for this reason, λ₂ is called the rate of genetic drift.

Let us recall the fundamental hypotheses of the Wright model:

1) The population has a fixed size N;

2) The mutations occur independently;

3) The number of descendants has a binomial distribution;

4) The generations do not overlap.

Moron model. In 1958 P. A. P. Moran introduced a model whose basic assumption was that generations overlap. More precisely, it is assumed that at any time t ∈ a randomly chosen gamete dies, whereas another gamete, also randomly chosen, gives birth to one descendant. This descendant can be of the same genotype or of a different genotype, due to a mutation phenomenon. The transition probabilities of this model are

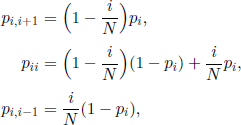
and p_ij =0 otherwise (i.e. for |i − j| > 1), where the quantities p_i were defined in [3.29]. Note that this is a particular random walk. We can prove that the associated eigenvalues are given by (J. Gani, in 1961, and S. Karlin and J. McGregor, in 1962)

where α₁ and α₂ are the mutation rates of genotype A to genotype B, respectively, of B to A. If there is no mutation, the eigenvalues are

An important characteristic of this model is that the eigenvalues λ_j depend on 1 − (α₁ + α₂) instead of (1 − α₁− α₂)_j, as it was the case in the Wright model. We will see in the following that this phenomenon is the consequence of the birth of only one gamete during a time unit, and that in models where it is allowed to give birth to two gametes in a time unit, λ_j will depend on 1 − (α₁ + α₂)², etc.

Therefore, the hypotheses of the Moran model are as follows:

1) The population has a fixed size N.

2) Events “birth” and “death” are independent, i.e.

3) Generations overlap.

4) The lifetime has an exponential distribution.

Karlin-McGregor model. The Wright model was generalized in 1965 by S. Karlin and J. McGregor, by considering a process of conditional multiplication. It is assumed that each of the N gametes reproduces independently of each other and that the number of descendants of any gamete has the same generating function G. From the resulting populations, only those of size N are considered. In the case where there are only two genotypes and mutations are allowed, we can prove that

[3.31]

and the eigenvalues are

In fact, only one hypothesis of the Wright model is modified in this model, allowing a more general distribution of the number of descendants. The other hypotheses are preserved, in particular the one of the independence of the mutations. If in the multiplication process considered here, the function G is supposed to have the expression G(w) = exp(μ(w − 1)) (which corresponds to a Poisson distribution), we actually obtain the Wright model.

Chia-Watterson model. In 1969 A. B. Chia and G. A. Watterson developed a model based on a conditional multiplication process, which includes all the models with two genotypes currently presented, with either non-overlapping or overlapping generations. The model can be described as follows: the gametes reproduce independently of each other, the distribution of the number of descendants of each gamete being specified by the generating function G; the number of all these descendants is supposed to be an r.v. M with distribution (M = m) = p_m, m ∈ . The population, formed by N existing individuals and by M newborn individuals, is maintained at a size N by a procedure of random sampling without replacement, such that R individuals are chosen from the N “old” individuals, whereas the other N − R are chosen from the newborns; here R is also an r.v. whose conditional distribution given M is (R = r | M =m) = q_mr. Note that the Karlin-McGregor model can be obtained from the current model for M = N and R =0 a.s.

For the Chia-Watterson model we can prove that we have

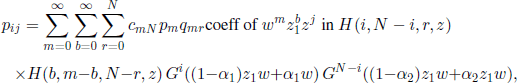
where c_mN = [coeff of w^m in G^N (w)]⁻¹,

and the eigenvalues are given by the formula

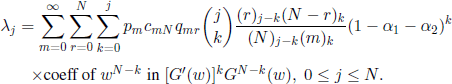
In the particular case where α₁ = α₂ = 0, we have , where d is the variance of the number of descendants of an individual during his life and μ* is the expected value of his lifetime; if α₁α₂ ≠ 0, we have .

This models is based on the following hypotheses:

1) The population has fixed size.

2) The mutations occur independently.

3) The lifetime has a geometric distribution.

4) The distribution of the number of descendants is the result of a conditional multiplication process, increasing a lifetime that has a geometric distribution.

5) There is a certain independence between the events of death and birth.

We will explain this last hypothesis. In this model, as opposed to the Moran model, we have

this dependence is generated by the fact that the information that a gamete died imposes restrictions on the values of variables M and R and these restrictions, in turn, influence the probability of its having produced any descendants. The independence we have here is a conditional independence, given the values of variables M and R, i.e.

Consequently, for M =1 and R = N − 1 a.s., i.e. considering the situation when only one individual replaces an “old” individual, the Chia-Watterson model is reduced to the Moran model.

Finally, let us mention the Chia model (1969), which is a generalization of the Chia-Watterson model, because more than two genotypes are allowed. An additional feature of this model is the variable size of the population.

In the following sections we present a model introduced by C. Cannings that includes some characteristics of all the models presented before. In this model, hypotheses (1) and (3) of Chia-Watterson model are maintained, whereas the others are modified as follows. Hypothesis (2) is weakened in order to allow an arbitrary distribution of mutations within a family. We need a structure where there is a correlation between individuals from the same family, i.e. we need the conditional probability that an individual had a mutation, given that a sister cell also had a mutation, to be different from the simple probability that an individual had a mutation. Such a generalization is useful because for many organisms, haploid included, the generation of descendants by repeated division of a small number of primary cells implies the independence of births of new individuals. Hypothesis (4) is also modified, allowing a more general distribution of the number of descendants. Finally, hypothesis (5) is modified in order to have a dependence between the events of birth and death. For instance, hypothesis (5) in the Moran model has to ensure that the individual that dies is not the same as the one who has descendants. This requirement corresponds to a real demographic phenomenon, fertility variation with age, which is not taken into account in models like the one of Chia and Watterson.

In the model we will present, as well as in all the other models, the main goal will be to find the eigenvalues of the associated Markov chain.

The construction method of this model differs from those used for the above models that were essentially based on the theory of multiplication processes. In the current case we will use “interchangeable” r.v.⁷ and Markov chains.

We will present four models: with two genotypes and without mutations, with several genotypes and without mutations, with two genotypes and mutations, with several genotypes and mutations. Clearly, the last model includes all the others; anyway, we also present the other models in order to be able to see, on the one hand, the connections between each model and the models presented in this section, and, on the other hand, the increasing complexity of the mathematical tools.

3.3.3. Models with two genotypes and without mutations

Let X(t) be the number of gametes of genotype A at time t ∈ ; it is clear that X(t) takes values in the set {0, 1, …, N}. Consider a sequence of interchangeable bi-dimensional r.v. (ξ_k, η_k), 1 ≤ k ≤ N, such that

[3.32]

The random vectors (ξ_k,η_k), 1 ≤ k ≤ N, have the following interpretation: (ξ_k takes the value 1 if the individual k survives and the value 0 in the opposite case, whereas η_k gives the number of descendants of the individual k. It is clear that relation [3.32] assures that the population size is constant and the variable X(t + 1) can be immediately obtained by

[3.33]

Note also that (X(t),t ∈ ) is a Markov chain with transition probabilities

[3.34]

In fact, it is worth noticing that it is not necessary to consider the random vectors (ξ_k,η_k), 1 ≤ k ≤ N, but only the r.v. θ_k = ξ_k + η_k, 1 ≤ k ≤ N, with the property ; indeed, we can write

[3.35]

and then we have

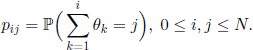
This remark shows that, by approaching the problem in this way, we obtain a simple equivalence between the two cases of non-overlapping and overlapping generations.

To obtain the eigenvalues of the Markov chain we proceed in a similar way as we did before for the other models. More precisely, we use the following result.

LEMMA 3.1.– Let P =(p_ij,0≤ i,j ≤ N)be the transition matrix of a Markov chain (X(t),t ∈ ). If

where B_j−1(i) is a polynomial in i of degree at most j − 1, then the eigenvalues of P are the coefficients λ_j, 0 ≤ j ≤ N, from the above formula.

The proof of this result can be found in [KAR 75].

THEOREM 3.2.– The eigenvalues of the transition matrix of the Markov chain given in [3.35] are λ₀ = 1 and

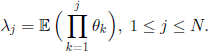
PROOF.– For i ≥ j we have

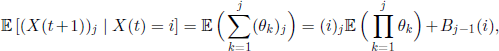
where B_j−1(i) is a polynomial in i, of degree at most j − 1. Since the above formula is also valid for i < j, because (i)j =0 and in the right-hand side term there are only two terms in i of degree less than j, we obtain the desired result using Lemma 3.1.

As the r.v. (θ_k, 1 ≤ k ≤ N) are interchangeable, note that we can calculate λ_j using any set of j variables chosen from θ₁,…,θ_n.

The following theorem is concerned with necessary conditions for the eigenvalues of the chain to be distinct.

THEOREM 3.3.– If (θ_i = 1) = 1, then all the eigenvalues are equal to 1. If (θ_i = 1) < 1, then

iff exactly N − K + 1 from the N individuals are characterized at each time instant by 0_i =0, i.e. at each time instant, there exist exactly N − K + 1 individuals that die without descendants.

PROOF.− It is clear that (θ_i, = 1) = 1 implies θ =(θ₁,…,θ_N) = 1, so λ_j =1,0 ≤ j ≤ N.

Let us now suppose that for N − K + 1 individuals we have 0_i =0; then, any subset of K elements of the set {θ₁, …, θ_n} contains at least one zero, so for any m ≥ K, and, consequently, λ_k =λ_k + 1 = · · · =λ_K+1 = 0. The proof of the converse is straightforward.

Let us now consider λ_j with j < K. As K − 1 of the θ_iS are not zero a.s., we obtain that . We are going to prove that λ_j−1> λ_j for j < K. As and variables θ_i are interchangeable, we get

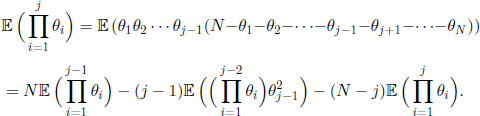
Therefore, λ_j ≤ λ_j−1 if and only if

and we have the equality λ_j =λ_j−1 if and only if the equality holds in the above formula. But (θ₁· · · θ_j−1(θ_j− 1)) > 0, because θ_j are not all zero a.s. and we are working under the hypothesis (θ_i = 1) < 1.

Theorem 3.2 can be used for obtaining the eigenvalues of some of the models presented in section 3.3.2.

For the Wright model, from the hypotheses we infer that 6 has a multinomial distribution

with x =(x₁,x₂, · · · ,x_n). Consequently, we obtain

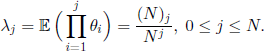
In the Moron model we have (θ = 1) = 1/N and (θ = (2, 0, 1, 1, …, 1)) = (N − 1)/N. Therefore

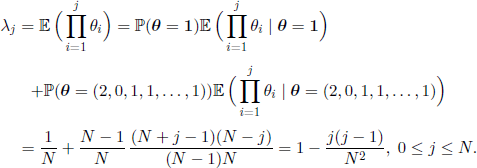
The interchangeable random variables bring more generality, as can be seen in the following simple example, which is a slight modification of the Moran model; more precisely, let us assume that the model satisfies the hypothesis that an individual that dies cannot have descendants. For this model, it is necessary to construct a new transition matrix, whose eigenvalues have to be computed. In fact, it suffices to specify the distribution of the descendants, which in this case is θ =(0, 2, 1, …, 1) or a permutation of this vector. This allows us to obtain

We end this section by mentioning that the eigenvalues λ₂ and λ₃ can be expressed in terms of the moments of θ_i. Indeed, we have

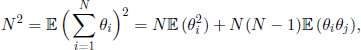
and we obtain

where Φ is the generating function of θ_i. Similarly, using and formula

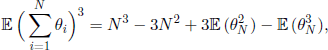
we obtain

3.3.4. Models with several genotypes and without mutations

Let us consider now a population of N individuals of p different genotypes and let X(t) = (X₁(t),…, X_p−1(t)) be the vector that specifies the number of individuals of genotype k at time t ∈ , 1≤ k ≤ p; obviously, we have . Using the r.v. ξ_i, η_i, θ_i, 1 ≤ i ≤ N, introduced in the previous section, we can write

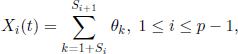
where

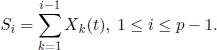
It is clear that (X(t), t ∈ ) is a Markov chain with transition matrix

[3.36]

where i_m and j_m,l ≤ m ≤ p − 1, are the components of the vectors i and j.

We can prove the following result.

THEOREM 3.4.– The eigenvalues of the Markov chain with transition matrix [3.36] are Ao = 1 and

[3.37]

with multiplicity order

J. Felsenstein studied the rate of extinction of k out of p initial alleles. He proved that there is a close connection between the extinction rate of the alleles and the probability G(i,k) that exactly i individuals randomly chosen are the descendants of exactly k individuals of the previous generation; moreover, he noted that in the models of Wright, Moran, and Karlin and McGregor, the probabilities G(k, k) are the same as the eigenvalues of the chain. Theorem 3.4 allows us to immediately prove this result.

Let θ =(θ₁, …, θ_n) and consider k arbitrary different numbers i₁, …, .i_k from the set {1, 2, …, N}; sampling k individuals from the new generation as if we randomly drew balls without replacement, we obtain

To obtain G(k,k) we have to sum the terms with the above expression and then to take the mean value with respect to the distribution of θ; thus we obtain

This formula allows the computation of the probability that, in a certain generation, there is a given number of different individuals. Indeed,

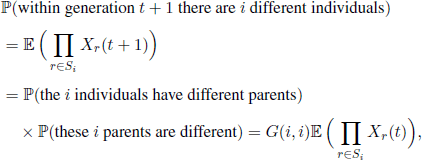
where S_i is an index set of i elements randomly chosen. Using a result of G. Malécot and the above equality, O. Kempthorne proved in 1967 that G(i, i) = λ_i,1≤ i ≤ N.

Note that in the Karlin-McGregor model with non-overlapping generations and without mutations, formula [3.37] becomes N, which allowed C. Cannings to prove in 1974 that λ₀ = 1 and

3.3.5. Models with two genotypes and mutations

For a population of N individuals of two genotypes A and B, let us denote as X(t) the number of individuals of genotype A at time t ∈ . For each individual i, 1 ≤ i ≤ N, we define a vector (ξ_i,η_i,η_i1,η_i2) by:ξ_i is the number of survivors from individual i (so ξ_i takes only the values 0 and 1), η_i is the number of descendants of the individual i, η_i1 is the number of individuals of genotype A produced by individuals of genotype A from the generation of descendants η_i, and η_i2 is the number of individuals of genotype A produced by individuals of genotype B from the same generation of descendants.

Let us assume that the vectors (ξ_i,η_i,η_i1,η_i2), 1 ≤ i ≤ N, are interchangeable. In order to have a constant size of population, we must impose that

Defining

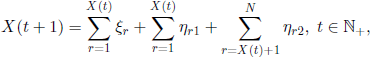
we note that, for individuals of genotype A, the r.v. η_r2, 1 ≤ r ≤ N, are not essential; they were introduced only for symmetry reasons. The transition matrix of the Markov chain (X(t),t ∈ ) of this model is given by

[3.38]

and we can prove the following result.

THEOREM 3.5.– For the transition matrix given in [3.38], the eigenvalues are λ₀ = 1 and

[3.39]

We will skip the proof, based on Lemma 3.1 and on the interchangeability hypothesis, and we will consider the important particular model of independent mutation rates. Let α₁ be the mutation rate of A to B and α₂ the mutation rate of B to A. If, in addition, we assume that the conditional distribution of the r.v. η_r1, respectively η_r2, given η_r, 1 ≤ r ≤ N, is binomial of parameter 1 − α₁, respectively 1 − α₂, we obtain

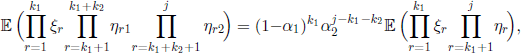
which allows us to write [3.39] as

[3.40]

All the following examples are particular cases of the model presented above.

First of all, if generations do not overlap, we have ξ_i, = 0 a.s. and formula [3.40] becomes

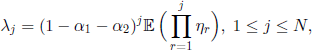
in accordance with the result of Karlin and McGregor.

If the r.v. (£j, 1 ≤ i ≤ N) are independent of (η_i, 1 ≤ i ≤ N), then we have from [3.40] that

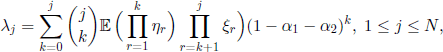
with the convention

In the Moran model with mutations, the hypothesis of independence of the r.v. (ξ_i, 1 ≤ i ≤ N) and (η_i, 1 ≤ i ≤ N) is satisfied and, moreover, we have η_iη_i= 0 a.s. for i ≠ j and (η_i) = 1/N, 1 ≤ j ≤ N. The above formula becomes

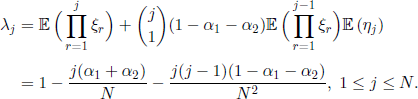
Finally, for the Chia-Watterson model, from [3.40] we obtain that

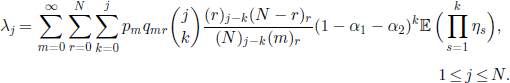
3.3.6. Models with several genotypes and mutations

Let us consider a population formed by N individuals of p different genotypes A₁, A₂, …, A_p, and let X(t) = (X₁(t),…, X_p(t)) be the vector of the numbers of genotypes A_k, 1 ≤ k ≤ p, at time t ∈ . Let us also introduce the random vectors (ξi, η_i, η_ijk, 1 ≤ i ≤ N, 1 ≤ j, k ≤ p), defined by: ξ_i, 1 ≤ i ≤ N, takes the value 1 or 0 if the individual i survives or dies, respectively; η_i, 1 ≤ i ≤ N, is the number of descendants of the individual i;η_ijk, 1≤ i ≤ N,1≤ j,k ≤ p, represents the number of descendants of genotype A_j from the individual i, assuming that it is of genotype A_k. We also assume that the vectors previously defined are interchangeable. Obviously, we have

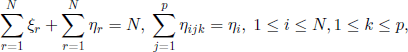
and we infer that

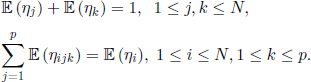
From these hypotheses we find that the process (X(t),t ∈ ) is a Markov chain with the state space formed by d-dimensional vectors, whose components are non-negative integers of sum N. If we let i =(i₁,i₂,… ,i_n) and j =(j₁,j₂,…,j_n), then the transition matrix is

[3.41]

with

Using the notation

formula [3.41] becomes

[3.42]

In order to find the eigenvalues of this chain, we need some preliminary work.

For two matrices A = (a_ij ,1≤ i ≤ m,1≤ j ≤ n) and B =(b_ij, 1 ≤ i ≤ q, 1 ≤ j ≤ r), their tensor product or Kronecker product is a matrix, denoted by A ⊗ B, with mq rows and nr columns, given by

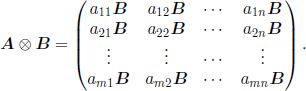
The tensor product of two vectors u =(u₁ …, u_m) and v =(v₁ …, v_n) is an mn-dimensional vector defined by

We note that the matrix A₁⊗ A₂ has the columns a1_j ⊗ a_2k, where a1_j, 1 ≤ j ≤ n₁ are the columns of the matrix A₁ and a_2j, 1 ≤ j ≤ n₂ are the columns of the matrix A₂. Generally, if we denote by the tensor product of matrices A_i, 1 ≤ i ≤ k, then the columns of the matrix are given by So, we can identify any column of the matrix if the vector is specified; we will denote by this column.

A vector is said to precede the vector in lexicographic order, and we denote this by , if there exists an r, 1 ≤ r ≤ k, such that for 1 ≤ j ≤ r − 1 and (if r =1 we only ask that ).

We order the columns according to the lexicographic order of the “index” vectors .

The vectors and are called equivalent (modulo a permutation) if there exists a permutation π of the set {1, …, k} such that .

For squared matrices A_i, of order n we will describe how we can obtain the collapsed direct product D() starting from the tensor product .

Using what we presented above, the columns of can be written as , with . For a fixed vector , we denote by the set of all the vectors equivalent to ; let be the smallest element of in lexicographic order. Let us define a new matrix A^k* whose columns are given by

where and δ() = 0 for all . In other words, we replace the column in the matrix by the sum of all the columns (the sum is done over all the vectors ) and the columns , by 0 vectors. We obtain the collapsed direct product by eliminating the zero columns and the corresponding raws; we can easily prove that this is a squared matrix of order .

We owe the main result of this section to C. Cannings.

THEOREM 3.6.– ([CAN 74]) The eigenvalues of the transition matrix [3.42] are λ₀ = 1 and the eigenvalues of the matrices

where .

All the theorems presented in this section are particular cases of Theorem 3.6. For instance, Theorem 3.4 is a particular case with , where I is the identity matrix of order p − 1.

For the Karlin-McGregor model we have , and, if the mutations are independent, then , where α_ij is the mutation rate of genotype A_j to genotype A_i. Thus we can write C_i = η_i Γ*, 1 ≤ i ≤ N, where Γ* is a square matrix of order p − 1 with entries , 1 ≤ i, j ≤ p − 1. If the eigenvalues of the matrix Γ = (α_ij, 1 ≤ i, j ≤ p) are 1, γ₂, …, γ_P, then we can prove that the eigenvalues of Γ* are γ₂, …, γ_P. Moreover, if we denote as Γ*^k the k-fold tensor product of the matrix Γ*, then the eigenvalues of the matrix D(Γ*^k) are , 2 . From Theorem 3.6 we get that the eigenvalues of P are obtained by multiplying the eigenvalues of D(Γ*^k) by (η₁η₂ · · · η_k); so, they are

which is in accordance with the result obtained by S. Karlin and J. McGregor by other methods.

3.3.7. Models with partitioned population

In this section we assume that the population is partitioned into q classes, each of them of fixed size . To simplify the presentation, we consider the case without mutations and we assume that the population is composed of individuals of two genotypes, say A and B.

The frequency of genotype A (and, implicitly, of genotype B) within different classes at different time moments t ∈ is given by the random vector X(t) = (X₁(t),…,X_q(t)), where X_j(t), 1 ≤ j ≤ q, denotes the number of individuals of genotype A in the class j at time t.

Let us define the vectors (ξ_ijk,η_ijk), 1≤ i ≤ N,1≤ j,k ≤ q, as follows: ξ_ijk is the number of survivors of the individual i from the class k, belonging to the class j, and η_ijk is the number of descendants of i from the class k, belonging to the class j. Obviously, we have

[3.43]

where we have denoted as Y_k(t) the set of individuals of genotype A in the class k at time t. For r = (r₁, …, r_q) we denote by Y_kr(t) the set of individuals of genotype A in the class k, given that there exist r_k such indexes. Under these hypotheses, (X(t),t ∈ ) is a Markov chain with state space Ω = {(i₁, i₂, …, i_q)| 1 ≤ i_j ≤ N_j, 1 ≤ j ≤ q} and transition matrix

[3.44]

with s =(s₁, …, s_q). We can note that the random vectors (ξ_ijk, η_ijk) appear in formulas [3.43] and [3.44] only through the sums θ_ijk = ξ_ijk + η_ijk; therefore, these formulas can be written as

[3.45]

[3.46]

As we have considered fixed size classes, we need to impose the condition

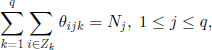
where Z_k is the index set of the class k. Note that, under the hypotheses of our model, we find that there exist j and k such that the number of individuals from the class j at time t which are descendants from individuals of the class k is constant. Consequently, a characteristic of our model is that even the movement between classes is stochastic. We will also assume that the reproduction and survival of individuals within classes are stochastically identical; this means that the r.v. (θ_ijk,l ≤ i ≤ N, 1 ≤ j, k ≤ q) are interchangeable with respect to i.

Let us define the matrices Θ_i, 1 ≤ i ≤ N, whose (j, k) entry, 1 ≤ j, k ≤ q, is θ_ijk, where i is an arbitrary element of Z_k. Denoting by the collapsed direct product, as in the previous section, we define a new matrix obtained from by keeping only the rows and columns corresponding to those vectors i =(i₁, …, i_v) that have at most N₁ components equal to 1,N₂ components equal to 2, etc.

THEOREM 3.7.– ([CAN 74]) The eigenvalues of the transition matrix [3.46] are λ₀ = 1, together with the eigenvalues of the matrices

[3.47]

This theorem implies that the number of absorbing states of the chain depends on the way the individuals move from one class to the other. For instance, if all the subpopulations communicate, there are only two absorbing states, but if all the subpopulations are isolated, there are 2^q absorbing states.

The model presented here contains many of the previous models as particular cases, because we can give different interpretations to the classes the population is divided into.

First, if we interpret the classes as being haploid colonies, we have a migration model. For such a model, genetic arguments lead to the study of Markov chains with state spaces having a certain symmetry; this is the reason why, for fixed v, 1 ≤ v ≤ N, the dominant eigenvalue is the eigenvalue of a matrix whose order is much lower than that of matrices [3.47]. This idea is the basis of the use by P. A. P. Moran of the coefficient of parentage for the study of a migration model, whose main results are, following Cannings, particular cases of Theorem 3.7.

Second, we can see the classes as being age groups. In this case, important simplifications can be done. Indeed, ξ_ijk = 0 for j ≠ k + 1 and ξ_ijk = 0 or 1 for j = k + 1, because an individual that survives will have to move to the next age group; we also have η_ijk = 0 for j ≠ 1, because all the descendants belong to the first age group.

3.3.8. Genealogy models for large size populations

In order to model certain traits of biological populations that change along time, it is often necessary to take into account the correlations between individuals following their ancestry. This ancestry could be purely genetic, but it can also have other causes; for instance, for a population living in a given space, it is possible for those individuals that are separated by small distances to have a tendency to approach one another. Modeling these correlations is more difficult from a mathematical point of view; studies devoted to this problem used either spatial branching processes [FLE 78], or point processes [MAT 78], or the identity by descent method [MAL 69].

The model we present here was introduced by J. F C. Kingman [KIN 82] and it can be applied to haploid populations, that is to those populations where an individual has only one parent. For genealogical studies of a diploid population, one can see [WAC 78].

The basic idea of this model consists of selecting n individuals of a certain generation and, looking backward in time, record the moments (generations) where there are common ancestors. Usually, after a time interval long enough (i.e. after a number of generations comparable to the size of the population), all the n selected individuals have the same common ancestor. If we want to mathematically describe the genealogical tree during the time period thus defined, an appropriate model for a large-size population is seen to be a Markov process with finite state space, called an n-coalescent process.

To make it even clearer, let us consider the Wright-Fisher model, where the successive generations G₀, G₁, … do not overlap, each of them has fixed size N, and the number of descendants of individual j is given by the r.v. η_j, 1 ≤ j ≤ N. It is clear that the r.v. η_j satisfy relation

[3.48]

moreover, we assume that they are independent and have a symmetric multinomial joint distribution, i.e.

[3.49]

Note that the identification of the “inverse” structure of this model is particularly simple, because relation [3.49] means that each individual of generation G_r “chooses” his parent randomly, independently and uniformly within the N individuals of generation G_r−1. If two individuals are randomly drawn from generation G_r, then the probability that they have the same parent is 1/N, whereas the probability that they have the same ancestor in generation G_r−2 is [1 − (1/N)](1/N), etc. Generally, the probability that they have different ancestors in generation G_r−S is [1 − (1/N)]^S.

A more difficult problem is to compute the probability γ(N, s) that all the individuals of generation G_r have the same ancestor in generation G_r−S. Taking into account that 1−γ(N, s) is the probability of the union of the events “individuals i and j of generation G_r have different ancestors in generation G_r−s” for all i < j, we obtain

[3.50]

A better upper bound can be obtained in these inequalities (see [KIN 80]), yielding

[3.51]

where the constant 3 is the best possible. Inequalities [3.50] and [3.51] show that, for a large size N, it is necessary to go backward a number of generations comparable to N in order to find a common ancestor of all the individuals of generation G_r.

There are some good reasons to consider that generations G_r are also defined for negative values of r. Let us fix r and choose n ≤ N particular individuals i₁, i₂, …, i_n from G_r. The genealogical tree of these individuals and of their ancestors can be described by a sequence of equivalence relations , on the set {1, 2, …, n}, such that the couple (J, k) ∈ if the individuals i_j and i_k have a common ancestor in the generation G_r−S. Let

We easily see that

[3.52]

and that γ(N, s) is the probability to have in the particular case n = N. Note also that every equivalence class with respect to relation corresponds to an individual from G_r−S (but the converse is not true!). If two individuals of generation G_r−S have the same parent in generation G_r−s−1, then the corresponding equivalence classes with respect to relation form in only one equivalence class; otherwise, these equivalence classes will be distinct with respect to . Consequently, the sequence is a homogenous Markov chain with state space the set ε_n of all the equivalence relations on {1, 2, …, n} and with transition probabilities

calculated as follows. From relation [3.52] we obtain that p(ξ,ζ) = 0 unless ξ ⊂ ζ. For the case ξ ⊂ζ, let C_α, 1 ≤ α ≤ α, be the equivalence classes with respect to relation ζ and C_αβ, 1 ≤ β ≤ b_α, 1 ≤ α ≤ α, be the equivalence classes with respect to relation ξ. Note that we have

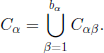
In order to calculate the probabilities p(ξ,ζ) in this case, it is convenient to consider the following urn model. Assume that balls labeled C_αβ, 1 ≤ β ≤ b_α, 1 ≤ α ≤ α, are randomly, independently, and uniformly placed in N urns, such that for different values of α the corresponding urns should be different. Then p(ξ,ζ) is the probability that for any α, 1 ≤ α ≤ α, all the balls C_αβ, 1 ≤ β ≤ b_α, are in the same urn. It is clear that p(ξ,ζ) depends only on N, a, b₁, b₂, …, b_α, that can be computed using combinatorial methods. For our purpose, we only need here to prove that p(ξ,ζ) is of order 1/N², except for the case where (the notation means that relation ζ was obtained from relation ξ by the juxtaposition of two of its equivalence classes). To be more specific, we can prove that

[3.53]

where

[3.54]

we have denoted here by |ξ| the number of equivalence classes of ξ.

In matrix notation, we obtain that P_N = (p(ξ, ζ), ξ, ζ ∈ ε_r) satisfies relation

[3.55]

as N → ∞. It is well known that stochastic matrices are contracting operators with respect to the norm

moreover, the contractions verify the inequality⁸

[3.56]

Using this inequality for A_s = P_N, B_s = exp((1/N)Q), 1 ≤ s ≤ r, where r =[Nt] for fixed t > 0, and taking into account [3.55], we obtain

Consequently, we have

in other words, if , then this is a process with values in ε_n which is weekly convergent to a Markov process whose generator (transition intensity matrix) is Q. This process is called the n-coalescent process.

We need to stress here that the n-coalescent process is a model for the genealogy study of a haploid population not only under the hypotheses of the Wright-Fisher model; we have chosen this case only for simplicity reasons. In fact, there are many other models that leads to the study of an n-coalescent process.

For instance, if the symmetric multinomial distribution [3.49] is replaced by an exchangeable distribution of the r.v. η_j and these r.v. are also assumed to be independent from one generation to another, then it can be proven that the sequence of relations on the set {1, 2, …, N} is a Markov chain. In this case, the transition probabilities are given by relation

[3.57]

where the quantities a,b₁,.. .b_a are determined from the known relations ξ and ζ as before, , and the sum is over all the different indexes 1 ≤ j1, j₂, …, j_a ≤ N. For instance, if there are only two equivalence classes with respect to ξ and only one with respect to ζ, the above formula becomes

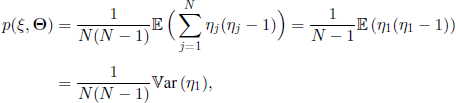
where, by means of [3.48], we have used (η₁) = 1.

If we assume that, as N→ ∞, the variance of the size of a typical family η₁ converges to a finite non-zero limit σ² and that the moments of η₁ are bounded, then we can directly prove that relation [3.57] yields

[3.58]

if ξ ≠ ζ; in this expression, the quantities q(ξ, ζ) are those given by [3.54]. As for the Wright-Fisher model, formula [3.58] implies that the process converges to the n-coalescent process. We note that in this case the variance of the size of the population modifies the natural time scale.

It is worth noticing here that even the hypothesis of constant size N of the population is not essential; if we do not assume constant size of the population, then we still can construct an n-coalescent process, by associating with the step from a generation G_r to another one G_r+1 a time interval equal to the local value 1/N.

To conclude, the n-coalescent process is a Markov process with finite state space ε_n, the set of all the equivalence relations on {1, 2, …, n}; the process starts from state A and has only one absorbing state 0, where A and 0 are, respectively, the finest and the coarsest equivalence relation on{l,2,…,n}; the transition intensities q(ξ, ζ) given by equation [3.54] completely define the process; note also that all the transitions of the process are of the type ξ → ζ, where .

Let us now find upper bounds for the absorption probability to state Θ. To this purpose, we will consider another Markov process obtained from the n-coalescent process through the procedure of “fusion.” It is known that, for f a surjective function defined on ε_n with values in another finite set S, the process generally is not a Markov process anymore. Nevertheless, for a function f such that, for all ξ ∈ ε_n and v ∈ S with f (ξ) ≠ v, the sum

[3.59]

depends on ξ only by means of u = f (ξ), then is a Markov process.

Let , where is the number of equivalence classes with respect to . Since yields |ξ| = |ζ| + 1, it implies that the sum [3.59] is zero, except for the case in which u = f (ξ) = v + 1, when it is equal to (l/2)u(u − 1). We obtain that is a quite simple Markov process. In fact, this is a pure death process (see section 2.5), with initial state n and transition intensity from r to r − 1

[3.60]

We note that the time T_n necessary for the n-coalescent process to arrive at the absorbing state 0 is the same as for the pure death process to arrive in the absorbing state 1. Consequently,

[3.61]

where the r.v. τ_r are independent and of a distribution given by

From [3.60] and [3.61] we obtain

which shows that the mean time to absorption of the n-coalescent process is bounded with respect to n.

If we define τ_r for any r ∈ , we have

[3.62]

and the series in this formula is a.s. convergent because (T) = 2. For θ > 0 we can write

which implies that the probability density function of the r.v. T is

Using [3.62] we obtain that

[3.63]

thus, we have obtained an upper bound, uniformly with respect to n, for the probability that the n-coalescent process does not reach the absorbing state until time t. For large values of t, the right-hand side member of inequality [3.63] is asymptotically equal to 3e^−t.

We can prove that, if (X(t),t ∈ ) is a pure death process whose transition intensities satisfy condition , then (Φθ (X(t))e^θt, t ∈ ) is a martingale for any θ > 0, where

In our framework, taking θ =1, we get Φ₁(x) = (x −1)/(x + 1), and we obtain that the process

is a martingale; in particular, we have

From the inequality (x − l)/(x + 1) ≥ 1/3, for x ≥ 2, we have

[3.64]

which is also an upper bound for the probability that the n-coalescent process does not reach the absorbing state up to time t. We conclude that formulas [3.63] and [3.64] give useful limits for the cases where t, and respectively n, are large enough.

3.4. Markov storage models

Storage models are used for the description and study of some economic phenomena, like reservoir models and risk models in insurance.

In this section we present some simple Markov models because further development would need complex mathematical tools, beyond the scope of this book. Note also that semi-Markov models are more adapted to the study of time evolution of a stock (commodities, water reservoir, money deposit, etc.).

3.4.1. Discrete-time models

A stock (or inventory) is an amount of goods or material stored for future sale or production. In discrete time, the stock level at time n, Z_n, satisfies the following recurrence relation

[3.65]

where η_n+1 is the amount of resource entered at time n + 1, ξ_n+1 is the demand over the time interval (n,n + 1], and f (Z_n + η_n+1,ξ_n+1) is the amount sold at time n + 1. In the standard case we suppose that the successive demands ξ₁, ξ₂,… are mutually independent r.v. with a common distribution, that the amounts of resource entering the stock are determined by a particular restocking policy, and that the function f is determined by this policy. It is clear that f(Z_n + η_n+1, ξ_n+1) ≤ ξ_n+1. Two restocking policies can be considered, whether we allow f(Z_n + η_n+1, ξ_n+1)> Z_n + η_n+1 or not.

a) Reserves are allowed. In this case f (Z_n + η_n+1, ξ_n+1) = ξ_n+1. Equation [3.65] becomes

[3.66]

and a negative inventory level indicates a reserve. The amount of reserve at time n + 1 is

[3.67]

b) Reserves are not allowed. In this case, demands are met only if they are “physically possible.” Consequently,

[3.68]

and equation [3.65] becomes

[3.69]

This policy can generate a deficit and the amount of this deficit at time n + 1 is

[3.70]

EXAMPLE 3.8.– (Storage model of (s, S)type). Let s, S, 0 ≤ s ≤ S < ∞, be two real numbers. It is supposed that the amount sold always equals the demand. The stocking policy is the following: if the available stock quantity is less than s, an order is placed to bring the stock level up to level S. Otherwise, no replenishment of stock is undertaken. Thus the amount received at time n + 1 is

[3.71]

and equation [3.65] written for this model is

[3.72]

In this model we assume that the refill process is controlled, i.e. the ordered quantity will eventually enter the stock, albeit with a certain delay. However, there are situations where these quantities are also random variables (the refill process is a stochastic process).

EXAMPLE 3.9.– In this model we suppose that there exists a real number x*, such that if the stock level Z_n ≥ x*, then no restock order is placed. If Z_n < x*, then an order is placed and a random amount X_n+1 enters the stock immediately. Consequently,

[3.73]

where ξ_n+1 is also a random variable.

EXAMPLE 3.10.– (Finite reservoir). Let us consider an example where the replenishment (the input amount), as well as the demand (the output amount), is r.v.; the objective of the study is to regulate the demands in order to maintain a desired stock level.

Let X_n+1 be the amount of water pumped into the reservoir (input) during the interval (n,n + 1], n ≥ 0. The r.v. X₁,X₂,… are supposed to be independent, with a common distribution. Due to the finite capacity of the reservoir, say c ∈ , the amount of water overflowing c is evacuated. Therefore, the amount of water which actually enters the reservoir is

where Z_n is the stock (water) level at time n. Water demands arrive at times n =1,2,... and the amount of the demand (output) at time n is ξ_n. The r.v. ξ₁,ξ₂,… are supposed to be independent, with common distribution. Moreover, we suppose that the r.v. (ξ_n) are independent of (X_n). The storage policy imposes the rule

In our case, equation [3.65] becomes

[3.74]

P. A. P. Moran assumed in his model that the water outputs are constant, i.e. ξ_n = m ∈ , n =1,2,.... We see that the sequence (Z_n,n ∈ ) defined in [3.74] is a homogenous Markov chain. If the input process has the discrete distribution

[3.75]

then the chain ) has c − m states and transition matrix P =(p(i,j),i,j = 0,l,...,c−m),with

For m < c/2, the transition matrix is given by

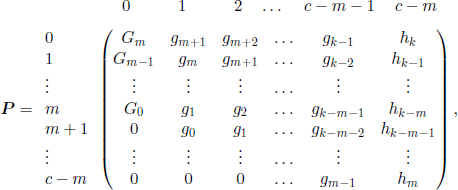
where

[3.76]

If the input process is characterized by a continuous distribution

the chain (Z_n,n ∈ ) has [0, c − m) as state space and, denoting , we have

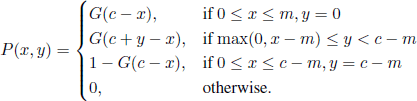
We would like to mention that most of the first articles on reservoir theory were devoted to the statistical equilibrium, i.e. to the asymptotic behavior of the chain (Z_n, n ∈ ) as n → ∞.

In the following we present the Lloyd model for reservoirs. We will be working under the hypotheses of the Moran model, except for the case when (x(n),n ∈ ) is a bounded Markov chain, i.e. it exists such that a.s. for all n ∈ . Additionally, we assume that the chain has a stationary (invariant) distribution . In this case ) is a Markov chain with transition probabilities

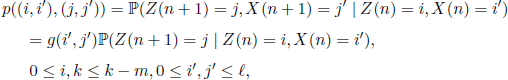
where

[3.77]

As the output policy asks the delivery of a water amount m, provided that such an amount is available, we obtain that

where

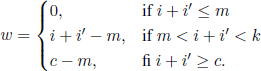
Therefore, we can prove that the distribution of the chain ((Z(n), X(n)), n ∈ ), i.e.

has a limit, as n → ∞, which satisfies the equations

[3.78]

as well as the equality

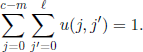
In the particular case where inputs are supposed to take only the values m − 1, m or m + 1, and the transition matrix whose elements are given in [3.77] has the expression

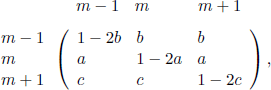
with 0 < min (a, b, c) ≤ max (a, b, c)< 1/2, choosing a = θ/r, b = θ/q, and c = θ/p (θ > 0, p + q + r = 1), we can prove that the Markov chain (X(n),n ∈ ) is stationary with the distribution

The meaning of the parameter θ can be understood from the following formula, which gives the correlation coefficient of the inputs

In reservoir theory, the problem of the first depletion time of a reservoir, stated for the first time by D. G. Kendall in 1957, has a particular interest.

Assuming that at time t =0 the reservoir contains an amount of water Z(0) = i > 0, we define

[3.79]

that represents the first-passage time of the chain to state 0. In the particular case where the inputs have a discrete distribution and m =1, for all n ∈ , we have

and the recurrence relation

We obtain f (l, i, 0) = g₀δ(i, 1) and

[3.80]

where g_i and h_i are given by [3.75] and [3.76]. If we introduce the notation

and

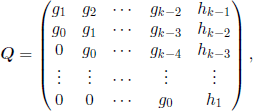
then equations [3.80] can be rewritten as Φ⁽ⁿ⁾ = QΦ⁽ⁿ⁻¹⁾,n ≥ 2; we successively find the solution of these equations for n =2,3,...,

[3.81]

where γ_i is the ith row of the matrix Q. Using this result we see that the generating function of T_i, is

[3.82]

where the existence of the inverse of I − θQ is guaranteed by a convenient choice of θ, for instance such that max_j |θg_j| < 1. Taking into account the particular form of the vector Φ⁽¹⁾, which has only the first component different from zero, formula [3.82] can be written as

[3.83]

where E is obtained from I − θQ by replacing the first row by γ_i.

If the inputs have a geometric distribution, i.e.

then formula [3.83] becomes

with

If the reservoir has an infinite capacity, i.e. c → ∞, relation [3.74] becomes

and, for m =1, we can prove that

[3.84]

where

If we let , then we have

[3.85]

where ζ is the largest solution of equation ζ = K(ζ) in the interval (0, 1) with

3.4.2. Continuous-time models

The theory of continuous-time storage models was initiated by P. A. P. Moran, J. Gani, and N. Prabhu in the years 1956–63. In these models we consider that the “inputs” define a continuous-time process X(t) and that the “outputs” are continuous with constant rate.

We present in the following only models for the risk in insurance and reservoir models.

EXAMPLE 3.11.– (Insurance risk) The theory of risk insurance concerns the business of an insurance company, and we make the following assumptions: (i) the total claim amount X(t) incurred by the company during the time interval (0, t] has a compound Poisson distribution

[3.86]

negative claims arising for ordinary whole-life annuities.⁹ The expected value of the claims during the interval (0, t] is λαt, where

and λα is called the net risk premium rate, (ii) The company receives premiums at constant rate β (−∞ < β < ∞). The difference β − λα is called the safety loading and we will assume that β and a have the same sign. The ratio ρ = β(Xa)⁻¹ > 0 is called Lundberg’s security factor.

The function

is called the risk reserve with initial value Z(0) = x ≥ 0. When this reserve becomes negative, the company is ruined. This event occurs at time T = T(x), where

The main topic in insurance risk is the study of the distribution of the r.v. T, the so-called ruin problem. The company needs to choose an initial reserve large enough to avoid ruin in a finite or infinite time horizon, with a specified probability [BUH 70, PRA 80]. So we are looking for an x such that

[3.87]

We recall that a process with stationary and independent increments, continuous in probability,¹⁰ whose sample paths are right continuous with left limits, is called a Levy process. Obviously, we can assume that X(0) = 0. We can prove that the characteristic function of X(t) is given by

where

[3.88]

with a ∈ ,

and M is a measure on , bounded on any bounded interval, such that

REMARK 3.12.–

1. If the measure M is concentrated at the origin with M({0}) = σ² > 0, then and

Then X(t) is the Brownian motion with drift.

2. If M does not have an atom at the origin and

we can write

where B(x) is a distribution function. Consequently, [3.88] becomes

and we obtain

where ψ(ω) is the characteristic function of B(x). Therefore, X(t) is a compound Poisson process.

If M({0}) = 0 and

then we can prove that

where d is called the shift of the process. In this case we have

where the sample paths of the processes X₁ (t) and X₂ (t) are positive. Note that if X(t)≥ 0 for all t ≥ 0, we obtain

[3.89]

EXAMPLE 3.13.– (A continuous-time model for reservoirs) Let us consider a water reservoir of infinite capacity and let X(t) denote the water pumped into the reservoir during the time interval (0, t]. We assume that (X(t),t ≥ 0) is a Levy process with characteristic function e−^tφ(ω),where φ(ω) is given by [3.89], with

If the water is continuously delivered at a unit rate (except when the reservoir is empty), then the amount of water in the reservoir at time t, denoted by Z(t), is given by

[3.90]

provided that the reservoir does not run dry during the time interval (0, t].

3.4.3. A generalized storage model

Relation [3.90] can be generalized in order to allow the description of a general stock level, without imposing the condition that the stock should be positive. Thus we obtain

[3.91]

with Z(0) ≥ 0, X(0) = 0, Y (t), and X(t) a Lévy process with increasing sample paths and no drift.

The Laplace transform of X(t) is , where

with M⁺ (0) ≤ ∞. If we introduce the following notation

then and .

In the stochastic integral equation [3.91] used for finding Z(t), the function

represents the time that the stock is empty during the time interval [0, t].

The following results concern the solution of equation [3.91] and its asymptotic behavior [PRA 80].

THEOREM 3.14.– The integral equation [3.91] has a unique solution

[3.92]

where

THEOREM 3.15.– Let Z(0) = x ≥ 0. If ρ < 1, then Z(t)converges in distribution, as t → ∞, to anr.v. Z whose Laplace transform is

If ρ ≥ 1, ρZ(t) → ∞ in distribution, as t → ∞.

The r.v.

[3.93]

has the same distribution as

[3.94]

which represents the first time that the stock runs empty, given that the initial stock level was x > 0, as well as the first hitting time of the set (− ∞, −x] by the Levy process Y(t).

To study the first time that the stock is empty, we have to consider the functional equation η = s + φ(η), s > 0, which has a unique solution η = rj(s) with η(∞) = ∞. Moreover, if ρ > 1, then , where η₀ is the largest solution of equation η₀ = φ(η₀) [PRA 80]. After these preliminary results, we can state the following theorem, whose proof can be found in [PRA 80].

THEOREM 3.16.− Assume that . Then:

(i)

(ii)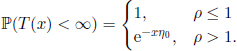

(iii)

(iv) If ρ 1, then

In the case of a reservoir study, we assume that the input X(t) has an absolutely continuous distribution with density k(x, t). Then, the r.v. T(x) is also absolutely continuous with the density

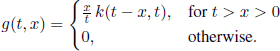
If we note

then the asymptotic behavior of T(x) as x → ∞ is given in the following theorem [PRA 80].

THEOREM 3.17.– For p < 1 and σ² < ∞ we have

[3.95]

In the case of an insurance study (see example 3.11) we are interested in the behavior of the r.v.

where x ≥ 0 and X(t) is a compound Poisson process (see [3.86]). The company needs to evaluate the non-ruin probability within a finite or infinite time horizon, i.e. . This is the so-called ruin problem in insurance risk theory. For α < 0 and β = − 1 we can obtain from Theorem 3.16 that

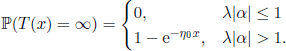
For α > 0 and β = 1 we have

and, if we also suppose that λα < 1, we obtain (T(0) = ∞) = 1 − λa.

3.5. Reliability of Markov models

3.5.1. Introduction to reliability

The design of reliable systems has become a compulsory requirement in our industrial society.

Reliability as a scientific field was born from military needs during the second world war. Afterwards, it was developed in space and nuclear programs of the United States and of the former Soviet Union. Obviously, important contributions are also due to laboratories in other parts of the world.

The researches of W. Weibull (1939) in Sweden, of B. Epstein and M. Sobel (1951), and those of Shannon on the construction of reliable systems starting from non reliable components, have set the basis of reliability theory. These last works led to the theory of coherent systems of Z.W. Birnbaum, J.D. Esary, and S.C. Saunders in the 60s. This theory, together with the introduction of fault trees, provided a theoretical basis and an important technique for the study of the reliability of complex systems.

The mathematical models used in reliability are probability theory, statistics, and, more specifically, stochastic processes.

Stochastic processes offer a natural mathematical basis for reliability study of discrete-time or continuous-time systems, with discrete or continuous state space. The stochastic processes mostly used in reliability are: renewal processes, Markov processes, semi-Markov processes, martingales, point processes, controlled processes, etc. The first two families of processes are particular cases of the third one and they are mainly used in the modeling of reliability (probabilistic approach). The following two families are applied more to statistical estimation of reliability. The last type of process is particularly used in system maintenance.

Semi-Markov systems are very general systems with numerous modeling possibilities in reliability. For instance, a system with cataleptic failures (sudden and complete) can be modeled by a semi-Markov system.

In fact, the system evolves by jumps from state to state at random times T_i, T₂,…. These times represent failures or end of reparation periods of the system’s components.

Repairable and non-repairable systems

We will study the random behavior of single-component systems subject to failures (breakdowns) that we observe over a period of time. For simplicity’s sake, we suppose that the system is new at time t = 0 when it starts to work and that there is only one type of failure.

The system starts to function at time t = 0, works for a certain time X₁ (random), when it breaks down. This r.v. X₁ is called the lifetime of the system. Then the system is repaired (or replaced) during a time period Y₁ (random), and, at the end of this period, the system starts again to function, etc. Such a system is said to be repairable. In the opposite case, when the component breaks down and cannot be either repaired or replaced, the system is said to be non-repairable.

The graphical description of the evolution of these two types of systems can be done in several ways, the phase diagram being the most common (see Figure 3.1).

Let the r.v. X be the lifetime of the system, with d.f. F,

If F is absolutely continuous, we denote as f the density function of the r.v. X, given by

In reliability, we always need to make the distinction between the occurrence (or arrival) of an event and its existence at time t. For instance, consider a component whose lifetime has a distribution function F and density function f. On the one hand, the statement “the failure of the component occurred at time t” means that this failure happened during the time interval (t, t + Δt], with Δt → 0; therefore, the probability of this event is f (t)Δt + o(Δt). On the other hand, the statement “the component is in a failure state at time t” means that the failure occurred at a time x ≤ t; the probability of this event is simply F(t).

Reliability and failure rate

The complementary function of F, 1 − F, denoted by , is called survival function or reliability of the system and it is denoted by R(t). Thus

and, for X absolutely continuous with density f we have

Consequently, we have

The hazard rate function, denoted by h(t), plays a major role in system reliability. For a failure process, it is called (instantaneous)failure rate and is denoted by λ(t); for a repair process, it is called (instantaneous)repair rate, denoted by μ(t). In survival analysis it is named risk rate (function). It is defined by

In order for a Borel function h on to be the hazard rate function of a certain r.v. X ≥ 0, it must satisfy the conditions

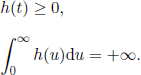
The cumulative hazard rate H(t) is defined by

and the total hazard rate is defined by

Note that H has an exponential distribution of parameter 1.

Maintainability and repair rate

The maintainability is defined as the probability that the system will be repaired during the time interval (0, t], given that it broke down at time t =0. Let Y denote the random repair time (failure time) and let M be the associated repair function, defined as the distribution function of Y,

The function M is called maintainability. The repair rate, denoted by μ(t), is given by

Mean times

The following mean times (if they exist) play a very important role in reliability studies, because they represent reliability indicators for systems and components and they are generally provided by the producers.

Mean time to failure, MTTF,

Mean time to repair, MTTR,

For multi-state systems we also have the following indicators.

Mean duration of good functioning after the repair, MUT (Mean Up Time).

Mean duration of failure, MDT (Mean Down Time).

Mean time between failures, MTBF,

It is worth noting that for single-component systems we have

therefore the formula MTBF = MTTF + MTTR holds only in this case.

In order for the MTTF to exist, there should exist a ξ > 0 such that

EXAMPLE 3.18.– If the density f of the r. v. X, with non-negative values, has the expression (Cauchy distribution)

then X does not have any moment. In fact, we have (X) = +∞.

In some applications it is interesting to know the mean residual lifetime at age t, given that it did not break down during the interval (0, t), called mean residual lifetime. It is defined by

where

The function L(t) satisfies the following properties:

1)

2)

3)

Fundamental relationships

The failure rate can be expressed by the formula

Therefore, the reliability satisfies the equation

whose solution is

Taking into account that the reliability at t =0 is equal to 1, we obtain the expression of the reliability in terms of the failure rate

Similarly, we obtain the equation satisfied by the maintainability

whose general solution is

We admit that M(0) = 0 and we get

Provided that the functions R(t) and 1 − M(t) are summable over the real half-line x ≥ 0, we have the following expressions for the mean times:

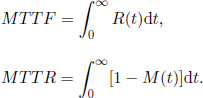
Exponential and weibull distributions

These two probability distributions are by far the most frequently used in reliability.

Exponential distribution. A system whose lifetime is modeled by an exponential distribution is a memoryless or Markovian system, that is, for any t > 0 and x > 0 we have . For the exponential distribution we have, for any t ≥ 0:

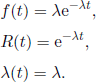
This distribution gives good modeling results for the lifetime of electronic components. However, its use in other application fields, like the modeling of mechanical components or of repair durations, is not always appropriate.

EXAMPLE 3.19.– Let us consider an electrical equipment with a constant failure rate A. The reliability of the equipment at time t is R(t) = exp(−λt). The probability that it fails during the time interval (t₁, t₂], t₁< t₂, is

The probability that it will be working at time t₂, given that it did not fail down between 0 and t₁, is

and

Weibull distribution. Thanks to the various shapes it can take according to different values of its parameters, the Weibull distribution is used in various reliability fields, particularly in the reliability of mechanical components. For the Weibull distribution we have:

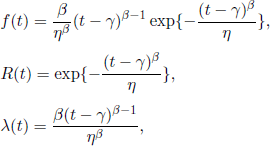
where β is the shape parameter, η the scale parameter, and 7 the location parameter. For β = 1 and γ = 0, we obtain the exponential distribution, which is, consequently, a particular case of the Weibull distribution. For γ = 0, we denote the Weibull distribution by W(β; η) Figure 3.2.

3.5.2. Some classes of survival distributions

Let F be a distribution function on . Let us denote by Λ(t) the cumulative survival rate function, i.e.

DEFINITION 3.20.– (IFRA and DFRA) We say that F is IFRA (DFRA) (increasing (decreasing) failure rate on average) if Λ(i)/t is an increasing (decreasing) function.

Equivalently, F is IFRA if

- is increasing,

or is decreasing.

EXAMPLE 3.21.– Let, be the distribution function of a Weibull r.v. We have

−

which is increasing for β ≥ 1, so F ∈ IFRA, and decreasing for β ≤ 1, so F ∈ DFRA. Consequently, the exponential distribution, that corresponds to β = 1, belongs to IFRA, as well as to DFRA.

DEFINITION 3.22.– (NBU and NWU) We say that F is NBU (NWU) (new better (worse) than used) if

In other words, the conditional survival probability of a component at time t + s, given that it did not break down before time t, is less than the survival probability at time s.

PROPOSITION 3.23.– (Relation between IFRA and NBU) We have the inclusion

PROOF– For F ∈ IFRA we have

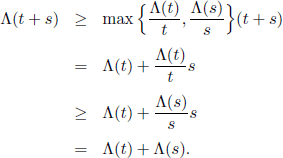
Therefore, for t ≥ s,

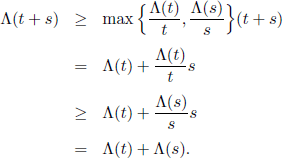
Thus

where

DEFINITION 3.24.– (NBUE and NWUE) We say that F is NBUE (NWUE) (new better (worse) than used in expectation) if and

This definition can also be written under the form

Indeed,

and, integrating by parts, we obtain

PROPOSITION 3.25.– We have the following inclusions:

– IFR ⊂ IFRA ⊂ NBU ⊂ NBUE;

– DFR ⊂ DFRA ⊂ NWU ⊂ NWUE.

The following two propositions show possible use of the results presented above.

PROPOSITION 3.26.– For a series system with n components with lifetimes T_i ∈ NBUE, 1 ≤ i ≤ n, the lifetime T of the system satisfies the inequality

PROPOSITION 3.27.– A series, a parallel or a k-out-of-n system, whose components have independent and IFRA lifetimes, has also an IFRA lifetime.

Availability of repairable systems

Unlike reliability, concerned with the functioning of the system during the whole interval [0, t], the availability is concerned only with the functioning of the system at an instant t, independently of any possible failure of the system prior to time t.

For the study of availability, let us consider the stochastic process X(t),t ≥ 0, with values in {0,1}, defined by

Instantaneous availability

The instantaneous availability of a system, denoted by A(t), is expressed as the probability that the system is operational at time t, i.e.

Using the previous definitions, we immediately establish the inequality

When the values of the availability are very close to unity, as is the case of standby safety systems, we will rather use instantaneous unavailability, denoted by and defined by

Asymptotic availability

This performance indicator represents the fraction of operational period per unit of time, when the system is in a “stationary probabilistic condition,” i.e. long enough after its start.

Mathematically, the asymptotic availability (or stationary availability) is defined by the following limit, if it exists,

Let X =(X_i;i = 1, 2,...) be the working times and Y =(Y_i;i = 1, 2,...) be the failure times of the system. If

– the r.v. Xi, i = 1, 2,... are i.i.d.,

– the r.v. Y_i, i = 1,2,... are i.i.d.,

– the r.v. X and Y are independent,

– at least one of X and Y is not a lattice,

then the stationary availability exists and is given by the relation

For the same reason as before, we will also use the notion of asymptotic unavailability, denoted by and defined by .

If X(t) is a Markov process with state space {0,1}, then represents the stationary distribution of this process, and, in this case, it always exists.

Note that for a non-repairable system we have A =0.

Mean availability

The mean availability, denoted by , is defined as the expected value of the system’s working time over [0, t],

Asymptotic mean availability

The asymptotic mean availability is defined by the relation

If exists, then we have .

Let us consider the example of a component with constant failure rate and repair rate λ and μ, respectively:

– for a non-repairable component

– for a repairable component

– the asymptotic unavailability

where τ is the mean repair time (τ = l/μ ). In the case where , the above formula reads: .

3.5.3. Discrete-time models

As will be seen in the following, reliability and related measures of Markov systems are well modeled and can be expressed under closed forms.

Let us consider a k-component system and let (X, (n), n ∈ ) be the performance process of component i ∈ C, with values in the finite state space of component i, denoted by E_i.

We also denote by the vector process with values in E′ = E₁× · · · × E_k, which jointly describes the states of the system’s components. A state of the system is given by the states of its components and is described by the corresponding element of E′, i.e. (x₁,..., x_k) ∈ E₁× · · · × E_k.

Let us also consider the process X_n with values in E ={1, ...,N}, where N =card(E′). Each element of E corresponds to an element of E′, for example through lexicographic order. Consequently, , where h is the bijection associated with lexicographic order.

EXAMPLE 3.28.– For a binary system of order 2 we have E₁ = E₂ = {0,1}, E′ ={(1,1), (1, 0), (0,1), (0, 0)}, and E ={1, 2, 3, 4}.

In reliability analysis, first of all we need to know whether the state of the system is a working state or a failure state. For this reason, we partition the state space E in two subsets U and D such that U ∪D = E, U ∩ D =Ø, where U contains the states of good functioning or working states and D contains the failure states or the repair states. To avoid degenerated cases, we assume from now on that U ≠ Ø and D ≠ Ø. The classic definitions of reliability measures (reliability, availability, maintainability) can be expressed for our model as follows.

1) Reliability, R(·). The reliability at time n, R(n), is defined as the probability that the system is in a working state at time n and that it did not visit failure states within the time interval [0, n],

[3.96]

2)Instantaneous availability, A(·). Instantaneous availability at time n, A(n), is defined as the probability that the system is in a working state at time n, independently of any possible failure on [0, n),

[3.97]

3)Maintainability, M(·). The maintainability at time n is defined as the probability that the system leaves the failure states up to time n, given that X₀∈ D,

[3.98]

PROPOSITION 3.29.– Let X and Y be two Markov systems independent of each other, with state spaces Ex and Ey, and transition junctions px and py. Then, the system formed by these two systems is also a Markov system with state space E′ = E_x × E_y and transition function and j, l ∈ E_Y.

The proposition stated above can be generalized for n Markov systems. It is obvious that this closure property is very important from a practical viewpoint, as we will see below, because a system whose components are Markov is itself a Markov process as well. So, if the processes Xi(n),..., X_k(n) are all Markov processes, then is also a Markov process. Moreover, X_n is a Markov process too.

Let us consider now a Markov chain (X_n) with state space E, transition function p, and initial distribution α; we will see below how the reliability measures of such a system can be computed. First of all, we need to consider partitions of matrices and vectors according to U and D. To this purpose, let us first rearrange the working states U = {1,..., r} and the failure states D = {r + 1,..., s}; thus we can write

PROPOSITION 3.30.– We have

Availability: A(n) = αpⁿ1_s,r,

Reliability:,

Maintainability: ,

where

Mean times

Let us denote by T the hitting time of set D and by Y the hitting time of U.

We have

[3.99]

where .

PROPOSITION 3.31.– The mean times can be expressed as follows:

[3.100]

[3.101]

where .

PROPOSITION 3.32.– For an ergodic system, the mean times under stationary distribution π =(π₁,π₂)can be expressed as follows:

[3.102]

[3.103]

where are the distributions of the hitting times of U and D when the initial distribution tt is stationary. The mean time between two failures is

[3.104]

PROPOSITION 3.33.– The variance of the hitting time of D, denoted by T, is given by

[3.105]

where

and

Obviously, we have .

EXAMPLE 3.34.– (a 3-state system) Let us consider

the transition matrix

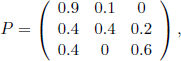
and the initial distribution

Reliability:

Mean time to failure:

Instantaneous availability:

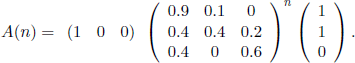
Stationary distribution:

Asymptotic availability:

The eigenvalues of P are λ₁ = 1, λ₂ =0.5, and λ₃ = 0.4. The eigenvalues of . Therefore, we obtain

– The rate of decreasing to A∞ of availability A(n), i.e.

– The rate of decreasing to 0 of reliability

3.5.4. Continuous-time models

We will apply the same formalism as we did for the Markov chain modeling presented in the previous section.

The classic definitions of reliability, availability, and maintainability for this model are expressed as follows:

1)Reliability: .

2)Instantaneous availability: .

3)Maintainability: .

REMARK 3.35.– The closure property given in proposition 3.29 for discrete-time Markov systems is also valid in the continuous-time case, with obvious analogous results.

Let us consider now a Markov process (X_t) with state space E, generator Q, transition function p(t), and stationary distribution α; we will see further on in this section how the performance indicators given above can be calculated for such a model.

The transition intensity matrix Q uniquely determines the transition matrix function P(t) due to the relationship

[3.106]

As we did in the discrete-time case, we need to consider partitions of matrices and vectors according to U and D. First, we rearrange the working states U ={1,..., r} and the failure states D ={r + 1,..., s}, and we have

Availability

As we have already seen, there are several indicators for the availability of a system: instantaneous availability, asymptotic (stationary) availability, mean availability over a time interval, and asymptotic mean availability. We give here the expression of the first two that are more used in practice.

PROPOSITION 3.36.– The instantaneous availability of a continuous-time Markov system as defined above is given by

[3.107]

PROOF.–

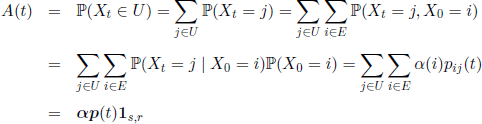
and, using relation [3.106], we achieve the proof.

The stationary availability, denoted by A∞, is given by

[3.108]

Reliability

Let T be the hitting time of the set D of failure states, T_D = inf {t ≥ 0 : X_t ∈ D}, with the convention inf Ø = +∞. We consider the process Y with state space , where A is an absorbing state, defined by

Note that (Y_t, t ≥ 0) is a Markov process with generator

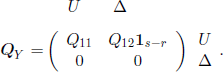
PROPOSITION 3.37.– The reliability of a continuous-time Markov system is given by .

PROOF-

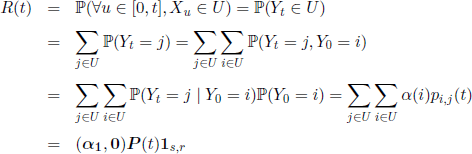
and relation [3.106] allows us to conclude.

Note that, in this proof, P(t) corresponds to the generator Q_Y of the process Y, i.e. P(t) = exp(tQ_Y).

Maintainability

PROPOSITION 3.38.– The maintainability of a continuous-time Markov system is given by .

PROOF.– The result can be proved following the same approach as for reliability.

Mean times

The mean times have been defined in the previous sectioi

PROPOSITION 3.39.–

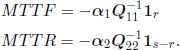
PROPOSITION 3.40.–

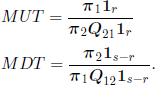
We also have

PROPOSITION 3.41.– We have

Phase-type distribution

Let us consider a Markov process X with generator Q and finite state space E ={1,..., s + 1}, with the partition U ={1,..., s} and D ={s + 1}. We suppose that all the states of U are transient and state s+1 is an absorbing state. The generator and the initial distribution vector are partitioned according to U and D,

and

DEFINITION 3.42.– A distribution function on [0, ∞) is said tc be of phase type (PH-distribution) if it is the d.f. of the absorption time of i Markov process as defined above. The couple (α, T) is called a representatior of F.

The distribution function of the absorption time to state s +1, for the initia distribution vector (α, α_s+1), is given by

[3.109]

Properties:

1)The absorption time distribution has an atom at x = 0. The density f of its absolutely continuous part is , for x > 0.

2)The Laplace-Stieltjes transform of F is given by

[3.110]

3)The (non-centered) moments are .

Let us denote by the space of matrices of dimension mn and let and the Kronecker sum of A and B is defined by A ⊕ B = (A ⊗ I_r) + (B ⊗ I_n), where ⊗ is the Kronecker product defined (see section 3.3.6), for

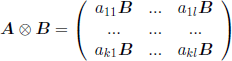
PROPOSITION 3.43.– (Convolution of two distribution functions of phase type [NEU 81]) Given two phase-type distribution functions F and G, with representations (α, T)and (β, S) of order M and N, respectively, their convolution F * G is a d.f of phase type with representation (γ, L), where

and γ =(α, α_N+1β).

PROPOSITION 3.44.– (Series and parallel systems [NEU 81]) Given two phase-type distribution functions F and G, with representations (α,T)and (β, S)of order M and N, respectively, then

1) The d.f. K given by K(x) = F(x)G(x)is a phase-type d.f. with representation (γ, L) and of order MN + M + N, with

and

2) The d.f. W given by W(x) = 1 − (1 − F(x))(1− G(x))is a phase-type d.f. with representation (α ⊗ β,T ⊗ S).

PROPOSITION 3.45 – (Asymptotic behavior [NEU81]) Let F be a phase-type d.f. of representation (α, T). If T is irreducible, then F is asymptotically exponential, i.e. , with −λ the eigenvalue of T having the greatest real part and K = αv, where v is the right eigenvector of T corresponding to the eigenvalue −λ.

---

1. Markov A.A., “Extension of the law of large numbers to quantities dependent on each other,” (in Russian) Izv. Fiz.-Mat. obsc, 2nd series, vol. 15, no. 4, 135–156, 1906.

2. We recall that

3. The word genetics comes from the Greek genao=to be born, and was coined by W. Bateson at the beginning of the last century.

4. In Greek, haploos=simple, diploos=double, eidos=shape, aspect, species.

5. We are talking here about somatic cells (of which body tissue is made) and not about sexual cells which are diploid.

6. In 1900 the Dutch botanist H. de Vries (1848-1935), the German botanist C. Correns (1864–1933), and the Austrian agronomist E. Tschermak (1871-1962) published several articles that confirmed the authenticity of Mendel’s heredity laws and their wide applicability.

7. The r.v. (ξ_n, 1 ≤ n ≤ p) are called interchangeable if their joint distribution function is symmetric, i.e. invariant to permutations.

8. The inequality can be proven by induction on r ∈ .

9. F*ⁿ is re-fold Stieltjes convolution of F, i.e. the distribution function of n i.i.d. r.v. with common distribution F (see 4.1).

10. The process is said to be continuous in probability if, for any ε > 0, we have