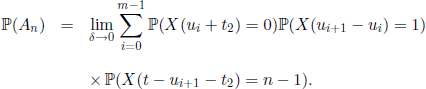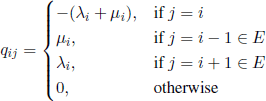Chapter 2

Simple Stochastic Models

This chapter presents stochastic models that, despite their simplicity, have been important for the development of the probability theory and of random modeling.

2.1. Urn models

An urn model (or scheme) is a system formed by urns that contain balls of different colors, to which we associate an experiment of successive ball drawings, with or without replacement in the urns, following some precise rules. These rules could consist in either putting in additional balls or taking out balls from some urns, or in changing the color of some balls at different stages of the experiment. The fundamental rule for computing the probability of a certain result of an experiment is that the random drawing from an urn with s balls is uniformly distributed, i.e. the probability of drawing any of the balls is 1/s.

In fact it is possible, at least theoretically, to associate an urn model with any random experiment with finite or countable number of outcomes [PÒL 54]. This was almost the only methodology at the beginning of probability theory, although urn models are not the only concepts used for discrete probabilistic models. A book of L. Hogben, entitled Chance and Choice by Cardpack and Chessboard (two volumes, 1950 and 1955, Max Parrish, London) presents other possible modeling ideas. Nevertheless, compared to card games, dice games, or chess, urns have the advantage of not being associated with a precise number like 52, 6, or 64. One can imagine a 17-sided die, a pack of 49 playing cards, etc., but all these have nothing to do with our “day-to-day experience.”

The following examples show how the conversion into urns’ language can be done.

1. The tossing of a perfect coin can be modeled as the drawing of a ball from an urn containing two balls labeled with the letters h and t (heads and tails). Similarly, rolling a die can be modeled by the drawing of a ball from an urn containing six balls labeled with the integers 1, 2, 3, 4, 5, and 6. Finally, drawing a card from a usual pack of playing cards can be seen as the drawing of a ball from an urn with 52 balls appropriately labeled.

2. The occurrence of an event of known probability p can be modeled by the drawing of a ball, say a white one, from an urn containing white and black balls in proportion p/(1 − p). Obviously, this is possible if and only if p is a rational number and we see here the limits of the method. A classic example (with p ≅ 0.515) is the birth of a boy. The successive drawings with replacement represent a prototype of Bernoulli scheme Bi(n, p), a fundamental concept in probability theory.

3. The successive dry or wet days in a town can be modeled by a three-urn system as follows [PÒL 54]. Each urn contains the same number of balls, say 1,000. Some of the balls are white (for dry days), the others are black (for wet days). The three urns, labeled 0, 1, and 2, have different compositions. The proportion “white balls/black balls” in the urn labeled 0 is equal to the proportion “dry days/wet days” throughout an year. The proportion “white balls/black balls” in the urn labeled 1 is equal to the proportion “dry days following a dry day/wet days following a dry day” throughout a year. The proportion “white balls/black balls” in the urn labeled 2 is equal to the proportion “dry days following a wet day/wet days following a wet day” throughout a year. The balls are successively drawn, their colors are recorded, and they are replaced in the original urns. Urn labeled 0 is only used for drawing the first ball. Whether this ball is white or black, the following drawing will be done from urn labeled 1 or 2, respectively. We keep drawing following this rule.

In fact, without saying it explicitly, we have here the representation of a two-state Markov chain (“dry days” and “wet days”) by means of an urn system. We have implicitly accepted the Markovian hypothesis for the succession between dry and wet days.

In fact, it can be seen that urn models are constructions mainly developed for illustrating theoretical concepts or facilitating the resolution of some probability problems. A list of urn models can be found in [JOH 77], as well as in [FEL 66, KOL 78b].

Some urn models (such as the Ehrenfest model) are presented in the following chapters. Although they are presented in a modern manner, the main aspects of the modeled phenomena will be clear.

It is often stated that probability theory has long been applied to casino games (roulette, dice, urns, etc.), called gambling games, but these studies made it possible to solve many important problems in sociology, demography, biology, engineering, etc. Urn models are mentioned and used in the monumental posthumous work Ars Conjectandi (1713) by Jakob Bernoulli (1654-1705), as well as in the famous Théorie Analytique des Probabilités (1812) by Pierre Simon de Laplace (1749-1827). The Ehrenfest model itself is a creation of the 18th century.

2.2. Random walks

The random walk is one of the simple stochastic models that is most useful. This type of model is used in physics, chemistry, biology, informatics, physiology of plants, technical studies, etc. There is a huge number of works on random walks, and we will mention here only some of them [GUT 88, HUG 96, RÉV 94, SPI76].

In an intuitive presentation of the random walk model, the state of the system is the position of a particle moving on the real line, in the plane or space, etc. So, the simplest random walk (called Bernoulli random walk) can be described as follows: a particle moves on the real line with one unit step, either one step to the right, with probability p, or one step to the left with probability q = 1 − p, where 0 < p < 1. Each step is supposed to be done in one time unit, such that the nth step occurs at time n. Moreover, it is supposed that the set of possible positions of the particle is the set of integers (the lattice of integers of ). The mathematical formulation is straightforward. Let be a sequence of i.i.d. random variables, with common distribution

so the r.v. (ξ_n + l)/2, n = 1,2,…, are Be(p), i.e. Bernoulli of parameter p. The position X(n) of the particle at time n is

[2.1]

where X(0) is its initial position. We find that the random walk model taken into account here is nothing but the sequence of partial sums of a sequence of i.i.d. r.v. Consequently, the random walk is a Markov chain (see below).

The problems related to the model defined in [2.1] arise from concrete situations. For instance: (a) what is the probability that the particle arrives in a given point? (b) if this probability is 1, how many steps (on average) are necessary to reach this point? (c) what is the probability that the particle returns to the starting point? (d) how long (on average) does the particle remain in a given state set?

We will take a closer look at the famous problem of gambler’s ruin: let a, b ∈ N₊, c = a + b; what is the probability that, starting from X(0) = a, the particle will reach 0 before reaching c? The problem got its name from the following context: two players A and B are involved in a series of plays of a game, with initial capitals a and b, respectively. At each play of the game, the probability that the players A and B win 1 unit is p and q, p + q = 1, respectively. The successive plays of the games are assumed to be independent. If X(n) denotes the fortune of the player A after n plays, then (X(n), n ≥ 1) is a random walk as described before. Each step of the particle to the right (left) means that the player A won (lost) a play. If the particle reaches the point 0 before reaching c, then A lost his capital, so he went bankrupt. Similarly, if the particle reaches the point c before reaching 0, then B went bankrupt.

This problem was stated for the first time by Christianus Huygens (1629-1695) in his work De Ratiociniis in Aleae Ludo published in 1657. He considered the particular case of a = b = 12, p = 5/12, and gave, without proof, the (correct) value of (5/7)¹² for the ratio of ruin probabilities of the two players. The first proof was given by Jakob Bernoulli, who reproduced the work of Huygens, accompanied by his commentaries, as the first part of his famous Ars Conjectandi. Using modern notation, Bernoulli’s solution is as follows. Let u(x) be the ruin probability of the player A, given that his initial capital is x. From the total probability formula we obtain the equations

[2.2]

with the limit conditions u(0) = 1, u(c) = 0. For solving the system [2.2] we write u(x) = (p + q)u(x), obtaining

and, by induction,

Denoting

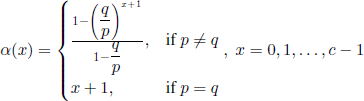
and adding the relations obtained for u(x) we obtain

Consequently,

which yields

and we finally obtain

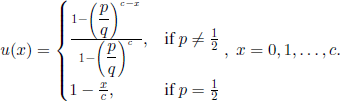
In the same way we obtain that the probability v(x) that the particle, starting from x, reaches c before reaching 0 (so the probability that B is ruined) is 1 − u(x), x = 0, 1,…, c. (An easier way to obtain v(x) is to exchange p with q and x with c − x in the previous expression of u(x)).

A similar argument can be used in order to obtain the mean value m(x) of the number of steps necessary for the particle to reach one of the points 0 or c, starting from the initial position x (i.e. the mean duration of the game). Note that m(x) satisfies the system of equations

with the limit conditions m(0) = m(c) = 0. The solution is

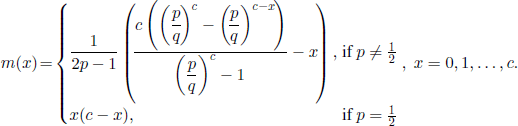
A modern probabilistic study of these problems uses the Markov chain theory [CHU 74, CHU 67, FEL 66, IOS 80, KAR75, KEM 60, RES 92, REV 75]. For instance, question (c) above can be expressed in terms of the recurrence or non-recurrence of the Markov chain (X(n), n ∈ ) with state space and transition probabilities P_i,i+1 = p, p_i,i−1 = q, P_i,j = 0 if |i − j| > 1 or i = j, i, j ∈ . It is interesting to note that this chain is recurrent (so, the probability of interest is 1, and, in fact, the chain returns an infinity of times to an arbitrary state i with probability 1) if and only if p′ = q′ = r′ = s′ = . An analogous result can be obtained if we generalize the model [2.1] by letting the possible positions of the particle be the points of the real plane with integer coordinates. In this case, starting from any point the particle can reach in one step one of the points (i + 1, j), (i − 1, j), (i, j + 1), or (i, j − 1), with probabilities p′, q′, r′, and s′, respectively, where p′ + q′ + r′ + s′ = 1. We can prove that the probability that the particle returns to its initial position is equal to 1 if and only if One can think that this property is true for any number of dimensions. But G. Pólya proved in 1921 that this was not the case: the Markov chain associated with the random walk in with m ≥ 3 is not recurrent. In the particular case of m = 3, considering that the probabilities that the particle reaches in one step one of the six neighboring points of the integer lattice of are all equal to 1/6, the probability that the particle returns to its initial position is equal to 0.340537, 330 … [SPI 76].

The term “random walk” was introduced in 1905 when Karl Pearson, in a paper entitled The problem of random walk, states the following problem: a person starts from a point O and walks yards in a straight line; then he turns through an arbitrary angle (i.e. the rotation angle follows a uniform distribution) and walks n yards in a second straight line. This procedure is repeated n times. We are looking for the probability that the person is at a distance between r and r + dr from his initial point O. Pearson states that he obtained the result for n = 2 and that a general solution can be obtained in the form of a power series of 1/n, when n is large. In fact, this result had already been obtained by Lord Rayleigh in 1880. He considered “the composition of n isoperiodic vibrations of unit amplitude and phases distributed at random,” a problem equivalent to Pearson’s problem. The asymptotic solution obtained by Rayleigh is (where is the amplitude of a vibration). Due to the difficulty of the problem, Rayleigh only considered the case where the phases have the exact values 0, π/2, π, and 3π/2, each of them with probability 1/4, so a bidimensional random walk. This is the first study of a random walk on a multidimensional lattice. For three dimensions, Rayleigh introduced the term random flight which did not survive, though very suggestive. In his subsequent works, Rayleigh discovered an important analogy between random walks and gas diffusion. In the end, this is to say that, starting from a random walk whose length of a step δ tends to 0, we can arrive at the Brownian motion process (or Wiener process, see the next section) and at other diffusion processes [FEL 66]. This method, exploited (even if in a heuristic manner) by Louis Bachelier¹ (1870–1946), was historically very rich: inspired by Bachelier, A. N. Kolmogorov developed the foundations of Markov processes.

We end these remarks on the use of random walks by presenting some generalizations and modifications of the model.

On the one hand, in the context of random walk and of its multidimensional generalizations, many applications require restrictions on the movement possibilities of the particle. This is done by modifying the transition probabilities of the associated Markov chain for the positions belonging to a given set. We have already seen such an example in gambler’s ruin problem, where the positions 0 and c are absorbing barriers.

On the other hand, we can get rid of the restriction on the movement of the particle by a unit step, keeping only the hypothesis of stochastic independence of the successive steps. More precisely, let (ξ_n, n > 1) be a sequence of i.i.d. r.v., with values in the Euclidean space . Then, relations [2.1], with X(0) an arbitrarily fixed point of , define a generalized random walk. From the various application fields of this model we can cite: insurance theory, system reliability, storage theory, queueing systems, etc.

Finally, coming back to the 1D case, if we suppose that each time the particle is in position i ∈ , it makes one step to the right or to the left with probabilities p_i, respectively q_i, or it remains in the same position with probability r_i, p_i + q_i + r_i, = 1, we obtain a non-homogenous random walk. Denoting by X(n) the particle’s position at time n ∈ , the chain (X(n), n ∈ ) is still Markovian, but the increments X(n + 1) − X(n), n ∈ , are no longer independent of n [KAR75, IOS 73, IOS 80]. The Ehrenfest model (see the next chapter) is a random walk of this type.

2.3. Brownian motion

2.3.1. Introduction

Let ξ_i, i > 1 be a sequence of i.i.d. r.v. with values in {−1, +1}, uniformly distributed. Let us consider the random walk called the simple random walk on , and the random walk , on . It is clear that S_n ~ Bi(n, 1/2). Let us also consider the simple random walk on the lattice Rh = {nh : n ∈ }, h > 0, of a particle starting from 0, whose movements are made at times t = nδ, n ∈ , δ > 0.

If X(t) denotes the position of the particle at time t = nδ, then

with X(0) = 0.

For t = nδ and s = mδ, with n > m, the r.v. X(t) and X(t + s) − X(s) are independent and identically distributed. Thus we have

Consequently, is a linear function of t. Let us set

[2.3]

where σ² is a constant.

We also have

so

[2.4]

Note that

[2.5]

and we obtain

[2.6]

Using the de Moivace theorere-Laplm, as δ → 0, we obtain

[2.7]

and finally

[2.8]

The process X(t), t > 0, is called Wiener process or Brownian motion. The constant σ² is called diffusion coefficient.

For all 0 ≤ s < t we also have

[2.9]

A definition of the Brownian motion can be given as follows.

A process (X(t), t ≥ 0) is called a Brownian motion or a Wiener process starting at 0 if the following conditions are fulfilled:

1. X(0) = 0 a.s.;

2. The sample paths are continuous a.s.;

3. (X(t), t ≥ 0) is aprocess with independent increments, i.e. ther.v. X(t+s) − X(t) is independent of X_u, u ≤ t for all ;

4. X(t + s) − X(t) is N(0, σ²s) distributed, for all .

This is equivalent to saying that for all 0 ≤ t₀ < t₁ < … < t_n, the r.v.

have a joint normal distribution with , and covariance matrix Γ, whose elements are

In fact, for t_l > t_k, we have

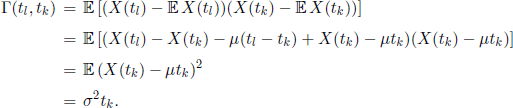
We can write

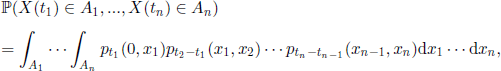
for all 0 ≤ t₁< … < t_n and , with

called transition density.

If σ² = 1 and μ = 0 the process is called standard. Any Brownian motion X(t) can be converted to the standard process through the transformation

A Brownian motion has continuous sample paths a.s., and almost all sample paths have infinite variation on any finite interval.

2.3.2. Basic properties

Some properties have already been mentioned in the previous paragraph. We will give further details here and will also present additional properties.

All through this section we will assume that σ = 1, i.e. we will be concerned only with standard Brownian motion. For a standard Brownian motion X(t), t > 0, the following properties are straightforward.

PROPOSITION 2.1.–

1)

2)

3)

4)

PROPOSITION 2.2.–

1) For a fixed time s > 0, the process X(t+s) − X(s), t ≥ 0, is a Brownian motion.

2) The process — X(t), t ≥ 0, is a Brownian motion.

3) The process cX(t/c²), t ≥ 0, with c ≠ 0, is a Brownian motion.

4) The process , defined by and tX(1/t) t > 0, is a Brownian motion.

The Brownian motion is a martingale with respect to its natural filtration and many other functions of this process are also martingales.

PROPOSITION 2.3.–

1) The Brownian motion X(t),t ≥ 0, is a martingale.

2) The process |X(t)|² − t, t ≥ 0, is a martingale.

3) The process e^X(t)−t/2, t ≥ 0, is a martingale, called the exponential martingale.

The following properties play an important role in the theory of stochastic integrals.

THEOREM 2.4.– (Doob’s maximal inequality in L²). For all t > 0,

The following two properties concern the sample paths of Brownian motion.

THEOREM 2.5.– The variations of the sample paths of the Brownian motion are infinite a.s.

THEOREM 2.6.– The sample paths of the Brownian motion are not differentiable a.s. for all t ≥ 0.

THEOREM 2.7.– We have

Reflection principle

Let X(t), t ≥ 0, be a Brownian motion in , with the diffusion coefficient σ². Let us denote by T the exit time from the open interval (a, b), with a < 0 and b > 0,

[2.10]

THEOREM 2.8.– We have

1) T < + ∞, a.s.;

2)

3)

For a ∈ , let T_a denote the first-passage time to a, i.e.

THEOREM 2.9.– (Reflection principle) Let a ∈ be a fixed number. Then the process , defined by

is a Brownian motion.

Markov property

The Brownian motion, just like any process with independent increments, is a Markov process.

Let P_t, t ≥ 0, be the associated transition semi-group. For any real Borel function f we have

and P₀ f(x) = f(x).

It is easy to prove the semi-group property (or Chapman-Kolmogorov identity)

Its (infinitesimal) generator L, defined by

gives, for , the set of bounded real functions defined on , two times continuously differentiable,

Consequently, the backward Kolmogorov equation can be written as

[2.11]

Similarly, the forward Kolmogorov equation can be written as

[2.12]

In physics, this equation is known under the name of heat or diffusion equation.

2.4. Poisson processes

The Poisson process is a mathematical model for a large variety of fields like physics (study of radioactive decay), biology (model for genetic mutations due to noxious radiation), telecommunication (especially in telephony), trade, insurance, road traffic, industry (reliability and quality statistical control) [HAI 67]. The name of the Poisson process comes from the great French mathematician and physicist Siméon Denis Poisson (1781-1840) who, during the last years of his life, became interested in applications of probability theory into administration and justice. His famous work Recherches sur la probabilité des jugements en matière criminelle et en matière civile, précédées des régles générales du calcul des probabilités (Bachelier, Paris, 1837) could be considered as a textbook of probability with applications to judicial practice. In this work, Poisson defines what we call today the “Poisson distribution.” The r.v. X(t) from a Poisson process represents the number of times that a specific event appeared during the time interval [0, t), t > 0 and X(0) = 0.

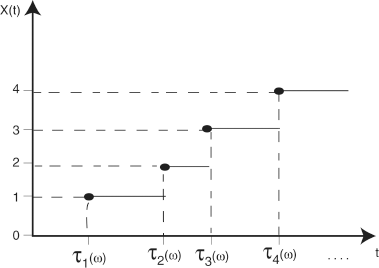
From this definition we see that every possible sample path of a Poisson process is a non-decreasing step function with unit steps (see Figure 2.1). The axioms satisfied by a Poisson process are the following:

(a) If 0 < t₁ < … < t_n, then the increments X(t_i) − X(t_i−1), 1 ≤ , are independent, i.e. the number of times the event occurs in disjoint time intervals are independent r.v. In this case, the process is said to have independent increments;

(b) The distribution of the r.v. X(t + h) − X(t) depends only on h²;

(c) There exists a constant λ > 0 such that

(d)

Using these postulates, one can compute the distribution of the r.v. X(t).³

Let . From (d) we obtain

Obviously,

Postulates (a) and (b) yield

so

Thus p₀(t) satisfies the differential equation = −λp₀(t), which has the solution p₀(t) = ce^−λt. The constant c is computed from condition p₀(0) = 1 and we obtain

In order to compute , note that p₁(t + h) = p₁(t)p₀(h) + P₀(t)p₁(h) and

for m ≥ 2. From postulates (c) and (d) we obtain

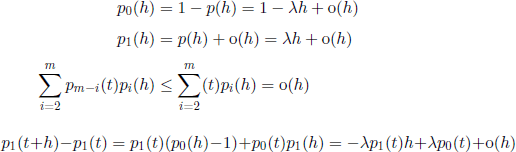
and

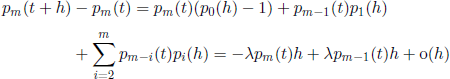
for m ≥ 2. Thus, letting t → 0, we obtain the system of differential equations

with initial conditions p_m(0) = 0, m ≥ 1. The easiest way of solving this system is to introduce the functions . In this way we obtain the much easier system]

with q₀ (t) = 1 and initial conditions q_m (0) = 0, m ≥ 1. From here, we obtain by induction that , and eventually

So, for all t ∈ ₊, the r.v. X(t) has a Poisson distribution of parameter λt. This implies that the expectation and the variance of X(t) are both equal to λt. Consequently, the parameter A is nothing but the mean number of occurrences per time unit of the specific event.

We have to mention that the usual definition of a Poisson process is based on the property of independent increments (postulate (a)) and on the fact that X(t) is Poisson distributed with parameter λt, . Obviously, this definition is equivalent to the one we have given above (postulates (a)-(d)), which is actually more intuitive.

Before continuing the presentation of the Poisson process, let us describe two generalizations of this process.

If λ( · ) is a non-decreasing real function on , we define the non-homogenous Poisson process as a process with independent increments (postulate (a)) such that X(t) − X(s), s < t, are Poisson distributed r.v. of parameter . The case that we have already studied, called homogenous, corresponds to the function λ(t) = λt. For the properties of non-homogenous Poisson processes (basically, the same as those of homogenous Poisson processes) we can see [IOS 73, RES 92].

Let us now define a more general class of stochastic processes, the point processes. Such a process is a finite or countable family of points randomly placed in an arbitrary space, for instance the gravels on a road, the stars in a region of the sky, the failure instants of a given system, etc. From a mathematical point of view, we admit that a point can be multiple.

Although the space where the points are considered can be an arbitrary topological space, we usually consider the case of the spaces , d ≥ 1.

Let (X_n, n ∈ ) be a sequence of random points in . Then, for any (the Borel σ-algebra of ),

is the random number of points in A. The family of r.v. (N(A), is called a point process if N(K) < ∞ for any compact set K of The r.v. N(A): are called counting variables of the point process (N(A), A ∈ .

The measure m defined on by

is called the mean measure of the process.

The process is called Poisson with mean measure m or Poisson random measure m if:

(a) for

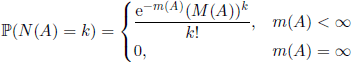
(b) for disjoint sets A₁ ,…, A_k of B(), the r.v. N(A₁), … N(A_k) are independent.

If the mean measure is a multiple of the Lebesgue measure, i.e. if a constant λ > 0 exists such that m(A) = λμ(A), with μ the Lebesgue measure, then the process is said to be homogenous.

Let us come back to the ordinary homogenous Poisson process P(λ) of parameter (or intensity) λ. We are interested in the distribution of the interval length between two successive occurrences of the event, i.e. between two successive jumps of its sample path.

Let τ_n, n ≥ 1, be the nth jump time (see Figure 2.1), i.e.

Thus τ₁ is the sojourn time in state 0, τ₂ − τ₁ is the sojourn time in state 1, etc.

THEOREM 2.10.– For the process P(λ) the sequence (τ_n − τ_n−1), n ≥ 1, with τ₀ = 0, is a sequence of i.i.d. r.v., with common exponential distribution of parameter λ.

PROOF.– Let us consider t₁, , and the events A_n = (τ₁ > t₁, τ₂ − τ₁ > t₂) ∩ (X(t) = n), n ∈ . We consider a partition t₁ + t₂ = u₀ + t₂ < u₁ + t₁ < … < u_m + t₂ = t of the interval [t₁ + t₂, t] and we set δ = max_0≤i≤m(u_i+1 − u_i). We have

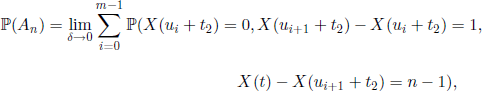
or, using postulates (a) and (b),

[2.13]

From [2.13] we obtain

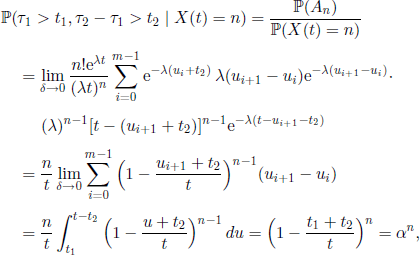
that implies

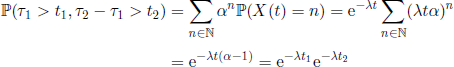
and the result is proved for τ₁ − τ₀ and τ₂ − τ₁. A similar calculation can be done for a finite number of r.v. τ_i+1 − τ_i,.

COROLLARY 2.11.– For all the values t and t_i, 1 ≤ i ≤ n, such that 0 ≤ t₁ ≤ … ≤ t_n ≤ t, we have

which is the common distribution function of the order statistics of a sample of size n from the uniform distribution on [0, t].

PROOF.– From Theorem 2.10 we get

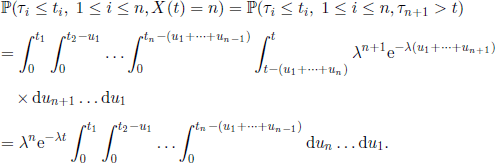
Using the change of variables x_i = u₁ + … + u_i, 1≤ i ≤ n, we obtain

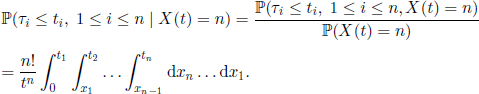
REMARK 2.12.–

1. From Theorem 2.10 we infer that the process P(λ) can be constructed as follows. Let (ξ_n, n ≥ 1) be a sequence of independent identically distributed r.v., of common distribution Exp(λ), i.e. exponential of parameter A. Then

is a Poisson process.

Generalizing this construction, we can define the compound Poisson process. Let F be a distribution function and (σ_n, n ≥ 1) a sequence of i.i.d. r.v. with common distribution function F. We consider that the sequences (σ_n, n ≥ 1) and (ξ_n, n ≥ 1) are independent. The process defined by the relations

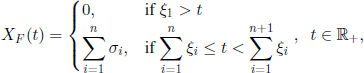
is called compound Poisson process and is denoted by P(λ, F). The process P(λ) can be seen as a compound Poisson process, with 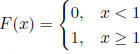. Note that the process P(λ, F) has independent increments. If F is continuous at the origin, then almost all the trajectories of the process P(λ, F) are step functions with jumps of amplitude σ₁, σ₂,…, separated by intervals of lengths ξ₁, ξ₂,….

It can be proven that

where F*ⁿ, n ≥ 1, is the convolution of order n of F and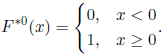

2. The nth jump time τ_n, n ≥ 1, is a sum of independent r.v. of distribution Exp(λ), which implies that its probability density is

An important property of the process P(λ) is its lack of memory or memoryless property. If the time is measured starting from a fixed moment t₀ and if we denote by τ₁⁽⁰⁾, τ₂⁽⁰⁾,… the jump times subsequent to t₀, then, through a direct computation⁴ we can prove that the sequence (τ_n+1(0)) − τ_n⁽⁰⁾, n ≥ 1) and τ₀⁽⁰⁾ has the properties stated in Theorem 2.10. This property can be used to prove that the process P(λ) is a homogenous Markov process with state space . Indeed, if 0 ≤ t₁< … < t_n+1 and , then

The last probability is equal to

which proves the homogenity of the process.

The infinitesimal generator of the process P(λ) is given by

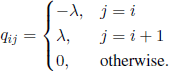
We end this section by mentioning that the Poisson process is not only a mathematical model for various natural and society phenomena but also has an outstanding theoretical importance (for instance, for the study of the general process with independent increments or for sums of independent r.v.), and it is often used for the construction of complex mathematical models.

2.5. Birth and death processes

The birth and death process is a mathematical model for describing phenomena where the variation of a random characteristic occurs by discrete jumps of one more unit (birth) or one less unit (death). Obviously, the Poisson process P(λ) is a particular case of the birth and death process.

Formally, the birth and death process is defined as a homogenous Markov process with state space E = {a, a + 1,… } ⊂ and generator

[2.14]

for i, j ∈ E, where μ_a = 0, λ_b = 0, with b = sup E (if E is finite), μ_i > 0, i − 1 ∈ E, λ_i, > 0, i + 1 ∈ E are given numbers.⁵ If E is an infinite set, it is possible that, for a given set of such numbers, there will be not only one birth and death process with generator [2.14], but several such processes. Anyway, there exists at least one process, called minimal, that we construct as follows. Let X(0) = i. The process stays in i a sojourn time ξ₁ of distribution Exp(λ_i + μ_i), then it jumps either to state i + 1 with probability or to i − 1 with probability . In this new state j (which is i − 1 or i + 1) the process stays a random time ξ₂ of distribution Exp(λ_j + μ_j), etc. The successive sojourn times ξ₁, ξ₂, … of the process X(0), X(ξ₁), X(ξ₁ + ξ₂), … are no longer independent r.v. They are only conditionally independent, given the states X(0), X(ξ₁), X(ξ₁ + ξ₂),….⁶ The dynamics of the process is analogous to that of the non-homogenous random walk, with the difference that the jump times are random and not fixed. A sufficient condition for the minimal process to be the unique Markov process with the generator [2.14] is (we suppose, without loss of generality, that )

where

More details on birth and death processes can be found in [IOS 73, KAR 75, MIH 78, WAN 92].

If μ_n = 0, n ∈ E, we obtain the pure birth process that is uniquely determined if and only if (with the convention ); similarly, if λ_n = 0, n ∈ E, the process is said pure death process that is uniquely determined by the values of μ_n, n ∈ E.

Another important case is the linear birth and death process obtained for .

---

1. Bachelier is the first author who described in detail many results of the mathematical theory of Brownian motion.

2. This postulate implies that the Poisson process is homogenous.

3. This distribution can also be directly obtained by way of a heuristic reasoning. Indeed, let us partition the time interval [0, t) in subintervals of length h small enough that the probability that an event occurs more than once in such a subinterval is zero (postulate (d)). From postulate (c) we obtain that in each subinterval the specific event either occurs once with probability λh or does not occur at all with probability 1 − λh. Taking into account the fact that the number of times the event occurs in disjoint time intervals are i.i.d. r.v. (postulates (a) and (b)), we can consider a binomial distribution Bi(n, p) with n = t/h and p = λh. As n(λh) = λt (constant), we obtain that X(t) has a Poisson distribution of parameter λt.

4. We use the memoryless property of the exponential distribution: ξ is an r.v. with Exp(λ) distribution if and only if for all . Intuitively, if a waiting time with an exponential distribution is cut into two parts, then the second part has the same exponential distribution, no matter which is the length of the first part. More generally, if η is an r.v. independent of ξ, then .

5. The birth and death process was first introduced by McKendrick in 1925 [MCK 26]. Feller in 1940 [FEL 39], without any knowledge of this work, basically defined the same process.

6. If X(0) = 1 and we set , then the r.v. σ_n+1 − σ_n, n ≥ 1, are independent (without conditioning).