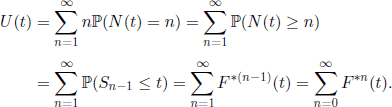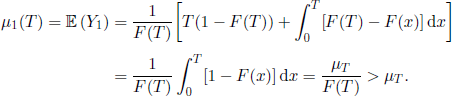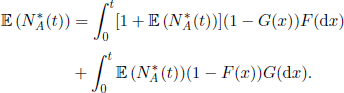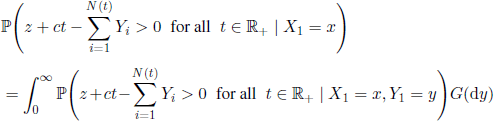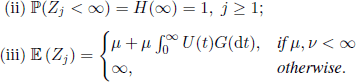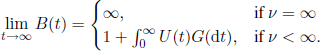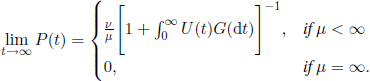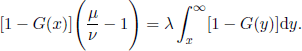Chapter 4

Renewal Models

Renewal theory was developed during the studies carried out on practical problems that arise from the degradation and replacement of components of complex systems. The fundamental theory can be found in [FEL 66], while [COX 62] is a monograph on the topic.

4.1. Fundamental concepts and examples

Note that, very often, to an arbitrary stochastic process there can naturally be associated sequences of i.i.d. r.v.

Let X₁ ,X₂,... be a sequence of real i.i.d. r.v., with the same d.f. F, F(−0) = 0, F(0) < 1, defined on a probability space . The sequence (S_n), where

[4.1]

is called a renewal chain (process).

In the applications that led to the renewal theory, the r.v. S₁, S₂, … represent the replacement (renewal) times of worn out components, while X₁, X₂, … are the working times (the times between successive arrivals). The expected value μ = (X_k), that exists and can be possibly +00, is called the mean lifetime of the components.

The counting function, i.e. the number of renewals during a time interval [0, t], is an r.v. defined by

[4.2]

and, for n ≥ 1, we have

where F*ⁿ (the n-fold Stieltjes convolution of F) is the distribution function of the r.v. S_n. More precisely,

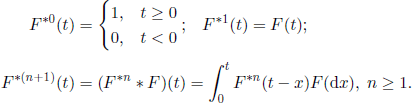
REMARK 4.1.–

1.In the particular case where F(t) = 1−e^−λt, t > 0, the counting process (N(t) – 1, t ≥ 0) is nothing but a Poisson process.

2.We consider that the time t = 0 is a renewal time, i.e. N(0) = 1, which is not the case for a Poisson process.

The expected value of the counting function at time t is called the renewal function and we denote it by U(t). We have

[4.3]

Obviously, the mean number of renewals during the interval (a, b] is U(b) − U(a).

Note that there exists at least one renewal in the time interval (0, t] if and only if X₁ ≤ t. Consequently, the mean number of renewals in the interval (0, t], given that X₁ = y ≤ t, is 1 plus the number of renewals during the interval (y,t]. Therefore,

which implies that U(t) verifies the equation

[4.4]

This equation is a particular case of what is called a renewal equation, that has the form

[4.5]

where F is a distribution function on , while h and g are functions that are bounded on finite intervals of , such that g(t) = h(t) = 0, t < 0.

THEOREM 4.2.–

(a)U is a non-decreasing and right continuous function, U(0) = 1 [see [4.3]] U(t) < ∞ for all ;

(b)Let h: h(t) = 0 for all t < 0, such that exists and is finite for all . Then

is the unique solution of the renewal equation [4.5] within the class of the functions h: , such that h(t) = 0 for all t < 0 and h is bounded on [0, t], t > 0.

EXAMPLE 4.3.– Let us assume that F is an exponential distribution Exp(A). Then, F(dy) = λe^−λy dy, y ≥ 0, and, for n ≥ 1, it can be proved by induction or by means of Laplace transform that

(Gamma distribution),

so

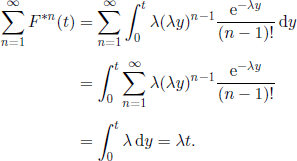
Thus, we obtain that

We will assume all throughout this section that μ = (X₁) < ∞.

THEOREM 4.4.– (Strong law of large numbers) We have

[4.6]

THEOREM 4.5.– (Central limit theorem) If then

[4.7]

THEOREM 4.6.– (Elementary renewal theorem) We have

[4.8]

THEOREM 4.7.– (Blackwell’s renewal theorem) If F is not arithmetic,¹ then for all h > 0 we have

[4.9]

If F is arithmetic on {nd; n ∈ }, then [4.9] is valid, provided that h is multiple of d.

The Blackwell’s renewal theorem is equivalent to the key renewal theorem for directly Riemann integrable functions introduced by Feller. We shall briefly present the directly Riemann integrable (DRI) functions. Let g be a function defined on [0, +00]. For any a > 0 and positive integer n, let us denote by the supremum and by the infimum of g on [(n — l)a, na]. The function g is said to be DRI if and are finite for every a > 0, and

PROPOSITION 4.8.– A sufficient condition for a function g to be DRI is that

a)g(t) ≥ 0 for any t ≥ 0;

b)g is non-increasing;

c)

THEOREM 4.9.– (Key renewal theorem) If F is not arithmetic and g: is DRI, then we have

[4.10]

In the case where F is arithmetic of period d and , then

[4.11]

REMARK 4.10.– Let us consider the case where Z : satisfies the renewal equation

with a given function and L an improper distribution function (i.e. L(∞) < 1), such that L(0) = 0. For this renewal equation, Theorem 4.9 cannot be applied.

Let us assume that there exists a k > 0 such that and let

, then ([FEL 66], vol. II, p. 362) we have provided that the integral of the right-hand side exists.

The results of renewal theory can be used in order to prove the existence of some “limit probabilities,” that express the equilibrium state of a random system with some specific properties. More precisely, we consider a stochastic process with a countable state space 1, 2,…, so that, with probability 1, there exists a random instant S₁ such that the evolution of the process after that moment is identical to the evolution of the process starting from time t = 0. For example, for a Markov process starting from a recurrent state, S₁ can be the first return time to the initial state.

From all we have seen before, we obtain that there exists a sequence of r.v.

0 = S₀ < S₁ < S₂ < S₃ < ... such that X_n = S_n — S_n-1, n ≥ 1, are i.i.d.

THEOREM 4.11.– Let Pk(t), , be the probability that the stochastic process is in state k at time t. If μ = , then there exist the non-negative constants pk, k , such that

PROOF.– Let q_k(t) be the probability that S₁ > t and that the process is in state k at time t. If F is the common distribution function of the r.v. X_n, n ∈ N₊, then

It is easy to check that P_k(t) satisfies the renewal equation

and, as 1 - F is a non-increasing function, from Theorem 4.9 we obtain

4.2. Waiting times

Let us consider a renewal process (S_n, n ∈ N) and, for an arbitrary fixed time t, let the r.v. X(t), Y (t), and L(t) be defined as follows:

1)X(t) = t — S_N(t)-1, called the spent waiting time or age;

2)Y (t) = S_N(t) - t, called the residual waiting time or residual lifetime;

3)L(t) = S_N(t) -S_N(t)-1, that is the duration between the two successive renewals containing t.

PROPOSITION 4.12.– The distribution functions of these three waiting times are given by

1)

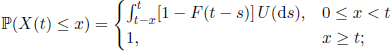
2)

3)

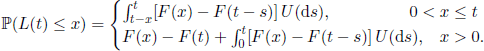
COROLLARY 4.13.– (Asymptotic behavior) We have

1)

2)

3)

EXAMPLE 4.14.– If F is an exponential distribution Exp(λ), we have

1)

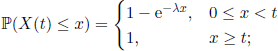
2)

3)

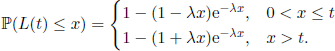
EXAMPLE 4.15.– (Waiting time paradox) Let us suppose that metros arrive in a station according to a Poisson process of parameter A. A person arriving at the station at time t can do the following reasonings about the time Y(t) he has to wait for the arrival of the next metro:

a)As the exponential distribution “forgets the past,” the mean waiting time for the next metro, i.e. , should be .

b)The moment when the passenger arrives at the station is randomly chosen between two successive arrivals, so, for reasons of symmetry, the mean waiting time should be .

On the one hand, the explanation of this paradox is that the r.v. L(t), that is the interval between two successive arrivals containing the instant t, does not follow an exponential distribution, but the distribution given in example 4.14. The mean value of this distribution is and not , as it was considered in (a). On the other hand, the r.v. Y(t) is exponentially distributed (see example 4.14) and we have for t→∞.

The waiting time paradox is a particular case of the paradox of backward recurrence time. Let us assume that a component of a certain type is replaced immediately after it fails. In order to determine the mean duration of good functioning of such a component, we can proceed as follows: at time t we choose a sample of working components for which we write down the duration of good functioning from the moment they started to work (before time t) up to the first failure. The mean value observed on this sample is considered as the mean duration of good functioning of the component. In fact, this reasoning is not correct because we determine the mean value of L(t), instead of the mean value of the r.v. X_n, ₊, that we are interested in. The relation between these two mean values is given, as t → ∞, by the formula

that is a consequence of corollary 4.13; for an exponential distribution of parameter A, this limit is 2A^-1.

Another problem that arises when we deal with renewal processes is to establish the distribution of the waiting time T up to the occurrence of the first interval between two successive renewals greater than or equal to a certain given value t₀ . To be more specific, T = S_n if X₁, X₂,..., X_n < t₀ and X_n+1 ≥ t₀ . Let us set T₁ = T + t₀ and let W be the distribution of the r.v. T₁. Obviously, W(t) = 0 for all t < t₀; we consider the mutually exclusive events X₁ > t₀ and X₁ = y ≤ t₀. Note that T₁ = t₀ in the first case, whereas in the second case the conditional distribution of T₁, given that X₁ = y, is W(t − y). Consequently,

[4.12]

for t ≥ t0.

Relation [4.12] can be regarded as a renewal equation of the form

[4.13]

where

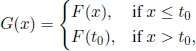
and

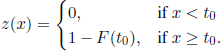
In the particular case where F is an exponential distribution of parameter A, the problem presented above is known as the gaps problem in a Poisson process.

In order to compute the moments of the distribution W, we consider the r.v. as the lifetime of a renewal process stopped with the probability 1 — F(to). Note also that the r.v. T satisfies equation [4.13], with z(t) = 1 — F(t₀) for all . Therefore,

and, in the Poisson case, we get

and

[4.14]

Similarly, we obtain

[4.15]

EXAMPLE 4.16.– Let us assume that, at a given point on a road, the successive cars moving in a single lane form a Poisson process. In order to cross the road at that given point, a pedestrian needs a time t₀ between two successive passages of the cars. So, he will cross the road during the first gap of the Poisson process.

If λt₀ > 1, then there exists a k > 0 such that e^(k−λ)t0 = k and, for large values of t, we have (see Remark 4.10)

[4.16]

Applying the Laplace transform in [4.12] we can obtain ([FEL 66], vol. II, p. 444)

[4.17]

where x⁺ = max(0, x), x ∈ .

REMARK 4.17.– If the cars move in two parallel lines and if for each line the successive passages form a Poisson process of parameter A, then we can consider that the successive passages of both lines form only one Poisson process of parameter 2A. In this case, the mean waiting time for crossing both lines is (e^4λto − 1)/λ (see [4.14]).

If the road crossing is done with a stop between the two lines, then the mean waiting time for crossing the road will be .

If λt₀ = 1, then the mean waiting time for crossing will be 30.24to with a stop between lines and 53.6to without a stop.

4.3. Modified renewal processes

Let us consider the case where S₀ > 0 is independent of X_n, n ≥ 1, and has the distribution function F₀ different from F. The process (S_n, ) is called modified renewal process or delayed renewal process. If we denote by U₀ the new renewal function, we can write

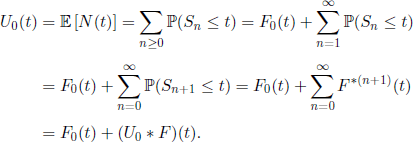
Therefore, U₀ satisfies the renewal equation

[4.18]

For h > 0 we have

[4.19]

If F is not arithmetic, then Blackwell’s renewal theorem implies

[4.20]

and, consequently, the number of renewals in (t, t + h] tends to the constant h/μ as t → ∞. Note also that the renewal rate does not depend on the initial distribution F₀. We would like to find the initial distribution F₀ such that , i.e. so that the renewal rate is constant. From [4.18] we see that the only possible choice is

[4.21]

In this case, the process is called stationary modified renewal process.

Another generalization can be obtained by assuming that the process can be stopped at each renewal time with probability q ∈ (0,1), or it can continue with probability p = 1 — q, independently of the evolution of the process up to that moment. Let (T_n, n ≥ 1) be a sequence of i.i.d. r.v., with

The sequences (T_n, n ≥ 1) and (X_n, n ≥ 1) are assumed to be independent. The r.v. T_n, n ≥ 1, can take the values 0 or 1, according to the decision made at the nth renewal to stop or to continue the renewal process. Let

Obviously, we have G(∞) = p.

Consequently, the evolution of the process that can be stopped is described by a sequence of i.i.d. r.v. that can take the value ∞, with distribution function G. If X_n = ∞, then the process is stopped at the nth renewal. The distribution function G is called improper (or defective), that is to say it has an atom at infinity.

The probability that the process will not be stopped during the first n renewals is pⁿ → 0 as n → ∞. Consequently, the process will be stopped with probability 1 after a finite number of steps. The mean number of steps up to the stopping time is

Note that the mean number of renewals on [0, ∞) is U(∞), so we get

The same result can be obtained from equation [4.4], replacing F by G.

Note also that the probability that S_n ≤ t and that the process is stopped at the nth renewal is qG*ⁿ (t), which implies that the probability that the process will be stopped before t is

Consequently, H(t) = qU(t) is the distribution function of the lifetime of the process. This function satisfies the renewal equation

4.4. Replacement models

Let us denote by X₁, X₂,... the lifetimes of identical components. When a component fails, it is immediately replaced by an identical one. So, the positive r.v. X₁,X₂,... are assumed to be independent, with the same distribution function F, whose mean value is denoted by μ.

The mean number of replacements during the interval [0, t] is U(t) and, from Theorem 4.7, we obtain

which means that for large values oft, the replacement rate is 1/μ. This implies that any replacement strategy that prescribes the component replacement prior to its failure will use more than 1/μ components per unit of time. Nevertheless, there are situations when failure in service can cause unacceptable damages (railways, aeronautical equipment, nuclear power plants, etc.).

Let us consider the age-replacement policy that consists of replacing a component either when it reaches an age T or when it fails, if this moment is prior to time T.

For large values of t, we would expect that the fraction of replaced components up to time t, due to their failure, to be F(T), and the corresponding fraction of replacements due to their age to be 1 — F(T). Let

and thus

For large values of t, the replacement rate will be 1/μT > 1/μ.

Let Y₁, Y₂,... denote the durations between replacements due to component failures. It is clear that these random variables are independent and have the same distribution. We have

where the r.v. N denotes the number of replacements due to age. Consequently,

and

and we obtain

[4.22]

So, for large values of t, the replacement rate due to failures is

[4.23]

Relation [4.23] suggests that, for some distribution functions F, the rate l/μ₁(T) could be lower than l/μ. This fact is relevant in the cases where the occurrence of failures during the service implies more expensive damages than the replacement costs.

It is worth noticing that, if F is an exponential distribution function, we have μ₁ = μ and the above strategy does not bring any improvement.

Let St (t) = (Y₁ > t) be the probability that there is no failure up to time t. We can easily see that St (t) has the expression

[4.24]

If F is differentiable, then [4.24] yields for t > T

Consequently, if and only if

[4.25]

The ratio is called (instantaneous) failure rate, because r(t)At is the probability that the component will fail during the interval (t, t + Δt], given that it worked up to time t. As T > t − nT, relation [4.24] is satisfied for distributions with increasing failure rate r(t).

In conclusion, regarding the probability that there will be no failure up to time t for distributions with increasing failure rate, the smaller T, the larger this probability will be.

In addition, [4.22] implies that μ = μ₁(∞). Therefore, in order to have l//xi(T) smaller than l/μ, it suffices that the function μ1 is decreasing. We have

[4.26]

and

if F has an increasing failure rate; thus, relation [4.26] shows that μ₁ (T) is increasing in this case.

Another replacement strategy is that of block replacement, where all the components of a certain type are replaced either simultaneously at times kT, k = 1, 2,..., or individually when failures occur. On the one hand, the advantage of this strategy compared to the previous one is that it avoids the recording of individual failures. On the other hand, this strategy uses on average more components per time unit than the previous one because there may be components that are replaced prior to their failure or before reaching ageT.

Let us investigate now if by using this strategy we can decrease the average number of replacements due to failures. Let N_B(t) and Ny(t) denote the

total number of replacements during the interval [0, t] when using the block-replacement policy and the age-replacement policy, respectively. The total number of replacements due to failures during the interval [0, t], in these two strategies, will be denoted by (t), respectively.

THEOREM 4.18.– ([BAR 65], pp. 67-69) Fo r all n ∈ we have

[4.27]

If F has an increasing failure rate, then

[4.28]

Inequality [4.27] implies that the average number of replacements during the interval [0, t] is greater for the block-replacement policy than for the replacement policy at a specified age; similarly, if F has an increasing failure rate, relation [4.28] implies that the average number of replacements due to failures during the interval [0, t] is greater for the block-replacement policy than for the age-replacement policy.

It can be proved ([BAR 65], p. 69) that equality holds in relation [4.28] for F exponential.

There are practical situations when replacements at fixed time moments are not appropriate (or even impossible), as is the case, for instance, for equipments working on random cycles, whose interruption for replacement purposes is not possible. In these cases we need a random-replacement policy. This policy is defined by a sequence of i.i.d. random variables (Y_n, n ≥ 1) of d.f. G. The sequence (Y_n, n ≥ 1) is assumed to be independent of the sequence (X_n, n ≥ 1) of intervals between the successive failures. If we let Z_n = min(X_n, Y_n), n ≥ 1, then Z_n, n ≥ 1, represents the durations between successive replacements, which define a renewal process with the distribution function

and we have

If N_A(t) is the total number of replacements during the interval [0, t], then applying Theorem 4.6 yields

For the number of replacements due to failures during the interval [0, t], denoted by N*(t), we can easily obtain

[4.29]

The distribution function K of the time elapsed between two successive failures satisfies the renewal equation

[4.30]

An important function from a practical point of view is the function denoted by R(x, t), representing the probability that a component operates without any replacement during the interval [t, t + x], given it started to work at time t. It can be proven ([BAR 65], p. 74) that R(x, t) satisfies the equation

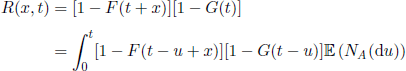
and, from Theorem 4.11, we obtain

4.5. Renewal reward processes

Let us assume that when the nth renewal occurs, n ≥ 1, a reward Y_n is given, such that the sequence of random variables ((X_n, Y_n), n ≥ 1) is i.i.d.; therefore, Y_n may depend only on X_n. The sum of the rewards up to time t is

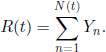
The asymptotic behavior of the r.v. R(t) is given in the following result.

THEOREM 4.19.– ([ROS 70], p. |Y_n| < ∞ and X_n < ∞, then

[4.31]

and

[4.32]

PROOF.– First note that

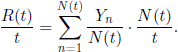
Second, applying the law of large numbers we have

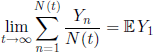
and

so we obtain [4.31].

As N(t) + 1 is a stopping time for the sequence (Y_n, n ≥ 1), by Wald’s equation we have

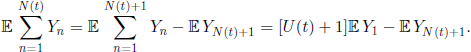
Relation [4.32] will follow from Theorem 4.6, if we show that . To this purpose, let

It can be easily checked that

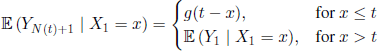
and thus g satisfies the renewal equation

[4.33]

where As , it follows that lim_t→∞ h(t) = 0 and

Note that the solution of equation [4.33] is (see Theorem 4.2)

For any ∈ > 0, there exists T > 0 such that h(t) < ∈ for all t ≥ T. Consequently,

Therefore

and we obtain

EXAMPLE 4.20.– The supply of a company with spare parts is done at the moment when there are N demands (N represents the capacity of one transport). It is assumed that the demands form a Poisson process of parameter A. For every demand that is not met, the company incurs a penalty equal to c per time unit. Let us denote by X₁, X₂,… the intervals between successive replenishment moments (the replenishment time is considered to be zero) and by Y₁, Y₂,… the penalties corresponding to these intervals. It is clear that

the sequence of random variables ((X_n,Y_n),n ≥ 1) is a renewal reward process. Therefore, for t large enough, the average penalty per time unit will be (see Theorem 4.19).

First, note that

where τ_i, 1 ≤ i ≤ N − 1, is the time between the ith and the (i + l)th demand. As τ_i, 1 ≤ i ≤ N—1, are exponentially distributed with parameter A, it follows that

Second, as X₁ = τ₁ + τ₂ + … + τ_N, we have Xs₁ = N/λ. Thus, for t large enough, the total average penalty on the interval [0, t] is c(N — l)t/2.

4.6. The risk problem of an insurance company

Let N(t) be the number of claims incurred by an insurance company over the time interval [0, t] and let us assume that it is a Poisson process. Assume, further, that the values of the successive claims Y₁, Y₂,... are i.i.d. r.v. with the same distribution function G. Let us denote by c the total cash inflow of the company per unit of time. If the initial capital of the company is z, then the capital at time t is

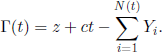
We are interested in the probability that the company will not be ruined. More precisely, we will study the function

Obviously,

where X₁ is the time of the first claim. Note that we have

[4.34]

and

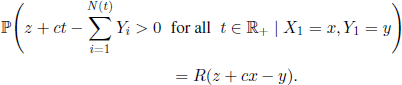
Consequently, the function R satisfies the equation

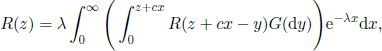
or, by change of variable t = z + cx,

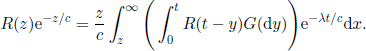
Differentiating this relation we obtain

which leads to

Integrating both sides with respect to z on the interval [0, w] we obtain

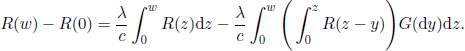
Interchanging the orders of integration and the change of variable s = z — y yields

[4.35]

If we let then from [4.35] we obtain

where

[4.36]

Equation [4.36] is a renewal equation corresponding to the improper density . Note that this probability density is improper because could have a value ≠ 1, where μ = (Y₁).

If , then R(z) = 0, since the average claim per unit of time exceeds the income rate c.

If then we have

and

where the constant k satisfies equation

and μ* is given by

4.7. Counter models

We consider a counter (or a recording mechanism) for the detection of the presence of a radio-active material. The impulses arrive at the counter, but some of them will not be recorded due to the counter inertia. This period of inertia is called locked time or dead time. Assume that an arriving impulse is recorded at time t = 0 and blocks the counter for a certain period. All the impulses that arrive during this period will not be recorded. The first impulse arriving after this locked period will be recorded, blocking in turn the counter, etc.

If the impulses that arrive at the counter during a locked period do not influence this locked time, then the counter is said to be of type I. On the contrary, if each arriving impulse has an influence on the locking time of the counter (even if it arrives at a moment when the counter is already locked), then the counter is said to be of type II.

4.7.1. Type I counters

Let us assume that the impulses arrive at the counter at times S₀ = 0, S₁, S₂,… and that at time t = 0 the counter is not locked. Let X_n = S_n — S_n-1, n ≥ 1, be the successive interarrival times of the particles and Y₀ , Y₁, Y₂,… be the successive locking times determined by the recorded particles. We make the following assumptions:

(i) The sequence (X_n,n ≥ 1) is a sequence of i.i.d. r.v., with common d.f. F,with F(0) = 0.

(ii) The sequence (Y_n,n ≥ 1) is a sequence of i.i.d. r.v., with common d.f. G,with G(0) = 0.

(iii) The sequences of r.v. (X_n,n ≥ 1) and (Y_n,n ≥ 1) are independent.

Let (N(t)). Obviously, N(t) + 1 is the number of particles arrived within the interval [0, t], t > 0.

Let us now introduce the sequence of non-negative integer numbers (n_i, j ∈ ), defined by the relations

Consequently, the successive registering times are and the elapsed times between successive registrations are

From the definition of the sequence of r.v. (n_j, j ∈ ) we see that (n_j − n_j-1, j ∈ ) is a sequence of independent r.v. with the same distribution. Consequently, the sequence (Z_j, j ∈ ) is also a sequence of independent r.v. with the same distribution. Let us also define T_n = Z₁ + … + Z_n, n ≥ 1, M(t) = max{n | T_n ≤ t}, and V(t) = (M(t)). Obviously, M(t) is the number of impulses registered within the interval [0, t].

It is worth noticing here that the ratio B(t) = (1 + U(t))/(1 + V(t)) is an indicator of the counter’s quality.

Let us denote by W_n the time interval after the nth registering when the counter is not locked, i.e. W_n = Z_n − Y_n−1. The sequence (W_n, n ≥ 1) is a sequence of random variables with the same distribution. The following result concerns their common distribution function K.

THEOREM 4.21.– ([PRA 65b], p. 177) We have

[4.37]

PROOF.– For Y₀ = t (fixed) we have W₁ = S_N(t)+1 - t, whose conditional distribution function, given Y₀ = t, is (see Proposition 4.12)

[4.38]

Integrating this relation with respect to the distribution of Y₀ we obtain [4.37].

From the definition of the variables Z_j, j ≥ 1, we see that they can take only finite values. The following theorem presents some properties of these variables.

THEOREM 4.22.– ([PRA 65b], p. 178) We have:

[4.39]

[4.40]

PROOF.– From relation Z_j = W_jY_j-1, the following equalities follow

and relation [4.39] is proved.

On the one hand, from [4.39], for θ > 0 we obtain

where is the Laplace transform of F. On the other hand, from the renewal equation [4.5] it follows

and

[4.41]

Using the properties of the Laplace transform, from [4.41] we obtain

since .

In order to prove relation [4.40], note first that max(Y₀, X₁) ≤ Z₁ ≤ Y₀ + X_n and that (Z₁) < ∞ if and only if μ, v < ∞. Second, from the definition of n₁ we have (n₁ | Y₀ = t) = 1 + U(t). Using Wald’s identity it follows that

Therefore,

If μ < ∞, note that

[4.42]

Indeed,

and we obtain [4.42] taking into account [4.40].

Let P(t) be the probability that at time t the counter is locked. The following result gives an expression of P and its asymptotic behavior.

THEOREM 4.23.– We have

[4.43]

and, if ν < ∞, then

[4.44]

PROOF.– From the definition of P(t) we have

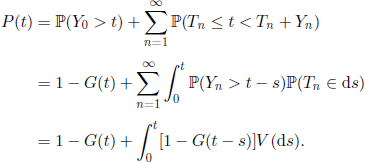
Since the function 1 - G(t), t ∈ R₊, is non-negative, non-increasing, and improper Riemann integrable over ₊, relation [4.44] is obtained from [4.43], applying Theorem 4.9.

In the following, we will illustrate the results presented above using some particular cases.

1. Poisson arrivals. In this case, F(x) = 1 − e^−λx, λ > 0, x ∈ ₊, and we obtain from [4.38]

as well as

and

The Laplace transform of the function H is

Since , we get

and, using the fact that F is exponential, we have

which yields

that is

Consequently,

and thus

Note that in this case U(t) = At, that implies

as well as

and

To conclude, relation [4.44] becomes

2. Counters with constant locking times. Let us assume that the locking time has a constant value d; in this case, the distribution function G has the form

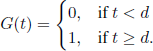
From relation [4.41] we obtain

which implies

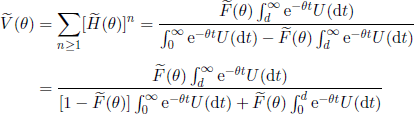
and, since , we obtain

Moreover, for μ < ∞, relation [4.42] leads to

and [4.43] and [4.44] become, respectively,

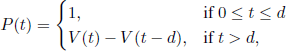
and

3. Counters with exponential locking times. By assuming that G(t) = 1 — e^-βt, β > 0, t ∈ ₊, relation [4.41] becomes

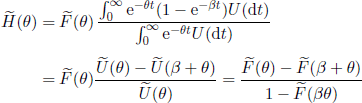
and relation [4.42] leads to

4.7.2. Type II counters

Let us assume now that the particles arrive at the counter following a Poisson process with rate A; let X₁, X₂,… be the successive interarrival times and Y₁, Y₂,… be the successive locking times determined by the arriving particles. The assumption of Poisson arrivals implies that the r.v. X₁, X₂, … are independent and exponentially distributed of parameter A. We will also make the following assumptions:

(i) The sequaence (Y_n, n ≥ 1) is a sequence of i.i.d. r.v. with common d.f. G.

(ii) The sequences of r.v. (X_n, n ≥ 1) and (Y_n, n ≥ 1) are independent.

(iii) A particle arrives and it is recorded at time t = 0.

As opposed to type I counters, where the particles arriving during a locked period of the counter have no influence on the counter, for the type II counters a particle arriving when the counter is locked causes a new locking of the counter. For instance, the particle arrived at time t = 0 locks the counter for a time Y₁; if there is another particle that arrives during the interval [0, Y₁], which means that Y₁ > X₁, then this second particle prompts a new locking of the counter of duration Y₂, such that the counter is locked for a period equal to max(Y₁,X₁ + Y₂) .

As we did for type I counters, let us denote by P(t) the probability that the counter is locked at time t. We will prove relation

[4.45]

Note that [the counter is not locked at time t | n particles arrived during the interval (0, t)] x (λt)ⁿe_−λt/n!. If we work under the assumption that there were n particles that arrived during the time interval [0,t], then the common distribution of the arrival times is the same as the common distribution of the order statistics for a sample of size n from the uniform distribution over [0,t] (see Corollary 2.11). Consequently, the probability that the length of locking times altogether ends at time t is

Therefore,

Moreover, we note that

[4.46]

If we denote by M(t) the mean number of particles registered during the interval (0, t], we will prove the relation

[4.47]

First, note that the probability that a particle arrives during the interval (t, t + At] is At + o(At); second, the probability that this particle does not find the counter locked during this interval is 1 — P(t) + o(At). Consequently, the probability of a recording during the time interval (t, t+Δt] is λΔt(l—P(t)) + o(Δt) and thus

which yields the differential equation

[4.48]

Integrating [4.48] we obtain [4.47].

4.8. Alternating renewal processes

Let us consider a system whose state space contains two states, denoted by 0 and 1; assume that these states represent the working state and respectively the repair state of the system. Initially, the system is in state 0 and it stays there a random time X₁; then it switches to state 1 where it stays for a time Y, afterward it moves to state 0 where it remains for a time X₂, etc. Let us make the following assumptions:

a) (X_n, n ≥ 1) is a sequence of i.i.d. r.v. with common d.f. F.

b) (Y_n, n ≥ 1) is a sequence of i.i.d. r.v. with common d.f. G.

c) The sequences (X_n,n ≥ 1) and (Y_n, n ≥ 1) are independent.

It is clear that the sequence (X_n + Y_n, n ≥ 1) is a sequence of i.i.d. r.v. with common d.f. H = F * G. If we assume that H is not arithmetic, then

[4.49]

where P(t) is the probability that the system is in state 0 at time t. To see that this relation holds, note first that

Second, we have

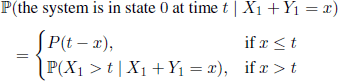
and we obtain

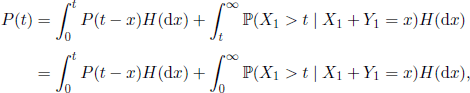
since Y₁ ≥ 0 a.s. Therefore, the function P(t) satisfies the renewal equation

whose solution is

[4.50]

with U(x) = Σ_n≥1 H*ⁿ(x). Applying Theorem 4.9 to [4.50], we get [4.49].

Let us present now how this result can be used for estimating the parameter λ of the Poisson process describing the particles’ arrival at type I and type II counters. For this purpose, let us note that the succession of locked times B_n and non-locked times K _n, n=1, 2…, forms an alternating renewal process, whose second component L_n has an exponential distribution of parameter A (due to the memoryless property of the exponential distribution). If Nz(t) denotes the number of renewals of the process Z_n = B_n + L_n, n ≥ 1, during the interval [0, t], we have (see Theorem 4.5)

[4.51]

where Y₁ is the locking time generated by the first particle.

Thus, for large values of t, relation [4.51] allows to estimate the parameter λ as follows:

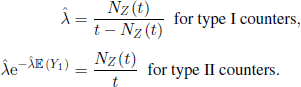
4.9. Superposition of renewal processes

For every n ≥ 1, let us consider k_n ∈ ₊ sequences of i.i.d. r.v. Additionally, let us assume that the k_n sequences are independent and have the distribution function F_ni, i = 1, 2,..., k_n. If we denote by N_ni(t), i = 1,2,...,k_n, the number of renewals within the interval [0, t] for the ith sequence, then the superposition N_n of these renewal processes is defined by

which is an r.v. that counts the total number of renewals up to time t for all the k_n renewal processes.

Note that, in general, there does not exist a renewal process whose number of renewals during the interval [0,t] is N_n(t), because, in the general case, the intervals between two successive renewals when considering all the k_n processes do not follow the same distribution and are not independent. Nevertheless, in some particular cases that we will present in the following two theorems, N_n(t) is a renewal process.

Let us consider N₁(t) and N₂(t), t ∈ ₊, two independent renewal processes with the same d.f. F of the intervals between two successive renewals.

THEOREM 4.24.– If and if N(t) = Ni(t) + N2(t), t ∈ ₊, is a renewal process, then N₁(t), N₂(t), and N(t) are Poisson processes.

PROOF.– Let us denote by H the distribution function of the intervals between two successive renewals for the renewal process N(t). Then

[4.52]

Let Y₁(t), Y₂(t), and Y (t), t ∈ R₊, be the processes defined in section 4.2, corresponding to the processes N₁(t), N₂(t), and N(t), respectively. Since Y (t) = min(Y₁(t), Y₂(t)), we have

From corollary 4.13, for t → ∞, we obtain

[4.53]

where . Differentiating² [4.53] with respect to x we obtain

so

[4.54]

If we set G(x) = 1 - F(x) and we differentiate [4.54], we obtain the differential equation

[4.55]

with the initial condition G(0) = 1. The solution of [4.55] is

where

Let us assume now that (N₁(t), t ∈ ₊) is a Poisson process and that (N₂(t), t ∈ ₊) is a renewal process independent of (N₁(t),t ∈ ₊), with the distribution function of the time between two successive renewals denoted by G.

THEOREM 4.25.– If and if N(t) = Ni(t) + N2(t), t ∈ ₊, is a renewal process, then (N₂(t),t ∈ ₊) and (N(t),t ∈ ₊) are Poisson processes.

PROOF.– Let H be the distribution function of the inter-renewal times of the process (N(t), t ∈ ₊). We have

[4.56]

and, following the same procedure as that used to obtain relation [4.53], we get

[4.57]

where . Differentiating relation [4.57] yields

and, taking into account [4.56], it follows

[4.58]

If we let λ₁ = λ(μ/ν — 1) and F(x) = 1 — G(x), x ∈ ₊, differentiating relation [4.58] we obtain the differential equation

whose solution is F(x) = e^−λ1x, x ∈ ₊, and we finally obtain

The superposition of a large number of renewal processes can be estimated by a Poisson process, under some conditions that are detailed in the next result.

THEOREM 4.26.– ([KAR 75], p. 223) For any n ∈ N₊, let us consider the independent renewal processes (N_ni(t), t ∈ R₊), with the corresponding distribution functions F_ni, i = 1, 2, … , k_n. We assume that

Then

if and only if

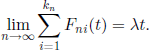
Note that the hypotheses of this theorem are satisfied in the particular case of F_ni(t) = F(t/n), k_n = n, where F is a distribution function with the properties F(0) = 0 and F′(0) = A > 0. Indeed,

and

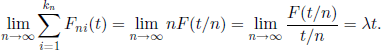
EXAMPLE 4.27.– Let us consider a system whose components satisfy the following assumptions:

1)The uninterrupted working times of the components are independent r.v.

2)The failure of a component determines the failure of the whole system (series systems).

3)Each component that breaks down is instantaneously replaced.

We are interested in the distribution of the time between two successive failures of the system. If the number of components is large enough and the distributions of the uninterrupted working times of the components satisfy the conditions of Theorem 4.26, then we can consider that the successive failures of the system form a Poisson process.

4.10. Regenerative processes

Let us consider a stochastic process (X(t),t ∈ ₊) taking values in (we can also consider the case ) and a renewal process (S_n,n ∈ ). We suppose that at instants S_n, the process (X(t),t ∈ ₊) regenerates (probabilistically, it starts anew), i.e. it behaves exactly as after time t = 0. To be more specific, we assume the following:

1) After each S_n, the process (X(t),t ∈ ₊) has the same finite-dimensional distributions as those of the entire process, i.e. for all n,k ∈ ₊, 0 < t₁ < … < t_k,t_i ∈ ₊, 1 ≤ i ≤ k, the random vectors (X(S_n + t_i), 1 ≤ i ≤ k) and (X(t_i), 1 ≤ i ≤ k) have the same distributions.

2)For each S_n, the process (X(t + S_n),t ∈ ₊) is independent of (S₀, S₁,..., S_n).

The part (X(t), t ∈ [S_n, S_n+1)) of the sample path is considered as the nth cycle of the process.

EXAMPLE 4.28.– Let us consider a Markov chain (X_n, n ∈ ) with values in . For any j ∈ , the return times to state j are regeneration moments. If the chain is recurrent, then the renewal process is not stopped.

Let F be the distribution function of S₁ (S₀ = 0) and, for A ∈ B(), let . We have

[4.59]

The second term of the right-hand member of [4.59] becomes

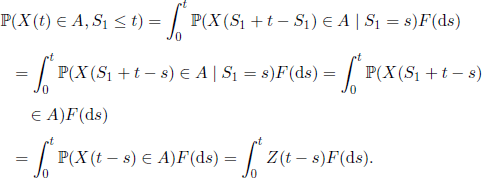
Thus [4.59] shows that Z(t) satisfies the renewal equation

[4.60]

with the solution

THEOREM 4.29.– ([SMI 55]) Let A ∈ be fixed and assume that the function K(·, A) is directly Riemann integrable. Then, if we note μ = (S₁), we have

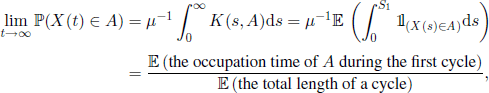
with the convention 1/∞ = 0.

PROOF.– We apply Theorem 4.9 and obtain

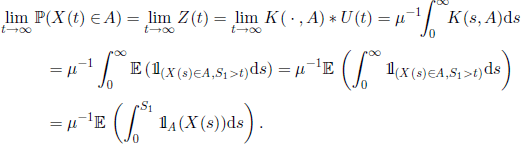
EXAMPLE 4.30.– (M/G/1 queue) Assume that the arrival process is Poisson with parameter (intensity) λ. The service discipline is “first come, first served” and the service time is a non-negative r.v. with distribution function G. A client arriving at time t = 0 initiates a service time that continues up to the moment when the first client and all his descendants are served, i.e. up to the moment when there is no client left in the queue and the service station can take a break. The following clients arrive after a random time exponentially distributed of parameter λ, and the service process starts again. If Q(t) denotes the number of clients in the system at time t, then (Q(t), t ∈ ⁺) is a regenerative process, where the regeneration epochs (S_n) are the moments when service times begin. From Theorem 4.29 we see that

The length of a cycle is the sum of the service time (ST) and the break time (exponential of parameter A); the occupation time of 0 is just the break time. Therefore, we obtain

---

1. A function F: for all t < 0, is said to be arithmetic if there exists a constant d > 0 such that F is constant on any open interval of the type (nd, (n + l) d) (lattice of period d).

2. In order to simplify our presentation, we assume that F is differentiable, but the result holds also in the general case.