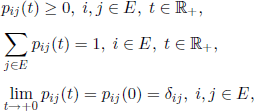Chapter 1
Introduction to Stochastic Processes
In this introductory chapter we present some notions regarding sequences of random variables (r.v.) and the most important classes of random processes.
1.1. Sequences of random variables
Let ![]() be a probability space and (An) a sequence of events in
be a probability space and (An) a sequence of events in ![]() .
.
– The set of ω ∈ Ω belonging to an infinity of An, that is,
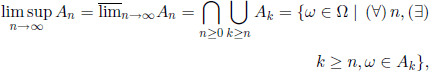
is called the upper limit of the sequence (An).
– The set of ω ∈ Ω belonging to all An except possibly to a finite number of them, that is,
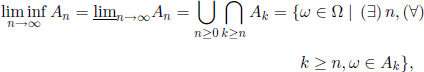
is called the lower limit of the sequence (An).
THEOREM 1.1.– (Borel-Cantelli lemma) Let (An) be a sequence of events in ![]() .
.
1. ![]() , them
, them ![]()
2. ![]() and (An) is a sequence of independent events, then
and (An) is a sequence of independent events, then ![]()
Let (Xn) be a sequence of r.v. and X an r.v., all of them defined on the same probability space ![]() . The convergence of the sequence (Xn) to X will be defined as follows:
. The convergence of the sequence (Xn) to X will be defined as follows:
1. Almost sure ![]()
2. In probability ![]() if for any ε > 0,
if for any ε > 0,
![]() .
.
3. In distribution (or weekly, or in law) ![]() pointwise in every continuity point of FX, where FXn and FX are the distribution functions of Xn and X, respectively.
pointwise in every continuity point of FX, where FXn and FX are the distribution functions of Xn and X, respectively.
4. In mean of order ![]() for all n ∈ N+, and if
for all n ∈ N+, and if ![]() . The most commonly used are the cases p = 1 (convergence in mean) and p = 2 (mean square convergence).
. The most commonly used are the cases p = 1 (convergence in mean) and p = 2 (mean square convergence).
The relations between these types of convergence are as follows:
The convergence in distribution of r.v. is a convergence property of their distributions (i.e. of their laws) and it is the most used in probability applications. This convergence can be expressed by means of characteristic functions.
THEOREM 1.2.– (Lévy continuity theorem) The sequence (Xn) converges in distribution to X if and only if the sequence of characteristic functions of (Xn) converges pointwise to the characteristic function of X.
EXAMPLE 1.3.– Let X1, X2,… be independent r. v. such that ![]()
![]() and
and ![]() . We have
. We have ![]() , but Xn is not almost surely convergent to 1 as n → ∞.
, but Xn is not almost surely convergent to 1 as n → ∞.
Indeed, for any ∈ > 0 we have
![]()
Consequently, ![]() .
.
To analyze the convergence a.s., we recall the following condition: ![]()
![]() , if and only if, for any ∈ > 0 and 0 < δ < 1, there exists an n0 such that for any n > n0
, if and only if, for any ∈ > 0 and 0 < δ < 1, there exists an n0 such that for any n > n0
As for any ∈ > 0, δ ∈ (0,1), and ![]() we have
we have
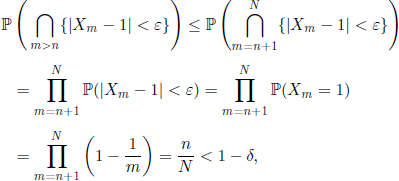
it does not exist an n0 such that relation [1.2] is satisfied, so we conclude that Xn does not converge a.s.
EXAMPLE 1.4.– Let us consider the probability space ![]() , with Ω = [0,1],
, with Ω = [0,1], ![]() , and
, and ![]() the Lebesgue measure on
the Lebesgue measure on ![]() . Let the r.v. X and the sequence of r.v
. Let the r.v. X and the sequence of r.v![]() be defined by
be defined by
![]()
and
![]()
On the one hand, as

we obtain that ![]() . Thus (Xn) does not converge in probability. On the other hand, the characteristic functions of the r.v.
. Thus (Xn) does not converge in probability. On the other hand, the characteristic functions of the r.v. ![]() , and X are
, and X are

and, respectively,
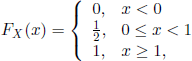
so ![]() .
.
Let us consider a sequence of r.v. (Xn,n ≥ 1) and suppose that the expected values ![]() , exist. Let
, exist. Let
DEFINITION 1.5.– The sequence (Xn,n ≥ 1) is said to satisfy the weak or the strong law of large numbers if ![]() , respectively.
, respectively.
Obviously, if a sequence of r.v. satisfies the strong law of large numbers, then it also satisfies the weak law of large numbers.
The traditional name “law of large numbers” that is still in use nowadays should be clearly understood: it is indeed a “true” mathematical theorem! We do indeed still speak of laws of large numbers to express vaguely but correctly the sense of a convergence of frequency toward probability, but we also tend to believe sometimes that a return to equilibrium will always occur in the end, and this is a big error of which we are often unaware.
Let us present now some “classic laws of large numbers.”
THEOREM 1.6.– (Markov) Let (Xn,n ≥ 1) be a sequence of r.v. such that ![]() and
and ![]() If
If
then (Xn, n ≥ 1) satisfies the weak law of large numbers.
PROOF.– Chebyshev’s inequality applied to Yn defined in equation [1.3] yields

and thus we obtain
![]()
COROLLARY 1.7.– (Chebyshev) Let (Xn,n ≥ 1) be a sequence of independent r.v. such that ![]() If there exists an M, 0 < M < ∞, such that
If there exists an M, 0 < M < ∞, such that ![]() then (Xn,n ≥ 1) satisfies the weak law of large numbers.
then (Xn,n ≥ 1) satisfies the weak law of large numbers.
PROOF.– In our case we have
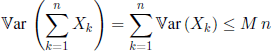
and condition [1.4] is verified.
THEOREM 1.8.– (Kolmogorov) Let (Xn, n ≥ 1) be a sequence of independent r.v. such that ![]() , and
, and 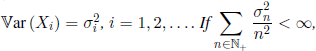 , then (Xn,n ≥ 1) satisfies the strong law of large numbers.
, then (Xn,n ≥ 1) satisfies the strong law of large numbers.
COROLLARY 1.9.– In the settings of Corollary 1.7, the sequence of r.v. (Xn,n ≥ 1) satisfies the strong law of large numbers.
EXAMPLE 1.10.– Let (Xn) be a sequence of i.i.d. r.v. of distribution P.1 For any Borel set B, the r.v. ll (Xn ∈ B) are i.i.d., with common expected value P(B). Using the law of large numbers, Corollary 1.9, we have ![]()
This argument justifies the estimation of probabilities by frequencies.
EXAMPLE 1.11.– Let (Xn) be a sequence of r.v. that take the values ![]() ,
, ![]() , with probabilities
, with probabilities ![]() and
and ![]()
We have ![]() and
and ![]() ar (Xk) = 2, k = 2,3,.... Consequently, the sequence (Xn) satisfies the strong law of large numbers (see Corollary 1.9).
ar (Xk) = 2, k = 2,3,.... Consequently, the sequence (Xn) satisfies the strong law of large numbers (see Corollary 1.9).
EXAMPLE 1.12.– Let (Xn) be a sequence of r.v. that take the values ![]() ,
, ![]() , with probabilities
, with probabilities ![]() and
and ![]()
We have ![]() and
and ![]() , which yields
, which yields
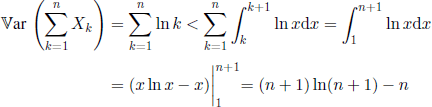
and
![]()
Consequently, the hypotheses of Theorem 1.6 are fulfilled and the sequence (Xn) satisfies the weak law of large numbers.
It is easy to see that in applications we often have to deal with random variables composed of an important number of independent elements. Under very general conditions, such sum variables are normally distributed. This fundamental fact can be mathematically expressed in one of the forms (depending on the conditions) of the central limit theorem. To state the central limit theorem, we consider (Xn, n ≥ 1) a sequence of r.v. and we introduce the following notation:
![]()
A central limit theorem gives sufficient conditions for the random variable
![]()
to converge in distribution to the standard normal distribution N(0, 1).
We see that, if the r.v. (Xn, n ≥ 1) are independent, then ![]() and
and ![]() are standard r.v., because
are standard r.v., because ![]() and
and ![]() .
.
We give now a central limit theorem important in probability and mathematical statistics.
THEOREM 1.13.– Let (Xn, n ≥ 1) be a sequence of independent identically distributed r.v. with mean a and finite positive variance a2. Then, the sequence of r.v. ![]() , is convergent in distribution to the normal distribution N(0,1). Zn is said to be asymptotically normal.
, is convergent in distribution to the normal distribution N(0,1). Zn is said to be asymptotically normal.
PROOF.- Let φ(t) be the characteristic function of (X1 — a) (hence of all (Xn — a), n ≥ 1). Then the characteristic function of Zn is 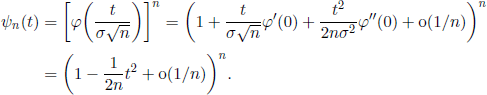
THEREFORE, ![]() and, using Theorem 1.2, we obtain
and, using Theorem 1.2, we obtain ![]() .
.
COROLLARY 1.14.– (De Moivre-Laplace) If X ~ Bi(n,p) and q = 1 — p, then ![]() is asymptotically normal N(0,1), as n —>∞.
is asymptotically normal N(0,1), as n —>∞.
PROOF.- This result is a direct consequence of Theorem 1.13, because X = ![]() , with (Xn, n ≥ 1) i.i.d. random variables, Xn ~ Be(p).
, with (Xn, n ≥ 1) i.i.d. random variables, Xn ~ Be(p).
EXAMPLE 1.15.– We roll a die n times and we consider the r.v. N = number of six. Starting from which value n of N do we have 9 out of 10 chances to get ![]()
As N is a binomial r.v. Bi(n, 1/6), for n large enough we can use Corollary 1.14 to approach the r.v. ![]() by a normal r.v. N(0, 1). Then, the condition
by a normal r.v. N(0, 1). Then, the condition ![]() can be written as
can be written as ![]() . From relation
. From relation ![]() which can be written as 2Φ(x) − 1 = 0.9,2 we obtain x = 1.645 (using the table of the standard normal distribution). Thus we have nine out of 10 chances to have
which can be written as 2Φ(x) − 1 = 0.9,2 we obtain x = 1.645 (using the table of the standard normal distribution). Thus we have nine out of 10 chances to have ![]() if the inequality
if the inequality ![]() 1.645 is satisfied, that is, if
1.645 is satisfied, that is, if
EXAMPLE 1.16.– Suppose that the lifetime of a component is an exponentially distributed r.v. with parameter λ = 0.2 x 10-3h-1. When a component breaks down, it is immediately replaced with a new identical one. What is the probability that after 50,000 hours the component which will be working will be at least the 10th used from the beginning?
Let us denote by Sn the sum of n independent exponential random variables that represent the lifetimes of the first n components. From the properties of the exponential distribution, we have ![]() . Using Theorem 1.13, we can approach
. Using Theorem 1.13, we can approach ![]() by a standard normal random variable, which is equivalent to saying that we can approach Sn by a normal r.v. N(n/λ,
by a standard normal random variable, which is equivalent to saying that we can approach Sn by a normal r.v. N(n/λ, ![]() /λ) = N(5000n, 5000
/λ) = N(5000n, 5000![]() ). The fact that the component which will be working after 50,000 hours will be at least the 10th used means that we have S9< 50,000, so we need only to compute
). The fact that the component which will be working after 50,000 hours will be at least the 10th used means that we have S9< 50,000, so we need only to compute ![]() , with S9 ~ N (45,000,15,000). Thus we obtain the required probability
, with S9 ~ N (45,000,15,000). Thus we obtain the required probability
![]()
EXAMPLE 1.17.– A restaurant can serve 75 meals a day. We know from experience that 20% of the clients that reserved would not eventually show up.
a) The owner of the restaurant accepts 90 reservations. What is the probability that more than 50 clients show up?
b)How many reservations should the owner of the restaurant accept in order to have a probability greater than or equal to 0.9 that he will be able to serve all the clients who will show up?
If n is the number of clients who reserved, the number N of clients who will come has a binomial distribution with parameters n and p = 0.8. Using corollary 1.14, this binomial distribution is approached by a normal distribution with the same mean and variance.
a) ![]() Consequently,
Consequently,
![]()
b) We have to solve the inequality ![]() with respect to N. On the one hand, we have
with respect to N. On the one hand, we have
![]()
and, on the other hand, we have $(1.281) = 0.9. So we need to have ![]() , that is,
, that is, ![]() . By letting
. By letting ![]() we get the inequality 0.8x2 + 0.5124x − 75 < 0 and finally obtain x < 9.367503, 097, i.e. n ≤ 87.
we get the inequality 0.8x2 + 0.5124x − 75 < 0 and finally obtain x < 9.367503, 097, i.e. n ≤ 87.
1.2. The notion of stochastic process
A stochastic or a random process is a family of r.v. ![]() defined on the same probability space
defined on the same probability space ![]() , with values in a measurable space
, with values in a measurable space ![]() .
.
The set E can be either ![]() or
or ![]() , and in this case
, and in this case ![]() is the σ-algebra of Borel sets, or an arbitrary finite or countable infinite discrete set, and in this case
is the σ-algebra of Borel sets, or an arbitrary finite or countable infinite discrete set, and in this case ![]() .
.
The index set I is usually ![]() (in this case the process is called chain) or
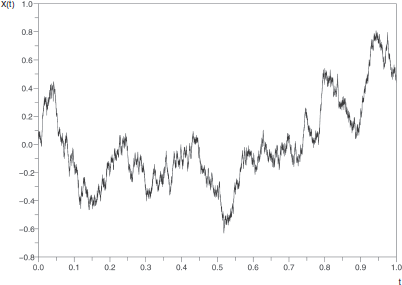
(in this case the process is called chain) or ![]() , and the parameter t is interpreted as being the time. The function
, and the parameter t is interpreted as being the time. The function ![]() is called a realization or a sample path of the process (see Figure 1.1).
is called a realization or a sample path of the process (see Figure 1.1).
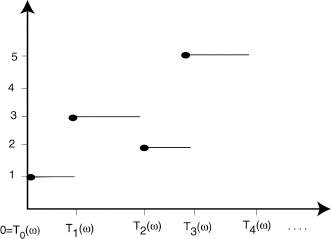
If the evolution of a stochastic process is done by jumps from state to state and if almost all its sample paths are constant except at isolated jump times, then the process is called a jump process.
EXAMPLE 1.18.– Let us consider the process ![]() , with state space E =
, with state space E = ![]() , describing the evolution of a population, the number of failures of a component, etc. Then Xt(ω) = X(t, ω) = i ∈ E means that the population has i individuals at time t, or that the component has failed i times during the time interval (0, t].
, describing the evolution of a population, the number of failures of a component, etc. Then Xt(ω) = X(t, ω) = i ∈ E means that the population has i individuals at time t, or that the component has failed i times during the time interval (0, t].
The times T0(ω),T1(ω), ... (Figure 1.2) are the jump times (transition times) for the particular sample path ω ∈ Ω. The r.v. ζ = supn Tn is the lifetime of the process.
The stochastic processes can be studied either by means of their finite-dimensional distributions or by considering the type of dependence between the r.v. of the process. In the latter case, the nature of the process is given by this type of dependence.
The distribution of a stochastic process X, i.e. ![]() , is specified by the knowledge of its finite-dimensional distributions. For a real-valued
, is specified by the knowledge of its finite-dimensional distributions. For a real-valued
process we define
for any t1, ..., tn ∈ I and x1, ..., xn ∈ ![]() .
.
The process is said to be given if all the finite-dimensional distributions Ft1 ,...,tn (·, ..., ·), t1, ..., tn ∈ I, are given.
The finite-dimensional distributions must satisfy the following properties:
1) for any permutation (i1, ..., in) of (1, ..., n),
![]()
2) for any 1 ≤ k ≤ n and x1, ..., xn ∈ ![]() ,
,
![]() .
.
Let X = (Xt;t ∈ I) and Y = (Yt;t ∈ I) be two stochastic processes on the same probability space ![]() , with values in the same measurable space (E, ∈ ).
, with values in the same measurable space (E, ∈ ).
DEFINITION 1.19.– (Stochastically equivalent processes in the wide sense) If two stochastic processes X and Y satisfy
![]()
for all n ∈ N∗, t1, ..., tn ∈ I, and A1, ..., An ∈ E, then they are called stochastically equivalent in the wide sense.
DEFINITION 1.20.– (Stochastically equivalent processes) If two stochastic processes X and Y satisfy
![]()
then they are called stochastically equivalent.
DEFINITION 1.21.– (Indistinguishable processes) If two stochastic processes X and Y satisfy
![]()
then they are called indistinguishable.
PROPOSITION 1.22.– We have the following implications: X,Y indistinguishable ![]() X,Y stochastically equivalent
X,Y stochastically equivalent ![]()
![]() X, Y stochastically equivalent in the wide sense.
X, Y stochastically equivalent in the wide sense.
PROPOSITION 1.23.– If the processes X and Y are stochastically equivalent and right continuous, then they are indistinguishable.
DEFINITION 1.24.– (Version or modification of a process) If the process Y is stochastically equivalent to the process X, then we say that Y is a version or a modification of the process X.
DEFINITION 1.25.– (Continuous process) Aprocess X with values in aBorel space (E, ∈ ) is said to be continuous a.s. if, for almost all ω, the function ![]() is continuous.
is continuous.
PROPOSITION 1.26.– (Kolmogorov continuity criterion) A real process X has a continuous modification if there exist the constants α, β, C > 0, such that ![]() for all t and s.
for all t and s.
1.3. Martingales
1.3.1. Stopping time
Let ![]() be a probability space. An increasing sequence of σ-algebras,
be a probability space. An increasing sequence of σ-algebras, ![]() , is called a filtration of
, is called a filtration of ![]() . A sequence (Xn,n ∈
. A sequence (Xn,n ∈ ![]() ) of r.v. is said to be F-adapted if Xn is
) of r.v. is said to be F-adapted if Xn is ![]() n -measurable for all
n -measurable for all ![]() . Usually, a filtration is associated with the sequence of r.v.
. Usually, a filtration is associated with the sequence of r.v. ![]() , that is, we have
, that is, we have ![]() n and the sequence will be F-adapted. This is called the natural filtration of
n and the sequence will be F-adapted. This is called the natural filtration of ![]() .
.
DEFINITION 1.27.– Let ![]() be a filtration of
be a filtration of ![]() . A stopping time for F (or F-adapted, or F-stopping time) is an r.v. T with values in
. A stopping time for F (or F-adapted, or F-stopping time) is an r.v. T with values in ![]() satisfying one of the following (equivalent) conditions:
satisfying one of the following (equivalent) conditions:
![]()
If ![]() , T is said to be adapted to the sequence
, T is said to be adapted to the sequence ![]() . In this case we note
. In this case we note ![]() .
.
EXAMPLE 1.28.– (Hitting time) Let ![]() be a sequence of r.v. with values in
be a sequence of r.v. with values in ![]() d and
d and ![]() . The r.v. T = inf
. The r.v. T = inf![]() is a stopping time, adapted to the sequence (Xn, n ∈
is a stopping time, adapted to the sequence (Xn, n ∈ ![]() ) and is called the hitting time of B. Indeed,
) and is called the hitting time of B. Indeed,
![]()
Properties of stopping times
1.The set ![]() is a σ-algebra called the σ-algebra of events prior to T.
is a σ-algebra called the σ-algebra of events prior to T.
2. If S and T are stopping times, then S + T, S ⋀ T, and S ⋁ T are also stopping times.
3.If ![]() is a sequence of stopping times, then
is a sequence of stopping times, then ![]() is also a stopping time.
is also a stopping time.
4.If S and T are stopping times such that ![]() S ≤ T, then
S ≤ T, then ![]() s ⊆ T.
s ⊆ T.
![]()
PROPOSITION 1.29.– (Wald identity) If T is a stopping time with finite expected value, adapted to an i.i.d. and integrable random sequence (Xn,n ∈ ![]() ), then
), then
1.3.2. Discrete-time martingales
We will consider in the following that every filtration F is associated with the corresponding random sequence.
DEFINITION 1.30.– A sequence of r.v. (Xn, n ∈ ![]() ) is an
) is an
1)Xn F-martingale if
(a)Xn is F-adapted for all n;
(b)E |Xn | < ∞ for all n ∈ ![]() ;
;
(c) ![]()
![]() for all n ∈
for all n ∈ ![]() .
.
2)F-submartingale if it satisfies (a), (b), and (c) with <.
3) F-supermartingale if it satisfies (a), (b), and (c) with >.
Note that condition (c) is equivalent to ![]() .
.
EXAMPLE 1.31.– Let ![]() be a sequence of i.i.d. r.v. such that
be a sequence of i.i.d. r.v. such that ![]() and
and ![]() . The random walk (see section 2.2)
. The random walk (see section 2.2) ![]() , is a submartingale for the natural filtration of (ζn) if p > 1/2, a martingale if p = 1/2, and a supermartingale if p < 1/2. Indeed, we have
, is a submartingale for the natural filtration of (ζn) if p > 1/2, a martingale if p = 1/2, and a supermartingale if p < 1/2. Indeed, we have ![]() Consequently,
Consequently,
EXAMPLE 1.32.– Let X be a real r.v. with ![]() and let F be an arbitrary filtration. Then, the sequence
and let F be an arbitrary filtration. Then, the sequence ![]() is a martingale. Indeed,
is a martingale. Indeed,
![]()
EXAMPLE 1.33.– (A martingale at the casino) A gambler bets 1 euro the first time, if he loses he bets ![]() 2 the second time, etc.
2 the second time, etc. ![]() k−1 the kth time. He stops gambling when he wins for the first time. At every play, he wins or loses his bet with a probability of 1/2. This strategy will make him eventually win the game. Indeed, when he stops playing at a random time N, he would have won 2N − (1 + 2 + ··· + 2N − 1) =
k−1 the kth time. He stops gambling when he wins for the first time. At every play, he wins or loses his bet with a probability of 1/2. This strategy will make him eventually win the game. Indeed, when he stops playing at a random time N, he would have won 2N − (1 + 2 + ··· + 2N − 1) = ![]() 1.
1.
If Xn is the r.v. defined as the fortune of the gambler after the nth game, we have
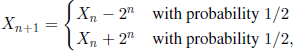
if he loses up to the nth game. Consequently ![]() (Xn+1 | Xn,..., X1) = Xn.
(Xn+1 | Xn,..., X1) = Xn.
On the other hand, the expected value of the loss is

because N is a geometrically distributed r.v. with parameter 1/2 and ![]() for n ≥ N. Consequently, the strategy of the player is valid only if his initial fortune is greater than the casino’s.
for n ≥ N. Consequently, the strategy of the player is valid only if his initial fortune is greater than the casino’s.
1.3.3. Martingale convergence
THEOREM 1.34.– (Doob’s convergence theorem) Every supermartingale, submartingale or martingale bounded in L1 converges a.s. to an integrable r.v.
EXAMPLE 1.35.– If X is an r.v. on ![]() with finite expected value and
with finite expected value and ![]() is a filtration of
is a filtration of ![]() , then
, then
![]()
THEOREM 1.36.– If (Xn) is an uniformly integrable martingale, i.e.
![]()
then there exists X integrable such that ![]() , and we have
, and we have![]() .
.
A martingale (Xn) for ![]() is said to be a square integrable if
is said to be a square integrable if ![]() for all n ≥ 1.
for all n ≥ 1.
THEOREM 1.37.– (Strong convergence theorem) If (Xn) is a square integrable martingale, then there exists an r.v. X such that ![]() .
.
THEOREM 1.38.– (Stopping theorem) Let (Xn) be a martingale (resp. a submartingale) for (![]() n). If S and T are two stopping times adapted to (
n). If S and T are two stopping times adapted to (![]() n) such that
n) such that
1) ![]() and
and ![]()
2) ![]() and
and ![]()
then ![]()
1.3.4. Square integrable martingales
Let (Mn, n ≥ 0) be a square integrable martingale, i.e.
![]()
The process ![]() is a submartingale and Doob’s decomposition gives
is a submartingale and Doob’s decomposition gives
![]()
where Xn is a martingale, and < M >n is a predictable increasing process, that is, ![]() -measurable for all n ≥ 1.
-measurable for all n ≥ 1.
THEOREM 1.39.– If (Mn) is a square integrable martingale, with predictable process < M >n, and if
1) ![]()
2) ![]()
for all ![]()
then
![]()
and
![]()
where (an) is a sequence increasing to infinity.
1.4. Markov chains
Markov chains and processes represent probabilistic models of great importance for the analysis and study of complex systems. The fundamental concepts of Markov modeling are the state and the transition.
1.4.1. Markov property
It is clear that the situation of a physical system at a certain moment can be completely specified by giving the values of a certain number of variables that describe the system. For instance, a physical system can often be specified by giving the values of its temperature, pressure, and volume; in a similar way, a particle can be specified by its coordinates with respect to a coordinate system, by its mass and speed. The set of such variables is called the state of the system, and the knowledge of the values of these variables at a fixed moment allows us to specify the state of the system, and, consequently, to describe the system at that precise moment.
Usually, a system evolves in time from one state to another, and is thus characterized by its own dynamics. For instance, the state of a chemical system can change due to a modification in the environment temperature and/or pressure, whereas the state of a particle can change because of interaction with other particles. These state modifications are called transitions.
In many applications, the states are described by continuous variables and the transitions may occur at any instant. To simplify, we will consider a system with a finite number of states, denoted by E = {1, 2, . . ., N}, and with transitions that can occur at discrete-time moments. So, if we set X(n) for the state of the system at time n, then the sequence X(0), X(1), . . ., X(n) describes the “itinerary” of the system in the state space, from the beginning of the observation, up to the fixed time n; this sequence is called a sample path (realization or trajectory) of the process (see section 1.2).
In most of the concrete situations, the observation of the process makes us come to the conclusion that the process is random. Consequently, to a sample path of the process a certain probability
![]()
needs to be associated. Elementary techniques of probability theory show that these probabilities can be expressed in terms of the conditional probabilities
![]()
for all ![]() and for any states i0, i1, . . ., in+1 ∈ E. This means that it is necessary to know the probability that the system is in a certain state in+1 ∈ E after the (n + 1)th transition,
and for any states i0, i1, . . ., in+1 ∈ E. This means that it is necessary to know the probability that the system is in a certain state in+1 ∈ E after the (n + 1)th transition, ![]() , knowing its history up to time n. Computing all these conditional probabilities renders the study of a real phenomenon modeled in this way very complicated. The statement that the process is Markovian is equivalent to the simplifying hypothesis that only the last state (i.e. the current state) counts for its future evolution. In other words, for a Markov process we have (the Markov property)
, knowing its history up to time n. Computing all these conditional probabilities renders the study of a real phenomenon modeled in this way very complicated. The statement that the process is Markovian is equivalent to the simplifying hypothesis that only the last state (i.e. the current state) counts for its future evolution. In other words, for a Markov process we have (the Markov property)
DEFINITION 1.40.– The sequence of r.v. ![]() defined on
defined on ![]() , with values in the set E, is called a Markov chain (or discrete-time Markov process) with a finite or countable state space, if the Markov property is satisfied.
, with values in the set E, is called a Markov chain (or discrete-time Markov process) with a finite or countable state space, if the Markov property is satisfied.
A Markov chain is called nonhomogenous or homogenous (with respect to time) whether or not the common value of the two members of [1.6] (i.e. the function p(n, i, j)) depends on n. This probability is called transition function (or probability) of the chain.
For more details on the study of discrete-time Markov processes with finite or countable state space, see [CHU 67, IOS 80, KEM 60, RES 92].
So, the Markovian modeling is adapted to physical phenomena or systems whose behavior is characterized by a certain memoryless property, in the sense specified in [1.6]. For real applications, it is very difficult often even impossible to know whether a physical system has a Markovian behavior or not; in fact, it is important to be able to justify this Markovian behavior (at least as a first approximation of the phenomenon) and thus to obtain a model useful for the study of the phenomenon.
Note that the Markovian modeling can also be used in the case in which a fixed number of states, not only the last one, determines the future evolution of the phenomenon. For instance, suppose that we take into account the last two visited states. Then, we can define a new process with n2 states, where the states are defined as couples of states of the initial process; this new process satisfies property [1.6] and the Markovian model is good enough, but with the obvious drawback of computational complexity.
PROPOSITION 1.41.– If the Markov property (1.6) is satisfied, then
for all ![]() and i0, i1, ..., in,j1, ...jm ∈ E.
and i0, i1, ..., in,j1, ...jm ∈ E.
REMARK 1.42.– The more general relation
can be proved for any A ∈ σ(Xk;k ≥ n + 1). The equalities between conditional probabilities have to be understood in the sense of almost surely ![]() . We will often write
. We will often write ![]() instead of
instead of ![]()
![]()
1.4.2. Transition function
Throughout this chapter, we will be concerned only with homogenous Markov chains and the transition function will be denoted by p(i, j). It satisfies the following properties:
A matrix that satisfies [1.9] and [1.10] is said to be stochastic.
From [1.8], taking A = (Xn+1 = j), we obtain
The probability ![]() does not depend on n and will be denoted by p(m)(i, j).
does not depend on n and will be denoted by p(m)(i, j).
The matrix p = (p(i, j); i, j ∈ E) is called the transition matrix of the chain, and p(m)(i, j) is the (i, j) element of the matrix pm.
From the following matrix equality
we obtain
for all ![]() . Equality [1.12] (or [1.13]) is called the Chapman-Kolmogorov identity (or equality).
. Equality [1.12] (or [1.13]) is called the Chapman-Kolmogorov identity (or equality).
EXAMPLE 1.43.– Binary component. Consider a binary component starting to work at time n = 0. The lifetime of the component has a geometric distribution on ![]() of parameter p. When a failure occurs, it is replaced with a new, identical component. The replacement time is a geometric random variable of parameter q. Denote by 0 the working state, by 1 the failure state, and let Xn be the state of the component at time n ≥ 0. Then Xn is an r.v. with values in E = {0, 1}. It can be shown that
of parameter p. When a failure occurs, it is replaced with a new, identical component. The replacement time is a geometric random variable of parameter q. Denote by 0 the working state, by 1 the failure state, and let Xn be the state of the component at time n ≥ 0. Then Xn is an r.v. with values in E = {0, 1}. It can be shown that ![]() is a Markov chain with state space E and transition matrix
is a Markov chain with state space E and transition matrix
![]()
Using the eigenvalues of the matrix p, we obtain
![]()
EXAMPLE 1.44.– A queuing model. A service unit (health center, civil service, tasks arriving in a computer, etc.) can serve customers (if any) at times 0,1, 2,.... We suppose that during the time interval (n, n + 1] there are ξn clients arriving, ![]() , where the r.v. ξ0, ξ1, ξ2, ... are i.i.d. and
, where the r.v. ξ0, ξ1, ξ2, ... are i.i.d. and ![]() pk, k ≥ 0, Σk≥0pk = 1. Let m be the number ofplaces available in the queue (m can also take the value +∞). When a customer arrives and sees m clients waiting to be served, then he leaves without waiting. Let Xn be the number of customers in the queue at time n (including also the one that is served at that moment). We have
pk, k ≥ 0, Σk≥0pk = 1. Let m be the number ofplaces available in the queue (m can also take the value +∞). When a customer arrives and sees m clients waiting to be served, then he leaves without waiting. Let Xn be the number of customers in the queue at time n (including also the one that is served at that moment). We have
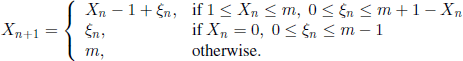
The process ![]() is a Markov chain with state space E = {0,1,…, m}, because Xn+1 depends only on the independent r.v. Xn and ξn. The transition function is given by
is a Markov chain with state space E = {0,1,…, m}, because Xn+1 depends only on the independent r.v. Xn and ξn. The transition function is given by
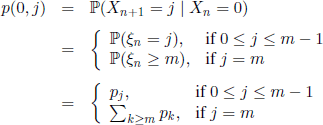
and, for 1≤i≤m
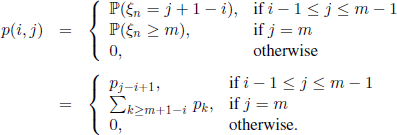
EXAMPLE 1.45.– Storage model. A certain product is stocked in order to face a random demand. The stockpile can be replenished at times 0, 1, 2, … and the demand in the time interval (n, n + 1] is considered to be a discrete ![]() -valued r.v. ξn. The r.v. ξ0, ξ1, ξ2, ... are supposed to be i.i.d. and
-valued r.v. ξn. The r.v. ξ0, ξ1, ξ2, ... are supposed to be i.i.d. and ![]()
![]()
The stocking strategy is the following: let m, M ∈ ![]() , be such that m < M; if, at an arbitrary time
, be such that m < M; if, at an arbitrary time ![]() , the inventory level is less or equal to m, then the inventory is brought up to M. Whereas, if the inventory level is greater than m, no replenishment is undertaken.
, the inventory level is less or equal to m, then the inventory is brought up to M. Whereas, if the inventory level is greater than m, no replenishment is undertaken.
If Xn denotes the stock level just before the possible supply at time n, we have
![]()
The same approach as in example 1.44 can be used in order to show that ![]() is a Markov chain and subsequently obtain its transition function.
is a Markov chain and subsequently obtain its transition function.
1.4.3. Strong Markov property
Let ![]() be a Markov chain defined on
be a Markov chain defined on ![]() , with values in E. Consider the filtration
, with values in E. Consider the filtration ![]() be a stopping time for the chain X (i.e. for the filtration
be a stopping time for the chain X (i.e. for the filtration ![]() and
and ![]() be the σ-algebra of events prior to τ. We want to obtain the Markov property (relation [1.6]) in case that the “present moment” is random.
be the σ-algebra of events prior to τ. We want to obtain the Markov property (relation [1.6]) in case that the “present moment” is random.
PROPOSITION 1.46.– For all ![]() such that
such that ![]() , we have
, we have
REMARK 1.47.– We can prove more general relations as follows: if B is an event subsequent to τ, i.e. B ∈ σ(Xτ+k, k ≥ 0), then
DEFINITION 1.48.– Relation [1.15] is called the strong Markov property.
If X0 = j a.s., j ∈ E, then the r.v.
![]()
with the convention inf Ø = ∞, is called the sojourn time in state j and it is a stopping time for the family ![]() .
.
PROPOSITION 1.49.– The sojourn time in a state j ∈ E is a geometric r.v. of parameter 1 − p(j, j) with respect to the probability ![]() for
for ![]() .
.
1.5. State classification
DEFINITION 1.50.– Let X = (Xn, n ∈ ![]() ) be a Markov chain defined on
) be a Markov chain defined on ![]() , with values in E (finite or countable). We call a state j ∈ E accessible from state i ∈ E (we write i → j) if there exists an
, with values in E (finite or countable). We call a state j ∈ E accessible from state i ∈ E (we write i → j) if there exists an ![]() such that p(n)(i, j) > 0. The states i and j are said to communicate if i → j and j → i; this will be denoted by i ↔ j.
such that p(n)(i, j) > 0. The states i and j are said to communicate if i → j and j → i; this will be denoted by i ↔ j.
Note that relation i → j is transitive, i.e. if i → j and j → k then i → k.
DEFINITION 1.51.– A class of states is a subset C of E that satisfies one of the two following properties:
1)The set C contains only one state i ∈ E and relation i ↔ i is not verified.
2)For all i, j ∈ C we have i ↔ j and C is maximal with this property, i.e. it is not possible to increase C by another state which communicates with all the other states of C.
EXAMPLE 1.52.– Let X = (Xn, n ∈ ![]() ) be a Markov chain with values in E = {0, 1, 2, 3} and of transition matrix
) be a Markov chain with values in E = {0, 1, 2, 3} and of transition matrix
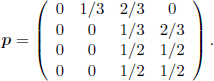
The matrices pm, m ≥ 2, have all the entries on the second column equal to zero. Consequently, the classes are C1= {0}, C2 = {1}, and C3 = {2,3}.
DEFINITION 1.53.– 1. A property concerning the states of E, such that the validity for a state i ∈ E implies the validity for all states from the class of i, is called a class property.
2. A class of states C is called closed if Σj∈C p(i, j) = 1 for all i ∈ C. In other words, the matrix (p(i,j); i, j ∈ C) is a stochastic matrix; thus, Σj∈c p(n) {i, j) = 1 for all i ∈ C and n ∈ ![]() .
.
3. If a closed class contains only one state, then this state is called absorbing
4. If the state space E consists of only one closed class, then the chain is called irreducible.
5.A state i ∈ E is said to be essential if i → j yields j → i; otherwise i is called inessential.
6. If i → i, then the greatest common divisor of n ∈ ![]() such that p(n)(i, i) > 0 is called the period of i and will be denoted by d%. If di = 1, then the state i is called aperiodic.
such that p(n)(i, i) > 0 is called the period of i and will be denoted by d%. If di = 1, then the state i is called aperiodic.
PROPOSITION 1.54.– Let C be a closed class of period d and C0, C1, …, Cd−1 be the cyclic subclasses.
1. If i ∈ Cr and p(n)(i,j) > 0, then j ∈ Cn+r.
2.If i ∈ Cr, we have
![]()
(The class subscripts are considered mod d).
We will denote by ![]() , the probabilities on σ(Xn; n ∈
, the probabilities on σ(Xn; n ∈ ![]() ) defined by
) defined by
![]()
and by ![]() i the corresponding expected values.
i the corresponding expected values.
If α = (α(i), i ∈ E) is a probability on E, i.e. ![]() then
then ![]() and
and ![]() is the corresponding expected value.
is the corresponding expected value.
DEFINITION 1.55.– Let ηi,i ∈ E, be the first-passage time to state i. The state i ∈ E is said to be recurrent (or persistent) if ![]() . In the opposite case, i.e. if
. In the opposite case, i.e. if ![]() , the state i is said to be transient. If i is a recurrent state, then if
, the state i is said to be transient. If i is a recurrent state, then if ![]() , i is said to be positive recurrent, and if μi = ∞, then i is said null recurrent.
, i is said to be positive recurrent, and if μi = ∞, then i is said null recurrent.
PROPOSITION 1.56.– A state i ∈ E is recurrent or transient, if the series ![]() is divergent, respectively convergent.
is divergent, respectively convergent.
PROPOSITION 1.57.– Let (Xn, n ∈ ![]() ) be a Markov chain with finite state space E. Then:
) be a Markov chain with finite state space E. Then:
1) there exists at least a recurrent state;
2) a class is recurrent iff it is closed.
PROPOSITION 1.58.– Let X = (Xn, n ∈ ![]() ) be a Markov chain with finite state space. Then any recurrent class C of X is positive. If the chain X is irreducible, then it is positive recurrent (i.e. all states are positive recurrent).
) be a Markov chain with finite state space. Then any recurrent class C of X is positive. If the chain X is irreducible, then it is positive recurrent (i.e. all states are positive recurrent).
1.5.1. Stationary probability
DEFINITION 1.59.– A probability distribution π on E is said to be stationary or invariant for the Markov chain X = (Xn, n ∈ ![]() ) with transition matrix P = (p(i, j); i, j ∈ E) if, for all j ∈ E,
) with transition matrix P = (p(i, j); i, j ∈ E) if, for all j ∈ E,
Relation [1.17] can be written in matrix form
where π = (π(i); i ∈ E) is a row vector. From [1.18] we can easily prove that
and
PROPOSITION 1.60.– We suppose that the transition matrix is such that the limits
exist for all i, j ∈ E and do not depend on i. Then, there are two possibilities:
1) π(j) = 0 for all j ∈ E and, in this case, there is no stationary probability;
2) Σj∈E π(j) = 1 and, in this case, π = (π(j); j ∈ E) is a stationary probability and it is unique.
DEFINITION 1.61.– A Markov chain is said to be ergodic if, for all i, j ∈ E, the limits limn→∞p(n)(i, j) exist, are positive, and do not depend on i.
PROPOSITION 1.62.– An irreducible, aperiodic, and positive recurrent Markov chain is ergodic.
PROPOSITION 1.63.– A finite Markov chain is ergodic if and only if
A Markov chain verifying [1.22] is called regular.
PROPOSITION 1.64.– A Markov chain with finite or countable state space E has a unique stationary probability if and only if the state space contains one and only one recurrent positive class.
COROLLARY 1.65.– A finite ergodic Markov chain (i.e. regular) has a unique stationary probability.
1.6. Continuous-time Markov processes
The concept of Markovian dependence in continuous time was introduced by A. N. Kolmogorov in 1931. The first important contributions are those of B. Pospisil, W. Feller, and W. Doeblin, and the standard references are [BLU 68, DYN 65, GIH 74].
1.6.1. Transition function
Let E be a finite or countable set and ![]() , be a matrix function with the properties:
, be a matrix function with the properties:
where δij is the Kronecker symbol.
A family of r.v. ![]() with values in E is called a Markov process homogenous with respect to time, with state space E, if
with values in E is called a Markov process homogenous with respect to time, with state space E, if
for all 0 ≤ t0 < t1 <…< tn, t ≥ 0, i0, i1, …,in−1, i, j ∈ E, n ≤ 1. We will suppose that the sample paths t → X(t, ω) are right-continuous with left limits a.s. The matrix P(t), called the transition matrix function of the process, satisfies the Chapman-Kolmogorov equation
which can be written under matrix form
![]()
The functions pij (t) have some remarkable properties:
1) For all i, j ∈ E, the function Pij(t) is uniformly continuous on [0, ∞).
2) For all i,j ∈ E, the function pij (t) is either identically zero, or positive, on (0, ∞).
3) For all ![]() exists and it is finite.
exists and it is finite.
4) For all ![]() exists and
exists and ![]() . A state z is said to be stable if qi < ∞, instantaneous if qi = ∞, and absorbing if qi = 0.
. A state z is said to be stable if qi < ∞, instantaneous if qi = ∞, and absorbing if qi = 0.
PROPOSITION 1.66.– If E is finite, then there is no instantaneous state.
PROPOSITION 1.67.– The sample paths of the process are right continuous a.s. if and only if there is no instantaneous state.
1.6.2. Kolmogorov equations
If qi < ∞ for all i ∈ E, then the matrix Q = (qij,i,j ∈ E), where qii = —qi, is called the infinitesimal generator of the process or transition intensity matrix. Generally, we have qij ≥ 0 for i ≠ j and qii ≤ 0. Additionally,
If E is finite, then [1.26] becomes
Relation [1.27] is a necessary and sufficient condition such that pij (t) satisfy the differential equations
or, in matrix form,
![]()
Equations [1.28] are called Kolmogorov backward equations. In addition, if qj < ∞, j ∈ E, and the limit
![]()
is uniform with respect to i ≠ j, then we have
Equations [1.29] are called Kolmogorov forward equations.
Note the important fact that, if E is finite, then the two equations [1.28] and [1.29] are satisfied. In this case, from these two systems of equations, with initial conditions pij(0)= δij, i, j ∈ E (or under matrix form P(0) = I), we obtain
Consequently, the transition intensity matrix Q uniquely determines the transition matrix function P(t).
The first jump time or the sojourn time in a state is defined by
![]()
Then ![]() is the distribution function of the sojourn time in state i.
is the distribution function of the sojourn time in state i.
PROPOSITION 1.68.– For i, j ∈ E, we have
and the r.v. T1 and XT1 are ![]() -independent.
-independent.
The successive jump times of the process can be defined as follows:
![]()
The lifetime of the process is the r.v. ![]() , then the process is regular (non-explosive); in the opposite case, if
, then the process is regular (non-explosive); in the opposite case, if ![]() , the process is called non-regular (explosive).
, the process is called non-regular (explosive).
If Tn+1 > Tn a.s. for all n ≥ 1, then (X(t),t ≥ 0) is said to be a jump process.
PROPOSITION 1.69.– There exists a stochastic matrix (aij,i, j ∈ E) with aii = 0, i ∈ E, such that
This means that the successively visited states form a Markov chain Yn = XTn, called the embedded chain, with transition function A. Given the successively visited states of the process, the sojourn times in different states are mutually independent.
REMARK 1.70.– We have
PROPOSITION 1.71.– (Reuter’s explosion condition) A jump Markov process is regular iff the only non-negative bounded solution of equation Qy = y is y = o.
PROPOSITION 1.72.– A necessary and sufficient condition for a Markov process (X(t),t ≥ 0) to be regular is ![]() a.s.
a.s.
PROPOSITION 1.73.– (Kolmogorov integral equation) For i, j ∈ E, we have
for i non-absorbing, and Pij (t) = δij for i absorbing.
Let us denote by ηi the first-passage time to state i, i.e. ηi = inf (t ≥ T1|Xt=i). A state i ∈ E is said to be:
– recurrent if ![]() ;
;
– transient if ![]() ;
;
– positive recurrent if it is recurrent and ![]() ;
;
– null recurrent if it is recurrent and μii = ∞.
For α = (αi, i ∈ E) a probability on E, we define
![]()
The probabilities Pi(t) = Pα(Xt = i), i ∈ E, t ≥ 0, are called state probabilities. If pi = pi(0) = Pα(X0 = j), j ∈ E, then the state probabilities satisfy the equations
A probability π = (πj, j ∈ E) on E is said to be stationary or invariant if Pπ(Xt = j) = πj, for all j ∈ E, t ≥ 0. This condition can be written in the matrix form πP(t) = π for all t ≥ 0. From [1.35] it can be inferred that (πj, j ∈ E) is stationary if and only if ![]() .
.
A Markov process (X(t),t > 0) is said to be ergodic if there exists a probability π on E such that, for all i, j ∈ E, we have
![]()
or, equivalently,
![]()
for all i ∈ E.
PROPOSITION 1.74.– For any state i of E, we have
![]()
PROPOSITION 1.75.– If the Markov process (X(t),t > 0) is irreducible (i.e. the chain (Yn, n ∈ ![]() ) is so) and it has an invariant probability π, then for any positive and bounded function g on E, we have
) is so) and it has an invariant probability π, then for any positive and bounded function g on E, we have
![]()
1.7. Semi-Markov processes
A semi-Markov process is a natural generalization of a Markov process. Its future evolution depends only on the time elapsed from the last transition.
The semi-Markov processes that we will present are minimal semi-Markov processes associated with Markov renewal processes, with finite state spaces E. Consequently, we do not have to take into account instantaneous states and the sojourn times of a process form, almost surely on ![]() +, a dense set.
+, a dense set.
1.7.1. Markov renewal processes
Let the functions Qij, i, j ∈ E, defined on the real line, be non-decreasing, right continuous, and such that Qij (∞) ≤ 1; they will be called mass functions. Besides, if we have
![]()
with ![]() , the matrix function Q(t) = (Qij(t),i, j ∈ E), t ∈
, the matrix function Q(t) = (Qij(t),i, j ∈ E), t ∈ ![]() +, is called a semi-Markov kernel (matrix) on the state space E. On E we consider the σ-algebra
+, is called a semi-Markov kernel (matrix) on the state space E. On E we consider the σ-algebra ![]() .
.
Let us consider the Markov transition function P((i, s), {j} x[0,t]) defined on the measurable space ![]() by
by
![]()
Then [BLU 68, DYN 65, GIH74], there exists a Markov chain ((Jn,Tn),n ∈ ![]() ) with values in
) with values in ![]() , such that the transition function is given by
, such that the transition function is given by
If we set X0 = T0, Xn =Tn — Tn_1, n ≥ 1, then the process ((Jn, Xn),n ∈ ![]() ) is a Markov chain with values in E x R+ and a transition function given by
) is a Markov chain with values in E x R+ and a transition function given by
Obviously,
![]()
where ![]()
DEFINITION 1.76.– The processes ((Jn,Tn), n ∈ ![]() ) and ((Jn,Xn),n ∈
) and ((Jn,Xn),n ∈ ![]() ) are called Markov renewal process (MRP) and, respectively, J — X process.
) are called Markov renewal process (MRP) and, respectively, J — X process.
Note that (Jn,n ∈ ![]() ) is a Markov chain with values in E and transition matrix p = (Pij, i, j ∈ E), with pij = Qij(∞).
) is a Markov chain with values in E and transition matrix p = (Pij, i, j ∈ E), with pij = Qij(∞).
The n-fold matrix Stieltjes convolution ![]() is defined by
is defined by
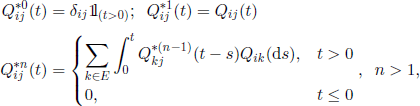
and we have
1.7.2. Semi-Markov processes
We will suppose that
![]()
and define
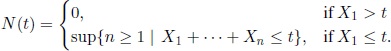
DEFINITION 1.77.– The jump stochastic process (Zt, t ∈ ![]() +), where
+), where
is said to be a semi-Markov process associated with the MRP (Jn, Tn).
We only present some notions regarding semi-Markov processes here, for they will be detailed in Chapter 5.
The jump times are T0 < T1 < T2 < · · · < Tn < … and the inter-jump times are X1, X2, ….
Obviously,
![]()
For any i, j ∈ E we define the distribution function Fij by
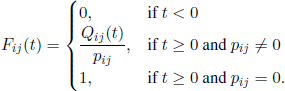
Note that Fij is the distribution function of the sojourn time in state i, knowing that the next visited state is j. These distribution functions are called conditional transition functions.
The transition functions of the semi-Markov process are defined by
We denote by Nj(t) the number of times the semi-Markov process visits state j during the time interval (0, t]. For i, j ∈ E we let
The function t → Ψij(t) is called the Markov renewal function. This function is the solution of the Markov renewal equation
The transition probabilities [1.40] satisfy the Markov renewal equation
1. In fact, the distribution (or law) of an r.v. is a probability on ![]() , i.e. on the Borel sets of
, i.e. on the Borel sets of ![]() .
.
2. Φ is the d.f. of N (0, 1).