9.3 Equivalent Labelings for Trellis Encoders
Conventionally, CM designs based on CENCs either optimize the encoder for a constellation labeled by a SP labeling (TCM), or simply connect an encoder designed for binary transmission with the BRGC (BICM). Of course, none of these approaches is optimal. Instead, a joint optimization over the labeling universe ![]() (see Section 2.5.2) and the CENC universe
(see Section 2.5.2) and the CENC universe ![]() (see Section 2.6.1) should be performed. This problem is very difficult, even for the simplest cases. As an example, we consider the design of a trellis encoder based on an
(see Section 2.6.1) should be performed. This problem is very difficult, even for the simplest cases. As an example, we consider the design of a trellis encoder based on an ![]() CENC with
CENC with ![]() and an
and an ![]() -ary constellation. In this case, the labeling universe includes
-ary constellation. In this case, the labeling universe includes ![]() different binary labelings and the CENC universe (discarding catastrophic encoders) includes about
different binary labelings and the CENC universe (discarding catastrophic encoders) includes about ![]() encoders.5 An exhaustive search for this quite simple configuration would require checking about 6 billion combinations of encoders and labelings.
encoders.5 An exhaustive search for this quite simple configuration would require checking about 6 billion combinations of encoders and labelings.
In this section we address the problem of the joint design of the CENC and the labeling for a trellis encoder, which, based on the analysis in the previous sections, can be used in combination with a BICM decoder. The analysis is based on a classification of binary labelings, which allows us to formally prove that in any trellis encoder the NBC can be replaced by many other labelings (including the BRGC) without causing any performance degradation, provided that the encoder is properly selected. This is also used to explain the asymptotic equivalence between BICM-T and TCM presented in Section 9.2.3.
9.3.1 Equivalent Trellis Encoders
We have seen in Fig. 9.4 that if the interleaver is removed in BICM, its performance over the AWGN channel is improved. Moreover, we showed that in terms of MED, a properly designed BICM-T performs asymptotically as well as TCM (see Tables 9.3 and 9.4). The transmitters for TCM andBICM-T for the ![]() -state (overall constraint length
-state (overall constraint length ![]() ) CENC are shown in Fig. 9.5 (a) and c, respectively. A careful examination of the results in Table 9.3 reveals that the optimal trellis encoder found when analyzing BICM-T, in fact, is equivalent to the one proposed by Ungerboeck 30 years ago. For a 4PAM constellation, Ungerboeck's SP labeling (NBC) can be generated using the BRGC plus one binary addition (which we call transform) applied to its inputs, as shown in Fig. 9.5 (b) (see also Example 2.12). If the transform is included in the mapper, the encoder in Fig. 9.5 (a) is obtained, while if it is included in the CENC, the trellis encoder in Fig. 9.5 (c) is obtained. This equivalence also applies to encoders with larger number of states6 and simply reveals that for 4PAM a TCM transceiver based on the BRGC will have identical performance to Ungerboeck's TCM if the encoder is properly modified, where the modification is the application of a simple transform.
) CENC are shown in Fig. 9.5 (a) and c, respectively. A careful examination of the results in Table 9.3 reveals that the optimal trellis encoder found when analyzing BICM-T, in fact, is equivalent to the one proposed by Ungerboeck 30 years ago. For a 4PAM constellation, Ungerboeck's SP labeling (NBC) can be generated using the BRGC plus one binary addition (which we call transform) applied to its inputs, as shown in Fig. 9.5 (b) (see also Example 2.12). If the transform is included in the mapper, the encoder in Fig. 9.5 (a) is obtained, while if it is included in the CENC, the trellis encoder in Fig. 9.5 (c) is obtained. This equivalence also applies to encoders with larger number of states6 and simply reveals that for 4PAM a TCM transceiver based on the BRGC will have identical performance to Ungerboeck's TCM if the encoder is properly modified, where the modification is the application of a simple transform.

Figure 9.5 Three equivalent trellis encoders: (a) encoder for TCM, (b) equivalent encoder, and (c) encoder for BICM; (a) Ungerboeck's CENC 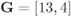 from Table 9.4 and the NBC; (c) Optimal CENC
from Table 9.4 and the NBC; (c) Optimal CENC  Table 9.3 and the BRGC. The trellis encoder in (b) shows how a transformation based on a binary addition can be included in the mapper (to go from (b) to (a)) or in the code (to go from (b) to (c))
Table 9.3 and the BRGC. The trellis encoder in (b) shows how a transformation based on a binary addition can be included in the mapper (to go from (b) to (a)) or in the code (to go from (b) to (c))
To formally study this equivalence, we consider the trellis encoder in Fig. 2.4, where for simplicity we assume that ![]() . For a given constellation
. For a given constellation ![]() and overall constraint length
and overall constraint length ![]() , a CM encoder is fully defined by the CENC matrix
, a CM encoder is fully defined by the CENC matrix ![]() and the labeling of the constellation
and the labeling of the constellation ![]() , and thus, a trellis encoder is defined by the pair
, and thus, a trellis encoder is defined by the pair ![]() . In this section we show how a joint optimization over all
. In this section we show how a joint optimization over all ![]() (i.e., over the CENC universe) and
(i.e., over the CENC universe) and ![]() (i.e., over the labeling universe) can be restricted, without loss of generality, to a joint optimization over all
(i.e., over the labeling universe) can be restricted, without loss of generality, to a joint optimization over all ![]() and over a subset of
and over a subset of ![]() .
.
The output of a given trellis encoder ![]() at time
at time ![]() depends only on
depends only on ![]() information bits. Using (2.90), the transmitted symbol at time
information bits. Using (2.90), the transmitted symbol at time ![]() can then be expressed as
can then be expressed as
where ![]() ,
, ![]() and
and ![]() , i.e.,
, i.e., ![]() , where
, where ![]() was used in (2.90). From now on, we use the notation
was used in (2.90). From now on, we use the notation ![]() to explicitly show the dependence of the mapper on the binary labeling
to explicitly show the dependence of the mapper on the binary labeling ![]() .
.
The following definition gives a condition for the trellis encoders to be equivalent, where this equivalence implies equivalence in terms of BEP and WEP.
In the following, we use ![]() to denote the set of all binary invertible
to denote the set of all binary invertible ![]() matrices and
matrices and ![]() to denote the set of all reduced column echelon binary matrices (see Definition 2.14) of size
to denote the set of all reduced column echelon binary matrices (see Definition 2.14) of size ![]() .
.
Theorem 9.9 shows that a full search over ![]() and
and ![]() will include many pairs of equivalent trellis encoders. Therefore, an optimal trellis encoder with given parameters can be found by searching over a subset of
will include many pairs of equivalent trellis encoders. Therefore, an optimal trellis encoder with given parameters can be found by searching over a subset of ![]() and the whole set
and the whole set ![]() or vice versa. Here we choose the latter approach, searching over a subset of
or vice versa. Here we choose the latter approach, searching over a subset of ![]() .
.
The following theorem will be used to develop an efficient search algorithm we introduce in the next section. For a proof of the following theorem, we refer the reader to the references we provide in Section 9.4.
Theorem 9.10 shows that all binary matrices ![]() can be uniquely generated by finding all the invertible matrices
can be uniquely generated by finding all the invertible matrices ![]() (the set
(the set ![]() ) and all the different reduced column echelon matrices
) and all the different reduced column echelon matrices ![]() (the set
(the set ![]() ). In particular, we have
). In particular, we have

In Table 9.5, the values for ![]() and
and ![]() for
for ![]() are shown. In this table we also show the number of binary labelings (
are shown. In this table we also show the number of binary labelings (![]() ), i.e., the number of matrices
), i.e., the number of matrices ![]() in the labeling universe.
in the labeling universe.
Table 9.5 Number of modified Hadamard classes (![]() ), their cardinality (
), their cardinality (![]() ), and the total number of labelings (
), and the total number of labelings (![]() ) for different values of
) for different values of ![]()
| 2 | 4 | 240 | ||||
| 1 | 6 | 168 | 20 160 | |||
| 2 | 24 | 40 320 |
A modified Hadamard class is defined as the set of matrices ![]() that can be generated via (9.54) using the same reduced column echelon matrix
that can be generated via (9.54) using the same reduced column echelon matrix ![]() . There are thus
. There are thus ![]() modified Hadamard classes, each with cardinality
modified Hadamard classes, each with cardinality ![]() .
.
As a consequence of Theorems 9.9 and 9.10, the two trellis encoders ![]() and
and ![]() are equivalent for any
are equivalent for any ![]() and
and ![]() , where
, where ![]() and
and ![]() are given by the factorization (9.54). In other words, all nonequivalent trellis encoders can be generated using one member of each modified Hadamard class only, and thus, a joint optimization over all
are given by the factorization (9.54). In other words, all nonequivalent trellis encoders can be generated using one member of each modified Hadamard class only, and thus, a joint optimization over all ![]() and
and ![]() can be reduced to an optimization over all
can be reduced to an optimization over all ![]() and
and ![]() with no loss in performance. This means that the search space is reduced by at least a factor of
with no loss in performance. This means that the search space is reduced by at least a factor of ![]() . For example, for
. For example, for ![]() -ary constellations (
-ary constellations (![]() ), the total number of different binary labelings that must be tested is reduced from
), the total number of different binary labelings that must be tested is reduced from ![]() to
to ![]() . Moreover, as shown in Section 9.3.4, this can be reduced even further if the constellation
. Moreover, as shown in Section 9.3.4, this can be reduced even further if the constellation ![]() possesses certain symmetries.
possesses certain symmetries.
9.3.2 Modified Full Linear Search Algorithm
The problem of finding the set ![]() of reduced column echelon matrices for a given
of reduced column echelon matrices for a given ![]() can be solved by using a modified version of the so-called full linear search algorithm (FLSA). Such a modified full linear search algorithm (MFLSA) generates one member of each modified Hadamard class, namely, the labeling that corresponds to a reduced column echelon matrix
can be solved by using a modified version of the so-called full linear search algorithm (FLSA). Such a modified full linear search algorithm (MFLSA) generates one member of each modified Hadamard class, namely, the labeling that corresponds to a reduced column echelon matrix ![]() . Its pseudocode is shown in Algorithm 1. In this algorithm, the (row) vector
. Its pseudocode is shown in Algorithm 1. In this algorithm, the (row) vector ![]() denotes the decimal representation of the columns of the matrix
denotes the decimal representation of the columns of the matrix ![]() . The first labeling generated (line 1) is always the NBC. Then the algorithm proceeds by generating all permutations thereof, under the condition that no power of two (
. The first labeling generated (line 1) is always the NBC. Then the algorithm proceeds by generating all permutations thereof, under the condition that no power of two (![]() ) is preceded by a larger value. By Definition 2.14, this simple condition assures that only reduced column echelon matrices are generated.
) is preceded by a larger value. By Definition 2.14, this simple condition assures that only reduced column echelon matrices are generated.
Table 9.6 Output of the MFLSA for ![]() (read row by row)
(read row by row)
| 01234567 | 10234567 | 12034567 | 12304567 | 12340567 | 12345067 | 12345607 | 12345670 |
| 01243567 | 10243567 | 12043567 | 12403567 | 12430567 | 12435067 | 12435607 | 12435670 |
| 01245367 | 10245367 | 12045367 | 12405367 | 12450367 | 12453067 | 12453607 | 12453670 |
| 01245637 | 10245637 | 12045637 | 12405637 | 12450637 | 12456037 | 12456307 | 12456370 |
| 01245673 | 10245673 | 12045673 | 12405673 | 12450673 | 12456073 | 12456703 | 12456730 |
| 01234657 | 10234657 | 12034657 | 12304657 | 12340657 | 12346057 | 12346507 | 12346570 |
| 01243657 | 10243657 | 12043657 | 12403657 | 12430657 | 12436057 | 12436507 | 12436570 |
| 01246357 | 10246357 | 12046357 | 12406357 | 12460357 | 12463057 | 12463507 | 12463570 |
| 01246537 | 10246537 | 12046537 | 12406537 | 12460537 | 12465037 | 12465307 | 12465370 |
| 01246573 | 10246573 | 12046573 | 12406573 | 12460573 | 12465073 | 12465703 | 12465730 |
| 01234675 | 10234675 | 12034675 | 12304675 | 12340675 | 12346075 | 12346705 | 12346750 |
| 01243675 | 10243675 | 12043675 | 12403675 | 12430675 | 12436075 | 12436705 | 12436750 |
| 01246375 | 10246375 | 12046375 | 12406375 | 12460375 | 12463075 | 12463705 | 12463750 |
| 01246735 | 10246735 | 12046735 | 12406735 | 12460735 | 12467035 | 12467305 | 12467350 |
| 01246753 | 10246753 | 12046753 | 12406753 | 12460753 | 12467053 | 12467503 | 12467530 |
| 01234576 | 10234576 | 12034576 | 12304576 | 12340576 | 12345076 | 12345706 | 12345760 |
| 01243576 | 10243576 | 12043576 | 12403576 | 12430576 | 12435076 | 12435706 | 12435760 |
| 01245376 | 10245376 | 12045376 | 12405376 | 12450376 | 12453076 | 12453706 | 12453760 |
| 01245736 | 10245736 | 12045736 | 12405736 | 12450736 | 12457036 | 12457306 | 12457360 |
| 01245763 | 10245763 | 12045763 | 12405763 | 12450763 | 12457063 | 12457603 | 12457630 |
| 01234756 | 10234756 | 12034756 | 12304756 | 12340756 | 12347056 | 12347506 | 12347560 |
| 01243756 | 10243756 | 12043756 | 12403756 | 12430756 | 12437056 | 12437506 | 12437560 |
| 01247356 | 10247356 | 12047356 | 12407356 | 12470356 | 12473056 | 12473506 | 12473560 |
| 01247536 | 10247536 | 12047536 | 12407536 | 12470536 | 12475036 | 12475306 | 12475360 |
| 01247563 | 10247563 | 12047563 | 12407563 | 12470563 | 12475063 | 12475603 | 12475630 |
| 01234765 | 10234765 | 12034765 | 12304765 | 12340765 | 12347065 | 12347605 | 12347650 |
| 01243765 | 10243765 | 12043765 | 12403765 | 12430765 | 12437065 | 12437605 | 12437650 |
| 01247365 | 10247365 | 12047365 | 12407365 | 12470365 | 12473065 | 12473605 | 12473650 |
| 01247635 | 10247635 | 12047635 | 12407635 | 12470635 | 12476035 | 12476305 | 12476350 |
| 01247653 | 10247653 | 12047653 | 12407653 | 12470653 | 12476053 | 12476503 | 12476530 |
9.3.3 NBC and BRGC
Another way of interpreting the result in Theorem 9.9 is that for any trellis encoder ![]() , a new equivalent trellis encoder can be generated using an encoder
, a new equivalent trellis encoder can be generated using an encoder ![]() and a labeling
and a labeling ![]() that belongs to the same modified Hadamard class as the original labeling
that belongs to the same modified Hadamard class as the original labeling ![]() . One direct consequence of this result is that any trellis encoder using the NBC labeling can be constructed using the BRGC and an appropriately selected encoder. To clarify this, consider the following example.
. One direct consequence of this result is that any trellis encoder using the NBC labeling can be constructed using the BRGC and an appropriately selected encoder. To clarify this, consider the following example.
The above relation between the NBC and the BRGC is generalized to an arbitrary order ![]() in the following theorem.
in the following theorem.
Theorem 9.15 can be understood as follows. Any trellis encoder using the NBC ![]() and a CENC
and a CENC ![]() is equivalent to a trellis encoder using the BRGC
is equivalent to a trellis encoder using the BRGC ![]() and a CENC
and a CENC ![]() with
with ![]() given by (2.56). Example 9.14 and Theorem 9.15 explain, in part, the results obtained in Section 9.2.3, where it is shown that BICM-T with the optimal encoders and the BRGC perform asymptotically as well as TCM. The “in part” comes from the fact that in BICM-T a (suboptimal) BICM receiver is used while in TCM an ML decoder is used.
given by (2.56). Example 9.14 and Theorem 9.15 explain, in part, the results obtained in Section 9.2.3, where it is shown that BICM-T with the optimal encoders and the BRGC perform asymptotically as well as TCM. The “in part” comes from the fact that in BICM-T a (suboptimal) BICM receiver is used while in TCM an ML decoder is used.
9.3.4  and
and  Constellations
Constellations
While all the previous results are fully general in the sense that they are valid for any constellation, any memoryless channel, and any receiver, in this section we study well-structured one- and two-dimensional constellations, i.e., ![]() PAM and (
PAM and (![]() PSK) constellations defined in Section 2.5.
PSK) constellations defined in Section 2.5.
![]() PAM constellations are symmetric around zero. Because of this, two trellis encoders based on an
PAM constellations are symmetric around zero. Because of this, two trellis encoders based on an ![]() PAM constellation, the first one using the labeling
PAM constellation, the first one using the labeling ![]() and the second one using a “reverse” labeling
and the second one using a “reverse” labeling
are equivalent for any ![]() . This result implies that the number of binary labelings that give nonequivalent trellis encoders is
. This result implies that the number of binary labelings that give nonequivalent trellis encoders is ![]() . To generate only the
. To generate only the ![]() nonequivalent labelings for
nonequivalent labelings for ![]() PAM, the MFLSA in Algorithm 1 can be modified as follows. Replace
PAM, the MFLSA in Algorithm 1 can be modified as follows. Replace ![]() on lines
on lines ![]() and
and ![]() with
with ![]() , where the integer function
, where the integer function ![]() is defined as
is defined as ![]() if
if ![]() and
and ![]() otherwise. This has the effect of only generating labelings, in which the all-zero label is among the first
otherwise. This has the effect of only generating labelings, in which the all-zero label is among the first ![]() positions.
positions.
A trellis encoder based on an ![]() PSK constellation is not affected by a circular rotation of its labeling, i.e., without loss of generality it can be assumed that the all-zero label is assigned to the constellation point
PSK constellation is not affected by a circular rotation of its labeling, i.e., without loss of generality it can be assumed that the all-zero label is assigned to the constellation point ![]() . The consequence of this is that for
. The consequence of this is that for ![]() PSK constellations, the number of reduced column echelon matrices that give nonequivalent trellis encoders is reduced further by a factor of
PSK constellations, the number of reduced column echelon matrices that give nonequivalent trellis encoders is reduced further by a factor of ![]() . For
. For ![]() the labelings can be obtained from the MFLSA by setting
the labelings can be obtained from the MFLSA by setting ![]() in line
in line ![]() , which gives the FLSA.
, which gives the FLSA.
9.4 Bibliographical Notes
BICM-T was introduced in [1] and later analyzed in detail in [2] for a rate ![]() encoder and 4PAM, where the performance analysis developed in this chapter as well as the optimal encoders were also introduced. Very recently, it was shown in [3] that for BICM-T, the asymptotic loss in terms of PEP introduced by the suboptimal BICM receiver is bounded by
encoder and 4PAM, where the performance analysis developed in this chapter as well as the optimal encoders were also introduced. Very recently, it was shown in [3] that for BICM-T, the asymptotic loss in terms of PEP introduced by the suboptimal BICM receiver is bounded by ![]() . Furthermore, [3] also shows that this loss is in fact zero for a wide range of linear codes, including all rate
. Furthermore, [3] also shows that this loss is in fact zero for a wide range of linear codes, including all rate ![]() CENCs we studied in this chapter.
CENCs we studied in this chapter.
TCM designs based on SP are considered heuristic [4, pp. 525, 531], [5, Section 3.4], and thus, they do not necessarily lead to an optimal design [6, p. 680]. Indeed, the results in [7, Tables 2–3], [8, Chapter 6; 9] show the suboptimality of using an SP labeling. For a good explanation about this, we refer the reader to [10, Section I]. The problem of using non-SP labelings for TCM has been studied in the literature. In [6, Section 13.2.1], a trellis encoder that uses a rate ![]() ODS CENC and a 4PSK constellation labeled by the BRGC was presented (see also [11, Example 18.2]). The same configuration was presented in [6, Problem 13–11], where the problem of selecting an appropriate labeling for a given encoder was analyzed. Another example is the so-called pragmatic TCM [12, Section 8.6, 13] (see also [14 15, Section 9.2.4]), where a non-SP labeling was used together with an off-the-shelf MFHD/ODS CENC. For 4PSK, this labeling corresponds to the BRGC, but for larger constellations it is not a Gray labeling (although it has a particular structure). A similar labeling was also used in [16]. A binary labeling for BICM-T was heuristically proposed in [1] for
ODS CENC and a 4PSK constellation labeled by the BRGC was presented (see also [11, Example 18.2]). The same configuration was presented in [6, Problem 13–11], where the problem of selecting an appropriate labeling for a given encoder was analyzed. Another example is the so-called pragmatic TCM [12, Section 8.6, 13] (see also [14 15, Section 9.2.4]), where a non-SP labeling was used together with an off-the-shelf MFHD/ODS CENC. For 4PSK, this labeling corresponds to the BRGC, but for larger constellations it is not a Gray labeling (although it has a particular structure). A similar labeling was also used in [16]. A binary labeling for BICM-T was heuristically proposed in [1] for ![]() PAM constellations for
PAM constellations for ![]() .
.
The idea of using a Gray labeling and an MFHD CENC in fact dates back to [17 18], which correspond to the first pragmatic TCM approaches. Trellis encoders using a constellation labeled by the BRGC were designed in [7] where a search over CENCs maximizing the MED was performed. In [8, Chapter 6; 9], and in the same spirit of the ODS CENCs, Zhang used a non-Gray non-SP labeling and tabulated trellis encoders with optimal spectrum. Gray-coded TCM codes for fading channels were studied in [19–21].
The classification of labelings is inspired by the one in [22], where the so-called Hadamard classes were used to solve a related search problem in source coding and where the FLSA was also introduced. The modified Hadamard classes introduced in this chapter are narrower than the regular Hadamard classes defined in [22], each including ![]() reduced column echelon matrices. For a proof of Theorem 9.10, we refer the reader to [23, p. 187, Corollary 1].
reduced column echelon matrices. For a proof of Theorem 9.10, we refer the reader to [23, p. 187, Corollary 1].
The idea of applying a linear transformation to the labeling/encoder was first introduced in [8, Fig. 6.5], (see also [9 24, 25, Chapter 2]). The equivalence between TCM encoders and encoders optimized for the BRGC and the NBC as well as the relationship between the encoders in [2 26] were first pointed out to us by R. F. H. Fischer [27]. In the same way the encoders in [26, Table I], (which we reproduced in Table 9.4) and [2, Table III] are equivalent, it was shown in [25, Chapter 2], that the encoders found in [8, Chapter 6], using a non-Gray labeling are equivalent to those found with a Gray-labeled constellation in [7]. The formalism of using modified Hadamard classes to study the equivalence of trellis encoders was introduced in [28 29], where the MFLSA was also introduced and trellis encoders with optimum distance spectrum were tabulated.
In a related work, Wesel et al. introduced in [10] the concept of edge profile (EP) of a labeling, and argued that in most of the cases, the EP can be used to find equivalent trellis encoders in terms of MED. The EP is also argued to be a good indication of the quality of a labeling for TCM in [10, Section I]; however, its optimality is not proven. Nevertheless, all the labelings found in [28] have optimal EP. This makes us conjecture that good trellis encoders can be found by using the EP of [10] on top of the Hadamard-based classification. This approach would indeed reduce the search space; however, the optimality would not be guaranteed.
References
- [1] Stierstorfer, C., Fischer, R. F. H., and Huber, J. B. (2010) Optimizing BICM with convolutional codes for transmission over the AWGN channel. International Zurich Seminar on Communications, March 2010, Zurich, Switzerland.
- [2] Alvarado, A., Szczecinski, L., and Agrell, E. (2011) On BICM receivers for TCM transmission. IEEE Trans. Commun., 59 (10), 2692–2702.
- [3] Ivanov, M., Alvarado, A., Brännström, F., and Agrell, E. (2014) On the asymptotic performance of bit-wise decoders for coded modulation. IEEE Trans. Inf. Theory, 60 (5), 2796–2804.
- [4] Proakis, J. G. (2000) Digital Communications, 4th edn, McGraw-Hill.
- [5] Schlegel, C. B. and Perez, L. C. (2004) Trellis and Turbo Coding, 1st edn, John Wiley & Sons.
- [6] Barry, J. B., Lee, E. A., and Messerschmitt, D. G. (2004) Digital Communication, 3rd edn, Springer.
- [7] Du, J. and Kasahara, M. (1989) Improvements of the information-bit error rate of trellis code modulation systems. Trans. IEICE, E 72 (5), 609–614.
- [8] Zhang, W. (1996) Finite state systems in mobile communications. PhD dissertation, University of South Australia, Adelaide, Australia.
- [9] Zhang, W., Schlegel, C., and Alexander, P. (1994) The bit error rate reduction for systematic 8PSK trellis codes by a Gray scrambler. IEEE International Conference on Universal Wireless Access, April 1994, Melbourne, Australia.
- [10] Wesel, R. D., Liu, X., Cioffi, J. M., and Komninakis, C. (2001) Constellation labeling for linear encoders. IEEE Trans. Inf. Theory, 47 (6), 2417–2431.
- [11] Lin, S. and Costello, D. J. Jr. (2004) Error Control Coding, 2nd edn, Prentice Hall, Englewood Cliffs, NJ.
- [12] Clark, G. C. Jr. and Cain, J. B. (1981) Error-Correction Coding for Digital Communications, 2nd edn, Plenum Press.
- [13] Viterbi, A. J., Wolf, J. K., Zehavi, E., and Padovani, R. (1989) A pragmatic approach to trellis-coded modulation. IEEE Commun. Mag., 27 (7), 11–19.
- [14] Wolf, J. K. and Zehavi, E. (1995)
 codes: pragmatic trellis codes utilizing punctured convolutional codes. IEEE Commun. Mag., 33 (2), 94–99.
codes: pragmatic trellis codes utilizing punctured convolutional codes. IEEE Commun. Mag., 33 (2), 94–99. - [15] Morelos-Zaragoza, R. H. (2002) The Art of Error Correcting Coding, 2nd edn, John Wiley & Sons.
- [16] Hagenauer, J. and Sundberg, C.- E. (1988) On the performance evaluation of trellis-coded 8-PSK systems with carrier phase offset. Arch. Elektron. Uebertragungstechnik, 5 (42), 274–284.
- [17] Odenwalder, J. P., Viterbi, A. J., Jacobs, I. M., and Heller, J. A. (1973) Study of information transfer optimization for communication satellites. Technical Report NASA-CR-114561, Linkabit Corporation, San Diego, CA.
- [18] Digeon, A. (1977) On improving bit error probability of QPSK and 4-level amplitude modulation systems by convolutional coding. IEEE Trans. Commun., COM-25 (10), 1238–1239.
- [19] Du, J. and Vucetic, B. (1990) New
 -PSK trellis codes for fading channels. Electron. Lett., 26 (16), 1267–1269.
-PSK trellis codes for fading channels. Electron. Lett., 26 (16), 1267–1269. - [20] Du, J. and Vucetic, B. (1991) New 16-QAM trellis codes for fading channels. Electron. Lett., 27 (12), 1009–1010.
- [21] Du, J. and Vucetic, B. (1995) Construction of new MPSK trellis codes for fading channels. IEEE Trans. Commun., 43 (2/3/4), 776–478.
- [22] Knagenhjelm, P. and Agrell, E. (1996) The Hadamard transform—a tool for index assignment. IEEE Trans. Inf. Theory, 42 (4), 1139–1151.
- [23] Birkhoff, G. and Mac Lane, S. (1977) A Survey of Modern Algebra, 4th edn, Macmillan, New York.
- [24] Gray, P. K. and Rasmussen, L. K. (1995) Bit error rate reduction of TCM systems using linear scramblers. IEEE International Symposium on Information Theory (ISIT), September 1995, Whistler, BC, Canada.
- [25] Gray, P. K. (1999) Serially concatenated trellis coded modulation. PhD dissertation, University of South Australia, Adelaide, Australia.
- [26] Ungerboeck, G. (1982) Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory, 28 (1), 55–67.
- [27] Fischer, R. F. H. Private communication, Jan. 2011.
- [28] Alvarado, A., Graell i Amat, A., Brännström, F., and Agrell, E. (2012) On the equivalence of TCM encoders. IEEE International Symposium on Information Theory (ISIT), July 2012, Cambridge, MA.
- [29] Alvarado, A., Graell i Amat, A., Brännström, F., and Agrell, E. (2013) On optimal TCM encoders. IEEE Trans. Commun., 61 (6), 2178–2189.
