15
Binary Response Variable
Many statistical problems involve binary response variables. For example, we often classify things as dead or alive, occupied or empty, healthy or diseased, male or female, literate or illiterate, mature or immature, solvent or insolvent, employed or unemployed, and it is interesting to understand the factors that are associated with an individual being in one class or the other. In a study of company insolvency, for instance, the data would consist of a list of measurements made on the insolvent companies (their age, size, turnover, location, management experience, workforce training, and so on) and a similar list for the solvent companies. The question then becomes which, if any, of the explanatory variables increase the probability of an individual company being insolvent.
The response variable contains only 0s or 1s; for example, 0 to represent dead individuals and 1 to represent live ones. Thus, there is only a single column of numbers for the response, in contrast to proportion data where two vectors (successes and failures) were bound together to form the response (see Chapter 14). An alternative is allowed by R in which the values of the response variable are represented by a two-level factor (like ‘dead’ or ‘alive’, ‘male’ or ‘female’, etc.).
The way that R treats binary data is to assume that the values of the response come from a binomial trial with sample size 1. If the probability that an individual is dead is p, then the probability of obtaining y (where y is either dead or alive, 0 or 1) is given by an abbreviated form of the binomial distribution with n = 1, known as the Bernoulli distribution:
The random variable y has a mean of p and a variance of p(1 − p), and the object is to determine how the explanatory variables influence the value of p. The trick to using binary response variables effectively is to know when it is worth using them, and when it is better to lump the successes and failures together and analyse the total counts of dead individuals, occupied patches, insolvent firms or whatever. The question you need to ask yourself is whether or not you have unique values of one or more explanatory variables for each and every individual case. If the answer is ‘yes’, then analysis with a binary response variable is likely to be fruitful. If the answer is ‘no’, then there is nothing to be gained, and you should reduce your data by aggregating the counts to the resolution at which each count does have a unique set of explanatory variables. For example, suppose that all your explanatory variables were categorical (say sex (male or female), employment (employed or unemployed) and region (urban or rural)). In this case there is nothing to be gained from analysis using a binary response variable because none of the individuals in the study have unique values of any of the explanatory variables. It might be worthwhile if you had each individual's body weight, for example; then you could ask whether, when you control for sex and region, heavy people are more likely to be unemployed than light people. In the absence of unique values for any explanatory variables, there are two useful options:
- analyse the data as a contingency table using Poisson errors, with the count of the total number of individuals in each of the eight contingencies (2 × 2 × 2) as the response variable (see Chapter 13) in a dataframe with just eight rows
- decide which of your explanatory variables is the key (perhaps you are interested in gender differences), then express the data as proportions (the number of males and the number of females) and recode the binary response as a count of a two-level factor – the analysis is now of proportion data (e.g. the proportion of all individuals that are female) using binomial errors (see Chapter 14)
If you do have unique measurements of one or more explanatory variables for each individual, these are likely to be continuous variables such as body weight, income, medical history, distance to the nuclear reprocessing plant, geographic isolation, and so on. This being the case, successful analyses of binary response data tend to be multiple regression analyses or complex analyses of covariance, and you should consult Chapters 10 and 11 for details on model simplification and model criticism.
In order to carry out modelling on a binary response variable we take the following steps:
- create a single vector containing 0s and 1s (or one of two factor levels) as the response variable
- use glm with family=binomial
- you can change the link function from the default logit to complementary log-log
- fit the model in the usual way
- test significance by deletion of terms from the maximal model, and compare the change in deviance with chi-squared
- note that there is no such thing as overdispersion with a binary response variable, and hence no need to change to using quasi-binomial when the residual deviance is large
- plot(model) is rarely informative with binary response variables, so model checking is more than usually challenging
The choice of link function is generally made by trying both links and selecting the link that gives the lowest deviance. The logit link that we used earlier is symmetric in p and q, but the complementary log-log link is asymmetric.
Incidence Functions
In this example, the response variable is called incidence; a value of 1 means that an island was occupied by a particular species of bird, and 0 means that the bird did not breed there. The explanatory variables are the area of the island (km2) and the isolation of the island (distance from the mainland, km).
island <- read.csv("c:\temp\isolation.csv")attach(island)names(island)
[1] "incidence" "area" "isolation"
There are two continuous explanatory variables, so the appropriate analysis is multiple regression. The response is binary, so we shall do logistic regression with binomial errors. We begin by fitting a complex model involving an interaction between isolation and area:
model1 <- glm(incidence~area*isolation,binomial)
Then we fit a simpler model with only main effects for isolation and area:
model2 <- glm(incidence~area+isolation,binomial)
Now we compare the two models using anova:
anova(model1,model2,test="Chi")
Analysis of Deviance Table
Model 1: incidence ~ area * isolationModel 2: incidence ~ area + isolation
Resid. Df Resid. Dev Df Deviance Pr(>Chi)1 46 28.2522 47 28.402 -1 -0.15043 0.6981
The simpler model is not significantly worse, so we accept this for the time being, and inspect the parameter estimates and standard errors:
summary(model2)
Coefficients:
Estimate Std. Error z value Pr(>|z|)(Intercept) 6.6417 2.9218 2.273 0.02302 *area 0.5807 0.2478 2.344 0.01909 *isolation -1.3719 0.4769 -2.877 0.00401 **
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 68.029 on 49 degrees of freedomResidual deviance: 28.402 on 47 degrees of freedom
AIC: 34.402
Number of Fisher Scoring iterations: 6
The estimates and their standard errors are in logits. Area has a significant positive effect (larger islands are more likely to be occupied), but isolation has a very strong negative effect (isolated islands are much less likely to be occupied). This is the minimal adequate model. We should plot the fitted model through the scatterplot of the data. It is much easier to do this for each variable separately, like this:
windows(7,4)par(mfrow=c(1,2))xv <- seq(0,9,0.01)
modela <- glm(incidence~area,binomial)modeli <- glm(incidence~isolation,binomial)
yv <- predict(modela,list(area=xv),type="response")plot(area,incidence,pch=21,bg="yellow")lines(xv,yv,col="blue")
xv2 <- seq(0,10,0.1)yv2 <- predict(modeli,list(isolation=xv2),type="response")plot(isolation,incidence,pch=21,bg="yellow")lines(xv2,yv2,col="red")
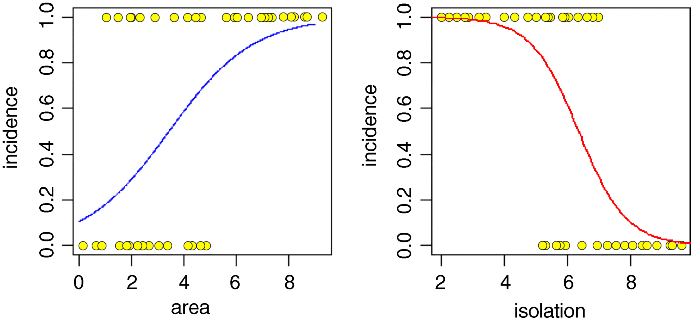
This is well and good, but it is very difficult to know how good the fit of the model is when the data are shown only as 0s or 1s. It is sensible to compute one or more intermediate probabilities from the data, and to show these empirical estimates (ideally with their standard errors) on the plot in order to judge whether the fitted line is a reasonable description of the data.
For the purposes of demonstration, we divide the ranges of area and of isolation into (say) three, count how many successes and failures occurred in each interval, calculate the mean proportion incidence in each third, p, and add these estimates to the plot as points along with their standard error bars ![]() . Start by using cut to obtain the break points on the two axes:
. Start by using cut to obtain the break points on the two axes:
ac <- cut(area,3)ic <- cut(isolation,3)tapply(incidence,ac,sum)
(0.144,3.19] (3.19,6.23] (6.23,9.28]7 8 14
tapply(incidence,ic,sum)
(2.02,4.54] (4.54,7.06] (7.06,9.58]12 17 0
There were seven data points indicating occupation (success) in the lowest third of the area axis and 14 in the highest third. There were 12 data points indicating occupation (success) in the lowest third of range of values for isolation and none in the highest third. Note the convention for labelling intervals: (a, b] means include the right-hand endpoint, b (the square bracket), but not the left one, a (the round bracket).
Now count the total number of islands in each interval using table:
table(ac)
ac(0.144,3.19] (3.19,6.23] (6.23,9.28]21 15 14
table(ic)
ic(2.02,4.54] (4.54,7.06] (7.06,9.58]12 25 13
The probability of occupation is given by dividing the number of successes by the number of cases:
tapply(incidence,ac,sum)/ table(ac)
(0.144,3.19] (3.19,6.23] (6.23,9.28]0.3333333 0.5333333 1.0000000
tapply(incidence,ic,sum)/ table(ic)
(2.02,4.54] (4.54,7.06] (7.06,9.58]1.00 0.68 0.00
The idea is to plot these mean proportions and their standard errors (![]() ) along with the regression line from the model to see how close the model gets to the three calculated proportions:
) along with the regression line from the model to see how close the model gets to the three calculated proportions:
xv <- seq(0,9,0.01)yv <- predict(modela,list(area=xv),type="response")plot(area,incidence,pch=21,bg="yellow")lines(xv,yv,col="blue")
d <- (max(area)-min(area))/3left <- min(area)+d/2mid <- left+dright <- mid+dxva <- c(left,mid,right)pa <- as.vector(tapply(incidence,ac,sum)/ table(ac))se <- sqrt(pa*(1-pa)/table(ac))
xv <- seq(0,9,0.01)yv <- predict(modela,list(area=xv),type="response")lines(xv,yv,col="blue")
points(xva,pa,pch=16,col="red")for (i in 1:3) lines(c(xva[i],xva[i]),c(pa[i]+se[i],pa[i]-se[i]),col="red")
xv2 <- seq(0,10,0.1)yv2 <- predict(modeli,list(isolation=xv2),type="response")plot(isolation,incidence,pch=21,bg="yellow")lines(xv2,yv2,col="red")
d <- (max(isolation)-min(isolation))/3left <- min(isolation)+d/2mid <- left+dright <- mid+dxvi <- c(left,mid,right)pi <- as.vector(tapply(incidence,ic,sum)/ table(ic))se <- sqrt(pi*(1-pi)/table(ic))
points(xvi,pi,pch=16,col="blue")for (i in 1:3) lines(c(xvi[i],xvi[i]),c(pi[i]+se[i],pi[i]-se[i]),col="blue")

You can see at once that the fit for the right-hand graph of incidence against isolation is excellent; the logistic is a very good model for these data. In contrast, the fit for the left-hand graph of incidence against area is poor; at low values of area the model (blue line) underestimates the observed data (red point with error bars) while for intermediate values of area the model (blue line) overestimates the observed data (red point with error bars).
This approach of plotting the two effects separately would not work, of course, if there were a significant interaction between area and isolation; then you would need to produce conditioning plots of incidence against area for different degrees of isolation.
ANCOVA with a Binary Response Variable
In this example the binary response variable is parasite infection (infected or not) and the explanatory variables are weight and age (continuous) and sex (categorical). We begin with data inspection:
infection <- read.csv("c:\temp\infection.csv")attach(infection)names(infection)
[1] "infected" "age" "weight" "sex"
For the continuous explanatory variables, weight and age, it is useful to look at box-and-whisker plots of the data:
windows(7,4)par(mfrow=c(1,2))plot(infected,weight,xlab="Infection",ylab="Weight",col="lightblue")plot(infected,age,xlab="Infection",ylab="Age", col="lightgreen")
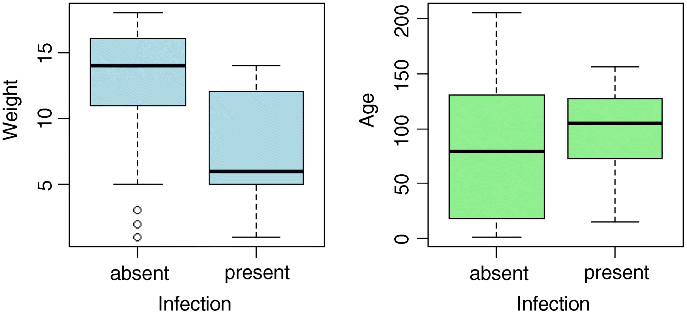
Infected individuals are substantially lighter than uninfected individuals, and occur in a much narrower range of ages. To see the relationship between infection and gender (both categorical variables) we can use table:
table(infected,sex)
sexinfected female maleabsent 17 47present 11 6
This indicates that the infection is much more prevalent in females (11/28) than in males (6/53).
We get down to business, as usual, by fitting a maximal model with different slopes for each level of the categorical variable:
model <- glm(infected~age*weight*sex,family=binomial)summary(model)
Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -0.109124 1.375388 -0.079 0.937age 0.024128 0.020874 1.156 0.248weight -0.074156 0.147678 -0.502 0.616sexmale -5.969109 4.278066 -1.395 0.163age:weight -0.001977 0.002006 -0.985 0.325age:sexmale 0.038086 0.041325 0.922 0.357weight:sexmale 0.213830 0.343265 0.623 0.533age:weight:sexmale -0.001651 0.003419 -0.483 0.629
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 83.234 on 80 degrees of freedomResidual deviance: 55.706 on 73 degrees of freedomAIC: 71.706
Number of Fisher Scoring iterations: 6
It certainly does not look as if any of the high-order interactions are significant. Instead of using update and anova for model simplification, we can use step to compute the AIC for each term in turn:
model2 <- step(model)
Start: AIC= 71.71
First, it tests whether the three-way interaction is required:
Df Deviance AIC- age:weight:sex 1 55.943 69.943<none> 55.706 71.706
Step: AIC= 69.94
This causes a reduction in AIC of just 71.7 – 69.9 = 1.8 and hence is not significant, so the three-way interaction is eliminated.
Next, it looks at the two-way interactions and decides which of the three to delete first:
Df Deviance AIC- weight:sex 1 56.122 68.122- age:sex 1 57.828 69.828<none> 55.943 69.943- age:weight 1 58.674 70.674
Step: AIC= 68.12
Only the removal of the weight–sex interaction causes a reduction in AIC, so this interaction in deleted and the other two interactions are retained. Let us see if we would have been this lenient:
summary(model2)
Call:
glm(formula = infected ~ age + weight + sex + age:weight + age:sex,family = binomial)
Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -0.391572 1.264850 -0.310 0.7569age 0.025764 0.014918 1.727 0.0842 .weight -0.036493 0.128907 -0.283 0.7771sexmale -3.743698 1.786011 -2.096 0.0361 *age:weight -0.002221 0.001365 -1.627 0.1037age:sexmale 0.020464 0.015199 1.346 0.1782
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 83.234 on 80 degrees of freedomResidual deviance: 56.122 on 75 degrees of freedomAIC: 68.122
Neither of the two interactions retained by step would figure in our model (p > 0.10). We shall use update to simplify model2:
model3 <- update(model2,~.-age:weight)anova(model2,model3,test="Chi")
Analysis of Deviance Table
Model 1: infected ~ age + weight + sex + age:weight + age:sexModel 2: infected ~ age + weight + sex + age:sex
Resid. Df Resid. Dev Df Deviance Pr(>Chi)1 75 56.1222 76 58.899 -1 -2.777 0.09562 .
So there is no really persuasive evidence of an age–weight term (p = 0.096).
model4 <- update(model2,~.-age:sex)anova(model2,model4,test="Chi")
Analysis of Deviance Table
Model 1: infected ~ age + weight + sex + age:weight + age:sexModel 2: infected ~ age + weight + sex + age:weight
Resid. Df Resid. Dev Df Deviance Pr(>Chi)1 75 56.1222 76 58.142 -1 -2.0203 0.1552
Note that we are testing all the two-way interactions by deletion from the model that contains all two-way interactions (model2): p = 0.1552, so nothing there, then.
What about the three main effects?
model5 <- glm(infected~age+weight+sex,family=binomial)summary(model5)
Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) 0.609369 0.803288 0.759 0.448096age 0.012653 0.006772 1.868 0.061701 .weight -0.227912 0.068599 -3.322 0.000893 ***sexmale -1.543444 0.685681 -2.251 0.024388 *
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 83.234 on 80 degrees of freedomResidual deviance: 59.859 on 77 degrees of freedomAIC: 67.859
Number of Fisher Scoring iterations: 5
Weight is highly significant, as we expected from the initial boxplot, sex is quite significant, and age is marginally significant. It is worth establishing whether there is any evidence of non-linearity in the response of infection to weight or age. We might begin by fitting quadratic terms for the two continuous explanatory variables:
model6 <- glm(infected~age+weight+sex+I(weight^2)+I(age^2),family=binomial)summary(model6)
Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -3.4475839 1.7978359 -1.918 0.0552 .age 0.0829364 0.0360205 2.302 0.0213 *weight 0.4466284 0.3372352 1.324 0.1854sexmale -1.2203683 0.7683288 -1.588 0.1122I(weight^2) -0.0415128 0.0209677 -1.980 0.0477 *I(age^2) -0.0004009 0.0002004 -2.000 0.0455 *
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 83.234 on 80 degrees of freedomResidual deviance: 48.620 on 75 degrees of freedomAIC: 60.62
Number of Fisher Scoring iterations: 6
Evidently, both relationships are significantly non-linear. It is worth looking at these non-linearities in more detail, to see if we can do better with other kinds of models (e.g. non-parametric smoothers, piecewise linear models or step functions). A good start is often a generalized additive model when we have continuous covariates:
library(mgcv)model7 <- gam(infected~sex+s(age)+s(weight),family=binomial)plot.gam(model7)
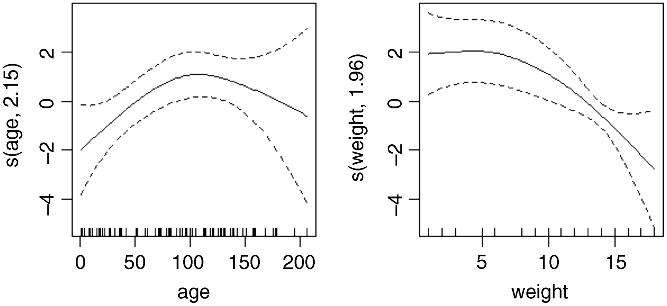
These non-parametric smoothers are excellent at showing the humped relationship between infection and age, and at highlighting the possibility of a threshold at weight ![]() in the relationship between weight and infection.
in the relationship between weight and infection.
We can now return to a GLM to incorporate these ideas. We shall fit age and age^2 as before, but try a piecewise linear fit for weight, estimating the threshold weight at a range of values (say, 8–14) and selecting the threshold that gives the lowest residual deviance; this turns out to be a threshold of 12 (a bit higher than it appears from the gam plot, above). The piecewise regression is specified by the term:
I((weight – 12) * (weight > 12))
The I (‘as is’) is necessary to stop the * being evaluated as an interaction term in the model formula. What this expression says is: regress infection on the value of weight–12, but only do this when weight>12 is true; otherwise, assume that infection is independent of weight.
model8 <- glm(infected~sex+age+I(age^2)+I((weight-12)*(weight>12)),family=binomial)summary(model8)
Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -2.7511382 1.3678824 -2.011 0.0443 *sexmale -1.2864683 0.7349201 -1.750 0.0800 .age 0.0798629 0.0348184 2.294 0.0218 *I(age^2) -0.0003892 0.0001955 -1.991 0.0465 *I((weight - 12) * (weight > 12)) -1.3547520 0.5350853 -2.532 0.0113 *
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 83.234 on 80 degrees of freedomResidual deviance: 48.687 on 76 degrees of freedomAIC: 58.687
Number of Fisher Scoring iterations: 7
model9 <- update(model8,~.-sex)
anova(model8,model9,test="Chi")
model10 <- update(model8,~.-I(age^2))
anova(model8,model10,test="Chi")
The effect of sex on infection is not quite significant (p = 0.071 for a chi-squared test on deletion), so we leave it out. The quadratic term for age does not look highly significant here (p = 0.0465), but a deletion test gives p = 0.011, so we retain it. The minimal adequate model is therefore model9:
summary(model9)
Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -3.1207552 1.2665593 -2.464 0.0137 *age 0.0765784 0.0323376 2.368 0.0179 *I(age^2) -0.0003843 0.0001846 -2.081 0.0374 *I((weight - 12) * (weight > 12)) -1.3511706 0.5134681 -2.631 0.0085 **
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 83.234 on 80 degrees of freedomResidual deviance: 51.953 on 77 degrees of freedomAIC: 59.953
Number of Fisher Scoring iterations: 7
We conclude there is a humped relationship between infection and age, and a threshold effect of weight on infection. The effect of sex is marginal, but might repay further investigation (p = 0.071).
Further Reading
- Collett, D. (1991) Modelling Binary Data, Chapman & Hall, London.
- Cox, D.R. and Snell, E.J. (1989) Analysis of Binary Data, Chapman & Hall, London.
