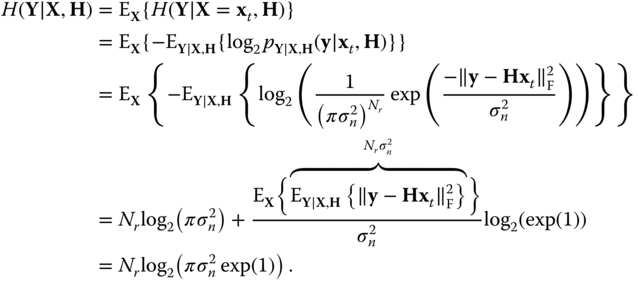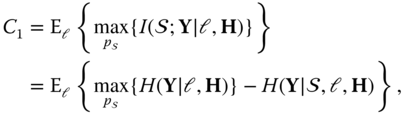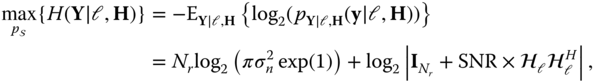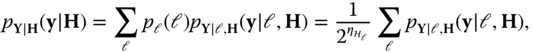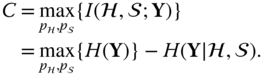Chapter 5
Information Theoretic Treatment for SMTs
Previously discussed space modulation techniques (SMTs) are novel wireless communication systems that deploy multiple transmit antennas at the transmitter and uses spatial symbols to convey additional information bits. They propose a new way to convey information between a source and destination nodes that is not trivial. One of the major elements to fully understand the capabilities of SMTs is the derivation of the capacity for such techniques. Several attempts were made in literature to derive the capacity of SMTs, and different assumptions were made to facilitate such analysis [202–206]. Most existing studies derive SMTs capacity by following conventional multiple–input multiple–output (MIMO) capacity derivation. A common assumption in literature is that SMTs have two information symbols: spatial and signal symbols. Spatial information symbols are represented by the indexes of the different transmit antennas, while signal symbols are drawn from arbitrary signal constellation diagram. However, representing the spatial symbols by the indexes of transmit antennas is not accurate. Assuming for instance that there exist multiple transmit antennas and are located at the same spatial location in space, the size of the spatial constellation diagram is one and no data can be conveyed through spatial symbols. Hence, the indexes of the transmit antennas are not the source of spatial information, and the spatial bits are encoded in the Euclidean difference between the different channel paths associated with the different transmit antennas. As such, spatial symbols should be represented by the channel vectors associated with the transmit antennas. The assumption that the indexes of the transmit antennas are the source of the spatial information led to the conclusion that SMT capacity is different for different channel statistics and can be achieved if the signal constellation follows a complex Gaussian distribution, similar to conventional spatial multiplexing (SMX) systems [25]. However, in SMT, data are transmitted by an ordinary symbol drawn from arbitrary constellation diagram and by activating a single antenna among the set of available transmit antennas. Hence, the capacity analysis for SMTs is not trivial and requires investigation beyond existing theory.
Considering the working mechanism of SMTs where two information symbols are transmitted and jointly decoded, a joint consideration of spatial and signal symbols is needed when deriving the theoretical capacity. In this chapter, information theoretic treatment of SMTs is presented and discussed. It is shown that the mutual information of SMTs approaches the capacity limit if the distribution of the signal constellation symbols multiplied by the spatial constellation symbols follows a complex Gaussian distribution. Therefore and for each channel statistics, the distribution of the signal symbols must be shaped such that the product of the channel and the symbol is complex Gaussian distribution. First attempts in this direction were foreseen in [51, 55], where capacity analysis for quadrature spatial modulation (QSM) over line‐of‐sight (LOS) and 3D‐millimeter‐wave (mmWave) channels was reported.
5.1 Evaluating the Mutual Information
5.1.1 Classical Spatial Multiplexing MIMO
To fully understand the differences between both classical MIMO systems and SMTs, the mutual information of SMX‐MIMO system is derived. In SMX‐MIMO system, there exist no spatial symbols and only signal symbols are present. Incoming data bits modulate complex signal symbols, and these symbols are the only means for conveying information. In principle, 
signal symbols are transmitted simultaneously from 
transmit antennas [25, 207–209].
By definition, the mutual information, 
, is the amount of information gained about the transmitted vector space 
when knowing the received vector space 
, and is given by
where 
denotes the entropy function.
The entropy of the received vector 
knowing 
is
where 
is the Frobenius norm, and 
is the probability distribution function (PDF) of 
given 
, and is given by
where 
is the PDF of 
given 
and 
, and is given by
The received vector 
was defined previously in Chapter 2 and is given by
where 
is the noise vector with each element 
. Hence, assuming deterministic 
and 
, 
.
From (5.2) and (5.3), the entropy of 
given 
is
The entropy of 
given 
and 
is [25]
5.1.2 SMTs
When deriving the mutual information for SMTs, the way information bits are modulated and transmitted needs to be considered. In SMX, as discussed above, all transmitted information bits are modulated in the 
‐length vector 
, which is transmitted simultaneously over the MIMO channel matrix 
. However, the communication protocol is totally different in SMTs.
For simplicity, let us first consider a space shift keying (SSK) transmitted signal over a multiple‐input single‐output (MISO) channel. In an SSK system, incoming information bits activate a transmit antenna index, 
, to transmit a constant symbol, say 
. Hence, the received signal 
is
where 
is the 
th channel element. In (5.9), the information bits are not modulated in 
. Rather, 
is the spatial symbol that conveys information bits. To explain this further, consider a single‐input single‐output (SISO)‐additive white Gaussian noise (AWGN) channel transmitting the symbol 
. Hence, the received signal is
In (5.10), the information bits are modulated in 
, and 
is just an index representing which symbol out of the available symbols is transmitted and contains no information. Now, comparing (5.10) with (5.9) clearly highlight that the incoming data bits modulate a spatial symbol 
from 
, which is done by activating only one antenna at a time. Therefore, 
is just an index that contains no information, and all information bits are modulated in the different 
vectors.
To elaborate further, let us now compare the received signals in spatial modulation (SM) and SMX for a MISO system,
where 
is an 
‐dimensional channel vector. From (5.11) and (5.12), it can be seen that, different to SMX, SM modulates information bits in the channel and in the transmitted signal, where the information bits are transmitted in the spatial and signal symbols 
and 
, respectively. Furthermore, as in SSK, 
is used as an index to differentiate between the different 
channel elements of 
and carries no information. The different 
elements of 
are the spatial symbols, 
, that carry information bits.
In summary, the information bits in SMTs are modulated in the spatial symbol, 
, and the signal symbol, 
. Therefore, the mutual information is the amount of information gained about both the spatial and signal constellation spaces 
and 
by knowing the received vector space 
, and is given by
It is important to note that there is no averaging over the channel 
in (5.13) since 
is used to convey information, where the spatial constellation space, 
, is generated from 
.
The entropy of 
is
where
where 
is the PDF of receive vector space 
given spatial and signal constellation diagrams 
and 
, respectively, and is given by
where the received vector 
, as defined in Chapter 3, is given by
Therefore, assuming deterministic 
and 
, 
.
From (5.14) and (5.15), the entropy of 
is
The entropy of 
knowing 
and 
is
Finally, substituting (5.18) and (5.19) in (5.13), the mutual information for SMTs is
Unfortunately, no closed‐form expression is available for (5.8) and (5.20), and numerical methods should be used.
5.2 Capacity Analysis
5.2.1 SMX
By definition, the capacity is the maximum number of bits that can be transmitted without any errors. Hence, the capacity for SMX is given by [116]
where
- the maximization is done over the choices of the PDF of possible transmitted vector space
, 
, - the mutual information
is given in (5.1), - and
does not depend on the distribution of 
. Therefore, the maximization is reduced to the maximization of 
.
From [3], the distribution that maximizes the entropy is the zero mean complex Gaussian distribution 
. As such, 
is maximized if 
with 
denoting the variance of 
, and 
is an 
‐length all zeros vector. From (5.5), the received vector is complex Gaussian distributed if the transmitted vector space is also a complex Gaussian distributed, 
.
Assuming complex Gaussian‐distributed transmitted vector, the PDF of 
given 
is given by
where 
denotes the determinant.
From (5.22) and by following similar steps as discussed for (5.7), the maximum entropy of 
is
Thus, by substituting (5.7) and (5.23) in (5.21), the capacity of SMX is derived as [25]
Note, 
is assumed that leads to 
.
5.2.2 SMTs
5.2.2.1 Classical SMTs Capacity Analysis
In most studies, when calculating the capacity of SMTs, the spatial information bits are assumed to be conveyed through the index of the activated transmit antennas 
and not the different 
spatial symbols. Hence, the mutual information is written as [205, 210]
where the chain rule for information is used [211], since both the spatial and signal constellation symbols are assumed to be independent. The capacity is then calculated by maximizing the mutual information in (5.25) over the choice of 
,
where it is assumed that the PDF of 
that maximizes 
would also maximize 
.
The right‐hand side of (5.26) is assumed to be the maximum mutual information between signal constellation symbols 
and the received vector 
,
where 
does not depend on the distribution of 
, and therefore, the maximization is reduced to the maximization of 
.
As discussed earlier, and from [3], the entropy is maximized by a zero mean complex Gaussian random variable (RV). Hence, the entropy 
is maximized when 
, which is achieved when 
. Hence and following the same steps as in (5.19),
where
The received vector 
knowing the transmitted signal symbol 
, the indexes of the active transmit antennas 
and the channel matrix 
, is 
. Hence and from (5.19)
Substituting (5.28) and (5.30) in (5.27) gives
The left‐hand side of (5.26) can be written as
Note, 
is assumed to be a discrete RV.
Substituting (5.31) and (5.32) in (5.26), the capacity is formulated as,
From [210], and as can be seen from (5.33), the distribution of the antenna index 
plays a major role in the capacity. Therefore, the maximization in (5.26) should have been performed over the choices of the distribution of the transmit antenna indexes as well as the signal symbols. Thus, the capacity in (5.33) is rewritten as
Because the signal constellation symbols are assumed to be continuous and the antenna indexes are discrete, obtaining closed‐form solution of (5.34) is very sophisticated [210]. Therefore, most of the existing literature attempts to calculate the capacity by assuming the distribution of the antenna indexes to be discrete uniform (DU) [203–205, 210, 212, 213].
Assuming that 
follows a DU distribution, 
, where 
is the number of bits modulated in the spatial domain. The capacity in (5.34) becomes
The PDF of 
given 
, and assuming DU distributed 
is
where 
is given in (5.29).
where
is the number of bit modulated in the signal domain.
From (5.37), and noting that 
is assumed to follow a DU distribution rather than maximizing over it, the maximum number of bits that could be transmitted in the spatial domain is capped. However, in capacity, the number of bit should increase to infinity as the signal‐to‐noise‐ratio (SNR) increases. Hence, the capacity in (5.37) is the maximum mutual information that can be transmitted assuming that DU distributed 
.
Finally, in (5.34) and (5.37), it is clear that complex Gaussian‐distributed symbols would maximize 
. However, it is not certain that such distribution would maximize 
as well. This is because 
depends on the joint distribution of both spatial and signal symbols [213]. Also, the distinction of which transmit antennas are activated depends on the Euclidean difference among channel paths from each transmit antenna to all receive antennas, and not on the indexes of the active antennas [213]. As discussed earlier, if two transmit antennas are located at the same spatial position, they will have identical channel paths and the cardinality of the spatial constellation diagram is one. Thereby, no information bits can be conveyed in the spatial domain even though two or more transmit antennas exist. Therefore, as will be shown in next section, the capacity for SMTs should be calculated by maximizing over the spatial and signal symbols instead of the antenna indexes and signal symbol [51, 55, 56].
5.2.2.2 SMTs Capacity Analysis by Maximing over Spatial and Constellation Symbols
As explained in the previous section and Section 5.1.2, the SMT capacity should be derived by maximizing the mutual information over the PDFs of the two different SMTs symbols, spatial and signal symbols. Therefore, the capacity for SMTs is defined as
where
- the mutual information
is given in (5.13), - and
does not depend on 
nor 
. Therefore, the maximization is reduced to the maximization of 
.
The received signal in (5.17) can be rewritten as
where 
is the SMT symbol. The received signal, 
, is complex Gaussian distributed if the SMT symbol, 
, also follows a complex Gaussian distribution, i.e., 
.
Assuming that the transmitted SMT symbol is complex Gaussian distributed, the PDF of the received vector space, 
, is
From (5.41), and following the same steps as discussed for (5.19), the maximum entropy of 
is
Hence, and using (5.19), the capacity of SMT in (5.39) can be derived as
Comparing the existing SMT capacity in (5.34), and SMX capacity in (5.24), to SMTs capacity in (5.43), the following can be observed:
- Similar to SMX and classical SMT analysis, the capacity equation does not depend on the constellation symbols.
- In the derived SMTs capacity in (5.43), the channel is a mean to convey information and the capacity does not depend on the channel. Therefore, there is no averaging over the channel.
In summary, SMTs have only one single theoretical capacity formula regardless of the considered fading channel. Such capacity is achievable if the SMT symbol 
is complex Gaussian distributed. However, for any particular channel, proper shaping of the constellation symbols is needed to achieve the theoretical capacity.
Figure 5.1 Comparison between the derived capacity in (5.43) and the MIMO capacity (5.24) over Rayleigh, Rician 
dB, and Nakagami‐
fading channel, for 
.
To illustrate this, the derived capacity in (5.43) is compared to the MIMO capacity formula in [202–206], which is given in (5.24) for 
, and the results are depicted in Figure 5.1. In [202–206], SMTs capacity is different for different techniques and antithetic channel statistics. Yet, it is shown in [51, 55] and as discussed in this chapter that single capacity formula is derived for all SMTs and for any channel statistics. It is evident from the figure that the expected anticipated classical SMTs capacity falls far below the true capacity for such techniques. It is shown in Figure 5.1 that SMTs can actually achieve 8.47, 19, and 25.6 bits more than the classical capacity for Rayleigh, Nakagami‐
, and Nakagami‐
channels, respectively.
Such capacity is attainable, as discussed previously, if 
. Thus,
- using the product distribution theory [214];
- assuming
for simplicity and without losing generality; - knowing that a zero mean complex normal RV,
, has a Rayleigh distribution amplitude, uniformly distribution phase, and a joint PDF given by
(5.44)
the distribution of the used signal constellation symbols has to be shaped depending on the distribution of the channel so that it solves
In the following section, illustrative examples for SSK and SM systems are presented to highlight how the theoretical channel capacity can be achieved.
5.3 Achieving SMTs Capacity
5.3.1 SSK
In SSK systems, only spatial constellation symbols exist and no signal symbols are transmitted, i.e. 
. Therefore, the capacity is achieved when each element of 
follows 
. Hence, SSK can achieve the capacity when the channel follows a Rayleigh distribution. However, the spatial symbol diagram 
of an SSK system over Rayleigh fading channel does not always follow a complex Gaussian distribution. In a small‐scale SSK system (i.e. assuming small number of transmit antennas), 
at each time instant is actually uniformly distributed. However and for large‐scale SSK, the elements of 
are complex Gaussian distributed. Therefore, it is anticipated that SSK system will achieve the capacity when deploying large‐scale MIMO configuration over Rayleigh fading channel. To further explain this, the histograms for the real parts of the spatial constellation diagram, 
, for an SSK system over Rayleigh fading channel, with 
and 
are compared to the PDF of a Gaussian distribution in Figure 5.2. It is shown in the figure that 
is uniformly distributed for a small number of transmit antennas, 
; whereas, it follows a Gaussian distribution for large number of transmit antennas, 
. This is because at each time instance, 4 unique possible symbols exist for 
and they are chosen equally probable. Therefore, 
follows a uniform distribution. However, for 
, there are 512 spatial symbols that are not necessarily unique, i.e. symbols would repeat and occur more than others following a Gaussian distribution. As such, for large number of transmit antennas even though the spatial symbols are chosen equally likely, the chosen symbol is not unique in the set of spatial symbols 
, and probability it occurs follows a Gaussian distribution.
Figure 5.2 Histogram of the real part of the spatial constellation diagram, 
, for SSK with 
and 
compared to the PDF of the Gaussian distribution.
Figure 5.3 The capacity of SMTs compared to simulated mutual information of SSK over Rayleigh fading channel for 
and 
.
Figure 5.4 The capacity of SMT compared to simulated mutual information of SSK over Rayleigh, Rician with 
dB, and Nakagami‐
, where 
and 
.
The mutual information performance of SSK system over Rayleigh fading channel for variable number of transmit antennas from 
with multiple of 2 step size are depicted in Figure 5.3. The derived theoretical capacity in (5.43) for SMTs is depicted as well. In all results, 
is assumed. It can be seen from the figure that for a small number of transmit antennas, SSK mutual information, are far below the capacity. However, as the number of antennas increases, the gap between the mutual information curves and the capacity curve dilutes. For instance, with 
and 
, an SSK is shown to follow the capacity up to 6 bits per channel use, before it starts to deviate and floor at 10 bits and 11 bits, respectively, which is the maximum number of bits that can be transmitted by SSK system using 1024 and 2048 transmit antennas, respectively. However, using 
, the mutual information curve follows the capacity for up to 0.5 bits before it starts to deviate and floor. The reason for this is discussed before, where SSK system is shown to achieve the capacity if 
, which is approximately attainable for large number of transmit antennas over Rayleigh fading channel.
The mutual information results for SSK systems over different channel distributions including Rayleigh, Rician with 
dB, and Nakagami‐
for 
and 
are shown in Figure 5.4. Again and as discussed before, 
if 
was large enough and the channel follows a Rayleigh distribution. Furthermore, in Figure 5.4, the mutual information of SSK system over Rician and Nakagami‐
fading channels are, respectively, 6 and 9.4 dB worse than that of the Rayleigh fading channel. Moreover, SSK over Rayleigh fading channel reaches the maximum mutual information of 
bits 8 dB earlier than Rician and Nakagami‐
fading channels. Hence, for an SSK system to achieve the capacity, a large number of transmit antennas are needed along with Rayleigh fading channel.
5.3.2 SM
Considering a transmission of an SM signal over Rayleigh fading channel gives
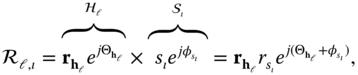
where 
and 
are the amplitude and the phase of 
, respectively, and 
and 
are the amplitude and the phase of 
, respectively. Now,
- A complex Gaussian distribution random variable has a Rayleigh distributed amplitude and uniform distributed phase.
- Rayleigh fading channel has Rayleigh distributed amplitude and uniform distributed phase.
Hence, for 
, the amplitude and phase of 
should be 
and 
, i.e. the constellation symbols have to follow a circular uniform (CU) distribution. Incoming data bits are usually assumed to be uniformly distributed. Therefore, different to any other distribution, CU signal constellation symbols can be realizable. For instance, phase shift keying (PSK) are distributed according to discrete CU distribution. Hence, CU distribution can be approximated by a PSK signal constellation diagram. The larger the size of the used PSK modulation, the closer the approximation to CU. This means that SM performance over Rayleigh fading channels can be enhanced by transmitting more bits in the signal domain.
Figure 5.5 shows the histogram of the phase of a randomly generated symbols modulated using 
and 128 size PSK modulation, and the PDF of 
. From the figure, it can be seen that as the size of the considered PSK modulation increases, the phase distribution of the generated symbols gets closer to 
, where for 
it is discrete uniform distributed 
. Hence, CU distributed symbols can be simply achieved by using large size PSK constellation diagram.
Figure 5.5 Histogram of the phase of a randomly generated symbols modulated using 
‐,16‐, and 
‐size PSK modulation compared to the uniform distribution.
Figure 5.6 PDF of 
plotted against histogram of 
using 
‐PSK modulation over MISO Rayleigh fading channel with 
.
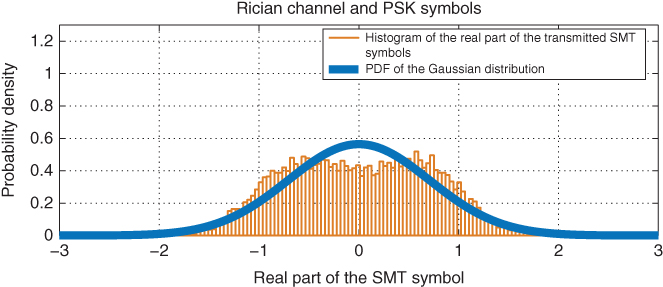
Figure 5.7 PDF of 
plotted against histogram of 
using 
‐PSK modulation over MISO Rician fading channel with 
dB and 
.
Figures 5.6–5.9 show the PDF of 
plotted against the histogram of the real part of the resultant transmitted SM symbol 
, respectively, over MISO Rayleigh and Rician (
dB) fading channels with 
. In Figures 5.6 and 5.7, 128‐PSK constellation diagram is considered. Whereas, in Figures 5.8 and 5.9, 128‐Gaussian‐distributed symbols are assumed to form the signal constellation diagram. Figures 5.8 and 5.9 show that Gaussian‐distributed symbols will not lead to 
being a complex Gaussian distribution. Though, considering PSK as illustrated in Figure 5.6, the distribution of 
is shown to accurately follow a complex Gaussian distribution. Therefore, SM is anticipated to achieve the capacity when implemented on a large‐scale MIMO system and using CU distributed symbols over Rayleigh fading channels. However and for non‐Rayleigh fading channels, CU distribution will not lead to 
being a complex Gaussian distribution as shown in Figure 5.7. Hence and for each channel type, the used constellation symbols need to be shaped such that they solve (5.45).
Figure 5.8 PDF of 
plotted against histogram of 
using 
complex Gaussian‐distributed symbols over MISO Rayleigh fading channel with 
.
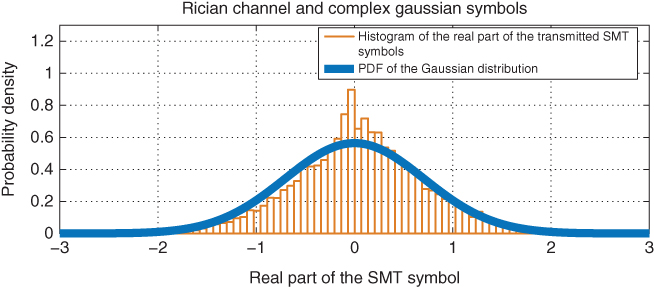
Figure 5.9 PDF of 
plotted against histogram of 
using 
complex Gaussian‐distributed symbols over MISO Rician fading channel with 
dB and 
.
Figure 5.10 The capacity of SMT compared to the simulated mutual information of SM using PSK constellations, and Gaussian‐distributed constellations, over Rayleigh fading channel, where 
, 
, and 
.
An example for the previous discussion is shown in Figure 5.10, where the mutual information performance for SM system over Rayleigh fading channels assuming large‐scale MIMO configuration with 
, 
and with 1024‐PSK constellation diagram and Gaussian‐distributed signal constellation are depicted. The theoretical capacity in (5.43) is shown in the figure as well. The results show that CU distribution, which is obtainable through 1024‐PSK constellation diagram, is required to achieve the theoretical capacity limit. This contradicts conventional theory for MIMO system where complex Gaussian‐distribution symbols are needed to achieve the capacity. As illustrated in Figure 5.10, Gaussian‐distributed signal constellation symbols, even though not practically possible to generate, perform 1 bit less than that of CU distribution symbols. These results highlight that SM systems can achieve the capacity with large number of transmit antennas and large PSK constellation size.
It should be also noted that the deviation from the theoretical capacity curve at high SNR is mainly due to the limited number of spatial and signal symbols. For mutual information curves to follow the capacity curve over the entire SNR range, continuous distributions with infinite number of symbols are required, which is not attainable.
5.4 Information Theoretic Analysis in the Presence of Channel Estimation Errors
5.4.1 Evaluating the Mutual Information
5.4.1.1 Classical Spatial Multiplexing MIMO
The mutual information for SMX in the presence of channel estimation errors (CSE) can be written as [152]
where 
is the estimated channel and is related to the perfect channel by
where 
is an 
channel estimation error matrix, assumed to follow a complex Gaussian distribution with zero mean and variance 
, 
, with 
being a parameter that captures the quality of the channel estimation as discussed in previous chapters. Assuming, for instance, least square (LS) channel estimation algorithm at the receiver, 
[192].
The entropy of 
given the estimated channel 
, is written as
where 
is the PDF of 
, knowing 
. Plugging (5.48) in (5.5) then gives
Knowing that 
, the PDF of 
and 
knowing 
is
and consequently
where 
it the PDF of 
.
Plugging (5.52)in (5.49) gives
The entropy of 
, knowing 
, and the estimated channel, 
, is
where the same steps as in (5.7) were followed, and 
is given in (5.51).
Finally, from (5.49), (5.54), and (5.47),
Comparing the mutual information of SMX in the presence of CSE in (5.55) to that with no CSE in (5.8), it can be seen that CSE can be thought of as an additional noise term with a power proportional to the power of the transmitted signal. The mutual information with no CSE in (5.8) can be easily deduced from (5.55) by setting 
.
5.4.1.2 SMTs
In the previous section, the presence of channel estimation errors were shown to degrade the performance of typical MIMO systems. It is also anticipated that CSE will have similar impact on SMTs as it impacts both transmitted symbols. However and in SMTs, CSE will cause a mismatch in the considered spatial constellation diagram at the receiver. It is like using quadrature amplitude modulation (QAM) constellation diagram at the transmitter while considering PSK at the receiver. Therefore, for SMTs in the presence of CSE at the receiver, the spatial constellation diagram, 
, is different than 
, where 
is generated from the estimated channel 
instead of 
. Now, assume that the 
th spatial symbol, 
, is transmitted, and the receiver decodes 
, there will be no errors as the same spatial symbol is decoded. As such and even though the received spatial symbol is not identical to the transmitted spatial symbol, 
, it still carries the same information about the transmitted spatial symbol. Therefore, the mutual information for SMTs in the presence of CSE is formulated as
The right‐hand side of (5.56) gives
where 
is the PDF of the received vector 
, and is given by
where 
is the PDF of spatial symbols 
and
Note, by plugging (5.48) in (5.17), the received vector can be written as
where 
is a subset of 
generated depending on the used SMT, in the same way, 
is generated. Note, both 
and 
are complex Gaussian RVs with zero‐mean and 
and 
variances, respectively.
Plugging (5.58) in (5.57) leads to
The entropy of 
, given the spatial and signal constellation diagrams, 
and 
, is given by
where 
is given in (5.59).
Finally, from (5.61), (5.62), and (5.56), the mutual information of SMTs in the presence of CSE is given by
Comparing the mutual information of SMTs in the presence of CSE (5.63) to that with no CSE in (5.20) and to the mutual information of SMX in the presence of CSE in (5.55), the CSE in SMTs not only affect the SNR, where the noise increases by a power proportional to the power of the transmitted signal symbol, 
, but it also impacts the spatial constellation symbols. As explained earlier, in the presence of CSE, the spatial constellations search space is generated from the estimated channel, 
, and not the perfect channel, 
. Yet, if the correct 
th spatial symbol is chosen, there will be no error.
5.4.2 Capacity Analysis
5.4.2.1 Spatial Multiplexing MIMO
The capacity of SMX in the presence of CSE is calculated by maximizing the mutual information in (5.47),
where
- the maximization is done over the choices of the PDF of possible transmitted vector
, 
, - and
does not depend on 
. Therefore, the maximization is reduced to the maximization of 
.
From [3], and as discussed in previous sections, the distribution that maximizes the entropy is the zero mean complex Gaussian distribution. As such, 
is maximized if 
. Thus
where 
, and 
, 
are assumed.
Following the same steps as in (5.7)
Plugging (5.66) and (5.54) in (5.64) gives [152]
Comparing the capacity of SMX in the presence of CSE (5.67) to that with no CSE in (5.24), it can be seen that (5.24) can be easily deduced from (5.67) by setting 
. Furthermore, SMX capacity in the presence of CSE depends on the power of the transmitted vector, and it is distribution where as can be seen there is an averaging over 
in the left side of (5.67).
Finally, from (5.50), and knowing that the noise vector 
, the received vector follows complex Gaussian distribution, if the summation 
is complex Gaussian distributed. Consequently, 
and 
each has to be complex Gaussian distributed, where the sum of two complex Gaussian distributions is complex Gaussian distributed. However, this is not possible, since 
is assumed to be deterministic. Hence, the transmitted vector 
is complex Gaussian distributed, if 
follows a complex Gaussian distribution. However, 
is a complex Gaussian distribution RV and if 
follows a complex Gaussian distribution, 
cannot be a complex Gaussian‐distributed RV. This is because the multiplication of two complex Gaussian RVs is not a complex Gaussian RV. Thereby, the capacity for SMX in the presence of CSE cannot be achieved. Furthermore, the distribution of transmitted symbols that maximize (5.66) is needed to calculate the left‐hand side of (5.67). However, and from the previous discussion, there is no distribution that maximizes (5.66). Thus, the capacity in (5.67) besides not achievable, it cannot be calculated.
Assuming that the CSE noise variance is proportional with the channel noise, 
, [192, 215], the capacity of SMX in the presence of CSE in (5.67) can be lower bounded by [152]
The lower bound capacity in (5.68) can be achieved at high SNR by using maximum‐likelihood (ML) receiver and complex Gaussian‐distributed symbols, which are the requirements to achieve capacity neglecting CSE.
Figure 5.11 The lower capacity of SMX in the presence of CSE compared to the simulated mutual information of SMX in the presence of CSE over MISO Rayleigh fading channels, 
complex Gaussian distributed symbols, 
and 
.
Figure 5.11 compares the lower capacity bound in (5.68) to the simulated mutual information of SMX in the presence of CSE over a MISO Rayleigh fading channels, with 
bits, 1024 complex Gaussian‐distributed symbols, and 
. It can be seen that simulated mutual information follows 
until 18 bits, where the simulated mutual information saturates at 20 bits. The saturation is because a complex Gaussian random variable has an infinite number of values, but in this example, only 1024 symbols are used. At low SNR, both 
and 
are dominant in (5.50) as they have larger power than 
, and therefore, the received vector is not complex Gaussian distribution. Note, as discussed earlier with 
and 
being complex Gaussian distributed their multiplication is not complex Gaussian distributed. Therefore, at low SNR, 
is a lower bound. In Figure 5.11, 
is 0.16 bits lower than the simulated mutual information. As the SNR increases, both 
and 
decrease, and the complex Gaussian‐distributed transmitted vector becomes dominant. Consequently, the received vector becomes complex Gaussian distributed. In Figure 5.11 at high SNR, the simulated mutual information closely follow 
.
5.4.2.2 SMTs
The capacity is derived by maximizing the mutual information in (5.56) as
where 
does not depend on 
and 
, and therefore, the maximization was reduced to 
. Moreover, as discussed in Section 5.1.2, there is no averaging over the channel as the channel is used as a way to convey information.
As discussed in Section 5.2.2.2, the entropy 
is maximized when 
. Hence
where 
, 
, and 
is assumed.
Plugging (5.70) and (5.62) in (5.69), the capacity of SMTs in the presence of CSE is
As in the case of perfect channel knowledge at the receiver side, the capacity of SMTs in the presence of CSE is a single theoretical equation that does not depend on the fading channel. However, in the presence of CSE, the capacity of SMT depends on the distribution of the signal constellation symbols.
As 
is complex Gaussian distributed, 
is complex Gaussian distributed, and the capacity in (5.71) is achievable if
This can be achieved by tailoring the signal constellation symbols for each fading channel, such that the PDF of the tailored signal constellation symbols, assuming for simplicity and without loss of generality 
, solves
where 
is the PDF of the summation of the two RVs 
and 
,
and 
is the PDF of the CSE noise, 
, which is assumed to be complex Gaussian distributed. Note, the PDF of the sum of two RVs is given by the convolution of the PDFs of the two RVs [214].
Substituting (5.74) in (5.73) gives
Different to SMX, SMTs can achieve capacity in the presence of CSE as long as the used constellation diagram solves (5.75). Note, the distribution of the constellation diagram that solves (5.75) is the one to use to calculate the capacity in (5.71). In the following section, examples of how to achieve capacity for SSK and SM in the presence of CSE are given.
5.4.3 Achieving SMTs Capacity
5.4.3.1 SSK
SSK does not have signal symbols, 
. Therefore, to achieve the capacity, 
. Note, the sum of two independent complex normal distributed RVs is also a complex normal distributed RV [214]. Hence and in the presence of complex Gaussian distributed CSE noise, SSK can achieve the capacity only when the channel is a large‐scale Rayleigh fading channel. The mutual information performance of SSK system over Rayleigh fading channel for different number of transmit antennas, 
, and 
is depicted in Figure 5.12. The derived theoretical capacity curve in (5.71) for SMTs is depicted as well. In all results, 
is assumed.
From Figure 5.12, it can be seen that the larger the number of transmit antennas, the closer the mutual information to the theoretical capacity curve. For 
, the mutual information for SSK over Rayleigh fading channel and in the presence CSE is shown to follow the capacity very closely up to 5 bits. After 5 bits, the mutual information deviates because the number of transmit antennas is finite, whereas a Rayleigh distributed RV continues with an infinite number of values, or in this case infinite number of transmit antennas.
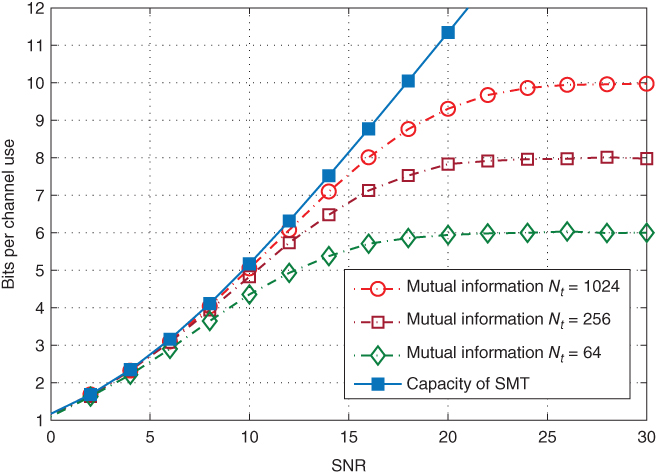
Figure 5.12 The capacity of SMTs compared to simulated mutual information of SSK over Rayleigh fading channel in the presence of CSE for 
, and 
, and 
.
5.4.3.2 SM
Following similar discussion as in the previous section and Section 5.3.2, SM would achieve the capacity if large signal and spatial constellation symbols are considered over Rayleigh fading channels while using PSK constellation diagram.
Figure 5.13 The capacity of SMT compared to the simulated mutual information of SM using PSK constellations, and Gaussian‐distributed constellations, over Rayleigh fading channel in the presence of CSE, where 
, 
, and 
.
An example is shown in Figure 5.13, where the mutual information performance for SM system over Rayleigh fading channels in the presence of CSE for large‐scale MIMO with 
, 
and with 32‐PSK constellation diagram and Gaussian‐distributed signal constellation are depicted. The theoretical capacity in (5.71) is shown in the figure as well. The results show that CU distribution, which is obtainable through 32‐PSK constellation diagram, is required to achieve the theoretical capacity limit. This again contradicts the belief that complex Gaussian‐distributed symbols are needed to achieve the SMTs capacity. It is illustrated in Figure 5.13 that using Gaussian‐distributed signal constellation symbols, even though not practically possible to generate, perform 0.5 bit less than that of CU distribution symbols at low SNR and 0.8 bit less at high SNR. These results highlight that SM systems can achieve the capacity in the presence of CSE with large number of transmit antennas and large PSK constellation diagram.
Furthermore, and from Figure 5.13, it can be seen that SM using PSK follows the theoretical capacity curve up to 4.7 bits at SNR
dB. Beyond that value, it started to slowly deviate mainly due to the limiting number of spatial and signal symbols as discussed before. To achieve the capacity for the entire range of SNR, continuous distributions with infinite number of symbols are required, which is not attainable.
Finally, from Figures 5.12 and 5.13, and comparing SMT to SMX, different to SMX, SMT can achieve the capacity in the presence of CSE. Furthermore, SMT capacity in the presence of CSE can be achieved easily by
- increasing the number of transmit antennas, which as explained in Chapter 3 comes at a very small cost, where SMTs need only one radio frequency (RF)‐chain;
- and in the case of SM by using CU distributed signal symbols, which are easily obtained by using PSK, as for other SMT systems by using constellation symbols with a distribution that solves (5.75).
5.5 Mutual Information Performance Comparison
A mutual information performance comparison between SM, QSM, and SMX is presented in Figures 5.14 and 5.15 for Rayleigh and Nakagami‐
fading channels, respectively, with 
and 
and 
. Moreover, the theoretical capacity of SMT is depicted for reference. It can be seen that SM offers 0.7 bit performance gain for 
. However, for larger spectral spectral efficiency, 
, SMX outperforms SM by about 1.2 bits and performs 0.6 bits better than QSM. The better performance of SMX can be attributed to the use of smaller signal constellation diagram in comparison with SM and QSM, 93.75% and 75% smaller constellation size, respectively. The same can be seen for QSM and SM, where QSM offers 0.5 bit better performance than SM, as QSM modulates more information bits in the spatial domain than SM, it requires smaller signal constellation diagram.
Figure 5.14 The capacity of SMT compared to the simulated mutual information of SM, QSM, and SMX over Rayleigh fading channels for different spectral efficiency, where 
and 
and 
.
In Figure 5.15 for Nakagami‐
fading channel, different to Rayleigh fading channels, SM is shown to offer nearly the same performance as SMX for 
where 0.3 bit difference is noticed at low SNR but diminishes as SNR increases. Also, SM is shown to outperform QSM by 0.75 bit. Though, for Rayleigh fading channels and for 
as shown in Figure 5.14, SM demonstrates better performance than SMX by about 0.3 bit.
It is also important to note that SM and QSM mutual information curves are far below the theoretical capacity limit for such systems, nearly 4 and 4.7 bits degradation can be observed for Rayleigh and Nakagami‐
channels, respectively, in Figures 5.14 and 5.15. Enhancing their performance and diminishing this gap can be achieved through proper design of the signal constellation diagram for each channel statistics as discussed earlier.
Figure 5.15 The capacity of SMT compared to the simulated mutual information of SM, QSM, and SMX over Nakagami‐
fading channels for different spectral efficiencies, where 
and 
and 
.
The capacity of SMT is compared to the simulated mutual information of SM, QSM, and SMX in the presence of CSE with 
in Figure 5.16, where 
and 
and 
. Again for small spectral efficiency, SM performs 0.25 bit better performance than SMX. However, for larger spectral efficiency, SMX offers 1 bit better performance than SM and 0.5 bit better than QSM and reaches maximum mutual information 6 dB earlier than SM and QSM. Yet, in Figure 5.16, SM is performing 3.8 bits less than the maximum SMT capacity, as the used signal constellation diagram is not tailored for SM with 
. Therefore, it is anticipated that SM and QSM would offer better performance than SMX if their signal constellations diagrams are designed for SM and QSM with 
in accordance with (5.75). Finally, because QSM modulates more bits in the spatial domain than SM, in Figure 5.16, QSM offers 0.6 bit better performance than SM.
Figure 5.16 The capacity of SMT compared to the simulated mutual information of SM, QSM, and SMX over Rayleigh fading channels in the presence of CSE with 
for different spectral efficiencies, where 
and 
and 
.