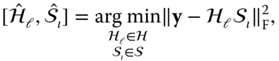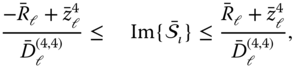Chapter 3
Space Modulation Transmission and Reception Techniques
In this chapter, the different space modulation techniques (SMTs) available in literature will be discussed. These include space shift keying (SSK) [89], generalized space shift keying (GSSK) [69], spatial modulation (SM) [37], generalized spatial modulation (GSM) [67], quadrature space shift keying (QSSK) [65], quadrature spatial modulation (QSM) [65], generalized quadrature space shift keying (GQSSK), generalized quadrature spatial modulation (GQSM) and the advanced SMTs including differential space shift keying (DSSK), differential spatial modulation (DSM) [63], differential quadrature spatial modulation (DQSM) [153], space–time shift keying (STSK) [78], and trellis coded spatial modulation (TCSM) [154] systems.
SMTs are unique multiple‐input multiple‐output (MIMO) transmission schemes that utilize the differences among different channel paths to convey additional information bits. In such systems, one or more of the available transmit antennas at the transmitter are activated at one particular time instant and all other antennas are turned off. The channel path from each transmit antenna to all receive antennas denotes a spatial constellation symbol denoted by ![]() or
or ![]() in this book, where
in this book, where ![]() denotes the spatial constellation diagram generated for the
denotes the spatial constellation diagram generated for the ![]() channel matrix
channel matrix ![]() , and
, and ![]() and
and ![]() are the number of transmit and receive antennas, respectively. At each time instance, the active transmit antennas transmit a modulated or unmodulated radio frequency (RF) signal. A common advantage for such systems is the ability to design MIMO transmitters with single RF‐chain, which promises implementation cost reduction, low computational complexity, and high‐energy efficiency. This is unlike conventional MIMO systems, such as spatial multiplexing (SMX), where each transmit antenna is driven by one RF‐chain, and independent data streams are transmitted from the available antennas. In such MIMO systems, the Euclidean difference among different channel vectors is utilized to transmit cochannel signals to increase the data rate. However, all antennas must be active, and the receiver needs to resolve the cochannel interference (CCI) to correctly estimate the transmitted data.
are the number of transmit and receive antennas, respectively. At each time instance, the active transmit antennas transmit a modulated or unmodulated radio frequency (RF) signal. A common advantage for such systems is the ability to design MIMO transmitters with single RF‐chain, which promises implementation cost reduction, low computational complexity, and high‐energy efficiency. This is unlike conventional MIMO systems, such as spatial multiplexing (SMX), where each transmit antenna is driven by one RF‐chain, and independent data streams are transmitted from the available antennas. In such MIMO systems, the Euclidean difference among different channel vectors is utilized to transmit cochannel signals to increase the data rate. However, all antennas must be active, and the receiver needs to resolve the cochannel interference (CCI) to correctly estimate the transmitted data.
In SMTs, the transmitted data are either modulated by a complex signal symbol, ![]() , drawn from an arbitrary constellation diagram,
, drawn from an arbitrary constellation diagram, ![]() , such as quadrature amplitude modulation (QAM), or phase shift keying (PSK), or unmodulated RF signals. Hence, the received signal at the input of the receive antennas is given by
, such as quadrature amplitude modulation (QAM), or phase shift keying (PSK), or unmodulated RF signals. Hence, the received signal at the input of the receive antennas is given by
where ![]() is the
is the ![]() ‐length transmitted vector,
‐length transmitted vector, ![]() is an
is an ![]() ‐dimensional additive white Gaussian noise (AWGN) with zero mean and covariance matrix of
‐dimensional additive white Gaussian noise (AWGN) with zero mean and covariance matrix of ![]() . As such, the signal‐to‐noise ratio (SNR) at the receiver input, assuming normalized channel
. As such, the signal‐to‐noise ratio (SNR) at the receiver input, assuming normalized channel ![]() , is given by
, is given by ![]() .
.
The received signal is then processed by a maximum‐likelihood (ML) decoder to jointly estimate the spatial symbol, ![]() , and the signal symbol,
, and the signal symbol, ![]() , as
, as
where ![]() is the Frobenius norm. The estimated spatial and constellation symbols are then used to retrieve transmitted data bits by inversing the mapping procedure considered at the transmitter.
is the Frobenius norm. The estimated spatial and constellation symbols are then used to retrieve transmitted data bits by inversing the mapping procedure considered at the transmitter.
3.1 Space Shift Keying (SSK)
SSK is the simplest form of the family of SMTs [89] even though it was proposed after SM [37]. In the SSK system, the data are transmitted through spatial symbols only, and the transmitted signal is unmodulated RF signal considered to indicate the spatial index of the active transmit antenna. At each time instant, ![]() bits modulate a transmit antenna with an index,
bits modulate a transmit antenna with an index, ![]() , among the set of existing
, among the set of existing ![]() transmit antennas. Only that particular antenna is active and transmits a fixed unmodulated RF signal. In Figure 3.1, the cosine part of the RF carrier,
transmit antennas. Only that particular antenna is active and transmits a fixed unmodulated RF signal. In Figure 3.1, the cosine part of the RF carrier, ![]() , is considered and any other fixed signal can be utilized. Therefore, SSK scheme requires no RF‐chain at the transmitter, and the transmitter can be entirely designed through RF switches [40]. Since no information is modulated on the carrier signal, it can be generated once and stored for further use in all other transmissions. An RF digital to analog converter (DAC) with an internal memory [155] can be utilized to store the RF signal and continuously transmits it at each symbol time. However, the RF DAC board generally produces low output power, and power amplifier (PA) will be needed to boost the signal output power before transmitted by the antennas.
, is considered and any other fixed signal can be utilized. Therefore, SSK scheme requires no RF‐chain at the transmitter, and the transmitter can be entirely designed through RF switches [40]. Since no information is modulated on the carrier signal, it can be generated once and stored for further use in all other transmissions. An RF digital to analog converter (DAC) with an internal memory [155] can be utilized to store the RF signal and continuously transmits it at each symbol time. However, the RF DAC board generally produces low output power, and power amplifier (PA) will be needed to boost the signal output power before transmitted by the antennas.

Figure 3.1 SSK system model with single RF‐chain and with  transmit and
transmit and  receive antennas.
receive antennas.
As such, SSK transmitter is an RF switch with single input and ![]() RF outputs. The incoming
RF outputs. The incoming ![]() bits control the RF switch and determine the active port at each particular time instant. An illustration of the spatial symbols and the mapping table for
bits control the RF switch and determine the active port at each particular time instant. An illustration of the spatial symbols and the mapping table for ![]() is shown in Figure 3.2. Such RF switches are generally very cheap and cost roughly around 1–3 US$. The RF switching time including the rise and fall times of a pulse,
is shown in Figure 3.2. Such RF switches are generally very cheap and cost roughly around 1–3 US$. The RF switching time including the rise and fall times of a pulse, ![]() , plays a major role in determining the maximum data rate of the SSK scheme. The maximum data rate that can be transmitted in SSK scheme is given by
, plays a major role in determining the maximum data rate of the SSK scheme. The maximum data rate that can be transmitted in SSK scheme is given by
Hence, a slow switching time degrades the spectral efficiency of SSK scheme, whereas a fast switching time achieves increased data rates. A study in [156] investigated the impact of RF switches on the achievable data rate of SM system. Different RF switches are available commercially with various switching times ranging from about 20 ns to a few microseconds. It should also be noted that there exists several RF switches that can support a different number of transmit antennas; ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , and can be obtained easily with very low cost [157, 158]. However, the switching time depends on the transistor technology and number of output ports and generally increases with increasing the number of output ports for the same technology. In some cases, like the 16 output switch, the decoder bit information has to be fed through a serial communication protocol such as serial peripheral interface (SPI). Therefore, the time overhead introduced by SPI has to be added to the RF switching time [40].
, and can be obtained easily with very low cost [157, 158]. However, the switching time depends on the transistor technology and number of output ports and generally increases with increasing the number of output ports for the same technology. In some cases, like the 16 output switch, the decoder bit information has to be fed through a serial communication protocol such as serial peripheral interface (SPI). Therefore, the time overhead introduced by SPI has to be added to the RF switching time [40].

Figure 3.2 An example of SSK constellation diagram with the mapping table for  .
.
To demonstrate the working mechanism of SSK‐MIMO system, an example is discussed in what follows. Assume that the incoming data bits ![]() bits are to be transmitted at one time instant from
bits are to be transmitted at one time instant from ![]() transmit antennas. Considering the mapping table in Figure 3.2, the incoming bits,
transmit antennas. Considering the mapping table in Figure 3.2, the incoming bits, ![]() , activate the fourth transmit antenna,
, activate the fourth transmit antenna, ![]() , and transmit the carrier signal through the RF switch. Therefore, the transmitted RF signal vector is given by
, and transmit the carrier signal through the RF switch. Therefore, the transmitted RF signal vector is given by
Hence,
- there is no constellation symbol,
 ;
; - all incoming data bits are modulated in the spatial domain, where the spatial constellation diagram is
 , and
, and  is the
is the 
 ‐length column of
‐length column of  .
.
3.2 Generalized Space Shift Keying (GSSK)
GSSK [69] generalizes the SSK scheme by activating more than one transmit antenna at the same time. The activated antennas transmit the same data symbol and the transmitted energy is divided among them. Hence, the spatial and signal constellations diagrams for GSSK are as follows:
- The spatial diagram is
(3.5)where

 is the
is the  combination of active antennas in the space .
combination of active antennas in the space . - The cardinality of the signal constellation diagram is one,
 . That is similar to SSK scheme, where data are conveyed solely through spatial symbols.
. That is similar to SSK scheme, where data are conveyed solely through spatial symbols.
One of the major advantages of such generalization is that it allows for an arbitrary number of transmit antennas. It is important to note that SSK scheme can work only for ![]() being a power of two integers. In GSSK, however, any number of transmit antennas can be considered.
being a power of two integers. In GSSK, however, any number of transmit antennas can be considered.
A system model for GSSK scheme with ![]() antennas and arbitrary
antennas and arbitrary ![]() receive antennas is depicted in Figure 3.3. The system model is similar to SSK with the only difference in the RF switch part. In GSSK scheme considering the mapping table shown in Figure 3.3, two RF switches are needed. The first switch with two outputs selects an antenna based on the most significant bit,
receive antennas is depicted in Figure 3.3. The system model is similar to SSK with the only difference in the RF switch part. In GSSK scheme considering the mapping table shown in Figure 3.3, two RF switches are needed. The first switch with two outputs selects an antenna based on the most significant bit, ![]() . The other switch with four outputs selects an antenna based on the other bits,
. The other switch with four outputs selects an antenna based on the other bits, ![]() and
and ![]() . As such, two transmit antennas are activated at one time instant in the considered example. In general,
. As such, two transmit antennas are activated at one time instant in the considered example. In general, ![]() antennas among the available
antennas among the available ![]() antennas can be activated, and the system model can be designed based on the mapping table. In principle, an RF switch with
antennas can be activated, and the system model can be designed based on the mapping table. In principle, an RF switch with ![]() outputs can be considered or multiple RF switches can be used to support the selections from the mapping table.
outputs can be considered or multiple RF switches can be used to support the selections from the mapping table.

Figure 3.3 GSSK system model with single RF‐chain and with  transmit and
transmit and  receive antennas.
receive antennas.
The number of data bits that can be transmitted at any particular time instant for GSSK is given by ![]() bits. Please note that for
bits. Please note that for ![]() bits, as the example considered in Figure 3.3,
bits, as the example considered in Figure 3.3, ![]() and
and ![]() can support such spectral efficiency as illustrated in the mapping table shown in Figure 3.4. However, such mapping table requires sophisticated RF switching circuits that can be simplified by considering
can support such spectral efficiency as illustrated in the mapping table shown in Figure 3.4. However, such mapping table requires sophisticated RF switching circuits that can be simplified by considering ![]() antennas instead of
antennas instead of ![]() , as shown in Figure 3.3.
, as shown in Figure 3.3.

Figure 3.4 An example of GSSK constellation diagram with the mapping table for  and
and  .
.
As multiple antennas transmit at the same time instant, transmit antenna synchronization is required. This is a drawback for GSSK where it increases the hardware complexity of the transmitter. Such synchronization is not required for SSK scheme since only one antenna is active at a time. Again, the unmodulated RF signal is generated once and stored in an RF DAC memory to be used regularly. The output from the RF memory is splitted through an RF splitter with ![]() outputs. The splitter can be thought of as a power divider of the input signal by the number of output ports of the RF splitter. The splitter outputs are then transmitted from
outputs. The splitter can be thought of as a power divider of the input signal by the number of output ports of the RF splitter. The splitter outputs are then transmitted from ![]() antennas determined by the RF switches.
antennas determined by the RF switches.
To demonstrate the working mechanism of GSSK system, let ![]() be the data bits to be transmitted at one time instant from
be the data bits to be transmitted at one time instant from ![]() transmit antennas, while activating
transmit antennas, while activating ![]() antennas at a time. Considering the mapping table shown in Figure 3.3, antennas
antennas at a time. Considering the mapping table shown in Figure 3.3, antennas ![]() and
and ![]() will be activated and the transmitted RF signal vector is given by
will be activated and the transmitted RF signal vector is given by ![]() , where
, where ![]() and
and ![]() .
.
3.3 Spatial Modulation (SM)
SM is the first proposed technique among the set of SMTs and most existing methods are derived as special or generalized cases from it [37]. However, prior work in [159] caught the name of SSK, but it works totally different than the discussed SSK scheme above. In [159], two antennas exist at the transmitter, where one antenna is active for bit “0” and both antennas are active for bit “1.” The idea is extended such that quadrature phase shift keying (QPSK) and binary phase shift keying (BPSK) signals can be transmitted to increase the data rate. This is a typical MIMO system that aims at enhancing the diversity by applying a repetition coding among antennas. The idea to modulate data bits in the spatial index of transmit antennas where suggested for the first time when proposing SM [37, 71].
An SM system model with single RF chain and RF switch is shown in Figure 3.5. Let ![]() denote the data bits to be transmitted at one particular time instant. In SM,
denote the data bits to be transmitted at one particular time instant. In SM, ![]() data bits can be transmitted at any particular time instant. The incoming serial data bits are converted to parallel data bits through serial/parallel shift register and grouped into two groups. The first group contains
data bits can be transmitted at any particular time instant. The incoming serial data bits are converted to parallel data bits through serial/parallel shift register and grouped into two groups. The first group contains ![]() bits and activates one antenna among the set of
bits and activates one antenna among the set of ![]() antennas using the RF switch. The second group with
antennas using the RF switch. The second group with ![]() bits modulates a signal constellation symbol from arbitrary
bits modulates a signal constellation symbol from arbitrary ![]() –QAM/PSK or any other constellation diagram. Hence, as illustrated in Figure 3.6, the spatial and signal constellation diagrams are
–QAM/PSK or any other constellation diagram. Hence, as illustrated in Figure 3.6, the spatial and signal constellation diagrams are
- The spatial diagram is
 .
. - The signal constellation space is
 , where
, where  is the
is the  symbol drawn from the considered
symbol drawn from the considered  ‐QAM/PSK diagram.
‐QAM/PSK diagram.

Figure 3.5 SM system model with single RF‐chain and with  transmit and
transmit and  receive antennas.
receive antennas.

Figure 3.6 An example of SM constellation diagram with  and 4‐QAM modulation.
and 4‐QAM modulation.
The modulated complex symbol is processed by an IQ modulator to generate the RF carrier signal as
which is then transmitted from the active antenna ![]() .
.
To better explain this, an example is given in what follows. Assume that ![]() input data bits are to be transmitted at a particular time instant using SM. The first group of data bits
input data bits are to be transmitted at a particular time instant using SM. The first group of data bits ![]() determines the active antenna index
determines the active antenna index ![]() , i.e.
, i.e. ![]() . The second group of data bits
. The second group of data bits ![]() selects the symbol
selects the symbol ![]() . A mapping table for SM with
. A mapping table for SM with ![]() and
and ![]() is given in Table 3.1. The resultant symbol vector after the RF switch can be written as
is given in Table 3.1. The resultant symbol vector after the RF switch can be written as
Table 3.1 SM mapping table for ![]() and 4‐QAM modulation.
and 4‐QAM modulation.
| Bits | Symbol bits | Symbols | Spatial bits | Antenna index |
| 0000 | 00 | +1+j | 00 | 1 |
| 0001 | 01 | −1+j | 00 | 1 |
| 0010 | 10 | −1−j | 00 | 1 |
| 0011 | 11 | +1−j | 00 | 1 |
| 0100 | 00 | +1+j | 01 | 2 |
| 0101 | 01 | −1+j | 01 | 2 |
| 0110 | 10 | −1−j | 01 | 2 |
| 0111 | 11 | +1−j | 01 | 2 |
| 1000 | 00 | +1+j | 10 | 3 |
| 1001 | 01 | −1+j | 10 | 3 |
| 1010 | 10 | −1−j | 10 | 3 |
| 1011 | 11 | +1−j | 10 | 3 |
| 1100 | 00 | +1+j | 11 | 4 |
| 1101 | 01 | −1+j | 11 | 4 |
| 1110 | 10 | −1−j | 11 | 4 |
| 1111 | 11 | +1−j | 11 | 4 |
Compared to other MIMO techniques, SM is shown to have many advantages that are
- interchannel interference (ICI) is totally avoided by SM, since only one antenna is active at a time;
- transmit antenna synchronization is not required;
- single RF‐chain can be used similar to other SMTs. Therefore, transmitter complexity and cost are reduced significantly;
- the ML receiver complexity is much less than other MIMO techniques such as SMX as will be discussed later;
- bit error performance, which will be discussed in Chapter 4, demonstrates that SM can achieve better error performance as compared to SMX MIMO system.
3.4 Generalized Spatial Modulation (GSM)
GSM is an expansion to SM similar to GSSK scheme [67]. In GSM, as shown in Figure 3.7, a group of transmit antennas, two or more, are activated at any particular time instant and transmit the same signal. Hence, the spatial constellation diagram is the same as in GSSK, and the signal constellation diagrams are the same as in SM. Thus, an overall spectral efficiency equal to ![]() is achieved by GSM scheme.
is achieved by GSM scheme.

Figure 3.7 GSM system model with single RF‐chain, multiple RF switches and with  transmit antennas,
transmit antennas,  active antennas at a time and
active antennas at a time and  receive antennas.
receive antennas.
A mapping table for ![]() ,
, ![]() , and BPSK modulation achieving
, and BPSK modulation achieving ![]() bits is shown in Table 3.2. Activating more than one antenna at a time reduces the required number of transmit antennas for a specific spectral efficiency and allows the use of
bits is shown in Table 3.2. Activating more than one antenna at a time reduces the required number of transmit antennas for a specific spectral efficiency and allows the use of ![]() being a number that is not necessarily a power of 2. However, transmitted energy should be divided among all active antennas, and transmit antennas need to be synchronized. Similar to GSSK, the number of transmit antennas might slightly increase to simplify the RF switching circuits as discussed before.
being a number that is not necessarily a power of 2. However, transmitted energy should be divided among all active antennas, and transmit antennas need to be synchronized. Similar to GSSK, the number of transmit antennas might slightly increase to simplify the RF switching circuits as discussed before.
Table 3.2 GSM mapping table with ![]() ,
, ![]() and BPSK modulation.
and BPSK modulation.
| Bits | Symbol bits | Symbols | Spatial bits | Active antenna index |
| 0000 | 0 | +1 | 000 | 1,2 |
| 0001 | 1 | −1 | 000 | 1,2 |
| 0010 | 0 | +1 | 001 | 1,3 |
| 0011 | 1 | −1 | 001 | 1,3 |
| 0100 | 0 | +1 | 010 | 1,4 |
| 0101 | 1 | −1 | 010 | 1,4 |
| 0110 | 0 | +1 | 011 | 1,5 |
| 0111 | 1 | −1 | 011 | 1,5 |
| 1000 | 0 | +1 | 100 | 2,3 |
| 1001 | 1 | −1 | 100 | 2,3 |
| 1010 | 0 | +1 | 101 | 2,4 |
| 1011 | 1 | −1 | 101 | 2,4 |
| 1100 | 0 | +1 | 110 | 2,5 |
| 1101 | 1 | −1 | 110 | 2,5 |
| 1110 | 0 | +1 | 111 | 3,4 |
| 1111 | 1 | −1 | 111 | 3,4 |
Another scheme called variable generalized spatial modulation (VGSM) proposed in [72] where the number of activated antennas is not fixed, i.e. depending on the bits to modulate in the spatial domain the number of activated antennas can vary from only one active to all antennas are active and transmitting the same signal symbol. As such, VGSM can further reduce the number of required transmit antennas for a specific spectral efficiency, where the number of bits that can be modulated in the spatial domain is ![]() . Hence, VGSM can achieve similar data rate of
. Hence, VGSM can achieve similar data rate of ![]() , as discussed for GSM system, with only
, as discussed for GSM system, with only ![]() antennas as illustrated in Table 3.3.
antennas as illustrated in Table 3.3.
Table 3.3 VGSM with ![]() and BPSK modulation.
and BPSK modulation.
| Bits | Symbol bits | Symbols | Spatial bits | Antenna index |
| 0000 | 0 | +1 | 000 | 1 |
| 0001 | 1 | −1 | 000 | 1 |
| 0010 | 0 | +1 | 001 | 2 |
| 0011 | 1 | −1 | 001 | 2 |
| 0100 | 0 | +1 | 010 | 3 |
| 0101 | 1 | −1 | 010 | 3 |
| 0110 | 0 | +1 | 011 | 4 |
| 0111 | 1 | −1 | 011 | 4 |
| 1000 | 0 | +1 | 100 | 1,2 |
| 1001 | 1 | −1 | 100 | 1,2 |
| 1010 | 0 | +1 | 101 | 1,3 |
| 1011 | 1 | −1 | 101 | 1,3 |
| 1100 | 0 | +1 | 110 | 1,4 |
| 1101 | 1 | −1 | 110 | 1,4 |
| 1110 | 0 | +1 | 111 | 2,3 |
| 1111 | 1 | −1 | 111 | 2,3 |
3.5 Quadrature Space Shift Keying (QSSK)
QSSK was proposed to enhance the spectral efficiency of SSK scheme [65, 70]. As discussed at the beginning of this chapter, in SSK system, either the cosine part or the sine part of the carrier signal is transmitted. However, QSSK idea is to utilize both parts to increase the data rate and enhance the performance of SSK scheme. This is done by transmitting the cosine part of the carrier from one antenna ![]() and the sine part from another or the same antenna
and the sine part from another or the same antenna ![]() . Incoming data bits determine the active antennas. Hence, the spectral efficiency of QSSK is given by
. Incoming data bits determine the active antennas. Hence, the spectral efficiency of QSSK is given by ![]() .
.
Table 3.4 QSSK mapping table for ![]() .
.
| Bits | In‐phase bits | In‐phase antenna | Quadrature bits | Quadrature antenna |
| 0000 | 00 | 1 | 00 | 1 |
| 0001 | 00 | 1 | 01 | 2 |
| 0010 | 00 | 1 | 10 | 3 |
| 0011 | 00 | 1 | 11 | 4 |
| 0100 | 01 | 2 | 00 | 1 |
| 0101 | 01 | 2 | 01 | 2 |
| 0110 | 01 | 2 | 10 | 3 |
| 0111 | 01 | 2 | 11 | 4 |
| 1000 | 10 | 3 | 00 | 1 |
| 1001 | 10 | 3 | 01 | 2 |
| 1010 | 10 | 3 | 10 | 3 |
| 1011 | 10 | 3 | 11 | 4 |
| 1100 | 11 | 4 | 00 | 1 |
| 1101 | 11 | 4 | 01 | 2 |
| 1110 | 11 | 4 | 10 | 3 |
| 1111 | 11 | 4 | 11 | 4 |
A system model for QSSK technique is shown in Figure 3.8, and a mapping table with ![]() is given in Table 3.4. Let
is given in Table 3.4. Let ![]() denote the data bits to be transmitted at a particular time instant using QSSK scheme with
denote the data bits to be transmitted at a particular time instant using QSSK scheme with ![]() . The incoming bits sequence is divided into two groups each with
. The incoming bits sequence is divided into two groups each with ![]() bits. The first group
bits. The first group ![]() will activate the antenna index
will activate the antenna index ![]() to transmit the cosine part of the carrier. The second group
to transmit the cosine part of the carrier. The second group ![]() activates the antenna index,
activates the antenna index, ![]() , which transmits the sine part of the carrier. Hence, the spatial and signal constellation diagrams for QSSK system are defined as
, which transmits the sine part of the carrier. Hence, the spatial and signal constellation diagrams for QSSK system are defined as
- The spatial diagram is
 .
. - The signal diagram is
 .
.

Figure 3.8 QSSK system model.
It is important to note that the cardinality of the signal diagram set is one and no data is transmitted in the signal domain. Similar to SSK and GSSK, data are transmitted exclusively in the spatial domain. As such, the transmitted vector for QSSK system in the previous example is given by,
Please note that the cosine and the sine parts of the carrier signal are orthogonal and transmitting them simultaneously causes no ICI similar to SSK and SM algorithms. Also and even though two transmit antennas might be active at a time, no RF chain is needed as in SSK scheme. Hence, all inherent advantages of SSK scheme are retained but with an additional ![]() bits that can be transmitted. However, the transmit antennas must be synchronized to start the transmission simultaneously. Again, RF signals are stored in an RF memory and repeatedly used for transmission. Two RF DAC memories are needed for QSSK scheme. One memory storing the in‐phase component of the carrier signal while the other one stores the quadrature component of the carrier signal. In addition, in QSSK scheme, there is a possibility that in‐phase and quadrature bits will modulate the same transmit antennas as shown in Table 3.4. Hence, an RF combiner is needed before each transmit antenna connecting identical outputs from the RF switches as illustrated in Figure 3.8.
bits that can be transmitted. However, the transmit antennas must be synchronized to start the transmission simultaneously. Again, RF signals are stored in an RF memory and repeatedly used for transmission. Two RF DAC memories are needed for QSSK scheme. One memory storing the in‐phase component of the carrier signal while the other one stores the quadrature component of the carrier signal. In addition, in QSSK scheme, there is a possibility that in‐phase and quadrature bits will modulate the same transmit antennas as shown in Table 3.4. Hence, an RF combiner is needed before each transmit antenna connecting identical outputs from the RF switches as illustrated in Figure 3.8.
3.6 Quadrature Spatial Modulation (QSM)
QSM can be thought of as an amendment to SM system by utilizing the quadrature spatial dimension similar to QSSK [48, 65, 70, 73]. However, in QSM, the transmitted symbol is utilized to convey information bits and can be obtained from an arbitrary complex signal constellation diagram. Thus, the spatial constellation diagram is the same as for QSSK, while the signal constellation diagram is ![]() .
.
A system model for QSM is depicted in Figure 3.10. Similar to SM, QSM can be designed with a single RF‐chain even though two antennas might be active at one time instant. The incoming data bits, ![]() with
with ![]() bits, are to be transmitted in one time slot using QSM system. The incoming bits are grouped into three groups. The first one contains
bits, are to be transmitted in one time slot using QSM system. The incoming bits are grouped into three groups. The first one contains ![]() bits, which is used to choose the signal symbol
bits, which is used to choose the signal symbol ![]() . The other two
. The other two ![]() bits determine the indexes of the two antennas to activate,
bits determine the indexes of the two antennas to activate, ![]() and
and ![]() , resulting in spatial symbol
, resulting in spatial symbol ![]() . A constellation illustration for QSM system is shown in Figure 3.9. The first antenna index,
. A constellation illustration for QSM system is shown in Figure 3.9. The first antenna index, ![]() , will transmit the modulated in‐phase part of the RF carrier by the real part of complex symbol
, will transmit the modulated in‐phase part of the RF carrier by the real part of complex symbol ![]() . Whereas the second antenna will be transmitting the quadrature part of the carrier signal modulated by imaginary part of the complex symbol
. Whereas the second antenna will be transmitting the quadrature part of the carrier signal modulated by imaginary part of the complex symbol ![]() . The output from the RF‐chain is given by
. The output from the RF‐chain is given by
The modulated cosine part of the carrier by ![]() will be transmitted from antenna
will be transmitted from antenna ![]() through the first RF switch, and the sine part of the carrier modulated by
through the first RF switch, and the sine part of the carrier modulated by ![]() is transmitted from antenna
is transmitted from antenna ![]() through the second RF switch.
through the second RF switch.
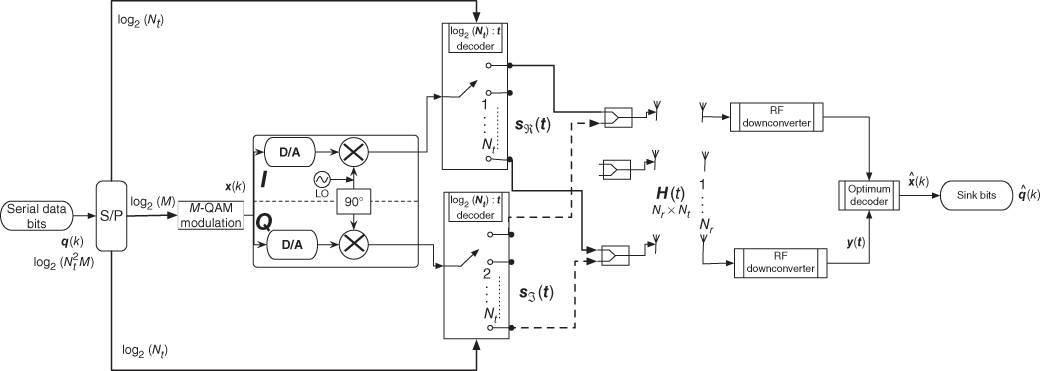
Figure 3.9 QSM system model with single RF‐chain, two RF switches,  transmit antennas and
transmit antennas and  receive antennas.
receive antennas.

Figure 3.10 An illustration for QSM signal and spatial constellation diagrams.
Consider an incoming sequence of bits given by ![]() is to be transmitted from
is to be transmitted from ![]() antennas and 4‐QAM modulation. The first two data bits
antennas and 4‐QAM modulation. The first two data bits ![]() modulate a 4‐QAM symbol,
modulate a 4‐QAM symbol, ![]() . The second group,
. The second group, ![]() modulates the antenna index
modulates the antenna index ![]() used to transmit
used to transmit ![]() , resulting in
, resulting in ![]() . The last group
. The last group ![]() indicates that the transmit antenna
indicates that the transmit antenna ![]() will be used to transmit
will be used to transmit ![]() and resulting in
and resulting in ![]() . Hence, the spatial and signal symbols are
. Hence, the spatial and signal symbols are ![]() and
and ![]() , respectively, and the resultant RF vector at the transmit antennas is given by
, respectively, and the resultant RF vector at the transmit antennas is given by
It is important to note that it is possible to have ![]() if identical spatial bits are to be transmitted as discussed above for QSSK system. Hence, one transmit antenna might be active at one time instant. To facilitate this, RF combiners are needed to connect the identical outputs from the RF switches to the corresponding antenna as shown in Figure 3.10.
if identical spatial bits are to be transmitted as discussed above for QSSK system. Hence, one transmit antenna might be active at one time instant. To facilitate this, RF combiners are needed to connect the identical outputs from the RF switches to the corresponding antenna as shown in Figure 3.10.
3.7 Generalized QSSK (GQSSK)
A system model for GQSSK is depicted in Figure 3.11 with the mapping table for ![]() and
and ![]() and the way they can be connected to the RF switches. Following similar concept as in GSSK, a subset of transmit antennas can be activated at a time to transmit the in‐phase part of the carrier and another subset to transmit the quadrature part of the carrier in GQSSK. Therefore, the number of data bits that can be transmitted in GQSSK scheme is
and the way they can be connected to the RF switches. Following similar concept as in GSSK, a subset of transmit antennas can be activated at a time to transmit the in‐phase part of the carrier and another subset to transmit the quadrature part of the carrier in GQSSK. Therefore, the number of data bits that can be transmitted in GQSSK scheme is ![]() , and the spatial and signal constellation diagrams are
, and the spatial and signal constellation diagrams are
- The spatial diagram is
(3.11)where

 is the
is the  active antennas combination in the space containing all used antenna combinations.
active antennas combination in the space containing all used antenna combinations. - The signal diagram for GQSSK contains only one symbol
 .
.

Figure 3.11 GQSSK system model with illustration for 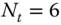 an
an  achieving
achieving  bits.
bits.
To illustrate the working principle of this system, an example is given in what follows. Consider the mapping table in Figure 3.11 and assume ![]() and
and ![]() . The number of data bits that can be transmitted using GQSSK at one time instant is
. The number of data bits that can be transmitted using GQSSK at one time instant is ![]() bits, which is double the number of bits in GSSK system. Assume that
bits, which is double the number of bits in GSSK system. Assume that ![]() bits are to be transmitted at one time instant. The sequence of bits is divided into half. The first half
bits are to be transmitted at one time instant. The sequence of bits is divided into half. The first half ![]() indicates that the second antenna combination,
indicates that the second antenna combination, ![]() and
and ![]() , will be transmitting the real part of the carrier. Hence, the real transmitting vector is
, will be transmitting the real part of the carrier. Hence, the real transmitting vector is ![]() . Similarly, the second half
. Similarly, the second half ![]() indicates that the fourth antenna combination,
indicates that the fourth antenna combination, ![]() and
and ![]() , will be transmitting the quadrature part of the carrier resulting in the transmitted vector
, will be transmitting the quadrature part of the carrier resulting in the transmitted vector ![]() . The real and imaginary vectors are added coherently and the resultant RF vector at the input of transmit antennas is
. The real and imaginary vectors are added coherently and the resultant RF vector at the input of transmit antennas is

which is transmitted over the MIMO channel. Note, the spatial symbol for this example is ![]() .
.
3.8 Generalized QSM (GQSM)
Modulating the RF carrier in GQSSK system by an arbitrary complex symbol drawn from a signal constellation diagram will lead to GQSM as shown in Figure 3.12. In GQSM, a subset of transmit antennas is considered at each time instant to separately transmit the real and the imaginary parts of complex symbol, ![]() and
and ![]() . As in QSM, the real part modulates the in‐phase part of the carrier, whereas the imaginary part modulates the quadrature component of the carrier signal. The spectral efficiency of GQSM is then given by
. As in QSM, the real part modulates the in‐phase part of the carrier, whereas the imaginary part modulates the quadrature component of the carrier signal. The spectral efficiency of GQSM is then given by ![]() . The discussion of GQSM system is similar to GQSSK except that the signal constellation diagram is the same as in QSM where it conveys
. The discussion of GQSM system is similar to GQSSK except that the signal constellation diagram is the same as in QSM where it conveys ![]() bits. Mapping tables for
bits. Mapping tables for ![]() ,
, ![]() , and
, and ![]() ‐QAM is given in Figure 3.12.
‐QAM is given in Figure 3.12.

Figure 3.12 GQSM system model with illustration for  ,
,  and
and  ‐QAM achieving 9 bits (s Hz)
‐QAM achieving 9 bits (s Hz) .
.
3.9 Advanced SMTs
3.9.1 Differential Space Shift Keying (DSSK)
In all previous discussions for optimum receiver of the different presented SMTs so far, the MIMO channel matrix should be perfectly known at the receiver. The perfect knowledge of the channel matrix is idealistic, as discussed in the previous chapter, and channel estimation techniques should be used to obtain an estimate for ![]() . However, a scheme called DSSK is proposed in [63] aimed at alleviating this condition, where the requirement for channel knowledge at the receiver in SSK is totally avoided in DSSK. The idea is that the receiver will rely on the received signal block at time
. However, a scheme called DSSK is proposed in [63] aimed at alleviating this condition, where the requirement for channel knowledge at the receiver in SSK is totally avoided in DSSK. The idea is that the receiver will rely on the received signal block at time ![]() ,
, ![]() , and the signal block received at time
, and the signal block received at time ![]() ,
, ![]() , to decode the message.
, to decode the message.
A system model for DSSK with the a mapping table for ![]() is shown in Figure 3.13.1 Another mapping table for
is shown in Figure 3.13.1 Another mapping table for ![]() is shown in Table 3.5. The mapping table is designed with the following conditions:
is shown in Table 3.5. The mapping table is designed with the following conditions:
- All columns should have only one nonzero element. This means that only one transmit antenna will be active at one particular time instant similar to SSK scheme. As such, ICI is totally avoided, and single RF‐chain can be used with proper RF switching design.
- All rows should not have the same symbol more than once. This also indicates that during the transmission time block, each symbol is transmitted only once.
It is shown in [63] that the spectral efficiency of DSSK is smaller than that of SSK scheme for the same ![]() value and equal only for the case of
value and equal only for the case of ![]() , where DSSK transmits
, where DSSK transmits ![]() bits each
bits each ![]() time slots. As such, the spectral efficiency of DSSK is
time slots. As such, the spectral efficiency of DSSK is ![]() bits. However, in DSSK, the number of transmit antennas that can be used for communication is flexible and the power of two requirement as in SSK scheme is alleviated. For instance, with
bits. However, in DSSK, the number of transmit antennas that can be used for communication is flexible and the power of two requirement as in SSK scheme is alleviated. For instance, with ![]() , 2 bits can be transmitted on 3 time slots using DSSK, whereas 3 bits can be transmitted on the three time slots when using SSK scheme with only two transmit antennas. The spectral efficiency of DSSK decays further for larger number of transmit antennas.
, 2 bits can be transmitted on 3 time slots using DSSK, whereas 3 bits can be transmitted on the three time slots when using SSK scheme with only two transmit antennas. The spectral efficiency of DSSK decays further for larger number of transmit antennas.
As in SSK, DSSK also does not have signal constellation symbols. However, its spatial constellation diagram contains a ![]() spatial symbols, where each symbol is an
spatial symbols, where each symbol is an ![]() square matrix containing a different permutation of the channel matrix. For example, for
square matrix containing a different permutation of the channel matrix. For example, for ![]() , the spatial constellation diagram is
, the spatial constellation diagram is

In DSSK, the transmission begins with known symbol (bits), which maps to specific transmission matrix ![]() . The next transmitted symbol is generated by multiplying the chosen spatial symbols
. The next transmitted symbol is generated by multiplying the chosen spatial symbols ![]() with a delayed version of the transmitted signal
with a delayed version of the transmitted signal ![]() , such that the next transmitted signal is
, such that the next transmitted signal is
Note, for simplicity, ![]() is assumed.
is assumed.
The main idea behind DSSK is that the channel state information (CSI) at the receiver is not needed. The symbol ![]() is an
is an ![]() square matrix indicating which antenna is active at time instance
square matrix indicating which antenna is active at time instance ![]() as shown in Table 3.5, where
as shown in Table 3.5, where ![]() . As in (3.14), the transmitted symbol is
. As in (3.14), the transmitted symbol is

Figure 3.13 Differential space shift keying system model with the mapping table for  .
.
Table 3.5 DSSK mapping table for ![]() achieving a spectral efficiency of
achieving a spectral efficiency of ![]() bits Hz
bits Hz![]() .
.
| Bits | DSSK symbol |
| 00 |  |
| 01 |  |
| 11 |  |
| 10 |  |
| Not used |  |
| Not used |  |
Assuming that the channel is quasi‐static such that ![]() , which is generally assumed for space–time systems, the received signals at
, which is generally assumed for space–time systems, the received signals at ![]() and
and ![]() time slots are
time slots are
and

Hence, the ML decoder for DSSK scheme is given by
where ![]() is a space containing all possible symbols of
is a space containing all possible symbols of ![]() . Note that the ML for DSSK in (3.18) does not require any knowledge of the MIMO channel.
. Note that the ML for DSSK in (3.18) does not require any knowledge of the MIMO channel.
3.9.2 Differential Spatial Modulation (DSM)
DSM is very similar to DSSK with the difference that transmitted symbols are now modulated [63]. Hence, the achievable spectral efficiency for DSM is given by ![]() . DSM has the same spatial constellation diagram as DSSK and has a signal constellation diagram containing all possible signal symbols permutations. For instance, assuming BPSK constellation diagram and
. DSM has the same spatial constellation diagram as DSSK and has a signal constellation diagram containing all possible signal symbols permutations. For instance, assuming BPSK constellation diagram and ![]() , the signal constellation diagram is
, the signal constellation diagram is

Note, in general, it is required that the signal constellation must have equal unit energy, such as ![]() ‐PSK constellations. This is required to maintain the closure property where the multiplication of any two transmitted vectors results in another vector from the existing set. Similar receiver as discussed for DSSK can be considered here as well, where
‐PSK constellations. This is required to maintain the closure property where the multiplication of any two transmitted vectors results in another vector from the existing set. Similar receiver as discussed for DSSK can be considered here as well, where ![]() is for example as showing in the mapping table for
is for example as showing in the mapping table for ![]() and
and ![]() ‐PSK is given in Table 3.6.
‐PSK is given in Table 3.6.
Table 3.6 DSM mapping table for ![]() and
and ![]() ‐PSK modulation achieving a spectral efficiency of
‐PSK modulation achieving a spectral efficiency of ![]() bits Hz
bits Hz![]() .
.
| Bits | DSM symbol |
| 000 |  |
| 001 |  |
| 010 |  |
| 011 |  |
| 100 |  |
| 101 |  |
| 110 |  |
| 111 |  |
3.9.3 Differential Quadrature Spatial Modulation (DQSM)
The extension of DSM to the QSM technique is proposed recently in [97]. A system model for DQSM is depicted in Figure 3.14. The incoming data bits are partitioned into three groups. The first group containing ![]() bits modulates an
bits modulates an ![]()
![]() ‐QAM symbols,
‐QAM symbols, ![]() , to be transmitted in
, to be transmitted in ![]() time instants. The other two groups each with
time instants. The other two groups each with ![]() bits modulate two sets of active antennas, which will transmit the real and imaginary parts of the signal symbol, respectively.
bits modulate two sets of active antennas, which will transmit the real and imaginary parts of the signal symbol, respectively.
The first spatial symbol, ![]() , represents the permutation matrix,
, represents the permutation matrix, ![]() , used to generate the transmitter block that transmits the real part of the constellation symbol,
, used to generate the transmitter block that transmits the real part of the constellation symbol, ![]() . The other spatial symbol,
. The other spatial symbol, ![]() , denotes the permutation matrix,
, denotes the permutation matrix, ![]() , that will generate the transmitter block which transmits the imaginary part of the constellation symbol,
, that will generate the transmitter block which transmits the imaginary part of the constellation symbol, ![]() . The real symbol vector,
. The real symbol vector, ![]() , and the imaginary symbol vector,
, and the imaginary symbol vector, ![]() , are, respectively, multiplied with
, are, respectively, multiplied with ![]() and
and ![]() , where each element of the symbol vectors is multiplied by the corresponding column vector of the permutation matrix to generate
, where each element of the symbol vectors is multiplied by the corresponding column vector of the permutation matrix to generate ![]() and
and ![]() . It should be mentioned, though, that there are
. It should be mentioned, though, that there are ![]() possible permutation matrices and only
possible permutation matrices and only ![]() are considered. It is also assumed that
are considered. It is also assumed that ![]() . Therefore,
. Therefore, ![]() , where
, where ![]() denoting a set of all possible permutation matrices. Similarly,
denoting a set of all possible permutation matrices. Similarly, ![]() ,
, ![]() ,
, ![]() .
.

Figure 3.14 DQSM system model with arbitrary number of transmit,  , and receive,
, and receive,  , antennas and specific modulation order,
, antennas and specific modulation order,  , utilizing single RF‐chain transmitter.
, utilizing single RF‐chain transmitter.
To maintain the inherent advantages of QSM and similar to DSSK and DSM systems, transmitter blocks with ![]() dimension are designed in such away that
dimension are designed in such away that
- At each time instant and to maintain single RF‐chain transmitter, a single transmit antenna is active to transmit the real part of the complex symbol and another or the same antenna to transmit the imaginary part of the data symbol. As such, each column of the transmitter block contains only one nonzero real value and one nonzero imaginary value.
- A transmit antenna is activated only once during the duration of one transmitter block.
- The closure property of the transmitted blocks is maintained, as discussed above, to facilitate differential modulation and demodulation.
To better explain the transmitter procedure of DQSM, an example is given in what follows considering ![]() and
and ![]() ‐QAM modulation. The possible permutation matrices with
‐QAM modulation. The possible permutation matrices with ![]() antennas along with the mapping bits are illustrated in Table 3.7. Let the incoming data bits to be transmitted at
antennas along with the mapping bits are illustrated in Table 3.7. Let the incoming data bits to be transmitted at ![]() time slots using DQSM be
time slots using DQSM be ![]() . The first group with
. The first group with ![]() data bits,
data bits, ![]() , modulates
, modulates ![]() 4‐QAM symbols as,
4‐QAM symbols as,

The other two groups each with ![]() bits,
bits, ![]() and
and ![]() , modulate two spatial indexes,
, modulate two spatial indexes, ![]() and
and ![]() , respectively. The first index,
, respectively. The first index, ![]() , denotes the permutation matrix that will be used to transmit the real parts of the transmitted symbols,
, denotes the permutation matrix that will be used to transmit the real parts of the transmitted symbols,
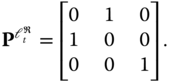
The second index, ![]() , denotes the permutation matrix that will be used to transmit the imaginary parts of the transmitted symbols as
, denotes the permutation matrix that will be used to transmit the imaginary parts of the transmitted symbols as

The real symbols vector, ![]() , and the imaginary symbols ,vector
, and the imaginary symbols ,vector ![]() , are, respectively, multiplied with
, are, respectively, multiplied with ![]() and
and ![]() , where each element in the symbol vectors is multiplied by the corresponding column vector of the permutation matrix to generate
, where each element in the symbol vectors is multiplied by the corresponding column vector of the permutation matrix to generate

and

To facilitate differential demodulation, each transmitted block, ![]() , is multiplied by the previously transmitted block,
, is multiplied by the previously transmitted block, ![]() , and the generated real and imaginary blocks are coherently added and transmitted over the MIMO channel matrix and suffer from an AWGN at the receiver inputs as shown in Figure 3.14.
, and the generated real and imaginary blocks are coherently added and transmitted over the MIMO channel matrix and suffer from an AWGN at the receiver inputs as shown in Figure 3.14.
Table 3.7 DQSM bits mapping and permutation matrices for ![]() transmit antennas.
transmit antennas.
| Bits | Permutations | ||
| 00 |  |  | |
| 01 |  |  | |
| 10 |  |  | |
| 11 |  |  |
The received signal for the ![]() block is then given by
block is then given by
At the receiver, the received signals at each receive antenna are first demodulated through an IQ demodulator. Then, the obtained real, ![]() , and imaginary,
, and imaginary, ![]() , signals are differentially demodulated to retrieve the transmitted bits as will be discussed in what follows.
, signals are differentially demodulated to retrieve the transmitted bits as will be discussed in what follows.
The received real signal at time ![]() is
is
Assuming quasi‐static channel where ![]() , the received real part of the signal can be written as
, the received real part of the signal can be written as
Similarly, the received imaginary part can be obtained.
The optimum joint ML differential detector is given by

where ![]() and
and ![]() , respectively, denote the detected real and imaginary matrices, and
, respectively, denote the detected real and imaginary matrices, and ![]() and
and ![]() denote a set with
denote a set with ![]() dimension containing, respectively, all possible real and imaginary transmission matrices. The estimated matrices are used to retrieve the original information bits through an inverse mapping procedure considering the same mapping rules applied at the transmitter.
dimension containing, respectively, all possible real and imaginary transmission matrices. The estimated matrices are used to retrieve the original information bits through an inverse mapping procedure considering the same mapping rules applied at the transmitter.
3.9.4 Space–Time Shift Keying (STSK)
STSK [79, 90, 92, 160] is another generalization MIMO transmission scheme that is based on the concept of SMTs. In STSK, incoming data bits activate a dispersion matrix to be transmitted from multiple transmit antennas. Different designs for the dispersion matrices are reported in literature. It is shown in [79] that different MIMO schemes can be obtained as special cases from STSK with proper design of the dispersion matrices. The spectral efficiency of STSK systems is

where ![]() is the number of total dispersion matrices,
is the number of total dispersion matrices, ![]() is the number of used dispersion matrices for each transmitted block, and
is the number of used dispersion matrices for each transmitted block, and ![]() is the time slots needed to transmit one dispersion matrix. The dispersion matrices
is the time slots needed to transmit one dispersion matrix. The dispersion matrices ![]() ,
, ![]() can be designed to achieve any of the previously discussed modulation schemes. For instance and assuming
can be designed to achieve any of the previously discussed modulation schemes. For instance and assuming ![]() ,
, ![]() ,
, ![]() , the following dispersion matrices can be designed:
, the following dispersion matrices can be designed: ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Now if SSK is targeted,
. Now if SSK is targeted, ![]() , and a fixed transmitted symbol,
, and a fixed transmitted symbol, ![]() , is transmitted at each time instant. The spectral efficiency is then
, is transmitted at each time instant. The spectral efficiency is then ![]() bits. Assume that the incoming data bits at one time instant are
bits. Assume that the incoming data bits at one time instant are ![]() , which modulate
, which modulate ![]() to be transmitted at this particular time. If SM is to be configured,
to be transmitted at this particular time. If SM is to be configured, ![]() ‐QAM /PSK symbols are then modulated by another
‐QAM /PSK symbols are then modulated by another ![]() bits, and the modulated complex symbol is multiplied by the corresponding modulated dispersion matrix. Similarly, QSM and QSSK can be configured where the real part of the complex is multiplied by a dispersion matrix and the imaginary part is multiplied by another dispersion matrix, i.e.
bits, and the modulated complex symbol is multiplied by the corresponding modulated dispersion matrix. Similarly, QSM and QSSK can be configured where the real part of the complex is multiplied by a dispersion matrix and the imaginary part is multiplied by another dispersion matrix, i.e. ![]() .
.
Also, other MIMO schemes can be designed. Consider, for instance, the following dispersion matrices:




where ![]() ,
, ![]() , and
, and ![]() . Using these dispersion matrices, orthogonal space–time coding techniques, such as Alamouti code, combined with SMTs can be configured [121, 161–168].
. Using these dispersion matrices, orthogonal space–time coding techniques, such as Alamouti code, combined with SMTs can be configured [121, 161–168].
A mapping table for ![]() bits spectral efficiency,
bits spectral efficiency, ![]() ,
, ![]() , where
, where ![]() dispersion matrices are selected at each time
dispersion matrices are selected at each time ![]() and
and ![]() (BPSK) modulation is shown in Table 3.8. Please note that the number of possible combination in this configuration is six and only four combinations are considered as in generalized space modulation techniques (GSMTs). Two incoming data bits determine the active combination of transmitted matrices and two other bits determine the BPSK symbols to be transmitted over the two time slots. Each symbol is multiplied by the corresponding dispersion matrix and the resultant matrices are added coherently and then transmitted. The receiver task is to determine the set of active matrices and an estimate of the possible transmitted symbols.
(BPSK) modulation is shown in Table 3.8. Please note that the number of possible combination in this configuration is six and only four combinations are considered as in generalized space modulation techniques (GSMTs). Two incoming data bits determine the active combination of transmitted matrices and two other bits determine the BPSK symbols to be transmitted over the two time slots. Each symbol is multiplied by the corresponding dispersion matrix and the resultant matrices are added coherently and then transmitted. The receiver task is to determine the set of active matrices and an estimate of the possible transmitted symbols.
Table 3.8 STSK mapping table for ![]() ,
, ![]() and BPSK modulation.
and BPSK modulation.
| Bits | Dispersion matrices | BPSK symbols | STSK codeword |
| 0000 | +1, +1 | ||
| 0001 | +1, −1 | ||
| 0010 | −1, +1 | − | |
| 0011 | −1, −1 | − | |
| 0100 | +1, +1 | ||
| 0101 | +1, −1 | ||
| 0110 | −1, +1 | − | |
| 0111 | −1, −1 | − | |
| 1000 | +1, +1 | ||
| 1001 | +1, −1 | ||
| 1010 | −1, +1 | − | |
| 1011 | −1, −1 | − | |
| 1100 | +1, +1 | ||
| 1101 | +1, −1 | ||
| 1110 | −1, +1 | − | |
| 1111 | −1, −1 | − |
3.9.5 Trellis Coded‐Spatial Modulation (TCSM)
The last scheme that will be discussed in this chapter is different than all previous schemes since it includes channel coding techniques [169]. TCSM attracted significant interest in literature and many variant schemes have been developed [154, 162, 170–172]. The idea of TCSM is to apply trellis coded modulation (TCM) to the spatial domain [173, 174]. TCM is an efficient modulation technique that conserves bandwidth through convolutional coding by doubling the number of constellation points of a signal. In TCM, the ![]() incoming bits are mapped to
incoming bits are mapped to ![]() bits using a convolutional encoder as illustrated in Figure 3.15. The basic idea is to use set partitioning to allow certain transitions among consecutive bits. An example of set partitioning for 8‐PSK constellation diagram is depicted in Figure 3.16. Designing the sets such that they have maximum possible Euclidean distances among all possible symbol transitions in the set is shown to significantly enhance the performance [173].
bits using a convolutional encoder as illustrated in Figure 3.15. The basic idea is to use set partitioning to allow certain transitions among consecutive bits. An example of set partitioning for 8‐PSK constellation diagram is depicted in Figure 3.16. Designing the sets such that they have maximum possible Euclidean distances among all possible symbol transitions in the set is shown to significantly enhance the performance [173].

Figure 3.15 An example of rate 1/2 TCM encoder with the state diagram and convolutional encoder.

Figure 3.16 An example of TCM set partitioning for 8‐PSK constellation diagram.
In TCSM, the similar concept is applied to the spatial constellation symbols. The possible transition states for ![]() antennas constellation along with the considered convolutional encoder are shown in Figure 3.17. As shown in figure, the antennas are partitioned in two sets, where Ant 1 and Ant 3 form a set and Ant 2 and Ant 4 form the other set. There is no possible transition between Ant 1 and Ant 2. Similarly, there is no transition between Ant 3 and Ant 4. Assuming that the antennas are horizontally aligned, the spacing between Ant 1 and Ant 3 is much larger than the spacing between Ant 1 and Ant 2. Therefore, the probability of correlation among each set elements is lower, which enhances the performance.
antennas constellation along with the considered convolutional encoder are shown in Figure 3.17. As shown in figure, the antennas are partitioned in two sets, where Ant 1 and Ant 3 form a set and Ant 2 and Ant 4 form the other set. There is no possible transition between Ant 1 and Ant 2. Similarly, there is no transition between Ant 3 and Ant 4. Assuming that the antennas are horizontally aligned, the spacing between Ant 1 and Ant 3 is much larger than the spacing between Ant 1 and Ant 2. Therefore, the probability of correlation among each set elements is lower, which enhances the performance.

Figure 3.17 TCSM possible transition states for  antennas along with the considered convolutional encoder.
antennas along with the considered convolutional encoder.
The idea of applying TCM in the spatial domain can be applied to all previously discussed SMTs. Spatial constellation symbols can be grouped in sets and special conditions among set elements can be guaranteed through the convolutional encoder.
3.10 Complexity Analysis of SMTs
3.10.1 Computational Complexity of the ML Decoder
One of the main advantages of SMTs is that they allow for simple receiver architecture with reduced complexity as compared to SMX and other MIMO systems. The receiver complexity is computed as the number of real multiplication and division operations needed by each algorithm [175]. Considering the SMT‐ML receiver in (3.2), the computational complexity is calculated as
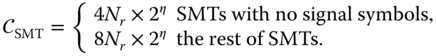
Note that each complex multiplication is a four real multiplications ![]() . For SM, QSM, and other similar systems, (3.2) can be written as
. For SM, QSM, and other similar systems, (3.2) can be written as ![]() , where the multiplication,
, where the multiplication, ![]() , requires four real multiplications and evaluating the square needs another four operations. These operations are done
, requires four real multiplications and evaluating the square needs another four operations. These operations are done ![]() times and over the cardinality of the set
times and over the cardinality of the set ![]() , which is
, which is ![]() . Therefore, QSM and SM requires
. Therefore, QSM and SM requires ![]() operations. For SSK and similar systems, the first multiplication does not exist and only the square operation need to be evaluated. As such, the number of needed operations is
operations. For SSK and similar systems, the first multiplication does not exist and only the square operation need to be evaluated. As such, the number of needed operations is ![]() . Similarly, for SMX system, the multiplication
. Similarly, for SMX system, the multiplication ![]() requires
requires ![]() operations and the square operations needs
operations and the square operations needs ![]() operations done over
operations done over ![]() possible symbols. Thereby, the number of required operations is
possible symbols. Thereby, the number of required operations is ![]() .
.
3.10.2 Low‐Complexity Sphere Decoder Receiver for SMTs
In this section, two sphere decoders (SDs) tailored for SMTs are considered. The first scheme called SMT‐Rx and the second called SMT‐Tx.
First, for ease of derivation, the real‐valued equivalent of the complex‐valued model in (3.2) is described as [176],
where


3.10.2.1 SMT‐Rx Detector
The SMT‐Rx is a reduced‐complexity and close‐to‐optimum average bit error ratio (ABER)‐achieving decoder, which aims at reducing the receive search space. The detector can formally be written as [86],
where ![]() is the
is the ![]() th row of
th row of ![]() ,
, ![]() is the
is the ![]() th element of
th element of ![]() , and
, and

where ![]() .
.
The idea behind SMT‐Rx is that it keeps combining the received signals as long as the Euclidean distance in (3.39) is less or equal to the radius ![]() . Whenever a point is found to be inside the sphere, the radius,
. Whenever a point is found to be inside the sphere, the radius, ![]() , is updated with the Euclidean distance of that point. The point with the minimum Euclidean distance is considered to be the solution.
, is updated with the Euclidean distance of that point. The point with the minimum Euclidean distance is considered to be the solution.
3.10.2.2 SMT‐Tx Detector
Conventional SD is designed for SMX, where all antennas are active at each time instance and transmitting different symbols [114, 177–179]. But, in SMT, there is none or only one constellation symbol transmitted from the active transmit antenna(s) depending on the used SMT. In [38, 87], a modified SD algorithm designed for SM only was presented. In this section, a generalized SD named SMT‐Tx tailored to any SMTs system is described.
Similar to conventional SDs, the SMT‐Tx scheme searches for points that lie inside a sphere with a radius ![]() centered at the received point. Every time a point is found inside the sphere, the radius is decreased until only one point is left inside the sphere.
centered at the received point. Every time a point is found inside the sphere, the radius is decreased until only one point is left inside the sphere.
Th SD in (3.35) can be thought of as an inequality described by
Let ![]() be Cholesky factorized as
be Cholesky factorized as ![]() , where
, where ![]() is an upper triangular matrix. Define
is an upper triangular matrix. Define ![]() and
and ![]() , then add
, then add ![]() to the both sides of (3.41), which yields,
to the both sides of (3.41), which yields,
Let ![]() ,
,
3.10.2.3 Single Spatial Symbol SMTs (SS‐SMTs)
For nonquadrature SMTs with only one spatial symbol, such as SM and GSM, ![]() is a two elements length vector,
is a two elements length vector, ![]() and
and ![]() , where
, where ![]() is an
is an ![]() square identity matrix.
square identity matrix.
Thus, (3.43) can be written as

where ![]() is the
is the ![]() element of
element of ![]() .
.
The necessary conditions for the point ![]() to lie inside the sphere are
to lie inside the sphere are
Solving (3.45) and (3.46) gives the bounds
where ![]() .
.
Every time a point is found inside the sphere, the radius ![]() is updated with
is updated with
The point with the smallest radius is the solution; hence, the last point is found inside the sphere.
3.10.2.4 Double Spatial Symbols SMTs (DS‐SMTs)
For quadrature SMTs with two spatial symbols, such as QSM, ![]() is an upper‐triangular matrix. Hence, (3.43) can be rewritten as
is an upper‐triangular matrix. Hence, (3.43) can be rewritten as
From (3.50), the necessary conditions for the point ![]() to lie inside the sphere is
to lie inside the sphere is
Solving (3.51) and (3.52) results in the following the bounds:
Note, different to conventional MIMO systems, that the channel matrix does not have to be full rank for SD to work, i.e., SMT‐SD works for ![]() as well as
as well as ![]() .
.
3.10.2.5 Computational Complexity
The detailed number of multiplication operations needed by SS–SMT–SD is shown in Table 3.9, where ![]() (3.47) and
(3.47) and ![]() (3.48) are the number of points in the bounds (3.47) and (3.48), respectively.
(3.48) are the number of points in the bounds (3.47) and (3.48), respectively.
Table 3.9 Detailed complexity analysis of SS‐SMTs‐SD.
| Operation | Number of multiplications |
| (3.47) | |
| (3.48) | |
| (3.49) |
Hence, the total complexity of SS–SMT–SD is
The detailed number of multiplication operations needed by SS‐SMT‐SD is shown in Table 3.10, where ![]() (3.53) and
(3.53) and ![]() (3.54) are the number of points in the bounds (3.53) and (3.54), respectively.
(3.54) are the number of points in the bounds (3.53) and (3.54), respectively.
Table 3.10 Detailed complexity analysis of DS‐SMTs‐SD.
| Operation | Number of multiplications |
| (3.53) | |
| (3.54) | |
| (3.49) |
Hence, the total complexity of DS‐SMT‐SD is,
3.10.2.6 Error Probability Analysis and Initial Radius
The pairwise error probability (PEP) of deciding on the point ![]() given that the point
given that the point ![]() is transmitted can be written as
is transmitted can be written as
The probability of error in (3.57) can be thought of as two mutually exclusive events depending on whether the transmitted point ![]() is inside the sphere or not. In other words, the probability of error for SMT–SD can be separated in two parts as [180],
is inside the sphere or not. In other words, the probability of error for SMT–SD can be separated in two parts as [180],
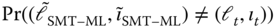 : The probability of deciding on the incorrect transmitted symbol and/or used antenna combination, given that the transmitted point
: The probability of deciding on the incorrect transmitted symbol and/or used antenna combination, given that the transmitted point  is inside the sphere.
is inside the sphere. : The probability that the transmitted point
: The probability that the transmitted point  is outside the set of points
is outside the set of points  considered by the SMT–SD.
considered by the SMT–SD.
From (3.58), SMT–SD will have a near optimum performance when,
The probability of not having the transmitted point ![]() inside
inside ![]() can be written as
can be written as
where ![]() is the
is the ![]() row of
row of ![]() , and
, and

is a central chi‐squared random variable (RV) with ![]() degrees of freedom,
degrees of freedom, ![]() is the
is the ![]() element of
element of ![]() , and the cumulative distribution function (CDF) of a chi‐squared RV is given by [120],
, and the cumulative distribution function (CDF) of a chi‐squared RV is given by [120],

where ![]() is the lower incomplete gamma function given by
is the lower incomplete gamma function given by
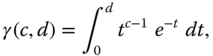
and ![]() is the gamma function given by
is the gamma function given by

The initial radius considered in SMT–SD is a function of the noise variance as given in [181],
where ![]() is a constant chosen to satisfy (3.59). This can be done by setting
is a constant chosen to satisfy (3.59). This can be done by setting ![]() and back solving (3.60). For
and back solving (3.60). For ![]() ,
, ![]() , respectively.
, respectively.
3.11 Transmitter Power Consumption Analysis
The approximate transmitter power consumption for the different SMTs and GSMTs is calculated in what follows. In particular, the transmitter designs for SSK, SM, QSSK, QSM, GSSK, GSM, GQSSK, and GQSM are considered in the analysis. The results are compared to SMX system with the previously presented transmitter design.
For power consumption analysis, the EARTH power model is considered, which describes the relation between the total power supplied or consumed by a transceiver system and the RF transmit power under the assumptions of full load and sleep mode [182, 183].
Therefore and through the EARTH model, the power consumptions for SMX, SSK, SM, QSM, and QSSK systems are calculated as follows [[40, 182], Eq. (1.2), p. 7]:
where ![]() denotes the minimum consumed power per RF‐chain,
denotes the minimum consumed power per RF‐chain, ![]() is the slope of the load dependent power consumption,
is the slope of the load dependent power consumption, ![]() is the total RF transmit power [182],
is the total RF transmit power [182], ![]() is the consumed power by a single RF switch, and
is the consumed power by a single RF switch, and ![]() denotes the number of needed single pole double through (SPDT) RF switches to implement the transmitter of the corresponding scheme. It should be noted here that different RF switches with variable number of output terminals can be considered and will lead to different results. However, SPDT switches are widely available and achieve the least switching time, which in turn means maximum possible data rate for SMTs. Each SPDT switch is connected to two transmit antennas. Hence, the number of needed RF switches to achieve a target spectral efficiency,
denotes the number of needed single pole double through (SPDT) RF switches to implement the transmitter of the corresponding scheme. It should be noted here that different RF switches with variable number of output terminals can be considered and will lead to different results. However, SPDT switches are widely available and achieve the least switching time, which in turn means maximum possible data rate for SMTs. Each SPDT switch is connected to two transmit antennas. Hence, the number of needed RF switches to achieve a target spectral efficiency, ![]() , for each SMT scheme is calculated as
, for each SMT scheme is calculated as
In [182], the relation between the power consumption for various base station types as a function of the RF output power is reported. Four types of base stations are considered in the conducted study in [182] including Macro, Micro, Pico, and Femto cells base stations. Any of these models can be considered in the presented comparative study between different systems. Here Macro‐type base station is assumed, and the reported numbers in [[182], Table 1.2, p. 8] are adopted, which are ![]() = 53 W,
= 53 W, ![]() , and
, and ![]() = 6.3 W. In addition, the consumed power by a single SPDT RF switch is assumed to be
= 6.3 W. In addition, the consumed power by a single SPDT RF switch is assumed to be ![]() mW [184]. It is important to note that even
mW [184]. It is important to note that even ![]() and
and ![]() have the same formula, the total consumed power is not equal since the number of required RF switches to achieve a target spectral efficiency is not the same. Similarly,
have the same formula, the total consumed power is not equal since the number of required RF switches to achieve a target spectral efficiency is not the same. Similarly, ![]() and
and ![]() are not equal.
are not equal.
For the generalized version of SMTs, GSMTs, the anticipated power consumption depends on the value of ![]() and
and ![]() . For a specific spectral efficiency, the needed number of transmit antennas by each GSMT system can be calculated and used to compute the required number of RF switches. Assume,
. For a specific spectral efficiency, the needed number of transmit antennas by each GSMT system can be calculated and used to compute the required number of RF switches. Assume, ![]() , the number of antennas for specific
, the number of antennas for specific ![]() is
is

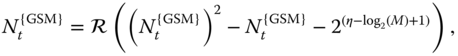


where ![]() denotes a positive root greater than one of the polynomial function.
denotes a positive root greater than one of the polynomial function.
As such, the power consumption for GSSK, GSM, GQSM, and GQSSK systems is calculated as
Again, ![]() and
and ![]() have the same formula, but the total consumed power is not equal since the number of required RF switches to achieve a target spectral efficiency in not the same. Similarly,
have the same formula, but the total consumed power is not equal since the number of required RF switches to achieve a target spectral efficiency in not the same. Similarly, ![]() and
and ![]() are not equal. Assuming that SPDT RF switches, where each switch can serve two transmit antennas, the number of needed RF switches for the different GSMTs is given by
are not equal. Assuming that SPDT RF switches, where each switch can serve two transmit antennas, the number of needed RF switches for the different GSMTs is given by
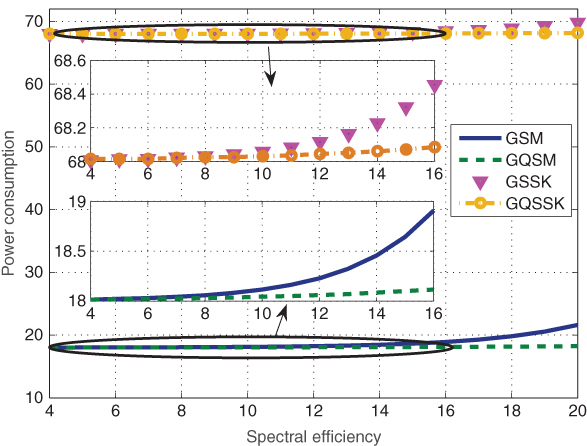
Figure 3.18 Transmitter power consumption for GSM, GQSM, GSSK, and GQSSK MIMO systems. For GSM and GQSM,  is assumed.
is assumed.
3.11.1 Power Consumption Comparison
The transmitter power consumptions for all SMTs and GSMTs are discussed in what follows. Results for SMTs are illustrated in Figure 3.19 and for GSMTs are shown in Figure 3.18. The consumed power by each system is depicted versus the target spectral efficiency, which is varied from ![]() = 4 to 20 bits. For SM, QSM, GSM, and GQSM,
= 4 to 20 bits. For SM, QSM, GSM, and GQSM, ![]() ‐QAM is assumed, and for GSMTs,
‐QAM is assumed, and for GSMTs, ![]() is considered. Besides the required number of transmit antennas to achieve a target spectral efficiency for all schemes is computed and illustrated in Figure 3.20. The number of needed RF switches can be calculated from the computed number of transmit antennas and used in the power analysis. For all systems, SPDT RF switches are considered, where each switch is connected to two transmit antennas. Interesting results are noticed in the figures, where SSK and GSSK demonstrate very low power consumption for relatively low spectral efficiencies. However, both schemes demonstrate a significant increase in power consumption at higher spectral efficiencies, where SSK demonstrates the maximum power consumption among all SMTs and SMX at
is considered. Besides the required number of transmit antennas to achieve a target spectral efficiency for all schemes is computed and illustrated in Figure 3.20. The number of needed RF switches can be calculated from the computed number of transmit antennas and used in the power analysis. For all systems, SPDT RF switches are considered, where each switch is connected to two transmit antennas. Interesting results are noticed in the figures, where SSK and GSSK demonstrate very low power consumption for relatively low spectral efficiencies. However, both schemes demonstrate a significant increase in power consumption at higher spectral efficiencies, where SSK demonstrates the maximum power consumption among all SMTs and SMX at ![]() bits. This is because SSK scheme needs
bits. This is because SSK scheme needs ![]() RF switches at 20 bits spectral efficiency, while GSSK needs 725 RF switches at that particular spectral efficiency. However, QSSK scheme requires only 512 RF switches, and GQSSK needs 23 switches at this spectral efficiency. For the same reason, the exponential growth of the SM and GSM power consumptions at higher spectral efficiencies can be explained, where SM needs
RF switches at 20 bits spectral efficiency, while GSSK needs 725 RF switches at that particular spectral efficiency. However, QSSK scheme requires only 512 RF switches, and GQSSK needs 23 switches at this spectral efficiency. For the same reason, the exponential growth of the SM and GSM power consumptions at higher spectral efficiencies can be explained, where SM needs ![]() switches and GSM needs 363 switches at
switches and GSM needs 363 switches at ![]() bits, while QSM and GQSM systems can be, respectively, implemented with 256 and 17 RF switches at this spectral efficiency. However, all SMTs and GSMTs except SSK and SM are shown to consume much less power than SMX system for all depicted spectral efficiencies. SM and SSK are shown to be power efficient schemes at moderate spectral efficiencies, where comparing SM to SMX at spectral efficiencies of
bits, while QSM and GQSM systems can be, respectively, implemented with 256 and 17 RF switches at this spectral efficiency. However, all SMTs and GSMTs except SSK and SM are shown to consume much less power than SMX system for all depicted spectral efficiencies. SM and SSK are shown to be power efficient schemes at moderate spectral efficiencies, where comparing SM to SMX at spectral efficiencies of ![]() bits is shown to, respectively, provide 150 W and 247 W gains.
bits is shown to, respectively, provide 150 W and 247 W gains.

Figure 3.19 Transmitter power consumption for SM, QSM, SSK, and QSSK MIMO systems. For SM and QSM,  is assumed. Also, for all SMTs, SPDT RF switches are considered in all systems.
is assumed. Also, for all SMTs, SPDT RF switches are considered in all systems.

Figure 3.20 Needed number of transmit antennas to achieve a target spectral efficiency for SSK, SM, QSSK, QSM, GSSK, GSM, GQSSK, and GQSM MIMO systems. For SM, QSM, GSM, and GQSM,  is assumed and for all GSMTs
is assumed and for all GSMTs  is considered.
is considered.
3.12 Hardware Cost
A rough estimate of the implementation cost for each SMTs and GSMTs system is calculated based on the available off‐the‐shelf components. The different implementation elements can be categorized as follows:
 : The cost of one RF‐chain (includes signal modulation, pulse shaping, and I/Q modulator blocks);
: The cost of one RF‐chain (includes signal modulation, pulse shaping, and I/Q modulator blocks); : The cost of a memory module such as microcontroller with a DAC chip;
: The cost of a memory module such as microcontroller with a DAC chip; : The cost of a serial to parallel converter;
: The cost of a serial to parallel converter; : The cost of one SPDT RF switch.
: The cost of one SPDT RF switch.
The cost of the required hardware items to implement the transmitter for each of SSK, QSSK, SM, QSM, and SMX is given by [40],
Similarly, the cost of the required hardware items to implement the transmitter for each of the GSMTs systems is calculated as
For evaluation and comparison purposes, the prices listed in Table 3.11 for the different elements are considered.
Table 3.11 Hardware items cost in US$.
| Item | Cost ($) |
| 180 [185] | |
| 4 [186] | |
| 2 [187] | |
| 2 [184] |
3.12.1 Hardware Cost Comparison
A rough estimate for the cost of deploying the transmitter of different SMTs and GSMTs is illustrated in Figures 3.21 and 3.22, respectively. ![]() is assumed for SM, QSM, GSM, and GQSM, and SPDT RF switch is assumed for all systems. Also,
is assumed for SM, QSM, GSM, and GQSM, and SPDT RF switch is assumed for all systems. Also, ![]() is considered for generalized systems.
is considered for generalized systems.
Similar trend as noticed for the power consumption is seen here as well. Hardware implementation costs for SSK and GSSK schemes increase exponentially with the increase of spectral efficiency due the exponential growth of the needed number of RF switches. However, it can be seen that implementing GSSK scheme costs much less than all other SMTs. This is because GSSK requires less number of transmit antennas for the same spectral efficiency and can be implemented without any RF‐chains, which in turn means less number of RF switches and reduced cost. For ![]() bits, the cost for implementing SSK system is shown to be very high and exceeds all other system costs. Similar trend can be seen as well for SM system and can be referred to the same reason as for SSK scheme. SMX implementation demonstrates the maximum cost for
bits, the cost for implementing SSK system is shown to be very high and exceeds all other system costs. Similar trend can be seen as well for SM system and can be referred to the same reason as for SSK scheme. SMX implementation demonstrates the maximum cost for ![]() bits. However, the cost of implementing SSK and SM, respectively, exceed the cost of SMX at
bits. However, the cost of implementing SSK and SM, respectively, exceed the cost of SMX at ![]() and
and ![]() bits. The implementation cost of QSM and QSSK is shown to be moderate and much lower than all other system's costs. Similar trends can be seen for GSMT's results in Figure 3.22. Again, implementing GSM and GSSK schemes is shown to cost much more than other schemes at high spectral efficiencies.
bits. The implementation cost of QSM and QSSK is shown to be moderate and much lower than all other system's costs. Similar trends can be seen for GSMT's results in Figure 3.22. Again, implementing GSM and GSSK schemes is shown to cost much more than other schemes at high spectral efficiencies.

Figure 3.21 Transmitter implementation cost for SM, QSM, SSK, and QSSK assuming  and SPDT RF switches.
and SPDT RF switches.

Figure 3.22 Transmitter implementation cost for GSM, GQSM, GSSK, and GQSSK assuming  and SPDT RF switches.
and SPDT RF switches.
3.13 SMTs Coherent and Noncoherent Spectral Efficiencies
The realizable spectral efficiencies for DQSM, QSM, DSM, SM, DSSK, and SSK systems with different number of transmit antennas, ![]() , and with
, and with ![]() ‐QAM/PSK modulation are compared in Figure 3.23. It can be seen from the figure that quadrature space modulation techniques (QSMTs), such as QSM and DQSM, offer an increase in spectral efficiency in comparison to their SMTs counterpart. Comparing QSM to SM, 1 bit more data can be attained with
‐QAM/PSK modulation are compared in Figure 3.23. It can be seen from the figure that quadrature space modulation techniques (QSMTs), such as QSM and DQSM, offer an increase in spectral efficiency in comparison to their SMTs counterpart. Comparing QSM to SM, 1 bit more data can be attained with ![]() , which increases to 2 and 3 bits for
, which increases to 2 and 3 bits for ![]() , respectively. As discussed earlier, this enhancement equals
, respectively. As discussed earlier, this enhancement equals ![]() , which increases logarithmically with the number of transmit antennas. SSK scheme is shown in Figure 3.23 to achieve the least spectral efficiency among all SMTs as it depends only on
, which increases logarithmically with the number of transmit antennas. SSK scheme is shown in Figure 3.23 to achieve the least spectral efficiency among all SMTs as it depends only on ![]() . SM, on the other hand, increases SSK's spectral efficiency by the number of transmitted bits in the signal domain,
. SM, on the other hand, increases SSK's spectral efficiency by the number of transmitted bits in the signal domain, ![]() . Similarly, QSM enhances SSK's spectral efficiency by
. Similarly, QSM enhances SSK's spectral efficiency by ![]() .
.
Finally, the spectral efficiency of differential space modulation techniques (DSMTs) is shown in Figure 3.23 to increase with an arbitrary number of transmit antennas, which is not necessarily being a power of 2. Furthermore, SMTs are shown to always achieve higher spectral efficiencies than DSMTs in Figure 3.23 for the same ![]() . Also, DQSM always achieve higher spectral efficiency than that of DSM system and achieving similar spectral efficiency for both schemes with 4‐QAM modulation is only possible with
. Also, DQSM always achieve higher spectral efficiency than that of DSM system and achieving similar spectral efficiency for both schemes with 4‐QAM modulation is only possible with ![]() for DQSM and
for DQSM and ![]() for DSM.
for DSM.

Figure 3.23 A comparison of achievable spectral efficiencies with variable number of transmit antennas,  , and with
, and with  ‐QAM modulation for different techniques including DQSM, QSM, DSM, SM, DSSK, and SSK systems.
‐QAM modulation for different techniques including DQSM, QSM, DSM, SM, DSSK, and SSK systems.