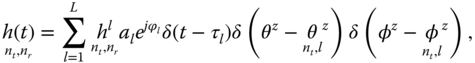Chapter 7
SMTs for Millimeter‐Wave Communications
Millimeter‐wave (mmWave) communications offer a plenty of frequency spectrum, ranging from 30 to 300 GHz, that can be exploited to achieve multi‐gigabits per second (Gb/s) data rates [257–259]. The E‐band at ![]() GHz offers 1 Gb s
GHz offers 1 Gb s![]() up to 10 Gb s
up to 10 Gb s![]() for typical distances of 3 km with an available worldwide low‐cost license [260]. Also, it has been demonstrated in [260–263] that wave propagation at E‐band has negligible atmospheric attenuation (less than 0.5 dB km
for typical distances of 3 km with an available worldwide low‐cost license [260]. Also, it has been demonstrated in [260–263] that wave propagation at E‐band has negligible atmospheric attenuation (less than 0.5 dB km![]() ) and is unaffected by dust, snow, and any other channel deterioration. Although heavy rain is shown to significantly impact the performance of E‐band mmWave systems. However, heavy rain usually occurs in limited part of the world [264], and the radio link can be designed to overcome the attenuation resulted from heavy rain [260]. As such, mmWave technology is one of the promising techniques for 5G and beyond wireless standards, and it has been adopted in several recent standards such as mmWave WPAN (IEEE 802.15.3c‐2009) [265], WiGig (IEEE 802.11ad) [266], and WirelessHD [267].
) and is unaffected by dust, snow, and any other channel deterioration. Although heavy rain is shown to significantly impact the performance of E‐band mmWave systems. However, heavy rain usually occurs in limited part of the world [264], and the radio link can be designed to overcome the attenuation resulted from heavy rain [260]. As such, mmWave technology is one of the promising techniques for 5G and beyond wireless standards, and it has been adopted in several recent standards such as mmWave WPAN (IEEE 802.15.3c‐2009) [265], WiGig (IEEE 802.11ad) [266], and WirelessHD [267].
The use of mmWave for multiple–input multiple–output (MIMO) systems requires careful design of propagation characteristics of radio signals. The signals at mmWave frequencies propagate in line‐of‐sight (LOS) environment and do not penetrate solid materials very well. Several experimental studies on mmWave outdoor channel modeling proved that the channel can be safely modeled as LOS or near LOS links [268–273]. The performance of several space modulation technique (SMT) systems over LOS mmWave channel has been studied in [51, 56, 210, 274–277]. Another experimental work conducted by New York University (NYU) Wireless Lab developed a three‐dimensional (3D) modeling of the mmWave channel [258, 259, 278–280]. The 3D channel models are comprehensive and fit the conducted measurements. The performance of quadrature spatial modulation (QSM) over the 3D mmWave channel model was studied in [55], and a performance comparison between spatial modulation (SM) and spatial multiplexing (SMX) systems over the 3D mmWave model is presented in [53, 54].
In this chapter, we will present both mmWave channel models, LOS and 3D, and discuss the performance of SMTs over such channel models.
7.1 Line of Sight mmWave Channel Model
In an LOS channel model, it is generally assumed that the antenna arrays at both the transmitter and the receiver are uniformly spaced and aligned to the broadside of each other. As such, the ![]() column of the
column of the ![]() LOS MIMO channel matrix,
LOS MIMO channel matrix, ![]() , can be modeled as [270, 272]
, can be modeled as [270, 272]
where ![]() is the distance between the transmitter antenna array and the receiver antenna array,
is the distance between the transmitter antenna array and the receiver antenna array, ![]() denotes the
denotes the ![]() transmit antenna vector containing all channel paths between the
transmit antenna vector containing all channel paths between the ![]() antenna and all receive antennas,
antenna and all receive antennas, ![]() is the distance vector between
is the distance vector between ![]() transmit antenna and all receive antennas, and
transmit antenna and all receive antennas, and ![]() is the carrier wavelength with
is the carrier wavelength with ![]() being the carrier frequency and
being the carrier frequency and ![]() denoting the speed of light. Furthermore, the signal‐to‐noise‐ratio (SNR) is defined as
denoting the speed of light. Furthermore, the signal‐to‐noise‐ratio (SNR) is defined as ![]() , where
, where ![]() .
.
7.1.1 Capacity Analysis
It is shown in Chapter 5 that the capacity of SMT systems is given by
where ![]() is the number of receiver antennas. It is also demonstrated that achieving the capacity depends on the channel, where the distribution of the multiplication of the spatial,
is the number of receiver antennas. It is also demonstrated that achieving the capacity depends on the channel, where the distribution of the multiplication of the spatial, ![]() , and signal,
, and signal, ![]() , symbols has to follow a complex Gaussian distribution
, symbols has to follow a complex Gaussian distribution ![]() , where
, where ![]() is an
is an ![]() ‐length of all zeros vector, and
‐length of all zeros vector, and ![]() is an
is an ![]() identity matrix.
identity matrix.
In what follows and for illustration purposes, the conditions under which the capacity of SM and QSM can be achieved for LOS mmWave channel are derived and discussed.
7.1.1.1 SM
In SM, the spatial and signal symbols are ![]() and
and ![]() , where
, where ![]() is a symbol drawn from a complex constellation diagram such as quadrature amplitude modulation (QAM) or phase shift keying (PSK).
is a symbol drawn from a complex constellation diagram such as quadrature amplitude modulation (QAM) or phase shift keying (PSK).
The spatial symbol generated from channel coefficients in (7.1) can be rewritten as
where ![]() . Hence, the transmitted SM symbol can be written as
. Hence, the transmitted SM symbol can be written as
To achieve the capacity, ![]() has to follow a complex Gaussian distribution. Knowing that the complex Gaussian distribution has Rayleigh distribution amplitude and uniform distribution phase, the capacity can be achieved if the phase of the spatial symbols is
has to follow a complex Gaussian distribution. Knowing that the complex Gaussian distribution has Rayleigh distribution amplitude and uniform distribution phase, the capacity can be achieved if the phase of the spatial symbols is ![]() , and the signal symbols are either Rayleigh distributed or complex Gaussian distributed. Note, the sum of two random phases with
, and the signal symbols are either Rayleigh distributed or complex Gaussian distributed. Note, the sum of two random phases with ![]() distribution is also a
distribution is also a ![]() .
.
7.1.1.2 QSM
For QSM, the spatial and signal symbols are ![]() and
and ![]() , respectively. Hence, and from (7.3), the transmitted QSM symbols are
, respectively. Hence, and from (7.3), the transmitted QSM symbols are
From (7.5) and from the discussion in the previous section for SM, the capacity can be achieved if the phase of the spatial symbol is uniformly distributed in the range ![]() , and the signal symbols are Rayleigh distributed.
, and the signal symbols are Rayleigh distributed.
7.1.1.3 Randomly Spaced Antennas
It is shown in previous sections that the capacity can be achieved if the different ![]() channel vectors follow a circular uniform distribution.
1 In other words, to achieve the capacity, the different
channel vectors follow a circular uniform distribution.
1 In other words, to achieve the capacity, the different ![]() channel vectors have to be i) not equal; ii) chosen equally likely; iii) and have an absolute value equal to the channel gain. The last two conditions are already fulfilled, because 1) the different
channel vectors have to be i) not equal; ii) chosen equally likely; iii) and have an absolute value equal to the channel gain. The last two conditions are already fulfilled, because 1) the different ![]() transmit antennas are chosen equally likely since no precoding is assumed and 2) the considered LOS mmWave channel is a phase shift with a constant amplitude as given in (7.1).
transmit antennas are chosen equally likely since no precoding is assumed and 2) the considered LOS mmWave channel is a phase shift with a constant amplitude as given in (7.1).
The first condition aims at decorrelating the MIMO channel matrix and is of significant research interest. Therefore, it has been intensively studied in literature, and an algorithm called optimally spaced antennas (OSA) is considered in [[270, 272, 274], and references therein]. In OSA, the distance between the neighbor transmit antennas, ![]() , and the neighbor receive antennas,
, and the neighbor receive antennas, ![]() , is chosen in a way that achieves an orthogonal channel as
, is chosen in a way that achieves an orthogonal channel as
However, it has been shown in [282] that the assumption of orthogonal channel paths in (7.6) is only valid for a number of receive antennas that is larger or equal to the number of transmit antennas, ![]() . But, for
. But, for ![]() , the channel will not be orthogonal, and the first condition will not be fulfilled. For example, for
, the channel will not be orthogonal, and the first condition will not be fulfilled. For example, for ![]() m,
m, ![]() GHz,
GHz, ![]() , and
, and ![]() cm the channel matrix
cm the channel matrix ![]() is
is
It can be clearly seen from (7.7) that the channel paths to the first receive antenna (![]() ) and to the third receive antenna (
) and to the third receive antenna (![]() ) are equal. Similarly, the channel paths to the second and fourth receive antennas,
) are equal. Similarly, the channel paths to the second and fourth receive antennas, ![]() and
and ![]() , are also equal. Thus, capacity cannot be achieved as the
, are also equal. Thus, capacity cannot be achieved as the ![]() channel paths are highly correlated.
channel paths are highly correlated.
To overcome the limitations of OSA in an unbalanced MIMO configuration, a method called randomly spaced antennas (RSA) was proposed in [51]. In RSA, the transmit and receive antennas are randomly distributed along the broadside of each other according to uniform distributions in the ranges of ![]() and
and ![]() , respectively, where
, respectively, where ![]() and
and ![]() are the maximum transmit and receive array lengths. This guarantees that the
are the maximum transmit and receive array lengths. This guarantees that the ![]() channel paths are not equal.
channel paths are not equal. ![]() and
and ![]() are chosen to be equal to the maximum transmit and receive array lengths if OSA was used,
are chosen to be equal to the maximum transmit and receive array lengths if OSA was used,
Using the same system setup for the example in (7.7), the maximum lengths of the transmit and receive antenna arrays are ![]() cm and
cm and ![]() cm. Based on the maximum lengths, the distances of the transmit and receive antennas to the start of the antenna array are chosen randomly according to uniform distribution in the ranges of
cm. Based on the maximum lengths, the distances of the transmit and receive antennas to the start of the antenna array are chosen randomly according to uniform distribution in the ranges of ![]() and
and ![]() , respectively. The resultant distances for the four transmit antennas are 2.7, 17.9, 26, and 30.4 cm from the start of the transmit array, and the two receive antennas are 2.6 and 8.3 cm from the start of the receive array. The channel matrix is then obtained as,
, respectively. The resultant distances for the four transmit antennas are 2.7, 17.9, 26, and 30.4 cm from the start of the transmit array, and the two receive antennas are 2.6 and 8.3 cm from the start of the receive array. The channel matrix is then obtained as,
It is evident from (7.10) that unlike (7.7), the four channel paths are not equal and the first condition is fulfilled even for ![]() .
.

Figure 7.1 Simulated mutual information comparison for mmWave‐SM over OSA and RSA channels, with  GHz,
GHz,  m,
m,  ,
,  and
and  , and
, and  .
.

Figure 7.2 ABER performance comparison for mmWave‐QSM over OSA and RSA channels, with  GHz,
GHz,  m,
m,  bits,
bits,  , and
, and  , and
, and  .
.
Figure 7.1 compares the mutual information of mmWave‐SM for ![]() bits,
bits, ![]() and
and ![]() , and
, and ![]() , while considering RSA and OSA channel design algorithms. It is seen in the figure that for unbalanced MIMO systems, where
, while considering RSA and OSA channel design algorithms. It is seen in the figure that for unbalanced MIMO systems, where ![]() , the performance of RSA algorithm is much better than the OSA method. Mutual information gains of
, the performance of RSA algorithm is much better than the OSA method. Mutual information gains of ![]() bits at SNR=
bits at SNR= ![]() and
and ![]() dB, respectively, can be clearly noticed in the figure. Besides it is demonstrated in Figure 7.1 that SM with RSA reaches the maximum mutual information of
dB, respectively, can be clearly noticed in the figure. Besides it is demonstrated in Figure 7.1 that SM with RSA reaches the maximum mutual information of ![]() bits, 36 dB earlier than OSA. These enhancements are because RSA algorithm insures that the channel follows a circular uniform distribution for unbalanced MIMO systems. However, in Figure 7.1, OSA is shown to have a better performance as compared to RSA for
bits, 36 dB earlier than OSA. These enhancements are because RSA algorithm insures that the channel follows a circular uniform distribution for unbalanced MIMO systems. However, in Figure 7.1, OSA is shown to have a better performance as compared to RSA for ![]() , where OSA offers
, where OSA offers ![]() , and
, and ![]() bits at SNR=
bits at SNR= ![]() , and
, and ![]() dB, respectively. Moreover, SM with OSA reaches the maximum mutual information 5 dB earlier than RSA. That is because circular uniform distribution is a continuous distribution, and RSA for small number of antennas offers a discrete circular uniform distribution. Hence, for RSA to perform better even for
dB, respectively. Moreover, SM with OSA reaches the maximum mutual information 5 dB earlier than RSA. That is because circular uniform distribution is a continuous distribution, and RSA for small number of antennas offers a discrete circular uniform distribution. Hence, for RSA to perform better even for ![]() , a very large number of transmit antennas should be used, i.e. large‐scale‐MIMO. Fortunately, this is not a problem with SMT as the computational complexity does not increase much with the number of transmit antennas. In addition, using mmWave allows more transmit antennas to be deployed in a small space. Yet, RSA by itself would not achieve the capacity as the signal symbol has to be especially shaped in accordance with the used SMT system to achieve the capacity. In Figure 7.1, uniformly distributed QAM symbols were used.
, a very large number of transmit antennas should be used, i.e. large‐scale‐MIMO. Fortunately, this is not a problem with SMT as the computational complexity does not increase much with the number of transmit antennas. In addition, using mmWave allows more transmit antennas to be deployed in a small space. Yet, RSA by itself would not achieve the capacity as the signal symbol has to be especially shaped in accordance with the used SMT system to achieve the capacity. In Figure 7.1, uniformly distributed QAM symbols were used.

Figure 7.3 Simulated mutual information comparison between SM, QSM, and SMX over LOS mmWave channel using OSA, with  GHz,
GHz,  m,
m,  and
and  bits, and
bits, and  .
.

Figure 7.4 Simulated mutual information comparison between SM with  and SMX with
and SMX with  over LOS mmWave channel, where
over LOS mmWave channel, where  GHz,
GHz,  m,
m,  bits, and
bits, and  .
.
The performance enhancement offered by RSA for ![]() can also be seen in the average bit error ratio (ABER) curves depicted in Figure 7.2. It can be seen that RSA offers 32 dB gain in the SNR for
can also be seen in the average bit error ratio (ABER) curves depicted in Figure 7.2. It can be seen that RSA offers 32 dB gain in the SNR for ![]() . However, for
. However, for ![]() , OSA offers better ABER performance than RSA, 3.5 and 2 dB can be noticed for
, OSA offers better ABER performance than RSA, 3.5 and 2 dB can be noticed for ![]() and
and ![]() , respectively.
, respectively.
7.1.1.4 Capacity Performance Comparison
Monte Carlo simulation results for the mutual information of SM, QSM, and SMX over LOS mmWave channel for ![]() and
and ![]() and
and ![]() are depicted in Figure 7.3. It is shown that for
are depicted in Figure 7.3. It is shown that for ![]() , SM offers 0.4 bit higher mutual information than SMX. However, for higher spectral efficiency,
, SM offers 0.4 bit higher mutual information than SMX. However, for higher spectral efficiency, ![]() , SMX outperforms QSM and SM, where it reaches the maximum mutual information 4 and 8 dB earlier.
, SMX outperforms QSM and SM, where it reaches the maximum mutual information 4 and 8 dB earlier.
Figure 7.4 depicts the simulated mutual information for SM with ![]() and SMX with
and SMX with ![]() , where
, where ![]() bits and
bits and ![]() . It can be seen that using a large number of transmit antennas for SM enhances the performance, where a gain of about 0.8 bit and 2 dB better than SMX is reported. Thus, large‐scale SMTs promises significant gains for LOS mmWave communication systems.
. It can be seen that using a large number of transmit antennas for SM enhances the performance, where a gain of about 0.8 bit and 2 dB better than SMX is reported. Thus, large‐scale SMTs promises significant gains for LOS mmWave communication systems.

Figure 7.5 ABER performance comparison between SM, QSM and SMX over LOS mmWave channel using RSA, with  GHz,
GHz,  m,
m,  and
and  bits,
bits,  , and
, and  .
.
7.1.2 Average Bit Error Rate Results
The ABER performance comparison for different spectral efficiencies and MIMO setups between SM, QSM, and SMX is depicted in Figures 7.5 and 7.6. As discussed in previous section, for ![]() , RSA is the best to use, and for
, RSA is the best to use, and for ![]() , OSA is a better choice. Therefore, in Figure 7.5 where
, OSA is a better choice. Therefore, in Figure 7.5 where ![]() , RSA is used, and in Figure 7.6, where
, RSA is used, and in Figure 7.6, where ![]() OSA is considered.
OSA is considered.

Figure 7.6 ABER performance comparison between SM, QSM and SMX over LOS mmWave channel using OSA, with  GHz,
GHz,  m,
m,  and
and  bits,
bits,  , and
, and  .
.
In Figure 7.5 where ![]() , it can be seen that for
, it can be seen that for ![]() bits, SM outperforms SMX by about 2.8 dB. However, for larger spectral efficiency,
bits, SM outperforms SMX by about 2.8 dB. However, for larger spectral efficiency, ![]() , SMX performs 1.5 dB better than SM. The same can be seen in Figure 7.6 for
, SMX performs 1.5 dB better than SM. The same can be seen in Figure 7.6 for ![]() , where for
, where for ![]() , SM performs 1.9 dB better than SMX. But, for larger spectral efficiency,
, SM performs 1.9 dB better than SMX. But, for larger spectral efficiency, ![]() , SMX performs 7.2 dB better than SM. That is because SMX uses much smaller constellation size as compared to SM at high spectral efficiencies. Furthermore and from both Figures 7.5 and 7.6, it can be seen that QSM offers 1.2 dB better performance than SMX for
, SMX performs 7.2 dB better than SM. That is because SMX uses much smaller constellation size as compared to SM at high spectral efficiencies. Furthermore and from both Figures 7.5 and 7.6, it can be seen that QSM offers 1.2 dB better performance than SMX for ![]() . Yet, for
. Yet, for ![]() , QSM performs 4.2 dB worse than SMX. That is because for
, QSM performs 4.2 dB worse than SMX. That is because for ![]() , RSA is used, which is designed so that QSM would achieve near capacity.
, RSA is used, which is designed so that QSM would achieve near capacity.
One of the advantages offered by mmWave communications is that a large number of antennas can be installed in small spaces. Furthermore, in SMTs and unlike SMX, increasing the number of transmit antennas comes with nearly no cost, as only a maximum of single radio frequency (RF) chain is needed as illustrated earlier. Hence, large‐scale SMTs are very good candidates for mmWave communications. Figure 7.7 demonstrates a comparison between SMX with ![]() and SM with a larger number of transmit antennas
and SM with a larger number of transmit antennas ![]() , where OSA is used and
, where OSA is used and ![]() . It can be seen that SM offers 2 dB better performance than SMX, where increasing the number of transmit antennas increased the size of the spatial constellation diagram and decreased the size of the needed signal constellation diagram. In conclusion, even though SMX offers better performance than SM for equal number of transmit antennas, SM would outperform SMX when using larger number of transmit antennas.
. It can be seen that SM offers 2 dB better performance than SMX, where increasing the number of transmit antennas increased the size of the spatial constellation diagram and decreased the size of the needed signal constellation diagram. In conclusion, even though SMX offers better performance than SM for equal number of transmit antennas, SM would outperform SMX when using larger number of transmit antennas.

Figure 7.7 ABER performance comparison between SM with  and SMX with
and SMX with  over LOS mmWave channel, where
over LOS mmWave channel, where  GHz,
GHz,  m,
m,  bits, and
bits, and  .
.
7.2 Outdoor Millimeter‐Wave Communications 3D Channel Model
In [258, 259, 278–280], NYU Wireless Lab proposed a 3D model for outdoor (mmWave) channels. The proposed model is comprehensive, and therefore, it is adopted in this section to study the ABER and capacity performance of the SMTs over outdoor mmWave channels.
The 3D mmWave channel model and measurements in [259] consider omni directional antennas operating at mmWave frequencies. The channel impulse response ![]() for the
for the ![]() th and
th and ![]() th transmit and receive antennas can be calculated using the double‐directional channel model proposed in [283, 284] and given by
th transmit and receive antennas can be calculated using the double‐directional channel model proposed in [283, 284] and given by
where ![]() is the
is the ![]() th subpath complex channel attenuation between the
th subpath complex channel attenuation between the ![]() th and
th and ![]() th transmit and receive antennas,
th transmit and receive antennas, ![]() ,
, ![]() , and
, and ![]() are the amplitude, phase, and absolute propagation delay of the
are the amplitude, phase, and absolute propagation delay of the ![]() th subpath,
th subpath, ![]() , and
, and ![]() are the vectors of azimuth/elevation angle of departure (AOD) and angle of arrival (AoA) for the
are the vectors of azimuth/elevation angle of departure (AOD) and angle of arrival (AoA) for the ![]() th and
th and ![]() th transmit and receive antennas, respectively, and
th transmit and receive antennas, respectively, and ![]() is the total number of multipath components.
is the total number of multipath components.
Assuming that the antenna arrays at both the transmitter and the receiver is uniformly spaced with distance ![]() and aligned along the
and aligned along the ![]() ‐dimension, the impulse response in (7.11) can be reduced to
‐dimension, the impulse response in (7.11) can be reduced to
where ![]() and
and ![]() denoting the elevation AOD and AOA for the
denoting the elevation AOD and AOA for the ![]() th and
th and ![]() th transmit and receive antennas, respectively.
th transmit and receive antennas, respectively.
From [285], the transfer function of the impulse response in (7.12) is given by

where ![]() is the carrier wavelength.
is the carrier wavelength.
The values of ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() in this chapter are generated using the 3D statistical channel model for outdoor mmWave communications derived in [259], where the frequency is 73 GHz, antenna gains are 24.5 dBi, and the distance at each particular time instance is varied equally likely in the range of
in this chapter are generated using the 3D statistical channel model for outdoor mmWave communications derived in [259], where the frequency is 73 GHz, antenna gains are 24.5 dBi, and the distance at each particular time instance is varied equally likely in the range of ![]() [259].
[259].
Furthermore, let ![]() be an
be an ![]() matrix containing all
matrix containing all ![]() complex MIMO channel attenuations, then, from [284],
complex MIMO channel attenuations, then, from [284],
where ![]() and
and ![]() are the transmitter and receiver correlation matrices, respectively, and
are the transmitter and receiver correlation matrices, respectively, and ![]() is a matrix whose elements obey the small‐scale Rician distribution with
is a matrix whose elements obey the small‐scale Rician distribution with ![]() dB [71]. From [286], the correlation matrices can be calculated by
dB [71]. From [286], the correlation matrices can be calculated by
where ![]() follows a uniform distribution in the range
follows a uniform distribution in the range ![]() .
.
The histogram of the amplitude ![]() and the phase
and the phase ![]() of the 3D mmWave channel model are plotted in Figures 7.8 and 7.9. From Figure 7.8, it can be seen that the amplitude of the 3D mmWave channel model can be fitted to a log‐normal with parameters in the range of
of the 3D mmWave channel model are plotted in Figures 7.8 and 7.9. From Figure 7.8, it can be seen that the amplitude of the 3D mmWave channel model can be fitted to a log‐normal with parameters in the range of ![]() and
and ![]() given by
given by

where ![]() if
if ![]() and zero otherwise, and
and zero otherwise, and ![]() denotes the set of all positive real numbers. Furthermore, it can be seen from Figure 7.9 that the phase of the 3D mmWave channel model can be fitted to a continues uniform distribution in the range of
denotes the set of all positive real numbers. Furthermore, it can be seen from Figure 7.9 that the phase of the 3D mmWave channel model can be fitted to a continues uniform distribution in the range of ![]() as
as
As the phase and amplitude of the 3D mmWave channel model are independent, the joint amplitude and phase probability distribution function (PDF) of the 3D mmWave channel model are,

Figure 7.8 Histogram of the amplitude of the 3D mmWave Channel model fitted to a log‐normal distribution.

Figure 7.9 Histogram of the phase of the 3D mmWave Channel model fitted to a uniform distribution.
Figure 7.10 illustrates the simulated mutual information of a QSM system over the 3D mmWave channel model and the lognormal channel model in (7.18) for different spectral inefficiencies ![]() , and
, and ![]() bits and different MIMO setups
bits and different MIMO setups ![]() ,
, ![]() and
and ![]() ,
, ![]() and
and ![]() , and
, and ![]() . The mutual information results for the 3D mmWave channel and for the log‐normal fading channel demonstrate close match for wide and pragmatic range of SNR values and for different number of transmit and receive antennas.
. The mutual information results for the 3D mmWave channel and for the log‐normal fading channel demonstrate close match for wide and pragmatic range of SNR values and for different number of transmit and receive antennas.

Figure 7.10 The simulated mutual information of QSM over the 3D mmWave channel model and the lognormal channel model for different spectral inefficiencies, and different MIMO setups.
7.2.1 Capacity Analysis
The capacity in (7.2) is only achievable if each element of the transmitted SMT symbol ![]() follows a complex Gaussian distribution. Hence, (i) substituting (7.18) in (5.45) and (ii) without loss of generality, consider SM system with
follows a complex Gaussian distribution. Hence, (i) substituting (7.18) in (5.45) and (ii) without loss of generality, consider SM system with ![]() as an example; the capacity is achieved if the signal symbols are shaped such that its PDF solves
as an example; the capacity is achieved if the signal symbols are shaped such that its PDF solves
From (7.19), it can be seen that for SM to achieve the capacity over the 3D‐mmWave channel, the constellation symbols have to be shaped, such that the PDF of the constellation symbols, ![]() , solves (7.19). Hence, it is a two‐stage process, where in the first stage,
, solves (7.19). Hence, it is a two‐stage process, where in the first stage, ![]() has to be found for the given mmWave channel statistics by solving (7.19). The second stage is to shape the constellation symbols to achieve
has to be found for the given mmWave channel statistics by solving (7.19). The second stage is to shape the constellation symbols to achieve ![]() . Signal shaping or other methods need to be considered to shape the constellation symbols such that their distribution follows the obtained
. Signal shaping or other methods need to be considered to shape the constellation symbols such that their distribution follows the obtained ![]() . This is an open design problem that is yet unsolved for SMTs as it is mathematically involved and requires further investigations and studies.
. This is an open design problem that is yet unsolved for SMTs as it is mathematically involved and requires further investigations and studies.
In almost all previous studies dealing with SM capacity over mmWave channel, as in [[210], and references therein], it is concluded that signal constellation symbols must be Gaussian to achieve the theoretical capacity. However, as discussed in Chapter 5, and shown in Section 7.1.1 and (7.19), complex Gaussian distribution is not always the needed distribution to achieve the theoretical capacity. For the 3D mmWave channel model and from (7.19), it is clear that complex Gaussian distribution is not the required distribution. Figure 7.11 shows the mutual information for SM system over the 3D mmWave channel model with ![]() ,
, ![]() , and
, and ![]() constellation size. The mutual information is computed for Gaussian distributed symbols and QAM symbols. It is clear from Figure 7.11 that Gaussian distribution does not achieve the capacity. In fact, the achieved mutual information using Gaussian distributed symbols is 0.4 bit less than the achieved mutual information using ordinary QAM symbols, which are uniformly distributed.
constellation size. The mutual information is computed for Gaussian distributed symbols and QAM symbols. It is clear from Figure 7.11 that Gaussian distribution does not achieve the capacity. In fact, the achieved mutual information using Gaussian distributed symbols is 0.4 bit less than the achieved mutual information using ordinary QAM symbols, which are uniformly distributed.

Figure 7.11 Mutual information for a SM system over 3D mmWave channel with  ,
,  and
and  constellation diagram assuming Gaussian distributed symbols and QAM symbols.
constellation diagram assuming Gaussian distributed symbols and QAM symbols.
A comparison between simulated mutual information of SM, QSM, and SMX for different spectral efficiencies (![]() , 8, and 12) is depicted in Figure 7.12, with
, 8, and 12) is depicted in Figure 7.12, with ![]() . Note, the minimum number of bits QSM can send for
. Note, the minimum number of bits QSM can send for ![]() is 5 bits. The theoretical channel capacity for SMT and SMX is also shown. It can be seen that for low spectral efficiency,
is 5 bits. The theoretical channel capacity for SMT and SMX is also shown. It can be seen that for low spectral efficiency, ![]() , SM and SMX have almost the same performance. Moreover, for
, SM and SMX have almost the same performance. Moreover, for ![]() and also
and also ![]() , QSM and SMX have almost the same performance. Yet, for
, QSM and SMX have almost the same performance. Yet, for ![]() , SMX offers higher mutual information than SM and QSM by about 1.63 bits and 1 bit higher, respectively. This enhancement can be attributed to the need of smaller constellation diagram of SMX as compared to SM and QSM systems. Please note that for
, SMX offers higher mutual information than SM and QSM by about 1.63 bits and 1 bit higher, respectively. This enhancement can be attributed to the need of smaller constellation diagram of SMX as compared to SM and QSM systems. Please note that for ![]() , SMX constellation size is about 99.6% and 97% smaller than the SM and QSM constellation sizes, respectively. The decrease in performance due to increasing the constellation size can also be seen when comparing QSM to SM for
, SMX constellation size is about 99.6% and 97% smaller than the SM and QSM constellation sizes, respectively. The decrease in performance due to increasing the constellation size can also be seen when comparing QSM to SM for ![]() . QSM is shown to perform 0.4 bit better than SM, and nearly the same as SMX, where SMX constellation size is only
. QSM is shown to perform 0.4 bit better than SM, and nearly the same as SMX, where SMX constellation size is only ![]() smaller than QSM, compared to 87.5% for SM.
smaller than QSM, compared to 87.5% for SM.
It is also shown that the SMT capacity is 12 dB higher than the SMX capacity. Moreover, at SNR![]() dB, the SMT capacity is 7.4 bits higher than the capacity of SMX. Thus and even though SMX outperforms SM and QSM, both SMT systems can achieve higher mutual information with proper design of the constellation symbols. Hence, solving (7.19) is of a great interest as it promises a great extension to the existing MIMO capacity.
dB, the SMT capacity is 7.4 bits higher than the capacity of SMX. Thus and even though SMX outperforms SM and QSM, both SMT systems can achieve higher mutual information with proper design of the constellation symbols. Hence, solving (7.19) is of a great interest as it promises a great extension to the existing MIMO capacity.

Figure 7.12 The capacity of SMT and SMX compared to the simulated mutual information of SM, QSM, and SMX over the 3D mmWave channel for different spectral efficiencies, where  , and
, and  and
and  .
.
7.2.2 Average Bit Error Rate Results
The ABER results for both SM and SMX with ![]() are demonstrated in Figure 7.13. The results are compared for spectral efficiencies of
are demonstrated in Figure 7.13. The results are compared for spectral efficiencies of ![]() , 8, 12, and 16. It can be seen that the performance of SM and SMX degrades with increasing the spectral efficiency. Also, SMX is shown to outperform SM performance by about 1.2, 4,
, 8, 12, and 16. It can be seen that the performance of SM and SMX degrades with increasing the spectral efficiency. Also, SMX is shown to outperform SM performance by about 1.2, 4, ![]() , and 14 dB for
, and 14 dB for ![]() , 8, 12, and 16, respectively. Another important observation from the figure is the significant degradation of SM performance with higher spectral efficiencies.
, 8, 12, and 16, respectively. Another important observation from the figure is the significant degradation of SM performance with higher spectral efficiencies.

Figure 7.13 ABER performance comparison between SMX and SM for different  , where
, where  , and
, and  ,
,  , and
, and  .
.
For the same MIMO setup, SMX uses smaller constellation diagram than SM, and it offers better ABER performance. However, as discussed in the previous chapters, in SMT, increasing the number of transmit antennas comes with nearly no cost. Hence, large‐scale SMT over mmWave communications is a cheep solution that can offer a better ABER performance than SMX. It is illustrated in Figure 7.14 for ![]() and
and ![]() , SM with
, SM with ![]() offers about 3.4 dB better performance than SMX with
offers about 3.4 dB better performance than SMX with ![]() . Note, SM with
. Note, SM with ![]() needs only 4 signal constellation symbols, i.e. 50% less than SMX with
needs only 4 signal constellation symbols, i.e. 50% less than SMX with ![]() , which needs 8 signal constellation symbols.
, which needs 8 signal constellation symbols.

Figure 7.14 ABER performance comparison between SMX and SM for different  ,
,  ,
,  for SMX and
for SMX and  for SM.
for SM.