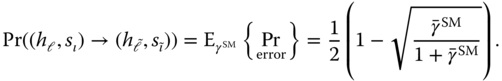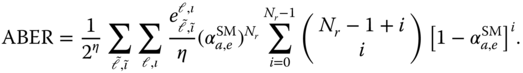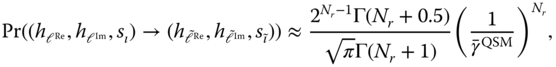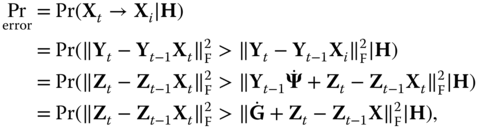Chapter 4
Average Bit Error Probability Analysis for SMTs
In this chapter, average bit error ratio (ABER) performance analysis for the different space modulation techniques (SMTs) discussed in previous chapter is presented. First, the ABER is computed for space shift keying (SSK), spatial modulation (SM), quadrature space shift keying (QSSK), and quadrature spatial modulation (QSM) over Rayleigh flat fading channels. Detailed derivation of the error probability is presented. As well, asymptotic analysis at high, but pragmatic, signal‐to‐noise‐ratio (SNR) values are also given for all schemes. Second, the average and asymptotic error probabilities for these schemes in the presence of Gaussian imperfect channel estimation and over Rayleigh fading channels are discussed and derived [52, 65, 68, 188]. Finally, a general framework for the performance analysis of the different SMTs over arbitrary fading channels, in the presence of spatial correlation and imperfect channel estimation, is derived and thoroughly discussed [46, 48, 72–75, 189].
4.1 Average Error Probability over Rayleigh Fading Channels
The derivation of the average error probability for SMTs can be computed by deriving the pairwise error probability (PEP). The PEP is defined as the error probability that a transmitted spatial and signal symbols, ![]() and
and ![]() , are received as another spatial and signal symbols,
, are received as another spatial and signal symbols, ![]() and
and ![]() , respectively, and is given by PEP
, respectively, and is given by PEP![]() [120].
[120].
4.1.1 SM and SSK with Perfect Channel Knowledge at the Receiver
The derivation of the error probability for SM and SSK is almost the same. SSK scheme can be treated as a special case from SM, and the probability of error for SSK scheme can be obtained as such.
4.1.1.1 Single Receive Antenna 
In what follows, the derivation is conducted for the special case where the receiver has single receive antenna. Later on, this is generalized to an arbitrary number of receive antennas.
For SM over multiple‐input single‐output (MISO) channel, the spatial and signal symbols are ![]() and
and ![]() , respectively, with
, respectively, with ![]() being the
being the ![]() th element of the
th element of the ![]() ‐length channel vector
‐length channel vector ![]() and
and ![]() is the
is the ![]() th modulation symbol. Note, SNR
th modulation symbol. Note, SNR ![]() , where for simplicity,
, where for simplicity, ![]() is assumed.
is assumed.
Assuming the maximum‐likelihood (ML)‐optimum receiver in (3.2) is used, the PEP is calculated as

where ![]() denotes the conjugate,
denotes the conjugate, ![]() is the
is the ![]() ‐function, and
‐function, and

is an exponential random variable (RV) with a probability distribution function (PDF) given by

with ![]() denoting the mean value and is given by
denoting the mean value and is given by
Therefore, the average PEP is
The formula in (4.5) is obtained for an exponential RV from [123, 190] as

Thus, the ABER of SM over MISO Rayleigh fading channels can be computed using the union bounding technique as [120]
with ![]() being the number of bits in error associated with the PEP event. The derived analytical ABER in (4.7) is compared to the simulated ABER for
being the number of bits in error associated with the PEP event. The derived analytical ABER in (4.7) is compared to the simulated ABER for ![]() , and
, and ![]() in Figure 4.1. The results in the figure validate the derived bound in (4.7).
in Figure 4.1. The results in the figure validate the derived bound in (4.7).

Figure 4.1 The derived analytical ABER of SM for MISO Rayleigh fading channels in (4.7) compared simulated ABER for  and
and  .
.
4.1.1.2 Arbitrary Number of Receive Antennas 
The previous derivations consider the special case of ![]() . For an arbitrary number of receive antennas,
. For an arbitrary number of receive antennas, ![]() , the PEP is given by
, the PEP is given by

where ![]() is the
is the ![]() th column of the
th column of the ![]() channel matrix
channel matrix ![]()

and ![]() is a chi‐squared RV with a PDF given by
is a chi‐squared RV with a PDF given by

where ![]() is the
is the ![]() th element of the
th element of the ![]() ‐length channel vector
‐length channel vector ![]() . Note,
. Note, ![]() is given in (4.4).
is given in (4.4).
Thus, the average PEP is given by [123, 191],

where ![]() . Note, from [123, 190] if
. Note, from [123, 190] if ![]() is a chi‐squared RV then,
is a chi‐squared RV then,

where ![]() .
.
Finally, the ABER for SM over Rayleigh fading multiple‐input multiple‐output (MIMO) channel is derived as
Figure 4.2 compares the derived analytical ABER bound in (4.13) to the simulated ABER for ![]() ,
, ![]() , and
, and ![]() . The accuracy of the bound is obvious in the figure where a close‐match between analytical and simulation curves can be clearly seen for all depicted SNR values greater than 5 dB.
. The accuracy of the bound is obvious in the figure where a close‐match between analytical and simulation curves can be clearly seen for all depicted SNR values greater than 5 dB.

Figure 4.2 The derived analytical ABER of SM over MISO Rayleigh fading channels in (4.13) compared to the simulated ABER for  ,
,  , and
, and  .
.
4.1.1.3 Asymptotic Analysis
Another very useful formula to obtain for such systems is the approximate average error probability, generally called asymptotic error probability, at high SNR values. Such formula clearly shows the diversity gain for such systems and can be utilized for optimization studies. The asymptotic error probability is derived based on the behavior of the PDF of ![]() around the origin. This can be obtained by taking Taylor series of
around the origin. This can be obtained by taking Taylor series of ![]() leading to
leading to

where ![]() denotes higher‐order terms that are ignored. The average PEP is then computed as [123, 191]
denotes higher‐order terms that are ignored. The average PEP is then computed as [123, 191]
It is evident that SM achieves a diversity gain of ![]() . This can be seen as well in Figures 4.1 and 4.2, where for MISO system in Figure 4.1, the diversity gain is 1 as there is only one receive antenna. For the MIMO system in Figure 4.2, the diversity gain is 2, which is equal to the number of receive antennas,
. This can be seen as well in Figures 4.1 and 4.2, where for MISO system in Figure 4.1, the diversity gain is 1 as there is only one receive antenna. For the MIMO system in Figure 4.2, the diversity gain is 2, which is equal to the number of receive antennas, ![]() .
.
For SSK, the ABER and asymptotic PEP can be computed by (4.13) and (4.15), respectively, by letting ![]() .
.
4.1.2 SM and SSK in the Presence of Imperfect Channel Estimation
The assumption of perfect channel knowledge at the receiver is impractical. In practical wireless systems, pilots are transmitted to estimate the channel at the receiver input. However and similar to transmitted data, transmitted pilots are corrupted by the additive white Gaussian noise (AWGN) at the receiver input, which leads to a mismatch between the exact channel and the estimated channel. The difference between both is generally called channel estimation errors (CSE). Generally, it is assumed that the true channel and the estimated channel are jointly ergodic and stationary processes. Also, the estimated channel and the estimation error are assumed to be orthogonal. Hence [192],
where ![]() denotes the
denotes the ![]() estimated channel matrix, and
estimated channel matrix, and ![]() denotes the CSE, which is a complex Gaussian random variable with zero mean and
denotes the CSE, which is a complex Gaussian random variable with zero mean and ![]() variance,
variance, ![]() . Note that
. Note that ![]() is a parameter that captures the quality of the channel estimation and can be appropriately chosen depending on the channel dynamics and estimation schemes.
is a parameter that captures the quality of the channel estimation and can be appropriately chosen depending on the channel dynamics and estimation schemes.
The derivation of the instantaneous PEP in the presence of imperfect channel knowledge at the receiver is similar to the derivation of perfect channel knowledge and is computed in what follows.
4.1.2.1 Single Receive Antenna 
In the presence of CSE, the ML‐optimum receiver for SM is given by

where ![]() is the
is the ![]() th element of the
th element of the ![]() ‐length estimated MISO channel vector
‐length estimated MISO channel vector ![]() .
.
Thus, the PEP for SM in the presence of CSE is given by

where ![]() is a complex Gaussian RV with zero mean and variance
is a complex Gaussian RV with zero mean and variance ![]() . Moreover,
. Moreover,

is an exponential RV with a mean value
where
Using the same method as discussed in Section 4.1.1.1 for perfect channel knowledge at the receiver, the ABER for SM over MISO Rayleigh fading channel with imperfect channel knowledge is given by [120, 123]
4.1.2.2 Arbitrary Number of Receive Antennas 
For an arbitrary number of receive antennas ![]() , the PEP is given by
, the PEP is given by

where ![]() is a chi‐squared RV with a PDF
is a chi‐squared RV with a PDF

and

where ![]() is the
is the ![]() th element of the
th element of the ![]() ‐length channel vector
‐length channel vector ![]() , and
, and ![]() is the
is the ![]() th vector of the
th vector of the ![]() estimated channel matrix
estimated channel matrix ![]() . Note,
. Note, ![]() is given in (4.20).
is given in (4.20).
Thus, and using similar procedure as in Section 4.1.1.2, the average PEP is given by [123, 191]

where 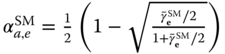 .
.
Finally, the ABER for SM over MIMO Rayleigh fading channels in the presence of CSE is given by
The derived ABER analytical bounds in (4.22) for MISO and in (4.27) for MIMO are depicted in Figure 4.3 and compared with the simulated ABER, for ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The depicted results validate the accuracy of the derived formulas for the ABER.
. The depicted results validate the accuracy of the derived formulas for the ABER.

Figure 4.3 The derived analytical ABER of SM over Rayleigh fading channels in the presence of CSE in (4.22) for MISO and in (4.27) for MIMO compared to the simulated ABER for  ,
,  ,
,  , and
, and  .
.
4.1.2.3 Asymptotic Analysis
The asymptotic PEP in the presence of CSE can be computed as
The obtained asymptotic formula allows deep investigations of several cases.
- Case I – Fixed
 : Assuming fixed CSE, i.e. the CSE is not a function of the SNR, the asymptotic PEP is given by
: Assuming fixed CSE, i.e. the CSE is not a function of the SNR, the asymptotic PEP is given by
where
 . It is clear from (4.29) that increasing the SNR has no impact on the average PEP, which leads to zero diversity order and an error floor will occur.
. It is clear from (4.29) that increasing the SNR has no impact on the average PEP, which leads to zero diversity order and an error floor will occur. - Case II – CSE is a function of SNR: In this case, the pilot symbols are assumed to be transmitted with the same energy as the symbols and the channel estimation error decreases as the SNR increases. Hence, the average asymptotic PEP is given by
(4.30)

The diversity order in this case is
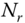 , and increasing the SNR enhances the performance. This gain can be seen in Figure 4.3 where the ABER results at high SNR have diversity gains of 1 and 2 for
, and increasing the SNR enhances the performance. This gain can be seen in Figure 4.3 where the ABER results at high SNR have diversity gains of 1 and 2 for  and
and  , respectively.
, respectively.
In the case of SSK scheme, the ABER and the asymptotic PEP can be calculated using (4.27) and (4.28), respectively, by letting ![]() .
.
4.1.3 QSM with Perfect Channel Knowledge at the Receiver
The average error probability of QSM and QSSK can be derived following similar steps as discussed before for SM and SSK systems [65, 70].
Assuming the ML‐optimum receiver in (3.2) is used, the PEP is given by

where ![]() and
and ![]() denote the real and imaginary parts of the complex number
denote the real and imaginary parts of the complex number ![]() , respectively;
, respectively; ![]() , and
, and ![]() is an exponential RV with a mean value given by
is an exponential RV with a mean value given by

Therefore, from [123], and as discussed in Section 4.1.1.1, the average PEP is

Thus, the ABER of QSM is
where ![]() .
.
For MIMO system with ![]() receive antennas, using the same methodology as discussed earlier, the ABER for QSM is
receive antennas, using the same methodology as discussed earlier, the ABER for QSM is
where ![]() .
.
Taking the Taylor series and ignoring higher‐order terms give the asymptotic average PEP of QSM as
where a diversity gain of ![]() is obtained. Figure 4.4 depicts the derived ABER analytical bounds (4.34) for MISO and in (4.35) for MIMO systems and compare it to the simulated ABER for QSM with
is obtained. Figure 4.4 depicts the derived ABER analytical bounds (4.34) for MISO and in (4.35) for MIMO systems and compare it to the simulated ABER for QSM with ![]() ,
, ![]() , and
, and ![]() . From the figure, simulation and analytical results demonstrate close‐match, and the diversity gains equal the number of receive antennas.
. From the figure, simulation and analytical results demonstrate close‐match, and the diversity gains equal the number of receive antennas.

Figure 4.4 The derived analytical ABER of QSM over Rayleigh fading channels in (4.34) for MISO and in (4.35) for MIMO compared to the simulated ABER for  ,
,  , and
, and  .
.
For QSSK, the ABER and PEP can be calculated using (4.34) and (4.36), respectively, by letting ![]() .
.
4.1.4 QSM in the Presence of Imperfect Channel Estimation
Following similar steps as discussed in Section 4.1.2.2 for SM, the ABER of QSM over MIMO Rayleigh fading channel in the presence of CSE is
where  and
and

Note, ![]() is given in (4.21). Figure 4.5 shows the derived bound and compares it to the simulated ABER for
is given in (4.21). Figure 4.5 shows the derived bound and compares it to the simulated ABER for ![]() ,
, ![]() , and
, and ![]() . The figure shows that the simulated ABER is bounded by (4.37). Furthermore and from the figure, QSM offers a diversity gain equal to the number of receive antennas.
. The figure shows that the simulated ABER is bounded by (4.37). Furthermore and from the figure, QSM offers a diversity gain equal to the number of receive antennas.

Figure 4.5 The derived analytical ABER of QSM over Rayleigh fading channels in the presence of CSE in (4.37) compared to the simulated ABER for  ,
,  , and
, and  .
.
The asymptotic error probability for QSM in the presence of CSE can be computed using similar steps as discussed earlier and is given by
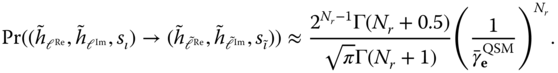
The asymptotic error probability can be analyzed for different cases based on the value of ![]() :
:
- Case I –
 : Assuming a fixed channel estimation error that remains constant even if the SNR changes, the average asymptotic PEP is given by
where
: Assuming a fixed channel estimation error that remains constant even if the SNR changes, the average asymptotic PEP is given by
where  . From (4.40), it can be seen that the diversity gain is zero, where changing the SNR would not change the PEP performance.
. From (4.40), it can be seen that the diversity gain is zero, where changing the SNR would not change the PEP performance. - Case II –
 : this is the general case, where pilot symbols are transmitted with the same energy as the data symbols. The asymptotic PEP is given by
(4.41)Similar to the assumption of perfect channel knowledge, a diversity gain of
: this is the general case, where pilot symbols are transmitted with the same energy as the data symbols. The asymptotic PEP is given by
(4.41)Similar to the assumption of perfect channel knowledge, a diversity gain of
 is achieved here as well.
is achieved here as well.
4.2 A General Framework for SMTs Average Error Probability over Generalized Fading Channels and in the Presence of Spatial Correlation and Imperfect Channel Estimation
The previous analysis for SM, SSK, QSSK, and QSM systems is valid only over Rayleigh flat fading channels where the channel phase distribution is uniform. The performance of SMTs over generalized fading channels, such as Nakagami‐![]() , Rician,
, Rician, ![]() –
–![]() , and others, attracted significant attention in literature [45, 84, 170, 193–197]. However, in all these analyses, the phase distribution of the generalized channel fading distribution is assumed to be uniform, which is needed for mathematical tractability and simplified analysis. Though, this assumption leads to inaccurate conclusions. It was shown in [195, 196] that increasing the
, and others, attracted significant attention in literature [45, 84, 170, 193–197]. However, in all these analyses, the phase distribution of the generalized channel fading distribution is assumed to be uniform, which is needed for mathematical tractability and simplified analysis. Though, this assumption leads to inaccurate conclusions. It was shown in [195, 196] that increasing the ![]() value of the Nakagami‐
value of the Nakagami‐![]() distribution enhances the performance of SMTs. This conclusion means that SMTs performance will be significantly enhanced for very large values of
distribution enhances the performance of SMTs. This conclusion means that SMTs performance will be significantly enhanced for very large values of ![]() . However, for
. However, for ![]() , the Nakagami‐
, the Nakagami‐![]() channel becomes Gaussian, and MIMO communication over Gaussian channels is impossible since it is not possible to resolve the different channel paths. This conclusion was reported recently, and a general framework for SMTs performance analysis over generalized fading channels is presented in [48, 73, 75]. In this section, the general framework for SMTs performance analysis over generalized fading channels and in the presence of spatial correlation and imperfect channel estimation is discussed in detail.
channel becomes Gaussian, and MIMO communication over Gaussian channels is impossible since it is not possible to resolve the different channel paths. This conclusion was reported recently, and a general framework for SMTs performance analysis over generalized fading channels is presented in [48, 73, 75]. In this section, the general framework for SMTs performance analysis over generalized fading channels and in the presence of spatial correlation and imperfect channel estimation is discussed in detail.
Consider a general MIMO system where the transmitter is equipped with ![]() transmit antennas and the receiver has
transmit antennas and the receiver has ![]() receive antennas. The received signal at any particular time is given by
receive antennas. The received signal at any particular time is given by
where ![]() denotes a correlated MIMO channel matrix given by
denotes a correlated MIMO channel matrix given by
where ![]() and
and ![]() being, respectively, the receiver and transmitter spatial correlation matrices as defined in Chapter 2, and
being, respectively, the receiver and transmitter spatial correlation matrices as defined in Chapter 2, and ![]() is the MIMO channel matrix. Assuming CSE at the receiver, the ML‐optimum receiver is written as
is the MIMO channel matrix. Assuming CSE at the receiver, the ML‐optimum receiver is written as
where ![]() is
is ![]() size space containing all possible transmitted vectors
size space containing all possible transmitted vectors ![]() , and
, and ![]() is the estimated MIMO channel matrix
is the estimated MIMO channel matrix
Thus, the PEP of SMTs over generalized and correlated MIMO channel matrix in the presence of CSE is given by
where ![]() ,
, ![]() ,
, ![]() ,
,  , and from [198], the alternative integral expression of the
, and from [198], the alternative integral expression of the ![]() ‐function is
‐function is ![]() .
.
The average PEP is computed by taking the expectation of (4.46) as
where ![]() denotes the moment‐generation function (MGF) of
denotes the moment‐generation function (MGF) of ![]() .
.
From [199], the Frobenius norm of ![]() can be expanded as
can be expanded as
where ![]() ,
, ![]() is the vectorization operator, where the columns of the matrix
is the vectorization operator, where the columns of the matrix ![]() are stacked in column vector, and
are stacked in column vector, and ![]() is the trace function.
is the trace function.
Let ![]() be an identical and independently distributed (i.i.d.) complex random vector with mean
be an identical and independently distributed (i.i.d.) complex random vector with mean ![]() , covariance matrix
, covariance matrix ![]() , and real and imaginary components with equal mean and variance. From [200] and for any Hermitian matrix
, and real and imaginary components with equal mean and variance. From [200] and for any Hermitian matrix ![]() , the MGF of
, the MGF of ![]() is
is
Hence, from (4.49) and (4.48), the MGF in (4.47) can be written as
where ![]() and
and
where ![]() and
and ![]() are the mean and variance of the channel
are the mean and variance of the channel ![]() , respectively,
, respectively, ![]() , with
, with ![]() being the Kronecker product, and
being the Kronecker product, and ![]() is an
is an ![]() ‐length all ones vector.
‐length all ones vector.
Substituting (4.50) in (4.47) gives
Finally, using (4.53), the ABER performance of SMTs over generalized correlated channels in the presence of CSE can be bounded by
Note, the ABER bound in (4.54) even though derived for SMTs is also valid for classical spatial multiplexing (SMX) MIMO systems as shown in the case of Rician fading channels in [199] and generalized fading channels in [54, 73, 74, 201]. Figure 4.6 validates the derived bound in (4.54), where it compares it to the simulated ABER of two SMT systems, SM and QSM, over correlated Rayleigh and Nakagami‐![]() fading channels, and in the presence of CSE, where
fading channels, and in the presence of CSE, where ![]() ,
, ![]() , and
, and ![]() . As can be seen from the figure, analytical and simulation results demonstrate close match for a wide and pragmatic range of SNR values and for the different channel conditions.
. As can be seen from the figure, analytical and simulation results demonstrate close match for a wide and pragmatic range of SNR values and for the different channel conditions.

Figure 4.6 The derived analytical ABER of SMTs in (4.54) compared with the simulated ABER of SM and QSM over correlated Rayleigh and Nakagami‐ fading channels in the presence of CSE, where
fading channels in the presence of CSE, where  ,
,  , and
, and  .
.
4.3 Average Error Probability Analysis of Differential SMTs
Performance analysis of differential space modulation techniques (DSMT) is presented hereinafter. The PEP for a DSMT can be formulated as follows:
where ![]() , and
, and ![]() .
.
Now, the left‐hand side of the inequality in (4.55) can be written as
Moreover, the right‐hand side can be written as
From (4.56) and (4.57), the PEP in (4.55) can be simplified to
Note that ![]() because
because ![]() .
.
Unfortunately, no closed‐form expression is available for the PEP in (4.58). Therefore, an approximate expression will be targeted in what follows. The approximation is based on assuming that ![]() for high SNR values [[120], p. 274]. Notice that both
for high SNR values [[120], p. 274]. Notice that both ![]() and
and ![]() are Gaussian random variables with zero mean and
are Gaussian random variables with zero mean and ![]() variance. Therefore, the mean of their product is also zero, and the variance is
variance. Therefore, the mean of their product is also zero, and the variance is ![]() . Consequently, as SNR increases,
. Consequently, as SNR increases, ![]() approaches zero and so the variance of
approaches zero and so the variance of ![]() .
.
Based on the previous approximation, (4.58) can be rewritten as
The average PEP is computed by taking the expectation of the PEP in (4.59)

where ![]() denotes the MGF of
denotes the MGF of ![]() .
.
Based on [123], the variable ![]() can be expanded as
can be expanded as
As in the previous section, the MGF of the variable ![]() can be expressed using the quadratic form expression as [48, 73, 200]
can be expressed using the quadratic form expression as [48, 73, 200]
where ![]() and
and ![]() are the mean vector and the covariance matrix of the vector
are the mean vector and the covariance matrix of the vector ![]() , respectively, and
, respectively, and ![]() .
.
Using (4.62), the average PEP can be upper bounded by

Finally, the ABER performance of DSMT can be bounded as
where ![]() is the number of bits error associated with the corresponding PEP event. In Figure 4.7, the derived bound in (4.64) is compared to the simulated ABER of differential spatial modulation (DSM) with
is the number of bits error associated with the corresponding PEP event. In Figure 4.7, the derived bound in (4.64) is compared to the simulated ABER of differential spatial modulation (DSM) with ![]() , and differential quadrature spatial modulation (DQSM) with
, and differential quadrature spatial modulation (DQSM) with ![]() , where
, where ![]() , and
, and ![]() ‐quadrature amplitude modulation (QAM) is used. From Figure 4.7, the simulated ABER validates the bound where it closely follows the bound for a wide range of SNR values.
‐quadrature amplitude modulation (QAM) is used. From Figure 4.7, the simulated ABER validates the bound where it closely follows the bound for a wide range of SNR values.
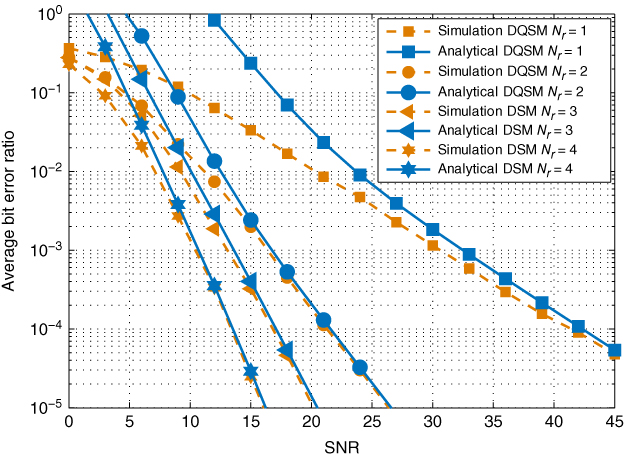
Figure 4.7 The derived analytical ABER of DSMTs in (4.64) compared with the simulated ABER of DSM and DQSM for  ‐QAM,
‐QAM,  ,
,  .
.
4.4 Comparative Average Bit Error Rate Results
In this section, Monte Carlo simulation results are presented to study the ABER performance of SMTs, generalized space modulation techniques (GSMTs), quadrature space modulation techniques (QSMTs), and DSMTs system with different configurations.
4.4.1 SMTs, GSMTs, and QSMTs ABER Comparisons
In Figure 4.9, the ABER of SMTs is presented and compared with SMX for ![]() bits. From the figure, it can be seen that QSSK offers the best performance compared to the rest of the SMTs, 2.5, 3, 3.7, and 7.6 dB better than SSK, QSM, SMX, and SM, respectively. This is because in QSSK all information bits are modulated in the spatial domain which is in Rayleigh fading channels more robust that the signal domain. This can also be seen in SSK where it performs better than QSM, SMX, and SM, 0.5, 1.2, and 5.1 dB, respectively. QSM and SM modulate part of the information bits in the signal domain as will as the spatial domain. However and even though QSSK and SSK modulate all information bits in the spatial domain, SSK performs 2.5 dB less than QSSK. This can be attributed to the need of much more transmit antennas in SSK than QSSK. In Figure 4.9, QSSK needs only
bits. From the figure, it can be seen that QSSK offers the best performance compared to the rest of the SMTs, 2.5, 3, 3.7, and 7.6 dB better than SSK, QSM, SMX, and SM, respectively. This is because in QSSK all information bits are modulated in the spatial domain which is in Rayleigh fading channels more robust that the signal domain. This can also be seen in SSK where it performs better than QSM, SMX, and SM, 0.5, 1.2, and 5.1 dB, respectively. QSM and SM modulate part of the information bits in the signal domain as will as the spatial domain. However and even though QSSK and SSK modulate all information bits in the spatial domain, SSK performs 2.5 dB less than QSSK. This can be attributed to the need of much more transmit antennas in SSK than QSSK. In Figure 4.9, QSSK needs only ![]() , while SSK requires
, while SSK requires ![]() . Comparing QSM to SM, QSM modulates more bits in the spatial domain than SM, and it offers 4.6 dB better performance than SM. With
. Comparing QSM to SM, QSM modulates more bits in the spatial domain than SM, and it offers 4.6 dB better performance than SM. With ![]() , QSM uses 4‐QAM to achieve
, QSM uses 4‐QAM to achieve ![]() bits. However, SM uses 32‐QAM to achieve the same spectral efficiency assuming similar number of transmit antennas. Finally, it can be seen that SMTs that modulate large bits in the spatial domain performs better than SMX. Yet, SMTs like SM that uses large signal constellation diagram perform worse than SMX.
bits. However, SM uses 32‐QAM to achieve the same spectral efficiency assuming similar number of transmit antennas. Finally, it can be seen that SMTs that modulate large bits in the spatial domain performs better than SMX. Yet, SMTs like SM that uses large signal constellation diagram perform worse than SMX.

Figure 4.8 ABER performance comparison between the SMTs, QSSK, SSK, QSM and SM, and SMX systems over Nakagami‐ fading channels for different number of transmit antennas and modulation orders achieving
fading channels for different number of transmit antennas and modulation orders achieving  bits with
bits with  antennas.
antennas.

Figure 4.9 ABER performance comparison between the SMTs, QSSK, SSK, QSM and SM, and SMX systems over Rayleigh fading channels for different number of transmit antennas and modulation orders achieving  bits with
bits with  antennas.
antennas.
The ABER results of SMTs and SMX over Nakagami‐![]() fading channels for
fading channels for ![]() and
and ![]() are presented in Figure 4.8, where
are presented in Figure 4.8, where ![]() for QSSK,
for QSSK, ![]() for SSK, and
for SSK, and ![]() for SM, QSM, and SMX. As in the case for Rayleigh fading channels in Figure 4.9, QSSK over Nakagami‐
for SM, QSM, and SMX. As in the case for Rayleigh fading channels in Figure 4.9, QSSK over Nakagami‐![]() fading channels offers the best performance with 1.3, 2.5, and 4 dB better performance than SMX and QSM, SSK, and SM, respectively. This can be attributed to the same reason as before where there exist no signal constellations and all the information bits are modulated in the spatial domain. Compared to Rayleigh, the performance gap between QSSK and the other systems is smaller, because it is harder to distinguish the different transmit antennas in Nakagami‐
fading channels offers the best performance with 1.3, 2.5, and 4 dB better performance than SMX and QSM, SSK, and SM, respectively. This can be attributed to the same reason as before where there exist no signal constellations and all the information bits are modulated in the spatial domain. Compared to Rayleigh, the performance gap between QSSK and the other systems is smaller, because it is harder to distinguish the different transmit antennas in Nakagami‐![]() fading channel compared to Rayleigh fading channels. This can also be seen in SSK, where it performs 1 dB worse than QSM even though it outperforms QSM performance over Rayleigh fading channels as shown in Figure 4.9. Furthermore, SM still demonstrates the worst performance as it uses large signal constellation diagram compared to all other systems. Finally, QSM is shown to offer nearly the same performance as SMX.
fading channel compared to Rayleigh fading channels. This can also be seen in SSK, where it performs 1 dB worse than QSM even though it outperforms QSM performance over Rayleigh fading channels as shown in Figure 4.9. Furthermore, SM still demonstrates the worst performance as it uses large signal constellation diagram compared to all other systems. Finally, QSM is shown to offer nearly the same performance as SMX.

Figure 4.10 ABER performance comparison between GSMTs, GQSSK, GSSK, GQSM and GSM, and SMX systems over Rayleigh fading channels for different number of transmit antennas and modulation orders achieving  bits with
bits with  antennas.
antennas.
Figure 4.10 depicts the ABER performance of generalized quadrature space shift keying (GQSSK) with ![]() , generalized space shift keying (GSSK) with
, generalized space shift keying (GSSK) with ![]() , generalized quadrature spatial modulation (GQSM) with
, generalized quadrature spatial modulation (GQSM) with ![]() , and generalized spatial modulation (GSM) with
, and generalized spatial modulation (GSM) with ![]() , and compares their performance to SMX with
, and compares their performance to SMX with ![]() over Rayleigh fading channel. All systems achieve
over Rayleigh fading channel. All systems achieve ![]() , and
, and ![]() is considered in all systems. From the figure, GQSSK offers the best performance with 1.2, 2, and 4.6 dB better performance than GSSK and SMX, GQSM, and GSM, respectively. As in QSSK, GQSSK offers this performance because all information bits are modulated in the spatial domain, while using small number of transmit antennas. This also can be seen for GSSK in Figure 4.10, where it offers the same performance as SMX and better performance than both GQSM and GSM. However, GQSSK performs better than GSSK as it uses less number of transmit antennas. Comparing the performance of QSSK in Figure 4.9 to GQSSK in Figure 4.10, it can be observed that QSSK achieves an ABER of
is considered in all systems. From the figure, GQSSK offers the best performance with 1.2, 2, and 4.6 dB better performance than GSSK and SMX, GQSM, and GSM, respectively. As in QSSK, GQSSK offers this performance because all information bits are modulated in the spatial domain, while using small number of transmit antennas. This also can be seen for GSSK in Figure 4.10, where it offers the same performance as SMX and better performance than both GQSM and GSM. However, GQSSK performs better than GSSK as it uses less number of transmit antennas. Comparing the performance of QSSK in Figure 4.9 to GQSSK in Figure 4.10, it can be observed that QSSK achieves an ABER of ![]() at an SNR
at an SNR ![]() dB while GQSSK achieves the same ABER at an SNR
dB while GQSSK achieves the same ABER at an SNR ![]() dB, i.e. GQSSK even though it uses less number of transmit antennas it performs 2.1 dB worse than QSSK. Even though GSMTs in general reduce the number of transmit antennas, they create correlation between the different spatial symbols, which increases the ABER. That is unlike QSMTs, where the reduction in the number of transmit antennas and the increase in the number of bits modulated in the spatial domain are attained while keeping the spatial symbols orthogonal.
dB, i.e. GQSSK even though it uses less number of transmit antennas it performs 2.1 dB worse than QSSK. Even though GSMTs in general reduce the number of transmit antennas, they create correlation between the different spatial symbols, which increases the ABER. That is unlike QSMTs, where the reduction in the number of transmit antennas and the increase in the number of bits modulated in the spatial domain are attained while keeping the spatial symbols orthogonal.
In summary, the more bits modulated in the spatial domain, the better is the performance of SMTs. Increasing the number of bits modulated in the spatial domain is best achieved through QSMTs. To increase the data rate, it is better to increase the number of transmit antennas, which as discussed in previous chapter comes at no extra hardware or computational complexity, nor energy consumption. Another way is to use GSMTs and generalized quadrature space modulation techniques (GQSMTs), which need less number of transmit antennas. However, they offer slightly worse performance than SMTs and QSMTs. Finally, SMTs offer the same performance as SMX or better, if the number of bits modulated in the signal domain is relatively similar to SMX. Though, as the number of bits modulated in the signal domain for SMTs increases, as compared to SMX, the worse the performance will be.
4.4.2 Differential SMTs Results
A comparison between DQSM with ![]() and 4‐QAM and DSM with
and 4‐QAM and DSM with ![]() and 8‐phase shift keying (PSK) is illustrated in Figure 4.11. Results for QSM with
and 8‐phase shift keying (PSK) is illustrated in Figure 4.11. Results for QSM with ![]() and 4‐QAM, SM with
and 4‐QAM, SM with ![]() and 4‐QAM, and SMX over Rayleigh fading channels and assuming
and 4‐QAM, and SMX over Rayleigh fading channels and assuming ![]() are depicted as well. Note, DSM and DQSM do not need channel state information (CSI) at the receiver. However, SM, QSM, and SMX assume full CSI knowledge at the receiver.
are depicted as well. Note, DSM and DQSM do not need channel state information (CSI) at the receiver. However, SM, QSM, and SMX assume full CSI knowledge at the receiver.
Interesting conclusions can be obtained from the depicted results in Figure 4.11. First, the ABER curves of DSM and DQSM intersect at a SNR ![]() dB, where DSM demonstrates slightly better performance for SNR
dB, where DSM demonstrates slightly better performance for SNR ![]() dB, whereas DQSM outperforms DSM for SNR
dB, whereas DQSM outperforms DSM for SNR ![]() dB. At pragmatic ABER values of about
dB. At pragmatic ABER values of about ![]() , DQSM outperforms DSM by around 2.3 dB. In addition, around the same ABER, SM is shown in Figure 4.11 to outperform DQSM and DSM by about 2.5 dB and 5 dB, respectively. Furthermore, QSM outperforms DQSM and DSM by about 1.2 and 2.5 dB, respectively.
, DQSM outperforms DSM by around 2.3 dB. In addition, around the same ABER, SM is shown in Figure 4.11 to outperform DQSM and DSM by about 2.5 dB and 5 dB, respectively. Furthermore, QSM outperforms DQSM and DSM by about 1.2 and 2.5 dB, respectively.
Finally, it can be seen from Figure 4.11 that SMX offers better performance than both DSMTs, while offering nearly the same performance as QSM, and 2.5 dB worse performance than SM. It should be noted, though, that different configurations might lead to different performances, but the trend is likely to remain the same.
In summary, DSMTs offer a relatively good performance without the need for a full CSI at the receiver, while retaining all advantages of SMTs since one antenna is active at a time and transmitter deployment through single radio frequency (RF)‐chain is anticipated.

Figure 4.11 ABER performance comparison between DQSM with  and
and  ‐QAM, DSM with
‐QAM, DSM with  and
and  ‐PSK, QSM with
‐PSK, QSM with  and
and  ‐QAM, SM with
‐QAM, SM with  and
and  ‐QAM, and SMX with
‐QAM, and SMX with  and BPSK over Rayleigh fading channels for
and BPSK over Rayleigh fading channels for  bits and
bits and  antennas.
antennas.