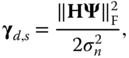Chapter 6
Cooperative SMTs
Cooperative communications create collaboration through distributed transmission/processing by allowing different nodes in a wireless network to share resources. The information for each user is sent out not only by the user but also by other collaborating users. This includes a family of configurations in which the information can be shared among transmitters and relayed to reach final destination in order to improve the systems overall capacity and coverage [209, 216–230]. As such, cooperative technologies have made their way toward wireless standards, such as IEEE 802.16 (WiMAX) [231] and long‐term evolution (LTE) [232] and have been incorporated into many modern wireless applications, such as cognitive radio and secret communications.
Driven by the several advantages of space modulation techniques (SMTs) and cooperative communication technologies, cooperative SMTs have been extensively investigated in the past few years. Reported results promise significant enhancements in spectral efficiency and network coverage [98, 206, 233–244].
In this chapter, cooperative SMTs are studied and analyzed. In particular, amplify and forward (AF), decode and forward (DF), and two‐way relaying (2WR) will be considered.
6.1 Amplify and Forward (AF) Relaying
In cooperative AF relaying, a source (S) and destination (D) nodes are communicating, and multiple or single AF relays participate in the communication protocol as illustrated in Figure 6.1.
Figure 6.1 AF cooperative SMT system model. A system with 
transmit antennas at the source, 
receive antennas at the destination, and with 
AF relays are considered.
At each particular time instant, 
bits are to be transmitted using any of the previously studied SMTs. In the first phase, the source, which is equipped with 
transmit antennas, applies an arbitrary SMT scheme and transmits the vector 
from the available transmit antennas as discussed in previous chapters. The transmitted signal is received by both the destination and the relay node R. Let 
denotes the 
multiple‐input multiple‐output (MIMO) channel matrix between the source and the destination. The received signal at the destination is then given by
where depending on the considered SMT, 
is the 
spatial symbol chosen from the spatial constellation diagram 
, where 
is generated form 
as discussed in Chapter 3. Moreover, 
is the 
signal constellation symbol chosen from the signal constellation diagram 
. Finally, 
is an 
‐length additive white Gaussian noise (AWGN) vector with zero mean and variance 
. Note, for simplicity, 
, and therefore, the signal‐to‐noise‐ratio (SNR) is 
.
In the depicted scenario in Figure 6.1, 
single‐antenna AF relays are assumed. Hence, the signal received at the 
relay in the first time slot is given by
where 
is the 
dimensional multiple‐input single‐output (MISO) channel vector between the source and the 
relay, which has similar characteristics as 
, and 
denotes the 
spatial symbol chosen from the spatial constellation diagram 
, where 
is generated, depending on the used SMT, from 
. Finally, 
is an AWGN with zero mean and variance 
seen at the input of the 
relay.
In conventional AF relaying, all the relays participate in the second phase by retransmitting the source signal to the destination in a predetermined orthogonal time slots. Therefore, 
time slots are needed for each symbol transmission. The relayed signal is an amplified version of the received signal at the relay node. As such, the amplification process is performed in the analog domain without further processing. Hence, the received signal at the destination can be written as
where 
denotes an 
‐dimensional single–input multiple–output (SIMO) channel vector between the 
relay and the destination, 
is the amplification factor, and 
is a colored Gaussian noise vector, 
, where 
, and 
and 
are an 
‐length all zeros vector and 
dimensional identity square matrix, respectively.
It is assumed that the receiver has full channel state information (CSI). Hence, the optimum maximum–likelihood (ML) detector assuming perfect time synchronization is given by
where the search is over 
and 
, with 
and 
denoting the number of bits modulated in the spatial and signal domains, respectively.
6.1.1 Average Error Probability Analysis
The ML receiver in (6.4) can be rewritten as
where 
denoting a space containing all possible transmitted vectors.
The pairwise error probability (PEP) of an AF cooperative system is given by
where 
, and 
.
Now,
where 
is a white Gaussian noise with zero mean and covariance given by
Plugging (6.7) in (6.6) and following the same steps as in (4.46),
where
The average PEP is then computed by taking the expectation of (6.9),
where 
and 
are the moment‐generation functions (MGFs) of 
and 
, respectively. Note, the upper bound in (6.13) is obtained by using 
in the integral in (6.12) [244].
Finally, the average bit error ratio (ABER) of AF cooperative system is
where 
is the number of bits in error associated with the corresponding PEP event.
For 
, then,
where 
, 
, and 
.
Assuming Rayleigh fading channels, the random variables (RVs) 
and 
are exponential RVs with means 
and 
, respectively, with 
and
The cumulative distribution function (CDF) of the RV 
, which is the result of the multiplication of the RVs 
, 
and 
, is given by [123, 245, 246],
and the probability distribution function (PDF) is given by [246]
where 
is the 
‐order modified Bessel function of the second kind.
Finally, the MGF of 
is given by [246]
where 
is the exponential integral function.
The MGF of the exponential RV 
is given by [123],
The ABER of AF SMTs over MISO Rayleigh fading channels can be calculated by substituting (6.19) and (6.20) in (6.14).
6.1.1.1 Asymptotic Analysis
At asymptotically high SNR values, and using Taylor series, the PDF of 
is simplified as
where 
is the digamma function with 
.
Thus, the average PEP can be computed as [247]
The diversity gain of 
is clearly seen in (6.22). Finally, the asymptotic ABER of AF SMTs over MISO Rayleigh fading channels can be computed by plugging (6.22) in (6.14).
Figure 6.2 Simulation, analytical, and asymptotic results for AF SSK system with 
, 
, and variable 
.
Figure 6.3 Analytical, simulation, and asymptotic results for an AF QSM system with 
, 
, and 4‐QAM modulation while varying 
.
Figure 6.4 AF cooperative QSM and SM performance comparison with 
bits and with 4‐QAM modulation assuming 
for QSM and 
for SM and 
and 
.
Figure 6.5 AF cooperative QSM and SM performance comparison with 
bits and with 4‐QAM modulation assuming 
for QSM and 
for SM and 
.
6.1.1.2 Numerical Results
In the first results shown in Figure 6.2, the performance of AF space shift keying (SSK) system is evaluated through Monte‐Carlo simulations and analytical formulas for 
, 
, and variable number of AF relays from 
. Results reveal that increasing the number of relays significantly enhances the ABER performance. Also, analytical and asymptotic curves are shown to closely match Monte Carlo simulation results for a wide range of SNR values and for the different number of relays. An increase in diversity with the increase of 
is also clear from the figure. Such increase in diversity gain is shown to provide about 25 dB gain in SNR at an ABER of 
. It should be noted, though, that the spectral efficiency is not identical for the depicted curves even though they all transmit the same number of data bits. This is because the number of needed orthogonal time slots for the AF scheme is 
, which increases with increasing 
. Therefore, an AF scheme with 
requires six time slots to convey source data to destination, whereas a system with 
requires only two time slots.
Results for AF quadrature spatial modulation (QSM) system with 
, 
, and 
while considering 4‐quadrature amplitude modulation (QAM) are shown in Figure 6.3. Again, higher 
value results in better error performance, and analytical and simulation results are shown to match closely for a wide range of SNR values. Also and as discussed for the previous results in Figure 6.2, increasing the value of 
enhances the performance and degrades the spectral efficiency as 
time slots are needed to convey the source information bits. A performance comparison between spatial modulation (SM) and QSM with single AF relay and for a spectral efficiency of 
bits is depicted in Figure 6.4 while assuming 4‐QAM modulation. QSM system is implemented with 
while SM considers 
to achieve the target spectral efficiency. Results show that QSM outperforms SM performance by about 1.7 dB. Similar comparison between SM and QSM but for a spectral efficiency of 
bits is shown in Figure 6.5. The target spectral efficiency is achieved by considering 4‐QAM for both schemes and assuming 
for QSM and 
for SM systems. A single AF cooperative relay is also considered. Again, QSM demonstrates better performance and a gain of about 1.7 dB can be clearly seen from the figure.
6.1.2 Opportunistic AF Relaying
Previous conventional AF relaying scheme requires 
time slots to convey the source message to the destination. To enhance the spectral efficiency, opportunistic relaying can be considered, where only the best relay participates in the relaying process. This relay is chosen by selecting the indirect link from the source to the 
relay and then to the destination, 
–
–
, that gives the minimum instantaneous error probability.
Following similar steps as in Section 6.1.1, the PEP for the 
relay link can be written as
The relay that minimizes (6.23) is selected to participate in the retransmission process. Hence, the chosen relay is formulated as
Please note that since only a single relay participates in the retransmission process, only two time slots are needed regardless of the number of relays in the network, and proper communication between the relays is assumed.
The ML receiver using opportunistic relaying is then given by
6.1.2.1 Average Error Probability Analysis
In opportunistic relaying, only one relay is retransmitting. Thus and following similar steps as in Section 6.1.1, the average PEP using opportunistic relaying can be written as
where
The CDF of 
can be written as [248]
where 
is given in (6.17).
Furthermore, the PDF is given by
Thus, the MGF of 
is given by
Plugging (6.30) in (6.26) results in the same average PEP as derived for conventional AF SMTs in (6.13). Hence, opportunistic AF relaying offers the same ABER performance as conventional AF relaying, but with an enhanced spectral efficiency.
6.1.2.2 Asymptotic Analysis
At high SNR values, and using Taylor series, the PDF of 
in (6.29) can simplified to
Hence, and using (6.26), the average PEP can be computed as
As in conventional AF relays, a diversity gain of 
is clearly seen in (6.32) for opportunistic relaying.
6.2 Decode and Forward (DF) Relaying
In DF relaying, all existing relays process the received signal and decode the transmitted information. It is generally assumed that an error detection mechanism is available and the relay can tell if the decoded bits are correct or not. If the relay decodes the source signal correctly, it participates in the second phase by forwarding the message to the destination. However, if an error is detected in the retrieved data at the relay, it remains silent at this particular time instant. The relays that will participate in the second phase are grouped in a set 
and allocated orthogonal slots. Therefore, the spectral efficiency will decay by a factor of 
, and required synchronization and signaling between relays is needed, with 
denoting the number of relays participating in the relaying phase. In practical DF systems, as in IEEE 802.16j standard [231] and other literature [248, 249], error detection techniques [250] are used and the relay participates in the cooperative phase if it detects the whole packet correctly. However, the simplified assumption made here facilitates the derived analysis of the error probability and commonly assumed in the literature (see [235, 237, 239, 248, 249, 251–253]). Besides the conducted analysis provides a benchmark for all practical systems.
6.2.1 Multiple single‐antenna DF relays
The source is equipped with multiple antennas and applies a specific SMT. However, in the first scenario considered here, single‐antenna DF relays are considered as shown in Figure 6.1. Similar to previous discussion for AF relaying, 
bits are to be transmitted by the source at each particular time instant. The signal received at the destination node through the direct link can be written as in (6.1). Also, the signal received at the 
relay in the first time slot is given by (6.2).
The relays apply the specific SMT‐ML decoder to decode the received source signal and retrieve the transmitted bits. If the retrieved bits are correct, the relay participates in the retransmission process. However, the relay is equipped with single antenna. Hence, the participating relay will forward the following message to the destination, 
. As such, the received signal at the destination from 
cooperative relay, 
, is given by
At the destination, the ML optimum detector is considered to jointly decode the received signals from the source and the cooperating relays:
6.2.2 Single DF Relay with Multiple Antennas
The previous DF system considers multiple DF relays each equipped with single transmit and receive antennas. Alternatively, DF relays with multiple transmit antennas can be considered as illustrated in Figure 6.6. In such case, the relay will apply the same SMT considered at the source and transmits identical data. A DF relay with 
antennas exists and participates in the retransmission phase if it detects the source signal correctly. The source and the destination nodes are the same as discussed before. The received signal at the destination is the same as given in (6.1). The signal received at the relay is given by
where 
is the 
square channel matrix between relay and the source, and 
is an 
‐length AWGN vector with zero‐mean and 
variance.
Figure 6.6 DF cooperative SMTs system model. A system with 
transmit antennas at the source, 
receive antennas at the destination, and with 
transmit and 
receive antennas at the DF relays are considered.
The relay decodes the signal using the ML decoder as
If the signal is decoded correctly, the relay retransmits the decoded symbol vector 
using the same SMT used at the transmitter. Therefore, the received signal at the destination in the cooperative phase is given by
where 
is an 
fading channel matrix between the relay and the destination, and 
is an 
‐length AWGN vector with zero‐mean and 
variance.
The destination node combines the received signals from the direct link and the cooperative link to detect the source signal as
6.2.3 Average Error Potability Analysis
6.2.3.1 Multiple Single‐Antenna DF Relays
In multiple single‐antenna DF relaying, the transmitted message is received via a direct link and through all relays that detected the transmitted SMT signal correctly. The average PEP that the 
relay detects the SMT signal incorrectly, and thus being off, is given by
As defined earlier in Section 6.1.1, 
is an exponential RV with a mean 
given in (6.16). Hence, and from (4.6),
In the considered multiple single‐antenna DF relays, different scenarios can be defined. In the first scenario, none of the available relays decoded the source message correctly. Therefore, all relays will be off and will not participate in the relaying phase. As such, the destination has to rely on the direct link signal to decode the message. In the second scenario, part of the relays decoded the signal correctly and are grouped in the set 
. Finally, all relays can decode the signal correctly and 
. Let the PEP given that the 
scenario occurs be 
. Then, the average 
for all scenarios is given by
In the first scenario, all relays are off and the receiver decodes only the direct link signal. Hence, the PEP of this scenario is
where 
is given in (6.10).
In the other two scenarios, 
relays detected the signal correctly and retransmitted it to the destination. Hence, the receiver will be receiving the signal from the direct link and from 
relaying links. Thus, and following the same steps as in Section 6.1.1, the PEP for the 
scenario is given by
where
where 
and 
are, as defined earlier in Section 6.1.1, exponential RVs with means 
and 
given in (6.16).
Plugging (6.42) and (6.43) in (6.41) gives
Taking the expectation of the PEP in (6.45), using (4.6) and following the same steps as in Section 6.1.1,
Note, 
is given in (6.20).
From [198], the PDF of 
, which is the result of the multiplication of two exponential RVs 
and 
, is given by
The MGF of 
is then given by
where 
is the incomplete Gamma function.
6.2.3.2 Single DF Relay with Multiple‐Antennas
From (6.46), the average PEP for a single DF relay is given by
where 
is an exponential RV with a mean 
. Hence, the MGF of 
is equal to the MGF of 
given in (6.20). Therefore, the average PEP in (6.49) can be rewritten as
From (6.39), and considering that the relay has 
receive antennas, the PEP of the relay detecting the transmitted SMT signal incorrectly and being off is
Different to single‐antenna relay, 
in (6.51) is a Chi‐squared RV and from [123, 191], the average PEP in (6.51) is given by
where 
.
6.2.3.3 Numerical Results
Simulation results for SM system with DF relays are illustrated in Figure 6.7, where 
, 
, and 
while considering binary phase shift keying (BPSK) modulation. Similar behavior as noted for AF relaying can be seen here as well. Increasing the number of relays significantly enhances the error performance due to the increase of diversity gain. Increasing 
from one to four enhances the SNR performance by about 12 dB at an ABER of 
. Such gain is achieved while degrading the spectral efficiency, as noted for AF system, since a maximum of 
time slots will be needed to convey the source information bits through 
DF relays. It is shown in the figure, as well, that analytical and simulation results closely match for a wide range of system parameters.
Figure 6.7 Simulation, analytical and asymptotic results for cooperative DF SM system with 
, 
, BPSK modulation and variable 
.
Increasing the modulation order to quadrature phase shift keying (QPSK) is shown to degrade the DF SM performance by about 
dB as shown in Figure 6.8. Furthermore, and as in previous results, Figure 6.8 shows that increasing the number of relays enhances the performance. From the figure, compared to no relays, using five relays offers a 20 dB gain in the SNR.
Figure 6.8 Simulation, analytical, and asymptotic results for cooperative DF SM system with 
, 
, and QPSK modulation and variable 
.
6.3 Two‐Way Relaying (2WR) SMTs
In all previously discussed cooperative networks, multiple orthogonal time slots are needed to broadcast information from a source node to a destination node. However, an enhanced spectral‐efficiency relaying algorithm that attracted significant interest in literature is 2WR [236, 242, 254–256]. In 2WR scheme, two source nodes are allowed to simultaneously transmit their data blocks toward a relay node. The relay node retrieves data bits from both nodes and applies network coding principle on the decoded messages. The new generated coded data block is then forwarded to both nodes. To receive the data from the other node, each node reverses the coding operation applied at the relay node.
A system model for 2WR protocol is illustrated in Figure 6.9, which consists of two source nodes, 
and 
, that exchange information with the aid of a relay node 
. The number of transmit antennas is, respectively, given by 
, 
, and 
for 
, 
and 
nodes. Similarly, the number of receive antennas is denoted by 
, 
, and 
.
Data transmission is performed in two consecutive phases, namely, transmission phase and relaying phase. In the transmission phase, both 
and 
nodes concurrently transmit 
bits toward the relay node using an SMT. A DF relay decodes the received data from both nodes and obtains an estimate for the 
bits. In the relaying phase, the relay precodes the estimated bits to generate a new message with 
bits that will be forwarded to both nodes using any of the discussed SMTs.
Figure 6.9 A two‐way relaying system model applying SMTs at any transmitting node. It is assumed that the sources 
and 
are equipped, respectively, with 
and 
transmit antennas and 
and 
receive antennas, and the relay has 
transmit and 
receive antennas.
In what follows, the transmission and reception protocols in both phases are described in detail.
6.3.1 The Transmission Phase
In this phase, both nodes 
and 
concurrently transmit 
bits toward the relay node, 
, using a specific SMT. In order to keep the same block length (i.e., 
bits) from both nodes, different nodes with unequal number of transmit antennas should use different modulation orders.
The transmitted block from 
is denoted by 
, while the transmitted block from 
is denoted by 
. Also, the transmitted vectors from nodes 
and 
are denoted by 
and 
, respectively, that are generated from their corresponding data blocks (i.e., 
and 
).
The received signal vector at the relay 
is denoted by 
and is given as follows:
where 
and 
are, respectively, the 
and 
MIMO channel matrices between node 
and the relay and node 
and the relay. Moreover, the vector 
is an 
‐length AWGN vector with zero mean and 
variance.
The ML detector is considered at the relay node to retrieve the transmitted vectors 
and 
as
where 
and 
represent the sets of all possible transmission vectors from nodes 
and 
, respectively. The detected vectors 
and 
are then, respectively, mapped back to their corresponding data blocks 
and 
.
6.3.2 The Relaying Phase
Upon obtaining the blocks 
and 
, the relay node processes them to obtain a third data block of size 
bits, denoted by 
. This is usually performed through a simple XOR operation as
The 
bits block is then used to obtain the transmission vector 
, which is transmitted from the relay node in this phase.
The received vectors at nodes 
and 
are
where 
and 
are, respectively, the 
and 
MIMO channel matrices between the relay and the nodes 
and 
, and 
and 
are the 
and 
length AWGN vectors at 
and 
nodes, respectively.
At nodes 
and 
, the ML detection is applied on the received signals in order to estimate the detected vectors 
as follows:
and
where 
is the set of all possible transmitted vectors from the relay node 
.
At the end of this phase, each node maps its detected vector into its corresponding bit block. Let 
denotes the obtained block at node 
, and 
is the obtained bits block at node 
. Consequently, each node can extract a corrupted version of the transmitted bits from the other node by performing an XOR operation with its own transmitted bits as
and
where 
being the corrupted version of 
obtained at node 
, and 
is the corrupted version of 
obtained at node 
.
At the end of both phases, each node has received 
bits from the other node. Compared to the conventional one‐way relaying systems, as discussed previously, 2WR can double the spectral efficiency. However, the cost of the improvement in the spectral efficiency is paid in the overall error performance at both nodes, which will be analyzed and discussed hereinafter.
6.3.3 Average Error Probability Analysis
The error performance at either nodes, 
or 
, is identical. Therefore, only the error performance at node 
is considered. Starting from (6.60), the received block 
can be expressed in terms of 
as follows:
where 
, 
, and 
are the error vectors in the transmitted block from 
, 
, and 
nodes, respectively, and all are of 
length. A specific bit in an error vector is 1 if the corresponding bit has been received in error. Otherwise, it is 0. For example, a specific bit in 
is 1 if the corresponding bits in 
and 
are not equal. The second line in (6.62) is obtained by substituting 
, the third line is obtained by substituting 
, the fourth line is obtained by substituting 
and 
, the fifth line is obtained by substituting 
where 
is an all zeros vector, and the last line is obtained using 
.
Now, the last line in (6.62) can be rewritten on a bit base as
where 
is an arbitrary bit in 
, and 
, 
, 
, and 
represent the corresponding bits in 
, 
, 
, and 
, respectively. The bit 
is correct if it is equal to 
. Hence, the bit error rate at 
, denoted by 
, can be expressed as follows:
Notice that 
occurs if only one of them is 1 or all of them are 1's. Thus, (6.64) can be expanded to
which can be further simplified to
where
and 
.
Also, it can be easily verified that 
. Therefore, (6.66) can be further simplified to
The parameter 
represents the ABER in the received block at the relay for the source 
given that the relay received the block from 
correctly. Similarly, 
is the average ABER in the received block from 
at the relay given that the relay received the 
block correctly, and 
represents the average ABER in the received block from the relay at node 
.
The computation of the average ABER can be obtained through the union bound technique. As such, 
is formulated as
where 
is the hamming distance between the two bit blocks corresponding to 
and 
. The probability 
can be expressed using (6.58) as
For a given 
, and as shown previously and in Chapter 4, the above probability can be expressed by means of 
‐function as
where 
.
Assuming Rayleigh fading channels, the probability in (6.74) can be averaged and upper bounded as
where 
and 
denotes the Kronecker product. A proof of (6.75) can be easily obtained considering the ABER derivations in Chapter 4.
Substituting (6.75) in (6.72), the probability 
can be upper bounded as
Following similar steps as used to obtain (6.78), 
can be derived and is given by
where 
is the hamming distance between the bit blocks corresponding to 
and 
. Following the same procedure in (6.72), (6.73), (6.74), (6.75), (6.76), the probability 
can be upper bounded by
where 
and 
. Please note that both 
and 
are identical (but not equal) due to the assumption that both 
and 
have same statistical fading model.
The last probability to be estimated in (6.71) is 
, which is given by
where 
represents the hamming distance between the bit blocks corresponding to 
and 
.
Now using (6.58), and similar to (6.74), the probability 
for a given 
can be expressed as
where 
and (6.80) can be rewritten as
where 
.
Therefore, 
can be computed by substituting (6.81) into (6.79) as follows:
Figure 6.10 Simulation and analytical results for the ABER versus the average SNR for 2WR QSM MIMO system. The block length is 
bits per channel use for each transmitting node. The nodes are assumed to have two transmit antennas and using 4‐QAM modulation order. The number of received antennas is varied from 
.
Finally, the average ABER at node 
( or node 
) can be expressed by substituting (6.76), (6.78), and (6.82) into (6.71).
6.3.3.1 Numerical Results
The ABER for 2WR QSM system is depicted in Figure 6.10 for 
, 
‐QAM, and 
is varied from 
. Considering this setup, each node will deliver 
bits by the end of the two phases. As illustrated in the figure, increasing the number of receive antennas at all nodes significantly improves the overall performance and a gain of about 9.2 dB can be noticed at an ABER of 
when having three receive antennas instead of two. In addition, depicted analytical and simulation results are shown to match closely and for the different depicted curves with variant number of receive antennas.
Another setup considering 
, 
‐QAM and the receive antennas are varied from 
is evaluated, and the results are shown in Figure 6.11. With these configurations, the spectral efficiency increases to 
bits for each transmitting node. Similar conclusions as drawn in the previous figure can be concluded here as well.
Figure 6.11 Simulation and analytical results for the ABER versus the average SNR for 2WR QSM MIMO system. The block length is 
bits per channel use from each transmitting node. Each node is assumed to be equipped with two transmit antennas and transmits an 4‐QAM symbol. The number of received antennas is varied from 
.