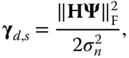Chapter 6
Cooperative SMTs
Cooperative communications create collaboration through distributed transmission/processing by allowing different nodes in a wireless network to share resources. The information for each user is sent out not only by the user but also by other collaborating users. This includes a family of configurations in which the information can be shared among transmitters and relayed to reach final destination in order to improve the systems overall capacity and coverage [209, 216–230]. As such, cooperative technologies have made their way toward wireless standards, such as IEEE 802.16 (WiMAX) [231] and long‐term evolution (LTE) [232] and have been incorporated into many modern wireless applications, such as cognitive radio and secret communications.
Driven by the several advantages of space modulation techniques (SMTs) and cooperative communication technologies, cooperative SMTs have been extensively investigated in the past few years. Reported results promise significant enhancements in spectral efficiency and network coverage [98, 206, 233–244].
In this chapter, cooperative SMTs are studied and analyzed. In particular, amplify and forward (AF), decode and forward (DF), and two‐way relaying (2WR) will be considered.
6.1 Amplify and Forward (AF) Relaying
In cooperative AF relaying, a source (S) and destination (D) nodes are communicating, and multiple or single AF relays participate in the communication protocol as illustrated in Figure 6.1.

Figure 6.1 AF cooperative SMT system model. A system with  transmit antennas at the source,
transmit antennas at the source,  receive antennas at the destination, and with
receive antennas at the destination, and with  AF relays are considered.
AF relays are considered.
At each particular time instant, ![]() bits are to be transmitted using any of the previously studied SMTs. In the first phase, the source, which is equipped with
bits are to be transmitted using any of the previously studied SMTs. In the first phase, the source, which is equipped with ![]() transmit antennas, applies an arbitrary SMT scheme and transmits the vector
transmit antennas, applies an arbitrary SMT scheme and transmits the vector ![]() from the available transmit antennas as discussed in previous chapters. The transmitted signal is received by both the destination and the relay node R. Let
from the available transmit antennas as discussed in previous chapters. The transmitted signal is received by both the destination and the relay node R. Let ![]() denotes the
denotes the ![]() multiple‐input multiple‐output (MIMO) channel matrix between the source and the destination. The received signal at the destination is then given by
multiple‐input multiple‐output (MIMO) channel matrix between the source and the destination. The received signal at the destination is then given by
where depending on the considered SMT, ![]() is the
is the ![]() spatial symbol chosen from the spatial constellation diagram
spatial symbol chosen from the spatial constellation diagram ![]() , where
, where ![]() is generated form
is generated form ![]() as discussed in Chapter 3. Moreover,
as discussed in Chapter 3. Moreover, ![]() is the
is the ![]() signal constellation symbol chosen from the signal constellation diagram
signal constellation symbol chosen from the signal constellation diagram ![]() . Finally,
. Finally, ![]() is an
is an ![]() ‐length additive white Gaussian noise (AWGN) vector with zero mean and variance
‐length additive white Gaussian noise (AWGN) vector with zero mean and variance ![]() . Note, for simplicity,
. Note, for simplicity, ![]() , and therefore, the signal‐to‐noise‐ratio (SNR) is
, and therefore, the signal‐to‐noise‐ratio (SNR) is ![]() .
.
In the depicted scenario in Figure 6.1, ![]() single‐antenna AF relays are assumed. Hence, the signal received at the
single‐antenna AF relays are assumed. Hence, the signal received at the ![]() relay in the first time slot is given by
relay in the first time slot is given by
where ![]() is the
is the ![]() dimensional multiple‐input single‐output (MISO) channel vector between the source and the
dimensional multiple‐input single‐output (MISO) channel vector between the source and the ![]() relay, which has similar characteristics as
relay, which has similar characteristics as ![]() , and
, and ![]() denotes the
denotes the ![]() spatial symbol chosen from the spatial constellation diagram
spatial symbol chosen from the spatial constellation diagram ![]() , where
, where ![]() is generated, depending on the used SMT, from
is generated, depending on the used SMT, from ![]() . Finally,
. Finally, ![]() is an AWGN with zero mean and variance
is an AWGN with zero mean and variance ![]() seen at the input of the
seen at the input of the ![]() relay.
relay.
In conventional AF relaying, all the relays participate in the second phase by retransmitting the source signal to the destination in a predetermined orthogonal time slots. Therefore, ![]() time slots are needed for each symbol transmission. The relayed signal is an amplified version of the received signal at the relay node. As such, the amplification process is performed in the analog domain without further processing. Hence, the received signal at the destination can be written as
time slots are needed for each symbol transmission. The relayed signal is an amplified version of the received signal at the relay node. As such, the amplification process is performed in the analog domain without further processing. Hence, the received signal at the destination can be written as

where ![]() denotes an
denotes an ![]() ‐dimensional single–input multiple–output (SIMO) channel vector between the
‐dimensional single–input multiple–output (SIMO) channel vector between the ![]() relay and the destination,
relay and the destination, ![]() is the amplification factor, and
is the amplification factor, and ![]() is a colored Gaussian noise vector,
is a colored Gaussian noise vector, ![]() , where
, where ![]() , and
, and ![]() and
and ![]() are an
are an ![]() ‐length all zeros vector and
‐length all zeros vector and ![]() dimensional identity square matrix, respectively.
dimensional identity square matrix, respectively.
It is assumed that the receiver has full channel state information (CSI). Hence, the optimum maximum–likelihood (ML) detector assuming perfect time synchronization is given by
where the search is over ![]() and
and ![]() , with
, with ![]() and
and ![]() denoting the number of bits modulated in the spatial and signal domains, respectively.
denoting the number of bits modulated in the spatial and signal domains, respectively.
6.1.1 Average Error Probability Analysis
The ML receiver in (6.4) can be rewritten as

where ![]() denoting a space containing all possible transmitted vectors.
denoting a space containing all possible transmitted vectors.
The pairwise error probability (PEP) of an AF cooperative system is given by
where ![]() , and
, and ![]() .
.
Now,
where ![]() is a white Gaussian noise with zero mean and covariance given by
is a white Gaussian noise with zero mean and covariance given by

Plugging (6.7) in (6.6) and following the same steps as in (4.46),
where

The average PEP is then computed by taking the expectation of (6.9),

where ![]() and
and ![]() are the moment‐generation functions (MGFs) of
are the moment‐generation functions (MGFs) of ![]() and
and ![]() , respectively. Note, the upper bound in (6.13) is obtained by using
, respectively. Note, the upper bound in (6.13) is obtained by using ![]() in the integral in (6.12) [244].
in the integral in (6.12) [244].
Finally, the average bit error ratio (ABER) of AF cooperative system is
where ![]() is the number of bits in error associated with the corresponding PEP event.
is the number of bits in error associated with the corresponding PEP event.
For ![]() , then,
, then,

where ![]() ,
, ![]() , and
, and ![]() .
.
Assuming Rayleigh fading channels, the random variables (RVs) ![]() and
and ![]() are exponential RVs with means
are exponential RVs with means ![]() and
and ![]() , respectively, with
, respectively, with ![]() and
and
The cumulative distribution function (CDF) of the RV ![]() , which is the result of the multiplication of the RVs
, which is the result of the multiplication of the RVs ![]() ,
, ![]() and
and ![]() , is given by [123, 245, 246],
, is given by [123, 245, 246],
and the probability distribution function (PDF) is given by [246]

where ![]() is the
is the ![]() ‐order modified Bessel function of the second kind.
‐order modified Bessel function of the second kind.
Finally, the MGF of ![]() is given by [246]
is given by [246]
where ![]() is the exponential integral function.
is the exponential integral function.
The MGF of the exponential RV ![]() is given by [123],
is given by [123],
The ABER of AF SMTs over MISO Rayleigh fading channels can be calculated by substituting (6.19) and (6.20) in (6.14).
6.1.1.1 Asymptotic Analysis
At asymptotically high SNR values, and using Taylor series, the PDF of ![]() is simplified as
is simplified as

where ![]() is the digamma function with
is the digamma function with ![]() .
.
Thus, the average PEP can be computed as [247]
The diversity gain of ![]() is clearly seen in (6.22). Finally, the asymptotic ABER of AF SMTs over MISO Rayleigh fading channels can be computed by plugging (6.22) in (6.14).
is clearly seen in (6.22). Finally, the asymptotic ABER of AF SMTs over MISO Rayleigh fading channels can be computed by plugging (6.22) in (6.14).

Figure 6.2 Simulation, analytical, and asymptotic results for AF SSK system with  ,
,  , and variable
, and variable  .
.

Figure 6.3 Analytical, simulation, and asymptotic results for an AF QSM system with  ,
,  , and 4‐QAM modulation while varying
, and 4‐QAM modulation while varying  .
.

Figure 6.4 AF cooperative QSM and SM performance comparison with  bits and with 4‐QAM modulation assuming
bits and with 4‐QAM modulation assuming  for QSM and
for QSM and  for SM and
for SM and  and
and  .
.

Figure 6.5 AF cooperative QSM and SM performance comparison with  bits and with 4‐QAM modulation assuming
bits and with 4‐QAM modulation assuming  for QSM and
for QSM and  for SM and
for SM and  .
.
6.1.1.2 Numerical Results
In the first results shown in Figure 6.2, the performance of AF space shift keying (SSK) system is evaluated through Monte‐Carlo simulations and analytical formulas for ![]() ,
, ![]() , and variable number of AF relays from
, and variable number of AF relays from ![]() . Results reveal that increasing the number of relays significantly enhances the ABER performance. Also, analytical and asymptotic curves are shown to closely match Monte Carlo simulation results for a wide range of SNR values and for the different number of relays. An increase in diversity with the increase of
. Results reveal that increasing the number of relays significantly enhances the ABER performance. Also, analytical and asymptotic curves are shown to closely match Monte Carlo simulation results for a wide range of SNR values and for the different number of relays. An increase in diversity with the increase of ![]() is also clear from the figure. Such increase in diversity gain is shown to provide about 25 dB gain in SNR at an ABER of
is also clear from the figure. Such increase in diversity gain is shown to provide about 25 dB gain in SNR at an ABER of ![]() . It should be noted, though, that the spectral efficiency is not identical for the depicted curves even though they all transmit the same number of data bits. This is because the number of needed orthogonal time slots for the AF scheme is
. It should be noted, though, that the spectral efficiency is not identical for the depicted curves even though they all transmit the same number of data bits. This is because the number of needed orthogonal time slots for the AF scheme is ![]() , which increases with increasing
, which increases with increasing ![]() . Therefore, an AF scheme with
. Therefore, an AF scheme with ![]() requires six time slots to convey source data to destination, whereas a system with
requires six time slots to convey source data to destination, whereas a system with ![]() requires only two time slots.
requires only two time slots.
Results for AF quadrature spatial modulation (QSM) system with ![]() ,
, ![]() , and
, and ![]() while considering 4‐quadrature amplitude modulation (QAM) are shown in Figure 6.3. Again, higher
while considering 4‐quadrature amplitude modulation (QAM) are shown in Figure 6.3. Again, higher ![]() value results in better error performance, and analytical and simulation results are shown to match closely for a wide range of SNR values. Also and as discussed for the previous results in Figure 6.2, increasing the value of
value results in better error performance, and analytical and simulation results are shown to match closely for a wide range of SNR values. Also and as discussed for the previous results in Figure 6.2, increasing the value of ![]() enhances the performance and degrades the spectral efficiency as
enhances the performance and degrades the spectral efficiency as ![]() time slots are needed to convey the source information bits. A performance comparison between spatial modulation (SM) and QSM with single AF relay and for a spectral efficiency of
time slots are needed to convey the source information bits. A performance comparison between spatial modulation (SM) and QSM with single AF relay and for a spectral efficiency of ![]() bits is depicted in Figure 6.4 while assuming 4‐QAM modulation. QSM system is implemented with
bits is depicted in Figure 6.4 while assuming 4‐QAM modulation. QSM system is implemented with ![]() while SM considers
while SM considers ![]() to achieve the target spectral efficiency. Results show that QSM outperforms SM performance by about 1.7 dB. Similar comparison between SM and QSM but for a spectral efficiency of
to achieve the target spectral efficiency. Results show that QSM outperforms SM performance by about 1.7 dB. Similar comparison between SM and QSM but for a spectral efficiency of ![]() bits is shown in Figure 6.5. The target spectral efficiency is achieved by considering 4‐QAM for both schemes and assuming
bits is shown in Figure 6.5. The target spectral efficiency is achieved by considering 4‐QAM for both schemes and assuming ![]() for QSM and
for QSM and ![]() for SM systems. A single AF cooperative relay is also considered. Again, QSM demonstrates better performance and a gain of about 1.7 dB can be clearly seen from the figure.
for SM systems. A single AF cooperative relay is also considered. Again, QSM demonstrates better performance and a gain of about 1.7 dB can be clearly seen from the figure.
6.1.2 Opportunistic AF Relaying
Previous conventional AF relaying scheme requires ![]() time slots to convey the source message to the destination. To enhance the spectral efficiency, opportunistic relaying can be considered, where only the best relay participates in the relaying process. This relay is chosen by selecting the indirect link from the source to the
time slots to convey the source message to the destination. To enhance the spectral efficiency, opportunistic relaying can be considered, where only the best relay participates in the relaying process. This relay is chosen by selecting the indirect link from the source to the ![]() relay and then to the destination,
relay and then to the destination, ![]() –
–![]() –
–![]() , that gives the minimum instantaneous error probability.
, that gives the minimum instantaneous error probability.
Following similar steps as in Section 6.1.1, the PEP for the ![]() relay link can be written as
relay link can be written as
The relay that minimizes (6.23) is selected to participate in the retransmission process. Hence, the chosen relay is formulated as

Please note that since only a single relay participates in the retransmission process, only two time slots are needed regardless of the number of relays in the network, and proper communication between the relays is assumed.
The ML receiver using opportunistic relaying is then given by

6.1.2.1 Average Error Probability Analysis
In opportunistic relaying, only one relay is retransmitting. Thus and following similar steps as in Section 6.1.1, the average PEP using opportunistic relaying can be written as
where

The CDF of ![]() can be written as [248]
can be written as [248]

where ![]() is given in (6.17).
is given in (6.17).
Furthermore, the PDF is given by
Thus, the MGF of ![]() is given by
is given by
Plugging (6.30) in (6.26) results in the same average PEP as derived for conventional AF SMTs in (6.13). Hence, opportunistic AF relaying offers the same ABER performance as conventional AF relaying, but with an enhanced spectral efficiency.
6.1.2.2 Asymptotic Analysis
At high SNR values, and using Taylor series, the PDF of ![]() in (6.29) can simplified to
in (6.29) can simplified to

Hence, and using (6.26), the average PEP can be computed as
As in conventional AF relays, a diversity gain of ![]() is clearly seen in (6.32) for opportunistic relaying.
is clearly seen in (6.32) for opportunistic relaying.
6.2 Decode and Forward (DF) Relaying
In DF relaying, all existing relays process the received signal and decode the transmitted information. It is generally assumed that an error detection mechanism is available and the relay can tell if the decoded bits are correct or not. If the relay decodes the source signal correctly, it participates in the second phase by forwarding the message to the destination. However, if an error is detected in the retrieved data at the relay, it remains silent at this particular time instant. The relays that will participate in the second phase are grouped in a set ![]() and allocated orthogonal slots. Therefore, the spectral efficiency will decay by a factor of
and allocated orthogonal slots. Therefore, the spectral efficiency will decay by a factor of ![]() , and required synchronization and signaling between relays is needed, with
, and required synchronization and signaling between relays is needed, with ![]() denoting the number of relays participating in the relaying phase. In practical DF systems, as in IEEE 802.16j standard [231] and other literature [248, 249], error detection techniques [250] are used and the relay participates in the cooperative phase if it detects the whole packet correctly. However, the simplified assumption made here facilitates the derived analysis of the error probability and commonly assumed in the literature (see [235, 237, 239, 248, 249, 251–253]). Besides the conducted analysis provides a benchmark for all practical systems.
denoting the number of relays participating in the relaying phase. In practical DF systems, as in IEEE 802.16j standard [231] and other literature [248, 249], error detection techniques [250] are used and the relay participates in the cooperative phase if it detects the whole packet correctly. However, the simplified assumption made here facilitates the derived analysis of the error probability and commonly assumed in the literature (see [235, 237, 239, 248, 249, 251–253]). Besides the conducted analysis provides a benchmark for all practical systems.
6.2.1 Multiple single‐antenna DF relays
The source is equipped with multiple antennas and applies a specific SMT. However, in the first scenario considered here, single‐antenna DF relays are considered as shown in Figure 6.1. Similar to previous discussion for AF relaying, ![]() bits are to be transmitted by the source at each particular time instant. The signal received at the destination node through the direct link can be written as in (6.1). Also, the signal received at the
bits are to be transmitted by the source at each particular time instant. The signal received at the destination node through the direct link can be written as in (6.1). Also, the signal received at the ![]() relay in the first time slot is given by (6.2).
relay in the first time slot is given by (6.2).
The relays apply the specific SMT‐ML decoder to decode the received source signal and retrieve the transmitted bits. If the retrieved bits are correct, the relay participates in the retransmission process. However, the relay is equipped with single antenna. Hence, the participating relay will forward the following message to the destination, ![]() . As such, the received signal at the destination from
. As such, the received signal at the destination from ![]() cooperative relay,
cooperative relay, ![]() , is given by
, is given by
At the destination, the ML optimum detector is considered to jointly decode the received signals from the source and the cooperating relays:

6.2.2 Single DF Relay with Multiple Antennas
The previous DF system considers multiple DF relays each equipped with single transmit and receive antennas. Alternatively, DF relays with multiple transmit antennas can be considered as illustrated in Figure 6.6. In such case, the relay will apply the same SMT considered at the source and transmits identical data. A DF relay with ![]() antennas exists and participates in the retransmission phase if it detects the source signal correctly. The source and the destination nodes are the same as discussed before. The received signal at the destination is the same as given in (6.1). The signal received at the relay is given by
antennas exists and participates in the retransmission phase if it detects the source signal correctly. The source and the destination nodes are the same as discussed before. The received signal at the destination is the same as given in (6.1). The signal received at the relay is given by
where ![]() is the
is the ![]() square channel matrix between relay and the source, and
square channel matrix between relay and the source, and ![]() is an
is an ![]() ‐length AWGN vector with zero‐mean and
‐length AWGN vector with zero‐mean and ![]() variance.
variance.

Figure 6.6 DF cooperative SMTs system model. A system with  transmit antennas at the source,
transmit antennas at the source,  receive antennas at the destination, and with
receive antennas at the destination, and with  transmit and
transmit and  receive antennas at the DF relays are considered.
receive antennas at the DF relays are considered.
The relay decodes the signal using the ML decoder as
If the signal is decoded correctly, the relay retransmits the decoded symbol vector ![]() using the same SMT used at the transmitter. Therefore, the received signal at the destination in the cooperative phase is given by
using the same SMT used at the transmitter. Therefore, the received signal at the destination in the cooperative phase is given by
where ![]() is an
is an ![]() fading channel matrix between the relay and the destination, and
fading channel matrix between the relay and the destination, and ![]() is an
is an ![]() ‐length AWGN vector with zero‐mean and
‐length AWGN vector with zero‐mean and ![]() variance.
variance.
The destination node combines the received signals from the direct link and the cooperative link to detect the source signal as
6.2.3 Average Error Potability Analysis
6.2.3.1 Multiple Single‐Antenna DF Relays
In multiple single‐antenna DF relaying, the transmitted message is received via a direct link and through all relays that detected the transmitted SMT signal correctly. The average PEP that the ![]() relay detects the SMT signal incorrectly, and thus being off, is given by
relay detects the SMT signal incorrectly, and thus being off, is given by
As defined earlier in Section 6.1.1, ![]() is an exponential RV with a mean
is an exponential RV with a mean ![]() given in (6.16). Hence, and from (4.6),
given in (6.16). Hence, and from (4.6),

In the considered multiple single‐antenna DF relays, different scenarios can be defined. In the first scenario, none of the available relays decoded the source message correctly. Therefore, all relays will be off and will not participate in the relaying phase. As such, the destination has to rely on the direct link signal to decode the message. In the second scenario, part of the relays decoded the signal correctly and are grouped in the set ![]() . Finally, all relays can decode the signal correctly and
. Finally, all relays can decode the signal correctly and ![]() . Let the PEP given that the
. Let the PEP given that the ![]() scenario occurs be
scenario occurs be ![]() . Then, the average
. Then, the average ![]() for all scenarios is given by
for all scenarios is given by
In the first scenario, all relays are off and the receiver decodes only the direct link signal. Hence, the PEP of this scenario is
where ![]() is given in (6.10).
is given in (6.10).
In the other two scenarios, ![]() relays detected the signal correctly and retransmitted it to the destination. Hence, the receiver will be receiving the signal from the direct link and from
relays detected the signal correctly and retransmitted it to the destination. Hence, the receiver will be receiving the signal from the direct link and from ![]() relaying links. Thus, and following the same steps as in Section 6.1.1, the PEP for the
relaying links. Thus, and following the same steps as in Section 6.1.1, the PEP for the ![]() scenario is given by
scenario is given by
where

where ![]() and
and ![]() are, as defined earlier in Section 6.1.1, exponential RVs with means
are, as defined earlier in Section 6.1.1, exponential RVs with means ![]() and
and ![]() given in (6.16).
given in (6.16).
Plugging (6.42) and (6.43) in (6.41) gives
Taking the expectation of the PEP in (6.45), using (4.6) and following the same steps as in Section 6.1.1,
Note, ![]() is given in (6.20).
is given in (6.20).
From [198], the PDF of ![]() , which is the result of the multiplication of two exponential RVs
, which is the result of the multiplication of two exponential RVs ![]() and
and ![]() , is given by
, is given by

The MGF of ![]() is then given by
is then given by

where ![]() is the incomplete Gamma function.
is the incomplete Gamma function.
6.2.3.2 Single DF Relay with Multiple‐Antennas
From (6.46), the average PEP for a single DF relay is given by
where ![]() is an exponential RV with a mean
is an exponential RV with a mean ![]() . Hence, the MGF of
. Hence, the MGF of ![]() is equal to the MGF of
is equal to the MGF of ![]() given in (6.20). Therefore, the average PEP in (6.49) can be rewritten as
given in (6.20). Therefore, the average PEP in (6.49) can be rewritten as

From (6.39), and considering that the relay has ![]() receive antennas, the PEP of the relay detecting the transmitted SMT signal incorrectly and being off is
receive antennas, the PEP of the relay detecting the transmitted SMT signal incorrectly and being off is
Different to single‐antenna relay, ![]() in (6.51) is a Chi‐squared RV and from [123, 191], the average PEP in (6.51) is given by
in (6.51) is a Chi‐squared RV and from [123, 191], the average PEP in (6.51) is given by

where ![]() .
.
6.2.3.3 Numerical Results
Simulation results for SM system with DF relays are illustrated in Figure 6.7, where ![]() ,
, ![]() , and
, and ![]() while considering binary phase shift keying (BPSK) modulation. Similar behavior as noted for AF relaying can be seen here as well. Increasing the number of relays significantly enhances the error performance due to the increase of diversity gain. Increasing
while considering binary phase shift keying (BPSK) modulation. Similar behavior as noted for AF relaying can be seen here as well. Increasing the number of relays significantly enhances the error performance due to the increase of diversity gain. Increasing ![]() from one to four enhances the SNR performance by about 12 dB at an ABER of
from one to four enhances the SNR performance by about 12 dB at an ABER of ![]() . Such gain is achieved while degrading the spectral efficiency, as noted for AF system, since a maximum of
. Such gain is achieved while degrading the spectral efficiency, as noted for AF system, since a maximum of ![]() time slots will be needed to convey the source information bits through
time slots will be needed to convey the source information bits through ![]() DF relays. It is shown in the figure, as well, that analytical and simulation results closely match for a wide range of system parameters.
DF relays. It is shown in the figure, as well, that analytical and simulation results closely match for a wide range of system parameters.

Figure 6.7 Simulation, analytical and asymptotic results for cooperative DF SM system with  ,
,  , BPSK modulation and variable
, BPSK modulation and variable  .
.
Increasing the modulation order to quadrature phase shift keying (QPSK) is shown to degrade the DF SM performance by about ![]() dB as shown in Figure 6.8. Furthermore, and as in previous results, Figure 6.8 shows that increasing the number of relays enhances the performance. From the figure, compared to no relays, using five relays offers a 20 dB gain in the SNR.
dB as shown in Figure 6.8. Furthermore, and as in previous results, Figure 6.8 shows that increasing the number of relays enhances the performance. From the figure, compared to no relays, using five relays offers a 20 dB gain in the SNR.

Figure 6.8 Simulation, analytical, and asymptotic results for cooperative DF SM system with  ,
,  , and QPSK modulation and variable
, and QPSK modulation and variable  .
.
6.3 Two‐Way Relaying (2WR) SMTs
In all previously discussed cooperative networks, multiple orthogonal time slots are needed to broadcast information from a source node to a destination node. However, an enhanced spectral‐efficiency relaying algorithm that attracted significant interest in literature is 2WR [236, 242, 254–256]. In 2WR scheme, two source nodes are allowed to simultaneously transmit their data blocks toward a relay node. The relay node retrieves data bits from both nodes and applies network coding principle on the decoded messages. The new generated coded data block is then forwarded to both nodes. To receive the data from the other node, each node reverses the coding operation applied at the relay node.
A system model for 2WR protocol is illustrated in Figure 6.9, which consists of two source nodes, ![]() and
and ![]() , that exchange information with the aid of a relay node
, that exchange information with the aid of a relay node ![]() . The number of transmit antennas is, respectively, given by
. The number of transmit antennas is, respectively, given by ![]() ,
, ![]() , and
, and ![]() for
for ![]() ,
, ![]() and
and ![]() nodes. Similarly, the number of receive antennas is denoted by
nodes. Similarly, the number of receive antennas is denoted by ![]() ,
, ![]() , and
, and ![]() .
.
Data transmission is performed in two consecutive phases, namely, transmission phase and relaying phase. In the transmission phase, both ![]() and
and ![]() nodes concurrently transmit
nodes concurrently transmit ![]() bits toward the relay node using an SMT. A DF relay decodes the received data from both nodes and obtains an estimate for the
bits toward the relay node using an SMT. A DF relay decodes the received data from both nodes and obtains an estimate for the ![]() bits. In the relaying phase, the relay precodes the estimated bits to generate a new message with
bits. In the relaying phase, the relay precodes the estimated bits to generate a new message with ![]() bits that will be forwarded to both nodes using any of the discussed SMTs.
bits that will be forwarded to both nodes using any of the discussed SMTs.

Figure 6.9 A two‐way relaying system model applying SMTs at any transmitting node. It is assumed that the sources  and
and  are equipped, respectively, with
are equipped, respectively, with  and
and  transmit antennas and
transmit antennas and  and
and  receive antennas, and the relay has
receive antennas, and the relay has  transmit and
transmit and  receive antennas.
receive antennas.
In what follows, the transmission and reception protocols in both phases are described in detail.
6.3.1 The Transmission Phase
In this phase, both nodes ![]() and
and ![]() concurrently transmit
concurrently transmit ![]() bits toward the relay node,
bits toward the relay node, ![]() , using a specific SMT. In order to keep the same block length (i.e.,
, using a specific SMT. In order to keep the same block length (i.e., ![]() bits) from both nodes, different nodes with unequal number of transmit antennas should use different modulation orders.
bits) from both nodes, different nodes with unequal number of transmit antennas should use different modulation orders.
The transmitted block from ![]() is denoted by
is denoted by ![]() , while the transmitted block from
, while the transmitted block from ![]() is denoted by
is denoted by ![]() . Also, the transmitted vectors from nodes
. Also, the transmitted vectors from nodes ![]() and
and ![]() are denoted by
are denoted by ![]() and
and ![]() , respectively, that are generated from their corresponding data blocks (i.e.,
, respectively, that are generated from their corresponding data blocks (i.e., ![]() and
and ![]() ).
).
The received signal vector at the relay ![]() is denoted by
is denoted by ![]() and is given as follows:
and is given as follows:
where ![]() and
and ![]() are, respectively, the
are, respectively, the ![]() and
and ![]() MIMO channel matrices between node
MIMO channel matrices between node ![]() and the relay and node
and the relay and node ![]() and the relay. Moreover, the vector
and the relay. Moreover, the vector ![]() is an
is an ![]() ‐length AWGN vector with zero mean and
‐length AWGN vector with zero mean and ![]() variance.
variance.
The ML detector is considered at the relay node to retrieve the transmitted vectors ![]() and
and ![]() as
as

where ![]() and
and ![]() represent the sets of all possible transmission vectors from nodes
represent the sets of all possible transmission vectors from nodes ![]() and
and ![]() , respectively. The detected vectors
, respectively. The detected vectors ![]() and
and ![]() are then, respectively, mapped back to their corresponding data blocks
are then, respectively, mapped back to their corresponding data blocks ![]() and
and ![]() .
.
6.3.2 The Relaying Phase
Upon obtaining the blocks ![]() and
and ![]() , the relay node processes them to obtain a third data block of size
, the relay node processes them to obtain a third data block of size ![]() bits, denoted by
bits, denoted by ![]() . This is usually performed through a simple XOR operation as
. This is usually performed through a simple XOR operation as
The ![]() bits block is then used to obtain the transmission vector
bits block is then used to obtain the transmission vector ![]() , which is transmitted from the relay node in this phase.
, which is transmitted from the relay node in this phase.
The received vectors at nodes ![]() and
and ![]() are
are
where ![]() and
and ![]() are, respectively, the
are, respectively, the ![]() and
and ![]() MIMO channel matrices between the relay and the nodes
MIMO channel matrices between the relay and the nodes ![]() and
and ![]() , and
, and ![]() and
and ![]() are the
are the ![]() and
and ![]() length AWGN vectors at
length AWGN vectors at ![]() and
and ![]() nodes, respectively.
nodes, respectively.
At nodes ![]() and
and ![]() , the ML detection is applied on the received signals in order to estimate the detected vectors
, the ML detection is applied on the received signals in order to estimate the detected vectors ![]() as follows:
as follows:
and

where ![]() is the set of all possible transmitted vectors from the relay node
is the set of all possible transmitted vectors from the relay node ![]() .
.
At the end of this phase, each node maps its detected vector into its corresponding bit block. Let ![]() denotes the obtained block at node
denotes the obtained block at node ![]() , and
, and ![]() is the obtained bits block at node
is the obtained bits block at node ![]() . Consequently, each node can extract a corrupted version of the transmitted bits from the other node by performing an XOR operation with its own transmitted bits as
. Consequently, each node can extract a corrupted version of the transmitted bits from the other node by performing an XOR operation with its own transmitted bits as
and
where ![]() being the corrupted version of
being the corrupted version of ![]() obtained at node
obtained at node ![]() , and
, and ![]() is the corrupted version of
is the corrupted version of ![]() obtained at node
obtained at node ![]() .
.
At the end of both phases, each node has received ![]() bits from the other node. Compared to the conventional one‐way relaying systems, as discussed previously, 2WR can double the spectral efficiency. However, the cost of the improvement in the spectral efficiency is paid in the overall error performance at both nodes, which will be analyzed and discussed hereinafter.
bits from the other node. Compared to the conventional one‐way relaying systems, as discussed previously, 2WR can double the spectral efficiency. However, the cost of the improvement in the spectral efficiency is paid in the overall error performance at both nodes, which will be analyzed and discussed hereinafter.
6.3.3 Average Error Probability Analysis
The error performance at either nodes, ![]() or
or ![]() , is identical. Therefore, only the error performance at node
, is identical. Therefore, only the error performance at node ![]() is considered. Starting from (6.60), the received block
is considered. Starting from (6.60), the received block ![]() can be expressed in terms of
can be expressed in terms of ![]() as follows:
as follows:
where ![]() ,
, ![]() , and
, and ![]() are the error vectors in the transmitted block from
are the error vectors in the transmitted block from ![]() ,
, ![]() , and
, and ![]() nodes, respectively, and all are of
nodes, respectively, and all are of ![]() length. A specific bit in an error vector is 1 if the corresponding bit has been received in error. Otherwise, it is 0. For example, a specific bit in
length. A specific bit in an error vector is 1 if the corresponding bit has been received in error. Otherwise, it is 0. For example, a specific bit in ![]() is 1 if the corresponding bits in
is 1 if the corresponding bits in ![]() and
and ![]() are not equal. The second line in (6.62) is obtained by substituting
are not equal. The second line in (6.62) is obtained by substituting ![]() , the third line is obtained by substituting
, the third line is obtained by substituting ![]() , the fourth line is obtained by substituting
, the fourth line is obtained by substituting ![]() and
and ![]() , the fifth line is obtained by substituting
, the fifth line is obtained by substituting ![]() where
where ![]() is an all zeros vector, and the last line is obtained using
is an all zeros vector, and the last line is obtained using ![]() .
.
Now, the last line in (6.62) can be rewritten on a bit base as
where ![]() is an arbitrary bit in
is an arbitrary bit in ![]() , and
, and ![]() ,
, ![]() ,
, ![]() , and
, and ![]() represent the corresponding bits in
represent the corresponding bits in ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. The bit
, respectively. The bit ![]() is correct if it is equal to
is correct if it is equal to ![]() . Hence, the bit error rate at
. Hence, the bit error rate at ![]() , denoted by
, denoted by ![]() , can be expressed as follows:
, can be expressed as follows:
Notice that ![]() occurs if only one of them is 1 or all of them are 1's. Thus, (6.64) can be expanded to
occurs if only one of them is 1 or all of them are 1's. Thus, (6.64) can be expanded to

which can be further simplified to
where
and ![]() .
.
Also, it can be easily verified that ![]() . Therefore, (6.66) can be further simplified to
. Therefore, (6.66) can be further simplified to
The parameter ![]() represents the ABER in the received block at the relay for the source
represents the ABER in the received block at the relay for the source ![]() given that the relay received the block from
given that the relay received the block from ![]() correctly. Similarly,
correctly. Similarly, ![]() is the average ABER in the received block from
is the average ABER in the received block from ![]() at the relay given that the relay received the
at the relay given that the relay received the ![]() block correctly, and
block correctly, and ![]() represents the average ABER in the received block from the relay at node
represents the average ABER in the received block from the relay at node ![]() .
.
The computation of the average ABER can be obtained through the union bound technique. As such, ![]() is formulated as
is formulated as
where ![]() is the hamming distance between the two bit blocks corresponding to
is the hamming distance between the two bit blocks corresponding to ![]() and
and ![]() . The probability
. The probability ![]() can be expressed using (6.58) as
can be expressed using (6.58) as
For a given ![]() , and as shown previously and in Chapter 4, the above probability can be expressed by means of
, and as shown previously and in Chapter 4, the above probability can be expressed by means of ![]() ‐function as
‐function as
where ![]() .
.
Assuming Rayleigh fading channels, the probability in (6.74) can be averaged and upper bounded as
where ![]() and
and ![]() denotes the Kronecker product. A proof of (6.75) can be easily obtained considering the ABER derivations in Chapter 4.
denotes the Kronecker product. A proof of (6.75) can be easily obtained considering the ABER derivations in Chapter 4.
Substituting (6.75) in (6.72), the probability ![]() can be upper bounded as
can be upper bounded as
Following similar steps as used to obtain (6.78), ![]() can be derived and is given by
can be derived and is given by

where ![]() is the hamming distance between the bit blocks corresponding to
is the hamming distance between the bit blocks corresponding to ![]() and
and ![]() . Following the same procedure in (6.72), (6.73), (6.74), (6.75), (6.76), the probability
. Following the same procedure in (6.72), (6.73), (6.74), (6.75), (6.76), the probability ![]() can be upper bounded by
can be upper bounded by
where ![]() and
and ![]() . Please note that both
. Please note that both ![]() and
and ![]() are identical (but not equal) due to the assumption that both
are identical (but not equal) due to the assumption that both ![]() and
and ![]() have same statistical fading model.
have same statistical fading model.
The last probability to be estimated in (6.71) is ![]() , which is given by
, which is given by
where ![]() represents the hamming distance between the bit blocks corresponding to
represents the hamming distance between the bit blocks corresponding to ![]() and
and ![]() .
.
Now using (6.58), and similar to (6.74), the probability ![]() for a given
for a given ![]() can be expressed as
can be expressed as
where ![]() and (6.80) can be rewritten as
and (6.80) can be rewritten as
where ![]() .
.
Therefore, ![]() can be computed by substituting (6.81) into (6.79) as follows:
can be computed by substituting (6.81) into (6.79) as follows:

Figure 6.10 Simulation and analytical results for the ABER versus the average SNR for 2WR QSM MIMO system. The block length is  bits per channel use for each transmitting node. The nodes are assumed to have two transmit antennas and using 4‐QAM modulation order. The number of received antennas is varied from
bits per channel use for each transmitting node. The nodes are assumed to have two transmit antennas and using 4‐QAM modulation order. The number of received antennas is varied from  .
.
Finally, the average ABER at node ![]() ( or node
( or node ![]() ) can be expressed by substituting (6.76), (6.78), and (6.82) into (6.71).
) can be expressed by substituting (6.76), (6.78), and (6.82) into (6.71).
6.3.3.1 Numerical Results
The ABER for 2WR QSM system is depicted in Figure 6.10 for ![]() ,
, ![]() ‐QAM, and
‐QAM, and ![]() is varied from
is varied from ![]() . Considering this setup, each node will deliver
. Considering this setup, each node will deliver ![]() bits by the end of the two phases. As illustrated in the figure, increasing the number of receive antennas at all nodes significantly improves the overall performance and a gain of about 9.2 dB can be noticed at an ABER of
bits by the end of the two phases. As illustrated in the figure, increasing the number of receive antennas at all nodes significantly improves the overall performance and a gain of about 9.2 dB can be noticed at an ABER of ![]() when having three receive antennas instead of two. In addition, depicted analytical and simulation results are shown to match closely and for the different depicted curves with variant number of receive antennas.
when having three receive antennas instead of two. In addition, depicted analytical and simulation results are shown to match closely and for the different depicted curves with variant number of receive antennas.
Another setup considering ![]() ,
, ![]() ‐QAM and the receive antennas are varied from
‐QAM and the receive antennas are varied from ![]() is evaluated, and the results are shown in Figure 6.11. With these configurations, the spectral efficiency increases to
is evaluated, and the results are shown in Figure 6.11. With these configurations, the spectral efficiency increases to ![]() bits for each transmitting node. Similar conclusions as drawn in the previous figure can be concluded here as well.
bits for each transmitting node. Similar conclusions as drawn in the previous figure can be concluded here as well.

Figure 6.11 Simulation and analytical results for the ABER versus the average SNR for 2WR QSM MIMO system. The block length is  bits per channel use from each transmitting node. Each node is assumed to be equipped with two transmit antennas and transmits an 4‐QAM symbol. The number of received antennas is varied from
bits per channel use from each transmitting node. Each node is assumed to be equipped with two transmit antennas and transmits an 4‐QAM symbol. The number of received antennas is varied from  .
.