Appendix A
Sine Waves in Circuits
A.1 Introduction
The material in this appendix is a fast review of linear circuit theory. This material is needed when applying the Smith chart to matching impedances. This theory describes the voltages and currents that result when sine waves at a fixed frequency are used to excite a network of linear components. Complex notation is used so that the phase relations in RLC networks can be analyzed as a function of frequency. The concepts of impedance, admittance, resistance, conductance, reactance, and susceptance are introduced. If the reader needs a slower pace, there are many texts available with problem sets. Working problems is an important part of learning this material and keeping it fresh.
A.2 Unit Circle and Sine Waves
On a simple grid of vertical and horizontal lines, label the center point as zero. This point is called the origin. Draw a circle with the center in mid page. This is called the unit circle. The horizontal line that goes through the origin is the x axis, the vertical line that goes through the origin is the y axis. The top of the circle is a y value of 1. The bottom is −1. The far left point has a y value of 0 and an x value of −1. Number the grid of lines so that every point on the circle can be given an x and y value from 0 to ±1.
Now draw a radial line from the origin to the circle at the point where y = 0.5. The radius is the hypotenuse of a triangle formed by the x and y distances. Note that any point on the circle must satisfy the relationship x2 + y2 = 1. This means that the x value here is 0.866 when the y value is 0.5. This point is often labeled (x, y) = (0.5, 0.866) (see Figure A.1).

Figure A.1 The unit circle and the point (0.5, 0.866).
Label the angle between the radius and the x axis β. When the angle is increased to 45°, the value of x and y are both 0.707. When the radius is vertical the value of x is 0 and the y value is 1.0. This point on the diagram is called (0, 1). The angle β = 90°.
Continue to increase the angle until the tip of the radius makes a full circle. In one revolution this angle is 360°. Two full cycles would result in an angle of 720°. When the angle is 150°, the y value returns to 0.5. When the angle is 270°, the y value is −1. This point is identified as (0, −1).
This vertical or y value in this diagram is called the sine of the angle. If the line is above the x axis the sine value is positive. If the line is below the x axis the sine value is negative. If the angle is labeled β, the equation that relates the y value to the angle β is
where sin is the abbreviation for sine. This equation is read “y equals sine of β.” The value of y is always between +1 and −1. When β is 0° or 180°, the value of y is 0. This means that sin (180°) = 0. When β = 90°, sin (90°) = 1.
The sine function is a ratio of line lengths using the unit circle. It is one of six trigonometric functions. The x value in the unit circle example above is called the cosine function. It is abbreviated as cos β. In equation form we can write
The value of the cosine function when β = 0° is 1: when β = 90° the value of cos β is 0. When β = 180° the value of cos β is −1.
Now rotate the radial counterclockwise at a constant rate starting with the tip at the point (1, 0). On a second graph, plot the vertical position of the tip against time. The curve that results (shown in Figure A.2) is called a sine wave. If the radial starts at (0, 1) and rotates at a steady rate, a cosine wave is formed. Sine waves and cosine waves have the same shape but the peak values occur at a different time. The cosine wave is said to lead the sine wave in phase by 90°. By convention any wave with this shape is called a sine wave.
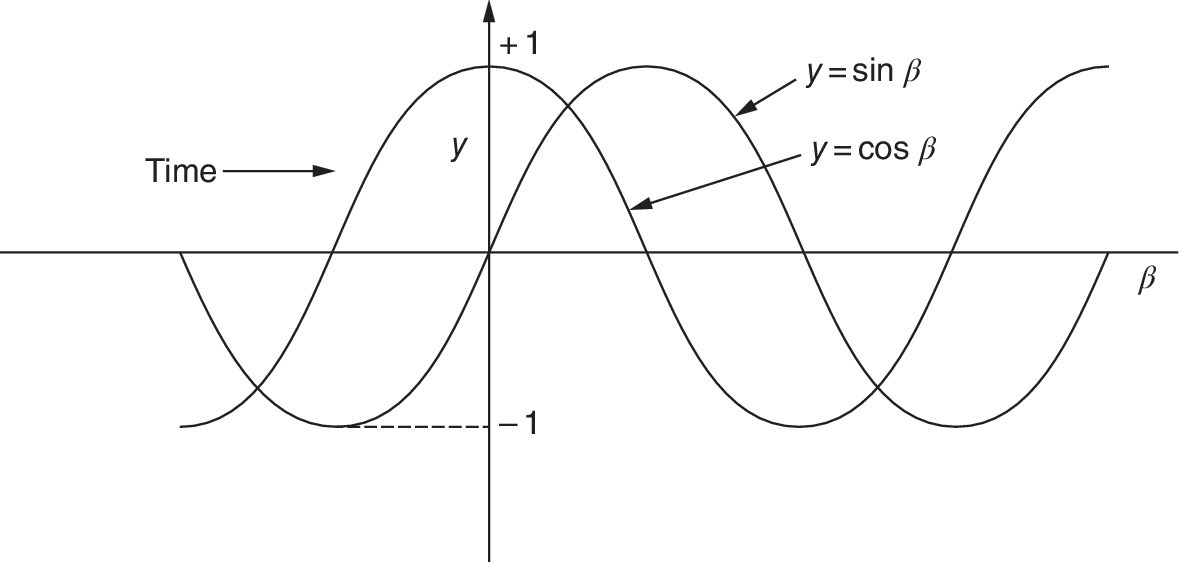
Figure A.2 A sine and cosine wave.
Problem Set A.2
- 1 Simplify sin 90° + cos 180° − sin 270°.
- 2 A unit radial has an x value of 0.707. What is the y value?
- 3 At what two angles does sin β = 0.707?
- 4 If sin β = 0.4 what is cos β?
- 5 What are the maximum and minimum values of the sine function?
A.3 Angles, Frequency, and rms
The measurement of angles dates well before man invented the calculus. Dividing the circle into 360 parts is a part of history. Some feel it would have made more sense to divide the circle into 100 parts rather than 360. In mathematics, the most useful way to measure angles involves the radius. Take a circle and wrap the radius along the circumference. The angle that is subtended by the radius is called a radian. Since 2π radians = 360°, we know that 1 radian is equal to 57.29°. This is not a nice even number. To get around the problem, electrical engineers measure angles in multiples of 2π. In other words, 2π radians equals 360°. An angle of π/2 radians is thus read as 90 electrical degrees. Most engineers refer to the angle as π/2 and omit the term radian. In the calculus the derivative of sin x is cos x, but only if the angles are in radian units.
The sine of 90° is equal to 1. The convention that is in constant use in engineering is sin(90°) = 1, which is written as sin(π/2) = 1.
It is very important to realize that the sine function only applies to angles. In one cycle the angle changes 360° or 2π radians. To generate sine waves at a given frequency, say at 60 Hz which is really 60 cycles/s, the number of degrees that must pass in 1 second is 60 times 360° or 60 times 2π radians. By convention the angle in radians at a time t is simply
where f is the conventional frequency in hertz and t is time in seconds. Since the term 2πf occurs often in electronics it is, by convention, labeled the Greek letter ω. The term ω is called the radian frequency.
where f is frequency in hertz. The angle β in radians as a function of time is
It is necessary to interpret all literature that describes sinusoidal responses as being in terms of radian frequency, not degrees frequency. A sine wave voltage would be described by
where V is the peak voltage value, v is the value of voltage at time t, and ω is the radian frequency. Often, just the lower case letter v is used and the reader understands it is a sine wave. It is time consuming to write sin ωt over and over. This understanding takes time to get used to. The sine waves in Figure A.2 are phase shifted by 90 electrical degrees. The cosine wave could have been written
where β = π/2.
The value V is called the peak value. The value v (in lower case) changes with time in a sinusoidal manner. This is also by convention. For current, the expression might be
The voltage V or the current I are peak values. The value measured by a voltmeter is often the heating value. This is the peak sine value divided by the square root of 2 or 0.707 V. In most electronics the peak value is used, not the rms value. This is also by convention. In power engineering V would mean the rms or heating value, not the peak value. The utility power in a home is 120 V rms. This voltage has a peak value of 169.7 V and a peak‐to‐peak value of 339 V.
The current that flows when a voltage is applied to a resistor R is by Ohm’s law V/R. The current can also be described by rotating a radial line. The rotating radius for the current points in the same direction as the voltage. The voltage and current are in phase. This means that when the voltage peaks the current also peaks. This rotating line is a vector as it has direction and intensity indicated by length.
Problem Set A.3
- 1 What is the value of sin(3π/2)?
- 2 What is the value of cos(−π/2)?
- 3 What is the radian frequency if the voltage vector rotates at twice per second?
- 4 At 100 Hz, how many degrees does the radial cover in 1 millisecond?
- 5 At 100 Hz, how many radians does the radial cover in 1 millisecond?
- 6 The voltage vector rotates once per microsecond. What is the frequency? What is the radian frequency?
- 7 A voltage has a peak value of 100 V. What is its rms value?
- 8 Write the equation for a sine wave at 1 kHz that leads another 1 kHz signal of equal amplitude by 30°.
- 9 A voltage 3 sin ωt is added to a voltage 4 cos ωt. What is the sum?
- 10 A voltage 3 sin ωt is added to a voltage 4 cos(ωt + π/6). What is the sum?
A.4 The Reactance of an Inductor
In the circuit in Figure A.3, a sinusoidal voltage is connected to an inductor at the moment of maximum voltage. This timing avoids generating any transients. The current starts at zero and increases as long as the voltage is positive. When the voltage is zero the current peaks. The current begins to decrease as the voltage goes negative. The current is zero when the voltage is at its negative peak. The current and voltage waveform are shown in Figure A.3.

Figure A.3 Sine wave voltage and current for an inductor. The current lags the voltage by 90°.
The current lags the voltage by 90 electrical degrees. If v = V sin ωt then the current I is equal to

where ω is the radian frequency, L is the inductance in henries, and V is the peak voltage.
This 90° relation between current and voltage occurs for every inductor handling sine wave signals. The ratio of peak voltage to peak current flow is called a reactance XL measured in ohms. The peaks do not occur at the same time.
If a steady current flows in an inductor that uses magnetic material, the material will saturate. This results in nonlinear behavior. Inductors that carry low‐frequency currents should not use magnetic materials without an adequate air gap.
When inductors are paralleled the total current that flows is given by
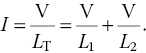
Eliminating V, it is easy to see that parallel inductors add using reciprocals.
Problem Set A.4
- 1 What is the reactance of a 1 mH inductor at 10 kHz?
- 2 What is the current flow in a 1 μH inductor at 2 MHz if the voltage is 1 V peak?
- 3 What is the inductance of a 10 μH inductor in parallel with an 8 μH inductor?
A.5 The Reactance of a Capacitor
In the circuit of Figure A.4, a sinusoidal voltage is applied to a capacitor at the moment the voltage starts going positive. This timing avoids generating any transients.

Figure A.4 Sine wave voltage and current for a capacitor. The voltage leads the current by 90°.
The current that flows depends on the rate of change of voltage which is maximum at the moment of contact. The current leads the voltage by 90 electrical degrees and is equal to
where ω is the radian frequency, C is the capacitance in farads, and V is the peak voltage. This 90° relationship between current and voltage occurs for every capacitor when there are sine waves. The ratio of peak voltage to peak current is called a reactance XC measured in ohms. The reactance is

When capacitors are placed in parallel their capacitances add directly.
When capacitors are put in series their reactances add directly. Using Equation A12 the reactance of series capacitors is

Eliminating ω it is easy to see that series capacitances add by using reciprocals.

Problem Set A.5
- 1 What is the reactance of a 0.001 μF capacitor at 100 MHz?
- 2 What is the parallel capacitance of 1 nF and 200 pF?
- 3 What is the capacitance of 0.001 μF and 0.002 μF in series?
- 4 What capacitance has a reactance of 50 ohms at 400 MHz?
A.6 An Inductor and a Resistor in Series
Assume a current is flowing in a series resistor and inductor. The voltage across the inductor peaks 90 electrical degrees before the voltage across the resistor. If the voltage across the resistor is IR sin ωt, then the voltage across the inductor is IωL cos ωt. The sum of these voltages is
Expand the right term, then equate the coefficients of sin ωt and cos ωt.
It is not difficult to show that
and
The ratio of V/I is called an impedance and is usually assigned the letter Z. In this case, the magnitude of the impedance in ohms of a resistor in series with an inductor is
Equations A19 and A20 are exactly the same as assigning a real value to a horizontal vector representing the voltage across the resistor and assigning an imaginary value to a vertical vector representing the voltage across the inductor. Using complex notation, the series RL circuit has an opposition to current flow equal to Z = R + jωL. The factor j is equal to the square root of −1. These vectors are shown in Figure A.5.

Figure A.5 The vectors representing the voltages in a series RL circuit.
The impedance Z in ohms using complex notations is
The reactance XL in ohms of the inductor is
A 10‐ohm resistor in series with a 1‐H inductor at 1 Hz has an impedance of (10 + 6.28 j) ohms. This means that if a sine wave current of 1 A were to flow in this impedance, the voltage across the resistor would be a 10‐V sine wave and the voltage across the inductor would be a 6.28‐V cosine wave. The total voltage is (102 + 6.282)½ V = 11.8 V. This is a sine wave voltage leading the voltage across the resistor by 32.3°.
Problem Set A.6
- 1 An inductor of 10 μH is in series with 50 ohms. What is the total impedance at 20 MHz?
- 2 An inductance has a reactance of 40 ohms at 50 MHz. What is the inductance?
- 3 An inductor of 3 μH is in series with 100 ohms. What is the phase angle between the current and voltage at 10 MHz?
- 4 At what frequency will an inductor of 20 nH have a reactance of 100 ohms?
A.7 A Capacitor and a Resistor in Series
When a resistor and a capacitor are placed in series, a current generates a voltage across the capacitor that peaks 90 electrical degrees after the voltage peaks across the resistor. If the voltage across the resistor is IR sin ωt, then the voltage across the capacitor is − IωL cos ωt. The sum of these voltages is
Expand the left term and equate coefficients of sin ωt and cos ωt. The voltage V is

and
In complex notation, the opposition to current flow for a resistor and capacitor in series is an impedance Z where
The magnitude of the impedance in ohms is
and the reactance of the capacitor is equal to
These vectors are shown in Figure A.6.
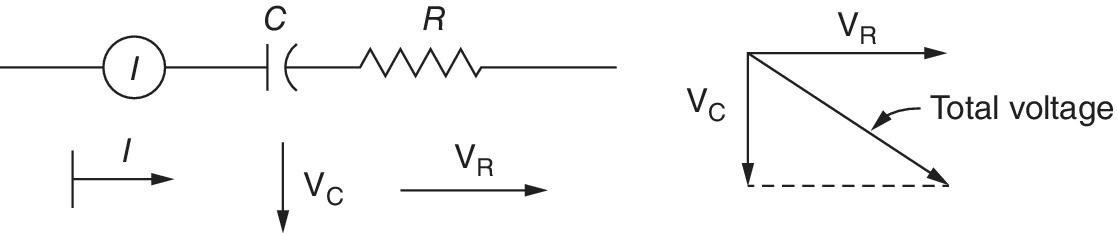
Figure A.6 The vectors representing the voltages in a series RC circuit.
A 3‐ohm resistor in series with a ½ farad capacitor at 2 Hz has an impedance of 3–0.159 j ohms. What this means is that if the voltage across the resistor is a 3‐V sine wave, the voltage across the capacitor is a delayed cosine wave of 0.159 V.
Problem Set A.7
- 1 At what frequency will a capacitor of 100 pF and a series resistor of 100 ohms have an impedance of 200 ohms?
- 2 In problem 1, at what frequency will the reactance double?
- 3 The series impedance in problem 1 is 300 ohms. What is the phase angle in degrees between the voltage and the current flow?
A.8 The Arithmetic of Complex Numbers
It is very convenient to use complex numbers to represent voltages, currents, impedances, and admittances. In a series circuit the voltages across components do not add directly as the peaks of voltages do not occur at the same time. In a parallel circuit the peaks of current do not occur at the same time. Complex numbers are the simplest way to solve these circuit problems. Here are the rules for addition, multiplication, and division of complex numbers.
- Addition. Add the real and imaginary terms separately.

- Multiplication. Use standard rules for multiplication where j2 = −1, j3 = −j and j4 = 1.

- Division requires the use of conjugates. The conjugate of (2 + 3 j) is (2 − 3 j). To divide by a complex number, multiply the numerator and denominator by the conjugate of the denominator. Here are two examples:


A.9 Resistance, Conductance, Susceptance, Reactance, Admittance, and Impedance
Resistor inductors and capacitors have the ability to oppose current flow. The unit that is used for resistance is the ohm abbreviated as Ω. The opposition to current flow by capacitors and inductors is called reactance and uses the symbol X. An impedance Z is a combination of resistance and reactance. These same components have the ability to accept current flow. The terms that are used are conductivity for a resistor and susceptance for a capacitor or inductor. The unit is the siemen, abbreviated as S.1 A combination of a conductance and a suseptance is called an admittance and uses the letter Y. In each case the measure of current acceptance is the reciprocal of current opposition. For example, a resistor of 10 Ω has a conductance of 0.1 siemens (S). It is the same resistor with two different measures. A capacitor has a reactance of −2 j Ω and a susceptance of 0.5 j S. It is the same capacitor. An inductor has a reactance of 5 j Ω and a susceptance of −0.2 j S. It is the same inductor. Any impedance can be described as a susceptance and visa versa. The ratio of voltage to current is fixed at any one frequency for a given network. It takes practice to get used to the language that is used.
When resistors are paralleled their conductances add. A 5‐Ω resistor in parallel with a 2‐Ω resistor is the sum of two conductances namely 1/5 + 1/2 = 7/10 S. To convert this conductance back to a resistance take the reciprocal which is 10/7 Ω.
When inductors are paralleled the same principle is used. Each inductor is described as a susceptance and these susceptances are added together. The result can be converted to a reactance by taking the reciprocal. To parallel an inductor of 2 j Ω with an inductor of 4 j Ω their susceptances are −0.5 j and −0.25 j S. Their sum is −0.75 j S. The reciprocal is a reactance of +1.33 j Ω.
When capacitors are paralleled each capacitor is described as a susceptance and the susceptances are added together. The result can be converted to a reactance by taking the reciprocal. To parallel a capacitor of −4 j ohms with a capacitor of −5 j ohms, their susceptances are +0.25 j and +0.2 j S. Their sum is +0.45 j S. To convert to a reactance the reciprocal is −2.22 j ohms.
The admittance Y of a resistor of 5 Ω in parallel with an inductor of 4 j Ω is found by converting the resistance to a conductance of 0.20 S and the inductor to a susceptance of −0.25 j S. The admittance is the sum Y = (0.20 − 0.25 j) S. To covert this to an impedance, take the reciprocal which is Z = (1.957 + 2.439 j) Ω.
The admittance Y of a resistor of 5 Ω in parallel with a capacitor of −2 j Ω is found by converting the resistance to a conductance of 0.2 S and the capacitor to a susceptance of +0.5 j S. The admittance is the sum Y = (0.2 + 0.5 j) S. The impedance of this parallel circuit is the reciprocal of Y which is Z = (0.69 − 1.76 j) Ω.
Problem Set A.9
In these problems use complex notation.
- 1 Two capacitors have a reactance of −2 j and −3 j ohms. What is the series reactance?
- 2 Two inductors have a reactance 0.5 j and 0.6 j ohms. What is the parallel reactance?
- 3 A resistor of 2 ohms is in series with an inductance of 3 j‐ohm reactance. What is the admittance in siemens?
- 4 A resistor of 3 ohms is in parallel with a capacitor with a reactance of −4 j ohms. What is the impedance in ohms?
- 5 In problem 4, what is the admittance in siemens?
- 6 A capacitor with a reactance of 2 j is in parallel with an inductance having a susceptance of −2 j. What is the impedance?
- 7 An impedance of 2 + 3 j is in series with an admission of 1 − 2 j. What is the impedance?
- 8 A susceptance of 3 + 2 j S is in series with an impedance of 2 − 3 j ohms. What is the total impedance?
A.10 Resonance
The reactance of an inductor is given in Equation A18. The reactance of a capacitor is give in Equation A22. The impedance of the two elements in series is
The frequency ω where Z = 0 is called the series resonant frequency. The frequency is

If there is a series resistance the impedance at the resonant frequency is this resistance.
The susceptance of an inductor is −j/ωL. The susceptance of a capacitor is jωC.
The frequency where the susceptances adds to zero is given by Equation A26. This frequency is called the parallel resonant frequency. This circuit is sometimes called a tank circuit. Ideally the impedance of a parallel resonant circuit is infinite at the resonant frequency.
A.11 Answers to Problems
Problem Set A.2
- 1 Sin 90° = 1, cos 180° = −1, sin 270° − 1. The sum is 1.
- 2 0.707.
- 3 45° and 135°.
- 4 Cos β = 0.917.
- 5 The limits are +1 and −1.
Problem Set A.3
- 1 Sin 3π/2 = −1
- 2 Cos − π/2 = 0.
- 3 4π.
- 4 36°.
- 5 π/5.
- 6 f = 1 MHz, 2π × 106 radians per second.
- 7 70.7 V
- 8 Sin(2000πt + π/6).
- 9 5 sin (ωt + 53°).
- 10 Sin ωt + 3.46 cos ωt.
Problem Set A.4
- 1 20π.
- 2 1/4π peak.
- 3 4.44 μH
Problem Set A.5
- 1 1.59 ohms.
- 2 1.2 nF.
- 3 0.666 nF.
- 4 398 pF.
Problem Set A.6
- 1 1.25 kΩ.
- 2 0.127 μH.
- 3 62°.
- 4 796 MHz.
Problem Set A.7
- 1 9.19 MHz.
- 2 18.38 MHz.
- 3 20.7°.
Problem Set A.8
- 1 −5 j.
- 2 1.1 j.
- 3 (2 − 3 j)/13.
- 4 12(4 − 3 j)/25.
- 5 1/3 + j/4.
- 6 12(4 − 3 j)/25.
- 7 2.2 + 3.4 j.
- 8 29/13 − 41 j/13.

