7
Repeated measurements
Repeated measurements occur in many areas of study. The measurements repeat in time, space, or both. However, they are normally relatively short, and therefore the standard time series methods cannot be used. In this chapter, we will introduce some methods and various models that are useful for analyzing repeated measures data. Empirical examples will be used for illustration.
7.1 Introduction
Many fields of study, such as medical and biological science, social science, and education, involve sets of relatively short time series where the application of standard time series methods introduced earlier is difficult, if not impossible. For instance, an experiment may involve measurements taken at some selected times (or locations) from subjects associated with several treatments. The term “subject” is often used because the phenomenon of repeated measurements commonly occurs in the areas of medical, social, and educational studies, where human subjects are involved. However, the term may refer to an animal, a company, or even a tool. For example, the following is a study involving the growth curve data on the body weights of 27 rats from Box (1950) given in Table 7.1. The subject is a rat that is assigned to one of three treatment groups (Control, Thiouracil, Thyroxin) and its weight is measured weekly for 5 weeks. The objective of the study is to test whether there are differences in growth rates between groups.
Table 7.1 Body weight of rats under three different treatments (1 = Control, 2 = Thyroxin, 3 = Thiouracil) with weight at five different time points (Week 0, Week 1, Week 2, Week 3, and Week 4).
| W0 | W1 | W2 | W3 | W4 | |
| 1 | 57 | 86 | 114 | 139 | 172 |
| 1 | 60 | 93 | 123 | 146 | 177 |
| 1 | 52 | 77 | 111 | 144 | 185 |
| 1 | 49 | 67 | 100 | 129 | 164 |
| 1 | 56 | 81 | 104 | 121 | 151 |
| 1 | 46 | 70 | 102 | 131 | 153 |
| 1 | 51 | 71 | 94 | 110 | 141 |
| 1 | 63 | 91 | 112 | 130 | 154 |
| 1 | 49 | 67 | 90 | 112 | 140 |
| 1 | 57 | 82 | 110 | 139 | 169 |
| 2 | 59 | 85 | 121 | 146 | 181 |
| 2 | 54 | 71 | 90 | 110 | 138 |
| 2 | 56 | 75 | 108 | 151 | 189 |
| 2 | 59 | 85 | 116 | 148 | 177 |
| 2 | 57 | 72 | 97 | 120 | 144 |
| 2 | 52 | 73 | 97 | 116 | 140 |
| 2 | 52 | 70 | 105 | 138 | 171 |
| 3 | 61 | 86 | 109 | 120 | 129 |
| 3 | 59 | 80 | 101 | 111 | 122 |
| 3 | 53 | 79 | 100 | 106 | 133 |
| 3 | 59 | 88 | 100 | 111 | 122 |
| 3 | 51 | 75 | 101 | 123 | 140 |
| 3 | 51 | 75 | 92 | 100 | 119 |
| 3 | 56 | 78 | 95 | 103 | 108 |
| 3 | 58 | 69 | 93 | 116 | 140 |
| 3 | 46 | 61 | 78 | 90 | 107 |
| 3 | 53 | 72 | 89 | 104 | 122 |
The type of time series data described previously differs from other time series data that we have studied earlier. First, although a series of measurements on a subject over time does constitute a univariate time series, it is often relatively short. More importantly, the main interest of the study is normally not about the stochastic nature of the series of any subject. Additionally, when several series of measurements were observed from several subjects, they do look like vectors of multiple time series, especially when the measurements of these subjects were observed at the same time points. However, the components of a vector constructed at each time point are measurements of the same phenomenon. For example, the components of the vector obtained from Table 7.1 will all be body weights. Certainly, the interest of the study is not the cross‐correlational structure of different component series from these subjects. Rather, subjects in each group constitute a random sample. The main interest is to study whether there are any differences between groups based on sample information from these groups. Since these series are measurements of the same phenomenon from several subjects that are often assumed to be independent, we refer to them as “repeated measurement data.” Other names such as “longitudinal data” or “panel data” are also used.
There are two factors in the experiment of repeated measurements, treatments, and time. Treatment is the first factor, often known as the between‐subjects factor because its levels change only between subjects. Time is the second factor, often known as within‐subjects factor because its values are changing over time on the same subject. In this factorial experiment, we are interested in finding whether (i) treatment means are different, (ii) treatment means are changing over time, and (iii) there are interactions between treatment and time.
In this chapter, we give a simple introduction to some normal distribution‐based methods. For more general treatments, we refer readers to Crowder and Hand (1990), Lindsey (1993), and Diggle, Liang, and Zeger (2013), among others.
7.2 Multivariate analysis of variance
7.2.1 Test treatment effects
To study the phenomenon described in Table 7.1, we can, in general, use Zi,j(i = 1, 2, …, m; j = 1, 2, …, ni) to denote the response of the jth subject for the ith treatment. Clearly, each Zij is a p‐dimensional random vector, where p is the total time period of the response. The subjects are elements of random samples collected from each of m populations (treatments) and can be arranged as follows:

Assume that (i) ![]() is a random sample of size ni from a multivariate normal population with mean vector μi, i = 1, 2, …, m; (ii) the random samples from different populations are independent; and (iii) all populations have a common variance–covariance matrix Σ. We can use multivariate analysis of variance (MANOVA) to investigate whether the population mean vectors are the same. Thus,
is a random sample of size ni from a multivariate normal population with mean vector μi, i = 1, 2, …, m; (ii) the random samples from different populations are independent; and (iii) all populations have a common variance–covariance matrix Σ. We can use multivariate analysis of variance (MANOVA) to investigate whether the population mean vectors are the same. Thus,
for i = 1, 2, …, m and j = 1, 2, …, ni where the errors eij are independent Np(0, Σ) variables, μ is an overall mean, and θi represents the ith treatment effect with ![]()
Note that a vector of observations can be written as
and it leads to the following decomposition

This is clearly the extension of the univariate analysis variance where we have
Total (corrected) sum of squares = Treatment sum of squares + Residual sum of squares.
For computation, the within‐sum of squares and cross product matrix can also be written as

where Si is the sample covariance matrix for the ith sample.
Thus, the hypothesis of no treatment effects
can be tested by comparing the relative sizes of the treatment (between) and residual (within) sums of squares and cross products summarized in the MANOVA table (Table 7.2):
Table 7.2 MANOVA table for comparing population mean vectors.
| Source of variation | Matrix of sum of squares and cross products (SSCP) | Degrees of freedom (d.f.) |
| Treatment (between) |
|
m − 1 |
| Residual (within) |
|
|
| Total (corrected for mean) |
|
|
In the univariate analysis of variance, we reject the null hypothesis when the treatment sum of squares is significantly larger than the residual sum of squares, or equivalently, when the residual sum of squares is a much smaller portion of the total sum of squares. Following the same logic, in multivariate analysis of variance, we reject H0 if the following ratio of generalized variances

is too small. The statistic Λ, originally proposed by Wilks (1932), is often known as Wilk's lambda. The sampling distribution of Wilk's lambda depends on the values of m and p. For example, with m = 3 and p ≥ 1, we have the following sampling distribution (see Johnson and Wichern, 2007, p. 303)

Alternatively, under H0, when ∑ni = n is large, we can also use the following Bartlett's approximation (Bartlett, 1954):

which has a chi‐square distribution with p(m – 1) degrees of freedom. Thus, we reject H0 if

7.2.2 Empirical Example 1 – First analysis on body weight of rats under three different treatments
data Rat;infile 'c:/Bookdata/WW7a.csv';input Treatment Week0 Week1 Week2 Week3 Week4;/* GLM procedure with MANOVA */proc glm data=Rat;class Treatment;model Week0 Week1 Week2 week3 week4 = Treatment /NOUNI;means Treatment;manova h = Treatment/printh printe htype=1 etype=1;run;
we get the following multivariate MANOVA table (Table 7.3).
Table 7.3 MANOVA table of comparing treatment mean vectors for body weights of rats.

Thus, the Wilk's lambda from Table 7.3 is Λ = |R|/|T + R|=0.259, and

which is much greater than the F0.05(10, 40)=2.08. Thus, the null hypothesis is rejected, and we conclude that the mean vectors of the three treatment groups are different. Using Bartlett's approximation, we have

which is greater than ![]() and hence the null hypothesis is rejected.
and hence the null hypothesis is rejected.
We now try to find out exactly when these mean differences occur in the experiment. The box plots for the three treatment groups over the four week‐long periods is given in Figure 7.2. It shows that the difference of the mean body weights for the three groups occurred in week 3 and week 4, which was also supported by the test results from the SAS GLM procedure.


Figure 7.2 The box plots for the three treatment groups over time.
If ODS Graphics are enabled, GLM also displays by default an interaction plot for this analysis. The following statements, which are the same as in the previous analysis but with ODS Graphics enabled, additionally produce Figure 7.3. The plot shows that there is no interaction between the groups.

Figure 7.3 Interaction plot.
7.3 Models utilizing time series structure
7.3.1 Fixed effects model
In the previous analysis, we assume that ei,j in model (7.1) are independent Gaussian vector white noise Np(0, Σ), where Σ is a general p × p variance–covariance matrix with p(p + 1)/2 elements. We do not utilize the fact that the elements in each p‐dimensional vector, ei,j = [ei,j,1, ei,j,2, …, ei,j,p]′, are time series, and that they are autocorrelated. In a repeated measurement study, to be more rigorous, we should first estimate the variance–covariance structure Σ and then incorporate this structure in the analysis.
More generally, we will consider a two‐factor fixed effects model that not only includes treatment effect but also time effect and treatment/time interaction effect as follows:
where αi, i = 1, …, m, represents the treatment effect, βt, t = 1, …, p, represents the time effect, γi,t represents time/treatment interaction effect, j = 1, …, ni, represents subject, and ![]() For the error term ei,j,t, we assume that
For the error term ei,j,t, we assume that ![]() if either i ≠ i′ or j ≠ j′. However, even though it is logical to assume the same variance–covariance structure for all subjects, we cannot assume
if either i ≠ i′ or j ≠ j′. However, even though it is logical to assume the same variance–covariance structure for all subjects, we cannot assume ![]() In fact,
In fact, ![]() when t ≠ t′, and its structure for the same subject clearly depends on time.
when t ≠ t′, and its structure for the same subject clearly depends on time.
The null hypotheses to be tested in Model (7.14) are:
The analysis of variance table used to test these hypotheses is summarized in Table 7.4. We normally test the interaction term first. When the interaction term is significantly different from 0, it implies that the factor effects are not additive, which makes the interpretation of the results complicated.
Table 7.4 Repeated measurement analysis of variance table.
| Source | SS | DF | Mean square |
| Treatment | SST | (m − 1) | SST/(m − 1) |
| Time (location) | SSL | (p − 1) | SSL/(p − 1) |
| Time*treatment | SSLT | (m − 1)(p − 1) | SSLT/[(m − 1)(p − 1)] |
| Error (time) | SSE | 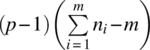 |
 |
By letting Zi,j = [Zi,j,1, …, Zi,j,p]′ be the (1 × p) vector for jth subject on the ith treatment and stacking these vectors into a column vector Y, that is, ![]() we can write Model in Eq. (7.14) in the following matrix form,
we can write Model in Eq. (7.14) in the following matrix form,
where Y is the (np × 1) vector of observations for Zi,j,t, X is the [np × (1 + m)(1 + p)]matrix of corresponding known constants, β is the [(1 + m)(1 + p) × 1] vector of parameters, and ε is a (np × 1) vector of random errors with mean vector 0 and variance–covariance matrix Ω = In ⊗ Σ, In is the n × n identity matrix,n = (n1 + ⋯ + nm) is the number of subjects, and Σ is the (p × p) common variance–covariance structure for all subjects. The generalized least square (GLS) estimator of β is
and variance–covariance matrix of ![]() is
is
Under normal assumptions, it is well known that ![]() follows a multivariate vector normal distribution with mean β and variance–covariance matrix (X′Ω−1X)−1, that is, N(β, (X′Ω−1X)−1).
follows a multivariate vector normal distribution with mean β and variance–covariance matrix (X′Ω−1X)−1, that is, N(β, (X′Ω−1X)−1).
7.3.2 Some common variance–covariance structures
Since a large number of parameters in a variance–covariance matrix will unfavorably affect the estimation efficiency, we should use the correlation pattern of the time series to simplify its form. The following are some commonly used variance–covariance matrices used in repeated measurement studies. Except for the first unstructured matrix, we introduce some simple and useful structures that contain only a small number of parameters.
- The unstructured matrix:

The form implies that variances and covariances at different times are not necessarily equal. There are p(p + 1)/2 parameters in the matrix.
- The identical and independent structure:
The form in Eq. (7.20) is the simplest one and contains only one parameter. It may be applicable in some applications especially when the repeated measurements are taken far apart such that the correlation between different times is effectively zero relative to the other variation.
- The independent but non‐identical structure:

This is a generalized form of Eq. (7.20), where the variances at different times are not necessarily equal. It contains p parameters.
- The structure of common symmetry:
The form in Eq. (7.22) assumes that E(ei,j,kei,j,ℓ) = σ2 if k = ℓ, and E(ei,j,kei,j,ℓ) = σ2ρ if k ≠ ℓ. There are only two parameters. However, it implies that (i) variances are equal at all times, and (ii) covariances and hence correlations are equal at all pairs of times. This strong assumption may not hold in many situations.
- The structure of heterogeneous common symmetry:
The form in Eq. (7.23) assumes that the variances at different times may be distinct, but the correlations are equal at all pairs of times. In this case, Σ contains (p + 1) parameters.
- The Toeplitz structure:
The form in Eq. (7.24) assumes that the correlations for any pairs separated by the same time lag are the same. It contains p parameters.
- The heterogeneous Toeplitz structure:
The form in Eq. (7.25) allows unequal variances and it contains (2p − 1) parameters.
- The AR(1) structure:

The form assumes the first‐order autoregressive structure, that is, the correlation with k time lags apart are ρk. It greatly simplifies the form and contains only two parameters.
- The heterogeneous AR(1) structure:
The form in Eq. (7.27) assumes the first‐order autoregressive structure but allows unequal variances. It contains (p + 1) parameters.
- The ARMA(1,1) structure:
The form in Eq. (7.28) assumes a general autoregressive moving average of order (1,1) structure, and it contains only three parameters.
More generally, AR(2), and ARMA(p, q) models can be used to represent the variance–covariance structure, which contain a much smaller number of parameters than the general form of Σ.
Since each mean vector of μi, i = 1, 2, …, m, is p‐dimensional, more explicitly we can write ![]() and after the hypotheses of no treatment, time, and treatment/time interaction effects are rejected, a very natural next step is to test
and after the hypotheses of no treatment, time, and treatment/time interaction effects are rejected, a very natural next step is to test
for each time t with t = 1, …, p. Through these careful further tests, one can find out exactly when these mean differences occur in the experiment. We will illustrate these in the following example.
7.3.3 Empirical Example II – Further analysis on body weight of rats under three different treatments
data rat;infile 'c:/Bookdata/WW7a.csv';input Treatment$ Week0 Week1 Week2 Week3 Week4;rat=_n_;weight=Week0; week=0; output;weight=Week1; week=1; output;weight=Week2; week=2; output;weight=Week3; week=3; output;weight=Week4; week=4; output;drop Week0-Week4;/*AR(1)covariance matrix*/proc mixed data=rat;class Treatment week rat;model weight = Treatment week Treatment*week;repeated/type=ar(1) sub=rat r rcorr;run;
The associated analysis of variance table is given in Table 7.5.
Table 7.5 Repeated measurement analysis of variance of body weights of rats with AR (1) covariance matrix.
| The mixed procedure | |||||
| Source | SS | DF | Mean Square | F Value | Pr > F |
| Treatment | 1 606.3504 | 2 | 803.1752 | 5.84 | 0.0086 |
| Week | 300 596.5704 | 4 | 75 149.1426 | 546.42 | <0.0001 |
| Treatment*week | 15 370.3528 | 8 | 1 921.2941 | 13.97 | <0.0001 |
| Error | 13 202.88 | 96 | 137.53 | ||
The results clearly reject the null hypotheses of Eq. (7.15). In addition to the treatment effect, there are strong time effect and treatment/time interaction effects, which can also be seen from Figure 7.1. More explicitly, we can summarize the test results for each week from the previous SAS repeated measurement analysis of variance in Table 7.6. They show that the treatments began to produce different results after week 2.
Table 7.6 Weekly treatment effect of body weights of rats.
| Week | Source | SS | DF | MS | F Value | Pr > F |
| 0 | Treatment | 10.1857 | 2 | 5.0929 | 0.24 | 0.7916 |
| 1 | Treatment | 36.5429 | 2 | 8.2715 | 0.27 | 0.7688 |
| 2 | Treatment | 601.3947 | 2 | 300.6974 | 3.17 | 0.0599 |
| 3 | Treatment | 3563.6058 | 2 | 781.8029 | 9.81 | 0.0008 |
| 4 | Treatment | 9204.1714 | 2 | 4602.0857 | 17.15 | <0.0001 |
For comparison, if we fit the model with general covariance matrix Σ, the associated analysis of variance table is given in Table 7.7. The degrees of freedom for the error term are reduced significantly.
Table 7.7 Repeated measurement analysis of variance for body weights of rats with an unspecified general covariance matrix.
| The mixed procedure | |||||
| Source | SS | DF | Mean Square | F Value | Pr > F |
| Treatment | 6 635.0486 | 2 | 3 317.5243 | 7.73 | 0.0026 |
| Week | 573 549.7372 | 4 | 143 387.4343 | 334.10 | <0.0001 |
| Treatment*week | 22 935.1224 | 8 | 2 866.8903 | 6.68 | 0.0001 |
| Error | 10 300.2048 | 24 | 429.1752 | ||
7.3.4 Random effects and mixed effects models
The model in Eq. (7.14) is a special case of the fixed effects model with two factors. When the levels of these factors are randomly selected, and we want to generalize the result from analysis to a much larger population, then the model becomes a random effects model. The model becomes a mixed effects model when some factors are random and some are fixed. For example, in Model (7.14), if treatments are randomly assigned, we have
where αi is random, i.i.d. ![]() independent of ei,j,t. The analysis of variance table for the fixed effects model, the random effects model, and the mixed effects model are the same as Table 7.7, but when a model contains a random factor like Eq. (7.30), it is important to note the following:
independent of ei,j,t. The analysis of variance table for the fixed effects model, the random effects model, and the mixed effects model are the same as Table 7.7, but when a model contains a random factor like Eq. (7.30), it is important to note the following:
- The variance of Zi,j,t is no longer equal to the variance of ei,j,t. Instead, if we also assume that Var(αi) =
 ,we have
,we have
- The model in (7.31) can also be written as
(7.32)

where the εi,j,t are now i.i.d.

- The Expected Mean Squares (EMS) for treatment is
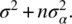 Hence, we can estimate the variance of the random treatment term using
(7.33)
Hence, we can estimate the variance of the random treatment term using
(7.33)
where s2 is the residual mean square error.
- The null and alternative hypotheses for the random treatment in Model (7.30) are now

7.4 Nested random effects model
In some applications, subjects are randomly selected from a population. For example, in agricultural studies, where researchers want to compare the effects of three different fertilizers in terms of the yield of a certain product such as tomatoes. In this case, “subjects” refers to plots of land. By realizing the effects of land, and more importantly, being interested in the effects of fertilizers on a wide variety of plots, the researchers may randomly select a certain number of plots of land from a population of plots when assigning fertilizers within their experiments. In such a case, we will consider the following nested random effects model:
where αi, βt, and γi,t are fixed effects defined in Eq. (7.14), but θj(i) is a random effect for subject j associated with treatment i. We assume that the θj(i) are i.i.d. ![]() which are independent of ei,j,t. The variance of Zi,j,t is no longer equal to the variance of ei,j,t. It becomes the sum of the variances of θj(i) and ei,j,t. Hence, the variance–covariance matrix of Zi,j = [Zi,j,1, …, Zi,j,p]′ becomes
which are independent of ei,j,t. The variance of Zi,j,t is no longer equal to the variance of ei,j,t. It becomes the sum of the variances of θj(i) and ei,j,t. Hence, the variance–covariance matrix of Zi,j = [Zi,j,1, …, Zi,j,p]′ becomes
where H is a matrix of ones.
Equivalently, we can rewrite the model in Eq. (7.34) as
where εi,j,t = θj(i) + ei,j,t. If the ei,j,t are i.i.d. N(0, σ2), then it can be shown that the variance and covariance of εi,j,t and hence Zi,j,t will follow the structure of common symmetry given in Eq. (7.22) of Section 7.3.2.
The analysis of variance table for this nested random effects model is now modified as given in Table 7.8.
Table 7.8 Repeated measurement analysis of variance table with nested random effects.
| Source | SS | df | Mean square | |
| Treatment | SST | (m − 1) | SST/(m − 1) | |
| Subjects (treatment) | SSB(T) | (n − m) | SSB(T)/(n‐m) | |
| Time (location) | SSL | (p − 1) | SSL/(p − 1) | |
| Treatment*time | SSLT | (m − 1)(p − 1) | SSLT/[(m − 1)(p − 1)] | |
| Error (time) | SSE | (p − 1)(n − m) | SSE/[(p − 1)(n − m)] | |
where ![]()
7.5 Further generalization and remarks
More generally, we can include some covariates in all the models introduced in Sections 7.3 and 7.4. For example, when subjects in the model are people, we may want to include related information, such as age, gender, education level, and others, in the model. Thus, we have
where the X's are covariates with associated coefficients c's.
With proper modifications, the model in (7.37) can be written in matrix form,
where the matrix X will now contain the values of covariates in addition to the values of 0 and 1 for factors, β is the vector of the associated parameters, and ε is a vector of normal random errors with mean vector 0 and variance–covariance matrix Ω = In ⊗ Σ, In is the n × n identity matrix, n is the number of subjects, and Σ is the (p × p) common variance–covariance structure for all subjects. The GLS estimator of β, ![]() is the best linear unbiased estimator that follows a multivariate vector normal distribution N(β, (X′Ω−1X)−1).
is the best linear unbiased estimator that follows a multivariate vector normal distribution N(β, (X′Ω−1X)−1).
It should be noted that although the examples illustrated in this chapter are equally spaced repeated measurements, the methods introduced can also be applied to cases when repeated measurements are unequally spaced. This is true even when a covariance structure such as an unstructured general covariance, a covariance of independent case, a covariance of common symmetry, or a covariance of heterogeneous common symmetry is used in the analysis. It should be noted, however, that most software such as SAS Proc Mixed may assume equally spaced times when a time series covariance structure like AR(1), ARMA(1, 1), or the Toeplitz form is specified in the analysis. In such a case, using the software may require some adjustment.
7.6 Another empirical example – the oral condition of neck cancer patients
We fit model (7.39) with the following SAS code for mixed models, where an unspecified covariance matrix is specified.
data oral;infile 'c:/Bookdata/WW7b.csv';input id trt age weight stage w0 w2 w4 w6;tc=w0; week=0; output;tc=w2; week=2; output;tc=w4; week=4; output;tc=w6; week=6; output;drop w0 w2 w4 w6;proc mixed data=oral;class trt age weight stage week;model tc = age weight stage trt week trt*week;random trt;run;
The associated analysis of variance table is given in Table 7.10. The results show that age, weight, and interaction term are all not significant. The time period, a week, is the only significant variable.
Table 7.10 Repeated measurement analysis of variance for the oral conditions of neck cancer patients with covariates and an unspecified general covariance matrix.
| Type 3 Tests of Fixed Effects | ||||
| Effect | Num df | Den df | F Value | Pr > F |
| Age | 1 | 68 | 0.28 | 0.5966 |
| Weight | 2 | 68 | 0.32 | 0.7280 |
| Stage | 0 | |||
| Treatment | 0 | |||
| Week | 3 | 68 | 13.13 | <0.0001 |
| Treatment*Week | 3 | 68 | 0.27 | 0.8480 |
In concluding this chapter, it should be pointed out that repeated measurements, clustered data, and longitudinal data are related, and we can use a mixed model to analyze all of them. However, the issues involved in these data sets are different, and some of the specifications used are also different. For further information and applications, we refer readers to Hand and Taylor (1987), Icaza and Jones (1999), Singer and Willett (2003), Fress (2004), Chen (2006), Dehlendorff (2007), Menard (2008), Coke and Tsao (2010), Davis and Ensor (2007), Fokianos (2010), Stram (2014), West, Welch, and Galecki et al. (2014), Bravo (2016), Heyse and Chan (2016), Li, Qian, and Su (2016), Ando and Bai (2017), Arellano, Blundell, and Bonhomme (2017), Broemeling (2017), Chalikias and Kounias (2017), Gile and Handcock (2017), Giordano, Rocca, and Parrella (2017), Islam and Chowdhury (2017), Nakashima (2017), Suarez et al. (2017), and Vogt and Linton (2017), among others.
Projects
- Find a repeated measurement data set of your interest, carry out its multivariate analysis variance, and complete your report with an appendix that contains your data set and analysis software code.
- Find a repeated measurement data set of your interest, carry out its analysis by incorporating a proper variance–covariance structure in the analysis, and complete your report with an appendix that contains your data set and analysis software code.
- Find a repeated measurement data set in a social science field, carry out its analysis with both fixed effect and random effect models, make comparisons, and complete your report with an appendix that contains your data set and analysis software code.
- Find a repeated measurement data set in a natural science related field, carry out its multivariate analysis variance, and complete your report with an appendix that contains your data set and analysis software code.
- For the data set in Project 4, carry out its analysis with both fixed effect and random effect models, make comparisons, and complete your report with an appendix that contains your data set and analysis software code.
References
- Ando, T. and Bai, J. (2017). Clustering huge number of financial time series: a panel data approach with high‐dimensional predictors and factor structures. Journal of the American Statistical Association 112: 1182–1198.
- Arellano, M., Blundell, R., and Bonhomme, S. (2017). Earnings and consumption dynamics: a nonlinear panel data framework. Econometrica 85: 693–734.
- Bartlett, M.S. (1954). A note on the multiplying factors for various χ2 approximation. Journal of the Royal Statistical Society Series B 16: 296–298.
- Box, G.E.P. (1950). Problems in the analysis of growth and wear curves. Biometrics 6: 262–289.
- Bravo, F. (2016). Local information theoretic methods for smooth coefficients dynamic panel data models. Journal of Time Series Analysis 37: 690–708.
- Broemeling, L.D. (2017). Bayesian Methods for Repeated Measures. Chapman and Hall/CRC.
- Chalikias, M. and Kounias, S. (2017). Optimal two treatment repeated measurement designs for three periods. Communications in Statistics: Theory and Methods 46: 200–209.
- Chen, W. (2006). An approximate likelihood function for panel data with a mixed ARMA(p,q) remainder disturbance model. Journal of Time Series Analysis 27: 911–921.
- Coke, G. and Tsao, M. (2010). Random effects mixture models for clustering electrical load series. Journal of Time Series Analysis 31: 451–464.
- Crowder, M.J. and Hand, D.J. (1990). Analysis of Repeated Measures. Chapman and Hall.
- Davis, G.M. and Ensor, K.B. (2007). Multivariate time‐series analysis with categorical and continuous variables in an LSTR model. Journal of Time Series Analysis 28: 867–885.
- Dehlendorff, C. (2007). Longitudinal Data Analysis of Asthma and Wheezing in Children. Technical University of Denmark.
- Diggle, P.J., Liang, K.Y., and Zeger, S.L. (2013). Analysis of Longitudinal Data, Oxford Statistical Science Series, 2e. Oxford University Press.
- Fokianos, K. (2010). Antedependence models for longitudinal data. Journal of Time Series Analysis 31: 494.
- Fress, E.W. (2004). Longitudinal and Panel Data – Analysis and Applications in the Social Sciences. Cambridge University Press.
- Gile, K. and Handcock, M.S. (2017). Analysis of networks with missing data with application to the national longitudinal study of adolescent health. Journal of the Royal Statistical Society Series C 66: 501–519.
- Giordano, F., Rocca, M.L., and Parrella, M.L. (2017). Clustering complex time‐series databases by using periodic components. Statistical Analysis and Data Mining 10: 89–106.
- Hand, D.J. and Taylor, C.C. (1987). Multivariate Analysis of Variance and Repeated Measures: A Practical Approach for Behavioural Scientists, 1e. Chapman & Hall/CRC.
- Heyse, J. and Chan, I. (2016). Review of statistical innovations in trials supporting vaccine clinical development. Statistics in Biopharmaceutical Research 8: 128–142.
- Icaza, G. and Jones, R. (1999). A state‐space EM algorithm for longitudinal data. Journal of Time Series Analysis 20: 537–550.
- Islam, M.A. and Chowdhury, R.I. (2017). Analysis of Repeated Measures Data. Springer.
- Johnson, R.A. and Wichern, D.W. (2007). Applied Multivariate Statistical Analysis, 6e. Prentice Hall.
- Li, D., Qian, J., and Su, L. (2016). Panel data models with interactive fixed effects and multiple structural breaks. Journal of the American Statistical Association 111: 1804–1819.
- Lindsey, J.K. (1993). Models for Repeated Measurements. New York: Oxford University Press.
- Menard, S. (2008). Handbook of Longitudinal Research, Design, Measurement, and Analysis. Academic Press, Elsevier.
- Nakashima, E. (2017). Modification of GEE1 and linear mixed‐effects models for heteroscedastic longitudinal Gaussian data. Communications in Statistics: Theory and Methods 46: 11110–11122.
- SAS Institute, Inc. (2015). SAS for Windows, 9.4, Cary, North Carolina.
- Singer, J.D. and Willett, J.B. (2003). Applied Longitudinal Data Analysis – Modeling Change and Event Occurrence. Oxford University Press.
- Stram, D.O. (2014). Design, Analysis, and Interpretation of Genome‐Wide Association Scans. Springer.
- Suarez, C.C., Klein, N., Kneib, T., Molenberghs, G., and Rizopoulos, D. (2017). Editorial “joint modeling of longitudinal and time‐to‐event data and beyond”. Biomedical Journal 59: 1101–1103.
- Vogt, M. and Linton, O. (2017). Classification of non‐parametric regression functions in longitudinal data models. Journal of the Royal Statistical Society Series B 79: 5–27.
- West, B.T., Welch, K.B., and Galecki, A.T. (2014). Linear Mixed Models: A Practical Guide Using Statistical Software, 2e. Chapman and Hall/CRC.
- Wilks, S.S. (1932). On the sampling distribution of the multiple correlation coefficient. Annals of Mathematical Statistics 3: 196–203.








