With the development of computers and the internet, we have had a data explosion. For example, a study of monthly cancer rates in the United States during the past 10 years can involve 50 or many hundreds or thousands of time series depending on whether we investigate the cancer rates for states, cities, or counties. Multivariate time series analysis methods are needed to properly analyze these data in a study, and these are different from standard statistical theory and methods based on random samples that assume independence. Dependence is the fundamental nature of the time series. The use of highly correlated high‐dimensional time series data introduces many complications and challenges. The methods and theory to solve these issues will make up the content of this book.

1.1 Introduction

In studying a phenomenon, we often encounter many variables, Z_i,t, where i = 1, 2, …, m, and the observations are taken according to the order of time, t. For convenience we use a vector, Z_t = [Z_1,t, Z_2,t, …, Z_m,t]′, to denote the set of these variables, where Z_i,t is the ith component variable at time t and it is a random variable for each i and t. The time t in Z_t can be continuous and any value in an interval, such as the time series of electric signals and voltages, or discrete and be a specific time point, such as the daily closing price of various stocks or the total monthly sales of various products at the end of each month. In practice, even for a continuous time series, we take observations only at digitized discrete time points for analysis. Hence, we will consider only discrete time series in this book, and with no loss of generalizability, we will consider Z_i,t, for i = 1, 2, …, m, t = 0, ± 1, ± 2, …, and hence Z_t = [Z_1,t, Z_2,t, …, Z_m,t]′, t = 0, ± 1, ± 2, ….

We call Z_t = [Z_1,t, Z_2,t, …, Z_m,t]′ a multivariate time series or a vector time series, where the first subscript refers to a component and the second subscript refers to the time. The fundamental characteristic of a multivariate time series is that its observations depend not only on component i but also time t. The observations between Z_i,s and Z_j,t can be correlated when i ≠ j, regardless of whether the times s and t are the same or not. They are vector‐valued random variables. Most standard statistical theory and methods based on random samples are not applicable, and different methods are clearly needed. The body of statistical theory and methods for analyzing these multivariate or vector time series is referred to as multivariate time series analysis.

Many issues are involved in multivariate time series analysis. They are different from standard statistical theory and methods based on a random sample that assumes independence and constant variance. In multivariate time series, Z_t = [Z_1,t, Z_2,t, …, Z_m,t]′, a fundamental phenomenon is that dependence exists not only in terms of i but also in terms of t. In addition, we have the following important issues to consider:

1. Fundamental concepts and representations related to dependence.

   We will introduce the variance–covariance and correlation matrix functions, vector white noise processes, vector autoregressive and vector moving average representations, vector autoregressive models, vector moving average models, and vector autoregressive moving average models.

2. Relationship between several multivariate time series.

   A multiple regression is known to be a useful statistical model that describes a relationship between a response variable and several predictor variables. The error term in the model is normally assumed to be uncorrelated noise with zero mean and constant variance. We will extend the results to a multivariate time series regression model where both response variables, and predictor variables are vectors. More importantly, not only are all components in the multivariate regression equation time series variables, but also the error term follows a correlated time series process.

3. Dimension reduction and model simplification.

   Without losing information, we will introduce useful methods of dimension reduction and representation including principal components and factor analysis in time series.

4. Representations of time variant variance–covariance structure.

   Unlike most classical linear methods, where the variance of error term has been assumed to be constant, in time series analysis a non‐constant variance often occurs and generalized autoregressive conditional heteroscedasticity (GARCH) models are been introduced. The literature and theory of GARCH models for univariate time series was introduced in chapter 15 of Wei (2006). In this book, we will extend the results to the multivariate GARCH models.

5. Repeated measurement phenomenon.

   Many fields of study, including medicine, biology, social science, and education, involve time series measurements of treatments for different subjects. They are multivariate time series but often relatively short, and the applications of standard time series methods are difficult, if not impossible. We will introduce some methods and various models that are useful for analyzing repeated measures data. Empirical examples will be used as illustrations.

6. Space and time series modeling.

   In many multivariate time series applications, the components i in Z_i,t refer to regions or locations. For example, in a crime study, the observations can be the crime rates of different counties in a state, and in a market study, one could look at the price of a certain product in different regions. Thus, the analysis will involve both regions and time, and we will construct space and time series models.

7. Multivariate spectral analysis.

   Similar to univariate time series analysis where one can study a time series through its autocovariance/autocorrelation functions and lag relationships or through its spectrum properties, we can study a multivariate time series through a time domain or a frequency domain approach. In the time domain approach we use covariance/correlation matrices, and in the frequency domain approach we will use spectral matrices. We will introduce spectral analysis for both multivariate stationary and nonstationary time series.

8. High dimension problem in multivariate time series.

   Because of high‐speed internet and the power and speed of the new generation of computers, a researcher now faces some very challenging phenomena. First, he/she must deal with an ever‐increasing amount of data. To find useful information and hidden patterns underlying the data, a researcher may use various data‐mining methods and techniques. Adding a time dimension to these large databases certainly introduces new aspects and challenges. In multivariate time series analysis, a very natural issue is the high dimension problem where the number of parameters may exceed the length of the time series. For example, a simple second order vector autoregressive VAR(2) model for the 50 states in the USA will involve more than 5000 parameters, and the length of the time series may be much shorter. For example, the length of the monthly observations for 20 years is only 240. Traditional time series methods are not designed to deal with these kinds of high‐dimensional variables. Even with today's computer power and speed, there are many difficult problems that remain unsolved. As most statistical methods are developed for a random sample, the use of highly correlated time series data certainly introduces a new set of complications and challenges, especially for a high‐dimensional data set.

The methods and theory to solve these issues will be the focus of this book. Examples and applications will be carefully chosen and presented.

1.2 Fundamental concepts

The m‐dimensional vector time series process, Z_t = [Z_1,t, Z_2,t, …, Z_m,t]′, is a stationary process if each of its component series is a univariate stationary process and its first two moments are time‐invariant. Just as a univariate stationary process or model is characterized by its moments such as mean, autocorrelation function, and partial autocorrelation function, a stationary vector time series process or model is characterized by its mean vector, correlation matrix function, and partial correlation matrix function.

1.2.1 Correlation and partial correlation matrix functions

Let Z_t = [Z_1,t, Z_2,t, …, Z_m,t]′, t = 0, ± 1, ± 2, … be a m‐dimensional stationary real‐valued vector process so that E(Z_i,t) = μ_i is constant for each i = 1, 2, …, m and the cross‐covariance between Z_i,t and Z_j,s, for all i = 1, 2, …, m and j = 1, 2, …, m, are functions only of the time difference (s − t). Hence, we have the mean vector

(1.1)

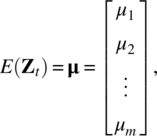
and the lag k covariance matrix

(1.2)

where

for k = 0, ± 1, ± 2, …, i = 1, 2, …, m, and j = 1, 2, …, m. As a function of k, Γ(k) is called the covariance matrix function for the vector process Z_t. Also, i = j, γ_i,i(k) is the autocovariance function for the ith component process, Z_i,t; and i ≠ j, γ_i,j(k) is the cross‐covariance function between component series Z_i,t and Z_j,t. The matrix Γ(0) can be easily seen to be the contemporaneous variance–covariance matrix of the process.

The covariance matrix function has the following properties:

1. Γ(k) = Γ′(−k). This follows because
   
2. |γ_i,j(k)| ≤ [γ_i,i(0)γ_j,j(0)]^1/2, for all i, j = 1, …, m, because of the Cauchy–Schwarz inequality.
3. The covariance matrix function is positive semidefinite in the sense that

(1.3)

for any set of time points t₁, t₂, …, t_n and any set of real vectors α₁, α₂, …, α_n. The result follows immediately from

The correlation matrix function for the vector process is defined by

(1.4)

for i = 1, 2, …, m, and j = 1, 2, …, m, where D is the diagonal matrix in which the ith diagonal element is the variance of the ith process; that is, D =  diag [γ_{1, 1}(0), γ_{2, 2}(0), …, γ_m,m(0)]. Thus, the ith diagonal element of ρ(k) is the autocorrelation function for the ith component series Z_i,t whereas the (i, j)th off‐diagonal element of ρ(k) is the cross‐correlation function between component series Z_i,t and Z_j,t.

Similarly, the correlation matrix functions have the following properties:

1. ρ(k) = ρ′(−k).
2. The correlation matrix function is positive semidefinite so that
   (1.5)

for any set of time points t₁, t₂, …, t_n and any set of real vectors α₁, α₂, …, α_n.

Other than the correlation matrix function, another useful function for describing a vector time series process is the partial correlation matrix function. The concept of a partial correlation matrix function was introduced much later, and there are different versions.

Heyse and Wei (1985) extended the definition of univariate partial autocorrelation to vector time series and derived the correlation matrix between Z_t and Z_t + s after removing the linear dependence of each on the intervening vectors Z_t + 1, …, Z_{t + s − 1}. This partial correlation matrix is defined as the correlation between the residual vectors

(1.6)

and

(1.7)

Let C_VU(s) be the covariance between V_{s − 1,t} and U_{s − 1,t + s}, i.e. C_VU(s) = Cov(V_{s − 1,t}, U_{s − 1,t + s}), Heyse and Wei (1985) showed that

(1.8)

(1.9)

and

(1.10)

where Thus, the partial autocorrelation matrix function is

(1.11)

where D_V(s) is the diagonal matrix in which the ith diagonal element is the square root of the ith diagonal element of C_VV(0) and D_U(s) is similarly defined for C_UU(0).

Tiao and Box (1981) defined the partial autoregression matrix at lag s, denoted by Φ_s,s, to be the last matrix coefficient when the data is fitted to a vector autoregressive process of order s. It can be shown that

(1.12)

Ansley and Newbold (1979) defined the multivariate partial autocorrelation matrix at lag s to be

(1.13)

where W_U(s) and W_V(s) are the symmetric square roots of C_UU(0) and C_VV(0)_, respectively, defined such that |W_U(s)|² = C_UU(0) and |W_V(s)|² = C_VV(0). However, it should be noted that although P(s), Φ_s,s and Q(s) all share the same cut‐off property for vector VAR(s) models, the elements of P(s) are proper correlation coefficient but those of Φ_s,s and Q(s) are not correlation coefficient except when m = 1; that is, except in the univariate case in which P(s) = Φ_s,s = Q(s). For more details, we refer readers to Wei (2006, chapter 16).

1.2.2 Vector white noise process

The m‐dimensional vector process, a_t, is said to be a vector white noise process with mean vector 0 and covariance matrix function Σ if

(1.14)

where Σ is a m × m symmetric positive definite matrix. Note that although the components of the white noise process are uncorrelated at different times, they may be contemporaneously correlated. It is a Gaussian white noise process if a_t also follows a multivariate normal distribution. Unless mentioned otherwise, a_t will be used to denote a Gaussian vector white noise process with mean vector 0 and covariance matrix function Σ, VWN(0, Σ), in this book.

1.2.3 Moving average and autoregressive representations of vector processes

A m‐dimensional stationary vector time series process Z_t that is purely nondeterministic can always be written as a linear combination of a sequence of vector white noises, that is

(1.15)

where and the sequence of m × m coefficient matrices Ψ_ℓ is square summable, in the sense that if we write and we have for all i = 1, 2, …, m and j = 1, 2, …, m. The B is the backshift operator such that B ^ja_t = a_t − j.

The infinite sum of random variables is defined as the limit in quadratic mean of the finite partial sums. Thus, Z_t in Eq. (1.15) is defined such that

(1.16)

The Eq. (1.15) is known as the vector moving average (MA) representation.

For a given sequence of covariance matrices, Γ(k), k = 0, ± 1, ± 2, …, the covariance matrix generating function is defined as

(1.17)

where the covariance matrix of lag k is the coefficient of B^k and B^−k. For a stationary vector process given in Eq. (1.15), it can be easily seen that

(1.18)

where

A vector time series process Z_t is said to be invertible if it can be written as a vector autoregressive (AR) representation

(1.19)

or equivalently,

(1.20)

where Π₀ = I, so that the sequence of m × m autoregressive coefficient matrices Π_ℓ is absolutely summable in the sense that if we write and we have for all i = 1, 2, …, m and j = 1, 2, …, m.

Projects

1. Find a univariate time series book, for example, Wei (2006, ch. 1–13), to review your background.
2. Write a detailed study plan on multivariate time series analysis and applications so that you can evaluate your accomplishments at the end of the semester if you use this book in your course.

References

1. Ansley, C.F. and Newbold, P. (1979). Multivariate partial autocorrelations. American Statistical Association Proceedings of Business and Economic Statistics Section, pp. 349–353.
2. Heyse, J.F. and Wei, W.W.S. (1985). Inverse and partial lag autocorrelation for vector time series. American Statistical Association Proceedings of Business and Economic Statistics Section, pp. 233–237.
3. MATLAB (matrix laboratory). A proprietary programming language developed by MathWorks. www.mathworks.com.
4. R Foundation. R: a free programming language and software environment for statistical computing and graphics, supported by the R Foundation for Statistical Computing. https://www.r‐project.org.
5. SAS Institute, Inc. (2015). SAS for Windows, 9.4. Cary, NC: SAS Institute, Inc.
6. Tiao, G.C. and Box, G.E.P. (1981). Modeling multiple time series with applications. Journal of the American Statistical Association 76: 802–816.
7. Wei, W.W.S. (2006). Time Series Analysis – Univariate and Multivariate Methods, 2e. Boston, MA: Pearson Addison‐Wesley.