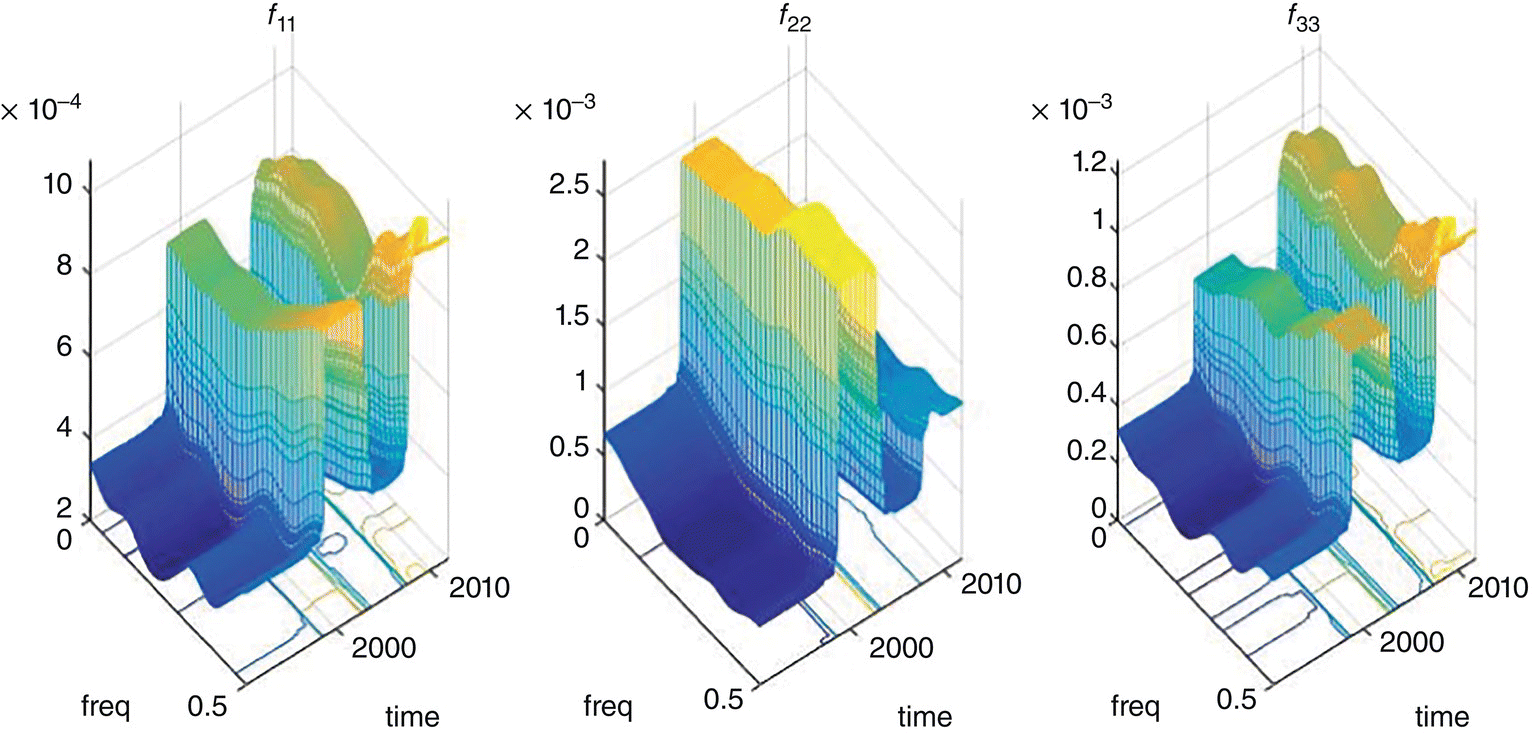
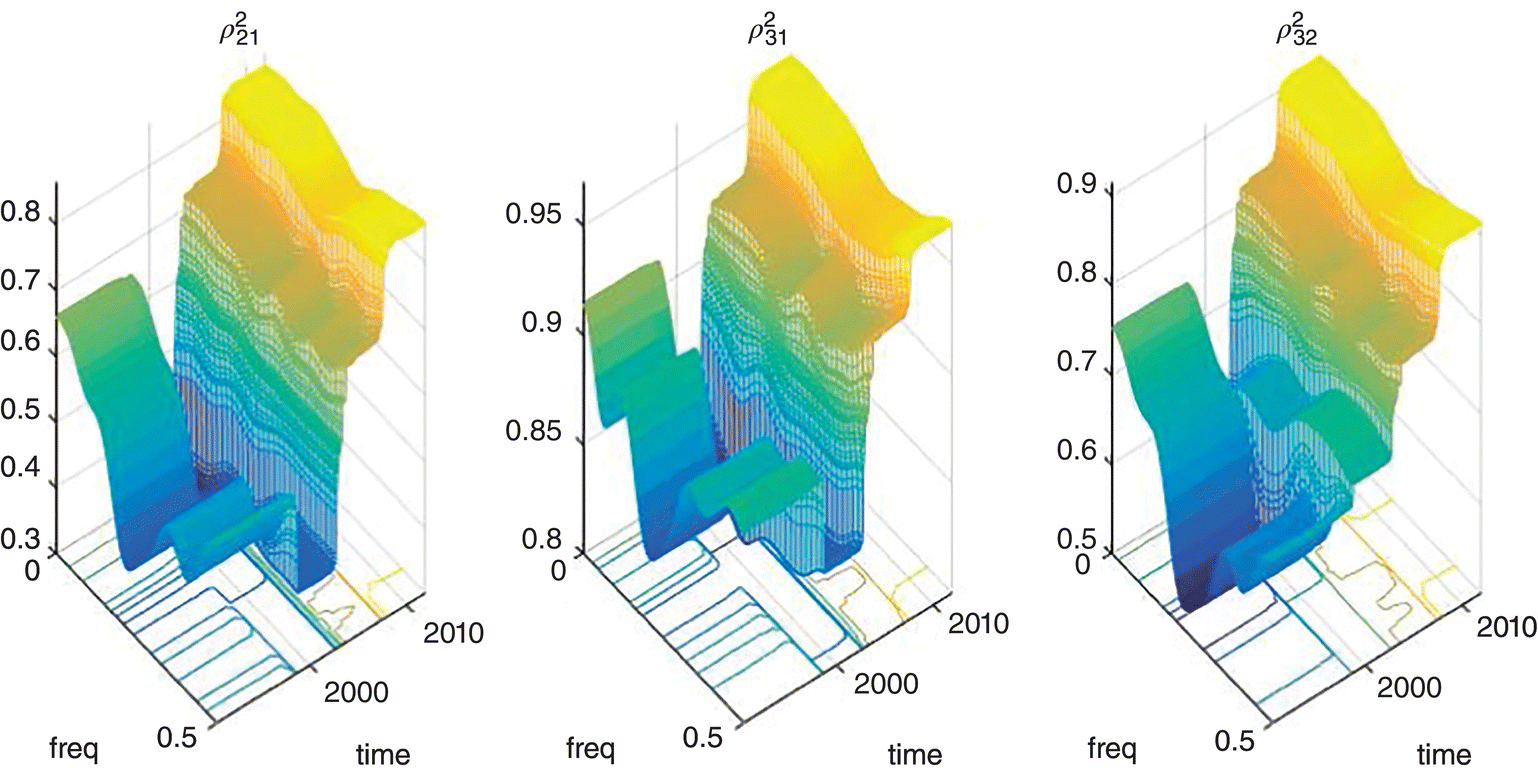
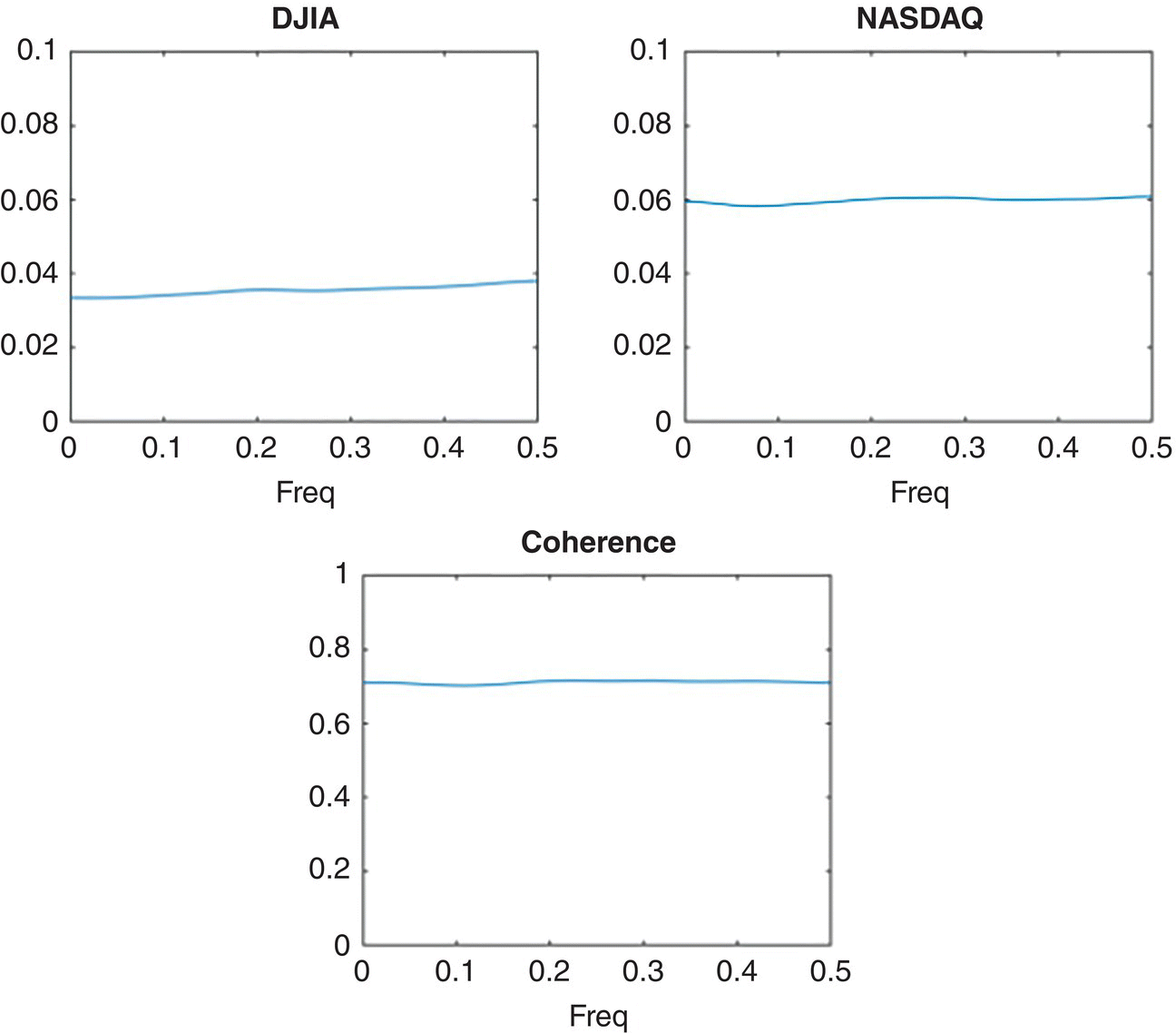
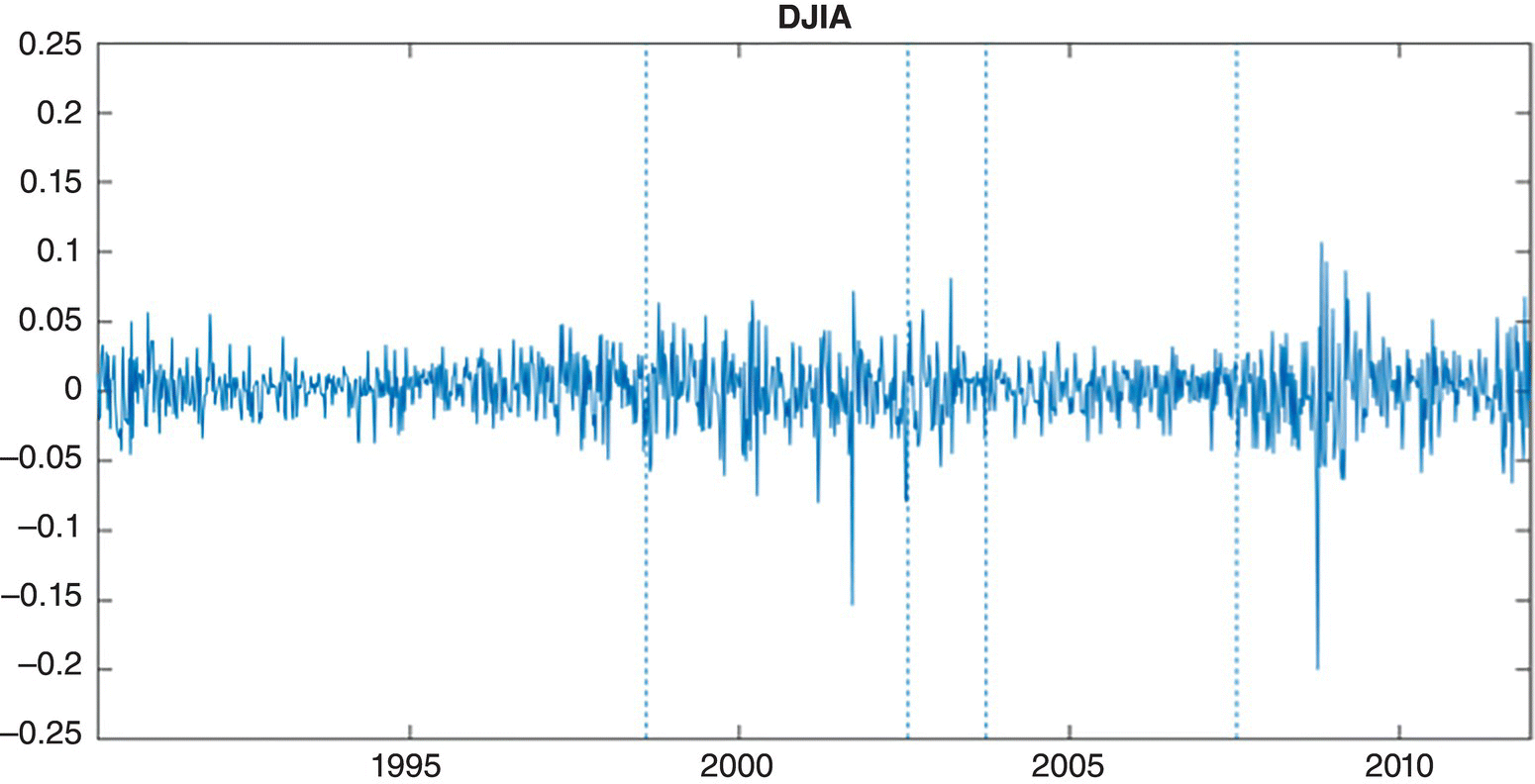
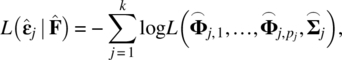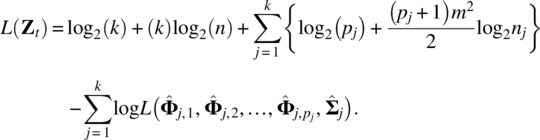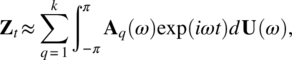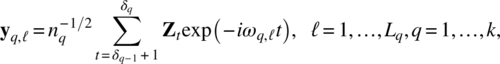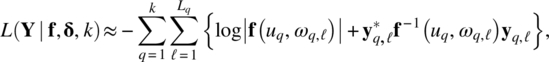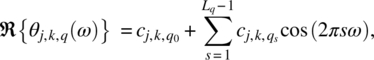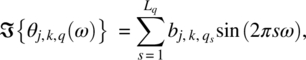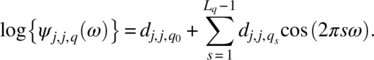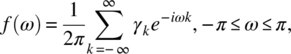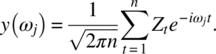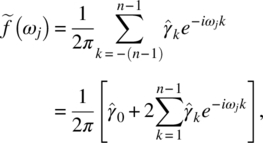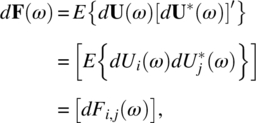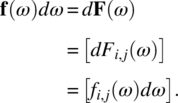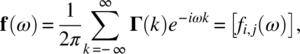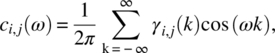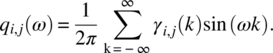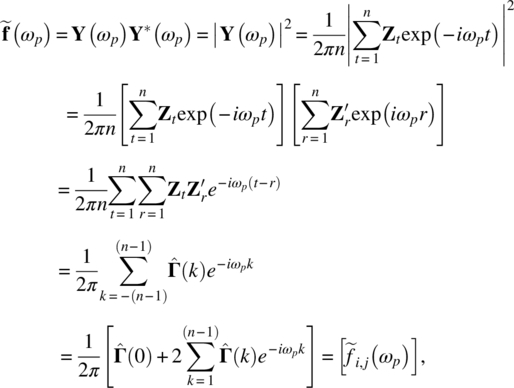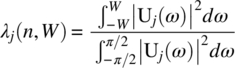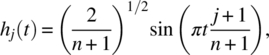Empirical Example 9.4 of nonstationary vector time series – analysis of financial data
function [f,gr,h] = Beta_derive1(x, yobs_tmp, chol_index, Phi_temp, tau_temp,...
Beta_temp, sigmasqalpha, nbasis)
global dimen
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Function used for optimization process for coefficients selected to % be changed
%
% Input:
% 1) x - initial values for coefficient of basis functions need to % be optimized
% 2) yobs_tmp - time series data within the segment
% 3) chol_index - index matrix
% 4) Phi_temp - which component changed
% 5) tau_temp - smoothing parameters
% 6) Beta_temp - current coefficients
% 7) sigmasqalpha - smoothing parameters for the constant in real % components
% 8) nbasis - number of basis functions used
% Main Outputs:
% 1) f - log posterior probability based on input parameters
% 2) gr - gradients for optimization process
% 3) h - Hessian matrix for optimization process
%
% Required programs: lin_basis_func
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%initilize Beta_1 and Beta_2: Beta_2 is for imaginary components
nBeta = nbasis + 1;
Beta_1 = zeros(nBeta,(dimen + dimen*(dimen-1)/2));
Beta_2 = zeros(nBeta,dimen*(dimen-1)/2);
select = chol_index(Phi_temp,:).*(1:dimen^2);
select = select(select∼=0);
x = reshape(x,nBeta,length(select));
Beta_temp(:,select) = x;
Beta_1(:,:) = Beta_temp(:,1:(dimen + dimen*(dimen-1)/2));
Beta_2(:,:) = Beta_temp(1:nBeta,(dimen + dimen*(dimen-1)/2 + 1): end);
dim = size(yobs_tmp); n = dim(1);
nfreq = floor(n/2); tt = (0:nfreq)/(2*nfreq);
yy = fft(yobs_tmp)/sqrt(n); y = yy(1:(nfreq+1),:); nf = length(y);
[xx_r, xx_i]=lin_basis_func(tt);
%theta's
theta = zeros(dimen*(dimen-1)/2,nf);
for i=1:dimen*(dimen-1)/2
theta_real = xx_r * Beta_1(:,i+dimen);
theta_imag = xx_i * Beta_2(:,i);
theta(i,:) = theta_real + sqrt(-1)*theta_imag;
end
%delta's
delta_sq = zeros(dimen,nf);
for i=1:dimen
delta_sq(i,:) = exp(xx_r * Beta_1(:,i));
end
if dimen==2 %Bivariate Time Series
if (mod(n,2)==1)%odd n
f = -sum(log(delta_sq(1,2:end))' + log(delta_sq(2,2:end))' + abs(y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,1)) + ...
abs(y(2:end,2) - theta(2:end).'.*y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,2))) - ...
0.5*(log(delta_sq(1,1))' + log(delta_sq(2,1))' + abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1)) + ...
abs(y(1,2) - theta(1).'.*y(1,1))^2.*exp(-xx_r(1,:)*Beta_1(:,2)));
else
f = -sum(log(delta_sq(1,2:nfreq))' + log(delta_sq(2,2:nfreq))' + abs(y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,1)) + ...
abs(y(2:nfreq,2) - theta(2:nfreq).'.*y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))) - ...
0.5*(log(delta_sq(1,1)) + log(delta_sq(2,1)) + abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1)) + ...
abs(y(1,2) - theta(1).'.*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))) - ...
0.5*(log(delta_sq(1,end)) + log(delta_sq(2,end)) + abs(y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,1)) + ...
abs(y(end,2) - theta(end).'.*y(end,1))^2.*exp(-xx_r(end,:)*Beta_1(:,2)));
end
f = f - (0.5.*(Beta_1(1,1)* Beta_1(1,1)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,1)'*Beta_1(2:nBeta,1))/tau_temp(1))*chol_index(Phi_temp,1) -...
(0.5.*(Beta_1(1,2)* Beta_1(1,2)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,2)'*Beta_1(2:nBeta,2))/tau_temp(2))*chol_index(Phi_temp,2) -...
(0.5.*(Beta_1(1,3)* Beta_1(1,3)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,3)'*Beta_1(2:nBeta,3))/tau_temp(3))*chol_index(Phi_temp,3) -...
(0.5.*(Beta_2(1:nBeta,1)'*Beta_2(1:nBeta,1))/tau_temp(4))*chol_index(Phi_temp,4);
gr1 = zeros(nBeta,1); gr2 = zeros(nBeta,1); gr3 = zeros(nBeta,1); gr4 = zeros(nBeta,1);
gr1(1) = Beta_1(1,1)/sigmasqalpha; gr1(2:nBeta,1) = Beta_1(2:nBeta,1)/tau_temp(1);
gr2(1) = Beta_1(1,2)/sigmasqalpha; gr2(2:nBeta,1) = Beta_1(2:nBeta,2)/tau_temp(2);
gr3(1) = Beta_1(1,3)/sigmasqalpha; gr3(2:nBeta,1) = Beta_1(2:nBeta,3)/tau_temp(3);
gr4(1:nBeta,1) = Beta_2(1:nBeta,1)/tau_temp(4);
h11(1,1)=1/sigmasqalpha; h11(2:nBeta,2:nBeta)=1/tau_temp(1)*eye(nbasis);
h22(1,1)=1/sigmasqalpha; h22(2:nBeta,2:nBeta)= 1/tau_temp(2)*eye(nbasis);
h33(1,1)=1/sigmasqalpha; h33(2:nBeta,2:nBeta)= 1/tau_temp(3)*eye(nbasis);
h44(1:nBeta,1:nBeta)=1/tau_temp(4)*eye(nBeta);
h42 = zeros(nBeta,nBeta); h32 = zeros(nBeta,nBeta);
if (mod(n,2)==1)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rk = -y(2:end,1).*conj(y(2:end,2)) - y(2:end,2).*conj(y(2:end,1));
ik = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,2)) + y(2:end,2).*conj(y(2:end,1)));
ck = 2*abs(y(2:end,1)).^2;
gr1 = gr1 + xx_r(2:end,:)'*(1-abs(y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:end,:)'*(1 - abs(y(2:end,2)-theta(2:end).'.*y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1).'.*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))));
temp_mat_31 = bsxfun(@times, xx_r(2:end,:),rk);
temp_mat_32 = bsxfun(@times, ck, bsxfun(@times, xx_r(2:end,:),xx_r(2:end,:)*Beta_1(:,3)));
gr3 = gr3 + sum( bsxfun(@times, (temp_mat_31+temp_mat_32), exp(-xx_r(2:end,:)*Beta_1(:,2)) ))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)');
temp_mat_41 = bsxfun(@times, ik, xx_i(2:end,:));
temp_mat_42 = bsxfun(@times, ck, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,1)));
gr4 = gr4 + sum( bsxfun(@times, (temp_mat_41 + temp_mat_42), exp(-xx_r(2:end,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(sqrt(-1)*(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Hessian
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
bigmat_h11 = kron(bsxfun(@times, abs(y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,1)), xx_r(2:end,:)),ones(nBeta,1)');
coefmat_h11 = repmat(xx_r(2:end,:), 1,nBeta);
h11 = h11 + reshape(sum(bsxfun(@times, bigmat_h11, coefmat_h11),1),nBeta,nBeta) +...
0.5*(abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))*xx_r(1,:)'*xx_r(1,:));
bigmat_h22 = kron(bsxfun(@times, abs(y(2:end,2)-theta(2:end).'.*y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,2)),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h22 = repmat(xx_r(2:end,:), 1,nBeta);
h22 = h22 + reshape(sum(bsxfun(@times, bigmat_h22, coefmat_h22),1),nBeta,nBeta) +...
0.5*(abs(y(1,2)-theta(1).'.*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))*xx_r(1,:)'*xx_r(1,:));
bigmat_h33 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck, xx_r(2:end,:)),ones(nBeta,1)');
coefmat_h33 = repmat(xx_r(2:end,:), 1,nBeta);
h33 = h33 + reshape(sum(bsxfun(@times, bigmat_h33, coefmat_h33),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_r(1,:)'*xx_r(1,:));
bigmat_h44 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck, xx_i(2:end,:)),ones(nBeta,1)');
coefmat_h44 = repmat(xx_i(2:end,:), 1,nBeta);
h44 = h44 + reshape(sum(bsxfun(@times, bigmat_h44, coefmat_h44),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_i(1,:)'*xx_i(1,:));
bigmat_h42_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck.*(xx_i(2:end,:)*Beta_2(:,1)),...
xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h42_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h42_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,2)).*ik, xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h42_2 = repmat(xx_r(2:end,:), 1,nBeta);
h42 = h42 + reshape(sum(bsxfun(@times, bigmat_h42_1, coefmat_h42_1) +...
bsxfun(@times, bigmat_h42_2, coefmat_h42_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)+...
sqrt(-1)*(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1)))*xx_i(1,:))'*xx_r(1,:));
bigmat_h32_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck.*(xx_r(2:end,:)*Beta_1(:,3)),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h32_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h32_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,2)).*rk, xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h32_2 = repmat(xx_r(2:end,:), 1,nBeta);
h32 = h32 + reshape(sum(bsxfun(@times, bigmat_h32_1, coefmat_h32_1) +...
bsxfun(@times, bigmat_h32_2, coefmat_h32_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)+...
(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:))'*xx_r(1,:));
h24=h42'; h23=h32';
else
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rk = -y(2:nfreq,1).*conj(y(2:nfreq,2)) - y(2:nfreq,2).*conj(y(2:nfreq,1));
ik = sqrt(-1)*(-y(2:nfreq,1).*conj(y(2:nfreq,2)) + y(2:nfreq,2).*conj(y(2:nfreq,1)));
ck = 2*abs(y(2:nfreq,1)).^2;
gr1 = gr1 + xx_r(2:nfreq,:)'*(1-abs(y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1)))) +...
0.5*(xx_r(end,:)'*(1-abs(y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:nfreq,:)'*(1 - abs(y(2:nfreq,2)-theta(2:nfreq).'.*y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1).'.*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2)))) + ...
0.5*(xx_r(end,:)'*(1 - abs(y(end,2)-theta(end).'.*y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,2))));
temp_mat_31 = bsxfun(@times,rk, xx_r(2:nfreq,:));
temp_mat_32 = bsxfun(@times,ck,bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,3)));
gr3 = gr3 + sum(bsxfun(@times, (temp_mat_31 + temp_mat_32), exp(-xx_r(2:nfreq,:)*Beta_1(:,2)) ))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)') +...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(-y(end,1).*conj(y(end,2)) - y(end,2).*conj(y(end,1)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,3))*xx_r(end,:)');
temp_mat_41 = bsxfun(@times, ik, xx_i(2:nfreq,:));
temp_mat_42 = bsxfun(@times, ck, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,1)));
gr4 = gr4 + sum( bsxfun(@times, (temp_mat_41 + temp_mat_42), exp(-xx_r(2:nfreq,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(sqrt(-1)*(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)') +...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(sqrt(-1)*(-y(end,1).*conj(y(end,2)) + y(end,2).*conj(y(end,1))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,1))*xx_i(end,:)');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Hessian
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
bigmat_h11 = kron(bsxfun(@times, abs(y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,1)), xx_r(2:nfreq,:)),ones(nBeta,1)');
coefmat_h11 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h11 = h11 + reshape(sum(bsxfun(@times, bigmat_h11, coefmat_h11),1),nBeta,nBeta) +...
0.5*(abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))*xx_r(1,:)'*xx_r(1,:))+...
0.5*(abs(y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,1))*xx_r(end,:)'*xx_r(end,:));
bigmat_h22 = kron(bsxfun(@times, abs(y(2:nfreq,2)-theta(2:nfreq).'.*y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,2)),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h22 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h22 = h22 + reshape(sum(bsxfun(@times, bigmat_h22, coefmat_h22),1),nBeta,nBeta) +...
0.5*(abs(y(1,2)-theta(1).'.*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))*xx_r(1,:)'*xx_r(1,:))+...
0.5*(abs(y(end,2)-theta(end).'.*y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,2))*xx_r(end,:)'*xx_r(end,:));
bigmat_h33 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck, xx_r(2:nfreq,:)),ones(nBeta,1)');
coefmat_h33 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h33 = h33 + reshape(sum(bsxfun(@times, bigmat_h33, coefmat_h33),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_r(1,:)'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*xx_r(end,:)'*xx_r(end,:));
bigmat_h44 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck, xx_i(2:nfreq,:)),ones(nBeta,1)');
coefmat_h44 = repmat(xx_i(2:nfreq,:), 1,nBeta);
h44 = h44 + reshape(sum(bsxfun(@times, bigmat_h44, coefmat_h44),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_i(1,:)'*xx_i(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*xx_i(end,:)'*xx_i(end,:));
bigmat_h42_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck.*(xx_i(2:nfreq,:)*Beta_2(:,1)),...
xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h42_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h42_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ik, xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h42_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h42 = h42 + reshape(sum(bsxfun(@times, bigmat_h42_1, coefmat_h42_1) +...
bsxfun(@times, bigmat_h42_2, coefmat_h42_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)+...
sqrt(-1)*(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1)))*xx_i(1,:))'*xx_r(1,:)) +...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,1))*xx_i(end,:)+...
sqrt(-1)*(-y(end,1).*conj(y(end,2)) + y(end,2).*conj(y(end,1)))*xx_i(end,:))'*xx_r(end,:));
bigmat_h32_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck.*(xx_r(2:nfreq,:)*Beta_1(:,3)),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h32_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h32_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*rk, xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h32_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h32 = h32 + reshape(sum(bsxfun(@times, bigmat_h32_1, coefmat_h32_1) +...
bsxfun(@times, bigmat_h32_2, coefmat_h32_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)+...
(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:))'*xx_r(1,:)) +...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,3))*xx_r(end,:)+...
(-y(end,1).*conj(y(end,2)) - y(end,2).*conj(y(end,1)))*xx_r(end,:))'*xx_r(end,:));
h24=h42'; h23=h32';
end
h1 = [h11,zeros(nBeta,2*nBeta+nBeta)];
h2 = [zeros(nBeta,nBeta),h22,-h23,-h24];
h3 = [zeros(nBeta,nBeta),-h32,h33,zeros(nBeta,nBeta)];
h4 = [zeros(nBeta,nBeta),-h42,zeros(nBeta,nBeta),h44];
gr = [gr1;gr2;gr3;gr4]; h = [h1;h2;h3;h4]; f = -f;
gr_index = (1:(4*nBeta)).*[kron(chol_index(Phi_temp,1:3),ones(nBeta,1)'), kron(chol_index(Phi_temp,4),ones(nBeta,1)')];
gr_index = gr_index(find(gr_index~=0));
gr = gr(gr_index); h = h(gr_index,gr_index);
elseif dimen==3
if (mod(n,2)==1) %odd n
f = -sum(log(delta_sq(1,2:end))' + log(delta_sq(2,2:end))' + log(delta_sq(3,2:end))' + ...
conj(y(2:end,1)).*y(2:end,1).*exp(-xx_r(2:end,:)*Beta_1(:,1)) + ...
conj(y(2:end,2) - theta(1,2:end).'.*y(2:end,1)).*(y(2:end,2) - theta(1,2:end).'.*y(2:end,1)).*exp(-xx_r(2:end,:)*Beta_1(:,2))+...
conj(y(2:end,3) -(theta(2,2:end).'.*y(2:end,1)+ theta(3,2:end).'.*y(2:end,2))).*(y(2:end,3) -(theta(2,2:end).'.*y(2:end,1)+ theta(3,2:end).'.*y(2:end,2))).*...
exp(-xx_r(2:end,:)*Beta_1(:,3))) - ...
0.5*(log(delta_sq(1,1))' + log(delta_sq(2,1))' + log(delta_sq(3,1))' + ...
conj(y(1,1)).*y(1,1).*exp(-xx_r(1,:)*Beta_1(:,1)) + ...
conj(y(1,2) - theta(1,1).'.*y(1,1)).*(y(1,2) - theta(1,1).'.*y(1,1)).*exp(-xx_r(1,:)*Beta_1(:,2))+...
conj(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*...
exp(-xx_r(1,:)*Beta_1(:,3)));
else
f = -sum(log(delta_sq(1,2:nfreq))' + log(delta_sq(2,2:nfreq))' + log(delta_sq(3,2:nfreq))' + ...
conj(y(2:nfreq,1)).*y(2:nfreq,1).*exp(-xx_r(2:nfreq,:)*Beta_1(:,1)) + ...
conj(y(2:nfreq,2) - theta(1,2:nfreq).'.*y(2:nfreq,1)).*(y(2:nfreq,2) - theta(1,2:nfreq).'.*y(2:nfreq,1)).*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))+...
conj(y(2:nfreq,3) -(theta(2,2:nfreq).'.*y(2:nfreq,1)+ theta(3,2:nfreq).'.*y(2:nfreq,2))).*(y(2:nfreq,3) -(theta(2,2:nfreq).'.*y(2:nfreq,1)+ theta(3,2:nfreq).'.*y(2:nfreq,2))).*...
exp(-xx_r(2:nfreq,:)*Beta_1(:,3))) - ...
0.5*(log(delta_sq(1,1))' + log(delta_sq(2,1))' + log(delta_sq(3,1))' + ..
conj(y(1,1)).*y(1,1).*exp(-xx_r(1,:)*Beta_1(:,1)) + ...
conj(y(1,2) - theta(1,1).'.*y(1,1)).*(y(1,2) - theta(1,1).'.*y(1,1)).*exp(-xx_r(1,:)*Beta_1(:,2))+...
conj(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*...
exp(-xx_r(1,:)*Beta_1(:,3)))-...
0.5*(log(delta_sq(1,1))' + log(delta_sq(2,1))' + log(delta_sq(3,1))' + ...
conj(y(end,1)).*y(end,1).*exp(-xx_r(end,:)*Beta_1(:,1)) + ...
conj(y(end,2) - theta(1,end).'.*y(end,1)).*(y(end,2) - theta(1,end).'.*y(end,1)).*exp(-xx_r(end,:)*Beta_1(:,2))+...
conj(y(end,3) -(theta(2,end).'.*y(end,1)+ theta(3,end).'.*y(end,2))).*(y(end,3) -(theta(2,end).'.*y(end,1)+ theta(3,end).'.*y(end,2))).*...
exp(-xx_r(end,:)*Beta_1(:,3)));
end
f = f - (0.5.*(Beta_1(1,1)* Beta_1(1,1)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,1)'*Beta_1(2:nBeta,1))/tau_temp(1))*chol_index(Phi_temp,1) -...
(0.5.*(Beta_1(1,2)* Beta_1(1,2)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,2)'*Beta_1(2:nBeta,2))/tau_temp(2))*chol_index(Phi_temp,2) -...
(0.5.*(Beta_1(1,3)* Beta_1(1,3)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,3)'*Beta_1(2:nBeta,3))/tau_temp(3))*chol_index(Phi_temp,3) -...
(0.5.*(Beta_1(1,4)* Beta_1(1,4)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,4)'*Beta_1(2:nBeta,4))/tau_temp(4))*chol_index(Phi_temp,4) -...
(0.5.*(Beta_1(1,5)* Beta_1(1,5)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,5)'*Beta_1(2:nBeta,5))/tau_temp(5))*chol_index(Phi_temp,5) -...
(0.5.*(Beta_1(1,6)* Beta_1(1,6)')/sigmasqalpha + 0.5.*(Beta_1(2:nBeta,6)'*Beta_1(2:nBeta,6))/tau_temp(6))*chol_index(Phi_temp,6) -...
(0.5.*(Beta_2(1:nBeta,1)'*Beta_2(1:nBeta,1))/tau_temp(7))*chol_index(Phi_temp,7)-...
(0.5.*(Beta_2(1:nBeta,2)'*Beta_2(1:nBeta,2))/tau_temp(8))*chol_index(Phi_temp,8)-...
(0.5.*(Beta_2(1:nBeta,3)'*Beta_2(1:nBeta,3))/tau_temp(9))*chol_index(Phi_temp,9);
gr1 = zeros(nBeta,1); gr2 = zeros(nBeta,1); gr3 = zeros(nBeta,1); gr4 = zeros(nBeta,1);
gr5 = zeros(nBeta,1); gr6 = zeros(nBeta,1); gr7 = zeros(nBeta,1); gr8 = zeros(nBeta,1);
gr9 = zeros(nBeta,1);
gr1(1) = Beta_1(1,1)/sigmasqalpha; gr1(2:nBeta) = Beta_1(2:nBeta,1)/tau_temp(1);
gr2(1) = Beta_1(1,2)/sigmasqalpha; gr2(2:nBeta) = Beta_1(2:nBeta,2)/tau_temp(2);
gr3(1) = Beta_1(1,3)/sigmasqalpha; gr3(2:nBeta) = Beta_1(2:nBeta,3)/tau_temp(3);
gr4(1) = Beta_1(1,4)/sigmasqalpha; gr4(2:nBeta) = Beta_1(2:nBeta,4)/tau_temp(4);
gr5(1) = Beta_1(1,5)/sigmasqalpha; gr5(2:nBeta) = Beta_1(2:nBeta,5)/tau_temp(5);
gr6(1) = Beta_1(1,6)/sigmasqalpha; gr6(2:nBeta) = Beta_1(2:nBeta,6)/tau_temp(6);
gr7(1:nBeta) = Beta_2(1:nBeta,1)/tau_temp(7);
gr8(1:nBeta) = Beta_2(1:nBeta,2)/tau_temp(8);
gr9(1:nBeta) = Beta_2(1:nBeta,3)/tau_temp(9);
h11(1,1)=1/sigmasqalpha; h11(2:nBeta,2:nBeta)=1/tau_temp(1)*eye(nbasis);
h22(1,1)=1/sigmasqalpha; h22(2:nBeta,2:nBeta)=1/tau_temp(2)*eye(nbasis);
h33(1,1)=1/sigmasqalpha; h33(2:nBeta,2:nBeta)=1/tau_temp(3)*eye(nbasis);
h44(1,1)=1/sigmasqalpha; h44(2:nBeta,2:nBeta)=1/tau_temp(4)*eye(nbasis);
h55(1,1)=1/sigmasqalpha; h55(2:nBeta,2:nBeta)=1/tau_temp(5)*eye(nbasis);
h66(1,1)=1/sigmasqalpha; h66(2:nBeta,2:nBeta)=1/tau_temp(6)*eye(nbasis);
h77(1:nBeta,1:nBeta)=1/tau_temp(7)*eye(nBeta);
h88(1:nBeta,1:nBeta)=1/tau_temp(8)*eye(nBeta);
h99(1:nBeta,1:nBeta)=1/tau_temp(9)*eye(nBeta);
h42 = zeros(nBeta,nBeta);
h53 = zeros(nBeta,nBeta);
h56 = zeros(nBeta,nBeta);
h59 = zeros(nBeta,nBeta);
h63 = zeros(nBeta,nBeta);
h68 = zeros(nBeta,nBeta);
h72 = zeros(nBeta,nBeta);
h83 = zeros(nBeta,nBeta);
h93 = zeros(nBeta,nBeta);
h98 = zeros(nBeta,nBeta);
if (mod(n,2)==1)
%%%%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%%%%
rk4 = -y(2:end,1).*conj(y(2:end,2)) - y(2:end,2).*conj(y(2:end,1));
ck4 = 2*abs(y(2:end,1)).^2;
rk5 = -y(2:end,1).*conj(y(2:end,3)) - y(2:end,3).*conj(y(2:end,1));
ck5 = 2*abs(y(2:end,1)).^2;
b = theta(3,:);
dk5 = y(2:end,2).*conj(y(2:end,1)).*(b(2:end).') + conj(y(2:end,2)).*y(2:end,1).*conj(b(2:end).');
rk6 = -y(2:end,2).*conj(y(2:end,3)) - y(2:end,3).*conj(y(2:end,2));
ck6 = 2*abs(y(2:end,2)).^2;
a = theta(2,:);
dk6 = y(2:end,1).*conj(y(2:end,2)).*(a(2:end).') + conj(y(2:end,1)).*y(2:end,2).*conj(a(2:end).');
ik7 = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,2)) + y(2:end,2).*conj(y(2:end,1)));
ck7 = 2*abs(y(2:end,1)).^2;
ik8 = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,3)) + y(2:end,3).*conj(y(2:end,1)));
ck8 = 2*abs(y(2:end,1)).^2;
dk8 = sqrt(-1)*(-y(2:end,2).*conj(y(2:end,1)).*(b(2:end).') + conj(y(2:end,2).*conj(y(2:end,1)).*(b(2:end).'))) ;
ik9 = sqrt(-1)*(-y(2:end,2).*conj(y(2:end,3)) + y(2:end,3).*conj(y(2:end,2)));
ck9 = 2*abs(y(2:end,2)).^2;
dk9 = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,2)).*(a(2:end).') + conj(y(2:end,1).*conj(y(2:end,2)).*(a(2:end).'))) ;
gr1 = gr1 + xx_r(2:end,:)'*(1-abs(y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:end,:)'*(1 - abs(y(2:end,2)-theta(1,2:end).'.*y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1,1).*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))));
gr3 = gr3 + xx_r(2:end,:)'*(1 - abs(y(2:end,3) - theta(2,2:end).'.*y(2:end,1) - theta(3,2:end).'.*y(2:end,2)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,3)))+...
0.5*(xx_r(1,:)'*(1 - abs(y(1,3) - theta(2,1).*y(1,1) - theta(3,1).*y(1,2))^2.*exp(-xx_r(1,:)*Beta_1(:,3))));
temp_mat_41 = bsxfun(@times, xx_r(2:end,:),rk4);
temp_mat_42 = bsxfun(@times, ck4, bsxfun(@times, xx_r(2:end,:), xx_r(2:end,:)*Beta_1(:,4)));
gr4 = gr4 + sum( bsxfun(@times, (temp_mat_41+temp_mat_42), exp(-xx_r(2:end,:)*Beta_1(:,2))))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,4))*xx_r(1,:)');
temp_mat_51 = bsxfun(@times, xx_r(2:end,:),rk5);
temp_mat_52 = bsxfun(@times, ck5, bsxfun(@times, xx_r(2:end,:), xx_r(2:end,:)*Beta_1(:,5)));
temp_mat_53 = bsxfun(@times, xx_r(2:end,:),dk5);
gr5 = gr5 + sum( bsxfun(@times, (temp_mat_51 + temp_mat_52 + temp_mat_53), exp(-xx_r(2:end,:)*Beta_1(:,3)) ))'+...
0.5* (exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,3)) - y(1,3).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,5))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,2).*conj(y(1,1)).*(b(1).') + conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_r(1,:)');
temp_mat_61 = bsxfun(@times, xx_r(2:end,:),rk6);
temp_mat_62 = bsxfun(@times, ck6, bsxfun(@times, xx_r(2:end,:), xx_r(2:end,:)*Beta_1(:,6)));
temp_mat_63 = bsxfun(@times, xx_r(2:end,:),dk6);
gr6 = gr6 + sum(bsxfun(@times, (temp_mat_61 + temp_mat_62 + temp_mat_63), exp(-xx_r(2:end,:)*Beta_1(:,3))))'+...
0.5* (exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,2).*conj(y(1,3)) - y(1,3).*conj(y(1,2)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_r(1,:)*Beta_1(:,6))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_r(1,:)');
temp_mat_71 = bsxfun(@times, ik7, xx_i(2:end,:));
temp_mat_72 = bsxfun(@times, ck7, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,1)));
gr7 = gr7 + sum( bsxfun(@times, (temp_mat_71 + temp_mat_72), exp(-xx_r(2:end,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(imag(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)');
temp_mat_81 = bsxfun(@times, ik8, xx_i(2:end,:));
temp_mat_82 = bsxfun(@times, ck8, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,2)));
temp_mat_83 = bsxfun(@times, xx_i(2:end,:),dk8);
gr8 = gr8 + sum( bsxfun(@times, (temp_mat_81 + temp_mat_82 + temp_mat_83), exp(-xx_r(2:end,:)*Beta_1(:,3))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,1).*conj(y(1,3)) + y(1,3).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,2))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(b(1).') + conj(y(1,1).*conj(y(1,2)).*(b(1).')))*xx_i(1,:)');
temp_mat_91 = bsxfun(@times, ik9, xx_i(2:end,:));
temp_mat_92 = bsxfun(@times, ck9, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,3)));
temp_mat_93 = bsxfun(@times, xx_i(2:end,:),dk9);
gr9 = gr9 + sum( bsxfun(@times, (temp_mat_91 + temp_mat_92 + temp_mat_93), exp(-xx_r(2:end,:)*Beta_1(:,3))))' + ...
0.5 * (exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,2).*conj(y(1,3)) + y(1,3).*conj(y(1,2))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_i(1,:)*Beta_2(:,3))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_i(1,:)');
%%%%%%%%%%%%%%%%%%%
%Hessian
%%%%%%%%%%%%%%%%%%%
bigmat_h11 = kron(bsxfun(@times, abs(y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,1)), xx_r(2:end,:)),ones(nBeta,1)');
coefmat_h11 = repmat(xx_r(2:end,:), 1,nBeta);
h11 = h11 + reshape(sum(bsxfun(@times, bigmat_h11, coefmat_h11),1),nBeta,nBeta) +...
0.5*(abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))*xx_r(1,:)'*xx_r(1,:));
bigmat_h22 = kron(bsxfun(@times, abs(y(2:end,2)-theta(1,2:end).'.*y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,2)),xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h22 = repmat(xx_r(2:end,:), 1,nBeta);
h22 = h22 + reshape(sum(bsxfun(@times, bigmat_h22, coefmat_h22),1),nBeta,nBeta) +...
0.5*(abs(y(1,2)-theta(1,1).*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))*xx_r(1,:)'*xx_r(1,:));
bigmat_h33 = kron(bsxfun(@times, abs(y(2:end,3) - theta(2,2:end).'.*y(2:end,1) - theta(3,2:end).'.*y(2:end,2)).^2.*...
exp(-xx_r(2:end,:)*Beta_1(:,3)),xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h33 = repmat(xx_r(2:end,:), 1,nBeta);
h33 = h33 + reshape(sum(bsxfun(@times, bigmat_h33, coefmat_h33),1),nBeta,nBeta) +...
0.5*(abs(y(1,3) - theta(2,1).'.*y(1,1) - theta(3,1).'.*y(1,2)).^2.*...
exp(-xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)'*xx_r(1,:));
bigmat_h44 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck4, xx_r(2:end,:)),ones(nBeta,1)');
coefmat_h44 = repmat(xx_r(2:end,:), 1,nBeta);
h44 = h44 + reshape(sum(bsxfun(@times, bigmat_h44, coefmat_h44),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_r(1,:)'*xx_r(1,:));
bigmat_h55 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck5, xx_r(2:end,:)),ones(nBeta,1)');
coefmat_h55 = repmat(xx_r(2:end,:), 1,nBeta);
h55 = h55 + reshape(sum(bsxfun(@times, bigmat_h55, coefmat_h55),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*xx_r(1,:)'*xx_r(1,:));
bigmat_h66 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck6, xx_r(2:end,:)),ones(nBeta,1)');
coefmat_h66 = repmat(xx_r(2:end,:), 1,nBeta);
h66 = h66 + reshape(sum(bsxfun(@times, bigmat_h66, coefmat_h66),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*xx_r(1,:)'*xx_r(1,:));
bigmat_h77 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck7, xx_i(2:end,:)),ones(nBeta,1)');
coefmat_h77 = repmat(xx_i(2:end,:), 1,nBeta);
h77 = h77 + reshape(sum(bsxfun(@times, bigmat_h77, coefmat_h77),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_i(1,:)'*xx_i(1,:));
bigmat_h88 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck8, xx_i(2:end,:)),ones(nBeta,1)');
coefmat_h88 = repmat(xx_i(2:end,:), 1,nBeta);
h88 = h88 + reshape(sum(bsxfun(@times, bigmat_h88, coefmat_h88),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*xx_i(1,:)'*xx_i(1,:));
bigmat_h99 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck9, xx_i(2:end,:)),ones(nBeta,1)');
coefmat_h99 = repmat(xx_i(2:end,:), 1,nBeta);
h99 = h99 + reshape(sum(bsxfun(@times, bigmat_h99, coefmat_h99),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*xx_i(1,:)'*xx_i(1,:));
bigmat_h42_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck4.*(xx_r(2:end,:)*Beta_1(:,4)),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h42_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h42_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,2)).*rk4, xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h42_2 = repmat(xx_r(2:end,:), 1,nBeta);
h42 = h42 + reshape(sum(bsxfun(@times, bigmat_h42_1, coefmat_h42_1) +...
bsxfun(@times, bigmat_h42_2, coefmat_h42_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,4))*xx_r(1,:)+...
(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:))'*xx_r(1,:));
bigmat_h53_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck5.*(xx_r(2:end,:)*Beta_1(:,5)),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h53_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h53_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*rk5, xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h53_2 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h53_3 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*dk5, xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h53_3 = repmat(xx_r(2:end,:), 1,nBeta);
h53 = h53 + reshape(sum(bsxfun(@times, bigmat_h53_1, coefmat_h53_1) +...
bsxfun(@times, bigmat_h53_2, coefmat_h53_2)+...
bsxfun(@times, bigmat_h53_3, coefmat_h53_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,5))*xx_r(1,:)+...
(-y(1,1).*conj(y(1,3)) - y(1,3).*conj(y(1,1)))*xx_r(1,:)+...
(y(1,2).*conj(y(1,1)).*(b(1).') + conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_r(1,:))'*xx_r(1,:));
bigmat_h56_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,1)).*y(2:end,2),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h56_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h56_2 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,2)).*y(2:end,1),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h56_2 = repmat(xx_r(2:end,:), 1,nBeta);
h56 = real(h56 + reshape(sum(bsxfun(@times, bigmat_h56_1, coefmat_h56_1) +...
bsxfun(@times, bigmat_h56_2, coefmat_h56_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,1)).*y(1,2))*xx_r(1,:)'*xx_r(1,:)+...
(conj(y(1,2)).*y(1,1))*xx_r(1,:)'*xx_r(1,:))));
bigmat_h59_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,1)).*y(2:end,2),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h59_1 = repmat(xx_i(2:end,:), 1,nBeta);
bigmat_h59_2 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,2)).*y(2:end,1),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h59_2 = repmat(xx_i(2:end,:), 1,nBeta);
h59 = imag(h59 + reshape(sum(bsxfun(@times, bigmat_h59_1, coefmat_h59_1) -...
bsxfun(@times, bigmat_h59_2, coefmat_h59_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,1)).*y(1,2))*xx_r(1,:)'*xx_i(1,:) -...
(conj(y(1,2)).*y(1,1))*xx_r(1,:)'*xx_i(1,:))));
bigmat_h63_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck6.*(xx_r(2:end,:)*Beta_1(:,6)),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h63_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h63_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*rk6, xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h63_2 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h63_3 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*dk6 , xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h63_3 = repmat(xx_r(2:end,:), 1,nBeta);
h63 = h63 + reshape(sum(bsxfun(@times, bigmat_h63_1, coefmat_h63_1) +...
bsxfun(@times, bigmat_h63_2, coefmat_h63_2)+...
bsxfun(@times, bigmat_h63_3, coefmat_h63_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,2)).^2*(xx_r(1,:)*Beta_1(:,6))*xx_r(1,:)+...
(-y(1,2).*conj(y(1,3)) - y(1,3).*conj(y(1,2)))*xx_r(1,:)+...
(y(1,2).*conj(y(1,1)).*(a(1).') + conj(y(1,2).*conj(y(1,1)).*(a(1).')))*xx_r(1,:))'*xx_r(1,:));
bigmat_h68_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,2)).*y(2:end,1),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h68_1 = repmat(xx_i(2:end,:), 1,nBeta);
bigmat_h68_2 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,1)).*y(2:end,2),...
xx_r(2:end,:)), ones(nBeta,1)');
coefmat_h68_2 = repmat(xx_i(2:end,:), 1,nBeta);
h68 = imag(h68 + reshape(sum(bsxfun(@times, bigmat_h68_1, coefmat_h68_1) -...
bsxfun(@times, bigmat_h68_2, coefmat_h68_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,2)).*y(1,1))*xx_r(1,:)'*xx_i(1,:)-...
(conj(y(1,1)).*y(1,2))*xx_r(1,:)'*xx_i(1,:))));
bigmat_h72_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,2)).*ck7.*(xx_i(2:end,:)*Beta_2(:,1)),...
xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h72_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h72_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,2)).*ik7, xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h72_2 = repmat(xx_r(2:end,:), 1,nBeta);
h72 = h72 + reshape(sum(bsxfun(@times, bigmat_h72_1, coefmat_h72_1) +...
bsxfun(@times, bigmat_h72_2, coefmat_h72_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)+...
imag(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1)))*xx_i(1,:))'*xx_r(1,:));
bigmat_h83_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck8.*(xx_i(2:end,:)*Beta_2(:,2)),...
xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h83_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h83_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*ik8, xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h83_2 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h83_3 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*(dk8), xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h83_3 = repmat(xx_r(2:end,:), 1,nBeta);
h83 = h83 + reshape(sum(bsxfun(@times, bigmat_h83_1, coefmat_h83_1) +...
bsxfun(@times, bigmat_h83_2, coefmat_h83_2)+...
bsxfun(@times, bigmat_h83_3, coefmat_h83_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,2))*xx_i(1,:)+...
(-y(1,1).*conj(y(1,3)) + y(1,3).*conj(y(1,1)))*xx_i(1,:)+...
imag(-y(1,2).*conj(y(1,1)).*(b(1).') + conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_i(1,:))'*xx_r(1,:));
bigmat_h93_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*ck9.*(xx_i(2:end,:)*Beta_2(:,3)),...
xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h93_1 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h93_2 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*ik9, xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h93_2 = repmat(xx_r(2:end,:), 1,nBeta);
bigmat_h93_3 = kron(bsxfun(@times,exp(-xx_r(2:end,:)*Beta_1(:,3)).*(dk9), xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h93_3 = repmat(xx_r(2:end,:), 1,nBeta);
h93 = h93 + reshape(sum(bsxfun(@times, bigmat_h93_1, coefmat_h93_1) +...
bsxfun(@times, bigmat_h93_2, coefmat_h93_2)+...
bsxfun(@times, bigmat_h93_3, coefmat_h93_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,2)).^2*(xx_i(1,:)*Beta_2(:,3))*xx_i(1,:)+...
(-y(1,2).*conj(y(1,3)) + y(1,3).*conj(y(1,2)))*xx_i(1,:)+...
imag(-y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_i(1,:))'*xx_r(1,:));
bigmat_h98_1 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,1)).*y(2:end,2),...
xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h98_1 = repmat(xx_i(2:end,:), 1,nBeta);
bigmat_h98_2 = kron(bsxfun(@times, exp(-xx_r(2:end,:)*Beta_1(:,3)).*conj(y(2:end,2)).*y(2:end,1),...
xx_i(2:end,:)), ones(nBeta,1)');
coefmat_h98_2 = repmat(xx_i(2:end,:), 1,nBeta);
h98 = real(h98 + reshape(sum(bsxfun(@times, bigmat_h98_1, coefmat_h98_1) +...
bsxfun(@times, bigmat_h98_2, coefmat_h98_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,1)).*y(1,2))*xx_i(1,:)'*xx_i(1,:)+...
(conj(y(1,2)).*y(1,1))*xx_i(1,:)'*xx_i(1,:))));
h24=h42'; h35=h53'; h65=h56'; h95=h59'; h36=h63';
h86=h68'; h27=h72'; h38=h83'; h39=h93'; h89=h98';
else
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rk4 = -y(2:nfreq,1).*conj(y(2:nfreq,2)) - y(2:nfreq,2).*conj(y(2:nfreq,1));
ck4 = 2*abs(y(2:nfreq,1)).^2;
rk5 = -y(2:nfreq,1).*conj(y(2:nfreq,3)) - y(2:nfreq,3).*conj(y(2:nfreq,1));
ck5 = 2*abs(y(2:nfreq,1)).^2;
b = theta(3,:);
dk5 = y(2:nfreq,2).*conj(y(2:nfreq,1)).*(b(2:nfreq).') + conj(y(2:nfreq,2)).*y(2:nfreq,1).*conj(b(2:nfreq).');
rk6 = -y(2:nfreq,2).*conj(y(2:nfreq,3)) - y(2:nfreq,3).*conj(y(2:nfreq,2));
ck6 = 2*abs(y(2:nfreq,2)).^2;
a = theta(2,:);
dk6 = y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).') + conj(y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).'));
ik7 = sqrt(-1)*(-y(2:nfreq,1).*conj(y(2:nfreq,2)) + y(2:nfreq,2).*conj(y(2:nfreq,1)));
ck7 = 2*abs(y(2:nfreq,1)).^2;
ik8 = sqrt(-1)*(-y(2:nfreq,1).*conj(y(2:nfreq,3)) + y(2:nfreq,3).*conj(y(2:nfreq,1)));
ck8 = 2*abs(y(2:nfreq,1)).^2;
dk8 = sqrt(-1)*( -y(2:nfreq,2).*conj(y(2:nfreq,1)).*(b(2:nfreq).') + conj(y(2:nfreq,2).*conj(y(2:nfreq,1)).*(b(2:nfreq).')));
ik9 = sqrt(-1)*(-y(2:nfreq,2).*conj(y(2:nfreq,3)) + y(2:nfreq,3).*conj(y(2:nfreq,2)));
ck9 = 2*abs(y(2:nfreq,2)).^2;
dk9 = sqrt(-1)*( -y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).') + conj(y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).')));
gr1 = gr1 + xx_r(2:nfreq,:)'*(1-abs(y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))))+...
0.5*(xx_r(end,:)'*(1-abs(y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:nfreq,:)'*(1 - abs(y(2:nfreq,2)-theta(1,2:nfreq).'.*y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1,1).*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2)))) +...
0.5*(xx_r(end,:)'*(1 - abs(y(end,2)-theta(1,end).*y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,2))));
gr3 = gr3 + xx_r(2:nfreq,:)'*(1 - abs(y(2:nfreq,3) - theta(2,2:nfreq).'.*y(2:nfreq,1) - theta(3,2:nfreq).'.*y(2:nfreq,2)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,3)))+...
0.5*(xx_r(1,:)'*(1 - abs(y(1,3) - theta(2,1).*y(1,1) - theta(3,1).*y(1,2))^2.*exp(-xx_r(1,:)*Beta_1(:,3))))+...
0.5*(xx_r(end,:)'*(1 - abs(y(end,3) - theta(2,end).*y(end,1) - theta(3,end).*y(end,2))^2.*exp(-xx_r(end,:)*Beta_1(:,3))));
temp_mat_41 = bsxfun(@times, xx_r(2:nfreq,:),rk4);
temp_mat_42 = bsxfun(@times, ck4, bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,4)));
gr4 = gr4 + sum( bsxfun(@times, (temp_mat_41+temp_mat_42), exp(-xx_r(2:nfreq,:)*Beta_1(:,2)) ))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,4))*xx_r(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(-y(end,1).*conj(y(end,2)) - y(end,2).*conj(y(end,1)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,4))*xx_r(end,:)');
temp_mat_51 = bsxfun(@times, xx_r(2:nfreq,:),rk5);
temp_mat_52 = bsxfun(@times, ck5, bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,5)));
temp_mat_53 = bsxfun(@times, xx_r(2:nfreq,:),dk5);
gr5 = gr5 + sum( bsxfun(@times, (temp_mat_51 + temp_mat_52 + temp_mat_53), exp(-xx_r(2:nfreq,:)*Beta_1(:,3)) ))'+...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,3)) - y(1,3).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,5))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,2).*conj(y(1,1)).*(b(1).')+conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_r(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,1).*conj(y(end,3)) - y(end,3).*conj(y(end,1)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,5))*xx_r(end,:)'+...
exp(-xx_r(end,:)*Beta_1(:,3))*(y(end,2).*conj(y(end,1)).*(b(end).') + conj(y(end,2).*conj(y(end,1)).*(b(end).')))*xx_r(end,:)');
temp_mat_61 = bsxfun(@times, xx_r(2:nfreq,:),rk6);
temp_mat_62 = bsxfun(@times, ck6, bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,6)));
temp_mat_63 = bsxfun(@times, xx_r(2:nfreq,:),dk6);
gr6 = gr6 + sum( bsxfun(@times, (temp_mat_61 + temp_mat_62 + temp_mat_63), exp(-xx_r(2:nfreq,:)*Beta_1(:,3)) ))'+...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,2).*conj(y(1,3)) - y(1,3).*conj(y(1,2)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_r(1,:)*Beta_1(:,6))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_r(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,2).*conj(y(end,3)) - y(end,3).*conj(y(end,2)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,2)).^2*(xx_r(end,:)*Beta_1(:,6))*xx_r(end,:)'+...
exp(-xx_r(end,:)*Beta_1(:,3))*(y(end,1).*conj(y(end,2)).*(a(end).') + conj(y(end,1).*conj(y(end,2)).*(a(end).')))*xx_r(end,:)');
temp_mat_71 = bsxfun(@times, ik7, xx_i(2:nfreq,:));
temp_mat_72 = bsxfun(@times, ck7, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,1)));
gr7 = gr7 + sum( bsxfun(@times, (temp_mat_71 + temp_mat_72), exp(-xx_r(2:nfreq,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(imag(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(imag(-y(end,1).*conj(y(end,2)) + y(end,2).*conj(y(end,1))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,1))*xx_i(end,:)');
temp_mat_81 = bsxfun(@times, ik8, xx_i(2:nfreq,:));
temp_mat_82 = bsxfun(@times, ck8, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,2)));
temp_mat_83 = bsxfun(@times, xx_i(2:nfreq,:),dk8);
gr8 = gr8 + sum( bsxfun(@times, (temp_mat_81 + temp_mat_82 + temp_mat_83), exp(-xx_r(2:nfreq,:)*Beta_1(:,3))))' + ...
0.5 * (exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,1).*conj(y(1,3)) + y(1,3).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,2))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(b(1).') + conj(y(1,1).*conj(y(1,2)).*(b(1).')))*xx_i(1,:)')+...
0.5 * (exp(-xx_r(end,:)*Beta_1(:,3))*(imag(-y(end,1).*conj(y(end,3)) + y(end,3).*conj(y(end,1))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,2))*xx_i(end,:)'+...
sqrt(-1)*exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,1).*conj(y(end,2)).*(b(end).') + conj(y(end,1).*conj(y(end,2)).*(b(end).')))*xx_i(end,:)');
temp_mat_91 = bsxfun(@times, ik9, xx_i(2:nfreq,:));
temp_mat_92 = bsxfun(@times, ck9, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,3)));
temp_mat_93 = bsxfun(@times, xx_i(2:nfreq,:),dk9);
gr9 = gr9 + sum( bsxfun(@times, (temp_mat_91 + temp_mat_92 + temp_mat_93), exp(-xx_r(2:nfreq,:)*Beta_1(:,3))))' + ...
0.5 * (exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,2).*conj(y(1,3)) + y(1,3).*conj(y(1,2))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_i(1,:)*Beta_2(:,3))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_i(1,:)')+...
0.5 * (exp(-xx_r(end,:)*Beta_1(:,3))*(imag(-y(end,2).*conj(y(end,3)) + y(end,3).*conj(y(end,2))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,2)).^2*(xx_i(end,:)*Beta_2(:,3))*xx_i(end,:)'+...
sqrt(-1)*exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,1).*conj(y(end,2)).*(a(end).') + conj(y(end,1).*conj(y(end,2)).*(a(end).')))*xx_i(end,:)');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Hessian
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
bigmat_h11 = kron(bsxfun(@times, abs(y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,1)), xx_r(2:nfreq,:)),ones(nBeta,1)');
coefmat_h11 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h11 = h11 + reshape(sum(bsxfun(@times, bigmat_h11, coefmat_h11),1),nBeta,nBeta) +...
0.5*(abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))*xx_r(1,:)'*xx_r(1,:))+...
0.5*(abs(y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,1))*xx_r(end,:)'*xx_r(end,:));
bigmat_h22 = kron(bsxfun(@times, abs(y(2:nfreq,2)-theta(1,2:nfreq).'.*y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,2)),xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h22 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h22 = h22 + reshape(sum(bsxfun(@times, bigmat_h22, coefmat_h22),1),nBeta,nBeta) +...
0.5*(abs(y(1,2)-theta(1,1).*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))*xx_r(1,:)'*xx_r(1,:))+...
0.5*(abs(y(end,2)-theta(1,end).*y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,2))*xx_r(end,:)'*xx_r(end,:));
bigmat_h33 = kron(bsxfun(@times, abs(y(2:nfreq,3) - theta(2,2:nfreq).'.*y(2:nfreq,1) - theta(3,2:nfreq).'.*y(2:nfreq,2)).^2.*...
exp(-xx_r(2:nfreq,:)*Beta_1(:,3)),xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h33 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h33 = h33 + reshape(sum(bsxfun(@times, bigmat_h33, coefmat_h33),1),nBeta,nBeta) +...
0.5*(abs(y(1,3) - theta(2,1).'.*y(1,1) - theta(3,1).'.*y(1,2)).^2.*...
exp(-xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)'*xx_r(1,:))+...
0.5*(abs(y(end,3) - theta(2,end).'.*y(end,1) - theta(3,end).'.*y(end,2)).^2.*...
exp(-xx_r(end,:)*Beta_1(:,3))*xx_r(end,:)'*xx_r(end,:));
bigmat_h44 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck4, xx_r(2:nfreq,:)),ones(nBeta,1)');
coefmat_h44 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h44 = h44 + reshape(sum(bsxfun(@times, bigmat_h44, coefmat_h44),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_r(1,:)'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*xx_r(end,:)'*xx_r(end,:));
bigmat_h55 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck5, xx_r(2:nfreq,:)),ones(nBeta,1)');
coefmat_h55 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h55 = h55 + reshape(sum(bsxfun(@times, bigmat_h55, coefmat_h55),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*xx_r(1,:)'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,1)).^2*xx_r(end,:)'*xx_r(end,:));
bigmat_h66 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck6, xx_r(2:nfreq,:)),ones(nBeta,1)');
coefmat_h66 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h66 = h66 + reshape(sum(bsxfun(@times, bigmat_h66, coefmat_h66),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*xx_r(1,:)'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,2)).^2*xx_r(end,:)'*xx_r(end,:));
bigmat_h77 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck7, xx_i(2:nfreq,:)),ones(nBeta,1)');
coefmat_h77 = repmat(xx_i(2:nfreq,:), 1,nBeta);
h77 = h77 + reshape(sum(bsxfun(@times, bigmat_h77, coefmat_h77),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*xx_i(1,:)'*xx_i(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*xx_i(end,:)'*xx_i(end,:));
bigmat_h88 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck8, xx_i(2:nfreq,:)),ones(nBeta,1)');
coefmat_h88 = repmat(xx_i(2:nfreq,:), 1,nBeta);
h88 = h88 + reshape(sum(bsxfun(@times, bigmat_h88, coefmat_h88),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*xx_i(1,:)'*xx_i(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,1)).^2*xx_i(end,:)'*xx_i(end,:));
bigmat_h99 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck9, xx_i(2:nfreq,:)),ones(nBeta,1)');
coefmat_h99 = repmat(xx_i(2:nfreq,:), 1,nBeta);
h99 = h99 + reshape(sum(bsxfun(@times, bigmat_h99, coefmat_h99),1),nBeta,nBeta) +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*xx_i(1,:)'*xx_i(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,2)).^2*xx_i(end,:)'*xx_i(end,:));
bigmat_h42_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck4.*(xx_r(2:nfreq,:)*Beta_1(:,4)),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h42_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h42_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*rk4, xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h42_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h42 = h42 + reshape(sum(bsxfun(@times, bigmat_h42_1, coefmat_h42_1) +...
bsxfun(@times, bigmat_h42_2, coefmat_h42_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,4))*xx_r(1,:)+...
(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:))'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,4))*xx_r(end,:)+...
(-y(end,1).*conj(y(end,2)) - y(end,2).*conj(y(end,1)))*xx_r(end,:))'*xx_r(end,:));
bigmat_h53_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck5.*(xx_r(2:nfreq,:)*Beta_1(:,5)),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h53_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h53_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*rk5, xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h53_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h53_3 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*dk5, xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h53_3 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h53 = h53 + reshape(sum(bsxfun(@times, bigmat_h53_1, coefmat_h53_1) +...
bsxfun(@times, bigmat_h53_2, coefmat_h53_2)+...
bsxfun(@times, bigmat_h53_3, coefmat_h53_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,5))*xx_r(1,:)+...
(-y(1,1).*conj(y(1,3)) - y(1,3).*conj(y(1,1)))*xx_r(1,:)+...
(y(1,2).*conj(y(1,1)).*(b(1).') + conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_r(1,:))'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,5))*xx_r(end,:)+...
(-y(end,1).*conj(y(end,3)) - y(end,3).*conj(y(end,1)))*xx_r(end,:)+...
(y(end,2).*conj(y(end,1)).*(b(end).') + conj(y(end,2).*conj(y(end,1)).*(b(end).')))*xx_r(end,:))'*xx_r(end,:));
bigmat_h56_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,1)).*y(2:nfreq,2),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h56_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h56_2 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,2)).*y(2:nfreq,1),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h56_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h56 = real(h56 + reshape(sum(bsxfun(@times, bigmat_h56_1, coefmat_h56_1) +...
bsxfun(@times, bigmat_h56_2, coefmat_h56_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,1)).*y(1,2))*xx_r(1,:)'*xx_r(1,:)+...
(conj(y(1,2)).*y(1,1))*xx_r(1,:)'*xx_r(1,:)))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*((conj(y(end,1)).*y(end,2))*xx_r(end,:)'*xx_r(end,:)+...
(conj(y(end,2)).*y(end,1))*xx_r(end,:)'*xx_r(end,:))));
bigmat_h59_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,1)).*y(2:nfreq,2),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h59_1 = repmat(xx_i(2:nfreq,:), 1,nBeta);
bigmat_h59_2 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,2)).*y(2:nfreq,1),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h59_2 = repmat(xx_i(2:nfreq,:), 1,nBeta);
h59 = imag(h59 + reshape(sum(bsxfun(@times, bigmat_h59_1, coefmat_h59_1) -...
bsxfun(@times, bigmat_h59_2, coefmat_h59_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,1)).*y(1,2))*xx_r(1,:)'*xx_i(1,:)-...
(conj(y(1,2)).*y(1,1))*xx_r(1,:)'*xx_i(1,:)))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*((conj(y(end,1)).*y(end,2))*xx_r(end,:)'*xx_i(end,:)-...
(conj(y(end,2)).*y(end,1))*xx_r(end,:)'*xx_i(end,:))));
bigmat_h63_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck6.*(xx_r(2:nfreq,:)*Beta_1(:,6)),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h63_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h63_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*rk6, xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h63_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h63_3 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*dk6, xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h63_3 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h63 = h63 + reshape(sum(bsxfun(@times, bigmat_h63_1, coefmat_h63_1) +...
bsxfun(@times, bigmat_h63_2, coefmat_h63_2)+...
bsxfun(@times, bigmat_h63_3, coefmat_h63_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,2)).^2*(xx_r(1,:)*Beta_1(:,6))*xx_r(1,:)+...
(-y(1,2).*conj(y(1,3)) - y(1,3).*conj(y(1,2)))*xx_r(1,:)+...
(y(1,2).*conj(y(1,1)).*(a(1).') + conj(y(1,2).*conj(y(1,1)).*(a(1).')))*xx_r(1,:))'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(2*abs(y(end,2)).^2*(xx_r(end,:)*Beta_1(:,6))*xx_r(end,:)+...
(-y(end,2).*conj(y(end,3)) - y(end,3).*conj(y(end,2)))*xx_r(end,:)+...
(y(end,2).*conj(y(end,1)).*(a(end).') + conj(y(end,2).*conj(y(end,1)).*(a(end).')))*xx_r(end,:))'*xx_r(end,:));
bigmat_h68_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,2)).*y(2:nfreq,1),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h68_1 = repmat(xx_i(2:nfreq,:), 1,nBeta);
bigmat_h68_2 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,1)).*y(2:nfreq,2),...
xx_r(2:nfreq,:)), ones(nBeta,1)');
coefmat_h68_2 = repmat(xx_i(2:nfreq,:), 1,nBeta);
h68 = imag(h68 + reshape(sum(bsxfun(@times, bigmat_h68_1, coefmat_h68_1) -...
bsxfun(@times, bigmat_h68_2, coefmat_h68_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,2)).*y(1,1))*xx_r(1,:)'*xx_i(1,:)-...
(conj(y(1,1)).*y(1,2))*xx_r(1,:)'*xx_i(1,:)))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*((conj(y(end,2)).*y(end,1))*xx_r(end,:)'*xx_i(end,:)-...
(conj(y(end,1)).*y(end,2))*xx_r(end,:)'*xx_i(end,:))));
bigmat_h72_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ck7.*(xx_i(2:nfreq,:)*Beta_2(:,1)),...
xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h72_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h72_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,2)).*ik7, xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h72_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h72 = h72 + reshape(sum(bsxfun(@times, bigmat_h72_1, coefmat_h72_1) +...
bsxfun(@times, bigmat_h72_2, coefmat_h72_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)+...
imag(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1)))*xx_i(1,:))'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,1))*xx_i(end,:)+...
imag(-y(end,1).*conj(y(end,2)) + y(end,2).*conj(y(end,1)))*xx_i(end,:))'*xx_r(end,:));
bigmat_h83_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck8.*(xx_i(2:nfreq,:)*Beta_2(:,2)),...
xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h83_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h83_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ik8, xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h83_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h83_3 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*(dk8), xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h83_3 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h83 = h83 + reshape(sum(bsxfun(@times, bigmat_h83_1, coefmat_h83_1) +...
bsxfun(@times, bigmat_h83_2, coefmat_h83_2)+...
bsxfun(@times, bigmat_h83_3, coefmat_h83_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,2))*xx_i(1,:)+...
(-y(1,1).*conj(y(1,3)) + y(1,3).*conj(y(1,1)))*xx_i(1,:)+...
imag(-y(1,2).*conj(y(1,1)).*(b(1).') + conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_i(1,:))'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,2))*xx_i(end,:)+...
(-y(end,1).*conj(y(end,3)) + y(end,3).*conj(y(end,1)))*xx_i(end,:)+...
imag(-y(end,2).*conj(y(end,1)).*(b(end).') + conj(y(end,2).*conj(y(end,1)).*(b(end).')))*xx_i(end,:))'*xx_r(end,:));
bigmat_h93_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ck9.*(xx_i(2:nfreq,:)*Beta_2(:,3)),...
xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h93_1 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h93_2 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*ik9, xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h93_2 = repmat(xx_r(2:nfreq,:), 1,nBeta);
bigmat_h93_3 = kron(bsxfun(@times,exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*(dk9), xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h93_3 = repmat(xx_r(2:nfreq,:), 1,nBeta);
h93 = h93 + reshape(sum(bsxfun(@times, bigmat_h93_1, coefmat_h93_1) +...
bsxfun(@times, bigmat_h93_2, coefmat_h93_2)+...
bsxfun(@times, bigmat_h93_3, coefmat_h93_3),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(2*abs(y(1,2)).^2*(xx_i(1,:)*Beta_2(:,3))*xx_i(1,:)+...
(-y(1,2).*conj(y(1,3)) + y(1,3).*conj(y(1,2)))*xx_i(1,:)+...
imag(-y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_i(1,:))'*xx_r(1,:))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(2*abs(y(end,2)).^2*(xx_i(end,:)*Beta_2(:,3))*xx_i(end,:)+...
(-y(end,2).*conj(y(end,3)) + y(end,3).*conj(y(end,2)))*xx_i(end,:)+...
imag(-y(end,1).*conj(y(end,2)).*(a(end).') + conj(y(end,1).*conj(y(end,2)).*(a(end).')))*xx_i(end,:))'*xx_r(end,:));
bigmat_h98_1 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,1)).*y(2:nfreq,2),...
xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h98_1 = repmat(xx_i(2:nfreq,:), 1,nBeta);
bigmat_h98_2 = kron(bsxfun(@times, exp(-xx_r(2:nfreq,:)*Beta_1(:,3)).*conj(y(2:nfreq,2)).*y(2:nfreq,1),...
xx_i(2:nfreq,:)), ones(nBeta,1)');
coefmat_h98_2 = repmat(xx_i(2:nfreq,:), 1,nBeta);
h98 = real(h98 + reshape(sum(bsxfun(@times, bigmat_h98_1, coefmat_h98_1) +...
bsxfun(@times, bigmat_h98_2, coefmat_h98_2),1),nBeta,nBeta)' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*((conj(y(1,1)).*y(1,2))*xx_i(1,:)'*xx_i(1,:)+...
(conj(y(1,2)).*y(1,1))*xx_i(1,:)'*xx_i(1,:)))+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*((conj(y(end,1)).*y(end,2))*xx_i(end,:)'*xx_i(end,:)+...
(conj(y(end,2)).*y(end,1))*xx_i(end,:)'*xx_i(end,:))));
h24=h42'; h35=h53'; h65=h56'; h95=h59'; h36=h63';
h86=h68'; h27=h72'; h38=h83'; h39=h93'; h89=h98';
end
ze = zeros(nBeta,nBeta);
h1 = [h11,repmat(ze,1,8)];
h2 = [ze,h22,ze,-h24,ze,ze,-h27,ze,ze];
h3 = [ze,ze,h33,ze,-h35,-h36,ze,-h38,-h39];
h4 = [ze,-h42,ze,h44,repmat(ze,1,5)];
h5 = [ze,ze,-h53,ze,h55,h56,ze,ze,h59];
h6 = [ze,ze,-h63,ze,h65,h66,ze,h68,ze];
h7 = [ze,-h72,ze,ze,ze,ze,h77,ze,ze];
h8 = [ze,ze,-h83,ze,ze,h86,ze,h88,h89];
h9 = [ze,ze,-h93,ze,h95,ze,ze,h98,h99];
gr = [gr1;gr2;gr3;gr4;gr5;gr6;gr7;gr8;gr9]; h = [h1;h2;h3;h4;h5;h6;h7;h8;h9]; f = -f;
gr_index = (1:(dimen^2*nBeta)).*kron(chol_index(Phi_temp,:),ones(nBeta,1)');
gr_index = gr_index(find(gr_index~=0));
gr = gr(gr_index); h = h(gr_index,gr_index);
end
function [f,gr,h] = Beta_derive2(x, yobs_tmp, chol_index, Phi_temp, tau_temp_1,...
tau_temp_2, Beta_temp_1, Beta_temp_2, sigmasqalpha, nbasis, nseg)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Function used for optimization process for coefficients are the same
% across segments
%
% Input:
% 1) x - initial values for coefficient of basis functions need to
% be optimized
% 2) yobs_tmp - time series data within the segment
% 3) chol_index - index matrix
% 4) Phi_temp - which component changed
% 5) tau_temp_1 - smoothing parameters for the first segment
% 6) tau_temp_2 - smoothing parameters for the second segment
% 7) Beta_temp_1 - current coefficients for the first segment
% 8) Beta_temp_2 - current coefficients for the second segment
% 9) sigmasqalpha - smoothing parameters for the constant in real
% components
% 10) nbasis - number of basis function used
% 11) nseg - number of observation in the first segment
% Main Outputs:
% 1) f - log posterior probability based on input parameters
% 2) gr - gradients for optimization process
% 3) h - Hessian matrix for optimization process
%
% Required programs: lin_basis_func, Beta_derive1
yobs_tmp_1 = yobs_tmp(1:nseg,:);
yobs_tmp_2 = yobs_tmp(nseg+1:end,:);
[f1,grad1,hes1] = Beta_derive1(x, yobs_tmp_1, chol_index, Phi_temp, tau_temp_1, Beta_temp_1, sigmasqalpha, nbasis);
[f2,grad2,hes2] = Beta_derive1(x, yobs_tmp_2, chol_index, Phi_temp, tau_temp_2, Beta_temp_2, sigmasqalpha, nbasis);
f = f1 + f2;
gr = grad1 + grad2;
h = hes1 + hes2;
function[PI,nseg_prop,xi_prop,tau_prop,Beta_prop,Phi_prop]=...
birth(chol_index,ts,nexp_curr,nexp_prop,...
tau_curr_temp,xi_curr_temp,nseg_curr_temp,Beta_curr_temp,Phi_curr_temp,....
log_move_curr,log_move_prop)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Does the birth step in the paper
%
% Input:
% 1) chol_index - index matrix
% 2) ts - TxN matrix of time series data
% 3) nexp_curr - current number of segment
% 4) nexp_prop - proposed number of segment
% 5) tau_curr_temp - current smoothing parameters
% 6) xi_curr_temp - current partitions
% 7) nseg_curr_temp - current number of observations in each segment
% 8) Beta_curr_temp - current coefficients
% 9) Phi_curr_temp - which component changed
% 10) log_move_curr - probability: proposed to current
% 11) log_move_prop - probability: current to proposed
% Main Outputs:
% 1) A - acceptance probability
% 2) nseg_prop - proposed number of observations in each segment
% 3) xi_prop - proposed partitions
% 4) tau_prop - proposed smoothing parameters
% 5) Beta_prop - proposed coefficients
% 6) Phi_prop - proposed indicator variable
%
% Required programs: postBeta1, Beta_derive1, whittle_like
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global nobs dimen nbasis nBeta sigmasqalpha tmin tau_up_limit
Beta_prop = zeros(nBeta,dimen^2,nexp_prop);
tau_prop = ones(dimen^2,nexp_prop,1);
nseg_prop = zeros(nexp_prop,1);
xi_prop = zeros(nexp_prop,1);
Phi_prop = zeros(nexp_prop,1);
%***************************************
%Drawing segment to split
%***************************************
kk = find(nseg_curr_temp>2*tmin); %Number of segments available for splitting
nposs_seg = length(kk);
seg_cut = kk(unidrnd(nposs_seg)); %Drawing segment to split
nposs_cut = nseg_curr_temp(seg_cut)-2*tmin+1; %Drawing new birthed partition
%************************************************
% Proposing new parameters, Beta, Phi, tau, xi
%************************************************
for jj=1:nexp_curr
if jj<seg_cut %nothing updated or proposed here
xi_prop(jj) = xi_curr_temp(jj);
tau_prop(:,jj) = tau_curr_temp(:,jj);
nseg_prop(jj) = nseg_curr_temp(jj);
Beta_prop(:,:,jj) = Beta_curr_temp(:,:,jj);
Phi_prop(jj) = Phi_curr_temp(jj);
elseif jj==seg_cut %updating parameters in the selected paritions
index = unidrnd(nposs_cut);
if (seg_cut==1)
xi_prop(seg_cut)=index+tmin-1;
else
xi_prop(seg_cut)=xi_curr_temp(jj-1)-1+tmin+index;
end
xi_prop(seg_cut+1) = xi_curr_temp(jj);
%Determine which Cholesky components should change here
Phi_prop(seg_cut) = randsample(2:2^(dimen^2),1);
Phi_prop(seg_cut+1) = Phi_curr_temp(jj);
%Drawing new tausq
select = find(chol_index(Phi_prop(seg_cut),:)~=0);
select_inv = find(chol_index(Phi_prop(seg_cut),:)==0);
zz = rand(dimen^2,1)'.*chol_index(Phi_prop(seg_cut),:);
uu = zz./(1-zz);
uu(find(uu==0))= 1;
tau_prop(:,seg_cut)= tau_curr_temp(:,seg_cut).*uu';
tau_prop(:,seg_cut+1) = tau_curr_temp(:,seg_cut).*(1./uu)';
%Drawing new values for coefficient of basis function for new birthed segments.
nseg_prop(seg_cut) = index+tmin-1;
nseg_prop(seg_cut+1) = nseg_curr_temp(jj)-nseg_prop(seg_cut);
Phi_need = Phi_prop(seg_cut);
for k=jj:(jj+1)
if k==jj
[Beta_mean_1, Beta_var_1,yobs_tmp_1] = postBeta1(chol_index, Phi_need, ...
k, ts, tau_prop(:,k), Beta_curr_temp(:,:,jj), xi_prop);
Beta_prop(:,select,k) = reshape(mvnrnd(Beta_mean_1,...
0.5*(Beta_var_1+Beta_var_1')),nBeta,length(select));
Beta_prop(:,select_inv,k) = Beta_curr_temp(:,select_inv,jj);
else
[Beta_mean_2, Beta_var_2,yobs_tmp_2] = postBeta1(chol_index, Phi_need, ...
k, ts, tau_prop(:,k), Beta_curr_temp(:,:,jj), xi_prop);
Beta_prop(:,select,k) = reshape(mvnrnd(Beta_mean_2,...
0.5*(Beta_var_2+Beta_var_2')),nBeta,length(select));
Beta_prop(:,select_inv,k) = Beta_curr_temp(:,select_inv,jj);
end
end
else %nothing updated or proposed here
xi_prop(jj+1) = xi_curr_temp(jj);
tau_prop(:,jj+1) = tau_curr_temp(:,jj);
nseg_prop(jj+1) = nseg_curr_temp(jj);
Beta_prop(:,:,jj+1) = Beta_curr_temp(:,:,jj);
Phi_prop(jj+1) = Phi_curr_temp(jj);
end
end
%Calculating Jacobian
ja = tau_curr_temp(:,seg_cut)./(zz.*(1-zz))'; ja = ja(ja~=Inf);
log_jacobian = sum(log(2*ja));
%*************************************************************
%Calculations related to proposed values
%*************************************************************
%=======================================================================
%Evaluating the Likelihood, Proposal and Prior Densities at the Proposed values
%=======================================================================
log_Beta_prop = 0;
log_tau_prior_prop = 0;
log_Beta_prior_prop = 0;
loglike_prop = 0;
for jj=seg_cut:seg_cut+1
if jj==seg_cut
Beta_mean = Beta_mean_1;
Beta_var = Beta_var_1;
yobs_tmp = yobs_tmp_1;
else
Beta_mean = Beta_mean_2;
Beta_var = Beta_var_2;
yobs_tmp = yobs_tmp_2;
end
pb = reshape(Beta_prop(:,select,jj), numel(Beta_prop(:,select,jj)),1);
%Proposed density for coefficient of basis functions
log_Beta_prop = log_Beta_prop - 0.5*(pb-Beta_mean)'*matpower(0.5*(Beta_var+Beta_var'),-1)*(pb-Beta_mean);
%Prior density for coefficient of basis functions
prior_tau = reshape([[repmat(sigmasqalpha,1,dimen^2-dimen*(dimen-1)/2) tau_prop((dimen + dimen*(dimen-1)/2 + 1):end,jj)'];...
reshape(kron(tau_prop(:,jj),ones(nbasis,1)), nbasis, dimen^2)], nBeta,(dimen^2));
prior_tau = reshape(prior_tau(:,select),length(select)*nBeta,1);
log_Beta_prior_prop = log_Beta_prior_prop - 0.5*(pb)'*matpower(diag(prior_tau),-1)*(pb);
log_tau_prior_prop = log_tau_prior_prop-length(select)*log(tau_up_limit); % Prior Density of tausq
[log_prop_spec_dens] = whittle_like(yobs_tmp,Beta_prop(:,:,jj));
loglike_prop = loglike_prop + log_prop_spec_dens; %Loglikelihood at proposed values
end
log_seg_prop = -log(nposs_seg);%Proposal density for segment choice
log_cut_prop = -log(nposs_cut);%Proposal density for partition choice
log_Phi_prop = -log(2^(dimen^2)-1); %proposal density for component choice
log_prior_Phi_prop = -log(2^(dimen^2)); %prior density for component choice
%Evaluating prior density for cut points at proposed values
log_prior_cut_prop = 0;
for k=1:nexp_prop-1
if k==1
log_prior_cut_prop=-log(nobs-(nexp_prop-k+1)*tmin+1);
else
log_prior_cut_prop=log_prior_cut_prop-log(nobs-xi_prop(k-1)-(nexp_prop-k+1)*tmin+1);
end
end
%Calculating Log Proposal density at Proposed values
log_proposal_prop = log_Beta_prop + log_seg_prop + log_move_prop + log_cut_prop + log_Phi_prop;
%Calculating Log Prior density at Proposed values
log_prior_prop = log_Beta_prior_prop + log_tau_prior_prop + log_prior_cut_prop + log_prior_Phi_prop;
%Calculating Target density at Proposed values
log_target_prop = loglike_prop + log_prior_prop;
%*************************************************************
%Calculations related to current values
%*************************************************************
%==============================================================================
%Evaluating the Likelihood, Proposal and Prior Densities at the Current values
%==============================================================================
[Beta_mean, Beta_var, yobs_tmp] = postBeta1(chol_index, Phi_need, seg_cut, ts, tau_curr_temp(:,seg_cut),...
Beta_curr_temp(:,:,seg_cut), xi_curr_temp);
pb = reshape(Beta_curr_temp(:,select,seg_cut),numel(Beta_curr_temp(:,select,seg_cut)),1);
%Current density for coefficient of basis functions
log_Beta_curr = -0.5*(pb-Beta_mean)'*matpower(0.5*(Beta_var+Beta_var'),-1)*(pb-Beta_mean);
%Prior density for coefficient of basis functions at current values
prior_tau = reshape([[repmat(sigmasqalpha,1,dimen^2-dimen*(dimen-1)/2) tau_curr_temp((dimen + dimen*(dimen-1)/2 + 1):end,seg_cut)'];...
reshape(kron(tau_curr_temp(:,seg_cut),ones(nbasis,1)), nbasis, dimen^2)], nBeta,(dimen^2));
prior_tau = reshape(prior_tau(:,select),length(select)*nBeta,1);
log_Beta_prior_curr = -0.5*(pb)'*matpower(diag(prior_tau),-1)*(pb);
log_tau_prior_curr = -length(select)*log(tau_up_limit); %prior density for smoothing parameters
[log_curr_spec_dens] = whittle_like(yobs_tmp,Beta_curr_temp(:,:,seg_cut));
loglike_curr = log_curr_spec_dens; %Loglikelihood at current values
log_Phi_curr = -log(1); %proposal for component choice
%Calculating Log Proposal density at current values
log_proposal_curr = log_Beta_curr + log_move_curr + log_Phi_curr;
%Evaluating prior density for partition current values
log_prior_cut_curr = 0;
for k=1:nexp_curr-1
if k==1
log_prior_cut_curr = -log(nobs-(nexp_curr-k+1)*tmin+1);
else
log_prior_cut_curr = log_prior_cut_curr-log(nobs-xi_curr_temp(k-1)-(nexp_curr-k+1)*tmin+1);
end
end
log_prior_Phi_curr = -log(2^(dimen^2)); %prior density for component choice
%Calculating Priors at Current Values
log_prior_curr = log_Beta_prior_curr + log_tau_prior_curr + log_prior_cut_curr + log_prior_Phi_curr;
%Evalulating Target densities at current values
log_target_curr = loglike_curr + log_prior_curr;
%*************************************************************
%Calculations acceptance probability
%*************************************************************
PI = min(1,exp(log_target_prop - log_target_curr +...
log_proposal_curr - log_proposal_prop + log_jacobian));
end
function[chol_index]=chol_ind(dimen)
chol_index = zeros(2^(dimen^2), dimen^2 );
k=0;
for i=0:dimen^2
C = nchoosek(1:dimen^2,i);
dim = size(C);
if i==0
k=k+1;
chol_index(1,:) = 0;
else
for j=1:dim(1)
k=k+1;
chol_index(k,C(j,:)) = 1;
end
end
end
end
function [result] = conv_diag(nobs, nBeta, nseg,nexp_curr, Beta_curr, tausq_curr, dimen)
% conv_diag Calculate convergence diagnostics for beta and tau sq params
% Get max eigenvalue of beta and tausq matrices across time and cov
idx = cumsum(nseg);
tausq_diag = zeros(nobs,dimen^2);
Beta_diag = zeros(nobs,nBeta,dimen^2);
for i=1:nexp_curr
if i==1
for k=1:dimen^2
tausq_diag(1:idx(i),k) = repmat(tausq_curr(k,i),nseg(i),1);
for j=1:nBeta
Beta_diag(1:idx(i),j,k)=repmat(Beta_curr(j,k),nseg(i),1);
end
end
else
for k=1:dimen^2
tausq_diag((idx(i-1)+1):idx(i),k) = repmat(tausq_curr(k,i),nseg(i),1);
for j=1:nBeta
Beta_diag((idx(i-1)+1):idx(i),j,k)=repmat(Beta_curr(j,k),nseg(i),1);
end
end
end
end
%calculate eigenval of symmetric transform
result = zeros(1,dimen^2*(nBeta+1));
for k=1:dimen^2
result(k) = real(max(eig(tausq_diag(:,k)*tausq_diag(:,k)')));
end
k=1;
for i=1:dimen^2
for j=1:nBeta
result(k+dimen^2) = real(max(eig(Beta_diag(:,j,i)*Beta_diag(:,j,i)')));
k=k+1;
end
end
end
function[PI,nseg_prop,xi_prop,tau_prop,Beta_prop,Phi_prop]=...
death(chol_index,ts,nexp_curr,nexp_prop,...
tau_curr_temp,xi_curr_temp,nseg_curr_temp,Beta_curr_temp,Phi_curr_temp,log_move_curr,log_move_prop)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Does the death step in the paper
%
% Input:
% 1) chol_index - index matrix
% 2) ts - TxN matrix of time series data
% 3) nexp_curr - current number of segment
% 4) nexp_prop - proposed number of segment
% 5) tau_curr_temp - current smoothing parameters
% 6) xi_curr_temp - current partitions
% 7) nseg_curr_temp - current number of observations in each segment
% 8) Beta_curr_temp - current coefficients
% 9) Phi_curr_temp - which component changed
% 10) log_move_curr - probability: proposed to current
% 11) log_move_prop - probability: current to proposed
% Main Outputs:
% 1) A - acceptance probability
% 2) nseg_prop - proposed number of observations in each segment
% 3) xi_prop - proposed partitions
% 4) tau_prop - proposed smoothing parameters
% 5) Beta_prop - proposed coefficients
% 6) Phi_prop - proposed indicator variable
%
% Required programs: postBeta1, Beta_derive_1, whittle_like
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global nobs dimen nBeta nbasis sigmasqalpha tmin tau_up_limit
Beta_prop = zeros(nBeta,dimen^2,nexp_prop);
tau_prop = ones(dimen^2,nexp_prop,1);
nseg_prop = zeros(nexp_prop,1);
xi_prop = zeros(nexp_prop,1);
Phi_prop = zeros(nexp_prop,1);
%***************************************
%Draw a partition to delete
%***************************************
cut_del=unidrnd(nexp_curr-1);
j=0;
for k = 1:nexp_prop
j = j+1;
if k==cut_del
%*********************************************************
%Calculations related to proposed values
%*********************************************************
xi_prop(k) = xi_curr_temp(j+1);
tau_prop(:,k) = sqrt(tau_curr_temp(:,j).*tau_curr_temp(:,j+1)); %Combine two taus into one
nseg_prop(k) = nseg_curr_temp(j) + nseg_curr_temp(j+1); %Combine two segments into one
Phi_prop(k) = Phi_curr_temp(j+1);
%============================================================
%Evaluate the Likelihood at proposed values
%============================================================
need = sum(Beta_curr_temp(:,:,k)-Beta_curr_temp(:,:,k+1));
need = need./need;
need(isnan(need))=0;
aa = zeros(2^(dimen^2),1);
for i=1:2^(dimen^2)
aa(i)=sum(chol_index(i,:)==need);
end
Phi_need = find(aa==dimen^2);
select = find(chol_index(Phi_need,:)~=0);
select_inv = find(chol_index(Phi_need,:)==0);
%Compute mean and variances for coefficents of basis functions
[Beta_mean, Beta_var, yobs_tmp]= postBeta1(chol_index, Phi_need, k, ts, tau_prop(:,k),...
Beta_curr_temp(:,:,k), xi_prop);
Beta_prop(:,select,k) = reshape(mvnrnd(Beta_mean,0.5*(Beta_var+Beta_var')),nBeta,length(select));
Beta_prop(:,select_inv,k) = Beta_curr_temp(:,select_inv,k);
%Loglikelihood at proposed values
[loglike_prop]=whittle_like(yobs_tmp,Beta_prop(:,:,k));
%========================================================================
%Evaluate the Proposal Densities at the Proposed values for tau, Phi, and Beta
%========================================================================
pb = reshape(Beta_prop(:,select,k), numel(Beta_prop(:,select,k)),1);
%Proposed density for coefficient of basis functions
log_Beta_prop = - 0.5*(pb-Beta_mean)'*matpower(0.5*(Beta_var+Beta_var'),-1)*(pb-Beta_mean);
log_seg_prop = -log(nexp_curr-1); %Proposal for segment choice
log_Phi_prop = -log(1); %proposal for component choice
%Calcualte Jacobian
log_jacobian = -sum(log(2*(sqrt(tau_curr_temp(select,j)) + sqrt(tau_curr_temp(select,j+1))).^2));
%log proposal probabililty
log_proposal_prop = log_Beta_prop + log_seg_prop + log_move_prop + log_Phi_prop;
%===================================================================
% Evaluate the PRIOR Densities at the Proposed values for tau, Phi, and Beta
%===================================================================
prior_tau = reshape([[repmat(sigmasqalpha,1,dimen^2-dimen*(dimen-1)/2) tau_prop((dimen + dimen*(dimen-1)/2 + 1):end,k)'];...
reshape(kron(tau_prop(:,k),ones(nbasis,1)), nbasis,...
dimen^2)], nBeta,(dimen^2));
prior_tau = reshape(prior_tau(:,select),length(select)*nBeta,1);
%Prior density for coefficient of basis functions
log_Beta_prior_prop = -0.5*(pb)'*matpower(diag(prior_tau),-1)*(pb);
%Prior Density of tausq
log_tau_prior_prop = -length(select)*log(tau_up_limit);
%Prior Density of Phi
log_Phi_prior_prop = -log(2^(dimen^2));
log_prior_prop = log_tau_prior_prop + log_Beta_prior_prop + log_Phi_prior_prop;
%*************************************************************
%Calculations related to current values
%*************************************************************
%===========================================================================
%Evaluate the Likelihood, Proposal and Prior Densities at the Current values
%===========================================================================
log_Beta_curr = 0;
log_tau_prior_curr = 0;
log_Beta_prior_curr = 0;
loglike_curr=0;
for jj=j:j+1
[Beta_mean, Beta_var, yobs_tmp]= postBeta1(chol_index, Phi_need, jj, ts, tau_curr_temp(:,jj),...
Beta_curr_temp(:,:,jj), xi_curr_temp);
pb = reshape(Beta_curr_temp(:,select,jj), numel(Beta_curr_temp(:,select,jj)),1);
%Current density for coefficient of basis functions
log_Beta_curr = log_Beta_curr -0.5*(pb-Beta_mean)'*matpower(0.5*(Beta_var+Beta_var'),-1)*...
(pb-Beta_mean);
prior_tau = reshape([[repmat(sigmasqalpha,1,dimen^2-dimen*(dimen-1)/2) tau_curr_temp((dimen + dimen*(dimen-1)/2 + 1):end,jj)'];...
reshape(kron(tau_curr_temp(:,jj),ones(nbasis,1)), nbasis,...
dimen^2)], nBeta,(dimen^2));
prior_tau = reshape(prior_tau(:,select),length(select)*nBeta,1);
%Prior density for coefficient of basis functions at current values
log_Beta_prior_curr = log_Beta_prior_curr - 0.5*(pb)'*matpower(diag(prior_tau),-1)*(pb);
[log_curr_spec_dens] = whittle_like(yobs_tmp,Beta_curr_temp(:,:,jj));
%Loglikelihood at proposed values
loglike_curr = loglike_curr + log_curr_spec_dens;
%prior density for smoothing parameters
log_tau_prior_curr = log_tau_prior_curr - length(select)*log(tau_up_limit);
end
log_Phi_curr = -log(2^(dimen^2)-1); %proposal for component choice
log_Phi_prior_curr = -log(2^(dimen^2)); %prior for component choice
%Calculate Log proposal density at current values
log_proposal_curr = log_move_curr + log_Beta_curr + log_Phi_curr;
%Calculate Priors at Current Vlaues
log_prior_curr = log_Beta_prior_curr + log_tau_prior_curr + log_Phi_prior_curr;
j=j+1;
else
xi_prop(k) = xi_curr_temp(j);
tau_prop(:,k) = tau_curr_temp(:,j);
nseg_prop(k) = nseg_curr_temp(j);
Beta_prop(:,:,k) = Beta_curr_temp(:,:,j);
Phi_prop(k) = Phi_curr_temp(j);
end
end
%=================================================
%Evaluate Target density at proposed values
%=================================================
log_prior_cut_prop=0;
for k=1:nexp_prop-1
if k==1
log_prior_cut_prop=-log(nobs-(nexp_prop-k+1)*tmin+1);
else
log_prior_cut_prop=log_prior_cut_prop-log(nobs-xi_prop(k-1)-(nexp_prop-k+1)*tmin+1);
end
end
log_target_prop = loglike_prop + log_prior_prop + log_prior_cut_prop;
%==================================================
%Evaluate Target density at current values
%==================================================
log_prior_cut_curr=0;
for k=1:nexp_curr-1
if k==1
log_prior_cut_curr=-log(nobs-(nexp_curr-k+1)*tmin+1);
else
log_prior_cut_curr=log_prior_cut_curr-log(nobs-xi_curr_temp(k-1)-(nexp_curr-k+1)*tmin+1);
end
end
log_target_curr = loglike_curr + log_prior_curr + log_prior_cut_curr;
%**********************************************************
%Calculations acceptance probability
%**********************************************************
PI = min(1,exp(log_target_prop - log_target_curr + ...
log_proposal_curr - log_proposal_prop + log_jacobian));
function [gr] = Gradient1(yobs_tmp, chol_index, Phi_temp, tau_temp,...
Beta_temp, sigmasqalpha, nbasis)
global dimen
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Calculate log gradients for coefficients selected to be different
%
% Input:
% 1) x - initial values for coefficient of basis functions need to
% be optimized
% 2) yobs_tmp - time series data within the segment
% 3) chol_index - index matrix
% 4) Phi_temp - which component changed
% 5) tau_temp - smoothing parameters
% 6) Beta_temp - current coefficients
% 7) sigmasqalpha - smoothing parameters for the constant in real
% components
% 8) nbasis - number of basis functions used
% Main Outputs:
% 2) gr - gradients for optimization process
%
% Required programs: lin_basis_func
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%initilize Beta_1 and Beta_2: Beta_2 is for imaginary components
nBeta = nbasis + 1;
Beta_1(:,:) = Beta_temp(:,1:(dimen + dimen*(dimen-1)/2));
Beta_2(:,:) = Beta_temp(1:nBeta,(dimen + dimen*(dimen-1)/2 + 1): end);
dim = size(yobs_tmp); n = dim(1);
nfreq = floor(n/2); tt = (0:nfreq)/(2*nfreq);
yy = fft(yobs_tmp)/sqrt(n); y = yy(1:(nfreq+1),:); nf = length(y);
[xx_r, xx_i]=lin_basis_func(tt);
%theta's
theta = zeros(dimen*(dimen-1)/2,nf);
for i=1:dimen*(dimen-1)/2
theta_real = xx_r * Beta_1(:,i+dimen);
theta_imag = xx_i * Beta_2(:,i);
theta(i,:) = theta_real + sqrt(-1)*theta_imag;
end
%delta's
delta_sq = zeros(dimen,nf);
for i=1:dimen
delta_sq(i,:) = exp(xx_r * Beta_1(:,i));
end
if dimen==2 %Bivariate Time Series
gr1 = zeros(nBeta,1); gr2 = zeros(nBeta,1); gr3 = zeros(nBeta,1); gr4 = zeros(nBeta,1);
gr1(1) = Beta_1(1,1)/sigmasqalpha; gr1(2:nBeta,1) = Beta_1(2:nBeta,1)/tau_temp(1);
gr2(1) = Beta_1(1,2)/sigmasqalpha; gr2(2:nBeta,1) = Beta_1(2:nBeta,2)/tau_temp(2);
gr3(1) = Beta_1(1,3)/sigmasqalpha; gr3(2:nBeta,1) = Beta_1(2:nBeta,3)/tau_temp(3);
gr4(1:nBeta,1) = Beta_2(1:nBeta,1)/tau_temp(4);
if (mod(n,2)==1)
%%%%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%%%%
rk = -y(2:end,1).*conj(y(2:end,2)) - y(2:end,2).*conj(y(2:end,1));
ik = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,2)) + y(2:end,2).*conj(y(2:end,1)));
ck = 2*abs(y(2:end,1)).^2;
gr1 = gr1 + xx_r(2:end,:)'*(1-abs(y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:end,:)'*(1 - abs(y(2:end,2)-theta(2:end).'.*y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1).'.*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))));
temp_mat_31 = bsxfun(@times, xx_r(2:end,:),rk);
temp_mat_32 = bsxfun(@times, ck, bsxfun(@times, xx_r(2:end,:),xx_r(2:end,:)*Beta_1(:,3)));
gr3 = gr3 + sum( bsxfun(@times, (temp_mat_31+temp_mat_32), exp(-xx_r(2:end,:)*Beta_1(:,2)) ))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)');
temp_mat_41 = bsxfun(@times, ik, xx_i(2:end,:));
temp_mat_42 = bsxfun(@times, ck, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,1)));
gr4 = gr4 + sum( bsxfun(@times, (temp_mat_41 + temp_mat_42), exp(-xx_r(2:end,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(sqrt(-1)*(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)');
else
%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%
rk = -y(2:nfreq,1).*conj(y(2:nfreq,2)) - y(2:nfreq,2).*conj(y(2:nfreq,1));
ik = sqrt(-1)*(-y(2:nfreq,1).*conj(y(2:nfreq,2)) + y(2:nfreq,2).*conj(y(2:nfreq,1)));
ck = 2*abs(y(2:nfreq,1)).^2;
gr1 = gr1 + xx_r(2:nfreq,:)'*(1-abs(y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1)))) +...
0.5*(xx_r(end,:)'*(1-abs(y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:nfreq,:)'*(1 - abs(y(2:nfreq,2)-theta(2:nfreq).'.*y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1).'.*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2)))) + ...
0.5*(xx_r(end,:)'*(1 - abs(y(end,2)-theta(end).'.*y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,2))));
temp_mat_31 = bsxfun(@times,rk, xx_r(2:nfreq,:));
temp_mat_32 = bsxfun(@times,ck,bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,3)));
gr3 = gr3 + sum( bsxfun(@times, (temp_mat_31 + temp_mat_32), exp(-xx_r(2:nfreq,:)*Beta_1(:,2)) ))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,3))*xx_r(1,:)') +...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(-y(end,1).*conj(y(end,2)) - y(end,2).*conj(y(end,1)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,3))*xx_r(end,:)');
temp_mat_41 = bsxfun(@times, ik, xx_i(2:nfreq,:));
temp_mat_42 = bsxfun(@times, ck, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,1)));
gr4 = gr4 + sum( bsxfun(@times, (temp_mat_41 + temp_mat_42), exp(-xx_r(2:nfreq,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(sqrt(-1)*(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)') +...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(sqrt(-1)*(-y(end,1).*conj(y(end,2)) + y(end,2).*conj(y(end,1))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,1))*xx_i(end,:)');
end
gr = [gr1;gr2;gr3;gr4];
gr_index = (1:(4*nBeta)).*[kron(chol_index(Phi_temp,1:3),ones(nBeta,1)'), kron(chol_index(Phi_temp,4),ones(nBeta,1)')];
gr_index = gr_index(find(gr_index~=0));
gr = gr(gr_index);
elseif dimen==3 %trivariate time series
gr1 = zeros(nBeta,1); gr2 = zeros(nBeta,1); gr3 = zeros(nBeta,1); gr4 = zeros(nBeta,1);
gr5 = zeros(nBeta,1); gr6 = zeros(nBeta,1); gr7 = zeros(nBeta,1); gr8 = zeros(nBeta,1);
gr9 = zeros(nBeta,1);
gr1(1) = Beta_1(1,1)/sigmasqalpha; gr1(2:nBeta) = Beta_1(2:nBeta,1)/tau_temp(1);
gr2(1) = Beta_1(1,2)/sigmasqalpha; gr2(2:nBeta) = Beta_1(2:nBeta,2)/tau_temp(2);
gr3(1) = Beta_1(1,3)/sigmasqalpha; gr3(2:nBeta) = Beta_1(2:nBeta,3)/tau_temp(3);
gr4(1) = Beta_1(1,4)/sigmasqalpha; gr4(2:nBeta) = Beta_1(2:nBeta,4)/tau_temp(4);
gr5(1) = Beta_1(1,5)/sigmasqalpha; gr5(2:nBeta) = Beta_1(2:nBeta,5)/tau_temp(5);
gr6(1) = Beta_1(1,6)/sigmasqalpha; gr6(2:nBeta) = Beta_1(2:nBeta,6)/tau_temp(6);
gr7(1:nBeta) = Beta_2(1:nBeta,1)/tau_temp(7);
gr8(1:nBeta) = Beta_2(1:nBeta,2)/tau_temp(8);
gr9(1:nBeta) = Beta_2(1:nBeta,3)/tau_temp(9);
if (mod(n,2)==1)
%%%%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%%%%
rk4 = -y(2:end,1).*conj(y(2:end,2)) - y(2:end,2).*conj(y(2:end,1));
ck4 = 2*abs(y(2:end,1)).^2;
rk5 = -y(2:end,1).*conj(y(2:end,3)) - y(2:end,3).*conj(y(2:end,1));
ck5 = 2*abs(y(2:end,1)).^2;
b = theta(3,:);
dk5 = y(2:end,2).*conj(y(2:end,1)).*(b(2:end).') + conj(y(2:end,2)).*y(2:end,1).*conj(b(2:end).');
rk6 = -y(2:end,2).*conj(y(2:end,3)) - y(2:end,3).*conj(y(2:end,2));
ck6 = 2*abs(y(2:end,2)).^2;
a = theta(2,:);
dk6 = y(2:end,1).*conj(y(2:end,2)).*(a(2:end).') + conj(y(2:end,1)).*y(2:end,2).*conj(a(2:end).');
ik7 = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,2)) + y(2:end,2).*conj(y(2:end,1)));
ck7 = 2*abs(y(2:end,1)).^2;
ik8 = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,3)) + y(2:end,3).*conj(y(2:end,1)));
ck8 = 2*abs(y(2:end,1)).^2;
dk8 = sqrt(-1)*(-y(2:end,2).*conj(y(2:end,1)).*(b(2:end).') + conj(y(2:end,2).*conj(y(2:end,1)).*(b(2:end).'))) ;
ik9 = sqrt(-1)*(-y(2:end,2).*conj(y(2:end,3)) + y(2:end,3).*conj(y(2:end,2)));
ck9 = 2*abs(y(2:end,2)).^2;
dk9 = sqrt(-1)*(-y(2:end,1).*conj(y(2:end,2)).*(a(2:end).') + conj(y(2:end,1).*conj(y(2:end,2)).*(a(2:end).'))) ;
gr1 = gr1 + xx_r(2:end,:)'*(1-abs(y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:end,:)'*(1 - abs(y(2:end,2)-theta(1,2:end).'.*y(2:end,1)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1,1).*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2))));
gr3 = gr3 + xx_r(2:end,:)'*(1 - abs(y(2:end,3) - theta(2,2:end).'.*y(2:end,1) - theta(3,2:end).'.*y(2:end,2)).^2.*exp(-xx_r(2:end,:)*Beta_1(:,3)))+...
0.5*(xx_r(1,:)'*(1 - abs(y(1,3) - theta(2,1).*y(1,1) - theta(3,1).*y(1,2))^2.*exp(-xx_r(1,:)*Beta_1(:,3))));
temp_mat_41 = bsxfun(@times, xx_r(2:end,:),rk4);
temp_mat_42 = bsxfun(@times, ck4, bsxfun(@times, xx_r(2:end,:),xx_r(2:end,:)*Beta_1(:,4)));
gr4 = gr4 + sum(bsxfun(@times, (temp_mat_41+temp_mat_42), exp(-xx_r(2:end,:)*Beta_1(:,2)) ))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,4))*xx_r(1,:)');
temp_mat_51 = bsxfun(@times, xx_r(2:end,:),rk5);
temp_mat_52 = bsxfun(@times, ck5, bsxfun(@times, xx_r(2:end,:),xx_r(2:end,:)*Beta_1(:,5)));
temp_mat_53 = bsxfun(@times, xx_r(2:end,:),dk5);
gr5 = gr5 + sum(bsxfun(@times, (temp_mat_51 + temp_mat_52 + temp_mat_53), exp(-xx_r(2:end,:)*Beta_1(:,3)) ))'+...
0.5* ( exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,3)) - y(1,3).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,5))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,2).*conj(y(1,1)).*(b(1).') + conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_r(1,:)');
temp_mat_61 = bsxfun(@times, xx_r(2:end,:),rk6);
temp_mat_62 = bsxfun(@times, ck6, bsxfun(@times, xx_r(2:end,:),xx_r(2:end,:)*Beta_1(:,6)));
temp_mat_63 = bsxfun(@times, xx_r(2:end,:),dk6);
gr6 = gr6 + sum(bsxfun(@times, (temp_mat_61 + temp_mat_62 + temp_mat_63), exp(-xx_r(2:end,:)*Beta_1(:,3)) ))'+...
0.5* (exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,2).*conj(y(1,3)) - y(1,3).*conj(y(1,2)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_r(1,:)*Beta_1(:,6))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_r(1,:)');
temp_mat_71 = bsxfun(@times, ik7, xx_i(2:end,:));
temp_mat_72 = bsxfun(@times, ck7, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,1)));
gr7 = gr7 + sum(bsxfun(@times, (temp_mat_71 + temp_mat_72), exp(-xx_r(2:end,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(imag(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)');
temp_mat_81 = bsxfun(@times, ik8, xx_i(2:end,:));
temp_mat_82 = bsxfun(@times, ck8, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,2)));
temp_mat_83 = bsxfun(@times, xx_i(2:end,:),dk8);
gr8 = gr8 + sum(bsxfun(@times, (temp_mat_81 + temp_mat_82 + temp_mat_83), exp(-xx_r(2:end,:)*Beta_1(:,3))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,1).*conj(y(1,3)) + y(1,3).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,2))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(b(1).') + conj(y(1,1).*conj(y(1,2)).*(b(1).')))*xx_i(1,:)');
temp_mat_91 = bsxfun(@times, ik9, xx_i(2:end,:));
temp_mat_92 = bsxfun(@times, ck9, bsxfun(@times,xx_i(2:end,:),xx_i(2:end,:)*Beta_2(:,3)));
temp_mat_93 = bsxfun(@times, xx_i(2:end,:),dk9);
gr9 = gr9 + sum(bsxfun(@times, (temp_mat_91 + temp_mat_92 + temp_mat_93), exp(-xx_r(2:end,:)*Beta_1(:,3))))' + ...
0.5 * (exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,2).*conj(y(1,3)) + y(1,3).*conj(y(1,2))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_i(1,:)*Beta_2(:,3))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_i(1,:)');
else
%%%%%%%%%%%%%%%%%%%%%%%%
%gradient
%%%%%%%%%%%%%%%%%%%%%%%%
rk4 = -y(2:nfreq,1).*conj(y(2:nfreq,2)) - y(2:nfreq,2).*conj(y(2:nfreq,1));
ck4 = 2*abs(y(2:nfreq,1)).^2;
rk5 = -y(2:nfreq,1).*conj(y(2:nfreq,3)) - y(2:nfreq,3).*conj(y(2:nfreq,1));
ck5 = 2*abs(y(2:nfreq,1)).^2;
b = theta(3,:);
dk5 = y(2:nfreq,2).*conj(y(2:nfreq,1)).*(b(2:nfreq).') + conj(y(2:nfreq,2)).*y(2:nfreq,1).*conj(b(2:nfreq).');
rk6 = -y(2:nfreq,2).*conj(y(2:nfreq,3)) - y(2:nfreq,3).*conj(y(2:nfreq,2));
ck6 = 2*abs(y(2:nfreq,2)).^2;
a = theta(2,:);
dk6 = y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).') + conj(y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).'));
ik7 = sqrt(-1)*(-y(2:nfreq,1).*conj(y(2:nfreq,2)) + y(2:nfreq,2).*conj(y(2:nfreq,1)));
ck7 = 2*abs(y(2:nfreq,1)).^2;
ik8 = sqrt(-1)*(-y(2:nfreq,1).*conj(y(2:nfreq,3)) + y(2:nfreq,3).*conj(y(2:nfreq,1)));
ck8 = 2*abs(y(2:nfreq,1)).^2;
dk8 = sqrt(-1)*(-y(2:nfreq,2).*conj(y(2:nfreq,1)).*(b(2:nfreq).') + conj(y(2:nfreq,2).*conj(y(2:nfreq,1)).*(b(2:nfreq).')));
ik9 = sqrt(-1)*(-y(2:nfreq,2).*conj(y(2:nfreq,3)) + y(2:nfreq,3).*conj(y(2:nfreq,2)));
ck9 = 2*abs(y(2:nfreq,2)).^2;
dk9 = sqrt(-1)*(-y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).') + conj(y(2:nfreq,1).*conj(y(2:nfreq,2)).*(a(2:nfreq).')));
gr1 = gr1 + xx_r(2:nfreq,:)'*(1-abs(y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,1))) + ...
0.5*(xx_r(1,:)'*(1-abs(y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,1))))+...
0.5*(xx_r(end,:)'*(1-abs(y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,1))));
gr2 = gr2 + xx_r(2:nfreq,:)'*(1 - abs(y(2:nfreq,2)-theta(1,2:nfreq).'.*y(2:nfreq,1)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))) + ...
0.5*(xx_r(1,:)'*(1 - abs(y(1,2)-theta(1,1).*y(1,1)).^2.*exp(-xx_r(1,:)*Beta_1(:,2)))) +...
0.5*(xx_r(end,:)'*(1 - abs(y(end,2)-theta(1,end).*y(end,1)).^2.*exp(-xx_r(end,:)*Beta_1(:,2))));
gr3 = gr3 + xx_r(2:nfreq,:)'*(1 - abs(y(2:nfreq,3) - theta(2,2:nfreq).'.*y(2:nfreq,1) - theta(3,2:nfreq).'.*y(2:nfreq,2)).^2.*exp(-xx_r(2:nfreq,:)*Beta_1(:,3)))+...
0.5*(xx_r(1,:)'*(1 - abs(y(1,3) - theta(2,1).*y(1,1) - theta(3,1).*y(1,2))^2.*exp(-xx_r(1,:)*Beta_1(:,3))))+...
0.5*(xx_r(end,:)'*(1 - abs(y(end,3) - theta(2,end).*y(end,1) - theta(3,end).*y(end,2))^2.*exp(-xx_r(end,:)*Beta_1(:,3))));
temp_mat_41 = bsxfun(@times, xx_r(2:nfreq,:),rk4);
temp_mat_42 = bsxfun(@times, ck4, bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,4)));
gr4 = gr4 + sum(bsxfun(@times, (temp_mat_41+temp_mat_42), exp(-xx_r(2:nfreq,:)*Beta_1(:,2)) ))' +...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(-y(1,1).*conj(y(1,2)) - y(1,2).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,4))*xx_r(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(-y(end,1).*conj(y(end,2)) - y(end,2).*conj(y(end,1)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,4))*xx_r(end,:)');
temp_mat_51 = bsxfun(@times, xx_r(2:nfreq,:),rk5);
temp_mat_52 = bsxfun(@times, ck5, bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,5)));
temp_mat_53 = bsxfun(@times, xx_r(2:nfreq,:),dk5);
gr5 = gr5 + sum( bsxfun(@times, (temp_mat_51 + temp_mat_52 + temp_mat_53), exp(-xx_r(2:nfreq,:)*Beta_1(:,3)) ))'+...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,3)) - y(1,3).*conj(y(1,1)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_r(1,:)*Beta_1(:,5))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,2).*conj(y(1,1)).*(b(1).') + conj(y(1,2).*conj(y(1,1)).*(b(1).')))*xx_r(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,1).*conj(y(end,3)) - y(end,3).*conj(y(end,1)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,1)).^2*(xx_r(end,:)*Beta_1(:,5))*xx_r(end,:)'+...
exp(-xx_r(end,:)*Beta_1(:,3))*(y(end,2).*conj(y(end,1)).*(b(end).') + conj(y(end,2).*conj(y(end,1)).*(b(end).')))*xx_r(end,:)');
temp_mat_61 = bsxfun(@times, xx_r(2:nfreq,:),rk6);
temp_mat_62 = bsxfun(@times, ck6, bsxfun(@times, xx_r(2:nfreq,:),xx_r(2:nfreq,:)*Beta_1(:,6)));
temp_mat_63 = bsxfun(@times, xx_r(2:nfreq,:),dk6);
gr6 = gr6 + sum(bsxfun(@times, (temp_mat_61 + temp_mat_62 + temp_mat_63), exp(-xx_r(2:nfreq,:)*Beta_1(:,3)) ))'+...
0.5*(exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,2).*conj(y(1,3)) - y(1,3).*conj(y(1,2)))*xx_r(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_r(1,:)*Beta_1(:,6))*xx_r(1,:)'+...
exp(-xx_r(1,:)*Beta_1(:,3))*(y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_r(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,2).*conj(y(end,3)) - y(end,3).*conj(y(end,2)))*xx_r(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,2)).^2*(xx_r(end,:)*Beta_1(:,6))*xx_r(end,:)'+...
exp(-xx_r(end,:)*Beta_1(:,3))*(y(end,1).*conj(y(end,2)).*(a(end).') + conj(y(end,1).*conj(y(end,2)).*(a(end).')))*xx_r(end,:)');
temp_mat_71 = bsxfun(@times, ik7, xx_i(2:nfreq,:));
temp_mat_72 = bsxfun(@times, ck7, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,1)));
gr7 = gr7 + sum(bsxfun(@times, (temp_mat_71 + temp_mat_72), exp(-xx_r(2:nfreq,:)*Beta_1(:,2))))' + ...
0.5*(exp(-xx_r(1,:)*Beta_1(:,2))*(imag(-y(1,1).*conj(y(1,2)) + y(1,2).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,2))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,1))*xx_i(1,:)')+...
0.5*(exp(-xx_r(end,:)*Beta_1(:,2))*(imag(-y(end,1).*conj(y(end,2)) + y(end,2).*conj(y(end,1))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,2))*2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,1))*xx_i(end,:)');
temp_mat_81 = bsxfun(@times, ik8, xx_i(2:nfreq,:));
temp_mat_82 = bsxfun(@times, ck8, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,2)));
temp_mat_83 = bsxfun(@times, xx_i(2:nfreq,:),dk8);
gr8 = gr8 + sum(bsxfun(@times, (temp_mat_81 + temp_mat_82 + temp_mat_83), exp(-xx_r(2:nfreq,:)*Beta_1(:,3))))' + ...
0.5 * (exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,1).*conj(y(1,3)) + y(1,3).*conj(y(1,1))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,1)).^2*(xx_i(1,:)*Beta_2(:,2))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(b(1).') + conj(y(1,1).*conj(y(1,2)).*(b(1).')))*xx_i(1,:)')+...
0.5 * (exp(-xx_r(end,:)*Beta_1(:,3))*(imag(-y(end,1).*conj(y(end,3)) + y(end,3).*conj(y(end,1))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,1)).^2*(xx_i(end,:)*Beta_2(:,2))*xx_i(end,:)'+...
sqrt(-1)*exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,1).*conj(y(end,2)).*(b(end).') + conj(y(end,1).*conj(y(end,2)).*(b(end).')))*xx_i(end,:)');
temp_mat_91 = bsxfun(@times, ik9, xx_i(2:nfreq,:));
temp_mat_92 = bsxfun(@times, ck9, bsxfun(@times,xx_i(2:nfreq,:),xx_i(2:nfreq,:)*Beta_2(:,3)));
temp_mat_93 = bsxfun(@times, xx_i(2:nfreq,:),dk9);
gr9 = gr9 + sum(bsxfun(@times, (temp_mat_91 + temp_mat_92 + temp_mat_93), exp(-xx_r(2:nfreq,:)*Beta_1(:,3))))' + ...
0.5 * (exp(-xx_r(1,:)*Beta_1(:,3))*(imag(-y(1,2).*conj(y(1,3)) + y(1,3).*conj(y(1,2))))*xx_i(1,:)' +...
exp(-xx_r(1,:)*Beta_1(:,3))*2*abs(y(1,2)).^2*(xx_i(1,:)*Beta_2(:,3))*xx_i(1,:)'+...
sqrt(-1)*exp(-xx_r(1,:)*Beta_1(:,3))*(-y(1,1).*conj(y(1,2)).*(a(1).') + conj(y(1,1).*conj(y(1,2)).*(a(1).')))*xx_i(1,:)')+...
0.5 * (exp(-xx_r(end,:)*Beta_1(:,3))*(imag(-y(end,2).*conj(y(end,3)) + y(end,3).*conj(y(end,2))))*xx_i(end,:)' +...
exp(-xx_r(end,:)*Beta_1(:,3))*2*abs(y(end,2)).^2*(xx_i(end,:)*Beta_2(:,3))*xx_i(end,:)'+...
sqrt(-1)*exp(-xx_r(end,:)*Beta_1(:,3))*(-y(end,1).*conj(y(end,2)).*(a(end).') + conj(y(end,1).*conj(y(end,2)).*(a(end).')))*xx_i(end,:)');
end
gr = [gr1;gr2;gr3;gr4;gr5;gr6;gr7;gr8;gr9];
gr_index = (1:(dimen^2*nBeta)).*kron(chol_index(Phi_temp,:),ones(nBeta,1)');
gr_index = gr_index(find(gr_index~=0));
gr = gr(gr_index);
end
gr=-gr;
function [gr] = Gradient2(yobs_tmp, chol_index, Phi_temp, tau_temp_1,...
tau_temp_2, Beta_temp_1, Beta_temp_2, sigmasqalpha, nbasis, nseg)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Calculate log gradients for coefficients selected to be then same
%
% Input:
% 1) x - initial values for coefficient of basis functions need to
% be optimized
% 2) yobs_tmp - time series data within the segment
% 3) chol_index - index matrix
% 4) Phi_temp - which component changed
% 5) tau_temp_1 - smoothing parameters for the first segment
% 6) tau_temp_2 - smoothing parameters for the second segment
% 7) Beta_temp_1 - current coefficients for the first segment
% 8) Beta_temp_2 - current coefficients for the second segment
% 9) sigmasqalpha - smoothing parameters for the constant in real
% components
% 10) nbasis - number of basis functions used
% 11) nseg - number of observations in the first segment
% Main Outputs:
% 2) gr - gradients for optimization process
%
% Required programs: lin_basis_func, Beta_derive1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
yobs_tmp_1 = yobs_tmp(1:nseg,:);
yobs_tmp_2 = yobs_tmp(nseg+1:end,:);
[grad1] = Gradient1(yobs_tmp_1, chol_index, Phi_temp, tau_temp_1, Beta_temp_1, sigmasqalpha, nbasis);
[grad2] = Gradient1(yobs_tmp_2, chol_index, Phi_temp, tau_temp_2, Beta_temp_2, sigmasqalpha, nbasis);
gr = grad1 + grad2;
function [Beta_out, m_out, m, yobs_tmp]=Hamilt1(chol_index, Phi_temp,...
j, yobs, tau_temp, Beta_temp, xi_temp)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Does HMC updates for the coefficents that are different
%
% Input:
% 1) chol_index - index matrix
% 2) Phi_temp - indicate variable that determine which coefficient
% should be different
% 3) j - one of two segments
% 4) yobs - time series observations
% 5) tau_temp - current smoothing parameters
% 6) Beta_temp - current coefficients
% 7) xi__temp - current partitions
% Main Outputs:
% 1) Beta_out - vector of coefficients
% 2) m_out - updated momentum variables
% 3) m - initial momentum variables
% 4) yobs_tmp - time series observations in selected segment
%
% Required programs: Gradient1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global nbasis sigmasqalpha dimen nBeta M ee
%pick right portion of the data
if j>1
yobs_tmp = yobs((xi_temp(j-1)+1):xi_temp(j),:);
else
yobs_tmp = yobs(1:xi_temp(j),:);
end
select = chol_index(Phi_temp,:).*(1:dimen^2);
select = select(select~=0);
ll = nBeta*length(select);
[gr]=Gradient1(yobs_tmp, chol_index, Phi_temp, tau_temp,...
Beta_temp, sigmasqalpha, nbasis);
Beta_old = reshape(Beta_temp(:,select),ll,1);
Beta_out = Beta_old;
% generate momentum variable
m = mvnrnd(zeros(ll,1),M*eye(ll))';
% determine leap number and step
stepsize = unifrnd(0,2*ee);
leap = randsample(1:2*ceil(1/ee),1);
%leap = randsample(1:(1/stepsize),1);
m_out = m + 0.5*gr*stepsize;
for i=1:leap
Beta_out = Beta_out + stepsize*(1/M)*eye(ll)*m_out;
Beta_temp(:,select) = reshape(Beta_out,nBeta,length(select));
if i==leap
[gr] = Gradient1(yobs_tmp, chol_index, Phi_temp, tau_temp,...
Beta_temp, sigmasqalpha, nbasis);
m_out = m_out + 0.5*gr*stepsize;
else
[gr] = Gradient1(yobs_tmp, chol_index, Phi_temp, tau_temp,...
Beta_temp, sigmasqalpha, nbasis);
m_out = m_out + 1*gr*stepsize;
end
end
m_out = -m_out;
function[Beta_out, m_out, m, yobs_tmp] = Hamilt2(chol_index, Phi_temp, j, yobs,...
tau_temp_1, tau_temp_2, Beta_temp_1, Beta_temp_2, xi_temp, nseg)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Does HMC updates for the coefficents that are the same
%
% Input:
% 1) chol_index - index matrix
% 2) Phi_temp - indicate variable that determine which coefficient
% should be different
% 3) j - the first segment
% 4) yobs - time series observations
% 5) tau_temp_1 - current smoothing parameters for the first segment
% 6) tau_temp_2 - current smoothing parameters for the second
% segment
% 7) Beta_temp_1 - current coefficients for the first segment
% 8) Beta_temp_2 - current coefficients for the second segment
% 9) xi__temp - current partitions
% 10) nseg - number of observation in the first segment
% Main Outputs:
% 1) Beta_out - vector of coefficients
% 2) m_out - updated momentum variables
% 3) m - initial momentum variables
% 4) yobs_tmp - time series observations in selected segment
%
% Required programs: Gradient2
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global dimen nbasis sigmasqalpha nBeta M ee
%pick right portion of the data
if j==1
yobs_tmp = yobs(1:xi_temp(j+1),:);
elseif j==length(xi_temp)-1
yobs_tmp = yobs(xi_temp(j-1)+1:end,:);
else
yobs_tmp = yobs(xi_temp(j-1)+1:xi_temp(j+1),:);
end
aa = zeros(2^(dimen^2),1);
for i=1:2^(dimen^2)
aa(i)=sum(chol_index(i,:)~=chol_index(Phi_temp,:));
end
Phi_inv = find(aa==dimen^2);
select = chol_index(Phi_inv,:).*(1:dimen^2);
select = select(select~=0);
ll = nBeta*length(select);
[gr] = Gradient2(yobs_tmp, chol_index, Phi_inv, tau_temp_1,...
tau_temp_2, Beta_temp_1, Beta_temp_2, sigmasqalpha, nbasis, nseg);
Beta_old = reshape(Beta_temp_1(:,select),ll,1);
Beta_out = Beta_old;
% generate momentum variable
m = mvnrnd(zeros(ll,1),M*eye(ll))';
% determine leap number and stepsize
stepsize = unifrnd(0,2*ee);
leap = randsample(1:2*ceil(1/ee),1);
m_out = m + 0.5*gr*stepsize;
for i=1:leap
Beta_out = Beta_out + stepsize*(1/M)*eye(ll)*m_out;
Beta_temp_1(:,select) = reshape(Beta_out,nBeta,length(select));
Beta_temp_2(:,select) = reshape(Beta_out,nBeta,length(select));
if i==leap
[gr] = Gradient2(yobs_tmp, chol_index, Phi_inv, tau_temp_1,...
tau_temp_2, Beta_temp_1, Beta_temp_2, sigmasqalpha, nbasis, nseg);
m_out = m_out + 0.5*gr*stepsize;
else
[gr] = Gradient2(yobs_tmp, chol_index, Phi_inv, tau_temp_1,...
tau_temp_2, Beta_temp_1, Beta_temp_2, sigmasqalpha, nbasis, nseg);
m_out = m_out + 1*gr*stepsize;
end
end
m_out = -m_out;
function [xx_r,xx_i]= lin_basis_func(freq_hat)% freq are the frequencies
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Produces linear basis functions
%
% Input:
% 1) xx_r - linear basis function for real Cholesky components
% 2) ts - linear basis function for imaginary Cholesky components
% Main Outputs:
% 1) freq_hat - frequencies used
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global nBeta dimen
nfreq_hat=length(freq_hat);
xx_r = ones((nfreq_hat),nBeta);
xx_i = ones((nfreq_hat),nBeta);
for j=2:nBeta
xx_r(:,j) = sqrt(2)* cos(2*pi*(j-1)*freq_hat)/(2*pi*(j-1));
end
for j =1:nBeta
xx_i(:,j) = sqrt(2)*sin(2*pi*j*freq_hat)/(2*pi*j);
end
function[ai] = matpower(a,alpha)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Calculate matrix power
%
% Input:
% 1) a - a matrix
% 2) alpha - desired power
% Main Outputs:
% 1) ai - matrix with desired power
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
small = .000001;
if numel(a) == 1
ai=a^alpha;
else
[p1, ~] = size(a);
[eve, eva] = eig(a);
eva = diag(eva);
eve = eve./(repmat((diag((eve)'*eve).^0.5),1,p1));
index = 1:p1;
index = index(eva>small);
evai = eva;
evai(index) = (eva(index)).^(alpha);
ai = eve*diag(evai)*(eve)';
end
end
function[Beta_mean,Beta_var,yobs_tmp] = postBeta1(chol_index, Phi_temp,...
j, yobs, tau_temp, Beta_temp, xi_temp)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Calculate the mean and variance of normal approximation for coefficient
% of basis functions that are different across segments
%
% Input:
% 1) chol_index - index matrix
% 2) Phi_temp - indicate variable that determine which coefficient
% should be different
% 3) j - one of two segments
% 4) yobs - time series observations
% 5) tau_temp - current smoothing parameters
% 6) Beta_temp - current coefficients
% 7) xi__temp - current partitions
% Main Outputs:
% 1) Beta_mean - mean of approximated distribution
% 2) Beta_var - variance of approximated distribution
% 3) yobs_tmp - time series observations in selected segment
%
% Required programs: Beta_derive1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global nbasis nBeta sigmasqalpha dimen options
%var_inflate_1 is for variance inflation for first real part of Cholesky components;
%var_inflate_1 is for variance inflation for rest of components
%pick right portion of the data
if j>1
yobs_tmp = yobs((xi_temp(j-1)+1):xi_temp(j),:);
else
yobs_tmp = yobs(1:xi_temp(j),:);
end
%provide initial values
x = zeros(chol_index(Phi_temp,:)*repmat(nBeta,dimen^2,1),1);
%optimization process
[Beta_mean,~,~,~,~,Beta_inv_var] = fminunc(@Beta_derive1, x, options, ...
yobs_tmp, chol_index, Phi_temp, tau_temp, Beta_temp, sigmasqalpha, nbasis);
%Beta_var = Beta_inv_vareye(size(Beta_inv_var));
Beta_var = matpower(Beta_inv_var,-1);
function[Beta_mean,Beta_var,yobs_tmp] = postBeta2(chol_index, Phi_temp, j, yobs,...
tau_temp_1, tau_temp_2, Beta_temp_1, Beta_temp_2, xi_temp, nseg)
global dimen options nbasis nBeta sigmasqalpha
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Calculate the mean and variance of normal approximation for coefficient
% of basis functions that are the same across segments
%
% Input:
% 1) chol_index - index matrix
% 2) Phi_temp - indicate variable that determine which coefficient
% should be different
% 3) j - the first segment
% 4) yobs - time series observations
% 5) tau_temp_1 - current smoothing parameters for the first segment
% 6) tau_temp_2 - current smoothing parameters for the second
% segment
% 7) Beta_temp_1 - current coefficients for the first segment
% 8) Beta_temp_2 - current coefficients for the second segment
% 9) xi__temp - current partitions
% 10) nseg - number of observation in the first segment
% Main Outputs:
% 1) Beta_mean - mean of approximated distribution
% 2) Beta_var - variance of approximated distribution
% 3) yobs_tmp - time series observations in selected segment
%
% Required programs: Beta_derive2
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%pick right portion of the data
if j==1
yobs_tmp = yobs(1:xi_temp(j+1),:);
elseif j==length(xi_temp)-1
yobs_tmp = yobs(xi_temp(j-1)+1:end,:);
else
yobs_tmp = yobs(xi_temp(j-1)+1:xi_temp(j+1),:);
end
aa = zeros(2^(dimen^2),1);
for i=1:2^(dimen^2)
aa(i)=sum(chol_index(i,:)~=chol_index(Phi_temp,:));
end
Phi_inv = find(aa==dimen^2);
%provide initial values
x = zeros(chol_index(Phi_inv,:)*repmat(nBeta,dimen^2,1),1);
%optimization process
[Beta_mean,~,~,~,~,Beta_inv_var] = fminunc(@Beta_derive2, x, options, yobs_tmp, chol_index, Phi_inv,...
tau_temp_1, tau_temp_2, Beta_temp_1, Beta_temp_2, sigmasqalpha, nbasis, nseg);
%Beta_var = Beta_inv_vareye(size(Beta_inv_var));
Beta_var = matpower(Beta_inv_var,-1);
function [log_whittle] = whittle_like(yobs_tmp, Beta)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Calculate local Whittle likelihood
%
% Input:
% 1) yobs_tmp - time series in the segment
% 2) Beta - coefficient of basis functions
% Main Outputs:
% 1) log_whitle - log local whittle likelihood
% Require programs: lin_basis_function
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global dimen
Beta_1 = Beta(:,1:(dimen + dimen*(dimen-1)/2));
Beta_2 = Beta(:,(dimen + dimen*(dimen-1)/2 + 1): end);
dim = size(yobs_tmp);
n = dim(1);
nfreq = floor(n/2);
tt = (0:nfreq)/(2*nfreq);
yy = fft(yobs_tmp)/sqrt(n);
y = yy(1:(nfreq+1),:);
nf = length(y);
[xx_r, xx_i]=lin_basis_func(tt);
%theta's
theta = zeros(dimen*(dimen-1)/2,nf);
for i=1:(dimen*(dimen-1)/2)
theta_real = xx_r * Beta_1(:,i+dimen);
theta_imag = xx_i * Beta_2(:,i);
theta(i,:) = theta_real + sqrt(-1)*theta_imag;
end
%delta's
delta_sq = zeros(dimen,nf);
for i=1:dimen
delta_sq(i,:) = exp(xx_r * Beta_1(:,i));
end
if dimen==2
if (mod(n,2)==1) %odd n
log_whittle = -sum(log(delta_sq(1,2:end))' + log(delta_sq(2,2:end))' + ...
conj(y(2:end,1)).*y(2:end,1).*exp(-xx_r(2:end,:)*Beta_1(:,1)) + ...
conj(y(2:end,2) - theta(2:end).'.*y(2:end,1)).*(y(2:end,2) - theta(2:end).'.*y(2:end,1)).*exp(-xx_r(2:end,:)*Beta_1(:,2))) - ...
0.5*(log(delta_sq(1,1))' + log(delta_sq(2,1))' + conj(y(1,1)).*y(1,1).*exp(-xx_r(1,:)*Beta_1(:,1)) - ...
conj(y(1,2) - theta(1).'.*y(1,1)).*(y(1,2) - theta(1).'.*y(1,1)).*exp(-xx_r(1,:)*Beta_1(:,2)));
else
log_whittle = -sum(log(delta_sq(1,2:nfreq))' + log(delta_sq(2,2:nfreq))' + ...
conj(y(2:nfreq,1)).*y(2:nfreq,1).*exp(-xx_r(2:nfreq,:)*Beta_1(:,1)) + ...
conj(y(2:nfreq,2) - theta(2:nfreq).'.*y(2:nfreq,1)).*(y(2:nfreq,2) - theta(2:nfreq).'.*y(2:nfreq,1)).*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))) - ...
0.5*(log(delta_sq(1,1)) + log(delta_sq(2,1)) + conj(y(1,1)).*y(1,1).*exp(-xx_r(1,:)*Beta_1(:,1)) + ...
conj(y(1,2) - theta(1).'.*y(1,1)).*(y(1,2) - theta(1).'.*y(1,1)).*exp(-xx_r(1,:)*Beta_1(:,2))) - ...
0.5*(log(delta_sq(1,end)) + log(delta_sq(2,end)) + conj(y(end,1)).*y((nfreq+1),1).*exp(-xx_r(end,:)*Beta_1(:,1)) + ...
conj(y(end,2) - theta(end).'.*y(end,1)).*(y(end,2) - theta(end).'.*y(end,1)).*exp(-xx_r(end,:)*Beta_1(:,2)));
end
elseif dimen==3
if (mod(n,2)==1) %odd n
log_whittle = -sum(log(delta_sq(1,2:end))' + log(delta_sq(2,2:end))' + log(delta_sq(3,2:end))' + ...
conj(y(2:end,1)).*y(2:end,1).*exp(-xx_r(2:end,:)*Beta_1(:,1)) + ...
conj(y(2:end,2) - theta(1,2:end).'.*y(2:end,1)).*(y(2:end,2) - theta(1,2:end).'.*y(2:end,1)).*exp(-xx_r(2:end,:)*Beta_1(:,2))+...
conj(y(2:end,3) -(theta(2,2:end).'.*y(2:end,1)+ theta(3,2:end).'.*y(2:end,2))).*(y(2:end,3) -(theta(2,2:end).'.*y(2:end,1)+ theta(3,2:end).'.*y(2:end,2))).*...
exp(-xx_r(2:end,:)*Beta_1(:,3))) - ...
0.5*(log(delta_sq(1,1))' + log(delta_sq(2,1))' + log(delta_sq(3,1))' + ...
conj(y(1,1)).*y(1,1).*exp(-xx_r(1,:)*Beta_1(:,1)) + ...
conj(y(1,2) - theta(1,1).'.*y(1,1)).*(y(1,2) - theta(1,1).'.*y(1,1)).*exp(-xx_r(1,:)*Beta_1(:,2))+...
conj(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*...
exp(-xx_r(1,:)*Beta_1(:,3)));
else
log_whittle = -sum(log(delta_sq(1,2:nfreq))' + log(delta_sq(2,2:nfreq))' + log(delta_sq(3,2:nfreq))' + ...
conj(y(2:nfreq,1)).*y(2:nfreq,1).*exp(-xx_r(2:nfreq,:)*Beta_1(:,1)) + ...
conj(y(2:nfreq,2) - theta(1,2:nfreq).'.*y(2:nfreq,1)).*(y(2:nfreq,2) - theta(1,2:nfreq).'.*y(2:nfreq,1)).*exp(-xx_r(2:nfreq,:)*Beta_1(:,2))+...
conj(y(2:nfreq,3) -(theta(2,2:nfreq).'.*y(2:nfreq,1)+ theta(3,2:nfreq).'.*y(2:nfreq,2))).*(y(2:nfreq,3) -(theta(2,2:nfreq).'.*y(2:nfreq,1)+ theta(3,2:nfreq).'.*y(2:nfreq,2))).*...
exp(-xx_r(2:nfreq,:)*Beta_1(:,3))) - ...
0.5*(log(delta_sq(1,1))' + log(delta_sq(2,1))' + log(delta_sq(3,1))' + ...
conj(y(1,1)).*y(1,1).*exp(-xx_r(1,:)*Beta_1(:,1)) + ...
conj(y(1,2) - theta(1,1).'.*y(1,1)).*(y(1,2) - theta(1,1).'.*y(1,1)).*exp(-xx_r(1,:)*Beta_1(:,2))+...
conj(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*(y(1,3) -(theta(2,1).'.*y(1,1)+ theta(3,1).'.*y(1,2))).*...
exp(-xx_r(1,:)*Beta_1(:,3)))-...
0.5*(log(delta_sq(1,end))' + log(delta_sq(2,end))' + log(delta_sq(3,end))' + ...
conj(y(end,1)).*y(end,1).*exp(-xx_r(end,:)*Beta_1(:,1)) + ...
conj(y(end,2) - theta(1,end).'.*y(end,1)).*(y(end,2) - theta(1,end).'.*y(end,1)).*exp(-xx_r(end,:)*Beta_1(:,2))+...
conj(y(end,3) -(theta(2,end).'.*y(end,1)+ theta(3,end).'.*y(end,2))).*(y(end,3) -(theta(2,end).'.*y(end,1)+ theta(3,end).'.*y(end,2))).*...
exp(-xx_r(end,:)*Beta_1(:,3)));
end
end
function[A,nseg_new,xi_prop,tau_prop,Beta_prop,Phi_prop,seg_temp]=...
within(chol_index,ts,nexp_temp,tau_temp,xi_curr_temp,nseg_curr_temp,Beta_curr_temp,Phi_temp)
global nobs dimen nBeta M prob_mm1 tmin
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Does the within-model move in the paper
%
% Input:
% 1) chol_index - index matrix
% 2) ts - TxN matrix of time series data
% 3) nexp_temp - number of segments
% 5) tau_temp - vector of smoothing parameters
% 6) xi_curr_temp - current partitions
% 7) nseg_curr_temp - current number of observations in each segment
% 8) Beta_curr_temp - current vector of coefficients
% 9) Phi_temp - which component changed
% 10) Z - together with Phi_temp, indicating how components should
% be update
% Main Outputs:
% 1) PI - acceptance probability
% 2) nseg_new - new number of observations in each segment
% 3) xi_prop - proposed partitions
% 4) tau_prop - proposed smoothing parameters
% 5) Beta_prop - proposed coefficients
% 6) Phi_prop - proposed indicator variable
%
% Required programs: postBeta1, postBeta2, Beta_derive1, Beta_derive2,
% whittle_like
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
xi_prop = xi_curr_temp;
Beta_prop = Beta_curr_temp;
nseg_new = nseg_curr_temp;
tau_prop = tau_temp;
Phi_prop = Phi_temp;
if nexp_temp>1
%*********************************************************
% If contains more than one segments
%*********************************************************
seg_temp = unidrnd(nexp_temp-1); %Drawing Segment to cut
u = rand;
cut_poss_curr = xi_curr_temp(seg_temp);
nposs_prior = nseg_curr_temp(seg_temp) + nseg_curr_temp(seg_temp+1) - 2*tmin+1;
%Determing if the relocation is a big jump or small jump
if u<prob_mm1
if nseg_curr_temp(seg_temp)==tmin && nseg_curr_temp(seg_temp+1)==tmin
nposs=1; %Number of possible locations for new cutpoint
new_index=unidrnd(nposs);%Drawing index of new cutpoint
cut_poss_new = xi_curr_temp(seg_temp)- 1 + new_index;
elseif nseg_curr_temp(seg_temp)==tmin
nposs=2; %Number of possible locations for new cutpoint
new_index=unidrnd(nposs);%Drawing index of new cutpoint
cut_poss_new = xi_curr_temp(seg_temp)- 1 + new_index;
elseif nseg_curr_temp(seg_temp+1)==tmin
nposs=2; %Number of possible locations for new cutpoint
new_index = unidrnd(nposs); %Drawing index of new cutpoint
cut_poss_new = xi_curr_temp(seg_temp) + 1 - new_index;
else
nposs=3;% Number of possible locations for new cutpoint
new_index = unidrnd(nposs);%Drawing index of new cutpoint
cut_poss_new = xi_curr_temp(seg_temp) - 2 + new_index;
end
else
new_index=unidrnd(nposs_prior);%
cut_poss_new = sum(nseg_curr_temp(1:seg_temp-1))- 1 + tmin+new_index;
end
xi_prop(seg_temp)=cut_poss_new;
if seg_temp>1
%Number of observations in lower part of new cutpoin
nseg_new(seg_temp) = xi_prop(seg_temp) - xi_curr_temp(seg_temp-1);
else
nseg_new(seg_temp) = xi_prop(seg_temp);
end
%Number of observations in upper part of new cutpoint
nseg_new(seg_temp+1) = nseg_curr_temp(seg_temp) + nseg_curr_temp(seg_temp+1) - nseg_new(seg_temp);
%===========================================================
%Evaluating the cut Proposal density for the cut-point at the cureent
%and proposed values
%===========================================================
if(abs(cut_poss_new-cut_poss_curr)>1)
log_prop_cut_prop=log(1-prob_mm1)-log(nposs_prior);
log_prop_cut_curr=log(1-prob_mm1)-log(nposs_prior);
elseif nseg_curr_temp(seg_temp)==tmin && nseg_curr_temp(seg_temp+1)==tmin
log_prop_cut_prop=0;
log_prop_cut_curr=0;
else
if (nseg_curr_temp(seg_temp)==tmin || nseg_curr_temp(seg_temp+1)==tmin)
%log_prop_cut_prop=log(1-prob_mm1)-log(nposs_prior)+log(1/2)+log(prob_mm1);
log_prop_cut_prop=log(1/2)+log(prob_mm1);
else
%log_prop_cut_prop=log(1-prob_mm1)-log(nposs_prior)+log(1/3)+log(prob_mm1);
log_prop_cut_prop=log(1/3)+log(prob_mm1);
end
if(nseg_new(seg_temp)==tmin || nseg_new(seg_temp+1)==tmin)
%log_prop_cut_curr=log(1-prob_mm1)-log(nposs_prior)+log(1/2)+log(prob_mm1);
log_prop_cut_curr=log(1/2)+log(prob_mm1);
else
%log_prop_cut_curr=log(1-prob_mm1)-log(nposs_prior)+log(1/3)+log(prob_mm1);
log_prop_cut_curr=log(1/3)+log(prob_mm1);
end
end
need = sum(Beta_curr_temp(:,:,seg_temp) - Beta_curr_temp(:,:,seg_temp+1));
need = need./need;
need(isnan(need))=0;
aa = zeros(2^(dimen^2),1);
for i=1:2^(dimen^2)
aa(i)=sum(chol_index(i,:)==need);
end
Phi_need = find(aa==dimen^2);
select = find(chol_index(Phi_need,:)~=0);
select_inv = find(chol_index(Phi_need,:)==0);
%=============================================================================
%Evaluating the Loglikelihood, Priors and Proposals at the current values
%=============================================================================
loglike_curr = 0;
for j=seg_temp:seg_temp+1
if j>1
yobs_tmp = ts((xi_curr_temp(j-1)+1):xi_curr_temp(j),:);
else
yobs_tmp = ts(1:xi_curr_temp(j),:);
end
%Loglikelihood at current values
[log_curr_spec_dens] = whittle_like(yobs_tmp,Beta_curr_temp(:,:,j));
loglike_curr = loglike_curr + log_curr_spec_dens;
end
%=============================================================================
%Evaluating the Loglikelihood, Priors and Proposals at the proposed values
%=============================================================================
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%For coefficient of basis functions that are the same across two segments %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if Phi_need ~=2^(dimen^2)
[Beta_out, m_out, m, ~] = Hamilt2(chol_index, Phi_need, seg_temp,...
ts, tau_prop(:,seg_temp), tau_prop(:,seg_temp+1),...
Beta_prop(:,:,seg_temp), Beta_prop(:,:,seg_temp+1), xi_prop, nseg_new(seg_temp));
Beta_prop(:,select_inv,seg_temp) = reshape(Beta_out,nBeta,length(select_inv));
Beta_prop(:,select_inv,seg_temp+1) = Beta_prop(:,select_inv,seg_temp);
m_curr_1 = -0.5*m'*((1/M)*eye(length(m)))*m;
m_prop_1 = -0.5*m_out'*((1/M)*eye(length(m_out)))*m_out;
else
m_curr_1 = 0;
m_prop_1 = 0;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% For coefficient of basis functions that are different across two segments %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
loglike_prop = 0;
yobs_tmp_2 = cell(2,1);
m_prop_2 = 0;
m_curr_2 = 0;
for j=seg_temp:seg_temp+1
[Beta_out, m_out, m, yobs_tmp]=Hamilt1(chol_index, Phi_need,...
j, ts, tau_prop(:,j), Beta_prop(:,:,j), xi_prop);
if j==seg_temp
yobs_tmp_2{1} = yobs_tmp;
else
yobs_tmp_2{2} = yobs_tmp;
end
Beta_prop(:,select,j) = reshape(Beta_out,nBeta,length(select));
m_curr_2 = m_curr_2 - 0.5*m'*((1/M)*eye(length(m)))*m;
m_prop_2 = m_prop_2 - 0.5*m_out'*((1/M)*eye(length(m_out)))*m_out;
end
%Loglikelihood at proposed values
for j=seg_temp:seg_temp+1
if j==seg_temp
[log_curr_spec_dens] = whittle_like(yobs_tmp_2{1},Beta_prop(:,:,j));
else
[log_curr_spec_dens] = whittle_like(yobs_tmp_2{2},Beta_prop(:,:,j));
end
loglike_prop = loglike_prop+log_curr_spec_dens;
end
%proposal density
log_proposal_curr = log_prop_cut_curr;
log_proposal_prop = log_prop_cut_prop;
%target density
log_prior_cut_prop=0;
log_prior_cut_curr=0;
for k=1:nexp_temp-1
if k==1
log_prior_cut_prop=-log(nobs-(nexp_temp-k+1)*tmin+1);
log_prior_cut_curr=-log(nobs-(nexp_temp-k+1)*tmin+1);
else
log_prior_cut_prop=log_prior_cut_prop - log(nobs-xi_prop(k-1)-(nexp_temp-k+1)*tmin+1);
log_prior_cut_curr=log_prior_cut_curr - log(nobs-xi_curr_temp(k-1)-(nexp_temp-k+1)*tmin+1);
end
end
log_target_prop = loglike_prop + log_prior_cut_prop + m_prop_1 + m_prop_2;
log_target_curr = loglike_curr + log_prior_cut_curr + m_curr_1 + m_curr_2;
else
%*********************************************************
% If contains only one segment
%*********************************************************
nseg_new = nobs;
seg_temp = 1;
%===========================================================================
%Evaluating the Loglikelihood, Priors and Proposals at the proposed values
%===========================================================================
Phi_need = 2^(dimen^2);
[Beta_out, m_out, m]=Hamilt1(chol_index, Phi_need,...
1, ts, tau_temp, Beta_curr_temp, xi_curr_temp);
Beta_prop(:,:,1) = reshape(Beta_out,nBeta,dimen^2);
m_curr = - 0.5*m'*((1/M)*eye(length(m)))*m;
m_prop = - 0.5*m_out'*((1/M)*eye(length(m_out)))*m_out;
%Loglike at proposed values
[loglike_prop] = whittle_like(ts,Beta_prop(:,:,1));
%Loglike at current values
[loglike_curr] = whittle_like(ts,Beta_curr_temp(:,:,1));
log_target_prop = loglike_prop + m_prop;
log_target_curr = loglike_curr + m_curr;
log_proposal_curr = 0;
log_proposal_prop = 0;
end
%*************************************************************
%Calculations acceptance probability
%*************************************************************
A = min(1,exp(log_target_prop-log_target_curr+log_proposal_curr-log_proposal_prop));
function [out, fitparams] = MultiSpect_diag(ts,varargin)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Program for the MCMC nonstationary multivariate spectrum analysis paper
% 07/02/2016
% Does the MCMC iterations for bivariate time series
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Extract information from the option parameters
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% If params is empty, then use the default parameters
if nargin==1
params = OptsMultiSpect();
else
params = varargin{1};
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%II) Run the estimation proceedure
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
warning('off','MATLAB:nearlySingularMatrix')
nloop = params.nloop;
%number of total MCMC iterations
nwarmup = params.nwarmup;
%number of warmup period
nexp_max = params.nexp_max;
%Input maximum number of segments
global dimen nobs nbasis nBeta sigmasqalpha tau_up_limit ...
prob_mm1 tmin var_inflate_1 var_inflate_2 options
options = optimset('Display','off','GradObj','on','Hessian','on','MaxIter',10000,...
'MaxFunEvals',10000,'TolFun',1e-5,'TolX',1e-5);
nbasis = params.nbasis;
%number of linear smoothing spline basis functions
nBeta = nbasis + 1;
%number of coefficients for real part of components
sigmasqalpha = params.sigmasqalpha;
%smoothing parameter for alpha
tau_up_limit = params.tau_up_limit;
%the prior for smoothing parameters
prob_mm1 = params.prob_mml;
%the probability of small jump, 1-prob of big jump
tmin = params.tmin;
%minimum number of observation in each segment
var_inflate_1 = params.v1(1);
var_inflate_2 = params.v1(1);
nfreq_hat = params.nfreq;
freq_hat=(0:nfreq_hat)'/(2*nfreq_hat);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% II) Run the estimation proceedure
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
dim = size(ts);
nobs = dim(1);
dimen = dim(2);
spect_hat = cell(nexp_max,1);
for j=1:nexp_max
spect_hat{j} = zeros(2,2,nfreq_hat+1,j,nloop+1);
end
nexp_curr = params.init; %initialize the number of segments
%initialize tausq
for j=1:nexp_curr
tausq_curr(:,j,1)=rand(4,1)*tau_up_limit;
end
%initilize the location of the changepoints for j=1:nexp_curr(1)
xi_curr = zeros(nexp_curr,1);
nseg_curr = zeros(nexp_curr,1);
for j=1:nexp_curr
if nexp_curr==1
xi_curr = nobs;
nseg_curr = nobs;
else
if j==1
nposs = nobs-nexp_curr*tmin+1;
xi_curr(j) = tmin + unidrnd(nposs)-1;
nseg_curr(j) = xi_curr(j);
elseif j>1 && j<nexp_curr
nposs=nobs-xi_curr(j-1)-tmin*(nexp_curr-j+1)+1;
xi_curr(j)=tmin+unidrnd(nposs)+xi_curr(j-1)-1;
nseg_curr(j)=xi_curr(j)-xi_curr(j-1);
else
xi_curr(j)=nobs;
nseg_curr(j)=xi_curr(j)-xi_curr(j-1);
end
end
end
%index matrix for which components of cholesky decomposition changed
chol_index = [0 0 0 0; 1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1;...
1 1 0 0; 1 0 1 0; 1 0 0 1; 0 0 1 1; 0 1 0 1;...
0 1 1 0; 1 1 1 0; 1 1 0 1; 0 1 1 1; 1 0 1 1;...
1 1 1 1];
% 1: no change; 2-5: one changes; 6-11: two changes; 12-15: three changes
% 16: all changed
Beta_curr = zeros(nBeta,4,nexp_curr);
Phi_temp = repmat(16,nexp_curr,1);
for j=1:nexp_curr
[Beta_mean, Beta_var,~] = postBeta1(chol_index, Phi_temp(j), j, ts, tausq_curr, Beta_curr, xi_curr);
Beta_curr(:,:,j) = reshape(mvnrnd(Beta_mean,0.5*(Beta_var+Beta_var')),nBeta,4);
end
Phi_curr=[repmat(16,nexp_curr-1,1);0];
%jumping probabilities
epsilon=zeros(nloop,1);
met_rat=zeros(nloop,1);
rat_birth=[];
rat_death=[];
%%%initialize .mat file
S.('ts') = ts;
S.('varargin') = varargin;
S.('nexp') = [];
S.('nseg') = [];
S.('xi') = {};
S.('Beta') = {};
S.('tausq') = {};
S.('spect_hat') = {};
S.('Spec_1') = {};
S.('Spec_2') = {};
S.('Coh') = {};
S.('Phi') = {};
if params.convdiag==1
S.('conv_diag') = [];
end
save(params.fname, '-struct', 'S', '-v7.3');
%create matfile object to use in MCMC sampler
out = matfile(params.fname, 'Writable', true);
%create data structures to store temporary results in between ouputs
Beta_tmp = cell(params.batchsize,1);
spect_hat_tmp = cell(params.batchsize,1);
nexp_tmp = zeros(params.batchsize,1);
nseg_tmp = cell(params.batchsize,1);
tausq_tmp = cell(params.batchsize,1);
xi_tmp = cell(params.batchsize,1);
Phi_tmp = cell(params.batchsize,1);
Spect_1_tmp = cell(params.batchsize,1);
Spect_2_tmp = cell(params.batchsize,1);
Coh_tmp = cell(params.batchsize,1);
if params.convdiag==1
convdiag_tmp = zeros(params.batchsize,4*nBeta+4);
end
% preallocate for the worst case memory use
for i=1:params.batchsize
Beta_tmp{i} = zeros(nBeta, 4, params.nexp_max);
spect_hat_tmp{i} = zeros(2,2,nfreq_hat+1,params.nexp_max);
nexp_tmp(i) = params.nexp_max;
nseg_tmp{i} = zeros(params.nexp_max,1);
tausq_tmp{i} = zeros(4,params.nexp_max);
xi_tmp{i} = zeros(params.nexp_max,1);
Phi_tmp{i} = zeros(params.nexp_max,1);
Spect_1_tmp{i} = zeros(nfreq_hat+1,nobs);
Spect_2_tmp{i} = zeros(nfreq_hat+1,nobs);
Coh_tmp{i} = zeros(nfreq_hat+1,nobs);
if params.convdiag==1
convdiag_tmp(i,:)=zeros(1,4*nBeta+4);
end
end
%set batch index
batch_idx = 1;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% run the loop
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for p=1:nloop
tic;
if(mod(p,100)==0)
fprintf('iter: %g of %g
' ,p, nloop)
end
if p<nwarmup
var_inflate_1=1;
var_inflate_2=1;
else
var_inflate_1=1;
var_inflate_2=1;
end
%========================
%BETWEEN MODEL MOVE
%========================
kk = length(find(nseg_curr>2*tmin)); %Number of available segments
%===========================
%Deciding on birth or death
if kk==0 %Stay where you (if nexp_curr=1) or join segments if there are no available segments to cut
if nexp_curr==1
nexp_prop = nexp_curr; %Stay
log_move_prop = 0;
log_move_curr = 0;
else
nexp_prop = nexp_curr-1; %death
log_move_prop = 0;
if nexp_prop==1
log_move_curr = 1;
else
log_move_curr = log(0.5);
end
end
else
if nexp_curr==1
nexp_prop = nexp_curr + 1; %birth
log_move_prop = 0;
if nexp_prop==nexp_max
log_move_curr = 0;
else
log_move_curr = log(0.5);
end
elseif nexp_curr==nexp_max
nexp_prop = nexp_curr-1; %death
log_move_prop = 0;
if nexp_prop==1
log_move_curr = 0;
else
log_move_curr = log(0.5);
end
else
u = rand;
if u<0.5
nexp_prop = nexp_curr+1; %birth
if nexp_prop==nexp_max;
log_move_curr = 0;
log_move_prop = log(0.5);
else
log_move_curr=log(0.5);
log_move_prop=log(0.5);
end
else
nexp_prop = nexp_curr-1; %death
if nexp_prop==1
log_move_curr = 0;
log_move_prop = log(0.5);
else
log_move_curr = log(0.5);
log_move_prop = log(0.5);
end
end
end
end
if nexp_prop<nexp_curr
%Do Death step
[met_rat(p),nseg_prop,xi_prop,tausq_prop,Beta_prop, Phi_prop]= death(chol_index,ts,nexp_curr,nexp_prop,...
tausq_curr,xi_curr,nseg_curr,Beta_curr,Phi_curr, log_move_curr,log_move_prop);
rat_death=[rat_death met_rat(p)];
elseif nexp_prop>nexp_curr
%Do Birth step
[met_rat(p),nseg_prop,xi_prop,tausq_prop,Beta_prop, Phi_prop]= birth(chol_index,ts,nexp_curr,nexp_prop,...
tausq_curr,xi_curr,nseg_curr,Beta_curr,Phi_curr,log_move_curr,log_move_prop);
rat_birth=[rat_birth met_rat(p)];
else
xi_prop=xi_curr;
nseg_prop=nseg_curr;
tausq_prop=tausq_curr;
Beta_prop=Beta_curr;
Phi_prop=Phi_curr;
met_rat(p) = 1;
end
u = rand;
if u<met_rat(p)
nexp_curr=nexp_prop;
xi_curr=xi_prop;
nseg_curr=nseg_prop;
tausq_curr=tausq_prop;
Beta_curr=Beta_prop;
Phi_curr=Phi_prop;
end
%========================
%WITHIN MODEL MOVE
%========================
%Drawing a new cut point and Beta simultaneously
%update coeffiecient of linear basis function
[epsilon(p),nseg_new,xi_prop,~,Beta_prop,Phi_prop,seg_prop]= ...
within(chol_index,ts,nexp_curr,tausq_curr, xi_curr,...
nseg_curr, Beta_curr, Phi_curr);
u = rand;
if (u<epsilon(p)|| p==1)
if nexp_curr>1
for j=seg_prop:seg_prop+1
Beta_curr=Beta_prop;
xi_curr=xi_prop;
nseg_curr=nseg_new;
Phi_curr=Phi_prop;
end
else
Beta_curr=Beta_prop;
end
end
%Drawing tau
for j=1:nexp_curr
for i=1:3
tau_a = nbasis/2;
tau_b = sum(Beta_curr(2:end,i,j).^2)/2;
u=rand;
const1 = gamcdf(1/tau_up_limit,tau_a,1/tau_b);
const2 = 1-u*(1-const1);
tausq_curr(i,j) = 1/gaminv(const2,tau_a,1/tau_b);
end
tau_a = nbasis/2;
tau_b = sum(Beta_curr(1:nBeta,4,j).^2)/2;
u=rand;
const1 = gamcdf(1/tau_up_limit,tau_a,1/tau_b);
const2 = 1-u*(1-const1);
tausq_curr(4,j) = 1/gaminv(const2,tau_a,1/tau_b);
end
%==================================
%Estimating Spectral Density
%==================================
[xx_r, xx_i] = lin_basis_func(freq_hat); %produce linear basis functions
for j =1:nexp_curr
%getting the coefficients of linear basis functions
g1 = Beta_curr(:,1:3,j);
g2 = Beta_curr(1:nBeta,4,j);
theta_real = xx_r * g1(:,3);
theta_imag = xx_i * g2;
theta = theta_real+sqrt(-1)*theta_imag;
delta_sq_hat = zeros(2,nfreq_hat+1);
for q=1:2
delta_sq_hat(q,:) = exp(xx_r * g1(:,q))';
end
%produce the spectral density matrix
for k=1:(nfreq_hat+1)
TT = eye(2);
TT(2,1) = -theta(k);
spect_hat{nexp_curr}(:,:,k,j,p+1) = ...
inv(TT)*diag(delta_sq_hat(:,k))*inv(TT');
end
end
%============================================
% Get time-varying spectra and coherence
%============================================
Spec_1_est = zeros(nfreq_hat+1,nobs);
Spec_2_est = zeros(nfreq_hat+1,nobs);
Coh_est = zeros(nfreq_hat+1,nobs);
% first spectrum
if((p+1)>nwarmup)
spec_hat_curr=squeeze(spect_hat{nexp_curr}(1,1,:,:,p+1));
for j=1:nexp_curr
if(j==1)
Spect_1_est(:,1:xi_curr(j))= repmat(spec_hat_curr(:,j),1,xi_curr(j));
else
Spect_1_est(:,xi_curr(j-1)+1:xi_curr(j))= ...
repmat(spec_hat_curr(:,j),1,xi_curr(j)-xi_curr(j-1));
end
end
end
% second spectrum
if((p+1)>nwarmup)
spec_hat_curr=squeeze(spect_hat{nexp_curr}(2,2,:,:,p+1));
for j=1:nexp_curr
if(j==1)
Spect_2_est(:,1:xi_curr(j))= repmat(spec_hat_curr(:,j),1,xi_curr(j));
else
Spect_2_est(:,xi_curr(j-1)+1:xi_curr(j))= ...
repmat(spec_hat_curr(:,j),1,xi_curr(j)-xi_curr(j-1));
end
end
end
% coherence
if((p+1)>nwarmup)
spec_hat_curr=abs(squeeze(spect_hat{nexp_curr}(2,1,:,:,p+1))).^2./...
(squeeze(spect_hat{nexp_curr}(1,1,:,:,p+1)).*squeeze(spect_hat{nexp_curr}(2,2,:,:,p+1)));
for j=1:nexp_curr
if(j==1)
Coh_est(:,1:xi_curr(j))=repmat(spec_hat_curr(:,j),1,xi_curr(j));
else
Coh_est(:,xi_curr(j-1)+1:xi_curr(j))=repmat(spec_hat_curr(:,j),1,xi_curr(j)-xi_curr(j-1));
end
end
end
%create convergence diagnostics
if params.convdiag==1
convdiag_curr=convdiag(nobs, nBeta, nseg_curr, nexp_curr, Beta_curr, tausq_curr);
end
%output to temporary container
Beta_tmp{batch_idx} = Beta_curr;
spect_hat_tmp{batch_idx} = spect_hat;
nexp_tmp(batch_idx) = nexp_curr;
nseg_tmp{batch_idx} = nseg_curr;
tausq_tmp{batch_idx} = tausq_curr;
xi_tmp{batch_idx} = xi_curr;
Phi_tmp{batch_idx} = Phi_curr;
if((p+1)>nwarmup)
Spect_1_tmp{batch_idx} = Spect_1_est;
Spect_2_tmp{batch_idx} = Spect_2_est;
Coh_tmp{batch_idx} = Coh_est;
end
if params.convdiag==1
convdiag_tmp=convdiag_curr;
end
if(mod(p,params.batchsize)==0)
%output data to .mat file
out.Beta((p-params.batchsize+1):p,1) = Beta_tmp;
out.spect_hat((p-params.batchsize+1):p,1) = spect_hat_tmp;
out.nexp((p-params.batchsize+1):p,1)=nexp_tmp;
out.nseg((p-params.batchsize+1):p,1)=nseg_tmp;
out.tausq((p-params.batchsize+1):p,1) = tausq_tmp;
out.xi((p-params.batchsize+1):p,1) = xi_tmp;
out.Phi((p-params.batchsize+1):p,1) = Phi_tmp;
out.Spect_1((p-params.batchsize+1):p,1) = Spect_1_tmp;
out.Spect_2((p-params.batchsize+1):p,1) = Spect_2_tmp;
out.Coh((p-params.batchsize+1):p,1) = Coh_tmp;
if params.convdiag==1
out.convdiag((p-params.batchsize+1):p,1:nbeta+1)=convdiag_tmp;
end
%reset temporary data containers
Beta_tmp = cell(params.batchsize,1);
spect_hat_tmp = cell(params.batchsize,1);
nexp_tmp = zeros(params.batchsize,1);
nseg_tmp = cell(params.batchsize,1);
tausq_tmp = cell(params.batchsize,1);
xi_tmp = cell(params.batchsize,1);
Phi_tmp = cell(params.batchsize,1);
Spect_1_tmp = cell(params.batchsize,1);
Spect_2_tmp = cell(params.batchsize,1);
Coh_tmp = cell(params.batchsize,1);
if params.convdiag==1
convdiag_tmp = zeros(params.batchsize,4*nBeta+4);
end
%reset batch index
batch_idx=0;
end
%increment batch index
batch_idx = batch_idx + 1;
tms(p) = toc;
if params.verb ==1
fprintf('sec / min hr: %g %g %g
' ,[tms(p),sum(tms(1:p))/60, sum(tms(1:p))/(60*60)]')
end
end
fitparams = struct('nloop', nloop, ...
'nwarmup', nwarmup, ...
'timeMean', mean(tms), ...
'timeMax', max(tms(2:end)), ...
'timeMin', min(tms),...
'timeStd', std(tms(2:end)));
end
function[spectra, coh] = MultiSpect_interval(zt, spect_matrices, fit, params, alphalevel)
dim = size(zt); nobs = dim(1); dimen=dim(2);
spectra = cell(dimen,1);
coh = cell(dimen,1);
if dimen==3
temp1 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
temp2 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
temp3 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
temp4 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
temp5 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
temp6 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
spect11 = zeros(params.nfreq+1,nobs,3);
spect22 = zeros(params.nfreq+1,nobs,3);
spect33 = zeros(params.nfreq+1,nobs,3);
coh21 = zeros(params.nfreq+1,nobs,3);
coh31 = zeros(params.nfreq+1,nobs,3);
coh32 = zeros(params.nfreq+1,nobs,3);
for j=1:nobs
if(mod(j,10)==0)
fprintf('Completed: %g of %g observations
' ,j, nobs)
end
for p=1:params.nloop
if(p>params.nwarmup)
if length(fit(fit(1).nexp_curr(p)).xi(:,p))==1
k=1;
else
k = min(find(j<=fit(fit(1).nexp_curr(p)).xi(:,p)));
end
temp1(:,p-params.nwarmup) = squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,k,p));
temp2(:,p-params.nwarmup) = squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,k,p));
temp3(:,p-params.nwarmup) = squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,3,:,k,p));
temp4(:,p-params.nwarmup) = abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,1,:,k,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,k,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,k,p)));
temp5(:,p-params.nwarmup) = abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,1,:,k,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,k,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,3,:,k,p)));
temp6(:,p-params.nwarmup) = abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,2,:,k,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,k,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,3,:,k,p)));
end
end
spect11(:,j,1) = mean(temp1,2); spect11(:,j,2:3) = quantile(temp1,[alphalevel/2, 1-alphalevel/2],2);
spect22(:,j,1) = mean(temp2,2); spect22(:,j,2:3) = quantile(temp2,[alphalevel/2, 1-alphalevel/2],2);
spect33(:,j,1) = mean(temp3,2); spect33(:,j,2:3) = quantile(temp3,[alphalevel/2, 1-alphalevel/2],2);
coh21(:,j,1) = mean(temp4,2); coh21(:,j,2:3) = quantile(temp4,[alphalevel/2, 1-alphalevel/2],2);
coh31(:,j,1) = mean(temp5,2); coh31(:,j,2:3) = quantile(temp5,[alphalevel/2, 1-alphalevel/2],2);
coh32(:,j,1) = mean(temp6,2); coh32(:,j,2:3) = quantile(temp6,[alphalevel/2, 1-alphalevel/2],2);
end
spectra{1}=spect11;spectra{2}=spect22;spectra{3}=spect33;
coh{1}=coh21;coh{2}=coh31; coh{3}=coh32;
elseif dimen==2
temp1 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
temp2 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
temp3 = zeros(params.nfreq+1,(params.nloop-params.nwarmup));
spect11 = zeros(params.nfreq+1,nobs,3);
spect22 = zeros(params.nfreq+1,nobs,3);
coh21 = zeros(params.nfreq+1,nobs,3);
for j=1:nobs
if(mod(j,10)==0)
fprintf('Completed: %g of %g observations
' ,j, nobs)
end
for p=1:params.nloop
if(p>params.nwarmup)
if length(fit(fit(1).nexp_curr(p)).xi(:,p))==1
k=1;
else
k = min(find(j<=fit(fit(1).nexp_curr(p)).xi(:,p)));
end
temp1(:,p-params.nwarmup) = squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,k,p));
temp2(:,p-params.nwarmup) = squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,k,p));
temp3(:,p-params.nwarmup) = abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,1,:,k,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,k,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,k,p)));
end
end
spect11(:,j,1) = mean(temp1,2); spect11(:,j,2:3) = quantile(temp1,[alphalevel/2, 1-alphalevel/2],2);
spect22(:,j,1) = mean(temp2,2); spect22(:,j,2:3) = quantile(temp2,[alphalevel/2, 1-alphalevel/2],2);
coh21(:,j,1) = mean(temp3,2); coh21(:,j,2:3) = quantile(temp3,[alphalevel/2, 1-alphalevel/2],2);
end
spectra{1}=spect11;spectra{2}=spect22;
coh{1}=coh21;
end
function[post_partitions]=MultiSpect_partition(zt, fit, params)
dim = size(zt);nobs = dim(1);
post_partitions = (histc(fit(1).nexp_curr(params.nwarmup+1:params.nloop),1:params.nexp_max)'/length(params.nwarmup+1:params.nloop))';
figure
histogram(fit(1).nexp_curr(params.nwarmup+1:params.nloop),'FaceAlpha',1,...
'Normalization','probability','BinMethod','integers','BinWidth',.5,'BinLimits',[1,10])
title('Histogram of the Number of Partitions')
xlabel('The number of partitions')
ylabel('Probability')
for j=1:params.nexp_max
kk=find(fit(1).nexp_curr(params.nwarmup+1:params.nloop)==j);
if ∼isempty(kk) && j>1
figure
hold
title(['Plot of Partition Points Given ',int2str(j), ' Segments'])
for k=1:j-1
plot(fit(j).xi(k,kk+params.nwarmup))
end
for k=1:j-1
figure
hold
title(['Histogram of Location of Partition ', int2str(k), ',' ' Given ',int2str(j), ' Segments'])
histogram(fit(j).xi(k,kk+params.nwarmup),'FaceAlpha',1,...
'Normalization','probability','BinMethod','integers','BinWidth',20,'BinLimits',[1,nobs])
end
end
end
end
function[spectra, coh] = MultiSpect_surface(zt, spect_matrices, fit, params)
dim = size(zt); nobs = dim(1); dimen=dim(2);
spectra = cell(dimen,1);
coh = cell(dimen,1);
if dimen==3
s_11=zeros(params.nfreq+1,nobs);
s_22=zeros(params.nfreq+1,nobs);
s_33=zeros(params.nfreq+1,nobs);
for p=1:params.nloop
if(p>params.nwarmup)
xi_curr=fit(fit(1).nexp_curr(p)).xi(:,p);
spec_hat_curr_11=squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,:,p));
spec_hat_curr_22=squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,:,p));
spec_hat_curr_33=squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,3,:,:,p));
for j=1:fit(1).nexp_curr(p)
if(j==1)
s_11(:,1:xi_curr)=s_11(:,1:xi_curr(j))+repmat(spec_hat_curr_11(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
s_22(:,1:xi_curr)=s_22(:,1:xi_curr(j))+repmat(spec_hat_curr_22(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
s_33(:,1:xi_curr)=s_33(:,1:xi_curr(j))+repmat(spec_hat_curr_33(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
else
s_11(:,xi_curr(j-1)+1:xi_curr(j))=s_11(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_11(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
s_22(:,xi_curr(j-1)+1:xi_curr(j))=s_22(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_22(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
s_33(:,xi_curr(j-1)+1:xi_curr(j))=s_33(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_33(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
end
end
end
end
coh_21=zeros(params.nfreq+1,nobs);
coh_31=zeros(params.nfreq+1,nobs);
coh_32=zeros(params.nfreq+1,nobs);
for p=1:params.nloop
if(p>params.nwarmup)
xi_curr=fit(fit(1).nexp_curr(p)).xi(:,p);
spec_hat_curr_21=abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,1,:,:,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,:,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,:,p)));
spec_hat_curr_31=abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,1,:,:,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,:,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,3,:,:,p)));
spec_hat_curr_32=abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,2,:,:,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(3,3,:,:,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,:,p)));
for j=1:fit(1).nexp_curr(p)
if(j==1)
coh_21(:,1:xi_curr(j))=coh_21(:,1:xi_curr(j))+repmat(spec_hat_curr_21(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
coh_31(:,1:xi_curr(j))=coh_31(:,1:xi_curr(j))+repmat(spec_hat_curr_31(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
coh_32(:,1:xi_curr(j))=coh_32(:,1:xi_curr(j))+repmat(spec_hat_curr_32(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
else
coh_21(:,xi_curr(j-1)+1:xi_curr(j))=coh_21(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_21(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
coh_31(:,xi_curr(j-1)+1:xi_curr(j))=coh_31(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_31(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
coh_32(:,xi_curr(j-1)+1:xi_curr(j))=coh_32(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_32(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
end
end
end
end
spectra{1}=s_11;spectra{2}=s_22;spectra{3}=s_33;
coh{1}=coh_21;coh{2}=coh_31; coh{3}=coh_32;
elseif dimen==2
s_11=zeros(params.nfreq+1,nobs);
s_22=zeros(params.nfreq+1,nobs);
for p=1:params.nloop
if(p>params.nwarmup)
xi_curr=fit(fit(1).nexp_curr(p)).xi(:,p);
spec_hat_curr_11=squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,:,p));
spec_hat_curr_22=squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,:,p));
for j=1:fit(1).nexp_curr(p)
if(j==1)
s_11(:,1:xi_curr)=s_11(:,1:xi_curr(j))+repmat(spec_hat_curr_11(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
s_22(:,1:xi_curr)=s_22(:,1:xi_curr(j))+repmat(spec_hat_curr_22(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
else
s_11(:,xi_curr(j-1)+1:xi_curr(j))=s_11(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_11(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
s_22(:,xi_curr(j-1)+1:xi_curr(j))=s_22(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_22(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
end
end
end
end
coh_21=zeros(params.nfreq+1,nobs);
for p=1:params.nloop
if(p>params.nwarmup)
xi_curr=fit(fit(1).nexp_curr(p)).xi(:,p);
spec_hat_curr_21=abs(squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,1,:,:,p))).^2./...
(squeeze(spect_matrices{fit(1).nexp_curr(p)}(1,1,:,:,p)).*squeeze(spect_matrices{fit(1).nexp_curr(p)}(2,2,:,:,p)));
for j=1:fit(1).nexp_curr(p)
if(j==1)
coh_21(:,1:xi_curr(j))=coh_21(:,1:xi_curr(j))+repmat(spec_hat_curr_21(:,j),1,xi_curr(j))/(params.nloop-params.nwarmup);
else
coh_21(:,xi_curr(j-1)+1:xi_curr(j))=coh_21(:,xi_curr(j-1)+1:xi_curr(j))+...
repmat(spec_hat_curr_21(:,j),1,xi_curr(j)-xi_curr(j-1))/(params.nloop-params.nwarmup);
end
end
end
end
spectra{1}=s_11;spectra{2}=s_22;
coh{1}=coh_21;
end
function [spect_hat, freq_hat, diagparams, fitparams] = MultiSpect(zt,varargin)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Program for the MCMC nonstationary multivariate spectrum % analysis paper
% Does the MCMC iterations for bivariate or trivariate time series
% Input:
% 1)zt - time series data. It should be T by N matrix. T is
% the length of the time series; N is the dimension (2 or 3)
% 2)varargin - Tunning parameters, which can be set % by the program % OptsMultiSpec.m
% See the documnetation in that program for details and default % values.
% Main Outputs:
% 1) spec_hat - a cell contains spectral matrix
% 2) freq_hat - vector of frequencies considered.
% 3) diagparams - contains draws of parameters, including:
% diagparams.tausq - smoothing parameters,
% diagparams.Beta - coefficients,
% diagparams.xi - locations of partitions
% diagparams.nseg - number of observations in each block,
% diagparams.nexp_curr - number of partitions,
% diagparams.Phi - set of coefficients that changed,
% diagparams.epsilon - acceptance rate of within-model move,
% diagparams.bet_birth - number of accepted birth step,
% diagparams.bet_death - number of accepted death step,
% diagparams.bet_within - number of accepted within step,
% diagparams.tms - tum time in second,
% diagparams.convdiag_out - an optional convergence diagnostic % output
% 4) fitparams - 6 dimensional structural array
% fitparams.nloop - number of iterations run
% fitparams.nwarmup - length of the burn-in
% fitparams.timeMean - average iteration run time time in % seconds
% fitparams.timeMax - maximum iteration run time in seconds
% fitparams.timeMin - minimum iteration run time in seconds
% fitparams.timeStd - standard deviation of iteration run times % in seconds
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % I) Extract information from the option parameters
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% If params is empty, then use the default parameters
if nargin==1
params = OptsMultiSpect();
else
params = varargin{1};
end
nloop = params.nloop;
%number of total MCMC iterations
nwarmup = params.nwarmup;
%number of warmup period
nexp_max = params.nexp_max;
%Input maximum number of segments
global dimen nobs nbasis nBeta sigmasqalpha tau_up_limit ...
prob_mm1 tmin M ee options
if verLessThan('matlab','9.2')
options = optimset('Display','off','GradObj','on','Hessian','on','MaxIter',10000,...
'MaxFunEvals',10000,'TolFun',1e-6,'TolX',1e-6);
else
options = optimoptions(@fminunc,'Display','off','GradObj','on','Hessian','on','MaxIter',10000,...
'MaxFunEvals',10000,'TolFun',1e-6,'TolX',1e-6,'Algorithm','trust-region');
end
nbasis = params.nbasis;
%number of linear smoothing spline basis functions
nBeta = nbasis + 1;
%number of coefficients
sigmasqalpha = params.sigmasqalpha;
%smoothing parameter for alpha
tau_up_limit = params.tau_up_limit;
%the prior for smoothing parameters
prob_mm1 = params.prob_mml;
%the probability of small jump, 1-prob of big jump
tmin = params.tmin;
%minimum number of observation in each segment
M = tau_up_limit;
%scale value for momentum variable
ee = params.ee;
%step size in HMC
nfreq_hat = params.nfreq;
freq_hat=(0:nfreq_hat)'/(2*nfreq_hat);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% II) Run the estimation proceedure
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
dim = size(zt);
nobs = dim(1);
dimen = dim(2);
ts = zt;
% ts = zeros(nobs,dimen);
% for i=1:dimen
% x = zt(:,i);
% xmat = [ones(length(x),1) linspace(1,length(x),% length(x))'];
% linfit=inv(xmat'*xmat)*xmat'*x;
% ts(:,i)=zt(:,i)- xmat*linfit;
% end
tausq = cell(nexp_max,1);
%big array for smoothing parameters
Beta = cell(nexp_max,1);
%big array for coefficients
spect_hat = cell(nexp_max,1);
xi = cell(nexp_max,1);
%Cutpoint locations xi_1 is first cutpoint, xi_) is beginning of timeseries
nseg = cell(nexp_max,1);
%Number of observations in each segment
Phi = cell(nexp_max,1);
%index for component change
tms = zeros(1,nloop);
for j=1:nexp_max
tausq{j}=ones(dimen^2,j,nloop+1);
Beta{j} = zeros(nBeta,dimen^2,j,nloop+1);
spect_hat{j} = zeros(dimen,dimen,nfreq_hat+1,j,nloop+1);
xi{j}=ones(j,nloop+1);
nseg{j}=ones(j,nloop+1);
Phi{j}=zeros(j,nloop+1);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% initilize the MCMC iteration
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
nexp_curr=nexp_max*ones(nloop+1,1);
%big array for number of segment
nexp_curr(1) = params.init;
%initialize the number of segments
%initialize tausq
for j=1:nexp_curr(1)
tausq{nexp_curr(1)}(:,j,1)=rand(dimen^2,1)*tau_up_limit;
end
%initilize the location of the changepoints for j=1:nexp_curr(1)
for j=1:nexp_curr(1)
if nexp_curr(1)==1
xi{nexp_curr(1)}(j,1) = nobs;
nseg{nexp_curr(1)}(j,1) = nobs;
else
if j==1
nposs = nobs-nexp_curr(1)*tmin+1;
xi{nexp_curr(1)}(j,1) = tmin + unidrnd(nposs)-1;
nseg{nexp_curr(1)}(j,1) = xi{nexp_curr(1)}(j,1);
elseif j>1 && j<nexp_curr(1)
nposs=nobs-xi{nexp_curr(1)}(j-1,1)-tmin*(nexp_curr(1)-j+1)+1;
xi{nexp_curr(1)}(j,1)=tmin+unidrnd(nposs)+xi{nexp_curr(1)}(j-1,1)-1;
nseg{nexp_curr(1)}(j,1)=xi{nexp_curr(1)}(j,1)-xi{nexp_curr(1)}(j-1,1);
else
xi{nexp_curr(1)}(j,1)=nobs;
nseg{nexp_curr(1)}(j,1)=xi{nexp_curr(1)}(j,1)-xi{nexp_curr(1)}(j-1,1);
end
end
end
%index matrix for which components of cholesky decomposition changed
chol_index = chol_ind(dimen);
xi_temp = xi{nexp_curr(1)}(:,1);
tau_temp = tausq{nexp_curr(1)}(:,:,1);
Beta_temp = Beta{nexp_curr(1)}(:,:,:,1);
Phi{nexp_curr(1)}(1:(end-1),1)=2^(dimen^2);
Phi_temp = repmat(2^(dimen^2),nexp_curr(1));
for j=1:nexp_curr(1)
[Beta_mean, Beta_var,~] = postBeta1(chol_index, Phi_temp(j), j, ts, tau_temp(:,j), Beta_temp(:,:,j,1), xi_temp);
if min(eig(0.5*(Beta_var+Beta_var')))<0
Beta{nexp_curr(1)}(:,:,j,1) = reshape(mvnrnd(Beta_mean,0.5*(eye(nBeta*dimen^2))),nBeta,dimen^2);
else
Beta{nexp_curr(1)}(:,:,j,1) = reshape(mvnrnd(Beta_mean,0.5*(Beta_var+Beta_var')),nBeta,dimen^2);
end
end
%jumping probabilities
epsilon=zeros(nloop,1);
met_rat=zeros(nloop,1);
bet_death = 0;
bet_birth = 0;
with = 0;
%create convergence diagnostics
if params.convdiag==1
convdiag_out = zeros((dimen^2)*nBeta+dimen^2,nloop);
convdiag_out(:,1)=conv_diag(nobs, nBeta, nseg{nexp_curr(1)}(:,1),...
nexp_curr(1), Beta{nexp_curr(1)}(:,:,:,1), tausq{nexp_curr(1)}(:,:,1),dimen);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% run the loop
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for p=1:nloop
tic;
if(mod(p,50)==0)
fprintf('iter: %g of %g
' ,p, nloop)
end
%========================
%BETWEEN MODEL MOVE
%========================
kk = length(find(nseg{nexp_curr(p)}(:,p)>2*tmin)); %Number of available segments
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Deciding on birth or death
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if kk==0 %Stay where you (if nexp_curr=1) or join segments if there are no available segments to cut
if nexp_curr(p)==1
nexp_prop = nexp_curr(p); %Stay
log_move_prop = 0;
log_move_curr = 0;
else
nexp_prop = nexp_curr(p)-1; %death
log_move_prop = 0;
if nexp_prop==1
log_move_curr = 1;
else
log_move_curr = log(0.5);
end
end
else
if nexp_curr(p)==1
nexp_prop = nexp_curr(p) + 1; %birth
log_move_prop = 0;
if nexp_prop==nexp_max
log_move_curr = 0;
else
log_move_curr = log(0.5);
end
elseif nexp_curr(p)==nexp_max
nexp_prop = nexp_curr(p)-1; %death
log_move_prop = 0;
if nexp_prop==1
log_move_curr = 0;
else
log_move_curr = log(0.5);
end
else
u = rand;
if u<0.5
nexp_prop = nexp_curr(p)+1; %birth
if nexp_prop==nexp_max;
log_move_curr = 0;
log_move_prop = log(0.5);
else
log_move_curr=log(0.5);
log_move_prop=log(0.5);
end
else
nexp_prop = nexp_curr(p)-1; %death
if nexp_prop==1
log_move_curr = 0;
log_move_prop = log(0.5);
else
log_move_curr = log(0.5);
log_move_prop = log(0.5);
end
end
end
end
xi_curr_temp = xi{nexp_curr(p)}(:,p);
Beta_curr_temp = Beta{nexp_curr(p)}(:,:,:,p);
nseg_curr_temp = nseg{nexp_curr(p)}(:,p);
tau_curr_temp = tausq{nexp_curr(p)}(:,:,p);
Phi_curr_temp = Phi{nexp_curr(p)}(:,p);
if nexp_prop<nexp_curr(p)
%Death step
[met_rat(p),nseg_prop,xi_prop,tausq_prop,Beta_prop, Phi_prop]= death(chol_index,ts,nexp_curr(p),nexp_prop,...
tau_curr_temp,xi_curr_temp,nseg_curr_temp,Beta_curr_temp,Phi_curr_temp, log_move_curr,log_move_prop);
elseif nexp_prop>nexp_curr(p)
%Birth step
[met_rat(p),nseg_prop,xi_prop,tausq_prop,Beta_prop, Phi_prop]= birth(chol_index,ts,nexp_curr(p),nexp_prop,...
tau_curr_temp,xi_curr_temp,nseg_curr_temp,Beta_curr_temp,Phi_curr_temp,log_move_curr,log_move_prop);
else
xi_prop=xi{nexp_curr(p)}(:,p);
nseg_prop=nseg{nexp_curr(p)}(:,p);
tausq_prop=tausq{nexp_curr(p)}(:,:,p);
Beta_prop=Beta{nexp_curr(p)}(:,:,p);
Phi_prop=Phi{nexp_curr(p)}(:,p);
met_rat(p) = 1;
end
u = rand;
if u<met_rat(p)
if nexp_prop<nexp_curr(p)
bet_death = bet_death + 1;
elseif nexp_prop>nexp_curr(p)
bet_birth = bet_birth + 1;
end
nexp_curr(p+1)=nexp_prop;
xi{nexp_curr(p+1)}(:,p+1)=xi_prop;
nseg{nexp_curr(p+1)}(:,p+1)=nseg_prop;
tausq{nexp_curr(p+1)}(:,:,p+1)=tausq_prop;
Beta{nexp_curr(p+1)}(:,:,:,p+1)=Beta_prop;
Phi{nexp_curr(p+1)}(:,p+1)=Phi_prop;
else
nexp_curr(p+1)=nexp_curr(p);
xi{nexp_curr(p+1)}(:,p+1)=xi{nexp_curr(p+1)}(:,p);
nseg{nexp_curr(p+1)}(:,p+1)=nseg{nexp_curr(p+1)}(:,p);
tausq{nexp_curr(p+1)}(:,:,p+1)=tausq{nexp_curr(p+1)}(:,:,p);
Beta{nexp_curr(p+1)}(:,:,:,p+1)=Beta{nexp_curr(p+1)}(:,:,:,p);
Phi{nexp_curr(p+1)}(:,p+1)=Phi{nexp_curr(p+1)}(:,p);
end
%========================
%WITHIN MODEL MOVE
%========================
%Drawing a new cut point and Beta simultaneously
%update coeffiecient of linear basis function
xi_curr_temp=xi{nexp_curr(p+1)}(:,p+1);
Beta_curr_temp=Beta{nexp_curr(p+1)}(:,:,:,p+1);
tau_temp=tausq{nexp_curr(p+1)}(:,:,p+1);
nseg_curr_temp=nseg{nexp_curr(p+1)}(:,p+1);
Phi_temp = Phi{nexp_curr(p+1)}(:,p+1);
[epsilon(p),nseg_new,xi_prop,tausq_prop,Beta_prop,Phi_prop,seg_temp]= ...
within(chol_index,ts,nexp_curr(p+1),tau_temp, xi_curr_temp,...
nseg_curr_temp, Beta_curr_temp,Phi_temp);
u = rand;
if (u<epsilon(p)|| p==1)
with = with + 1;
if nexp_curr(p+1)>1
for j=seg_temp:seg_temp+1
Beta{nexp_curr(p+1)}(:,:,j,p+1)=Beta_prop(:,:,j);
xi{nexp_curr(p+1)}(j,p+1)=xi_prop(j);
nseg{nexp_curr(p+1)}(j,p+1)=nseg_new(j);
Phi{nexp_curr(p+1)}(j,p+1)=Phi_prop(j);
end
else
Beta{nexp_curr(p+1)}(:,:,p+1)=Beta_prop;
end
else
Beta{nexp_curr(p+1)}(:,:,:,p+1)=Beta_curr_temp;
xi{nexp_curr(p+1)}(:,p+1)=xi_curr_temp;
nseg{nexp_curr(p+1)}(:,p+1)=nseg_curr_temp;
Phi{nexp_curr(p+1)}(:,p+1)=Phi_temp;
end
%Drawing tau
for j=1:nexp_curr(p+1)
for i=1:dimen^2
if ismember(i,1:dimen + dimen*(dimen-1)/2)
tau_a = nbasis/2;
tau_b = sum(Beta{nexp_curr(p+1)}(2:end,i,j,p+1).^2)/2;
u=rand;
const1 = gamcdf(1/tau_up_limit,tau_a,1/tau_b);
const2 = 1-u*(1-const1);
tausq{nexp_curr(p+1)}(i,j,p+1) = 1/gaminv(const2,tau_a,1/tau_b);
else
tau_a = nBeta/2;
tau_b = sum(Beta{nexp_curr(p+1)}(1:nBeta,i,j,p+1).^2)/2;
u=rand;
const1 = gamcdf(1/tau_up_limit,tau_a,1/tau_b);
const2 = 1-u*(1-const1);
tausq{nexp_curr(p+1)}(i,j,p+1) = 1/gaminv(const2,tau_a,1/tau_b);
end
end
end
tms(p) = toc;
if params.verb ==1
fprintf('sec / min hr: %g %g %g
' ,[tms(p),sum(tms(1:p))/60, sum(tms(1:p))/(60*60)]')
end
%==================================
%Estimating Spectral Density
%==================================
[xx_r, xx_i] = lin_basis_func(freq_hat); %produce linear basis functions
for j =1:nexp_curr(p+1)
%getting the coefficients of linear basis functions
g1 = Beta{nexp_curr(p+1)}(:,1:(dimen + dimen*(dimen-1)/2),j,p+1);
g2 = Beta{nexp_curr(p+1)}(1:nBeta,(dimen + dimen*(dimen-1)/2 + 1):end,j,p+1);
theta = zeros(dimen*(dimen-1)/2,(nfreq_hat+1));
for i=1:dimen*(dimen-1)/2
theta_real = xx_r * g1(:,i+dimen);
theta_imag = xx_i * g2(:,i);
theta(i,:) = (theta_real + sqrt(-1)*theta_imag).';
end
delta_sq_hat = zeros(2,nfreq_hat+1);
for q=1:dimen
delta_sq_hat(q,:) = exp(xx_r * g1(:,q)).';
end
%produce the spectral density matrix
for k=1:(nfreq_hat+1)
TT = eye(dimen);
TT(2,1) = -theta(1,k);
if dimen==3
TT(3,1) = -theta(2,k);
TT(3,2) = -theta(3,k);
end
spect_hat{nexp_curr(p+1)}(:,:,k,j,p+1) = ...
inv(TT)*diag(delta_sq_hat(:,k))*inv(TT');
end
end
%create convergence diagnostics
if params.convdiag==1
convdiag_out(:,p+1)=conv_diag(nobs, nBeta, nseg{nexp_curr(p+1)}(:,p+1),...
nexp_curr(p+1), Beta{nexp_curr(p+1)}(:,:,:,p+1), tausq{nexp_curr(p+1)}(:,:,p+1),dimen);
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% III) Collect outputs
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fitparams = struct('nloop', nloop, ...
'nwarmup', nwarmup, ...
'timeMean', mean(tms), ...
'timeMax', max(tms(2:end)), ...
'timeMin', min(tms),...
'timeStd', std(tms(2:end)));
if params.convdiag==1
diagparams = struct('tausq', tausq,...
'Beta', Beta,...
'xi', xi,...
'nseg', nseg,...
'nexp_curr', nexp_curr,...
'Phi', Phi,...
'epsilon', epsilon,...
'bet_birth', bet_birth,...
'bet_death', bet_death,...
'with', with,...
'time', tms,...
'convdiag_out', convdiag_out);
else
diagparams = struct('tausq', tausq,...
'Beta', Beta,...
'xi', xi,...
'nseg', nseg,...
'nexp_curr', nexp_curr,...
'Phi', Phi,...
'epsilon', epsilon,...
'bet_birth', bet_birth,...
'bet_death', bet_death,...
'with', with,...
'time', tms);
end
end
function [param] = OptsMultiSpect(varargin)
% This function sets the optional input arguments for the function
% MCBSpec().
%
% (I) ONLY DEFAULT PARAMETERS
% If only defult values for the parameters are desired, then either:
%
% a) the SECOND argument in MultiSpec() can be left missing, or
%
% b) params=setOptions() can be defined and used as the second
% argument of MultiSpec().
%
% (II) USING NONDEFAULT PARAMETERS
% If some options other than the default are desired:
%
% 1) Set all default parameters using (Ia) above.
%
% 2) Change desired parameters.
%
%
% PARAMETERS
%
% nloop - The number of iterations run.
% Default: 6000.
% nwarmup - The length of the burn-in.
% Default: 200.
% nexp_max- The maximum number of segments allowed, adjust % when time series get longer.
% Default: 10
% tmin - The minimum number of observation in each segment.
% Default: 100
% prob_mml- The probability of small jump, 1-prob of big
% jump.
% Default: 0.8
% nbasis - The number of linear smoothing spline basis
% functions.
% Default: 10
% tau_up_limit - The normal variance prior for smoothing
% parameters.
% Default: 10^4.
% sigmasqalpha - The smoothing parameter for alpha.
% Default: 10^4
% init - Initial number of partitions
% Default: 3
% nfreq - The number of frequencies for spectrm
% Default: 50
% verb - An indicator if the iteration number should be printed
% at the completion of each iteration. 1 is
% yes, 0 is
% no.
% covdiag - An indicator if the diagnostic should be
% ee - Step size in Hamiltonian Monte Carlo
% Default is 0.1
param = struct('nloop',10000, 'nwarmup',2000, ...
'nexp_max',10, 'tmin',60, 'prob_mml',0.8 , 'nbasis',10, ...
'tau_up_limit',10^5 , 'sigmasqalpha',10^5, 'init',3,...
'nfreq',50, 'verb',1, 'convdiag',0, 'ee',0.1);
param.bands = {};
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% read in data and implement the analysis
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fdata = csvread('C:/Bookdata/WW9.csv',1,1);
dimen = size(fdata);
nobs = dimen(1);
startDate = datenum('04-01-1990');
endDate = datenum('12-31-2011');
xData = linspace(startDate,endDate,nobs);
figure
subplot(1,3,1)
plot(xData,fdata(:,1))
title('DJIA')
datetick('x','yyyy','keeplimits')
subplot(1,3,2)
plot(xData,fdata(:,2))
title('NASDAQ')
datetick('x','yyyy','keeplimits')
subplot(1,3,3)
plot(xData,fdata(:,3))
title('S&P500')
datetick('x','yyyy','keeplimits')
params = struct('nloop',12000, 'nwarmup',4000, ...
'nexp_max',10, 'tmin',60, 'prob_mml',0.8 , 'nbasis',10, ...
'tau_up_limit',10^5, 'sigmasqalpha',10^5, 'init',2,...
'nfreq',50, 'verb',1, 'convdiag',0, 'ee', 0.05);
%%% Note: he code can be run using default parameters
%%% [spect_matrices, freq_hat, fit, fit_diag] = MultiSpect(zt)
rng(201701204);
[spect_matrices, freq_hat, fit, fit_diag] = MultiSpect(fdata,params);
[spect, coh] = MultiSpect_surface(fdata, spect_matrices, fit, params);
figure
subplot(1,3,1); meshc( xData, freq_hat,real(spect{1})); set(gca,'YDir','reverse'); title('$ f_{11}$','Interpreter','LaTex'); xlabel('time'); ylabel('freq'); datetick('x','yyyy','keeplimits')
subplot(1,3,2); meshc( xData, freq_hat,real(spect{2})); set(gca,'YDir','reverse'); title('$ f_{22}$','Interpreter','LaTex'); xlabel('time'); ylabel('freq'); datetick('x','yyyy','keeplimits')
subplot(1,3,3); meshc( xData, freq_hat,real(spect{3})); set(gca,'YDir','reverse'); title('$ f_{33}$','Interpreter','LaTex'); xlabel('time'); ylabel('freq'); datetick('x','yyyy','keeplimits')
figure
subplot(1,3,1); meshc( xData, freq_hat,real(coh{1})); set(gca,'YDir','reverse'); title('$
ho_{21}^2$','Interpreter','LaTex'); xlabel('time'); ylabel('freq'); datetick('x','yyyy','keeplimits')
subplot(1,3,2); meshc( xData, freq_hat,real(coh{2})); set(gca,'YDir','reverse'); title('$
ho_{31}^2$','Interpreter','LaTex'); xlabel('time'); ylabel('freq'); datetick('x','yyyy','keeplimits')
subplot(1,3,3); meshc( xData, freq_hat,real(coh{3})); set(gca,'YDir','reverse'); title('$
ho_{32}^2$','Interpreter','LaTex'); xlabel('time'); ylabel('freq'); datetick('x','yyyy','keeplimits')
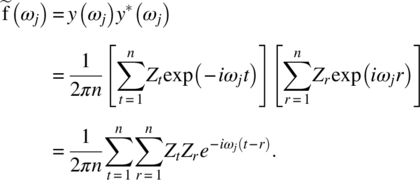
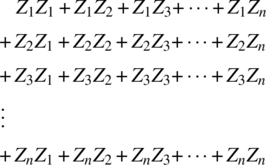
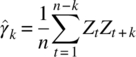
![]() for j = 1, 2, …, (n − 1)/2, are distributed independently and identically as the following Chi‐square distribution, that is
for j = 1, 2, …, (n − 1)/2, are distributed independently and identically as the following Chi‐square distribution, that is![]() is an unbiased estimate, since the sample spectrum is only defined at the Fourier frequencies and its variance is independent of the sample size n, it is a rather poor estimate of the spectrum. To solve this problem, we introduce a suitable kernel or spectral window to smooth the sample spectrum, that is,
is an unbiased estimate, since the sample spectrum is only defined at the Fourier frequencies and its variance is independent of the sample size n, it is a rather poor estimate of the spectrum. To solve this problem, we introduce a suitable kernel or spectral window to smooth the sample spectrum, that is,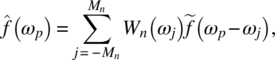
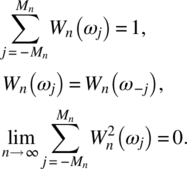
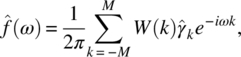
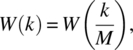
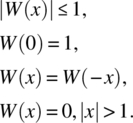
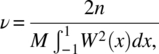
![]() has a distribution related to the Chi‐square distribution.
has a distribution related to the Chi‐square distribution. ![]() is an asymptotically unbiased estimate of f(ω) so that
is an asymptotically unbiased estimate of f(ω) so that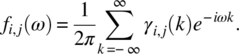
![]() for all i and j.
for all i and j.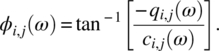
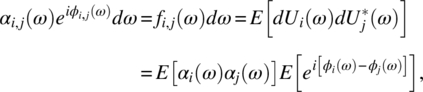
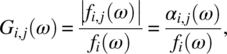
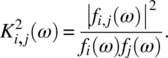
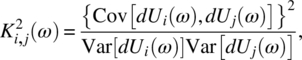
![]() close to 1 implies that the ω − frequency components of the two series are strongly linearly related, and a value of
close to 1 implies that the ω − frequency components of the two series are strongly linearly related, and a value of ![]() close to 0 implies that they are very weakly linearly related. It should be noted that just like the correlation coefficient between two random variables, the square coherency is invariant under linear transformations.
close to 0 implies that they are very weakly linearly related. It should be noted that just like the correlation coefficient between two random variables, the square coherency is invariant under linear transformations.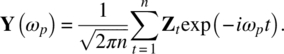
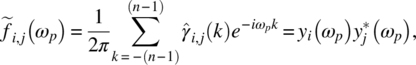
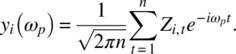
![]() has a distribution related to the sample variance–covariance matrix that is known as Wishart distribution with n degrees of freedom, which is the multivariate analog of the Chi‐square distribution. We refer readers to Goodman (1963), Hannan (1970), and Brillinger (2002) for further discussion of the properties of the periodogram and Wishart distribution.
has a distribution related to the sample variance–covariance matrix that is known as Wishart distribution with n degrees of freedom, which is the multivariate analog of the Chi‐square distribution. We refer readers to Goodman (1963), Hannan (1970), and Brillinger (2002) for further discussion of the properties of the periodogram and Wishart distribution.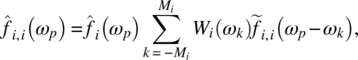
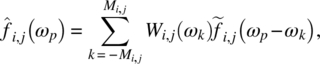
![]()
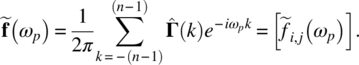
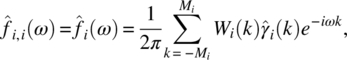
![]() is the sample autocovariance for the Zi,t series, Wi(k) is a suitable lag window, and Mi is the truncation point, and
is the sample autocovariance for the Zi,t series, Wi(k) is a suitable lag window, and Mi is the truncation point, and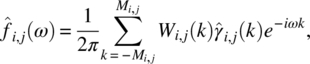
![]() is the sample cross‐covariance function between Zi,t and Zj,t, Wi,j(k) is a suitable lag window, and Mi,j is the corresponding truncation point. In this case, the estimations of the co‐spectrum, the quadrature spectrum, the cross‐amplitude spectrum, the phase spectrum, the gain function, and the squared coherency function are given by
is the sample cross‐covariance function between Zi,t and Zj,t, Wi,j(k) is a suitable lag window, and Mi,j is the corresponding truncation point. In this case, the estimations of the co‐spectrum, the quadrature spectrum, the cross‐amplitude spectrum, the phase spectrum, the gain function, and the squared coherency function are given by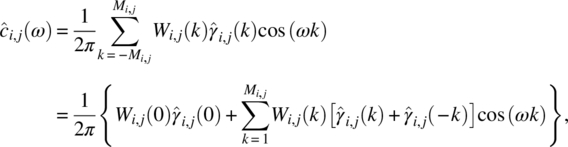
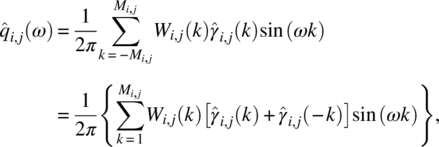
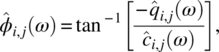
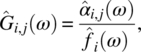
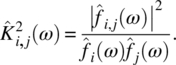
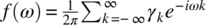 , it implies that the range of the frequencies is from −π to π. Given a time series of length n, due to symmetry, the Fourier frequencies used in the sample spectrum will be ωj = 2πj/n, with j = 0, 1, …, [n/2]. However, if one writes the spectral density as
, it implies that the range of the frequencies is from −π to π. Given a time series of length n, due to symmetry, the Fourier frequencies used in the sample spectrum will be ωj = 2πj/n, with j = 0, 1, …, [n/2]. However, if one writes the spectral density as 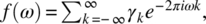 it implies that the range of the frequencies will be −1/2 to 1/2. In this case, the frequencies used in the sample spectrum will be ωj = j/n, with j = 0, 1, …, [n/2]. In the following discussions, we may use either one depending on what is used in software and the referenced papers.
it implies that the range of the frequencies will be −1/2 to 1/2. In this case, the frequencies used in the sample spectrum will be ωj = j/n, with j = 0, 1, …, [n/2]. In the following discussions, we may use either one depending on what is used in software and the referenced papers.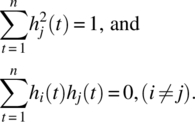
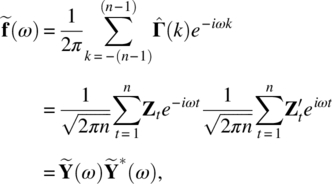
![]() is the discrete Fourier transform of Zt. The multitaper power spectral estimator at frequency ω is
is the discrete Fourier transform of Zt. The multitaper power spectral estimator at frequency ω is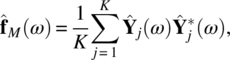
![]() is the tapered Fourier transform such that
is the tapered Fourier transform such that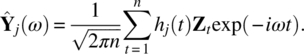
![]() Consequently, the first of the sequences, {h1(t), t = 1, …, n}, is chosen such that its corresponding spectral window or taper maximizing the concentration ratio in Eq. (9.63) over the interval (−W, W), which is equal to λ1(n,W). This is done by maximizing the power
Consequently, the first of the sequences, {h1(t), t = 1, …, n}, is chosen such that its corresponding spectral window or taper maximizing the concentration ratio in Eq. (9.63) over the interval (−W, W), which is equal to λ1(n,W). This is done by maximizing the power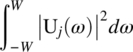
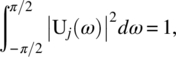
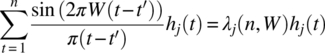
![]() through sine multitapers as shown in Eq. (9.65). Then, it further smooths the Cholesky components of the spectral matrix via the smoothing spline and penalized sum of squares, which allows different degrees of smoothness for different Cholesky elements.
through sine multitapers as shown in Eq. (9.65). Then, it further smooths the Cholesky components of the spectral matrix via the smoothing spline and penalized sum of squares, which allows different degrees of smoothness for different Cholesky elements.![]() has Cholesky decomposition such that
has Cholesky decomposition such that ![]() , where Γ is m × m lower triangular matrix. To obtain unique decomposition, the diagonal elements of Γ are constrained to be positive. The diagonal elements γj,j, j = 1, …, m, the real part of γj,k, ℜ(γj,k), and imaginary part of γj,k, ℑ(γj,k), j > k are smoothed by spline with different smoothing parameters. Suppose γ ∈ {γj,j, ℜ(γj,k), ℑ(γj,k), j > k, for j,k = 1, …, m}, we have
, where Γ is m × m lower triangular matrix. To obtain unique decomposition, the diagonal elements of Γ are constrained to be positive. The diagonal elements γj,j, j = 1, …, m, the real part of γj,k, ℜ(γj,k), and imaginary part of γj,k, ℑ(γj,k), j > k are smoothed by spline with different smoothing parameters. Suppose γ ∈ {γj,j, ℜ(γj,k), ℑ(γj,k), j > k, for j,k = 1, …, m}, we have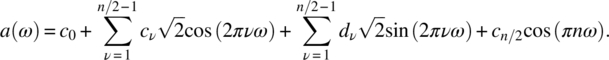
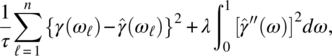
![]() is the estimator of γ(ωℓ); and λ is a smoothing parameter. The final form of the estimator is given by
is the estimator of γ(ωℓ); and λ is a smoothing parameter. The final form of the estimator is given by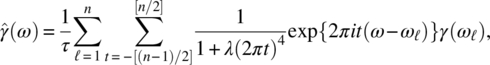
![]() , ℓ = 0, …, (n − 1)/2, are approximately independent complex multivariate normal random variables. The large‐sample distribution of
, ℓ = 0, …, (n − 1)/2, are approximately independent complex multivariate normal random variables. The large‐sample distribution of ![]() leads to the Whittle likelihood (Whittle, 1953, 1954),
leads to the Whittle likelihood (Whittle, 1953, 1954),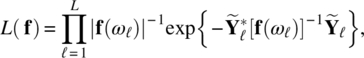

![]() . Let
. Let ![]() Θ = (θ1, …, θL), and D = {D1, …, DL},the modified Cholesky representation facilitates development of Bayesian sampler by noticing that the Whittle likelihood can be rewritten as
Θ = (θ1, …, θL), and D = {D1, …, DL},the modified Cholesky representation facilitates development of Bayesian sampler by noticing that the Whittle likelihood can be rewritten as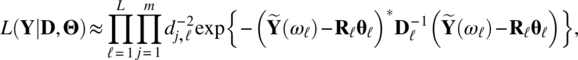

![]() . Let
. Let ![]() and
and ![]() Each component of the Cholesky decomposition is fitted by the Demmler–Reinsch basis functions for linear smoothing splines of Eubank and Hsing (2008) as follows
Each component of the Cholesky decomposition is fitted by the Demmler–Reinsch basis functions for linear smoothing splines of Eubank and Hsing (2008) as follows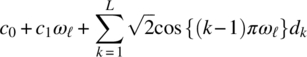
![]() be the associated parameters. We then have
be the associated parameters. We then have![]() and the priors on dj, dj,k, (re), and dj,k, (im) are chosen to be L–dimensional normal distributions
and the priors on dj, dj,k, (re), and dj,k, (im) are chosen to be L–dimensional normal distributions ![]() ,
, ![]() , and
, and ![]() , respectively. The hyperparameters
, respectively. The hyperparameters ![]()
![]() , and
, and ![]() are smoothing parameters, which control the amount of smoothness. As the smoothing parameters tend to zero, the spline becomes a linear fit; as the smoothing parameters tend to infinity, the spline will be an interpolating spline. Gibbs sampling with the Metropolis–Hastings algorithm is used to draw parameters from posterior distribution.
are smoothing parameters, which control the amount of smoothness. As the smoothing parameters tend to zero, the spline becomes a linear fit; as the smoothing parameters tend to infinity, the spline will be an interpolating spline. Gibbs sampling with the Metropolis–Hastings algorithm is used to draw parameters from posterior distribution.![]() are discrete Fourier transform of the time series, and define the negative log Whittle likelihood as
are discrete Fourier transform of the time series, and define the negative log Whittle likelihood as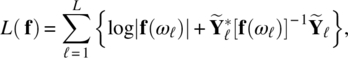
![]() is
is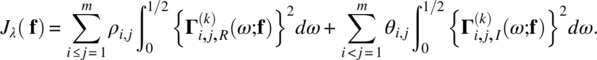
![]() at is a sequence of m‐dimensional vector white noise process, VWN(0, Σ), and
at is a sequence of m‐dimensional vector white noise process, VWN(0, Σ), and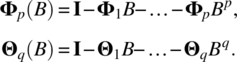
![]() and the sequence Ψj is square summable. The spectral density matrix of VARMA(p, q) model is given by
and the sequence Ψj is square summable. The spectral density matrix of VARMA(p, q) model is given by![]() and Ψ*(e−iω) is its conjugate transpose.
and Ψ*(e−iω) is its conjugate transpose.![]()
![]() and
and ![]() be the corresponding estimates of the parameter matrices. We have
be the corresponding estimates of the parameter matrices. We have![]()
![]() and at is a sequence of m‐dimensional vector white noise,
and at is a sequence of m‐dimensional vector white noise, ![]() Then, the spectral density matrix estimation of the underlying process is given by
Then, the spectral density matrix estimation of the underlying process is given by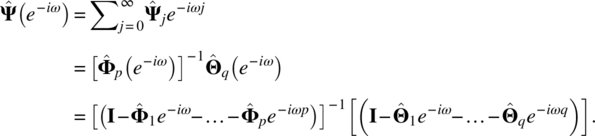
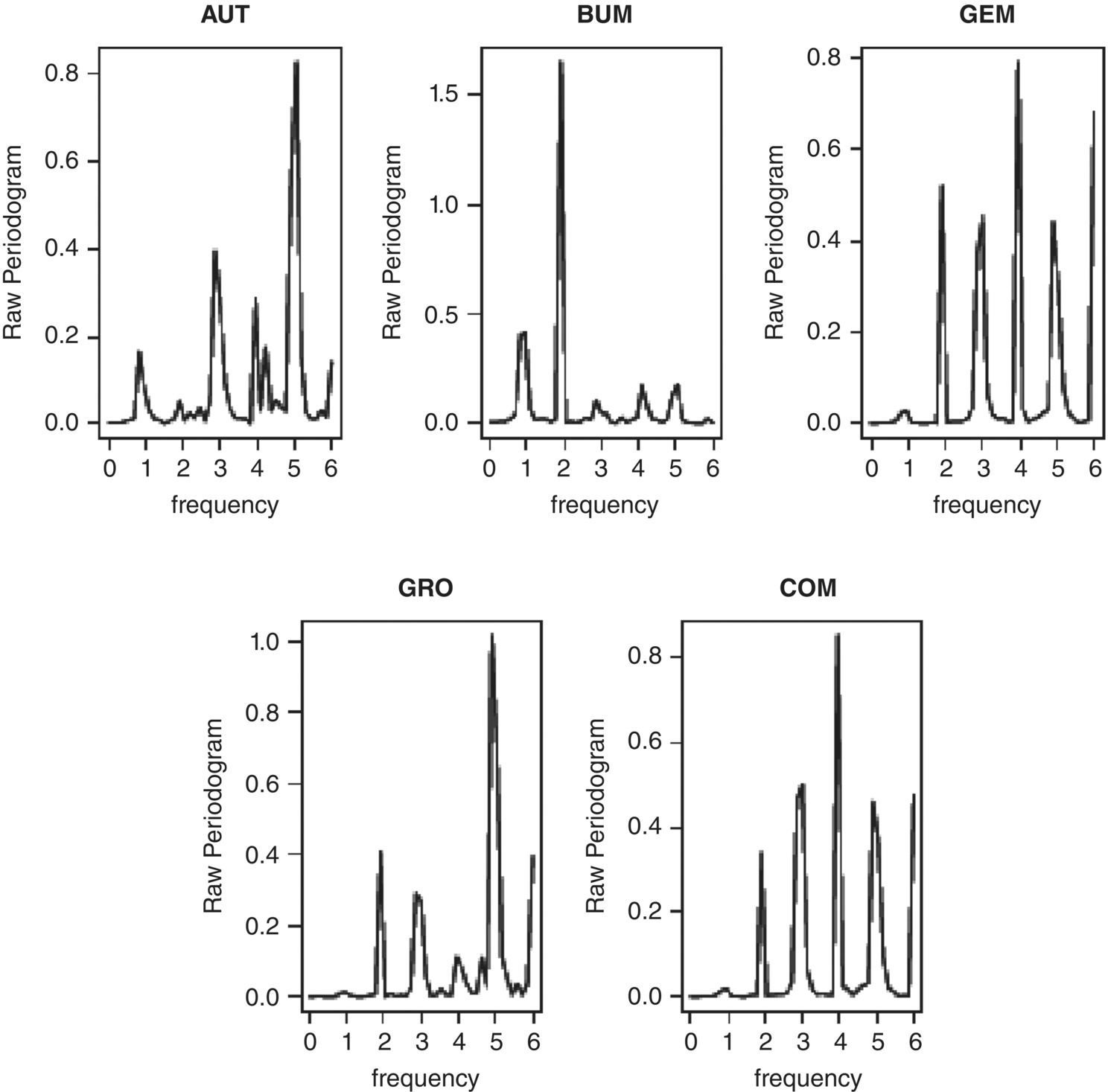
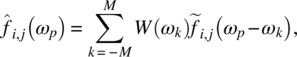
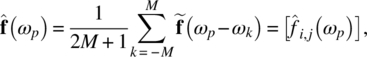
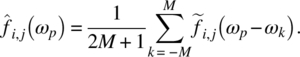
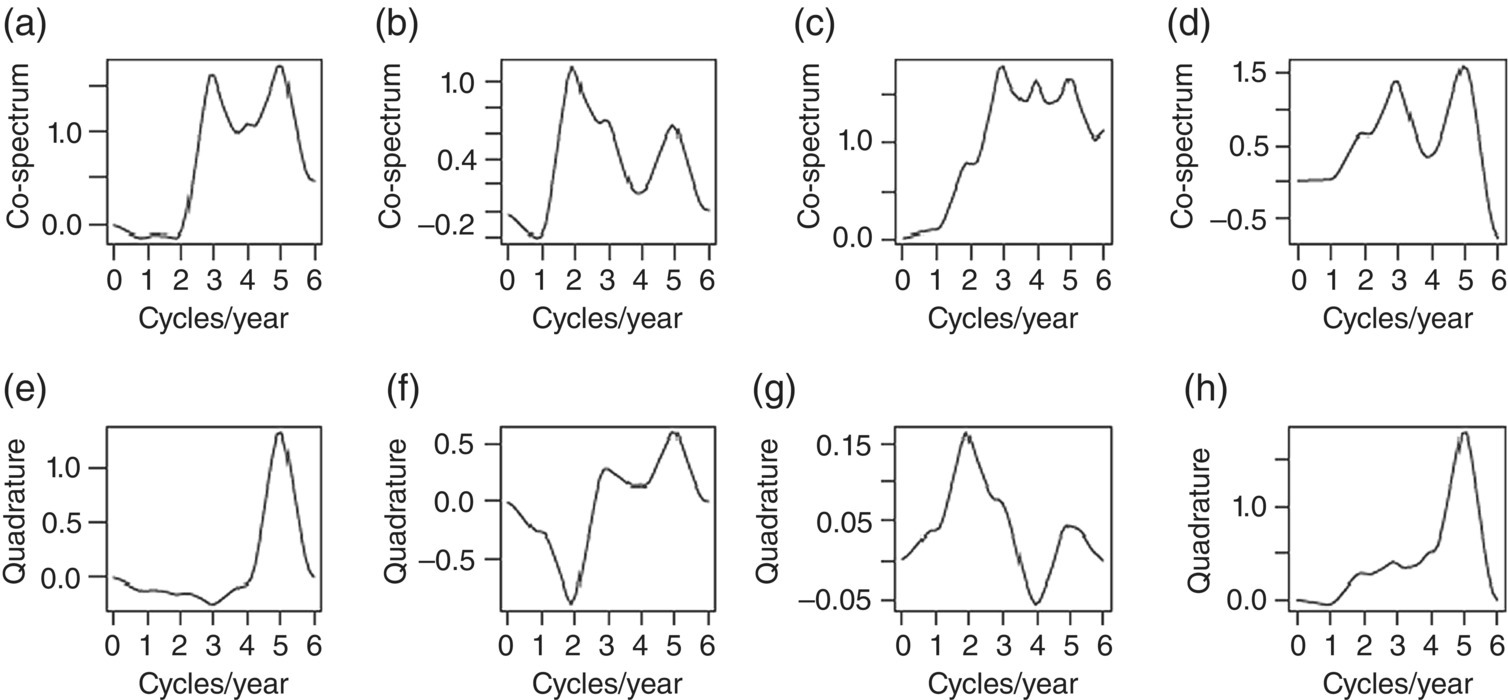
![]() are obtained, we can compute the estimated co‐spectra,
are obtained, we can compute the estimated co‐spectra, ![]() and the estimated quadrature spectra,
and the estimated quadrature spectra, ![]() as follows.
as follows.![]() and quadrature spectra,
and quadrature spectra, ![]() for j = 1, …, 4.
for j = 1, …, 4.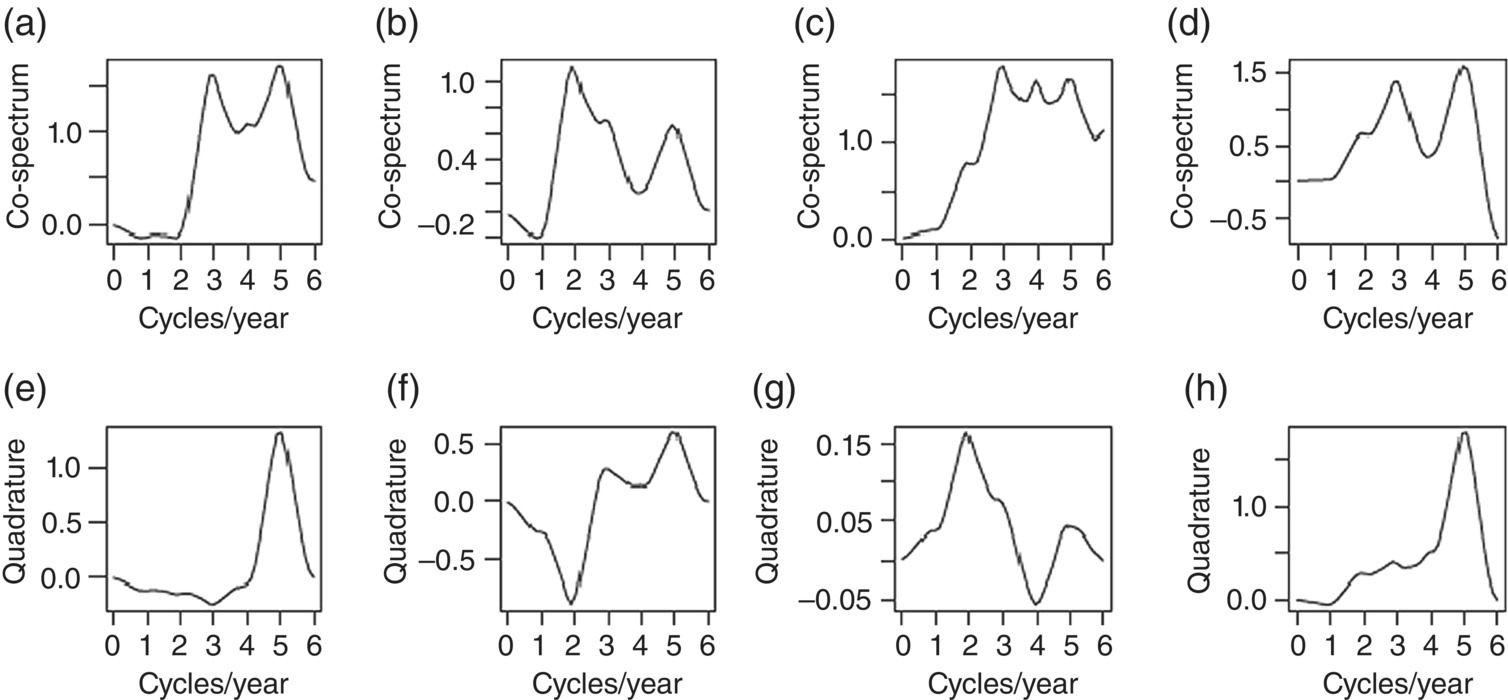
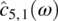 ,
, 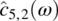 ,
, 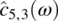 , and
, and 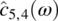 ; estimated quadrature spectra (e–h):
; estimated quadrature spectra (e–h): 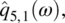
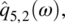
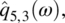 and
and 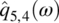 .
.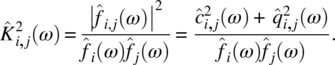
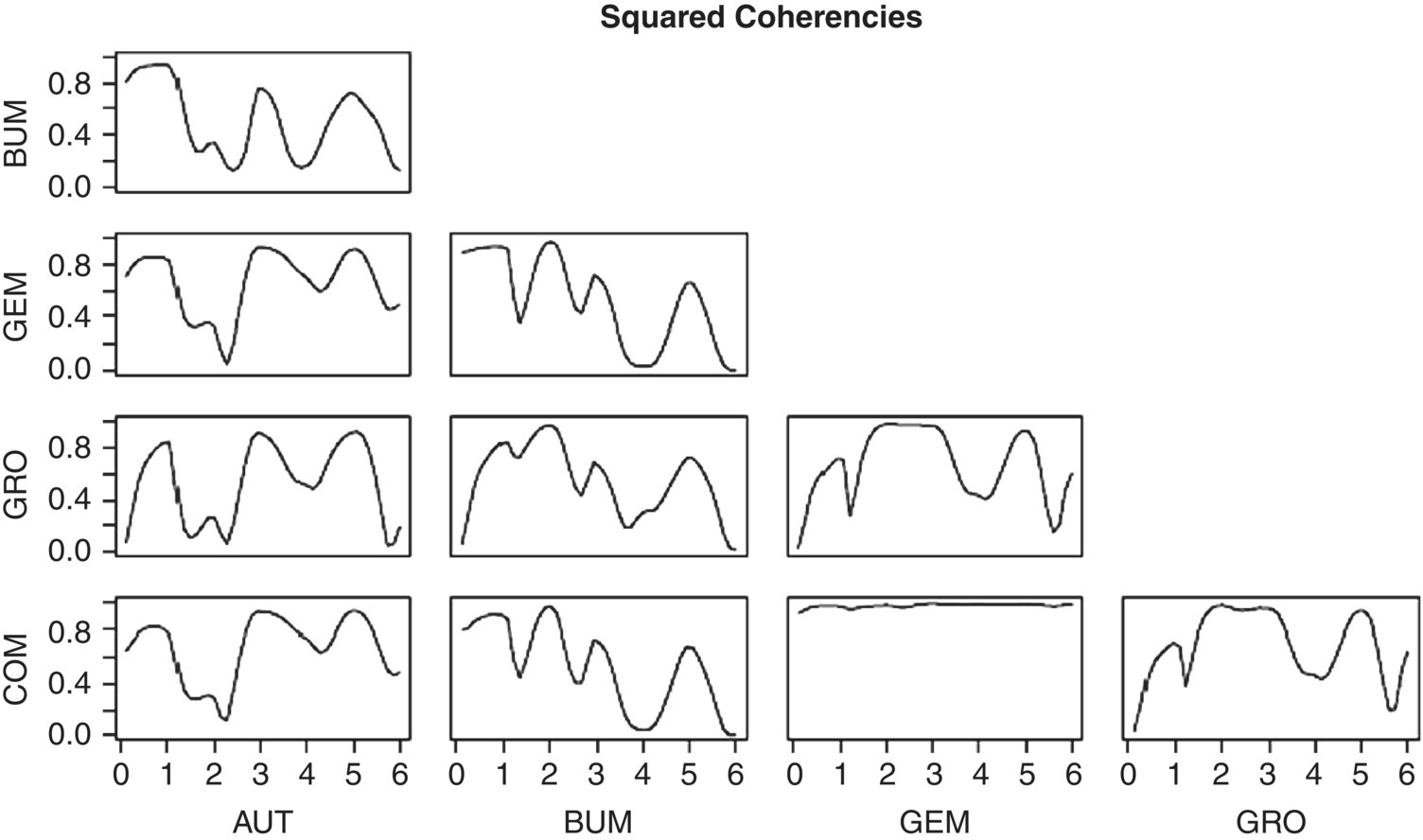
![]()
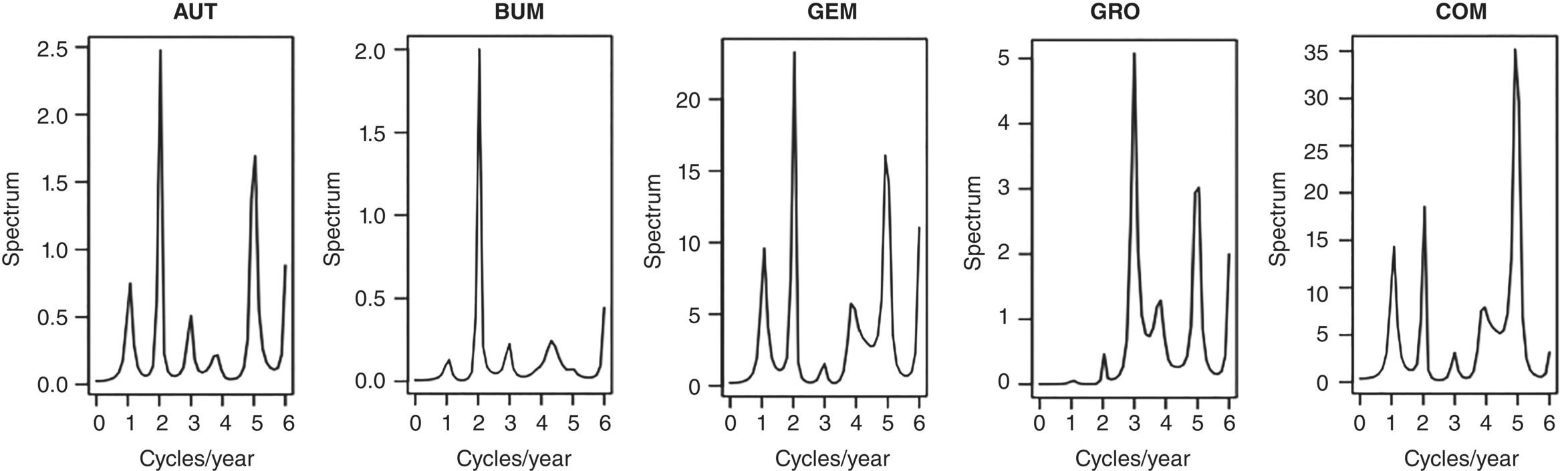
![]() and quadrature spectra,
and quadrature spectra, ![]() for j = 1, …, 4. Comparing with the kernel smoothed estimations given in Figure 9.4, again we see that there are some similarities and differences. However, the VAR estimation of the squared coherences as shown in Figure 9.10 is quite similar to the kernel estimation from Figure 9.5. Both estimation methods show that the estimated squared coherence between COM and GEM is large and constant across all frequencies, indicating a strong relationship between sales changes of consumer materials and general merchandise.
for j = 1, …, 4. Comparing with the kernel smoothed estimations given in Figure 9.4, again we see that there are some similarities and differences. However, the VAR estimation of the squared coherences as shown in Figure 9.10 is quite similar to the kernel estimation from Figure 9.5. Both estimation methods show that the estimated squared coherence between COM and GEM is large and constant across all frequencies, indicating a strong relationship between sales changes of consumer materials and general merchandise.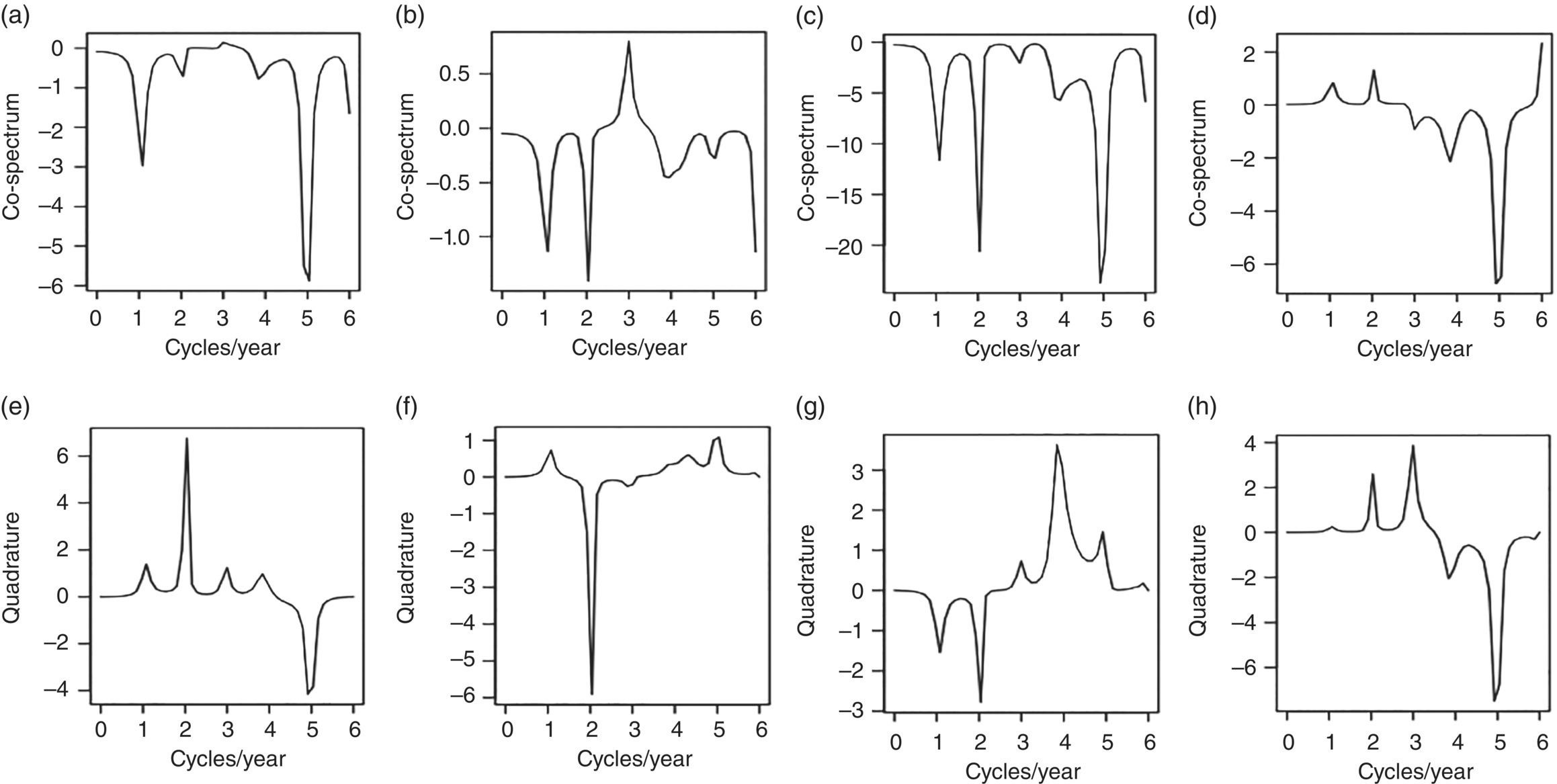
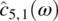 ,
, 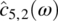 ,
, 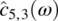 ,
, 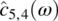 and estimated quadrature spectra (e–h):
and estimated quadrature spectra (e–h):  ,
, 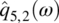 ,
, 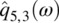 , and
, and 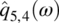 from the VAR(4) model.
from the VAR(4) model.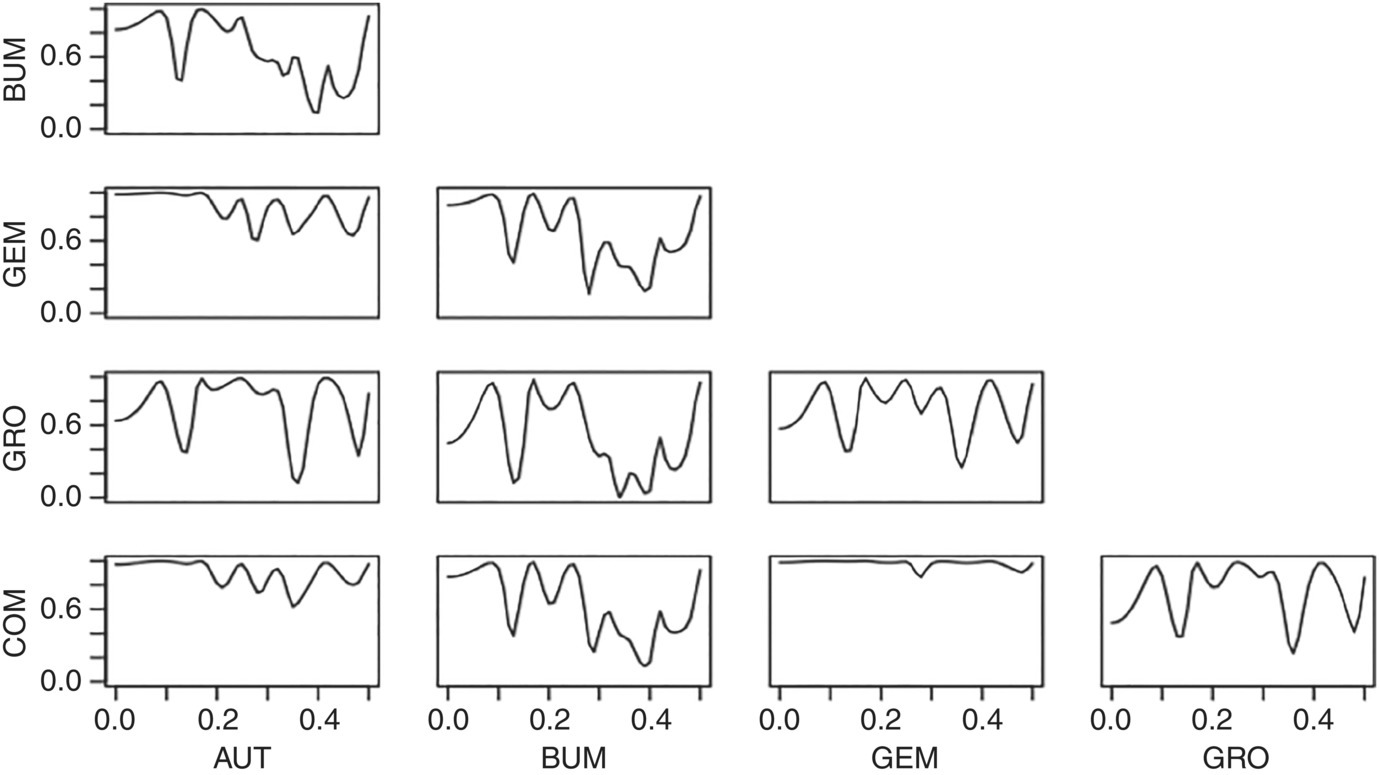
![]() given in Eq. (9.1), because the function ϕ(ω) = eiωt as a sine and cosine waves is stationary. Priestley (1965, 1966, and 1967) has pointed out that in this case, instead of using ϕ(ω) = eiωt, we need to consider an oscillatory function, which is a generalized Fourier transform,
given in Eq. (9.1), because the function ϕ(ω) = eiωt as a sine and cosine waves is stationary. Priestley (1965, 1966, and 1967) has pointed out that in this case, instead of using ϕ(ω) = eiωt, we need to consider an oscillatory function, which is a generalized Fourier transform,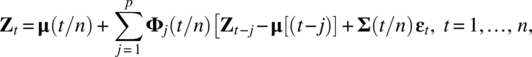
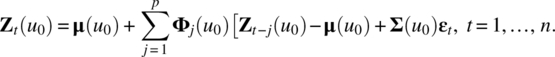
![]() has the Cholesky decomposition such that
has the Cholesky decomposition such that ![]() where L(u,ω) is a m × m lower triangular matrix. The method smooths the diagonal elements γj,j(u,ω), j = 1, …, m, the real part of γj,k(u,ω), ℜ{γj,k(u,ω)}, and the imaginary part of γj,k(u,ω), ℑ{γj,k(u,ω)}, for j > k separately with their own smoothing parameters. Let γ(u,ω) ∈ {γj,j(u,ω), ℜ(γj,k)(u, ω), ℑ(γj,k)(u,ω), j > k, for j, k = 1, …, m}. We have
where L(u,ω) is a m × m lower triangular matrix. The method smooths the diagonal elements γj,j(u,ω), j = 1, …, m, the real part of γj,k(u,ω), ℜ{γj,k(u,ω)}, and the imaginary part of γj,k(u,ω), ℑ{γj,k(u,ω)}, for j > k separately with their own smoothing parameters. Let γ(u,ω) ∈ {γj,j(u,ω), ℜ(γj,k)(u, ω), ℑ(γj,k)(u,ω), j > k, for j, k = 1, …, m}. We have![]() For the details, see Guo and Dai (2006).
For the details, see Guo and Dai (2006).![]() are m × m dimensional coefficient matrices of the VAR process. We define the entire class of piecewise VAR models as M and a model from this class as F ∈ M. The principle of MDL is to find the best fitting model from M as the one that produces the shortest code length. The code length of an object is the amount of memory space required to store the data Zt. The MDL has two components, a fitted model
are m × m dimensional coefficient matrices of the VAR process. We define the entire class of piecewise VAR models as M and a model from this class as F ∈ M. The principle of MDL is to find the best fitting model from M as the one that produces the shortest code length. The code length of an object is the amount of memory space required to store the data Zt. The MDL has two components, a fitted model ![]() and the portion that is unexplained by
and the portion that is unexplained by ![]() . The later component can be defined as the residuals
. The later component can be defined as the residuals ![]() . Let
. Let ![]() be the code length of fitted model
be the code length of fitted model ![]() and
and ![]() be the code length of the residuals of the jth segment. Then, the total code length of the data can be decomposed to
be the code length of the residuals of the jth segment. Then, the total code length of the data can be decomposed to![]() , we can further decompose
, we can further decompose ![]() by
by![]() . On the other hand, if integer I is upper‐bounded say IU, then log2IU bits are needed. Since nj is bounded by n, we have L(nj) = log2n and L(n1, …, nk) = klog2n (Hansen and Yu, 2001). It is known that a maximum likelihood estimate of a real parameter computed from n observations can be effectively encoded with (1/2)log2n bits. Because the total number of parameters in
. On the other hand, if integer I is upper‐bounded say IU, then log2IU bits are needed. Since nj is bounded by n, we have L(nj) = log2n and L(n1, …, nk) = klog2n (Hansen and Yu, 2001). It is known that a maximum likelihood estimate of a real parameter computed from n observations can be effectively encoded with (1/2)log2n bits. Because the total number of parameters in ![]() is (pj + 1)m2, we have
is (pj + 1)m2, we have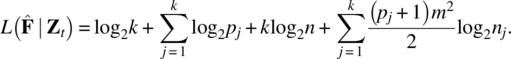
![]() is approximated by the negative of the loglikelihood of the fitted model
is approximated by the negative of the loglikelihood of the fitted model ![]() . Thus, we have
. Thus, we have