CHAPTER SIXTEEN: Security and Encryption

Chapter opener image: © Fon_nongkran/Shutterstock
Introduction
Security is a very important concern for every user of a computer in general, and a mobile device in particular. Valuable data, such as credit card numbers, can be stolen if not properly protected. One way to protect data is to encrypt it. As technology evolves and computers get more and more powerful, encryption algorithms that were once thought to be robust and safe may become weaker. When choosing an encryption algorithm, it is wise to check that it is still safe at the time we use it. In this chapter, we learn about various encryption algorithms and how we can use them to encrypt data.
16.1 Symmetric and Asymmetric Encryption
Encryption typically involves using a particular algorithm and a key in order to encrypt a message. A key is usually a string of characters. In cryptography, in order to test the strength of an encryption algorithm, we typically assume that the algorithm is known and assess the difficulty of finding its associated key. Thus, in addition to understanding how an encryption algorithm works, it is also important to understand how to generate a key for that algorithm.
An encryption system can be one way or two ways. One way means that once we have encrypted something, it is not possible to decrypt it. A one-way encryption system can be used to encrypt passwords. Usernames and encrypted passwords are typically stored in a database located on a server. Users connect to that server from a remote location and log in. The plaintext passwords are only known by the individual users and never stored on the server. Because the encryption process takes place on the server side and not on the client side, we do not cover one-way encryption in this chapter.
A two-way encryption system can be either symmetric or asymmetric. Symmetric encryption means that the key used to encrypt the plain message is the same as the key used to decrypt the encrypted message: there is only one key. That means that both the sender and the recipient of the message need to have that key. That, in turn, means that at least one person must have given the key to the other person. Since that key is secret, a challenge is to distribute that key in a secure manner, so that nobody else has access to it. If more than two people are involved, the challenge is even greater. People can decide to use a different key every time they send a message, in order to decrease the risk of having the key stolen by a third party. As always, there is a trade-off between practicality and security.
Asymmetric encryption means that the key used to encrypt the plain message is different from the key used to decrypt the encrypted message: there are two keys. One such system is RSA, which stands for Rivest, Shamir, and Adleman, its three inventors. In the RSA system, every person has a set of two keys, a public one (published) and a private one (secret). For example, if Alice and Bob are two users of the system, Alice can send a message to Bob, encrypting the message using the public key of Bob as follows:
encryptedMessage1 = rsa( publicKeyBob, message1 )
Alice knows Bob’s public key because it is public and published. Because that message has been encrypted using Bob’s public key, it can only be decrypted using Bob’s private key. Since Bob’s private key is private and secret, only Bob knows it. Thus, only Bob can decrypt that message. Bob decrypts the message as follows:
decryptedMessage1 = rsa( privateKeyBob, encryptedMessage1 )
Bob can reply to Alice, encrypting a message using Alice’s public key as follows:
encryptedMessage2 = rsa( publicKeyAlice, message2 )
Bob knows Alice’s public key because it is public and published. Because that message has been encrypted using Alice’s public key, it can only be decrypted using Alice’s private key. Since Alice’s private key is private and secret, only Alice knows it. Thus, only Alice can decrypt that message. Alice decrypts the message as follows:
decryptedMessage2 = rsa( privateKeyAlice, encryptedMessage2 )
RSA relies on the fact that finding the factors of a very large composite number is very hard. A composite number is the product of two prime numbers. For example, 143, which is equal to 13 times 11, is a composite number. The underlying mathematical foundations of RSA include group theory and modular algebra.
16.2 Symmetric Encryption: The Model (AES), Encryption App, Version 0
In Version 0, we explore symmetric encryption via a simple app. We also look into the issue of key distribution. We build a Model for encrypting and decrypting text using symmetric encryption and test it. There are many symmetric encryption algorithms available in the Android library. We use Advanced Encryption Standard (AES). We can access the list of encryption algorithms available on a device via the Security class by calling its getProviders method, and then iterating through all the providers. This is beyond the scope of this chapter.
The javax.crypto package contains classes and interfaces that encapsulate cryptology concepts, such as Cipher, KeyGenerator, and SecretKey. The Cipher class provides access to implementations of encryption and decryption algorithms. All of its methods are final (i.e., we cannot override them). TABLE 16.1 shows some selected methods of the Cipher class. Cipher does not have a public constructor. We use its getInstance static method to get a reference to a Cipher object. The parameter of the getInstance method is a String representing the name of the encryption algorithm, for example, AES. The doFinal method encrypts or decrypts an array of bytes into another array of bytes. Before calling doFinal, we should call the init method in order to specify three things:
▸ Whether
doFinalis going to encrypt or decrypt (the operation mode).▸ The encryption/decryption key.
▸ An element of randomness.
TABLE 16.1 Selected methods of the Cipher class
| Method | Description |
|---|---|
| public static Cipher getInstance( String transformation ) | Returns a Cipher for transformation, the name of an encryption algorithm. Throws a NoSuchAlgorithmException and a NoSuchPaddingException. |
| public byte [ ] doFinal( byte [ ] input ) | Encrypts input and other previously buffered bytes, and returns the resulting encrypted bytes. Throws an IllegalBlockSizeException, a BadPaddingException, and an IllegalStateException. |
| public void init( int opMode, Key key, SecureRandom random ) | Initializes this Cipher with the operation opMode, key and with random as a randomness source. Throws an InvalidKeyException and an IllegalParameterException. |
TABLE 16.2 Selected constructor of the SecureRandom class
| Method | Description |
|---|---|
| public SecureRandom( ) | Constructs a SecureRandom object using the default algorithm. We can use it to generate pseudo-random numbers. |
TABLE 16.3 Selected methods of the KeyGenerator class
| Method | Description |
|---|---|
| public static KeyGenerator getInstance( String algorithm ) | Returns a KeyGenerator that can generate a key for an encryption algorithm named algorithm. Throws a NoSuchAlgorithmException and a NullPointerException. |
| public void init( int keySize ) | Initializes this KeyGenerator for a key whose size is keySize bits. |
| public SecretKey generateKey( ) | Returns a SecretKey reference for this KeyGenerator. |
We can use the ENCRYPT_MODE and DECRYPT_MODE constants of the Cipher class to specify the mode, encryption or decryption. Key is an interface so it cannot be instantiated. The Secret-Key class implements the Key interface and encapsulates a secret key for a symmetric encryption algorithm. Thus, we can use it for the second parameter of init.
The third parameter’s type is SecureRandom. The SecureRandom class encapsulates the ability to generate cryptographically secure pseudo-random numbers. We can instantiate a SecureRandom object using the default constructor of the SecureRandom class, a subclass of Random, shown in TABLE 16.2. We can use the KeyGenerator class, shown in TABLE 16.3, to create a SecretKey. KeyGenerator does not have a public constructor. We use the getInstance static method to get a reference to a KeyGenerator object. The parameter of the getInstance method is a String representing the name of the encryption algorithm, for example, AES. The generateKey method returns a secret key of type SecretKey. Before calling generateKey, we should call the init method in order to specify the size of the key in bits.
We first write a class, part of our Model, to encapsulate the ability to encrypt and decrypt a String using the AES algorithm. EXAMPLE 16.1 shows the AESEncryption class. We can use it to generate a secret key and also to perform encryption and decryption using any key. It has a default constructor, two accessors for the secretKey instance variable, and the crypt method, which we can use to encrypt or decrypt a String. We need a SecretKey, a Cipher, and a SecureRandom reference in order to encrypt or decrypt a String. Thus, we declare three instance variables (secretKey, cipher, and rand) of these types (lines 11–13) so we can access them in the crypt method. Inside the constructor (lines 15–24), we instantiate cipher at line 17 and rand at line 18. We instantiate a KeyGenerator object for the AES algorithm at line 19, initialize it with a key size of 256 bits at line 20, and instantiate secretKey with it at line 21. We catch either a NoSuchAlgorithmException or a NoSuchPaddingException at line 22.

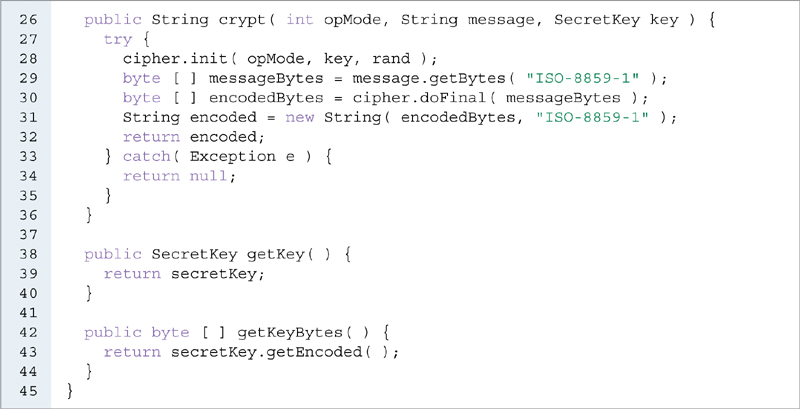
EXAMPLE 16.1 The AESEncryption class of the Encryption app, Version 0
We provide two accessors for the key of the algorithm, secretKey. The first one, getSecretKey, (lines 38–40), returns secretKey. The second one, getKeyBytes (lines 42–44), returns a representation of secretKey as an array of bytes. Generally, we need to distribute a key to remote users. If we want to distribute a key electronically, we can send an array of bytes to a user via a secure connection, using the getKeyBytes method to get a byte array representation of the key. We can also encrypt a key when we send it. Inside getKeyBytes, we call the getEncoded method of SecretKey, inherited from the Key interface, and shown in TABLE 16.4.
We can use the crypt method (lines 26–36) to either encrypt or decrypt a String using a given key. Its first parameter specifies whether we encrypt or decrypt. If we want to encrypt, we pass Cipher.ENCRYPT_MODE as the first argument. If we want to decrypt, we pass Cipher.DECRYPT_MODE. The third parameter represents an encryption key. In this example, we pass the key of this AESEncryption object. We initialize cipher using the mode specified by opMode with the key parameter key and rand (line 28). The doFinal method accepts an array of bytes parameter, so we convert the String parameter into an array of bytes at line 29. We use the ISO-8859-1 encoding standard to convert the array of bytes to a String: ISO-8859-1 is the default encoding standard for transmitting documents via the HTTP protocol with the MIME type; it provides a one-to-one mapping between a String and an array of bytes. At line 30, we call doFinal to crypt that array of bytes into another array of bytes, and convert that array of bytes to a String at line 31. We return that String at line 32. We catch all possible Exceptions at line 33 and return null at line 34 if an Exception occurs.
TABLE 16.4 The getEncoded method of the Key interface
| Method | Description |
|---|---|
| byte [ ] getEncoded( ) | Returns the encoded form of this Key as an array of bytes. |
In the MainActivity class, shown in EXAMPLE 16.2, we use the AESEncryption class to encrypt a String and decrypt its encrypted version into the original String. We also test that we can convert a key to an array of bytes, reconstruct a key from that array of bytes, and that the reconstructed key matches the original key. That is the type of operation that happens when we distribute a key electronically. At line 20, we instantiate aes, an AESEncryption instance variable. We encrypt the String original at lines 25–26 and output the encrypted String to Logcat the result at line 27. We decrypt the encrypted String at lines 28–29 and output the result to Logcat at line 30, which, as FIGURE 16.1 shows, is identical to the String we started with.


EXAMPLE 16.2 The MainActivity class of the Encryption app, Version 0
At lines 32–45, we simulate distributing a key and check that the key received matches the key sent. We start with the key of aes and convert it to an array of bytes at lines 32–33. At lines 34–36, we output the array of bytes as an object and a String equivalent of that array of bytes. We then assume that that array of bytes is sent to a user and reconstruct a key with it at lines 38–39. We retrieve the equivalent array of bytes for that reconstructed key at lines 40–41. Finally, at lines 42–45, we output the array of bytes as an object and a String equivalent of that array of bytes.

FIGURE 16.1 Logcat output from the Encryption app, Version 0
Figure 16.1 shows the output in Logcat. We can see two things: the memory addresses for both arrays of bytes are different, and their values are identical. Thus, this example shows that we can transfer a key from one user to another by transferring bytes.
16.3 Symmetric Encryption: Adding a View, Encryption App, Version 1
In Version 1, we add a user interface to enable the user to enter a String. We provide a button to encrypt that String and decrypt the encrypted String, thus, retrieving the original String.
EXAMPLE 16.3 shows the activity_main.xml file. We use a RelativeLayout to organize the various elements. We also make references to styles and strings defined in the styles.xml and strings.xml files. The styles.xml file uses colors that we have defined in the colors.xml file. EXAMPLES 16.4, 16.5, and 16.6 show those three files. The activity_main.xml file includes three TextViews on the left that we use as labels for the EditText (lines 20–26) and the two TextViews on the right (lines 37–42 and 53–58). We give ids to these three elements (lines 21, 38, 54) so we can retrieve them using the findViewById method in the MainActivity class. When the user enters something in the EditText and clicks on the button (lines 60–66), the encryptAndDecryptAES method executes (line 66). We update the two TextViews on the right accordingly, showing the encrypted String and the result of decrypting the encrypted String.


EXAMPLE 16.3 The activity_main.xml file of the Encryption app, Version 1

EXAMPLE 16.4 The strings.xml file of the Encryption app, Version 1

EXAMPLE 16.5 The colors.xml file of the Encryption app, Version 1


EXAMPLE 16.6 The styles.xml file of the Encryption app, Version 1
EXAMPLE 16.7 shows the MainActivity class. Inside the encryptAndDecryptAES method (lines 21–34), we retrieve user input and update the two TextViews on the right side of the screen. We get references to the EditText and the two TextViews at lines 22, 26–27, and 29–30. At line 23, we retrieve the user input. At lines 24–25, we encrypt it. We place the result in the TextView in the middle right of the screen at line 28. We decrypt the encrypted String at lines 31–32 and place the result in the other TextView at line 33.


EXAMPLE 16.7 The MainActivity class of the Encryption app, Version 1
FIGURE 16.2 shows the app running inside the emulator after the user typed in Android is fun and clicked on the button.

FIGURE 16.2 The Encryption app, Version 1, running inside the emulator
16.4 Asymmetric Encryption: Adding RSA to the Model, Encryption App, Version 2
In Version 2, we add RSA encryption to our Model and test it in the MainActivity class. We can use the RSAEncryption class, shown in EXAMPLE 16.8, to generate a set of private and public keys, and also to perform encryption and decryption using any key. This design is similar to the AESEncryption class. We declare three instance variables at lines 11–13: cipher, a Cipher reference, and the two keys—privateKey and publicKey. The constructor, at lines 15–25, instantiates cipher at lines 17 and generates the two keys at lines 18–22.


EXAMPLE 16.8 The RSAEncryption class of the Encryption app, Version 2
The KeyPairGenerator class has methods to generate a KeyPair, which encapsulates a pair of keys, one private and one public. TABLE 16.5 shows methods of these two classes. The KeyPairGenerator class is abstract and cannot be instantiated. However, we can use its getInstance static method to get a reference to a KeyPairGenerator (line 18). The getInstance method accepts a String parameter that represents the algorithm that the KeyPairGenerator will use to generate a KeyPair. The genKeyPair method (called at line 20) returns a KeyPair: we can retrieve the two keys using the getPrivate and getPublic methods of the KeyPair class (lines 21 and 22). The getPrivate and getPublic methods return a PrivateKey and PublicKey, respectively. Both are interfaces that inherit from the Key interface. Thus, we can assign their return values to the privateKey and publicKey instance variables (lines 21 and 22).We provide accessors for the two keys at lines 27–29 and 31–33. We also provide accessors for the byte array representation of the two keys, so that they can be transferred electronically. We can transfer the public key to a central location, probably on a server, so that other users can retrieve it. If we provide client software that generates the keys, there is no need to transfer the private key to each user and therefore the risk of compromising one or more private keys is much lower. If we have to transfer the private key to a particular user in a secure manner, we can encrypt it using an algorithm like AES.
TABLE 16.5 Selected methods of the KeyPair and KeyPairGenerator classes
| Class | Method | Description |
|---|---|---|
| KeyPairGenerator | public static KeyPairGenerator getInstance( String algorithm ) | Returns a KeyPairGenerator that uses the specified algorithm. |
| KeyPairGenerator | initialize( int keySize ) | Initializes this KeyPairGenerator with keySize (in bits). |
| KeyPairGenerator | KeyPair genKeyPair( ) | Generates and returns a new KeyPair. |
| KeyPair | PrivateKey getPrivate( ) | Returns the private key of this KeyPair. |
| KeyPair | PublicKey getPublic( ) | Returns the public key of this KeyPair. |
The crypt method (lines 43–53) is identical to the crypt method of the AESEncryption class, except that it uses a Cipher reference for RSA instead of AES.
The MainActivity class, shown in EXAMPLE 16.9, demonstrates how we can use the RSAEncryption class. Because the RSA encryption algorithm is asymmetric, we perform two tests. We declare an RSAEncryption instance variable at line 15 and instantiate it at line 21. We first encrypt with the public key and decrypt with the private key (lines 24–32), then we encrypt with the private key and decrypt with the public key (lines 34–42). FIGURE 16.3 shows that in both scenarios, we end up with the original String after successively encrypting and decrypting. We two encrypted Strings illustrate that the encryption is not symmetric. As indicated on the figure, the encrypted Strings are much longer than shown.


EXAMPLE 16.9 The MainActivity class of the Encryption app, Version 2

FIGURE 16.3 Logcat output of the Encryption app, Version 2
16.5 Symmetric and Asymmetric Encryption: Modifying the View, Encryption App, Version 3
In Version 3, we present the user with three buttons: the first one triggers AES encryption and decryption, as before, and the other two trigger RSA encryption and decryption, using the two scenarios available to us:
▸ One encrypting with the private key and decrypting with the public key.
▸ The other one encrypting with the public key and decrypting with the private key.
We modify the activity_main.xml file, the View, and add two buttons. The two buttons are coded at lines 67–74 and 76–83 of EXAMPLE 16.10. We give the AES button an id (line 60) so we can position the two new buttons relative to it. Also, since we now have three buttons, the AES button is no longer centered. Because RSA encrypting results in a String much larger than AES encrypting, we specify a bigger margin than before between the first row and second row of components (line 30).
We also define the button_rsa1 and button_rsa2 Strings in strings.xml.



EXAMPLE 16.10 The activity_main.xml file of the Encryption app, Version 3
EXAMPLE 16.11 shows the updated MainActivity class. Because we need to access the GUI components in three different methods, we add three instance variables for them at lines 14–16. We instantiate them using the findViewById method at lines 24–26. Note that it is important to set the content View (line 23) before we retrieve them. Otherwise, they will be null and the app will eventually crash at runtime. The encryptAndDecryptRSA1 and encryptAndDecryptRSA2 methods are very similar to the encryptAndDecryptAES method. The encryptAndDecryptRSA1 method encrypts with the private key (lines 46–47) and decrypts with the public key (lines 49–50). The encryptAndDecryptRSA1 method encrypts with the public key (lines 56–57) and decrypts with the private key (lines 59–60).


EXAMPLE 16.11 The MainActivity class of the Encryption app, Version 3

FIGURE 16.4 The Encryption app, Version 3, after the user clicks on RSA 1

FIGURE 16.5 The Encryption app, Version 3, after the user clicks on RSA 2
FIGURES 16.4 and 16.5 show the app after the user enters Android is fun and clicks on the RSA 1 button and RSA 2 button, respectively.
Chapter Summary
Encryption algorithms can be one way (something encrypted cannot be decrypted), symmetric (the same key is used for encryption and decryption), or asymmetric (a different key is used for encryption and decryption).
The
javax.cryptopackage provides interfaces and classes that encapsulate various cryptology concepts and functionalities.We can use the
KeyGeneratorclass to generate a key for a symmetric encryption algorithm.We can use the
KeyPairGeneratorclass to generate a pair of keys for an asymmetric encryption algorithm.Classes that encapsulate a key provide methods to convert a key object to an array of bytes and to reconstruct a key from an array of bytes. In this way, we can transfer a key electronically. Key distribution is an important issue.
We can use the
SecureRandomclass to generate a cryptographically secure pseudo-random number.The
Cipherclass provides access to implementations of encryption and decryption algorithms.The
doFinalmethod of theCipherclass encrypts or decrypts an array of bytes into another array of bytes.We can use the
ISO-8859-1encoding standard to convert an array of bytes to aStringand vice versa. It provides a one-to-one mapping between aStringand an array of bytes.Before calling the
doFinalmethod to encrypt or decrypt, we callinitto specify the mode (encryption or decryption), the key, and set an element of randomness.

Exercises, Problems, and Projects
Multiple-Choice Exercises
An asymmetric encryption algorithm uses the same key for encryption and decryption
True
False
In what package do we find interfaces and classes that encapsulate cryptology concepts and functions?
java.crypto
javax.crypto
android.crypto
android.algorithm
What class can we use to generate a private key and its corresponding public key for the RSA algorithm?
Key
KeyGenerator
KeyPairGenerator
SecretKey
What is the name of the class that provides implementations of various encryption and encryption algorithms?
Crypt
Encrypt
RSA
Cipher
The doFinal method of the class in question 4 converts
An array of bytes to a String
A String to an array of bytes
A String to a String
An array of bytes to an array of bytes
The first parameter of the init method of the class in question 4 is an int. If we want to encrypt, what value can we use?
Cipher.ENCRYPT_MODE
Cipher.ENCRYPT
Cipher.DECRYPT
Cipher.DECRYPT_MODE
The first parameter of the init method of the class in question 4 is an int. If we want to decrypt, what value can we use?
Cipher.ENCRYPT_MODE
Cipher.ENCRYPT
Cipher.DECRYPT
Cipher.DECRYPT_MODE
Fill in the Code
Write the code to declare and instantiate a Cipher object for the AES algorithm.
Write the code to declare and instantiate a Cipher object for the RSA algorithm.
Write the code to declare and instantiate a KeyGenerator object for the AES algorithm.
Write the code to declare and instantiate a KeyPairGenerator object for the RSA algorithm.
The variable keyPair is a KeyPairGenerator reference and has already been instantiated for the RSA algorithm. Write the code to retrieve the array of bytes for its private key.
The variable keyPair is a KeyPairGenerator reference and has already been instantiated for the RSA algorithm. Write the code to retrieve the array of bytes for its public key.
A String named s has been initialized. Write the code to convert it to an array of bytes using the ISO-8859-1 encoding standard.
An array of bytes has been initialized with some values. Write the code to convert it into a String using the ISO-8859-1 encoding standard.
A Cipher reference named myCipher has been declared and instantiated. The key myKey has also been declared and instantiated. Write the code to initialize myCipher so that it is ready to encrypt something with myKey.
A Cipher reference named myCipher has been declared, instantiated, and initialized for encryption with some key. Write the code to encrypt the array of bytes myBytes. Assign the result to a variable of your choice.
Write an App
Code an app similar to Version 1 in this chapter. Choose an encryption algorithm different from AES.
Code an app similar to Version 1 in this chapter. Use the init method whose second parameter is a Certificate instead.
Code an app that sends an email. Encrypt the body of the email with AES.
Code an app, using RSA, asking the user to enter a sentence. One button encrypts the sentence with the private key of user 1 and the public key of user 2 and displays the result in a TextView (user 2 can decrypt the sentence knowing that it comes from user 1). Another button decrypts the result back to the original sentence and displays it in another TextView.
Make an app that encrypts some user input using a Caesar cipher (every letter on the alphabet is shifted by a fixed number: for example, if the shift is 3, a becomes d, b becomes e, etc.).
Look at the Security class from the java.security package. Make an app that uses that class in order to retrieve all the encryption algorithms that are supported by your Android devices.
