The Effects of Pulling, Pushing, and Twisting Forces

Solid objects move when a force is applied to them. If they are constrained, they may not move in some way you can see. However, they will get squeezed or stretched internally. The force generates internal stresses that can cause the material to break. The way an object moves internally is the key to understanding a material’s behavior under load.

Every type of material has a unique way of stretching or compressing. Some materials are viscous, like a fluid; others are elastic, like a solid. Some materials fall in between, such as plastic and blood. They flow like a liquid yet can be stretched and recover to their original dimension like a solid. These materials are called viscoelastic and will be discussed in Chapter 6. The relationship between the force produced by a load and the movement of the material defines how it can be used.

Although a force can only produce tension, compression, and shear, it is convenient to think of loads being applied to an object in five ways:

• Tension

• Compression

• Shear

• Torsion

• Flexure

Tension is simply a force that pulls apart an object’s molecules, while compression is the opposite of tension and is the squeezing of an object’s molecules. Most materials have a higher compressive strength than tensile strength.

Shear is a set of opposing forces in the same plane. For example, if the bottom of a plate is rigidly attached to a surface and then the top of the plate is pushed parallel to the surface, a shear force will be applied to the plate. The shear force occurs when the force at the bottom of the plate resists the force on top of the plate. These opposing forces are transmitted as a shear force in the plate. If the plate were made from a stack of papers, the shear force would readily allow the papers to slide across one another. The ability to bear a shearing stress is the feature that defines solids. Solids resist shearing forces while fluids (gases and liquids) will flow until the shearing stresses are gone.

Torsion is a twisting force. For example, a rod that is held rigid at one end while a rotating force is applied at the other end will experience a torsional force on the rod. The outer surface has the highest stress and the centerline will have zero stress. The behavior of a design can be very different when subject to torsional loads as opposed to flexural or other loads. It is for this reason cross bracing is used in many structures. For example, a box-shaped structure like a bookshelf can have its torsional deflection reduced 100 fold by including cross bracing. Simpler diagonal bracing is also very effective, but this design generally permits three times more deflection than cross bracing. Torsional rigidity can also be improved by incorporating closed members such as tubing rather than open members such as U channels.

Torsion is important to understand in a variety of applications, such as the bookshelf previously mentioned, but also propulsion systems where all the power is transmitted by torque. Not only can this torque tear apart shafts but it can produce torsional vibrations that need to be stopped by changing material properties or with dampeners. Helmets must be designed for more than impact loading; they must reduce the twisting of the head. This can be done with membranes that allow a sliding action to occur between the shell and the head.

Flexure is a load that does not fall in line with the central axis of a part, like standing at the end of a diving board. This is an extremely common loading condition and is produced by an offset load that creates tensile loading in one half of a part and compressive loading in another half. If a bar is supported at both ends and a load is applied in the center, the material on the same side of the centerline as the load will be in compression whereas the material on the opposite side of the load will be in tension. In addition, the stress varies with the distance from the centerline. Flexural stress is harder to understand than the other stresses because it is a function of a part’s shape. For example, an I-beam is much stronger in one plane than an equivalent mass of square steel. This will be considered in more detail later.

Tension, compression, shear, torsion, and flexure—now get a paper clip, stick, or a ruler and try them all out. Pull, push, shear, twist, and bend and see how it behaves. Notice the ruler twists pretty easy. It is rigid in one axis but it can easily be twisted and bent in other axes. Now try twisting a pen. It is torsionally rigid. What appear to be strong objects can be very weak in some stress conditions. You can park a car on a pile of papers, but they are easy to shear or pull apart. While this will all be good fun, you will need some squishy clay to really see the effect of compression. Figure 3-1 shows a summary of these loading conditions.

Figure 3-1. Common loading conditions; these create tensile and/or compressive stresses

Why does a designer care about this? Because only you know what loads might be applied to your design and you must understand the stresses these loads will produce. We will discuss later how the shape of your design will dictate the intensity of these stresses and therefore how strong and rigid your design is. These terms have different meanings: strong means your design won’t easily break; rigid means it won’t easily deform.

Static Loads

When considering the behavior of a design, we typically start with evaluating how loads and twisting action are transmitted through an object. Loads move objects. Either they accelerate and move or they make small internal movements called strain. If you are sitting on a teeter-totter with someone of equal weight on the other side, the teeter-totter is balanced in a state of equilibrium. If you push up with your legs, that force propels you up and the other person down until they push back on the ground. If you extend a ruler over the edge of a desk and push down on it, you can feel the load in the hand holding the other end. If you push down further from the edge of the ruler, the resisting force you have to apply increases. The reaction to a force and a distance is called a moment. Moment is also referred to as a couple or torque. Equilibrium requires that the summation of all forces and moments on an object be equal to zero. This study of how forces transmit through a stationary object is called statics.

The term load can be used loosely—when we stand on a floor, we are putting a load on it. However, the term describes two things: force and direction. In the case of the floor, the force is your body weight and the direction is down in line with gravity. The loads and moments upon which an object is subject depend on both the magnitude of the load and its distance from a support. For example, the deflection of an overhung (cantilever) beam is sixteen times that of a beam simply supported at both ends. You can experiment with a ruler and different supports to get a real sense for this behavior. This perception of loads is intuitive for us because our limbs are a bunch of beams that are usually cantilevered. We know it is hard to hold something far from our body. We prefer our limbs to be supported at both ends, hence we like to put our elbows on the table while we are eating (a fork full of food is heavy!) so at least our upper arms are supported at both ends.

When a force is applied to an object, it follows Newton’s three laws of motion. The first two relate to dynamics. The first law is that every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied. This corresponds to the inertia of an object. Inertia is a property of matter and matter does not want to accelerate or decelerate on its own—it needs a force to make that happen.

Newton’s second law states that force is equal to mass times acceleration. Therefore, it takes force to accelerate a mass. The higher the mass or the higher the desired acceleration, the greater the required force. If you put a model rocket engine on a car, nothing interesting will happen, but if you put the same engine on a much less massive model rocket—wow!

Newton’s third law brings us right back to where we started with regards to statics. The third law states that for every action there is an equal and opposite reaction. When you stand on a bridge, the bridge is pushing up on you with the same force. You will have noticed this if you try stepping off a canoe. When you push off the canoe, the canoe can’t push back very well because it has low inertia and is floating on water so it gets pushed away from you.

Identifying all the forces with which an object must contend is necessary in evaluating a design. Some of these might not be obvious, such as the mechanic who uses a filter bracket as a footstep to service a turbocharger. The second biggest load this bracket would encounter is when the engine is being transported by rail and the cars smash into each other during latching. Think about the damage caused by the expansive force of ice in roads, or bird droppings on a car. Toyota recently recalled more than 800,000 cars because of the potential for a spider web to block the condensate drainage of the air conditioner and damage the air bag electronics.

Many forces in nature are trying to destroy your design in a beautifully natural way. The design world is full of these unanticipated usages and they must all be considered. Toy designers probably have the biggest challenge in this area—kids do amazing things!

Draw upon your creative insights, and think about how the object could be misused and what this might do to the object. Are screwdrivers only used to drive in screws? Of course not! Figures 3-2 and 3-3 show examples of misuse.

Figure 3-2. If you design doorknobs, doors, or door hinges you need to know about this traditional application

Figure 3-3. Garbage cans are not just for garbage; they are great places to rest a box. How heavy a box should it hold?

Forces are normally sketched out on free body diagrams, such as shown in Figure 3-4 and Figure 3-5.

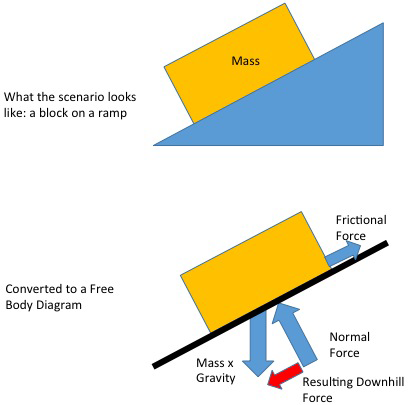
Figure 3-4. Free body diagram

Figure 3-5. Forces diagram of a car

This diagram indicates the load, direction, and type of force. Remember to consider the loads, temperatures, and other environments encountered during shipping, handling, and expected misusage as previously described.

Mechanics of Deformable Bodies

In addition to the reaction of an object to a load, another important characteristic of a material is its behavior as it is about to break. Designers care about how their products will stretch and deform because we understand the weak points and vulnerabilities of a product more than anyone else. Some materials, like glass, are brittle and hardly stretch before they break. Other materials, like wood, are ductile and stretch noticeably before they break. This ductility characteristic determines the existence of common warning signs (bending or stretching) prior to imminent failure. The category of deformable bodies includes all solids because they can develop internal stresses. The behavior of fluids will be described in Chapter 6.

A force’s effect on a material is dependent on the size of the area upon which the force is applied. The force per area is called stress and is simply equal to force divided by area:

where:

Strain is the same as stretch but refers specifically to the movement per unit length. Stress-strain diagrams have been developed for most materials by taking a sample of the material and applying force while monitoring its length. The force is continuously increased until the sample breaks.

Most materials you encounter are elastic. That is, over a certain range of stresses the strain is directly proportional to the stress (Hooke’s law). Moreover, when the stress is removed, the materials return to their original unstressed dimensions. Flexing of a material can be part of a compliant mechanism such as with springs and paper clips.

Both rubber bands and steel rods act like an elastic material. If supporting the same weight over the same cross-sectional area, a rubber band will stretch much more than steel. This difference in stretch is described by the slope of the stress-strain line and is called the modulus of elasticity (or Young’s modulus) and is equal to the difference in stress divided by the difference in strain:

where:

The unit for force is pound (lb) or Newton (N) in SI units. The units for stress are pounds per square inch (psi) or Pascal (Pa) in SI units. One Pascal equals one N/m². The conversion is: 1 psi = 6,895 Pa. Strain is measured in length per original length—this gives a strange unit of in./in. or mm/mm. Because the modulus of elasticity is stress divided by this unit canceling strain, the modulus of elasticity becomes psi or Pa. Table 3-1 shows the relationship between stress and strain for different materials before they break or permanently stretch.

What happens to a material as the stress is continually increased? The yield strength (or elastic limit) is reached, beyond which the material continues to stretch but will not completely recover if the stress is removed. This permanent stretching (called yielding or plastic strain) at stresses above the elastic limit occurs in what is called the plastic region. As the stress is further increased, the material finally breaks at a load called the ultimate strength. Figure 3-6 shows the relationship between stress and strain for ductile and brittle materials.

Where does the material for the stretching come from? In the elastic region, the stretching comes from the increased distance between atoms. In the plastic region, groups of atoms (crystals or grains) slip or deform to allow the stretch. As the material strains in one axis, it also strains in the perpendicular axes. This intuitive relationship is denoted by the ratio of strains called the Poisson’s ratio.

Figure 3-6. Stress-strain diagrams for ductile and brittle materials

Consider these practical implications of the relationship between stress and strain:

• Usually the most important stress level to consider is the yield strength rather than the ultimate strength. That is, all considerations of safety factors, fatigue strength, and impact loading are based on a value that will allow the material to completely recover from the applied stress. Notable exceptions are body armor and crash cushions where the energy of the impact is absorbed by taking the material up to or beyond its ultimate strength.

• The modulus of elasticity determines the flexibility of a material and is independent of its strength. However, an object’s size and shape is the most important determinant of its flexibility. For example, a thin stick blows readily in the wind whereas a thick trunk made of the same wood does not move at all. The relationship between shape and rigidity is presented in more detail later.

• The area under the stress-strain curve indicates a material’s toughness or energy absorption ability. The larger the area, the more energy the material can absorb before it breaks. For example, plastic may be weaker than ceramics but it is tougher.

• Unlike metals, typical composites like wood, fiberglass, and carbon fiber do not have the same stress-strain characteristics in all axes (known as anisotropic); therefore, the modulus of elasticity and yield strength will be different depending on orientation. If a load is pulling in the same direction as the fiber orientation, it will be much stiffer and stronger than if it is pulling perpendicular to their orientation. With a perpendicular load, the fiber strength is unused and only the bonding material (such as epoxy) offers resistance to the load. Metals are isotropic materials and have the same stress-strain relationships in all axes.

Shape

Before considering how an object’s shape affects its strength and rigidity, let’s recall that forces produce some combination of tension or compression. However, it is helpful to consider forces present in five different categories. As described previously, these are tension, compression, shear, flexural, or torsional loads.

Shear loading is sliding force whereby the molecules are being asked to slide against each other as opposed to being pulled apart as with tension or squeezed as with compression. In the case of fluids, the shear resistance is very low so it flows easily. The stresses produced by tension, compression, and shear are the easiest loads to calculate because they are simply calculated as force divided by cross-sectional area. Therefore, increasing the area of something, say using a 1/2-inch (12 mm) bolt instead of a 1/4-inch (6 mm) bolt, decreases the stress. Thick is good (but heavy).

Relationship Between Stress and Thickness

Corrugated cardboard is amazing material. Stiff, strong, and lightweight. This cardboard construction demonstrates an example of sandwich construction. This corrugated cardboard is made entirely of paper with a wavy (corrugated) section of paper sandwiched between the outer layers of flat cardboard. The corrugated cardboard is made rigid because the corrugations separate the flat cardboard, which does not stretch easily, away from the neutral axis. Imagine how floppy the cardboard would be if the corrugated section was flattened out and all the paper layers were laid on top of each other. Even if the flattened paper were replaced by thin sheet metal, it would still not be as rigid as the corrugated form. This increased rigidity and strength are only apparent when the composite is bent. In pure tension, it has virtually no effect—that is, the flattened paper would be as rigid as the corrugated paper if it were pulled at the ends. Figure 3-7 shows a relationship between thickness and stress.

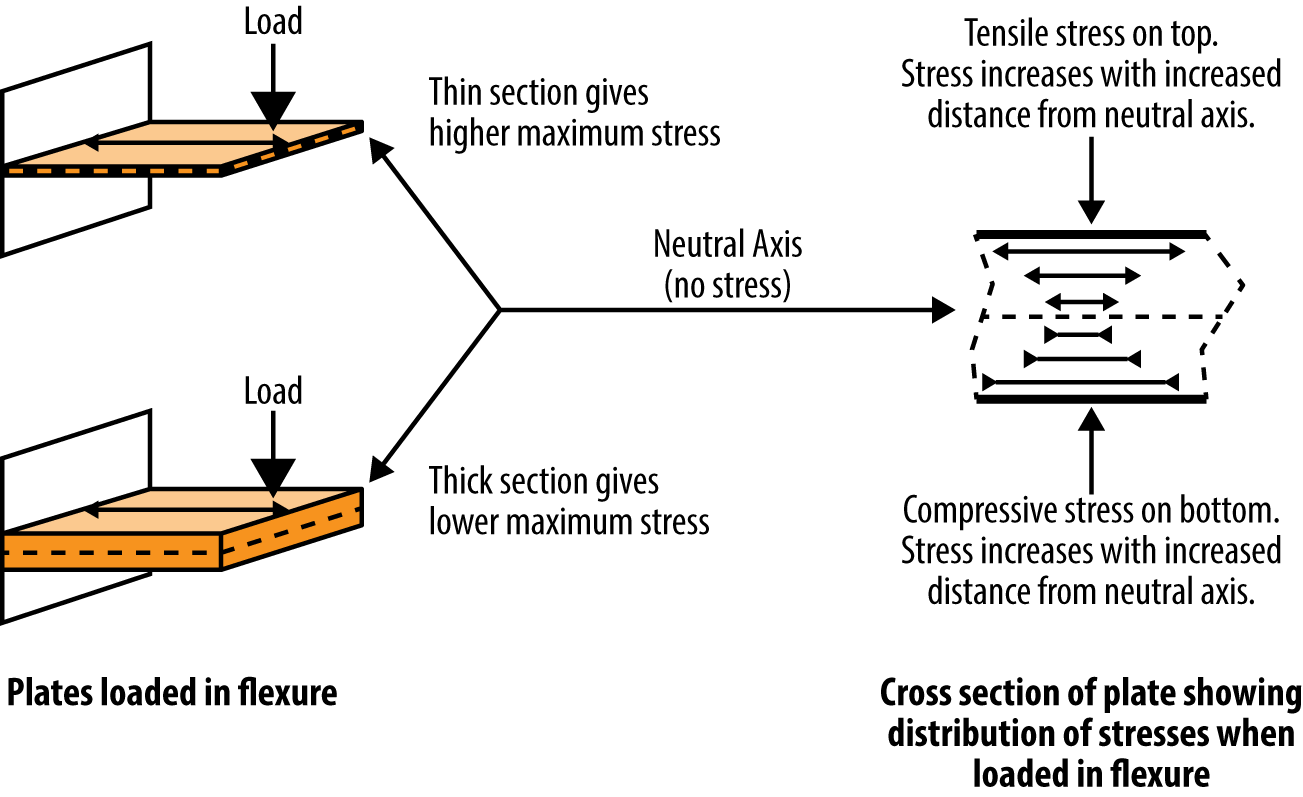
Figure 3-7. The relationship between thickness and internal stress

The relationship between rigidity and shape is described and quantified by the moment of inertia. Moment of inertia is specifically related to the shape of the cross section under load. In the case of flexural loading (a load that produces only a moment, not an axial or torsional force), the stress produced in the part is inversely proportional to the moment of inertia:

$$\sigma =\frac{Mc}{I}$$

where:

σ = flexural stress

M = moment on section equal to the force times distance

c = distance from neutral axis (usually, the only value of concern is the maximum c              value, which is half the thickness of the section)

I = moment of inertia

The higher the moment of inertia, the lower the stress produced under a given load. If a part is designed so the material is far away from its center, or neutral axis, it will have a higher moment of inertia than if all the material is bunched up around the center. In fact, the moment of inertia increases as a cubic function of the thickness. Figure 3-8 shows how a beam can be made 75% more rigid by changing its shape.

Figure 3-8. By changing the shape of the rectangular beam to that of an I-beam, the rigidity increases by over 75%, yet the weight is unchanged, however, this is only true in the vertical plane; in the horizontal plane, the I-Beam is 250% less rigid than in the vertical plane; this illustrates that if the direction of loading can be predicted, it is very beneficial to develop a shape that puts as much of the material as far as possible from the neutral axis

For a rectangular cross section, the formula for I is:

$$I=\frac{b{h}^3}{12}$$

where:

b = width of the section

h = thickness (or depth) of section

For a solid rod cross section, the formula for I is:

I = π r⁴/4

where:

r = radius of rod

A tube has a much higher moment of inertia than a solid rod of the same mass because the mass of the tube is located further from the center. Figure 3-9 shows two round shapes that have the same rigidity even though the tube is almost one half the weight of the rod. Unlike a tube, an I-beam is optimized for resisting bending in one plane. Therefore, a load must be positioned in a way that takes advantage of its shape.

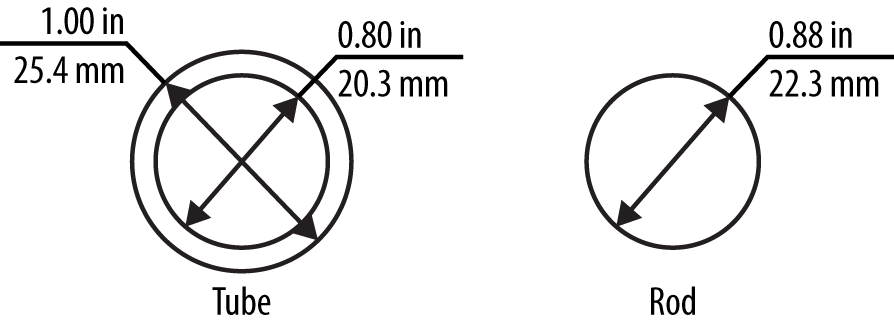
Figure 3-9. Tube versus solid rod

Section modulus is often used to describe the properties of a structural shape when dealing with structural steel. Section modulus is equal to the moment of inertia divided by the distance from the center of the shape to its furthest edge (c), such as the radius (r) or half the height (h) in the case of a rectangular shape:

Section modulus (S) = I/c

Torsion has a similar relationship except the design’s polar moment of inertia—that is, the shape from a twisting perspective—dictates the torsional shear stress. For example, a large-diameter pipe with a thin wall will have a higher polar moment of inertia than will a small-diameter pipe with a thick wall. Torsional shear stress (τ) is equal to the torque (T) times the distance from neutral axis to outer fiber (r) divided by the polar moment of inertia (J):

τ = T r/J

where:

τ = torsional shear

T = torque

r = radius from neutral axis to outer fiber

J = polar moment of πR⁴/2

Few items are under pure tension, compression, or shear. Some items, such as bolts, are designed to be under pure tension and shear only, but these are the exception. Consequently, understanding flexural behavior is essential for predicting potential failures.

Flexural behavior does not consider another phenomenon that will make parts fail at stresses well below their yield stress. This phenomenon is called buckling and is a common failure mechanism for long, slender objects. Buckling behavior, a well-understood phenomenon, is carefully considered in design calculations.

Stress Concentration

If you want to know where your design is most likely to break, look for sharp corners and notches. A sudden change in an object’s form, such as a sharp corner, notch, hole, or crack, will result in an increase in stress called a stress concentration. These geometric changes tend to squeeze (concentrate!) stresses into a smaller area, as shown in Figure 3-10. Stress concentrations also arise around microscopic fissures, which can lead to fatigue failure that will be described later. The mathematical analyses of stress concentrations are so complex that their amplifying values are obtained experimentally.

Figure 3-10. Stress concentration shown in sharp corner of flexed protractor by photoelastic visualization

Figure 3-11 shows a graph of stress concentration versus radius sharpness. This relationship between shape and stress concentration illustrates the importance of gradually bending mating surfaces. Cracks concentrate stresses.

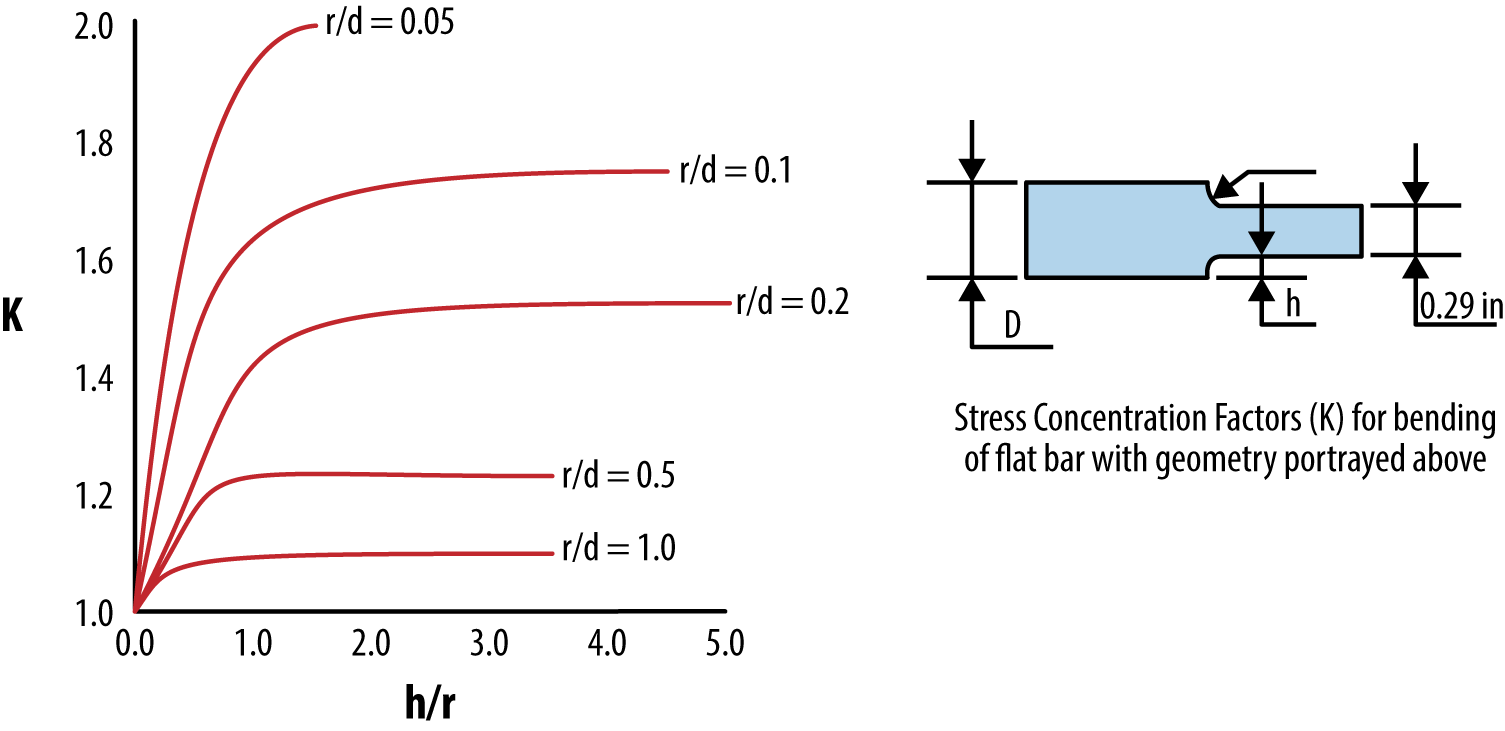
Figure 3-11. Stress concentration versus radius sharpness

Stress concentration effects are reduced by moving the abrupt change of form to a lesser stressed section of the object. The problem of stress concentrations has long been known, and boat builders would seek trees with natural fillets for use in highly loaded sections such as keels and mast connections. These valuable forms are stockpiled, as shown in Figure 3-12.

Figure 3-12. Wooden sections saved for highly loaded features in boat construction

In building construction, holes are drilled in the center of beams where very low stress exists (see the section “Relationship Between Shape, Stiffness, and Flexural Stress”) and away from the area of maximum moment. It is accepted practice in some applications to drill small holes at each end of a crack to reduce the stress concentration in this area and to stop the crack’s progress.

Ductile materials are less sensitive to stress concentrations than brittle materials because they deform when loaded. This reshaping redistributes the load over a broader area. Even though the brittle form of a material can often handle higher stresses, a ductile material can distribute stress and therefore actually handle a higher load.

Fatigue

As a material is continually loaded and unloaded, its maximum strength decreases. This gradual weakening is called fatigue, a name derived from an early misunderstanding of this phenomenon. The metal was thought to have become “tired” over time. Fatigue is now understood to be caused by movements within the material that cause cracks to propagate through the material’s grain boundaries. One solution to fatigue failure is to over-design an object—that is, use massive thicknesses to ensure longevity. However, understanding the rate of decline of a material’s strength is a more environmentally and cost-sensitive solution. Generally, if the stresses experienced by an object under cyclic tension and compression loading are less than one-half of the yield stress, the object will never fail due to fatigue. Therefore, highly efficient designs are produced only when the anticipated loading and fatigue characteristics are fully understood.

Fatigue failures often start at a stress concentration or at the surface of an object, where stresses are highest. Small surface cracks may be the first sign of fatigue. However, there may be no visible cracking because the cracks may be too small to see, start from inside the object, or be obscured. For example, the stress concentration at the corner of a notch in a shaft (such as the keyway) is a common location for fatigue cracking but this area cannot be observed unless the shafted assembly is completely torn apart.

Inspecting a broken object that is subject to fatigue failure will always show two different surface characteristics:

• The fatigue zone where cracks slowly propagated into the object

• The instantaneous zone where the crack accelerated quickly through the object

The relationship between the size of the fatigue zone and the instantaneous zone indicates the relative loading of an object. The instantaneous zone is produced when the effective area (total area minus fatigue zone) is too small to support a load. Therefore, if the instantaneous zone is small, the object was not heavily loaded. However, if the instantaneous zone is large, the object was heavily loaded.

The fatigue zone is identified by beachmarks, which are small ridges on the broken surface of a material. These beachmarks are produced by the crack propagation. They in turn plot the crack progression. Due to abrasion within the crack, older fatigue zone areas are smoother than new ones and can help identify the failure origin.

Buckling

Like fatigue, buckling is a failure mechanism that occurs at loads well below the material design strength. The best way to observe the buckling phenomenon is to stand carefully on an aluminum can, which should support your weight. With your full weight on the can, have someone else use two rulers to bend the sides of the can in slightly and the can will buckle and crush rapidly.

Buckling is the collapse of a material under compression when the object bends and folds at loads that it would normally support (as we saw with the can). Buckling is a principle concern in axially loaded beams and thin-walled cylinders and is caused by the large increase in stress when a part is shifted slightly off center. Depending on the design of the part, this will make the part unstable and cause it to collapse. Buckling calculations can become quite complicated but they are a function of the slenderness ratio of a part. Long, slender objects will buckle under compressive loading, while short, stout ones will not. Figure 3-13 shows the types of compression failures associated with slenderness.

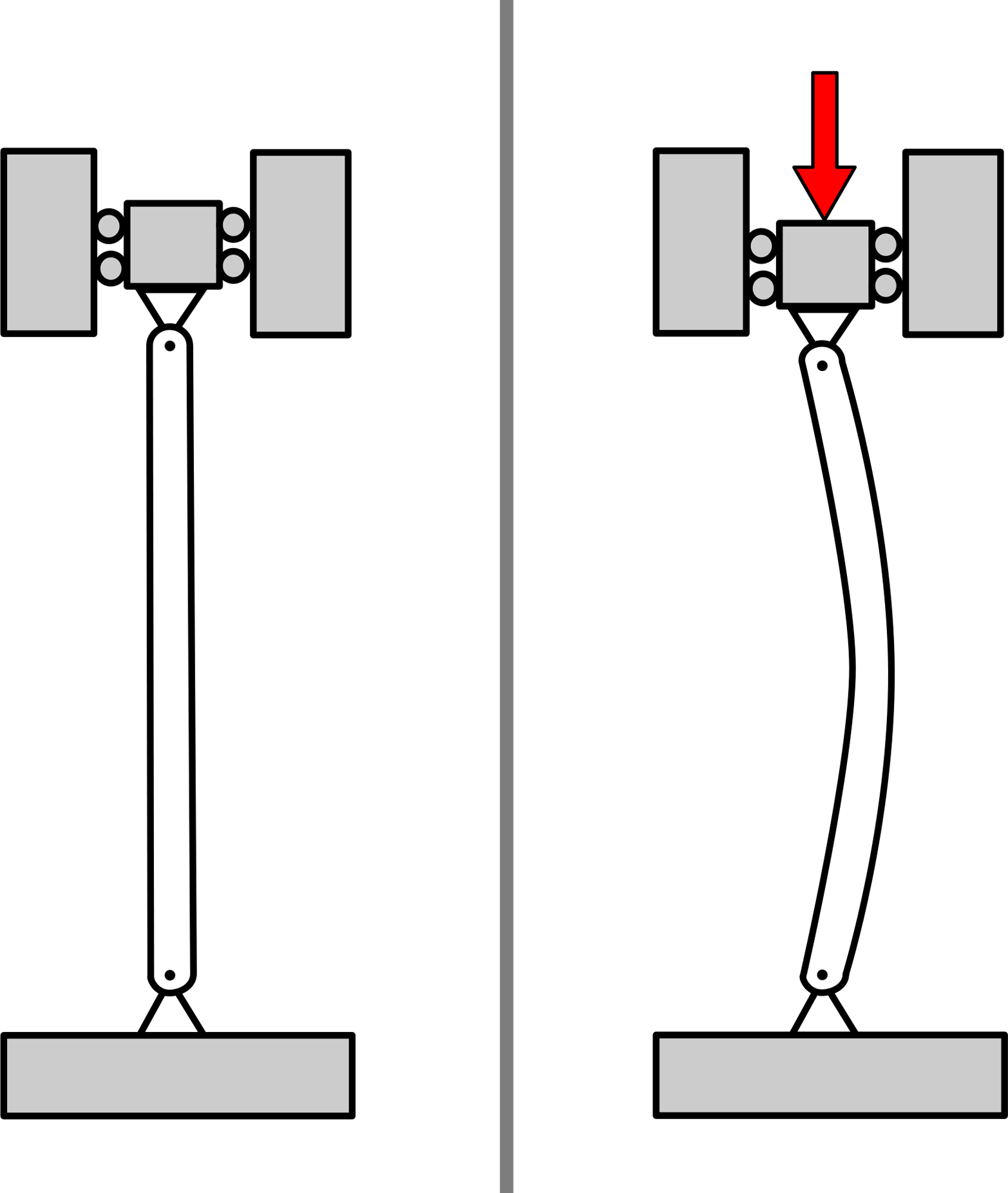
Figure 3-13. Long, slender objects fail (by buckling) at much lower loads than predicted by their yield stress

Thermal Expansion

Hot stuff expands, cold stuff contracts. If an object is not allowed to move freely, it produces high stress as it grows into an adjoining object. Heat increases atomic vibration and makes the atoms act as if they are bigger. Therefore, thermal expansion and temperature are directly related. The amount of expansion varies by material and is measured by the thermal expansion coefficient. Brass has a thermal expansion that is 50% more than steel. Aluminum thermally expands at twice the rate of steel, as shown in Table 3-2.

Thermal expansion or contraction is calculated by:

where:

If two materials expand into each other, either because they have different thermal expansion coefficients or they are at widely different temperatures, they develop stresses directly related to the strain they produce. That is, the strain produces stress. If a column or pipe is anchored at both ends and is axially constrained, the compressive stress generated by thermal expansion becomes high. Plastics are viscoelastic, meaning they will flow like a liquid. Therefore, they can reduce the stresses caused by thermal expansion to some degree by fluid flow.

The compressive stress generated by thermal expansion is calculated by:

where:

We are designers, not vibrating molecule specialists, so why should we care about this? Thermal expansion can break things and change their shape. While you might think your product lives a benign life on a store shelf and in someone’s home, when it is shipped in the belly of an airplane or on a giant containership plying the north Pacific, it is exposed to freezing temperatures. When it is stored in an attic or transported by truck, it can get very hot.

The force of thermal expansion creates high stresses when two materials with dissimilar thermal expansions (e.g., plastic and metal or aluminum and steel) are entrapped. The stresses can also be produced when a hot object is completely constrained by another object, which is why bridges have thermal expansion joints. Thermal expansion is a special problem for big items or those that experience large temperature changes because the effect is multiplied. Therefore, such things as piping systems and engine exhaust need to be thermally accommodated by including flexible joints or bends to the system’s design.

Failure Modes

You have built a prototype and it broke. Now what? Well, there is a lot of good news in the broken parts you are looking at. They contain a wealth of data to help you see what went wrong. Even if your device doesn’t break, it is still considered “failed” if it stops working the way it should. This section describes different ways devices stop working, from breakage to changing their shape and jamming.

Impact

Impact is a very rapidly applied load such as a hammer striking a nail. Stress waves, produced during impact, actually stack up on each other, amplifying the stress. Figure 3-14 shows an example of impact power.

Figure 3-14. Jackhammers amplify force by impact

Noise and Vibration

Noise and vibration are important issues in design. They impact the health and experience of a user. Both noise and vibration are mechanical phenomena, whether they be oscillating air molecules or solid material. While noise can be harmful, its gentle cousins of music and sound can be reassuring, comforting, and an essential part of a user experience. Vibration can help us understand how something is responding, whether it be damaged bearings or an intentional haptic feedback system. However, vibration can also produce fatigue failure and other damage to mechanical systems.

Closing Thoughts

Now for the juggling! You know the careful shaping of an object’s cross section lets you use the minimum amount of material and avoiding sharp corners reduces stress concentration. You know long, skinny shapes buckle, high loading cycles produce fatigue, impact amplifies stresses, corrosion can be hidden, and materials expand when they are heated. All of these factors go into keeping the loads under the yield stress of the materials.

If you were designing a water piping system, you would need to worry about many more things than simply its ability to move water from one place to another. You would think about what happens to the pipe when the water is turned off quickly (impact), what happens when it heats up (expands), and what happens at the elbows (stress concentration). You would also be thinking about the flexing of the pipe, the axial loading of the pipe supports, and the corrosion of fittings.

If you were designing a fancy new bicycle wheel, you would need to think about the load of the weighted bike traveling through the wheel, the impact of potholes, and the corrosion produced by water and road salt (not to mention what that will do to the bearings!) You would also think about how a rider might get their foot dangerously tangled in your wheel design and the side loads the wheel encounters if it tips over sideways. You would need to consider the pressure of the tire on the wheel and what the minimum cross section should look like. You know any cracking will probably originate from the sharp corners in your design and may not show up for a long time.

When you design a frame to support your new invention of a dog trampoline, you are thinking about the flexural stresses in the frame, their propensity to buckle, fatigue strength, corrosion, and vibration (maybe the frame resonates at the dog’s favorite jumping rate!). Welcome to the world of worry and good design.