You often use statistics to describe data. In doing so, measures of central tendency and measures of dispersion are often used. In this appendix you will have a chance to review these concepts. Doing so may help you better understand some aspects of regression analysis.
Population Versus Sample
Before discussing some descriptive statistics let us take a little detour to talk about populations and samples. A population represents the entire list of all possible measurement units. Some examples might help you understand this. Suppose you are interested in developing a model for sales at individual Abercrombie & Fitch stores in 2012. The population would be all Abercrombie & Fitch stores that were in business in 2012. If you were doing a study concerning students at the University of Iowa, the population would be all 30,328 students.
A sample is a subset of the population. Usually it is either impossible or very costly (or both) to use an entire population in a study. Think about trying to do a study that involves the entire population of students at the University of Iowa. It would be very difficult to locate and get the cooperation of all 30,328 students. And, even if you were successful, there are often students who drop out or enroll so the population changes frequently. To study students at the University of Iowa you would select a sample, or subset, of all students.
There are many ways in which you might select the sample. Some are good and others are not so good. A statistics text or a research methods text would provide you with information about the various ways by which you might select a sample. The important point here is for you to understand that you almost always work with only a subset of all the possible data. That is you work with a sample of data. It turns out that for various reasons a well-selected sample is likely to provide a more accurate view of the population than a census of the entire population.
The information you obtain from measures on a sample is called statistics. The average height of students at the University of Iowa calculated from a sample of perhaps 400 students would be a statistic. The actual average height for all University of Iowa students is some value that is unknown and maybe unknowable. This value is called a population parameter. You can get a good estimate of the true height of all University of Iowa students by using the average height based on your sample of 400 students (assuming you did a good job of selecting the sample).
In all aspects of statistical work you use Sample Statistics to estimate Population Parameters. Note the S’s go together and the P’s go together, which makes this relationship easy to remember. In statistical work, sample statistics are normally represented by English letters and population parameters are typically represented with Greek letters. For example, a sample mean is denoted 
while a population mean is denoted m.
Central Tendency
When you want to describe to someone the general case for some measurement, you use a measure of central tendency which may represent a “typical” case in the population. There are three primary measures of central tendency: (1) the mean, (2) the median, and (3) the mode.
The Mean
The mean is often called the average. You may have seen the mean represented by the symbol 
. To calculate the mean you add the values of all observations on the measurement and then divide by the number of observations. Suppose you have the following five observations: 1 5 3 4 2. When added these equal 15. To get the mean you would divide this sum by the number of observations (five). So, for this simple example, you get the mean as:
The Median
The median is another measure of central tendency. The median is the value that is in the middle of the data set if the values are arrayed from low to high (or high to low). Using the same five observations used above, if you order them from low to high you have: 1 2 3 4 5. The middle value is 3, so that is the median. In this case, the median and the mean are equal.
Think about this: What if in the data the five was 500? What effect would this have on the mean and the median? If the 5 was changed to 500 the data set would be: 1 2 3 4 500. The mean would now be 510/5 = 102. But, what about the median? The median is still 3. When you have data with one or more values that are very high or very low compared to other values the median might better represent the “typical” case than would the mean.
When you have an even number of observations there is no middle number. Consider these data: 1 2 3 4 5 6. There is no number that splits the data into two equal halves. In such a case, you use the average of the two middle values to represent the median (3 and 4 in this example). So you would say the median is 3.5.
The Mode
The mode is the value that occurs most frequently in a set of data. Consider the following data: 1 3 4 2 5 6 2 7 2 6. The mode would be equal to 2 since that value appears three times while other values appear only once or twice.
Dispersion
There are three measures of the degree of dispersion in data that are most common. These are the range, the standard deviation, and the variance. In addition, you will see a measure of dispersion called a “standard error.” This is a measure of dispersion for a statistic rather than for data.
The Range
The range for data is the distance between the lowest and the highest values. When provided in addition to a measure of central tendency, the range gives you a better feel for the data. Consider again the following data: 1 3 4 2 5 6 2 7 2 6. The range would be from 1 to 7.
The Standard Deviation
The standard deviation is a common way to express the average distance between each value and the mean of all the values. For the values 1 3 4 2 5 6 2 7 2 6 the mean is 3.8. None of the actual values equals the mean and each is some distance away from the mean.
The standard deviation is calculated by subtracting the mean from each of the 10 values and squaring that result. These values are then added together and divided by n - 1 (where n is the number of observations). Finally, you take the square root of that value to get the standard deviation. You normally use s to represent the sample standard deviation. (The population standard deviation is the Greek σ and is calculated in a similar manner except that the denominator is just n and the population mean μ is used in the numerator rather than the sample mean ). The calculation is:
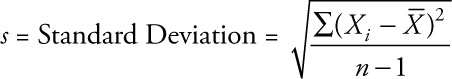
The Variance
The variance is the square of the standard deviation. So the variance is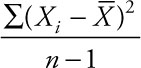 
You may wonder why both are important when one is just the square of the other. The standard deviation is much more easily understood by people as a measure of dispersion than is the variance. However, the variance has some very nice statistical properties that can be useful in advanced forms of data analysis. In fact, you could take a full semester course just studying analysis of variance (ANOVA) … that is studying various aspects and applications of the simple formula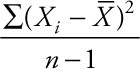 
To help you understand this, consider a hypothetical situation. Suppose you own a car dealership that sells an average of 364 cars a month. When you are reading a newsletter from a car dealer association you read that nationally the mean car sales per month for dealers is 400. That piece of information you would understand and could relate to your business.
As you read further you see that the variance is given as 10,000 cars squared per month. Wow!! That would be confusing. The 10,000 is a really big number in your mind and you are really confused by what a “car squared” means. You know what a Ford Focus is. But what is a Ford Focus squared? You see that a variance is not such a good way to describe dispersion to someone. But, what if you find the square root of 10,000 cars squared? It would be 100 cars and is the standard deviation. This is something that would make sense to you.
The Standard Error
It is easy for you to see that there is dispersion in data. But what about statistics? Is there a measure of dispersion for statistics? The answer is yes. Suppose that you and five friends do an experiment in which each of you goes to a mall and randomly selects seven people to interview. Each of you asks each person in your sample of seven some questions, one of which might be their ages. All six of you have a sample of seven ages. Do you think all six of the average ages from your six samples would be exactly the same? It is very (very very) unlikely. What is likely is that all six average ages will be different. They might be 34.5, 23.8, 46.7, 50.3, 23.9, and 32.7. You see that there would be a range from 23.8 to 50.3. That is, there would be dispersion in the sample statistic ().
A standard error is a measure of dispersion for a sample statistic and is analogous to a standard deviation. You will see the term standard error a number of times in the text and when you do regression in Excel. So now you have some idea what this term means.