Chapter 5

Point and Interval Estimates from a Regression Model

Chapter 5 Preview

When you have completed reading this chapter you will be able to:

• learn to calculate a point estimate based on a ­regression equation.

• understand that this point estimate is the best ­estimate based on regression statistics.

• learn to calculate an approximate 95% confidence interval centered on your point estimate.

• realize that regression with one independent (or causal) variable is quite limited for business applications.

• see that larger models with more causal variables can increase the explanatory power of regression.

• see that larger models with more causal variables can result in more narrow (more precise) approximate 95% confidence intervals.

Introduction

In chapter 3, you saw simple bivariate regression equations for women’s clothing sales and for college basketball team’s WP. In this chapter, you will learn to apply these two models. You will use both to make point estimate and approximate 95% confidence interval estimates for the dependent variables.

The Concept of a Point Estimate

A point estimate is a single value, or point. It is your best estimate of the value of a dependent variable, given some value(s) for the independent variables(s). The point estimate is generated directly from the regression equation. To illustrate, suppose that you have a very simple regression model as follows:

If per capita income is $30,000 then your point estimate of sales would be:

While this would be your best estimate it is likely to be wrong. This may sound disturbing to you. However, statistical theory supports the notion that this best estimate will be close to correct most of the time. It just may not be exactly right. Suppose in this example sales are in thousands of units. Your estimate of sales is really 50,000 units … not 50,001 or 49,999 but exactly 50,000. The business world is not so precise. If sales really turn out to be 50,001 and you estimated sales to be 50,000 you would look pretty good. But technically you would be wrong. Later in this chapter, you will see how to calculate point estimates for some of the models you have seen in previous chapters.

The Concept of Approximate 95% Confidence Interval Estimates

Because you would almost always be wrong (but close) with a point estimate you may want to provide a set of lower and upper bounds for an estimate such that you would have some level of confidence that the true value would be in that interval. To do this you need to know another statistic called the “standard error” of the estimate (SEE). The SEE is just called standard error in Excel.1 This measure is include in the output of almost every regression software program.2

The approximate 95% confidence interval is found by taking your point estimate plus and minus some amount that you can calculate if you know the standard error of the estimate (SEE). The way this is calculated is:

Point Estimate ± 2(Standard Error of the Estimate)

The number 2 in this calculation is an approximation for 1.96 from a t-table with a large number of degrees of freedom. This confidence interval is also an approximation because the true confidence interval bows away from the regression line as the dependent variable and the independent variable(s) move away from their respective mean values.

You will see this concept applied later in this chapter for regression models you have already seen. After seeing some examples of the concept you will find it easy to apply in your own situation.

There is a way to get an exact 95% confidence interval. The arithmetic is a bit more complex but it can be done.3 However, relying on the approximate 95% confidence interval is sufficient for most ­purposes.4

Point Estimates in Practice: Two Examples

Women’s Clothing Sales

Consider the following women’s clothing sales (WCS) model first introduced in chapter 2. In this model WCS was a function of personal income (PI). The model was:

In chapter 2, you put a value for personal income into this equation to get an estimate of WCS for that level of personal income. This was a point estimate because you obtained a single number for your answer. In that example, you estimated the dollar amount of WCS if personal income is 9,000 (billion dollars). You obtained:

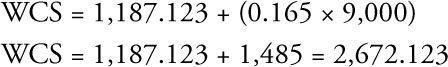
Thus, your estimate of WCS if personal income was 9,000 (billion dollars) is 2,672.123 (million dollars) or $2,672,123,000. Do you think this would be exactly right for that level of PI? Probably not!

Winning Percentage for College Basketball Teams

In the second example, consider the model for the WP of college basketball teams, also shown in chapter 2. The model was:

In chapter 2, you learned that if a team’s FG percentage is 45% your best estimate of the team’s WP would be:

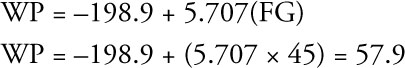
This probably seems awfully precise to you. Would you be sure the WP might not be 57.6% or maybe 58.1%? Again, probably not. But 57.9% would be your best point estimate. If you need to provide one number as your estimate, 59.7% would be the best number to give.

Approximate 95% Confidence Interval Estimates: Two Examples

While point estimates are useful, it is very unlikely that they will be exactly correct. Thus, it is often preferable to make an interval estimate in such a way that you can be 95% confident that the true value will be somewhere within the interval. You have seen that an approximation for a 95% confidence interval can be given as:

where YE is the point estimate and SEE is the standard error of the estimate.5

Before looking at examples, you should know exactly where to find the SEE in Excel’s regression output. Look at the partial output from an Excel regression in Table 5.1. You see that the SEE is in the top section of Excel’s output under the heading “Regression Statistics.” In this example, the SEE is 1.676. To calculate an approximate 95% confidence interval for this model you would have:

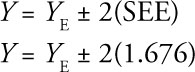
You would need the entire equation to get your point estimate (YE). For now the important thing is for you to know where to find the SEE in your regression results from Excel. In the examples that follow you will see how to do specific calculations.

Women’s Clothing Sales: Example One

As you have seen, the relationship between women’s clothing sales (WCS) and personal income (PI) is:

This is the point estimate. Table 5.2 provides the Excel output needed to get the approximate 95% confidence interval. Here you see that the SEE is 525.160.

You now have enough information to calculate the approximate 95% confidence interval. The point estimate of 2,672.123 is your starting point and the SEE is 525.160. The approximate 95% confidence interval is:

This is based on how WCS are influenced by only personal income. As shown in Table 5.2, the coefficient of determination (R2) is 0.173. Thus, this simple model only explains about 17.3% of the variation in WCS.

As you would expect WCS are influenced by more than just PI. As you learn more about regression you will see how you can include many other measures that may influence WCS into a regression model. If, in addition to personal income, you include the unemployment rate among women, an index of consumer sentiment, and measures to account for seasonality you can develop a much better regression model. If we include them the coefficient of determination increases to 0.966.6 This means that the more complete model explains 96.6% of the variation in WCS. Partial regression statistics for this model is shown in Table 5.3.

With the more complete model the approximate 95% confidence interval becomes narrower as follows:

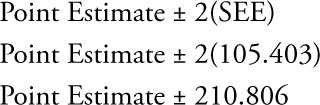
Compare this plus or minus range with the one for the simpler models (1,050.320).

You see that by including more causal variables two important things change. The coefficient of determination increases from 16.7% to 96.6%, and the standard error decreases from 525.160 to 105.403. As a result, the width of the approximate 95% confidence interval falls from 1,050.320 to 210.806. This allows you to be more precise in your estimates based on a regression model.

Basketball Winning Percentage Example

Statistics play an important role in sports, as illustrated by the book and the movie MONEYBALL, which was based on a true story. You have already seen one model of the collegiate basketball WP in which only the percentage of successful FG attempts was used as a causal variable. That model explained about 40% of the variation in WP. If you were to include other offensive and some defensive measures you could develop a model that would explain roughly 83% of the variation in WP.

The Regression Statistics for both these models are shown in Table 5.4. You see that in the larger regression model the explanatory power is about twice as high as with the smaller model and the SEE is much smaller.

For these two models, the widths of the approximate 95% confidence bands would be:

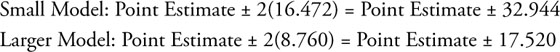
Again you see that the width of the approximate 95% confidence band depends on the model. Rarely is a model with only one independent variable sufficient in business applications. Starting with chapter 6 you will build on what you have learned about the basics of regression analysis to build larger, more complex, and more useful regression models.

What You Have Learned in Chapter 5

• You can calculate a point estimate based on a regression ­equation.

• You know that a point estimate is the best estimate based on regression statistics.

• You can calculate an approximate 95% confidence interval centered on your point estimate.

• You realize that regression with one independent (or causal) variable is quite limited for business applications.

• You have seen that larger models with more causal variables can increase the explanatory power of regression.

• You have seen that larger models with more causal variables can result in more narrow (more precise) approximate 95% confidence intervals.

NOTES