Besides exponential smoothing, another approach for analyzing time series is the so-called ARIMA, or Box–Jenkins models. ARIMA stands for “Autoregressive Integrated Moving Average.” These models are very popular, particularly among econometric forecasters. As we will see later in this chapter, ARIMA models can be seen as a generalization of exponential smoothing models. The popularity of ARIMA models is often explained by the logic that if exponential smoothing models are a special case of ARIMA models, then ARIMA models should outperform, or at least perform equivalent to, exponential smoothing. Unfortunately though, this logic does not seem to hold in reality. In large forecasting competitions (Makridakis 1993b; Makridakis and Hibon 2000), exponential smoothing models regularly beat ARIMA models in out-of-sample comparisons. Nevertheless, ARIMA models are still used in practice, and this chapter will briefly explore the mechanics of ARIMA time series modeling.
7.1 Autoregression
The first component of an ARIMA model is the autoregressive (AR) component. Autoregression means that we conceptualize current demand as being a function of previous demand. This is a slightly different (though mathematically somewhat similar) conceptualization of demand compared to exponential smoothing, where we saw demand as being driven by a constantly changing underlying but unobserved level of the time series. Specifically, if we see demand as driven by only the most recent demand, we can write the simplest form of an ARIMA model, also called an AR(1) model, as follows:

Equation (9) looks like a regression equation (see Chapter 8), with current demand being the dependent variable and previous demand being the independent variable. This is, in fact, how an AR(1) model is estimated—simply as a regression equation between previous and current demand. One can, of course, easily extend this and add additional terms to reflect a dependency of the time series that goes deeper into the past. For example, an AR(2) model would look as follows:

Estimating this model again follows a similar regression logic. In general, an AR(p) model is a regression model that predicts current demand with the p most recent past demand observations.
Trends in a time series are usually “filtered out” before an AR model is estimated by first-differencing the data. Further, it is straightforward to deal with seasonality in this context of AR models. One way of dealing with seasonality would be to deseasonalize data before analyzing a time series, for instance, by taking year-over-year differences. There is also an alternative to such preprocessing by simply including an appropriate demand term in the model equation. Suppose, for example, we examine a time series of monthly data with expected seasonality. We could model this seasonality by allowing current demand to be influenced by demand from 12 time periods ago. In the case of an AR(1) model with seasonality, we would write this specification as follows:
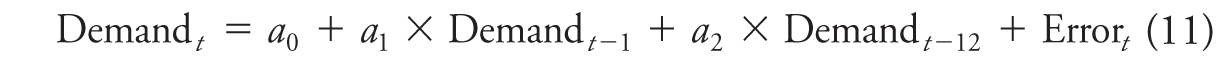
7.2 Integration
The next component of an ARIMA model is the “I,” which stands for the order of integration. Integration refers to taking differences of demand data prior to analysis. For example, an AR(1)I(1) model would look as follows:

To make things simple, the Greek letter Delta (Δ) is often used to indicate first differences. For example, one can write

Substituting equation (13) into equation (12) then leads to the following simplified form:

Taking first differences essentially means that, instead of examining demand directly, one analyzes changes in demand. As we have discussed in Chapter 4, this technique is employed to make the time series stationary before running a statistical model. This idea can be extended further. For example, an AR(1)I(2) model uses second differences by analyzing

which is akin to analyzing changes in the change in demand instead of demand itself.
To see how a time series becomes stationary through integration, consider the following example of a simple time series with a trend:

This time series is not stationary, since the mean of the series constantly changes by a factor a1 in each time period. If, however, we examine the first difference of the time series instead, we observe that in this case

The two error terms in equation (17) are simply the difference of two random variables, which again is just a random variable in itself. In other words, first differencing turned the time series from a nonstationary series into a stationary one. This effect is illustrated in Figure 7.1. The left part of the figure shows a nonstationary time series with a positive trend. The right hand side of the figure shows the first difference of the same demand observations. Clearly, these first differences now represent noise around a mean, thus making the series of first differences stationary.

Figure 7.1 First differencing a time series
Sometimes (though rarely), the process of first-order differencing is not enough to make a time series stationary, and second- or third-order differencing is needed. Further, some time series require taking the natural logarithm first (which can lead to a more constant variance of the series) or deseaonalizing the series. In practice, many manipulations can be used to achieve stationarity of the series, but differencing represents a very common transformation to achieve this objective.
One can of course argue that all these data manipulations distract from the actual objective. In the end, forecasting is about predicting the next demand in a series, and not about predicting the next first difference in demand. But notice that data manipulations such as first differencing can easily by reversed ex post. Suppose you have used an AR(1)I(1) model to predict the next first difference in demand (= Predicted ΔDt+1). Since you know the currently observed demand, you can simply construct a forecast for demand in period t+1 by calculating
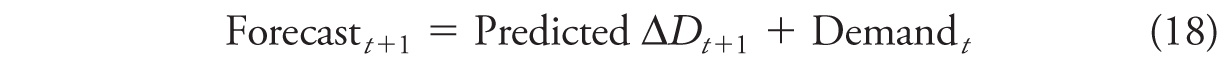
7.3 Moving Averages
This concludes the discussion of the “I” component of ARIMA models; what remains is to discuss the moving averages (MA) component. Note that this MA component in ARIMA models should not be confused with the MA forecasting method discussed in Section 6.1. This component simply represents an alternative conceptualization of serial dependence in a time series—but this time, the next demand does not depend on the previous demand but on the previous error, that is, the difference between what the model would have predicted and what we have actually observed. An MA(1) model can be represented as follows:

In other words, instead of seeing current demand as a function of previous demand, we conceptualize demand as a function of previous forecast errors. The difference between AR and MA models, as we shall see later this chapter, essentially boils down to a difference in how persistent random shocks are to the series. Whereas random shocks tend to “linger” for a long time in AR models, they more quickly disappear in MA models. MA models, however, are more difficult to estimate than AR models. While an AR model estimation is very similar to a standard regression, MA models have a bit of a “chicken-or–egg” problem: one has to create an initial error term to estimate the model, and all future error terms will directly depend on what that initial error term is. For that reason, MA models require estimation with more complex maximum likelihood procedures instead of the regular regression we can use for AR models.
MA models extend in a similar fashion as AR models do. An MA(2) model would see current demand as a function of the past two model errors, and an MA(q) model sees demand as a function of the past q model errors. More generally, when combining these components, one can see an ARIMA(p, d, q) model as a model that looks at demand that has been differenced d times, where this dth demand difference is seen as a function of the previous p (dth) demand differences and q forecast errors. Quite obviously, this is a very generic model for demand forecasting, and selecting the right model among this basically infinite set of possible models becomes a key challenge. One could apply a “brute force” technique, as in exponential smoothing, and simply examine which model among a wide range of choices fits best in an estimation sample. Yet, unlike in exponential smoothing, where the number of possible models was limited, there is a nearly unlimited number of models available here, since one could always go further into the past to extend the model. The next subsection will show how to use the autocorrelation function (ACF) to select a good ARIMA model.
7.4 Autocorrelation and Partial Autocorrelation
Two tools used in practice for identifying an adequate ARIMA model are the so-called autocorrelation function (ACF) and partial autocorrelation functions (PACF). For the ACF, one calculates the sample correlation (= CORREL function in Excel) between the current demand and the previous demand, between the current demand and the demand before the previous demand, and so on. By going n time periods into the past, this leads to n correlation coefficients between current demand and the demand lagged by n time periods. These correlations are called “autocorrelations,” because they describe the correlation of demand with itself (“auto” in Greek meaning “self”). Autocorrelations are usually plotted against lag order in a bar plot, the so-called “autocorrelation plot.” Figure 7.2 contains an example of such a plot. One frequently also sees horizontal lines in such an autocorrelation plot, which differentiate autocorrelations that are statistically significant from nonsignificant ones, that is, autocorrelation estimates that are higher (or lower, in the case of negative autocorrelations) than we would expect by chance. This can help in identifying the orders p and q of an ARIMA model.

Figure 7.2 AR, MA and Normally distributed series with their ACF and PACF
The partial ACF works similar by estimating first an AR(1) model, then an AR(2) model, and so on, and always recording the regression coefficients of the last term that is added to the equation. To illustrate how to calculate the ACF and the PACF, consider the following example. Suppose we have a demand time series, and calculate the correlation coefficient between demand in a current period and the time period before (r1 = 0.84), as well as the correlation coefficient between demand in a current period and demand in the time period before the previous one (r2 = 0.76). The first two entries of the ACF are then 0.84 and 0.76. Suppose now that we additionally estimate two regression equations:

Suppose that the results from this estimation show that θ1,1 = 0.87 and θ2,2 = 0.22. The first two entries of the PACF are then 0.87 and 0.22.
The ACF can be used to differentiate MA(1) and AR(1) processes from each other, as well as differentiate both of these processes from demand which represents simple draws from a distribution without any serial dependence. To illustrate this selection process, Figure 7.2 contains the time series and ACF plots of a series following an AR(1) process, an MA(1) process, and data which represents simple draws from a normal distribution. Note that all three series were generated using the same random draws to enhance comparability. One can see that the MA(1) series and the normal series look very similar; only a comparison of their ACFs reveals that while the normally distributed demand shows no autocorrelation in any time lag, the MA(1) series shows an autocorrelation going back one time period (but no further). The AR(1) process, however, looks very distinct in comparison. Shocks from the series tend to throw the series off from the long run average for longer periods of time. In other words, if demand drops, it will likely stay below average for some time before it recovers. This distinctive pattern is clearly visible in the ACF for the AR(1) process; the autocorrelation coefficients in the series are present in all four time lags depicted, though they slowly decrease as the time lag increases.
7.5 Discussion
One can show that using single exponential smoothing as a forecasting method is essentially equivalent to using an ARIMA(0,1,1) model as a forecasting method. With optimal parameters, the two series of forecasts produced will be the same. The logical conclusion is then that since ARIMA(0,1,1) models are a special case of ARIMA(p, d, q) models, ARIMA models represent a generalization of exponential smoothing and thus must be more effective at forecasting.
While this logic is compelling, it has not withstood empirical tests. Large forecasting competitions have repeatedly demonstrated that exponential smoothing models tend to dominate ARIMA models in out-of-sample comparisons (Makridakis and Hibon 2000). It seems that exponential smoothing is simply more robust. Further, with the more general state space modeling framework, the variety of exponential smoothing models has been extended such that many of these models are not simply special cases of ARIMA modeling anymore. Thus, ARIMA modeling is not necessarily preferred anymore as a forecasting method in general; nevertheless, the use of these models continues to enjoy some popularity. ARIMA modeling is recommended “for a series showing short-term correlation where the variation is not dominated by trend and seasonality, provided the forecaster has the technical expertise to understand how to carry out the method” (Chatfield 2007). If ARIMA models are used as a forecasting method, one usually does not need to consider a high differencing order. Most series can be well modeled with no more than two differences (i.e., d ≤ 2) and AR/MA terms up to order five (i.e., p, q ≤ 5) (Ali et al. 2015).
While ARIMA models focus on point forecasts, a similar class of models, called GARCH (generalized autoregressive conditional heteroscedasticity) focuses on modeling the uncertainty inherent in forecasts as a function of previous shocks (i.e., forecast errors). These models are often employed in stock market applications and stem from the observation that large shocks to the market in one period create more volatility in succeeding periods. The key to these models is to view the variance of forecast errors not as fixed, but as a function of previous errors, effectively creating a relationship between previous shocks to the time series and future uncertainty of forecasts. GARCH can be combined with ARIMA models since the former technique is focused at modeling the variance of a distribution while the latter models the mean. A good introduction to GARCH modeling is given in Engle (2001) and Batchelor (2010).
7.6 Key Takeaways
• ARIMA models explain time series based on autocorrelation, integration, and moving averages. They can be applied to time series with seasonality and trend.
• These models have not performed particularly well in demand forecasting competitions, but they are included in most forecasting software packages.
• Your software should identify the best differencing, AR, and MA orders automatically, as well as estimate the actual AR and MA coefficients. If not, ACF and PACF plots can be used to identify AR and MA orders.
• You will typically not need high AR, MA or differencing orders for the model to work.
