So far we have studied several forecasting algorithms. Most of these can have many different variants, depending on whether seasonality, trend, and so forth are included or not. The question therefore arises how to decide whether one algorithm does a better job at forecasting a given time series than another one—that is, we need to benchmark methods and find those that work the best in our context. We thus need forecast quality key performance indices (KPIs), or error measures.
Performance measurement is necessary for management; if we do not measure performance, it is hard to set goals and coordinate activities to a purpose. This statement is true for almost any aspect of a business, but particularly so for forecasting. However, it is counter to how society often treats forecasting (Tetlock and Gardner 2015). Pundits on television can make bold statements about the future without their feet being held to the fire; management gurus are praised when one of their predictions has come true, without ever considering their long-run record. A similar culture can exist in organizations—managerial gut judgments are taken as fact, without ever establishing whether the forecaster making the judgment has a history of being spot on, or mostly off. Even worse, forecasts are often made in such a way that it becomes impossible to examine their quality, particularly since the forecast does not include a proper time frame; the good news is that in demand forecasting, forecasts are usually quantified (“we expect demand for SKU X to be Y”) and come with a time frame (“Z months from now”). Such a specificity allows explicitly calculating the error in the forecast and thus making long-run assessments of this error. Unfortunately, despite these benefits of quantification, it still turns out that deciding whether a demand forecast is “good” or whether one forecasting algorithm is “better” than another is not completely straightforward—which is why we will devote this chapter to the topic.
The aim of this section is to introduce the concepts of bias and accuracy in forecast error measurement and to provide an overview of commonly used metrics for this purpose. Suppose we have calculated a single point forecast ![]() and later on observe the corresponding demand realization y. We will define the corresponding error as
and later on observe the corresponding demand realization y. We will define the corresponding error as

For instance, if ![]() = 10 and y = 8, then e = 10 – 8 = 2. This definition has the advantage that overforecasts (i.e.,
= 10 and y = 8, then e = 10 – 8 = 2. This definition has the advantage that overforecasts (i.e., ![]() > y) correspond to positive errors, while underforecasts (i.e.,
> y) correspond to positive errors, while underforecasts (i.e., ![]() < y) correspond to negative errors, in accordance with everyday intuition. Note that, with a slight rearrangement, this definition means that
< y) correspond to negative errors, in accordance with everyday intuition. Note that, with a slight rearrangement, this definition means that

or “actuals equal the model minus the error,” instead of “plus,” which is a common convention in modeling sciences such as statistics or machine learning, where one would define the error as e = y – ![]() . Such a definition would yield the unintuitive fact that overforecasts (or underforecasts) would correspond to negative (or positive) errors.
. Such a definition would yield the unintuitive fact that overforecasts (or underforecasts) would correspond to negative (or positive) errors.
As a matter of fact, our error definition, although common, is not universally accepted in forecasting research and practice, and many forecasters adopt the alternative error definition motivated by statistics and machine learning. Green and Tashman (2008) conducted a survey among practicing forecasters as to their favorite error definition and offered some additional commentary. Even our own definition of forecast error in Chapter 6 defines the error in its alternate form—mostly because this alternative definition makes exponential smoothing easier to explain and understand.
Whichever convention you adopt in your practical forecasting work, the key takeaway is that whenever you discuss errors, you need to make sure everyone is using the same definition. Note that this challenge does not arise if the only thing we are interested in are absolute errors.
Demand forecasts cannot be judged in their quality unless a sufficient number of forecasts have been made. As discussed in Chapter 1, if we examine just a single forecast error, we have no means of differentiating between bad luck and a bad forecasting method. Thus, we will not calculate the error of a single forecast and realization, but instead calculate errors of many forecasts made by the same method. Let us assume that we have n forecasts ![]() , . . .,
, . . ., ![]() and n corresponding actual realizations
and n corresponding actual realizations ![]() , . . .,
, . . ., ![]() , giving rise to n errors, that is,
, giving rise to n errors, that is,
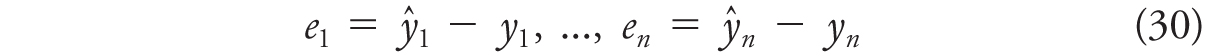
Our task is to summarize this (potentially very large) number of errors in a way that we can make sense of it. The simplest way of summarizing a large number of errors is to take its average. The mean error (ME) is the simple average of errors,

The ME tells us whether a forecast is “on average” on target. This is the key metric used to assess bias in a forecasting method. If ME = 0, then the forecast is on average unbiased, but if ME > 0, then we systematically overforecast demand, and if ME < 0, then we systematically underforecast demand. In either case, if ME ≠ 0 and the distance between ME and 0 is sufficiently large, we say that our forecast is biased.
While the notion of bias is an important one, quite often we are less interested in bias than in the accuracy of a forecasting method. While bias measures whether on average a forecast is on target, accuracy measures how close the forecast is to actual demand, on average. In other words, while the bias examines the mean of the forecast error distribution, the accuracy relates to the spread of the forecast error distribution. One often used metric to assess accuracy is the absolute difference between a point forecast ![]() and the corresponding realization y, that is,
and the corresponding realization y, that is,

where |.| means that we take the value between the “absolute bars,” that is, dropping any plus or minus sign. Thus, the absolute error cannot be negative. For instance, if the actual realization is y = 8, then a forecast of ![]() = 10 and one of
= 10 and one of ![]() = 6 would both be two units away from the actual in either direction, and the absolute error is 2 for either forecast. The mean absolute error (MAE) or mean absolute deviation (MAD)—both terms are used interchangeably—is the simple average of absolute errors,
= 6 would both be two units away from the actual in either direction, and the absolute error is 2 for either forecast. The mean absolute error (MAE) or mean absolute deviation (MAD)—both terms are used interchangeably—is the simple average of absolute errors,

Note here that we need to take absolute values before and not after summing the errors. For instance, assume that n = 2, e1 = 2, and e2 = – 2. Then |e1| + |e2| = |2| + |–2| = 2 + 2 = 4 ≠ 0 = |2 + (–2)| = |e1 + e2|. The MAE tells us whether a forecast is “on average” accurate, that is, whether it is “close to” or “far away from” the actual, without taking the sign of the error into account.
Let us consider an artificial example (cf. Figure 11.1). Assume that our point forecast is ![]() = (11, 11, . . ., 11), that is, we have a constant forecast of 11 for n = 10 months. Assume further that the actual observations are y = (10, 12, 10, 12, 10, 12, 10, 12, 10, 12). Then the errors are e = (1, -1, 1, -1, 1, -1, 1, -1, 1, -1) and ME = 0, that is, our flat forecast is unbiased. However, it is not very accurate, since MAD = 1. Conversely, assume that the forecast is
= (11, 11, . . ., 11), that is, we have a constant forecast of 11 for n = 10 months. Assume further that the actual observations are y = (10, 12, 10, 12, 10, 12, 10, 12, 10, 12). Then the errors are e = (1, -1, 1, -1, 1, -1, 1, -1, 1, -1) and ME = 0, that is, our flat forecast is unbiased. However, it is not very accurate, since MAD = 1. Conversely, assume that the forecast is ![]() = (9.5, 11.5, 9.5, 11.5, . . ., 9.5, 11.5). In this case, our errors are e = –(-0.5, -0.5, . . ., -0.5), and every single forecast is 0.5 unit too low. Therefore, ME = -0.5, and our forecasts are biased (more precisely, biased downward). However, these forecasts are more accurate than the original ones, since their MAE = 0.5. In other words, even though being unbiased often means that a forecast is more accurate, this relationship is not guaranteed, and forecasters sometimes have to decide whether they prefer a biased but more accurate method over an unbiased but less accurate one.
= (9.5, 11.5, 9.5, 11.5, . . ., 9.5, 11.5). In this case, our errors are e = –(-0.5, -0.5, . . ., -0.5), and every single forecast is 0.5 unit too low. Therefore, ME = -0.5, and our forecasts are biased (more precisely, biased downward). However, these forecasts are more accurate than the original ones, since their MAE = 0.5. In other words, even though being unbiased often means that a forecast is more accurate, this relationship is not guaranteed, and forecasters sometimes have to decide whether they prefer a biased but more accurate method over an unbiased but less accurate one.

Figure 11.1 Bias vs. accuracy
Which of the two forecasts shown in Figure 11.1 is better? This question cannot be answered in isolation. We usually want our forecasts to be unbiased, since over- and underforecasts cancel out in the long run for unbiased forecasts. This logic would favor the first set of forecasts. However, the second set of forecasts captures the zigzag pattern in the realizations better, at the expense of bias. To decide which forecast is “better,” we would need to assess which one leads to better decisions in plans that depend on the forecast, for example, which forecast yields lower stocks and out-of-stocks (which in turn depends, in addition to point forecasts, on accurate estimates of future residual variances and in fact on predictive distributions).
How strong a bias do our error measures need to exhibit to provide us with evidence that a forecasting method actually is biased? After all, it is highly unlikely that the average error is exactly equal to zero. To answer this question, we need to standardize the observed average forecast error by the observed variation in forecast errors—much akin to calculating a test statistic. This is the objective of the tracking signal, which is calculated as follows:

The tracking signal is constantly monitored. If it falls outside certain boundaries, the forecast is deemed biased. A general rule of thumb is that if the tracking signal consistently goes outside to range of ±4, that is, if the running sum of forecast errors is four times the average absolute deviation, then this constitutes evidence that the forecasting method has become biased.
One other very common point forecast accuracy measure, which is often used as an alternative to the MAE, works with squared errors, that is, e2. The square turns every negative number into a positive one, so similar to absolute deviations, squared errors will again always be nonnegative. In order to summarize multiple squared errors e12, . . ., en2, one can calculate the mean squared error (MSE),

The MSE is another measure of accuracy, not of bias. In the example in the previous section, the first (constant) forecast yields MSE = 1, whereas the second (zigzag) forecast yields MSE = 0.25.
Should one use absolute (i.e., MAE) or squared (i.e., MSE) errors to calculate the accuracy of a method? Squared errors have one important property: Because of the process of squaring numbers, they emphasize large errors much more than absolute errors. Indeed, suppose that in the example above we change a single actual realization from 10 to 20, without changing the forecasts. Then the MEs change a little to -1 and -1.5, the MAEs change slightly to 1.8 and 1.5, but the MSE changes drastically to 9 and 11.25.
Through the process of squaring errors, MSE becomes more sensitive to outlier observations than MAE—which can be a good thing (if outliers are meaningful) or distracting (if you do not want to base your decision making on outlier observations). If you use the MSE, it is always important to screen forecasts and actuals for large errors and to think about what these mean—if these are not important in the larger scheme of things, you may want to remove them from the forecast quality calculation or switch to an absolute error measure instead.
In addition, squared errors have one other technical but very important property: Estimating the parameters of a forecasting model by minimizing the MSE will always lead to unbiased errors, at least if we understand the underlying distribution well enough. The MAE does not have this property—optimizing the MAE may lead to systematically biased forecasts, especially when we forecast intermittent or count data (see Chapter 9 and Morlidge 2015 as well as Kolassa 2016a).
Finally, squared errors and the MSE are expressed in “squared units.” If, for example, the forecast and the actual demand are both expressed in dollars, the MSE will be denoted in “squared dollars.” This scale is rather unintuitive. One remedy is to take the square root of the MSE, to arrive at the root mean squared error (RMSE)—an error measure that is similar to a standard deviation and thus somewhat easier to interpret.
Note that all summary measures of error we considered so far (the ME, MAE/MAD, MSE, and RMSE) have one important weakness: They are not scale-independent. If a forecaster tells you that the MAE associated with forecasting a time series with a particular method is 15, you have no idea how good this number actually is. If average demand in that series is at about 2,000, an MAE of 15 would imply very good forecasts! If, however, the average demand in that series is only 30, then an MAE of 15 would be seen as evidence that it is very difficult to forecast the series. Thus, without knowing the scale of the series, interpreting any of these measures of bias and accuracy is difficult. One can always use them to compare different methods for the same series (i.e., method 1 has an MAE of 15 and method 2 has an MAE of 10 on the same series; thus method 2 seems better), but any comparison between series becomes challenging.
Typically, we will forecast not a single time series but multiple ones, for example, multiple SKUs, possibly in multiple locations. Each time series will be on a different order of magnitude. One SKU may sell tens of units per month, while another one may sell thousands. In such cases, the forecast errors will typically be on similar orders of magnitude—tens of units for the first SKU and thousands of units for the second SKU. Thus, if we use a point forecast quality measure like the MAE to decide, say, between different possible forecast algorithms applied to all series, our result will be completely dominated by the performance of the algorithms on the faster-moving SKU, although the slower-moving one may well be equally or more important. To address this issue, we will try to express all error summaries on a common scale, which we can then meaningfully summarize in turn. For this, we will consider both percentage errors and scaled errors.
11.2 Percentage and Scaled Errors
To scale forecast errors according to their time series, percentage errors express errors as a fraction of the corresponding actual demand realization, that is,

These percentage errors are often articulated as percentages instead of fractions. Thus, a forecast of ![]() = 10 and an actual realization of y = 8 will yield a percentage error of p = (10 – 8)/8 = 0.25, or 25 percent.
= 10 and an actual realization of y = 8 will yield a percentage error of p = (10 – 8)/8 = 0.25, or 25 percent.
As in the case of unscaled errors in the previous subsection, the definition we give for percentage errors in equation (36) is the most common one used, but it is not the only one encountered in practice. Some forecasters prefer to divide the error not by the actual (i.e., y) but by the forecast (i.e., ![]() ; see Green and Tashman 2009). One advantage of this alternative approach is that while the demand can occasionally be zero within the time series (creating a division by zero problem when using demand as a scale), forecasts are less likely to be zero. This modified percentage error otherwise has similar properties as the percentage error defined in equation (36), and the same key takeaway as for “simple” errors applies: all definitions have advantages and disadvantages, and it is most important to agree on a common error measure in a single organization so we do not compare apples and oranges.
; see Green and Tashman 2009). One advantage of this alternative approach is that while the demand can occasionally be zero within the time series (creating a division by zero problem when using demand as a scale), forecasts are less likely to be zero. This modified percentage error otherwise has similar properties as the percentage error defined in equation (36), and the same key takeaway as for “simple” errors applies: all definitions have advantages and disadvantages, and it is most important to agree on a common error measure in a single organization so we do not compare apples and oranges.
Percentage errors p1 = e1/![]() , . . ., pn = en/yn can be summarized in a similar way as “regular” errors. For instance, the mean percentage error is the simple average of pi,
, . . ., pn = en/yn can be summarized in a similar way as “regular” errors. For instance, the mean percentage error is the simple average of pi,

The MPE plays a similar role to the ME as a measure of “relative” bias. Similarly, we can calculate single absolute percentage errors (APEs),
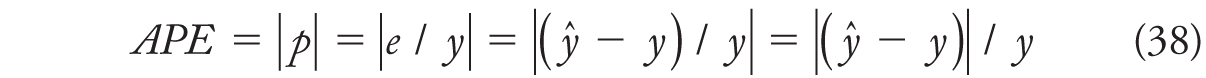
where one assumes y >0. APEs can then be summarized by averaging to arrive at the mean APE (MAPE),

which is an extremely common point forecast accuracy measure.
At this point, let us take a step back and look a little closer at the definition of percentage error. First, note that percentage errors are asymmetric. If we exchange the forecast ![]() and the actual y, then the error switches its sign, but the absolute error and the squared error do not change at all. In contrast, the percentage error changes in a way that depends on both
and the actual y, then the error switches its sign, but the absolute error and the squared error do not change at all. In contrast, the percentage error changes in a way that depends on both ![]() and y if we exchange the two. For instance,
and y if we exchange the two. For instance, ![]() = 10 and y = 8 yield p = 0.25 = 25 percent, but
= 10 and y = 8 yield p = 0.25 = 25 percent, but ![]() = 8 and y = 10 yield p = 0.20 = 20 percent. The absolute error is 2 and the squared error is 4 in either case. Thus, positive and negative forecast errors are treated differently with percentage error measures. Second, there is another problem here. If y = 0, then p entails a division by zero, which is mathematically undefined. If the actual realization is zero, then any nonzero error is an infinite fraction or percentage of it. Accordingly, if y becomes very small, p can become very large. There are various ways of dealing with this division by zero problem, some better, some not so good. Let us consider these in turn.
= 8 and y = 10 yield p = 0.20 = 20 percent. The absolute error is 2 and the squared error is 4 in either case. Thus, positive and negative forecast errors are treated differently with percentage error measures. Second, there is another problem here. If y = 0, then p entails a division by zero, which is mathematically undefined. If the actual realization is zero, then any nonzero error is an infinite fraction or percentage of it. Accordingly, if y becomes very small, p can become very large. There are various ways of dealing with this division by zero problem, some better, some not so good. Let us consider these in turn.
Some forecasting software “deals” with the problem by sweeping it under the rug: in calculating the MAPE, it only sums pi’s whose corresponding yi’s are greater than zero (Hoover 2006). Needless to say, this approach is not a good way of addressing the issue. It amounts to positing that we do not care at all about the forecast ![]() i if yi = 0, but if we make production decisions based on the forecast, then it will matter a lot whether prediction was
i if yi = 0, but if we make production decisions based on the forecast, then it will matter a lot whether prediction was ![]() i = 100 or
i = 100 or ![]() i = 1000 for an actual demand of zero—and such an error should be reflected in the forecast accuracy measure.
i = 1000 for an actual demand of zero—and such an error should be reflected in the forecast accuracy measure.
An alternative, which also addresses the asymmetry of percentage errors noted above, is to “symmetrize” the percentage errors by dividing the error not by the actual but by the average of the forecast and the actual (Makridakis 1993a), that is,

and then summarizing the absolute values of si’s as usual, yielding a symmetric MAPE (sMAPE),
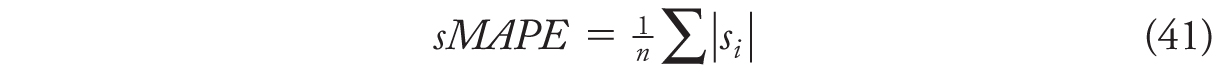
Assuming that at least one of ![]() and y are positive, s is well defined, and calculating the sMAPE poses no mathematical problems. In addition, s is symmetric in the sense above: if we exchange
and y are positive, s is well defined, and calculating the sMAPE poses no mathematical problems. In addition, s is symmetric in the sense above: if we exchange ![]() and y, then s changes its sign, but its absolute value |s| remains unchanged.
and y, then s changes its sign, but its absolute value |s| remains unchanged.
Unfortunately, some conceptual problems remain with this error definition as well. In particular, while the sMAPE is symmetric under exchange of forecasts and actuals, it introduces a new kind of asymmetry (Goodwin and Lawton 1999). If the actual realization is y = 10, then forecasts of ![]() = 9 and
= 9 and ![]() = 11 (an under- and overforecast of one unit, respectively) both result in APEs of 0.10 = 10 percent. However,
= 11 (an under- and overforecast of one unit, respectively) both result in APEs of 0.10 = 10 percent. However, ![]() = 9 yields |s| = 0.105 = 10.5 percent, whereas
= 9 yields |s| = 0.105 = 10.5 percent, whereas ![]() = 11 yields |s| = 0.095 = 9.5 percent. Generally, an underforecast
= 11 yields |s| = 0.095 = 9.5 percent. Generally, an underforecast ![]() = y – Δ by a difference Δ >0 will yield a larger |s| than an overforecast
= y – Δ by a difference Δ >0 will yield a larger |s| than an overforecast ![]() = y + Δ by the same amount, whereas the APE will be the same in both cases, |p| = Δ/y.
= y + Δ by the same amount, whereas the APE will be the same in both cases, |p| = Δ/y.
And this asymmetry is not the last of our worries. As noted above, using s instead of p means that we can mathematically calculate a symmetric percentage error even when y = 0. However, what does actually happen for this symmetrized error when y = 0? Let us calculate:

That is, whenever y = 0, the symmetric error s contributes 200 percent to the sMAPE, again completely regardless of the forecast ![]() (Boylan and Syntetos 2006). Dealing with zero demand observations in this way is not much better than simply disregarding errors whenever y = 0, as above.
(Boylan and Syntetos 2006). Dealing with zero demand observations in this way is not much better than simply disregarding errors whenever y = 0, as above.
Finally, we can calculate a percentage summary of errors in a different way to address the division by zero problem. The weighted MAPE (wMAPE) is defined as

A simple computation (Kolassa and Schuetz 2007) shows that we can interpret the wMAPE as a weighted average of APEs if all yi >0, where each APEi is weighted by the corresponding yi. That is, in the wMAPE, a given APE has a higher weight if the corresponding realization is larger, which makes intuitive sense. In addition, the wMAPE is mathematically defined even if some yi = 0, as long as not all yi = 0.
Now, the interpretation of wMAPE as a weighted average APE, with weights corresponding to actual yi, immediately suggests alternative weighting schemes. After all, while the actual yi is one possible measure of the “importance” of one APE, there are other possibilities of assigning an “importance” to an APE, like the cost of an SKU or its margin, or anything else. All these different measures of importance could be used in constructing an alternative wMAPE.
Apart from the problem with dividing by zero, which we can address by using the wMAPE, the APE has another issue, which does not necessarily invalidate its use, but which should be kept in mind. In forecasting demands, we have a natural lower bound of zero, both for actuals and for forecasts. It will (usually) not make sense to forecast ![]() = -10. Thus, our forecasts and actuals are constrained to 0 ≤
= -10. Thus, our forecasts and actuals are constrained to 0 ≤ ![]() , y < ∞. Now, assume that y = 10. Of course, a perfect forecast of
, y < ∞. Now, assume that y = 10. Of course, a perfect forecast of ![]() = 10 yields APE = |p| = 0 percent. A forecast of
= 10 yields APE = |p| = 0 percent. A forecast of ![]() = 0 yields APE = |p| = 1 = 100 percent, as does a forecast of
= 0 yields APE = |p| = 1 = 100 percent, as does a forecast of ![]() = 2× y = 20. However, a forecast of
= 2× y = 20. However, a forecast of ![]() = 30 yields APE = 200 percent. That is, the APE is bounded by 100 percent for underforecasts but unbounded for overforecasts (Figure 11.2).
= 30 yields APE = 200 percent. That is, the APE is bounded by 100 percent for underforecasts but unbounded for overforecasts (Figure 11.2).

Figure 11.2 The MAPE is bounded by underforecasts but unbounded by overforecasts
Thus, the APE is asymmetric as well: A forecast that can be either too high or too low may be penalized more strongly if it turns out to be too high than if it turns out to be too low.
Kolassa and Martin (2011) give a simple illustration of this effect that you can try at home. Take any standard six-sided die and forecast its roll. Assuming the die is not loaded, all six numbers from one to six are equally likely, and the average roll is 3.5. Thus, an unbiased forecast would also be 3.5. What MAPE would we expect from forecasting 3.5 for a series of many die rolls? We can simulate this expected MAPE empirically by rolling a die many times. Alternatively, we can calculate it abstractly, by noting that we have one chance in six in rolling a one, with an APE of |1-3.5|/1 = 250 percent, another one-in-six chance of rolling a two, with an APE of |2-3.5|/2 = 75 percent, and so on. It turns out that our expected MAPE is 70.97 percent.
We can use our dice to see what happens if we use a biased forecast of 4 instead of an unbiased forecast of 3.5. Little surprise here: the long-run MAPE of a forecast of 4 is worse than for a forecast of 3.5: it is 81.11 percent. However, what happens if our forecast is biased low instead of high? This time, we are in for a surprise: A forecast of 3 yields an expected MAPE of 60.83 percent, clearly lower than the MAPE for an unbiased forecast of 3.5. And an even more biased forecast of 2 yields a yet lower long-run MAPE of 51.67 percent. Try this with your dice at home!
Explaining this effect requires understanding the asymmetry of MAPE. Any forecast higher than 2 will frequently result in an APE that is larger than 100 percent, for example, if we roll a one. Such high APEs pull the average up more than lower APEs can pull it down. The bottom line is that the expected MAPE is minimized by a forecast that is heavily biased downward. Obviously, using this KPI can then lead to very dysfunctional incentives in forecasting.
Interestingly enough, this simple example also shows that alternatives to “plain vanilla” MAPE, such as the sMAPE or the MAPE with the forecast as a denominator, are also minimized by forecasts that differ from the actual long-run average. This asymmetry in the APE creates a perverse incentive to calculate a forecast that is biased low, rather than one that is unbiased but has a chance of exceeding the actual by a factor of 2 or more (resulting in an APE >100 percent). A statistically savvy forecaster might even be tempted to apply a “fudge factor” to the statistical forecasts obtained using his/her software, reducing all system-generated forecasts by 10 percent.
An alternative to using percentage errors is to calculate scaled errors, where the MAE/MAD, MSE, or RMSE (or indeed any other nonscaled error measure) are scaled by an appropriate amount. One scaled error measure is mean absolute scaled error (MASE; Hyndman and Koehler 2006; Hyndman 2006; Franses 2016). Its computation involves not only forecasts and actual realizations but also historical observations used to calculate forecasts. Specifically, assume that we have historical observations ![]() , . . . , yT, from which we calculate one-step-ahead, two-step-ahead, and later forecasts
, . . . , yT, from which we calculate one-step-ahead, two-step-ahead, and later forecasts ![]() T+1, . . . ,
T+1, . . . , ![]() T+h, which correspond to actual realizations yT+1, . . . , yT+h. Using this notation, we can write our MAE calculations as follows:
T+h, which correspond to actual realizations yT+1, . . . , yT+h. Using this notation, we can write our MAE calculations as follows:

Next, we calculate the MAE that would have been observed historically if we had used naïve one-step-ahead forecasts in the past—that is, simply using the previous demand observation as a forecast for the future. The naïve one-step forecast for period 2 is the previous demand y1, for period 3 the previous demand y2, and so forth. Specifically, we calculate

The MASE then is the ratio of MAE and MAE′:
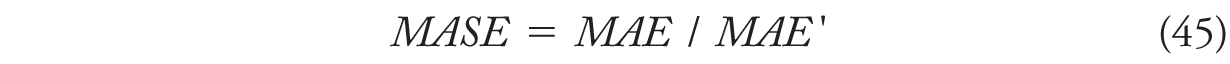
The MASE scales MAE by MAE′. It expresses whether our “real” forecast error (MAE) is larger than the in-sample naïve one-step-ahead forecast (MASE > 1) or smaller (MASE < 1). Since both numerator and denominator are on the level of the original time series, we can compare the MASE between different time series.
Two points should be kept in mind. First, the MASE is often miscalculated. Correct calculation requires using the in-sample, naïve forecast for MAE′, that is, basing the calculations on historical data used to estimate the parameters of a forecasting method. Instead, forecasters often use the out-of-sample, naïve forecast to calculate MAE′, that is, the data that the forecasting method is applied to. This miscalculation also results in a scaled quality measure that is comparable between time series and, as such, is quite defensible, but it simply is not “the” MASE as defined in literature.1 As always, one simply needs to be consistent in calculating, reporting, and comparing errors in an organization.
Second, as discussed above, a MASE > 1 means that our forecasts have a worse MAE than an in-sample, naïve, one-step-ahead forecast. This, at first glance, sounds disconcerting. Should we not expect to do better than the naïve forecast? However, a MASE > 1 could easily come about using quite sophisticated and competitive forecasting algorithms (e.g., Athanasopoulos et al. 2011 who found MASE = 1.38 for monthly, 1.43 for quarterly, and 2.28 for yearly data). For instance, you need to keep in mind that MAE in the MASE numerator is calculated from multistep-ahead forecasts, whereas MAE′ in the denominator is calculated from one-step-ahead forecasts. It certainly is not surprising that multistep-ahead forecasts are worse than one-step-ahead (naïve) forecasts, or MAE > MAE′, or MASE > 1.
What are the advantages of MASE compared to, say, MAPE? First, it is scaled, so the MASE of forecasts for time series on different scales is comparable. Insofar, it is similar to MAPE. However, MASE has two key advantages over MAPE. First, it is defined even when one actual is zero. Second, it penalizes over- and underforecasts equally, avoiding the problem we encountered in the dice-rolling example. On the other hand, MASE does have the disadvantage of being harder to interpret. A percentage error (as for MAPE) is simply easier to understand than a scaled error as a multiple of some in-sample forecast (as for MASE).
11.3 Assessing Prediction Intervals
Recall from Section 3.2 that a prediction interval of coverage q consists of a lower and an upper bound 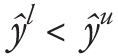 on future demand realizations y, such that we expect a certain given percentage q of future realizations to fall within the bracket
on future demand realizations y, such that we expect a certain given percentage q of future realizations to fall within the bracket  . How do we assess whether such an interval forecast is any good?
. How do we assess whether such an interval forecast is any good?
A single-interval forecast and a corresponding single-demand realization usually does not yield a lot of information. Suppose q = 80 percent. Even if the prediction interval captures the corresponding interval of the underlying probability distribution perfectly (which is referred to as “perfectly calibrated”), then the prediction interval is expected not to contain the true realization in one out of every five cases. If we observe just a few instances, there is little we can learn about the accuracy of our method of creating prediction intervals. Such a calibration assessment requires larger amounts of data.
Furthermore, the successful assessment of prediction intervals requires that the method of creating these intervals is fixed over time. Suppose we want to examine whether the prediction intervals provided by a forecaster are really 80 percent; if the method of how these intervals are created is not fixed during the time of observation, the forecaster could simply set very wide intervals for four of these time periods and a very narrow interval for the remaining time period, creating an 80 percent “hit rate.”
In summary, in order to assess the calibration of prediction interval forecasts, we will need multiple demand observations from a time period where the method used to create these intervals was fixed. Suppose we have n interval forecasts and that k of them contain the corresponding demand realization. We can then compute the true coverage rate k/n and compare it to the so-called nominal coverage rate q. If k/n ≈ q, then our interval forecast looks good. However, we will usually not exactly have k/n = q. Thus, the question arises how large the difference between k/n and q needs to be for us to reasonably conclude that our method of constructing interval forecasts is good or bad. To this purpose, we can use a statistical concept called “Pearson’s χ2 test.” We create a so-called contingency table (see Table 11.1) by noting how often our interval forecasts in fact covered the realization and how often we would have expected them to do so.
Table 11.1 Expected and observed coverage

We next calculate the following test statistic:

The symbol “χ” represents the small Greek letter “chi,” and this test is therefore often called a “chi-squared” test. We can then examine whether this calculated value is larger than the critical value of a χ2 distribution with 1 degree of freedom for a given α (i.e., statistical significance) level. This critical value is available in standard statistical tables or in standard statistical software, for example, using the = CHISQ.INV function in Microsoft Excel. If our calculated value from equation (46) is indeed larger than the critical value, then this can be seen as evidence for poor calibration, and we should consider improving our method of calculating prediction intervals.
As an example, let us assume we have n = 100 interval forecasts aiming at a nominal coverage probability of q = 95 percent, so we would expect qn = 95 of true realizations to be covered by the corresponding interval forecasts. Let us further assume that we actually observe k = 90 realizations that were covered by the interval forecast. Is this difference between observing k = 90 and expecting qn = 95 covered realizations statistically significant at a standard alpha level of α = 0.05? We calculate a test statistic of χ2 = (90 – 95)2/95 + (10 – 5)2/5 = 0.26 + 5.00 = 5.26. The critical value of a χ2 distribution with 1 degree of freedom for α = 0.05, calculated for example using Microsoft Excel by “= CHISQ.INV(0.95;1),” is 3.84, which is smaller than our test statistic. We conclude that our actual coverage is statistically significantly smaller than the nominal coverage we had aimed for and thus consider modifying our way of calculating prediction intervals.
11.4 Quality Measures for Count Data forecasts
Count data unfortunately pose particular challenges for forecast quality assessments. Some of the quality measures investigated so far can be seriously misleading for count data. For instance, the MAE does not work as expected for count data. This is a rather new discovery in the forecasting community (Morlidge 2015; Kolassa 2016a). The underlying reason is well known in statistics, but you will still find researchers and practitioners incorrectly measuring the quality of intermittent demand forecasts using MAE. After reading further, you will understand why such an approach is incorrect.
What is the problem with MAE and count data? There are two key insights to this. One is that we want a point forecast quality measure to guide us toward unbiased point forecasts. Put differently, we want any error measure to have a minimal expected value (or one of zero) if we feed it unbiased forecasts. Unfortunately, MAE does not conform to this requirement. Whereas MSE is in fact minimized and ME is zero in expectation for an unbiased forecast, MAE is not minimized by an unbiased forecast for count data. Specifically, it is easy to show that for any distribution, the forecast that minimizes the expected (mean) absolute error is not the expected value of distribution but its median (Hanley et al. 2001). This fact does not make a difference for a symmetric predictive distribution like normal distribution, since mean and median of a symmetric distribution are identical. However, the distributions we use for count data are hardly ever symmetric, and this deficiency of MAE thus becomes troubling.
Figure 11.3 shows three Poisson-distributed demand series with different means (0.05, 0.3, and 0.6), along with probability mass histograms turned sideways. Importantly, in all three cases, the median of the Poisson distribution is zero, meaning that the point forecast that minimizes MAE is zero. Turning this argument around, suppose we use MAE to find the “best” forecasting algorithm for a number of count data series. We find that a flat zero-point forecast minimizes MAE. This is not surprising after the discussion above. However, a flat zero forecast is obviously not useful. The inescapable conclusion is that we need to be very careful about using MAE for assessing point forecasts for count data!

Figure 11.3 Poisson–distributed count demand data
Unfortunately, this realization implies that all point forecast quality measures that are only scaled multiples of MAE are equally useless for count data. Specifically, this applies to MASE and wMAPE, which in addition is undefined if all demands in the evaluation period are zero. Finally, almost needless to say, MAPE does not make any sense for intermittent data, since APEs are undefined if y = 0. Happily, some quality measures do work (mostly) “as advertised” for count data. The ME is still a valid measure of bias. However, of course, highly intermittent demands can, simply by chance, have long strings of consecutive zero demands, so any nonzero forecast may look biased. Thus, detecting bias is even harder for count data than for continuous data.
Similarly, the MSE still retains its property of being minimized by the expectation of future realizations. Therefore, we can still use MSE to guide us toward unbiased forecasts. As discussed above, MSE can still not be meaningfully compared between time series of different levels. One could, however, scale RMSE by the series’ overall mean to obtain a scaled error measure that is comparable between series.
11.5 Key Takeaways
• There are numerous forecast accuracy measures.
• Different accuracy measures measure different things. There is no one “best” accuracy KPI. Consider looking at multiple ones.
• If you have only a single time series or series on similar scales, use MSE or MAE.
• If you have multiple series at different scales, use scaled or percentage errors. However, remember that these percentage errors can introduce asymmetries with respect to how they penalize over- and underforecasting.
• Always look at bias. Be aware that MAE and MAPE can mislead you into biased forecasts.
______________
1Hyndman and Koehler (2006) give a technical reason for proposing the in-sample MAE as the denominator.
