Next, we're going to talk about conditional probability. It's a very simple concept. It's trying to figure out the probability of something happening given that something else occurred. Although it sounds simple, it can be actually very difficult to wrap your head around some of the nuances of it. So get an extra cup of coffee, make sure your thinking cap's on, and if you're ready for some more challenging concepts here. Let's do this.

Conditional probability is a way to measure the relationship between two things happening to each other. Let's say I want to find the probability of an event happening given that another event already happened. Conditional probability gives you the tools to figure that out.

What I'm trying to find out with conditional probability is if I have two events that depend on each other. That is, what's the probability that both will occur?

In mathematical notation, the way we indicate things here is that P(A,B) represents the probability of both A and B occurring independent of each other. That is, what's the probability of both of these things happening irrespective of everything else.

Whereas this notation, P(B|A), is read as the probability of B given A. So, what is the probability of B given that event A has already occurred? It's a little bit different, and these things are related like this:

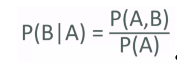
The probability of B given A is equal to the probability of A and B occurring over the probability of A alone occurring, so this teases out the probability of B being dependent on the probability of A.

It'll make more sense with an example here, so bear with me.

Let's say that I give you, my readers, two tests, and 60% of you pass both tests. Now the first test was easier, 80% of you passed that one. I can use this information to figure out what percentage of readers who passed the first test also passed the second. So here's a real example of the difference between the probability of B given A and the probability of A and B.

I'm going to represent A as the probability of passing the first test, and B as the probability of passing the second test. What I'm looking for is the probability of passing the second test given that you passed the first, that is, P (B|A).

So the probability of passing the second test given that you passed the first is equal to the probability of passing both tests, P(A,B) (I know that 60% of you passed both tests irrespective of each other), divided by the probability of passing the first test, P(A), which is 80%. It's worked out to 60% passed both tests, 80% passed the first test, therefore the probability of passing the second given that you passed the first works out to 75%.

OK, it's a little bit tough to wrap your head around this concept. It took me a little while to really internalize the difference between the probability of something given something and the probability of two things happening irrespective of each other. Make sure you internalize this example and how it's really working before you move on.