Alright, let's move on and do another more complicated example using some real Python code. We can then see how we might actually implement these ideas using Python.

Let's put conditional probability into action here and use some of the ideas to figure out if there's a relationship between age and buying stuff using some fabricated data. Go ahead and open up the ConditionalProbabilityExercise.ipynb here and follow along with me if you like.

What I'm going to do is write a little bit of Python code that creates some fake data:

from numpy import random 
random.seed(0) 
 
totals = {20:0, 30:0, 40:0, 50:0, 60:0, 70:0} 
purchases = {20:0, 30:0, 40:0, 50:0, 60:0, 70:0} 
totalPurchases = 0 
for _ in range(100000): 
    ageDecade = random.choice([20, 30, 40, 50, 60, 70]) 
    purchaseProbability = float(ageDecade) / 100.0 
    totals[ageDecade] += 1 
    if (random.random() < purchaseProbability): 
        totalPurchases += 1 
        purchases[ageDecade] += 1 

What I'm going to do is take 100,000 virtual people and randomly assign them to an age bracket. They can be in their 20s, their 30s, their 40s, their 50s, their 60s, or their 70s. I'm also going to assign them a number of things that they bought during some period of time, and I'm going to weight the probability of purchasing something based on their age.

What this code ends up doing is randomly assigning each person to an age group using the random.choice() function from NumPy. Then I'm going to assign a probability of purchasing something, and I have weighted it such that younger people are less likely to buy stuff than older people. I'm going to go through 100,000 people and add everything up as I go, and what I end up with are two Python dictionaries: one that gives me the total number of people in each age group, and another that gives me the total number of things bought within each age group. I'm also going to keep track of the total number of things bought overall. Let's go ahead and run that code.

If you want to take a second to kind of work through that code in your head and figure out how it works, you've got the IPython Notebook. You can go back into that later too. Let's take a look what we ended up with.

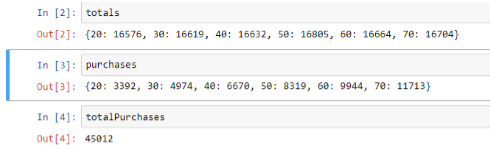
Our totals dictionary is telling us how many people are in each age bracket, and it's pretty evenly distributed, just like we expected. The amount purchased by each age group is in fact increasing by age, so 20-year-olds only bought about 3,000 things and 70-year-olds bought about 11,000 things, and overall the entire population bought about 45,000 things.

Let's use this data to play around with the ideas of conditional probability. Let's first figure out what's the probability of buying something given that you're in your 30s. The notation for that will be P(E|F) if we're calling purchase E, and F as the event that you're in your 30s.

Now we have this fancy equation that gave you a way of computing P(E|F) given P(E,F), and P(E), but we don't need that. You don't just blindly apply equations whenever you see something. You have to think about your data intuitively. What is it telling us? I want to figure out the probability of purchasing something given that you're in your 30s. Well I have all the data I need to compute that directly.

PEF = float(purchases[30]) / float(totals[30]) 

I have how much stuff 30-year-olds purchased in the purchases[30] bucket, and I know how many 30-year-olds there are. So I can just divide those two numbers to get the ratio of 30-year-old purchases over the number of 30-year-olds. I can then output that using the print command:

print ("P(purchase | 30s): ", PEF) 

I end up with a probability of purchasing something given that you're in your 30s of being about 30%:

P(purchase | 30s): 0.2992959865211 

Note that if you're using Python 2, the print command doesn't have the surrounding brackets, so it would be:

print "p(purchase | 30s): ", PEF 

If I want to find P(F), that's just the probability of being 30 overall, I can take the total number of 30-year-olds divided by the number of people in my dataset, which is 100,000:

PF = float(totals[30]) / 100000.0 
print ("P(30's): ", PF) 

Again, remove those brackets around the print statement if you're using Python 2. That should give the following output:

P(30's): 0.16619 

I know the probability of being in your 30s is about 16%.

We'll now find out P(E), which just represents the overall probability of buying something irrespective of your age:

PE = float(totalPurchases) / 100000.0 
print ("P(Purchase):", PE) 
 
P(Purchase): 0.45012 

That works out to be, in this example, about 45%. I can just take the total number of things purchased by everybody regardless of age and divide it by the total number of people to get the overall probability of purchase.

Alright, so what do I have here? I have the probability of purchasing something given that you're in your 30s being about 30%, and then I have the probability of purchasing something overall at about 45%.

Now if E and F were independent, if age didn't matter, then I would expect the P(E|F) to be about the same as P(E). I would expect the probability of buying something given that you're in your 30s to be about the same as the overall probability of buying something, but they're not, right? And because they're different, that tells me that they are in fact dependent, somehow. So that's a little way of using conditional probability to tease out these dependencies in the data.

Let's do some more notation stuff here. If you see something like P(E)P(F) together, that means multiply these probabilities together. I can just take the overall probability of purchase multiplied by the overall probability of being in your 30s:

print ("P(30's)P(Purchase)", PE * PF) 
 
P(30's)P(Purchase) 0.07480544280000001 

That worked out to about 7.5%.

Just from the way probabilities work, I know that if I want to get the probability of two things happening together, that would be the same thing as multiplying their individual probabilities. So it turns out that P(E,F) happening, is the same thing as P(E)P(F).

print ("P(30's, Purchase)", float(purchases[30]) / 100000.0) 
P(30's, Purchase) 0.04974 

Now because of the random distribution of data, it doesn't work out to be exactly the same thing. We're talking about probabilities here, remember, but they're in the same ballpark, so that makes sense, about 5% versus 7%, close enough.

Now that is different again from P(E|F), so the probability of both being in your 30s and buying something is different than the probability of buying something given that you're in your 30s.

Now let's just do a little sanity check here. We can check our equation that we saw in the Conditional Probability section earlier, that said that the probability of buying something given that you're in your 30s is the same as the probability of being in your 30s and buying something over the probability of buying something. That is, we check if P(E|F)=P(E,F)/P(F).

(float(purchases[30]) / 100000.0) / PF  

This gives us:

Out []:0.29929598652145134 

Sure enough, it does work out. If I take the probability of buying something given that you're in your 30s over the overall probability, we end up with about 30%, which is pretty much what we came up with originally for P(E|F). So the equation works, yay!

Alright, it's tough to wrap your head around some of this stuff. It's a little bit confusing, I know, but if you need to, go through this again, study it, and make sure you understand what's going on here. I've tried to put in enough examples here to illustrate different combinations of thinking about this stuff. Once you've got it internalized, I'm going to challenge you to actually do a little bit of work yourself here.