Let's put train/test into action. So you might remember that a regression can be thought of as a form of supervised machine learning. Let's just take a polynomial regression, which we covered earlier, and use train/test to try to find the right degree polynomial to fit a given set of data.
Just like in our previous example, we're going to set up a little fake dataset of randomly generated page speeds and purchase amounts, and I'm going to create a quirky little relationship between them that's exponential in nature.
%matplotlib inline import numpy as np from pylab import * np.random.seed(2) pageSpeeds = np.random.normal(3.0, 1.0, 100) purchaseAmount = np.random.normal(50.0, 30.0, 100) / pageSpeeds scatter(pageSpeeds, purchaseAmount)
Let's go ahead and generate that data. We'll use a normal distribution of random data for both page speeds and purchase amount using the relationship as shown in the following screenshot:
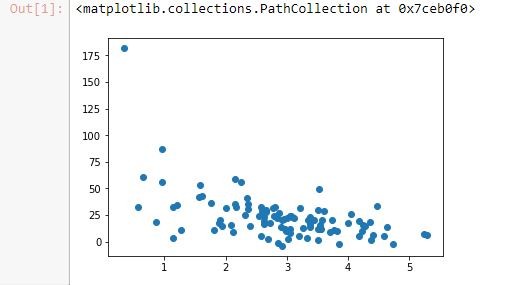
Next, we'll split that data. We'll take 80% of our data, and we're going to reserve that for our training data. So only 80% of these points are going to be used for training the model, and then we're going to reserve the other 20% for testing that model against unseen data.
We'll use Python's syntax here for splitting the list. The first 80 points are going to go to the training set, and the last 20, everything after 80, is going to go to test set. You may remember this from our Python basics chapter earlier on, where we covered the syntax to do this, and we'll do the same thing for purchase amounts here:
trainX = pageSpeeds[:80] testX = pageSpeeds[80:] trainY = purchaseAmount[:80] testY = purchaseAmount[80:]
Now in our earlier sections, I've said that you shouldn't just slice your dataset in two like this, but that you should randomly sample it for training and testing. In this case though, it works out because my original data was randomly generated anyway, so there's really no rhyme or reason to where things fell. But in real-world data you'll want to shuffle that data before you split it.
We'll look now at a handy method that you can use for that purpose of shuffling your data. Also, if you're using the pandas package, there's some handy functions in there for making training and test datasets automatically for you. But we're going to do it using a Python list here. So let's visualize our training dataset that we ended up with. We'll do a scatter plot of our training page speeds and purchase amounts.
scatter(trainX, trainY)
This is what your output should now look like:

Basically, 80 points that were selected at random from the original complete dataset have been plotted. It has basically the same shape, so that's a good thing. It's representative of our data. That's important!
Now let's plot the remaining 20 points that we reserved as test data.
scatter(testX, testY)

Here, we see our remaining 20 for testing also has the same general shape as our original data. So I think that's a representative test set too. It's a little bit smaller than you would like to see in the real world, for sure. You probably get a little bit of a better result if you had 1,000 points instead of 100, for example, to choose from and reserved 200 instead of 20.
Now we're going to try to fit an 8th degree polynomial to this data, and we'll just pick the number 8 at random because I know it's a really high order and is probably overfitting.
Let's go ahead and fit our 8th degree polynomial using np.poly1d(np.polyfit(x, y, 8)), where x is an array of the training data only, and y is an array of the training data only. We are finding our model using only those 80 points that we reserved for training. Now we have this p4 function that results that we can use to predict new values:
x = np.array(trainX) y = np.array(trainY) p4 = np.poly1d(np.polyfit(x, y, 8))
Now we'll plot the polynomial this came up with against the training data. We can scatter our original data for the training data set, and then we can plot our predicted values against them:
import matplotlib.pyplot as plt xp = np.linspace(0, 7, 100) axes = plt.axes() axes.set_xlim([0,7]) axes.set_ylim([0, 200]) plt.scatter(x, y) plt.plot(xp, p4(xp), c='r') plt.show()
You can see in the following graph that it looks like a pretty good fit, but you know that clearly it's doing some overfitting:

What's this craziness out at the right? I'm pretty sure our real data, if we had it out there, wouldn't be crazy high, as this function would implicate. So this is a great example of overfitting your data. It fits the data you gave it very well, but it would do a terrible job of predicting new values beyond the point where the graph is going crazy high on the right. So let's try to tease that out. Let's give it our test dataset:
testx = np.array(testX) testy = np.array(testY) axes = plt.axes() axes.set_xlim([0,7]) axes.set_ylim([0, 200]) plt.scatter(testx, testy) plt.plot(xp, p4(xp), c='r') plt.show()
Indeed, if we plot our test data against that same function, well, it doesn't actually look that bad.

We got lucky and none of our test is actually out here to begin with, but you can see that it's a reasonable fit, but far from perfect. And in fact, if you actually measure the r-squared score, it's worse than you might think. We can measure that using the r2_score() function from sklearn.metrics. We just give it our original data and our predicted values and it just goes through and measures all the variances from the predictions and squares them all up for you:
from sklearn.metrics import r2_score r2 = r2_score(testy, p4(testx)) print r2
We end up with an r-squared score of just 0.3. So that's not that hot! You can see that it fits the training data a lot better:
from sklearn.metrics import r2_score r2 = r2_score(np.array(trainY), p4(np.array(trainX))) print r2
The r-squared value turns out to be 0.6, which isn't too surprising, because we trained it on the training data. The test data is sort of its unknown, its test, and it did fail the test, quite frankly. 30%, that's an F!
So this has been an example where we've used train/test to evaluate a supervised learning algorithm, and like I said before, pandas has some means of making this even easier. We'll look at that a little bit later, and we'll also look at more examples of train/test, including k-fold cross validation, later in the book as well.
