Okay, let's actually build a full-blown recommender system that can look at all the behavior information of everybody in the system, and what movies they rated, and use that to actually produce the best recommendation movies for any given user in our dataset. Kind of amazing and you'll be surprised how simple it is. Let's go!
Let's begin using the ItemBasedCF.ipynb file and let's start off by importing the MovieLens dataset that we have. Again, we're using a subset of it that just contains 100,000 ratings for now. But, there are larger datasets you can get from GroupLens.org-up to millions of ratings; if you're so inclined. Keep in mind though, when you start to deal with that really big data, you're going to be pushing the limits of what you can do in a single machine and what Pandas can handle. Without further ado, here's the first block of code:
import pandas as pd
r_cols = ['user_id', 'movie_id', 'rating']
ratings = pd.read_csv('e:/sundog-consult/packt/datascience/ml-100k/u.data',
sep=' ', names=r_cols, usecols=range(3))
m_cols = ['movie_id', 'title']
movies = pd.read_csv('e:/sundog-consult/packt/datascience/ml-100k/u.item',
sep='|', names=m_cols, usecols=range(2))
ratings = pd.merge(movies, ratings)
ratings.head()
Just like earlier, we're going to import the u.data file that contains all the individual ratings for every user and what movie they rated, and then we're going to tie that together with the movie titles, so we don't have to just work with numerical movie IDs. Go ahead and hit the run cell button, and we end up with the following DataFrame.
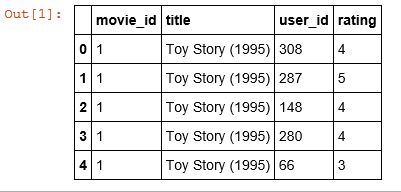
The way to read this is, for example, user_id number 308 rated Toy Story (1995) a 4 star, and user_id number 66 rated Toy Story (1995) a 3 star. And, this will contain every rating, for every user, for every movie.
And again, just like earlier, we use the wonderful pivot_table command in Pandas to construct a new DataFrame based on the information:
userRatings = ratings.pivot_table(index=['user_id'],
columns=['title'],values='rating') userRatings.head()
Here, each row is the user_id, the columns are made up of all the unique movie titles in my dataset, and each cell contains a rating:

What we end up with is this incredibly useful matrix shown in the preceding output, that contains users for every row and movies for every column. And we have basically every user rating for every movie in this matrix. So, user_id number 1, for example, gave 101 Dalmatians (1996) a 2-star rating. And, again all these NaN values represent missing data. So, that just indicates, for example, user_id number 1 did not rate the movie 1-900 (1994).
Again, it's a very useful matrix to have. If we were doing user-based collaborative filtering, we could compute correlations between each individual user rating vector to find similar users. Since we're doing item-based collaborative filtering, we're more interested in relationships between the columns. So, for example, doing a correlation score between any two columns, which will give us a correlation score for a given movie pair. So, how do we do that? It turns out that Pandas makes that incredibly easy to do as well.
It has a built-in corr function that will actually compute the correlation score for every column pair found in the entire matrix-it's almost like they were thinking of us.
corrMatrix = userRatings.corr() corrMatrix.head()
Let's go ahead and run the preceding code. It's a fairly computationally expensive thing to do, so it will take a moment to actually come back with a result. But, there we have it!

So, what do we have in the preceding output? We have here a new DataFrame where every movie is on the row, and in the column. So, we can look at the intersection of any two given movies and find their correlation score to each other based on this userRatings data that we had up here originally. How cool is that? For example, the movie 101 Dalmatians (1996) is perfectly correlated with itself of course, because it has identical user rating vectors. But, if you look at 101 Dalmatians (1996) movie's relationship to the movie 12 Angry Men (1957), it's a much lower correlation score because those movies are rather dissimilar, makes sense, right?
I have this wonderful matrix now that will give me the similarity score of any two movies to each other. It's kind of amazing, and very useful for what we're going to be doing. Now just like earlier, we have to deal with spurious results. So, I don't want to be looking at relationships that are based on a small amount of behavior information.
It turns out that the Pandas corr function actually has a few parameters you can give it. One is the actual correlation score method that you want to use, so I'm going to say use pearson correlation.
corrMatrix = userRatings.corr(method='pearson', min_periods=100) corrMatrix.head()
You'll notice that it also has a min_periods parameter you can give it, and that basically says I only want you to consider correlation scores that are backed up by at least, in this example, 100 people that rated both movies. Running that will get rid of the spurious relationships that are based on just a handful of people. The following is the matrix that we get after running the code:

It's a little bit different to what we did in the item similarities exercise where we just threw out any movie that was rated by less than 100 people. What we're doing here, is throwing out movie similarities where less than 100 people rated both of those movies, okay? So, you can see in the preceding matrix that we have a lot more NaN values.
In fact, even movies that are similar to themselves get thrown out, so for example, the movie 1-900 (1994) was, presumably, watched by fewer than 100 people so it just gets tossed entirely. The movie, 101 Dalmatians (1996) however, survives with a correlation score of 1, and there are actually no movies in this little sample of the dataset that are different from each other that had 100 people in common that watched both. But, there are enough movies that survive to get meaningful results.
