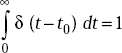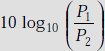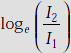Chapter 1
Mathematical Preliminaries
Mathematics is the backbone of all Sciences, Economics as well as all branches of Engineering.
The main objective of this chapter is to provide a brief and necessary background of the following main topics of mathematics:
- fundamentals of scalar and vector coordinate systems
- operations with del
- determinants and matrices
- series and identities
- trigonometric functions
- differentiation and integration formulae
- integral theorems and so on
- points/formulae to remember, solved problems, objective questions and exercise problems.
Mathematics is the backbone of science and engineering. For all analytical or computational purposes, mathematical background is essential. Mathematical modeling of systems is a common practice. The design and analysis of any antenna problem is possible only with mathematical concepts. No engineering system can be designed without using mathematics. Moreover, the solutions of antenna problems are simplified by mathematical approach.
In view of this, basics of mathematics is presented in this chapter.
1.1 FUNDAMENTALS OF SCALARS AND VECTORS
A scalar has magnitude and an algebraic sign. For example, temperature, mass, charge and work.
A vector has both magnitude and direction. For example, velocity, force, electric field and magnetic field.
In this book, a scalar is represented by simple letters like A, B and a vector is represented by bold-faced letters like A, B. Unit vectors are represented by small bold-faced letters like a, b.
The vector A is expressed in two forms:
- A = (Ax, Ay, Az). Ax, Ay, Az are known as the components of vector A.
- A = Ax ax + Ay ay + Az az . ax , ay , az are unit vectors along the coordinate axes.
The magnitude of A is written as A,
that is, A = |A|
The unit vector of A is a and it is given by
![]()
The sum and difference of two vectors are given by
The dot product is denoted by
A . B or B . A
A . B = B . A = AB cos q
= Ax Bx + Ay By + Az Bz
Here θ is the angle between the vectors A and B.
Dot product of two vectors is a scalar.
The cross product is denoted by A × B.
where an is the unit vector perpendicular to A and B
or 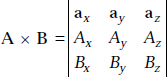
|
= ax [AyBz − AzBy] + ay [AzBx − AxBz] + az [AxBy − AyBx] |
where |
A = Axax + Ayay + Azaz |
and |
B = Bxax + Byay + Bzaz |
The cross product of two vectors is a vector.
1.2 COORDINATE SYSTEMS
Coordinate system is defined as a system which is used to represent a point in space.
Coordinate systems, basically, are of three types:
- Cartesian coordinate system
- Cylindrical coordinate system
- Spherical coordinate system
Cartesian Coordinate System
Here a point, P is represented by P (x, y, z). The variables are x, y and z.
A point obtained by the intersection of three planes given by
The unit of x, y and z is metre.
The Cartesian coordinates are represented in Fig. 1.1.
The three axes, x, y and z are mutually perpendicular to each other. These are said to be orthogonal to each other.
The unit vectors along the coordinate axes are represented by ax, ay and az. Their magnitude is unity and they are in the increasing directions of x, y and z axes respectively.
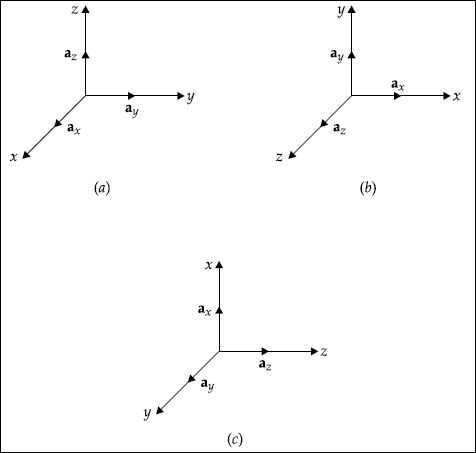
Fig. 1.1 Cartesian coordinate system
Properties of unit vectors
ax . ax = 1 |
ay . az = 0 |
ay . ay = 1 |
ax × ay = az |
az . az = 1 |
ay × az = ax |
ax × ax = 0 |
az × ax = ay |
ay × ay = 0 |
ay × ax = − az |
az × az = 0 |
az × ay = − ax |
ax . ay = 0 |
ax × az = − ay |
ax . az = 0 |
|
Cylindrical Coordinate System
Here, a point, P is represented by P (ρ, ϕ, z). ρ represents the radius of a cylinder, ϕ is called the azimuthal angle and z is the same as in Cartesian coordinate system.
The unit of ρ is metre.
The unit of ϕ is degree or radian.
The unit of z is metre.
In cylindrical coordinate system, a point is obtained by the intersection of three surfaces, namely,
a cylindrical surface, ρ = k1 (constant), metre
a plane, ϕ = α (constant), radian, and
another plane, z = k2 (constant), metre
All the three surfaces are mutually perpendicular to each other. These are said to be mutually orthogonal.
In this book, the term Cylindrical Coordinate system is used to indicate circular cylindrical coordinate system. However, a point in cylindrical coordinate system is shown in Fig. 1.2. The coordinate ρ is the radius of the cylinder. ϕ is measured from x-axis and z is the same as in Cartesian system.
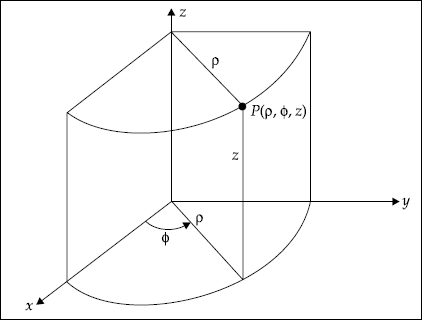
Fig. 1.2 A point in cylindrical coordinates
Here aρ , aϕ, az represent the unit vectors along the coordinates ρ, ϕ, z. Their magnitude is unity and they are in the increasing directions of ρ, ϕ, z respectively.
It is obvious that increase in ρ results in cylinders of higher radius. ϕ increases in anti-clockwise direction. z is the same as in Cartesian system.
The relations between x, y, z and ρ, ϕ, z:
x = ρ cos ϕ
y = ρ sin ϕ
z = z
and |
|
0 ≤ ρ < ∞ |
|
ϕ = tan−1 x, |
0 ≤ ϕ < 2π |
|
z = z, |
0 ≤ z < ∞ |
Dot products of ax, ay and az with aρ, aϕ and az are given by
ax.aρ = cos ϕ
ax. aϕ = − sin ϕ
ay. aρ = sin ϕ
ay. aϕ = cos ϕ
az. aρ = 0
az. aϕ = 0
The unit vectors of cylindrical coordinates in terms of Cartesian coordinates are given by
aρ = cos ϕ ax + sin ϕ ay
aϕ = − sin ϕ ax + cos ϕ ay
az = az
A vector, A = (Ax ax + Ay ay + Az az) is expressed in cylindrical coordinates as
A = (Aρ, Aϕ, Az) = [(Ax cos ϕ + Ay sin ϕ), (− Ax sin ϕ + Ay cos ϕ), Az]
That is |
Aρ = Ax cos ϕ + Ay sin ϕ |
|
Aϕ = − Ax sin ϕ + Ay cos ϕ |
|
Az = Az |
A is also written as
A = (Ax cos ϕ + Ay sin ϕ) aρ + (− Ax sin ϕ + Ay cos ϕ) aϕ + Az az.
Spherical Coordinate System
Here P (r, θ, ϕ) represents a point. r represents the radius of a sphere, θ is the angle of elevation measured from z-axis and ϕ is the azimuthal angle measured from x-axis.
A point is obtained by the intersection of three surfaces, namely,
a spherical surface, r = k (constant), metre
a cone, θ = α (constant), radian, and
a plane, ϕ = β (constant), radian
All these three surfaces are mutually perpendicular to each other.
These are said to be orthogonal.
ar, aθ, aϕ represent unit vectors along the coordinate axes. Their magnitude is unity and they are in the increasing directions of r, θ and ϕ axes.
A point in spherical coordinate system is shown in Fig. 1.3.
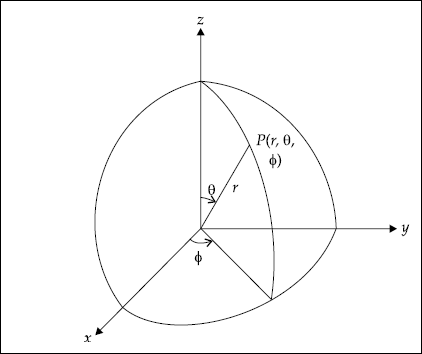
Fig. 1.3 A point in spherical coordinate system
Increase of r results in spheres of larger radii. θ increases in the clockwise direction and ϕ increases in the anti-clockwise direction.
The variables of Cartesian and spherical coordinates are related by
x = r sin θ cos ϕ, |
− ∞ < x < ∞ |
y = r sin θ sin ϕ, |
− ∞ < y < ∞ |
z = r cos θ, |
− ∞ < z < ∞ |
and

The relations between the variables of cylindrical and spherical coordinates are given by
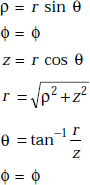
The unit vectors of spherical coordinates in terms of Cartesian coordinates are given by
ar = sin θ cos ϕ ax + sin θ sin ϕ ay + cos θ az
aθ = cos θ cos ϕ ax + cos θ sin ϕ ay − sin θ az
aϕ = − sin ϕ ax + cos ϕ ay
A vector,
A |
= |
(Ax, Ay, Az), is expressed in spherical coordinates as |
A |
= |
(Ar, Aθ, Aϕ) |
|
= |
[(Ax sin θ cos ϕ + Ay sin θ sin ϕ + Az cos θ), (Ax cos θ cos ϕ + Ay cos θ + sin ϕ − Az sin θ), (− Ax sin ϕ + Ay cos ϕ)] |
The dot products of ax, ay and az with ar, aθ and aϕ are given by
ax . ar = sin θ cos ϕ
ax . aθ = cos θ cos ϕ
ax . aϕ = − sin ϕ
ay . ar = sin θ sin ϕ
ay . aθ = cos θ sin ϕ
ay . aϕ = cos ϕ
az . ar = cos θ
az . aθ = − sin θ
az . aϕ = 0
Here,
Ar = Ax sin θ cos ϕ + Ay sin θ sin ϕ + Az cos θ
Aθ = Ax cos θ cos ϕ + Ay cos θ sin ϕ − Az sin θ
Aϕ = − Ax sin ϕ + Ay cos ϕ
The point A (x, y, z) = A (ρ, ϕ, z) = A (r, θ, ϕ) in Cartesian, cylindrical and spherical coordinate systems is shown in a single Fig. 1.4 to understand the concept at a glance.
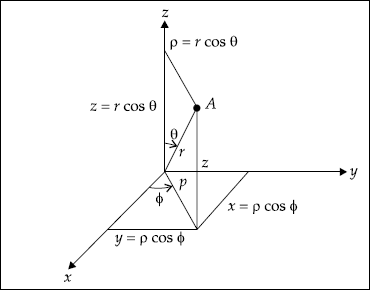
Fig. 1.4 Coordinates of a point in all the three systems
The relations for differential length, area and volume are given in Table 1.1.
Table 1.1 Differential Quantities in Different Coordinates

Relations between the polar coordinates (ρ, ϕ) and Cartesian coordinates (x, y) are:
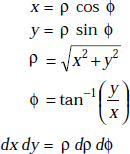
1.3 DEL (∇) OPERATOR
Definition The del or nabla is known as differential vector operator and is defined as

Del has units of 1/metre (1/m)
Del is operated in three ways.
1.4 GRADIENT OF A SCALAR, V (= ∇ V)
Gradient of a scalar is a vector and is defined as

Examples are gradient of temperature, gradient of electric potential and so on.
It gives the maximum space rate of change of the scalar. The scalar can be temperature, potential and so on.
1.5 DIVERGENCE OF A VECTOR, A (= ∇.A)
Divergence of a vector is a scalar and is defined as
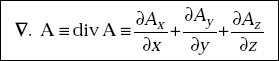
Divergence means the spreading or diverging of a quantity from a point. It is applicable to vectors only. The divergence of a vector indicates the net flow of quantities like gas, fluid, vapour, electric and magnetic flux lines. In other words, it is a measure of the difference between outflow and inflow.
The divergence of a vector is positive if the net flow is outward.
It is negative if the net flow is inward.
The fluid is said to be incompressible if the divergence is zero, that is, ∇ . A = 0 is the condition of incompressibility.
Examples and Features of Divergence
- Leaking air from a balloon yields positive divergence.
- Rushing of air into the drum under the carriage of a train yields negative divergence.
- Divergence of water or oil is almost zero and hence they are incompressible.
- Divergence of electric flux density is equal to volume charge density,
or, ∇ . D = ρv
- Divergence of magnetic flux density is equal to zero,
or, ∇ . B = 0
- Divergence of gradient of scalar electric potential is equal to the laplacian of the scalar,
or, ∇ . ∇V = ∇2 V.
1.6 CURL OF A VECTOR (≡ ∇ × A)
Curl of a vector is a vector and is defined as
Curl A

It is a measure of the tendency of a vector quantity to rotate or twist or curl. In other words, the rate of rotation or angular velocity at a point is the measure of curl.
As the curl of a vector represents rotation, it is also written as
curl A = rot A = ∇ × A
It may be noted that curl (gradient of a scalar) = ∇ × (∇V) is zero.
This means that the gradient of fields is irrotational. Also div (curl) = 0.
Examples:
- When a leaf floats in sea water and its rotation is about the z-axis, curl of velocity V is in the z-direction. When (∇ × V)z is positive, it represents rotation from x to y.
- For a rotating rigid body, the curl of velocity is in the direction of the axis of rotation. Its magnitude is equal to twice the angular speed of rotation.
In Cartesian coordinates,
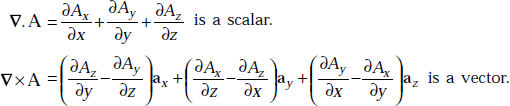
In cylindrical coordinates,
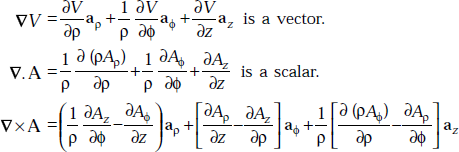
is a vector.
In spherical coordinates,
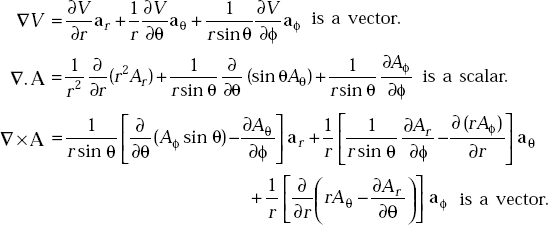
Vector identities
B . B |
= |
B2 |
B . B* |
= |
B2 |
B + C |
= |
C + B |
B . C |
= |
C . B |
C × B |
= |
− B × C |
(D + B) . C |
= |
D . C + B . C |
(D + B) × C |
= |
D × C + B × C |
D . B × C |
= |
B . C × D = C . D × B |
D × (B × C) |
= |
(D . C) B − (D . B) C |
(E × B) . (C × D) |
= |
E . B × (C × D) |
|
= |
(E . C) (B . D) − (E . D) (B . C) |
(E × B) × (C × D) |
= |
(E × B . D) C − (E × B . C) D |
∇ (VmV) |
= |
Vm∇V + V∇Vm |
∇ . (∇ × C) |
= |
0 |
∇ × ∇V |
= |
0 |
∇ (Vm + V) |
= |
∇Vm + ∇V |
∇ . (C + B) |
= |
∇ . C + ∇ . B |
∇ × (C + B) |
= |
∇ × C + ∇ × B |
∇ . (VC) |
= |
C . ∇V + V∇ . C |
∇ × (VC) |
= |
∇V × C + V∇ × C |
∇ (C . B) |
= |
(C . ∇) B + (B . ∇) C + C × (∇ × B) + B × (∇ × C) |
∇ . (C × B) |
= |
B . ∇ × C − C . ∇ × B |
∇ × (C × B) |
= |
C(∇ . B) − B (∇ . C) + (B . ∇) C − (C . ∇) B |
∇ × ∇ × C |
= |
∇ (∇ . C) − ∇2 C |
1.7 LAPLACIAN OPERATOR (∇2)
It is defined as ∇ . ∇. Its unit is ![]() It is a scalar differential operator. It is operated on a scalar as well as a vector.
It is a scalar differential operator. It is operated on a scalar as well as a vector.
Laplacian of a scalar electric potential (∇2 V), is a scalar.
Laplacian of an electric field (∇2 E), is a vector.
Laplacian of a scalar and a vector in different coordinate systems.
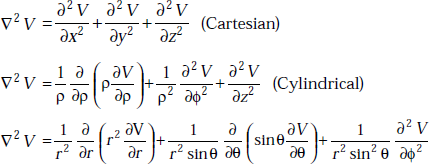
(Spherical)
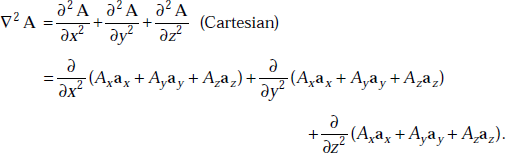
1.8 DIRAC DELTA
The properties of Dirac Delta are
δ (t − t0) = ∞ |
if t = t0 and |
= 0 |
otherwise |
Direct Delta is used to represent very short pulse of high amplitude. Sometimes it is also called unit impulse function.
At t = 0, it is represented by δ (t)
At t = t0, it is represented by δ (t – t0)
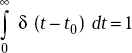
Dirac Delta is shown in Fig. 1.5.
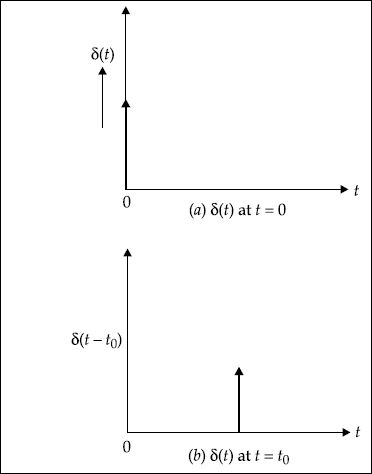
Fig. 1.5 Dirac Delta
1.9 DECIBEL AND NEPER CONCEPTS
Decibel (dB) is defined as ten times the common logarithm of the power ratio, that is,
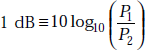
If P1 and P2 are input and output powers respectively of an electric circuit, then dB is negative if P2 > P1. This indicates power loss. If P1 > P2, dB is positive and this indicates power gain.
Decibel has no dimensions and it is used to express the ratio of two powers, voltages, currents or sound intensities.
One Bel (B) is equal to ten decibels.
When input and output currents and voltages are known, we have
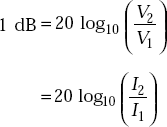
Neper (NP) It has no dimensions and is used to express the ratio of powers in communications.
A Neper is defined as the natural logarithm of the square root of the power ratio, that is,
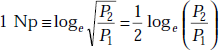
In terms of input and output currents or voltages, it is given by
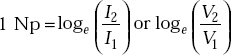
and 1 Np = 8.686 dB.
1.10 COMPLEX NUMBERS
By definition, a complex number is an ordered pair represented by
A ≡ (x, y)
where x is the real part and y is the imaginary part of A. Hence it is also represented as A = x + jy.
Here, ![]() is called imaginary unit.
is called imaginary unit.
Properties of Complex Numbers
- Two complex numbers are equal if their real parts are equal and their imaginary parts are also equal.
- If A1 = x1 + jy1, A2 = x2 + jy2 the sum of two complex numbers A1 and A2 is given by
A = A1 + A2 = (x1 + x2) + j (y1 + y2)
- Subtraction of A2 from A1 is given by
B = A1 − A2 = (x1 − x2) + j (y1 − y2)
- The product of A1 and A2 is
C
=
A1 A2 = (x1 + jy1) (x2 + jy2)
=
x1 x2 + jx1 y2 + jx2 y1 − y1 y2
=
(x1 x2 − y1 y2) + j (x1 y2 + x2 y1)
- The division of A1 by A2 is given by
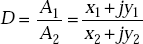
Multiplying numerator and denominator by (x2 – jy2), we get
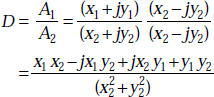
So
1.11 LOGARITHMIC SERIES AND IDENTITIES
This series converges for – 1 < x < 1.
It diverges for x = – 1
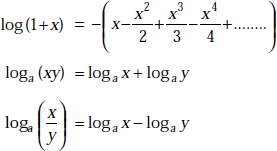
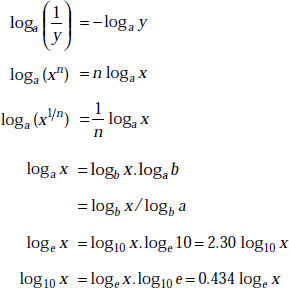
1.12 QUADRATIC EQUATIONS
A quadratic equation is represented by ax2 + bx + c = 0 where a, b and c are constants. Its roots are given by
|
|
|
|
The roots may be real or imaginary and may be equal or unequal depending on whether the quantity (b2 – 4ac) is positive, zero or negative.
1.13 CUBIC EQUATIONS
It is given by
By substituting ![]() for x, f (x) becomes
for x, f (x) becomes
y3 + dy + e = 0
Here,
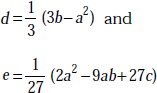
If
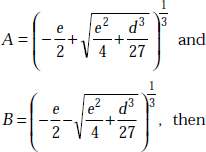
the three values of y are
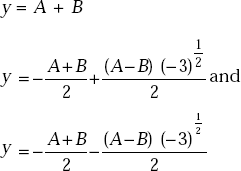
If 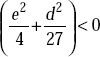 , the trigonometric solution is found by evaluating the cube roots of complex quantities. Then the angle ϕ is evaluated from
, the trigonometric solution is found by evaluating the cube roots of complex quantities. Then the angle ϕ is evaluated from
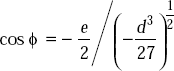
The values of y will be
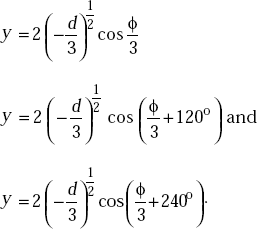
1.14 DETERMINANTS
A quantity ![]() is defined as a determinant.
is defined as a determinant.
It is said to be a second order determinant. Its value is given by
Example The value of a determinant
Similarly, 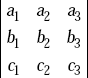 is called a determinant of the third order.
is called a determinant of the third order.
Example The value of a third order determinant 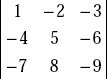
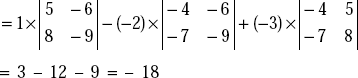
Application of Determinants
They are widely used in solving simultaneous equations and are also useful in developing the theory of matrices.
Minor of a Determinant
In a determinant 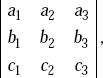 the minor of b3 is given by
the minor of b3 is given by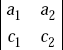 and the minor of c2 is given by
and the minor of c2 is given by 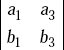
that is, the minor of an element in a determinant is a determinant obtained by deleting the row and the column which intersect at that element.
The Cofactor The cofactor of an element in a determinant is its minor with a suitable sign. The sign in the ith row and jth column is given by (– 1)i+j . Then the cofactor, B3 of b3 is (− 1)2 + 3 × minor of b3.
Properties of Determinants
- Value of the determinant remains the same after changing its rows into columns and columns into rows.
- Value of the determinant remains the same if any two rows or columns are interchanged but the sign changes.
- If two rows or columns are identical, the value of the determinant is zero.
- If each element of a row or column is multiplied by a factor, the determinant is multiplied by the same factor.
- If each element of a row consists of n terms, the determinant can be expressed as the sum of n determinants.
- When equi-multiples of the corresponding elements of one or more parallel lines are added to each element of a line, the determinant value remains the same.
1.15 MATRICES
A matrix is defined as a rectangular array of numbers or functions enclosed in brackets. These numbers or functions are known as the elements of the matrix.
Examples
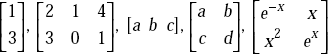
![]() is a matrix containing two rows and one column.
is a matrix containing two rows and one column.
Similarly, 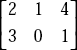 is a matrix containing two rows and three columns.
is a matrix containing two rows and three columns.
Here, a row means a horizontal line and a column means a vertical line.
Applications of Matrices
Matrices are widely used to solve linear systems of equations. They often appear as models of different problems. For example, in electrical circuits and numerical methods they are used for solving differential equations.
Types of Matrices
- Row Matrix—Example [1 2 3].
- Column Matrix—Example

- Square Matrix—Example
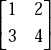
- Diagonal Matrix—Example
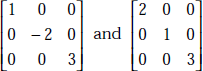
- Unit Matrix—Example

- Null Matrix—Example
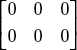
- Symmetric Matrix—Example
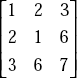
- Skew Symmetric Matrix—Example
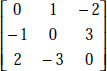
- Upper Triangular Matrix—Example
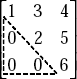
- Lower Triangular Matrix—Example
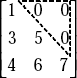
Properties of Matrices
- Two matrices A and B are equal if and, only if, they are of the same order and each element of A is equal to the corresponding element of B.
- The sum of A and B exists only when they are of the same order.
- The difference of A and B exists only when they are of the same order.
If

- Addition of matrices is commutative, that is, A + B = B + A.
- Addition and subtraction of matrices are associative, that is,
(A + B) − C = A + (B − C)= B + (A − C)
- The multiplication of a matrix, A by a scalar, K gives a matrix each element of which is K times the corresponding elements of A. The distributive law is valid for such a product,
that is, K (A + B) = KA + KB
- All the laws of ordinary algebra hold good for the addition or subtraction of matrices and their multiplication by scalars.
- Two matrices can be multiplied only when the number of columns in the first is equal to the number of rows in the second. Such matrices are said to be conformable.
- AB ≠ BA
Sometimes if AB exists, BA may not exist at all.
- IA = AI = A if A is a square matrix which has the same order as that of I.
- OA = AO = 0, where O is a null matrix.
- If AB = 0, it does not mean that A or B is a null matrix.
- Multiplication of matrices is associative, that is, (AB) C = A (BC) provided A, B are conformable for the product AB and B, C are conformable for the product BC.
- Multiplication of matrices is distributive, that is, A (B + C) = AB + AC provided A, B are conformable for AB and A, C are conformable for AC.
- If A is a square matrix, then A . A = A2 .
- The matrix obtained from a given matrix A by interchanging rows and columns is called Transpose of A denoted by A′.
- For a symmetric matrix, A′ = –A
- (AB)′ = B′. A′
- Adjoint of a matrix A is the transposed matrix of cofactors of A.
- If A is any matrix, then a matrix, B if it exists such that AB = BA = I, is called the Inverse of A. Both the matrix and its inverse must be non-singular. Inverse of a matrix, A is denoted by A-1 so that A . A-1 = A-1. A = I.
Also,
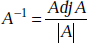
- Inverse of a matrix is unique.
- (AB)1 = B−1 A−1
- A matrix is said to be of rank r when it has at least one non-zero minor of order r and every minor of order higher than r vanishes. It means that the rank of a matrix is the largest order of any non-vanishing minor of the matrix.
1.16 FACTORIAL
Factorial of n is defined as the product of the first n natural numbers.
Factorial of n is represented by n! or ∠n
Using Stirling’s approximation, n! is evaluated from
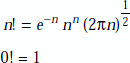
1.17 PERMUTATIONS
Permutations are defined as different possible arrangements which can be formed with a given number of items, taking some or all of them at a time.
The number of permutations of n different things taken r at a time is given by npr and ![]()
If p, q, r types of elements exist among n elements, then the number of permutations are given by
The number of permutations of n different things taken all at a time is npn.
1.18 COMBINATIONS
Combinations are defined as the number of possible groups which can be formed by taking some or all the number of things at a time irrespective of the order.
The number of combinations or groups of n different elements taken r at a time is given by ncr
where
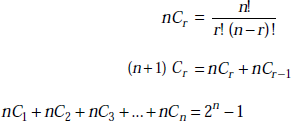
1.19 BASIC SERIES
Binomial Series These are given by
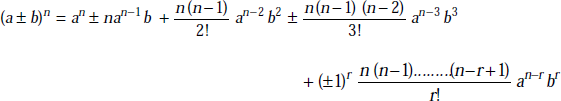
Here the last term shown is the (r + 1)th term.
If n is a positive integer, the series is finite and the last term is bn. If n is less than unity, the series is infinite and converges only when b < a. For any value of n, and convergent, when x2 is less than unity, we have
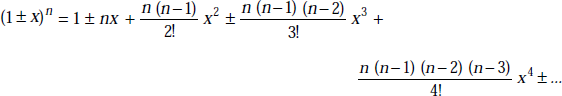
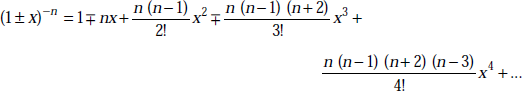
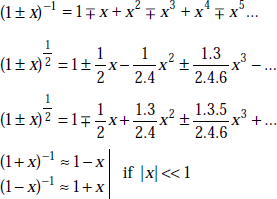
1.20 EXPONENTIAL SERIES
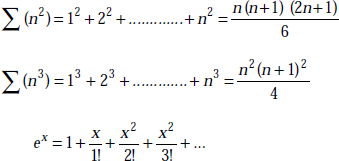
This series converges for all values of x.
For x = 1,

1.21 SINE AND COSINE SERIES
If x is a variable,
1.22 SINH AND COSH SERIES
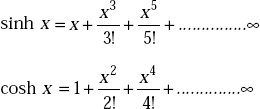
1.23 HYPERBOLIC FUNCTIONS
|
|
|
|
|
|
|
|
Similarly,
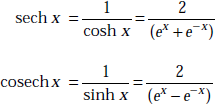
It may be noted that
sinh 0 = 0, cosh 0 = 0, and tanh 0 = 0
cosh x + sinh x = ex
cosh x + sinh x = e−x
cosh2 x − sinh2 x = 1
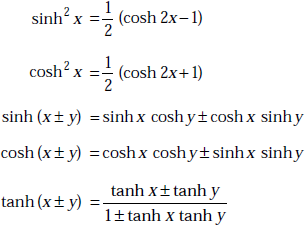
1.24 SINE, COSINE, TAN AND COT FUNCTIONS
For all values of θ,
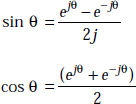
If
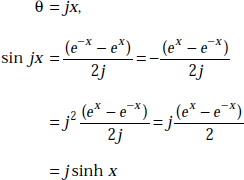
and ![]()
Similarly,
tan jx = j tanh x
sinh jx = j sin x
cosh jx = cos x
tanh jx = j tan x
sin (−x) = −sin x
cos (−x) = cos x
1 degree = 0.01745 radian
1 radian = 57.29577 degrees
sin2 x + cos2 x = 1
sin (x + y) = sin x cos y + cos x sin y
sin (x − y) = sin x cos y − cos x sin y
cos (x + y) = cos x cos y − sin x sin y
cos (x − y) = cos x cos y + sin x sin y
sin 2x = 2 sin x cos x
cos 2x = cos2 x − sin2 x

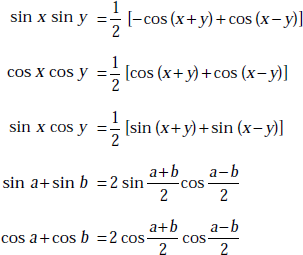
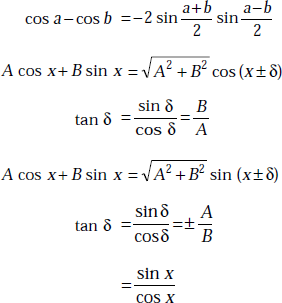
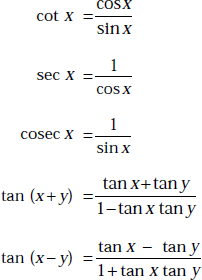
1.25 SOME SPECIAL FUNCTIONS
Gamma function
Γ (α) is defined as
This is true if α > 0
Beta function
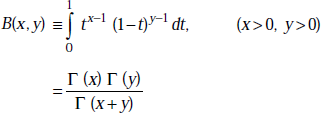
Error function

Bessel function
Bessel functions are a set of solutions for differential equations of a certain type. These are useful to obtain propagation characteristics of electromagnetic waves in circular waveguides.
Considering circular waveguides, solutions of the axial component is written conveniently in terms of Bessel function. For transverse magnetic wave, the solution is
for transverse electric wave
where |
Jn (Kc r) = Bessel function of the first kind |
|
r = radius of the guide |
|
Kc = cut-off wave number |
A, B, A1, B1, = constants
The solutions for the Bessel function are obtained for certain values of Kc. These values of Kc are known as eigen values. If Kc is to produce solution of the Bessel function, (Kc r) must be the roots of the Bessel function. Then
Jn (Kc r) = 0
The propagation parametres for nmth mode of TM waves are
Phase constant,
where ![]()
Also, 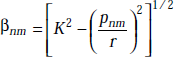
where |
pnm = the roots of the Bessel function |
|
K = free space wave number |
The cut-off wavelength for the TM wave,
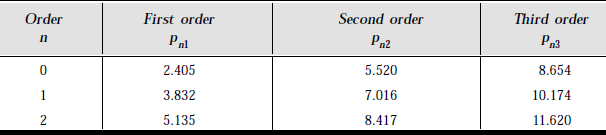
The roots of the Bessel function for TM mode are shown in Table 1.2.
Table 1.2 Roots of Bessel Function (TM)
The roots of the Bessel function for TE mode are shown in Table 1.3.
Table 1.3 Roots of Bessel Function (TE)

The propagation parametres for TEnm mode are
where ![]()
So,
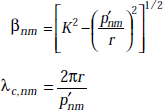
Guide wavelength,
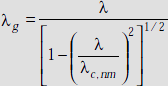
The variation of the first three orders of the Bessel function and their roots are shown in Fig. 1.6.
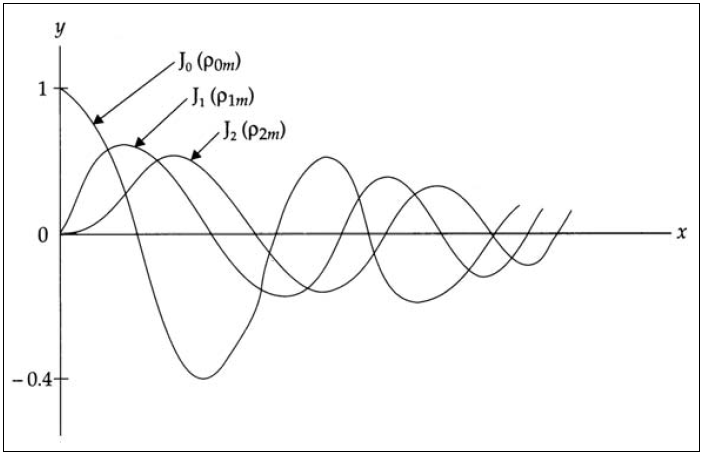
Fig. 1.6 Bessel function
Fresnel integral
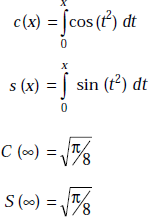
Sine integral
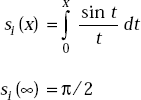
Cosine integral

Exponential integral
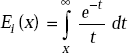
Logarithmic integral

1.26 PARTIAL DERIVATIVE
Assume z = f (x, y) is a real function of two independent real variables, x and y. If x is kept constant, say x = x1 and y is a variable, then f (x1, y) depends on y only. If the derivative of f (x, y1) with y for a value y = y1 exists, then the value of this derivative is called partial derivative of f (x, y) with respect to y at the point (x1, y1). It is represented by
1.27 SOME DIFFERENTIATION FORMULAE
Assume u, v to be functions of x and let a, n be the constants. Then,
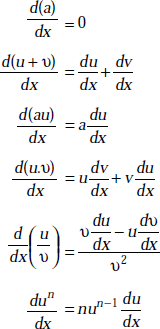
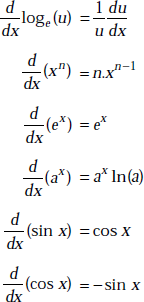
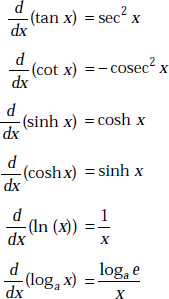

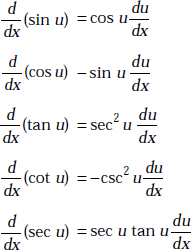
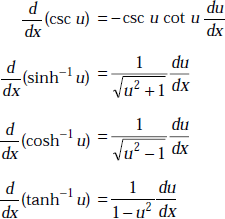
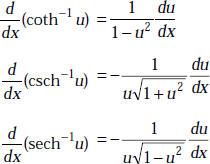
1.28 SOME USEFUL INTEGRATION FORMULAE
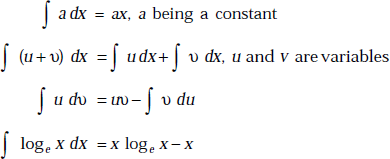
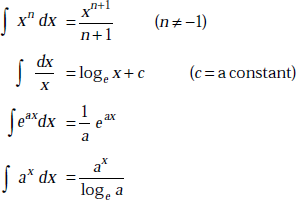
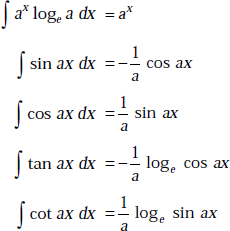
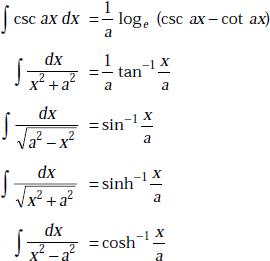
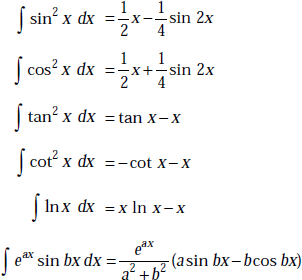

1.29 RADIAN AND STERADIAN
The radian is the measure of a plane angle. One radian is defined as a plane angle with its vertex at the centre of a circle of radius r which is subtended by an arc whose length is equal to r.
This is shown in Fig. 1.7. It is well known that the circumference of a circle is 2πr and there are 2π radians in a full circle.
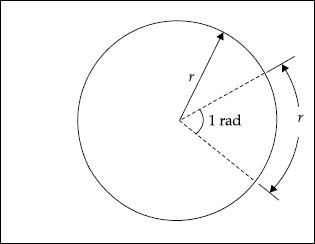
Fig. 1.7 Radian
Steradian is the measure of a solid angle. It is defined as the solid angle with its vertex at the centre for a sphere of radius r which is subtended by a spherical surface area equal to the area of a square, whose side length is r.
The differential area ds on the surface of a sphere of radius r is
ds = r2 sin θ dθ dϕ (m2)
The element of solid angle dΩ of the sphere is given by
This is illustrated in Fig. 1.8.
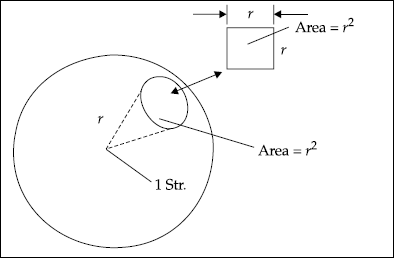
Fig. 1.8 Steradian
1.30 INTEGRAL THEOREMS
Stokes’s Theorem
If a field vector like H and its first derivatives are continuous at all points in a region of area S bounded by a closed curve, then Stokes’s theorem states that
where dS is along the outward normal to the surface. By Stokes theorem, surface integral is converted into line integral and vice versa.
Divergence Theorem
If a field vector like D and its first derivatives are continuous at all points in a region of volume V bounded by a closed elementary surface dS, then Divergence theorem states that
This means a surface integral is converted into volume integral and vice versa by Divergence theorem.
POINTS/FORMULAE TO REMEMBER
- Unit vector of a vector A is
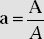
- The coordinate axes are perpendicular to each other.
- A point in Cartesian coordinate system is obtained by the intersection of three planes.
- A point in cylindrical coordinate system is obtained by the intersection of two planes and one cylindrical surface.
- A point in spherical coordinate system is obtained by the intersection of a plane, a spherical surface and a cone.
- Del, ∇ is a vector differential operator.
- The unit of ∇ is 1/m.
- Gradient of a scalar is a vector.
- Divergence of a scalar is a vector.
- Curl of a vector is a vector.
- 1 dB is defined as
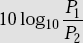
- 1 Neper is defined as
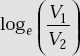
- 1 Neper = 8.686 dB.
- A determinant is represented by

- A matrix is defined as a rectangular array of numbers or functions enclosed in brackets.
- cos jx = cosh x
- sin jx = j sinh x
- 1 degree = 0.01745 radians
- 1 radian = 57.29 degrees
- The unit of magnetic scalar potential is ampere.
- The unit of magnetic vector potential is wb/m.
- Reflection coefficient is a complex quantity.
- Electric field, magnetic field, electric flux density, magnetic flux density, conductor current density, displacement current density, magnetic current density are vector quantities.
- The unit of Poynting vector is watts/m2.
- Torque is a vector and has unit of Newton-metre.
- The unit of solid angle is steradian.
- Stokes’ theorem gives the relation between a closed line integral and a surface integral.
- Divergence theorem gives the relation between a closed surface integral and a volume integral.
- The unit of magnetic current density is volts/m2.
- ∇2 is Laplacian scalar operator.
SOLVED PROBLEMS
Problem 1.1 If a vector A = ax + 2ay + 3az , find its magnitude and direction.
Solution A = ax + 2ay + 3az ,
The magnitude of
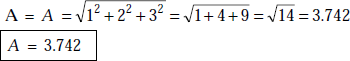
Its direction is given by unit vector, ![]()
Problem 1.2 If A = 2ax + 5ay + 6az and B = ax – 3ay + 6az, find A + B and A – B.
Solution
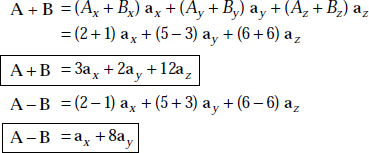
Problem 1.3 If A = ax + ay + 2az and B = 2ax + ay + az, find A.B.
Solution
A.B = AxBx + AyBy + AzBz
= 1.2 + 1.1 + 2.1 = 2 + 1 + 2 = 5
Problem 1.4 Given A = 2ax + ay + 2az and B = ax + 2ay + az, find A × B.
Solution
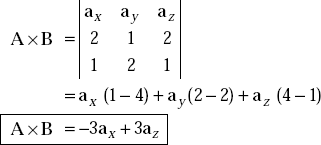
Problem 1.5 For A = (1,3,4) and B = (1, 0, 2), find A .B.
Solution
Here |
Ax = 1, |
Ay = 3, |
Az = 4 |
|
Bx = 1, |
By = 0, |
Bz = 2 |
|
A.B |
= |
AxBx + AyBy + AzBz |
|
|
= |
1 × 1 + 3 × 0 + 4 × 2 |
|
|
= |
1 + 0 + 8 = 9 |
Problem 1.6 In Cartesian coordinates, a point is described by P (1, 2, 4). What are the orthogonal planes whose intersection give this point?
Solution The planes which intersect at the point P (1, 2, 4) are:
x = 1
y = 2 and
z = 4
Problem 1.7 Represent the point P (0.5, 0.2, 0.1) in terms of unit vectors along the coordinate axes.
Solution At the point, P (0.5, 0.2, 0.1), the coordinates are x = 0.5, y = 0.2 and z = 0.1. Therefore, P is represented by a vector
Problem 1.8 How is a point P (2.0 m, π/4, 1.0 m) obtained in cylindrical coordinates?
Solution The point P (2.0 m, π/4, 1.0 m) is obtained by the intersection of a cylindrical surface, ρ = 2.0 m a plane, ϕ = π/4 and a plane, z = 1.0 m.
Problem 1.9 A point in Cartesian coordinates is given by P (1, 2, 3). Express it in cylindrical coordinates.
Solution The coordinates of P in Cartesian system are
The coordinates of P in cylindrical system are given by
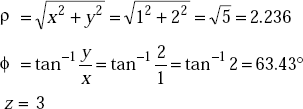
In cylindrical coordinates P is (2.236, 63.43°, 3).
Problem 1.10 If a vector, A is 4a x + 2ay + az, express it in cylindrical coordinate system.
Solution A = 4ax + 2ay + az
We have
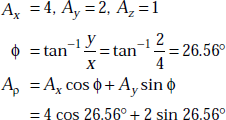
that is,
|
Aρ |
= |
3.57 + 0.894 = 4.46 |
|
Aϕ |
= |
−Ax sin ϕ + Ay cos ϕ |
|
|
= |
− 4 × 0.447 + 2 × 0.894 |
|
|
= |
− 1.789 + 1.789 |
|
|
= |
0 |
|
Az |
= |
1.0 |
A in cylindrical coordinates is
Problem 1.11 How is a point P (1.0m, 10°, 30°) obtained in spherical coordinates?
Solution The point P (1.0m, 10°, 30°) is obtained by the intersection of a sphere, r = 1.0m a cone, θ= 10° and a plane, ϕ = 30°.
Problem 1.12 If a point in Cartesian coordinates is given by P (1, 2, 3), express it in spherical coordinates.
Solution The Cartesian coordinates of P are
The coordinates of P in spherical system are given by
Problem 1.13 A scalar function, V is given by V = xyz2. Find the gradient of V.
Solution Grad
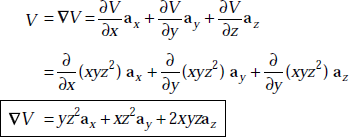
Problem 1.14 If a vector, B = 4xy2ax + 2y3ay + xyzaz, find the divergence of B.
Solution
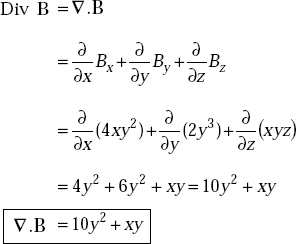
Problem 1.15 Given a vector, A = 3xax + yay + 5zaz, find the curl of A.
Solution
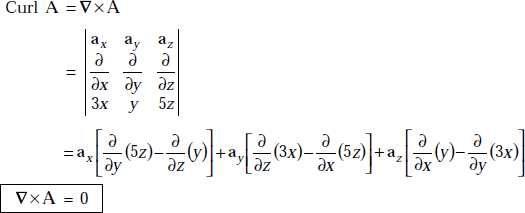
Problem 1.16 If the scalar potential is given by V = x2 – y2 – z2 volts, find the Laplacian of V.
Solution V = x2 – y2 – z2 volts
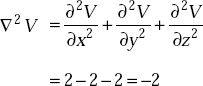
Problem 1.17 If power gain, Ap is 22, find its value in decibels.
Solution Power gain = 22
Ap in |
dB = 10 log10 22 |
|
= 13.424 dB |
Problem 1.18 When the ratio of output and input voltages of an amplifier is 95, find its gain in dB.
Solution AV = voltage gain = 95
AV in dB |
= 20 log10 95 |
|
= 39.55 dB |
Problem 1.19 If the power gain in a communication system is 16, what is its value in nepers?
Solution Ap = power gain = 16
Problem 1.20 If the current gain in a circuit is 34, what is its value in nepers?
Solution AI Current gain = 34
AI in Np |
= loge 34 |
|
= 3.526 |
Problem 1.21 If a complex number, A is given by 2 + j4, find its magnitude and phase.
Solution A = 2 + j4
|
|
|
|
Problem 1.22 If a complex number is given by A = 1 + j3, find its complex conjugate, magnitude of A and its phase.
Solution The complex conjugate of A is
|
A * = 1 − j3 |
|
|
|
|
Problem 1.23 If the amplitude of a complex number, A is 5.0 and its phase is 45°, find its real and imaginary parts.
Solution The given complex number
|
A = 5.0 ∠45° |
Its magnitude, |
ρ = 5.0 |
Its phase, |
ϕ = 45° |
So the real part of |
A = ρ cos ϕ = 5 cos 45° = 3.535 |
The imaginary part of |
A = ρ sin ° = 3.535 |
A is represented as 3.535 + j3.535. |
|
Problem 1.24 If A1 = 2 + j3 and A2 = 4 + j5, find the sum of A1 and A2.
Solution
A1 = 2 + j3, A2 = 4 + j5
A = A1 + A2 = 2 + j3 + 4 + j5 = 6 + j8
Problem 1.25 If A1 = j6 and A2 = 1 – j2, find A1 – A2.
Solution
A1 = j6, A2 = 1 − j2
A1 − A2 = j6 − 1+ j2 = −1 + j8
Problem 1.26 Given two complex numbers, A = 0.4 + j5, B = 2 + j3, find the product of A and B.
Solution A = 0.4 + j5
B = 2 + j3
The product,
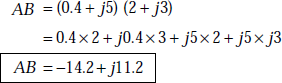
Problem 1.27 Given two complex numbers, A = 10 + j6 and B = 2 – j3, find the ratio of A and B.
Solution
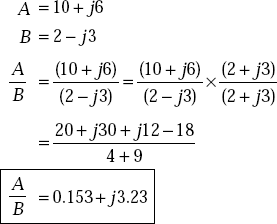
Problem 1.28 Find the roots of the quadratic equation x2 + 2x + 4 = 0.
Solution For x2 + 2x+4 =0, the roots are

Problem 1.29 For the determinant,  find the minor of 8 and 9.
find the minor of 8 and 9.
Solution The minor of the element, 8 is ![]()
The minor of the element, 9 is ![]()
Problem 1.30 For the determinant,  find the cofactor of 6 and 5.
find the cofactor of 6 and 5.
Solution The minor of 6 is ![]()
Its cofactor
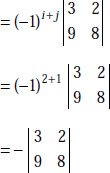
The minor of 5 is ![]()
Its cofactor

Problem 1.31 Find the factorial of 4 and 6.
Solution Factorial of 4 = 4 × 3 × 2 × 1 = 24
Factorial of 6 = 6 × 5 × 4 × 3 × 2 × 1 = 720
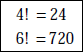
OBJECTIVE QUESTIONS
1. The wavelength of an EM wave depends on its velocity. |
(Yes/No) |
2. The velocity of an EM wave depends on the medium in which it propagates. |
(Yes/No) |
3. The unit vectors along the Cartesian coordinate axes are not mutually perpendicular to each other. |
(Yes/No) |
4. In cylindrical coordinates, ρ has the unit of degrees. (Yes/No) |
|
5. In cylindrical coordinates, ρ has the units of metres. |
(Yes/No) |
6. In spherical coordinates, θ increases in anticlockwise direction. |
(Yes/No) |
7. In cylindrical coordinates, ϕ increases in anticlockwise direction. |
(Yes/No) |
8. In spherical coordinates, θ increases in clockwise direction. |
(Yes/No) |
9. Del is a scalar operator. |
(Yes/No) |
10. ∇2 is a vector operator. |
(Yes/No) |
11. ∇2 can be operated on scalar and vector. |
(Yes/No) |
12. sin jx is equal to j sinh x. |
(Yes/No) |
13. sin jx is equal to j sin x. |
(Yes/No) |
14. cosh jx is cos x. |
(Yes/No) |
15. tanh jx is j tan x. |
(Yes/No) |
16. Fresnel integrals C(∞) = S(∞). |
(Yes/No) |
17. Fresnel integral, |
(Yes/No) |
18. Error function, erf (∞) = 1. |
(Yes/No) |
19. In cylindrical coordinates, ϕ = a constant is a plane. |
(Yes/No) |
20. In spherical coordinates, θ = a constant is a cone. |
(Yes/No) |
21. ax.aρ = sin ϕ. |
(Yes/No) |
22. ax.aϕ = sinϕ. |
(Yes/No) |
23. ay.aρ = 0. |
(Yes/No) |
24. az.aρ = 0. |
(Yes/No) |
(Yes/No) |
|
26. ay.aϕ = cos ϕ. |
(Yes/No) |
27. The gradient of a vector does not exist. |
(Yes/No) |
28. Divergence of a scalar does not exist. |
(Yes/No) |
29. Curl of a scalar exists. |
(Yes/No) |
30. Del (∇) has no units. |
(Yes/No) |
31. Divergence of water or oil is almost zero. |
(Yes/No) |
32. Divergence of gradient of scalar electric potential is the Laplacian of the potential. |
(Yes/No) |
33. j = (0, 1). |
(Yes/No) |
34. Complex conjugate of A = 2 + j5 is 2 – j5. |
(Yes/No) |
35. A complex number B = (x, y) is nothing but (x + jy). |
(Yes/No) |
36. |
|
37. 1 Neper = 8.686 dB |
(Yes/No) |
38. loge x = 0.434 log10 x |
(Yes/No) |
39. A . A = A . A* = A2. |
(Yes/No) |
40. Radar X-band is ________. |
|
41. The frequency range of radar mm-band is ________. |
|
42. The frequency range UHF is ________. |
|
43. The wavelength range of VHF band is ________. |
|
44. In cylindrical coordinates, ρ is the ________. |
|
45. In spherical coordinates, r is ________. |
|
46. dv in cylindrical coordinates is ________. |
|
47. dL in spherical coordinates is ________. |
|
48. Dot product of az and aϕ is ________. |
|
49. Dot product of ax and ar is ________. |
|
50. Dot product of ax and ay is ________. |
|
52. In spherical coordinates, ϕ varies between ________. |
|
53. The divergence of an incompressible fluid is ________. |
|
54. Del has ________ units. |
|
55. A point is obtained by the intersection of ________ in spherical coordinates. |
|
56. 1 NP is equal to ________. |
|
57. 1 dB is defined as ________. |
|
58. 1 NP is defined as ________. |
|
59. 0! is ________. |
|
60. For x << 1, (1 + xit)–1 = ________. |
|
61. For x<< 1, (1 + x)+1 = ________. |
|
62. sinh 0 is ________. |
|
63. tanh 0 is ________. |
|
64. cosh 0 is ________. |
|
65. Gamma function, |
|
Answers
1. Yes |
2. Yes |
3. No |
4. No |
5. Yes |
6. No |
7. Yes |
8. Yes |
9. No |
10. No |
11. Yes |
12. Yes |
13. Yes |
14. Yes |
15. Yes |
16. Yes |
17. Yes |
18. Yes |
19. Yes |
20. Yes |
21. No |
22. No |
23. No |
24. Yes |
25. Yes |
26. Yes |
27. Yes |
28. Yes |
29. No |
30. No |
31. Yes |
32. Yes |
33. Yes |
34. Yes |
35. Yes |
36. Yes |
37. Yes |
38. Yes |
39. Yes |
|
40. 8–12 GHz |
41. 40–300 GHz |
|
42. 300−3,000 MHz |
43. 10 – 1 m |
|
44. Radius of cylinder |
45. Radius of sphere |
|
46. p dϕ dϕ dz |
||
48. Zero |
49. sin θ cos ϕ |
|
50. Zero |
51. 0 and π |
|
52. 0 and 2π |
53. Zero |
|
54. 1/m |
55. A plane, a cone and a sphere |
|
|
57. |
|
58. |
|
|
60. 1 – x |
61. 1 + x |
|
62. Zero |
63. Zero |
|
64. One |
65. |
|
EXERCISE PROBLEMS
- Find the magnitude and direction for the vectors A = 5ax + 3ay + 2ay and B = 4ay + 0.5az.
- If A = (2, 4, 1) and B = (0, 0.1, 5), find A + B, A – B.
- If A = 6ax + 3az and B = 2ay + 5az, find A.B.
- When A = (2, 0, 7), B = (3, 2, 0), what is A × B??
- If a point in Cartesian coordinates is given by (2, 0, 4), express it in cylindrical and spherical coordinate systems.
- The electric scalar potential is given by V = 3x + 5y2 + 4z3. Find its gradient.
- For a vector A = 12ax + 2ay + 3az, find the divergence and curl.
- If a voltage gain is 22 dB, express it in nepers.
- Find the roots of the quadratic equation 5x2 + 2x + 4 = 0.
- What are the roots of the cubic equation given by x3 – 2x2 + 4x-8 = 0?
- Find the value of the determinant
 .
. - Find the minor of 0 in Problem 11.
- What is the cofactor of 4 and 3 in the determinant

- Find the value of (1 + x)1/2 if x = 0.01, using the series expansion.
- Find sin x if x = 0.2, using the series expansion.