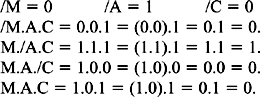Logic expressions
We begin our discussion of logic by asking how we can make an automatic device for controlling access to a bank vault. In finding an answer to this question, we shall arrive at a form of algebraic expression that always evaluates to either 0 or 1. To arrive at the simplest form of these expressions, you can learn a graphical method and a tabular method for simplifying logic expressions.
2.1 Logic – the bank vault
Three employees of a bank have access to the vault: the Manager, the Assistant Manager, and the Chief Cashier. In order to obtain access to the vault, any two of these persons must present themselves before an incorruptible person, the controller, who decides if access to the vault is permitted.
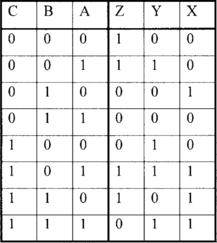
The controller makes a ‘truth table’, Figure 2.1, which he uses to determine whether access to the vault is permitted. When bank employees present themselves before him, he asks three questions, the answers to which are either ‘Yes’ or ‘No’:
Is the Assistant Manager present?
He then arrives at his decision by looking it up in the truth table. Note that there are eight possible sets of answers to these three yes/no questions1.
The controller realizes he could arrive at his decision in a different way. He writes down all the conditions that make Allow_access equal to ‘Yes’, Figure 2.2.
In order to write the expression for ‘Allow_access’ more concisely, the controller writes the symbol M instead of ‘Manager is present’ and writes the symbol /M (read as ‘not M’) instead of ‘Manager is NOT present’. He does likewise for the Assistant Manager and the Chief Cashier. The resulting expression is:
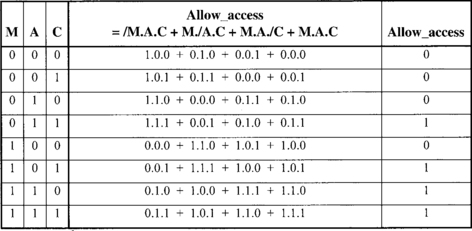
Allow_access = /M.A.C + M./A.C + M.A./C + M.A.C
Here a dot is used as an abbreviation for ‘AND’, and a + is used as an abbreviation for ‘OR’.
This expression has exactly the same meaning as the expression given in Figure 2.2. In order to arrive at his decision, the controller has to evaluate this logic expression every time bank employees present themselves before him. How does he evaluate this expression?
2.2 Evaluating the logic expression for the bank vault
If the Manager is present, the controller gives M the value 1; if the Manager is not present, the controller gives M the value 0. He also gives variable A a value of 0 or 1 according to the presence or absence of the Assistant Manager, and similarly for variable C.
For example, consider the situation where the Manager is present, the Assistant Manager is NOT present, and the Chief Cashier is present. The variables thus have the values M = 1, A = 0, and C = 1. To evaluate the expression for Allow_access, the controller applies the following rules2.
Let x stand for a particular value, 0 or 1, then:
| /0 = 1 | /0 = 1 |
| x.0 = 0 | x.0 = x |
| x + 0 = x | x + 1 = 1 |
The controller replaces the variables in the expression for Allow_access with their actual values, so that for this situation:
In more detail, the result of applying the rules given that M = 1, A = 0, C = 1:
Finally, the logical OR of these four values is:
0 + 1 + 0 + 0 = (0 + 1) + (0 + 0) = 1 + 0 = 1
That is, the value of Allow_access is 1, which means that access to the bank vault is allowed.
All eight possible combinations of the values of M, A, and C are listed in the table of Figure 2.3 together with the corresponding evaluations of Allow_access. The evaluations give the required results.
Note that the term /M.A.C may be regarded as detecting <MAC> = = <011>. Similarly, M./A.C detects <MAC> == <101>, M./A.C detects <MAC> == <101>, M.A./C detects <MAC> == <110>, and M.A.C detects <MAC> == <111>. Since these logic expressions detect various combinations of the input variables they are known as combinational or combinatorial logic expressions.
Using this detection property gives a simpler way of evaluating Allow_access. In the table of Figure 2.4, we can quickly write down the value of each of these so-called product terms. In the column headed /M.A.C we write 1 where <MAC> == <011> and write 0 everywhere else. We do the same for the other product term columns. Finally, we write a 1 in the Allow_access column wherever one or more of the product term columns in the same row contains a 1.
2.3 Another solution
The controller might have seen that the vault access rule is effectively that any two of the Manager, Assistant Manager, and Chief Cashier must be present. This would lead him to the expression:
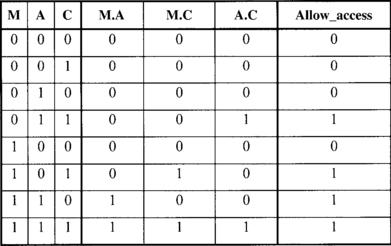
Allow_access = M.A + M.C + A.C
Allow_access = /M.A.C + M./A.C + M.A./C + M.A.C
How do we know that these two expressions perform the same function?
We construct the truth table for the simpler expression, Figure 2.5 and compare it with the truth table of Figure 2.4. The Allow_access columns in both truth tables are identical, therefore the two expressions represent the same function.
A question now arises: given an expression for a particular function, how do we arrive at the simplest expression that performs the same function?
2.4 Simplifying logical expressions*
Consider the members of an orchestra. We wish to classify the members according to what sort of instruments they play – string, wind, or percussion instruments. Some members play several types of instrument. We want to group the players on a rectangular field according to the types of instrument they play. How do we do this? Obviously we ask each member the three questions:
| Do you play Strings? | If Yes, set S = 1, /S = 0 |
| Do you play Percussion? | If Yes, set P = 1, /P = 0 |
| Do you play Wind? | If Yes, set W = 1, /W = 0 |
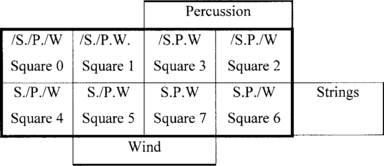
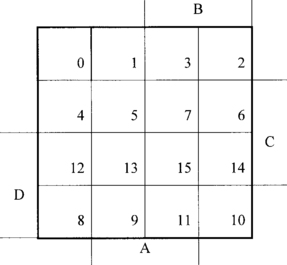
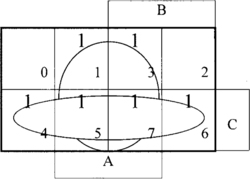
Since there are eight, (23), possible sets of answers, we divide the field into eight squares, one square for each possible set of answers. We give each square a number according to the scheme shown in Figure 2.6; the numbering scheme is important. A square number is obtained by regarding the three 0s and 1s in <SPW> as a pure binary number: for convenience, we write the number in decimal notation. We shall refer to the field with squares arranged in this way as a map. Furthermore, we arrange the squares on the map such that all string players are in the bottom part of the map, all percussion players are in the right-hand part of the map, and all wind players are in the middle two columns of the map.
The orchestra members in square 5, (= binary 101) are described by S./P.W, that is, they play strings, do not play percussion, and play wind. Similarly, the members in square 3, (= binary 011) are described by /S.P.W, they do not play strings, do play percussion, and do play wind.
And so on for all the eight squares.
It is usual to refer to terms such as S./P.W and /S.P.W as minterms. A minterm is the logical AND of all the variables in either their true or complemented form. Further, we can refer to a minterm by the number formed by writing 1 for a true variable and 0 for a complemented variable. Thus, minterm S. /P.W becomes 101 or 5, and /S.P.W becomes 011 or 3.
2.4.1 Using the squares
Suppose we wish to find where the members who play strings AND play percussion are located. We can proceed as follows:
Hence, all those that play strings AND play percussion, S.P, are in squares 6, 7.
So, those that play strings AND play percussion may be described by:
= S.P./W + S.P.W3
Note that S.P is a simpler way of expressing S.P./W + S.P.W.
Again, suppose we wish to find where the members who play strings OR percussion, (S + P), are located. We can proceed as follows:
All those that play strings are in squares 4, 5, 6, 7.
All those that play percussion are in squares 2, 3, 6, 7.
Hence, all those that play strings OR play percussion, (S + P), are in squares 2, 3, 4, 5, 6, 7, giving:
S + P = Squares 2, 3, 4, 5, 6, 7
= /S.P./W + /S.P.W + S./P./W + S./P.W + S.P./W + S.P.W
Note that S + P is a simpler way of expressing
2.4.2 Simplified logic for bank vault access
Going back to the bank vault access problem, we can use a map to simplify the original design solution:
Allow_access = /M.A.C + M./A.C + M.A./C + M.A.C
Allow_access(M, A, C) = minterm 011 + minterm 101 + minterm 110 + minterm 111
or Allow_access(M, A, C) = sum of minterms 3, 5, 6, 7
or Allow_access(M, A, C) = Σ3, 5, 6, 7
Note that it is necessary to write (M, A, C) to indicate the order in which the variables are written in order to obtain the numerical value of the minterm.
Draw a map, as shown in Figure 2.7 and write a 1 in each of the squares 3 (/M.A.C), 5 (M./A.C), 6 (M.A./C), and 7 (M.A.C). Squares 6 and 7 may be grouped together into a region described by M.A. Squares 5 and 7 group to become the region M.C, and squares 3 and 7 become A.C. So we can write the simplified expression by forming the OR of these groups:
Allow_access = M.A + M.C + A.C
We now have a graphical way of simplifying expressions.4
2.5 Rules for simplifying logical expressions using a map*
For the general function of three variables, F(C, B, A), output F depends on input variables C, B, and A. In order to simplify the function we use the following steps.
Step 1. Draw a map as in Figure 2.8. Label the bottom part C, the right-hand part B, and the middle part A.
Step 2. Where F is to have the value 1, write 1 into the corresponding square(s).
Step 3. Identify in your mind, all possible groups of squares with a 1 written in them. A group must contain 1, 2, 4, or 8 squares in the shape of a rectangle. The groups must be as large as possible. The right-hand and left-hand edges of the map are regarded as being the same edge – thus, for example, if squares 4 and 6 both contain a 1, they form a group of two.
A square containing a 1 may be in any number of groups.
Step 4. Examine each square containing a 1 – if there is only one group that contains that square, draw a loop around the group, or move onto another square containing a 1.
Step 5. Repeat step 4, until all squares containing a 1 have been examined.
Step 6. Re-examine any squares containing a 1 that are not in a group. These are those that may be grouped in more than one way. Choose a group for these squares.
Step 7. For each group, ask ‘Is this group entirely within region C?’ If it is, write C; if it is entirely outside region C, write /C. If the group lies only partly within C, do not write anything. Repeat this question for region B, then for region A. What you have written down is the logical description for that group.
Step 8. Repeat step 7 for all the groups.
Step 9. Write the result as the OR of the descriptions of all the groups.
An output, F, depends on inputs C, B, and A. The function is F(C B A) = Σ0, 1, 4, 5, 6. The map of the function is:

Group squares 0, 1, 4, 5, and ask the questions:
Is the group wholly within C? Answer: part of it is but part of it is not; so write nothing.
Is the group wholly within B? Answer: no; so write /B.
Is the group wholly within A? Answer: part of it is but part of it is not; so write nothing.
Thus, the group is described by /B.
Group squares 4, 6, and ask the questions:
Is the group wholly within C? Answer: yes; so write C.
Is the group wholly within B? Answer: part of it is but part of it is not; so write nothing.
Thus, the group is described by C./A.
F(C, B, A) = C./B./A + C.B./A + A
The term C./B./A is minterm 100 and maps to square 4.
The term C.B./A is minterm 110 and maps to square 6.
The term A is not a minterm; it maps to squares 1, 3, 5, 7.
Group squares 1, 3, 5, 7, and ask the questions:
Is the group wholly within C? Answer: part of it is but part of it is not;
Is the group wholly within B? Answer: part of it is but part of it is not;
Thus, the group is described by A.
Group squares 4, 5, 6, 7, and ask the usual questions:
G(C, B, A) = C./B + C./A + /C./B
C./B maps to squares 4, 5. C./A maps to squares 4, 6. /C./B maps to squares 0, 1.
This is the same map as Example 1.
Example 4 – Map for four variables
The squares on a four-variable map are arranged and numbered as shown in Figure 2.9 (Note that if the lower half of this map is folded over the top half, the new squares have a minterm number that is eight more than the square over which it now lies.) The new squares are labelled as region D.
F(D, C, B, A) = /D./C./B./A + /D./C./B.A + D./C./B./A + D./C./B.A + /D./A.
The map of the function is made using:
/D./C./B./A is minterm 0000 and maps to square 0.
/D./C./B.A is minterm 0001 and maps to square 1.
D./C./B./A is minterm 1000 and maps to square 8.
So the map of F(D, C, B, A) is:
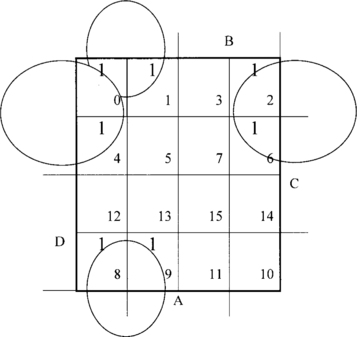
Group squares 0, 2, 4, 6 and describe the group by /D./A.
Group squares 0, 1, 8, 9 and describe the group by /C./B. (Note that the top and bottom edges of the map are regarded as being the same, as are the left-hand and right-hand edges.)
2.6 Karnaugh-Veitch program, KVMap*
The KVMap.exe program automates the map method for four variables labelled D, C, B, and A. (For three-variable problems use only the top half of the map and ignore D in the solution.) Enter the data for the truth table either by typing the value in the truth table or by clicking on a square in the map. (The program allows a square to be set to X as well as 0 or 1: we shall see the use of the X in Chapter 3.) Possible groups of squares, called prime implicants, are looped and listed automatically. Often the required logic expression is the OR of all the prime implicants but this is not always so. This is because not all the prime implicants may be essential to implement the function; that is, some prime implicants are not needed in the simplest possible solution, as in the following case.
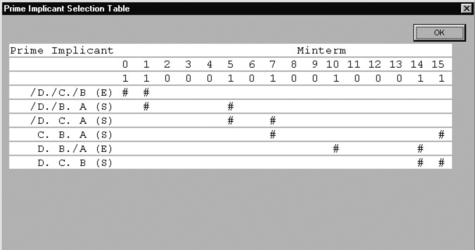
Consider the map of the function F(D, C, B, A) = Σ 0, 1, 5, 7, 10, 14, 15, shown in Figure 2.10. The prime implicant or loop (/D./C./B) covering minterms 0 and 1 is essential because it is the only loop containing minterm 0. Similarly, the prime implicant (D.B./A) covering minterms 10 and 14 is essential because it is the only prime implicant covering minterm 10. These two prime implicants /D./C./B and D.B./A are both flagged with an E to indicate that they are essential.
One way of looping the remaining minterms, 5, 7, and 15, is to loop minterms 1 and 5 (/D./B.A), and loop minterms 7 and 15 (C.B.A). Alternatively, minterms 5 and 7 may be looped (/D.C.A) and minterms 14 and 15 (D.C.B). All these prime implicants are flagged with an S, which indicates that it may or may not be needed; you, the designer, must make the choice. There are two possible solutions, both, of course, include the essential prime implicants.
F = /D./C./B + D.B./A + /D./B.A + C.B.A
F = /D./C./B + D.B./A + /D.C.A + D.C.B
Both solutions produce expressions that are equally simple.
2.6.1 Prime implicant selection table
Clicking on the Prime Implicant Selection Table button in program KVMap.exe gives a table that helps to select the prime implicants. For the current example, the table is shown in Figure 2.11. (You can print this table from the program.) The table shows all the possible prime implicants and the minterms that they cover. The second and third rows show all the minterms and their value, either 0 or 1. Reading across the row for prime implicant /D./C.B, the table shows that this loops minterms 0 and 1. Reading down the column for minterm 0, we see that this is the only prime implicant that loops minterm 0; this prime implicant must therefore be included in the solution, which is why it is flagged as essential, (E). We strike through this row and the columns for minterms 0 and 1. Similarly, we strike through the row for essential prime implicant D.B./A and the columns for minterms 10 and 14. The table now shows all the minterms that are looped more than once and are therefore to be selected by us. Thus we may choose to cover minterm 5 either by /D./B.A or by /D.C.A. Suppose we choose /D./B.A: we strike through the row for this prime implicant and the column for minterm 5. This leaves minterms 7 and 15 still uncovered; the proper choice now is prime implicant C.B.A, which covers both these minterms.
2.7 Quine–McCluskey method*
The KV map method is useful for expressions having four, or fewer, variables. For more variables, the maps effectively become three dimensional and are difficult to interpret. Not surprisingly, reduction of combinational logic expressions is usually done with the aid of a computer. The computer programs are often based on the algorithm described here5. Since it makes use of tables, it is often called a tabular method. The algorithm detects all the possible implicants, that is, all the possible loops that can be made on the KV map of the function. However, unlike the KV map method, this algorithm can be applied to any number of variables. A word of warning: the algorithm takes much longer to describe than to do! Once the algorithm has been practised a few times, it is quite easy, though tedious, to simplify logical functions by hand.
2.7.1 Finding pairs of adjacent minterms
The arrangement of the KV maps is such that adjacent squares represent minterms that differ in one, and only one, variable. For example, adjacent minterms 6 (/D.B.C./A) and 14 (D.B.C./A) differ only in variable D. Two properties follow from this. First, adjacent minterms always have a numerical difference that is a power of 2. Second, there is always one more 1 in the binary number for one minterm than the other. We call the number of 1s in a binary number its index. Thus, in the example, 6 = 0110 has an index of 2, and 14 = 1110 has an index of 3. This suggests the basis of an algorithm for detecting adjacent minterms, which may then be combined into an implicant.
These two properties alone, however, are not sufficient to correctly identify adjacent minterms. Thus, minterms 7 (0111, index 3) and 9 (1001, index 2) have numerical values that differ by a power of 2, yet they are not adjacent. We overcome this by noting that the minterm with the higher numerical value must also have the higher index. These three properties of adjacent squares imply that:
have index values that differ by 1, and
have numerical values that differ by a power of 2, and
the minterm with the higher index also has the higher numerical value
then, the two squares are adjacent.
An unsophisticated implementation of this algorithm would be to compare every minterm with every other minterm and test to see if they are adjacent. However, there is only a need to compare those minterms that have index values that differ by 1, so we will put the minterms into a list that is divided into groups of minterms having the same index value.
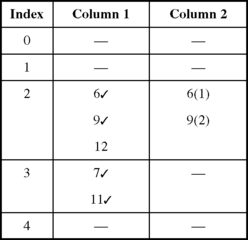
A function is given by F(D, C, B, A) = Σ 6, 7, 9, 12. We first evaluate the index values: 6 (0110, index 2), 7 (0111, index 3), 9 (1001, index 2), 11 (1011, index 3), 12 (1100, index 2). The list of minterms grouped according to their index is shown in Figure 2.12
The comparisons are shown in Figure 2.13 where each minterm in one index group is compared with every minterm in the next higher index group. If we are doing this by hand, a convenient way of writing this is shown in Figure 2.14. When minterms 6 and 7 are compared, and found to merge, mark both minterms in Column 1, and write 6(1) in Column 2, where the number in brackets is the numerical difference. Similarly, the comparison of minterms 9 and 11 gives marks against 9 and 11 in Column 1 and 9(2) in Column 2. When all comparisons have been made, the unmarked minterms in Column 1 do not merge while Column 2 indicates pairs of minterms. Thus, we have found prime implicants 12, 6(1), and 9(2). Since this example uses only four variables, we can verify that on the KV map, these prime implicants correspond to loops around 12, pair 6 and 7, and pair 9 and 11.
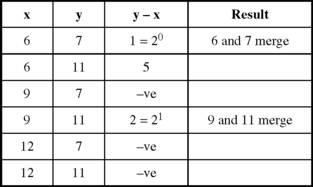
Figure 2.13 Comparison of the minterms shown in Figure 2.12
How do we turn these numbers – 12, 6(1), 9(2) – back into logical expressions using the variable names? Clearly, prime implicant 12, 1100 in binary, means minterm D.C./B./A. Prime implicant 6(1) means the logical OR of minterms 6 and 7; that is /D.C.B./A + /D.C.B.A = /D.C.B.(/A + A) = /D.C.B. A simple way of arriving at this result is to write minterm 6 as /D.C.B./A and then to strike out the variable that has a weight of 1, that is variable A. This leaves /D.C.B. Similarly, implicant 9(2) is written as D./C./B.A and then variable B is struck out, leaving D./C.A. The simplified function is thus: F = D.C./B./A + /D.C.B + D./C.A.
2.7.2 Finding larger groups of minterms
The procedure for finding pairs of minterms can be extended to detect larger groups.
A function is given by F(D, C, B, A) = Σ 1, 4, 10, 11, 12, 14, 15. We begin with the table shown in Figure 2.15. In Column 1, the minterms have been grouped according to their index. In Column 2, minterms 4 and 12 are merged to form pair 4(8), 10 and 11 form pair 10(1), 10 and 14 form pair 10(4), 12 and 14 form pair 12(2), 11 and 15 form pair 11(4), and 14 and 15 form pair 14(1). All these merged minterms are marked in Column 1.
Figure 2.16 shows Column 3 filled; the marks in Column 2 now indicate adjacent pairs of squares that have been merged into the groups of four shown in Column 3. As before, this has been achieved by comparing each implicant in each index group in Column 2 with each implicant in the next higher index group. The added requirement is that implicants can merge only if they have the same number in brackets. Thus, 10(1) and 14(1) merge into 10(1,4) and 10(4) and 11(4) merge into 10(4,1). The implicants 10(1,4) and 10(4,1) are in fact the same group of four minterms; both describe the group of minterms 10 + 0, 10 + 1, 10 + 4, and 10 + 1 + 4, that is, 10, 11, 14, and 15. No further simplification is possible since there are no possible comparisons in Column 3. The implicants are thus 1, which is unmarked in Column 1, 4(8) and 12(2), which are unmarked in Column 2, and 10(1, 4), which is unmarked in Column 3. A prime implicant selection table, as described in an earlier section, must now be used to select which of the prime implicants are required for the function. In this example, prime implicants 1, 4(8), and 10(1, 4) are essential, and prime implicant 12(2) is not required. The required function is thus F(D, C, B, A) = Σ 1, 4(8), 10(1,4) = /D./C./B.A+ ![]() .C./B./A + D.
.C./B./A + D.![]() .B.
.B.![]() = /D./C./B.A + C./B./A + D.B.
= /D./C./B.A + C./B./A + D.B.
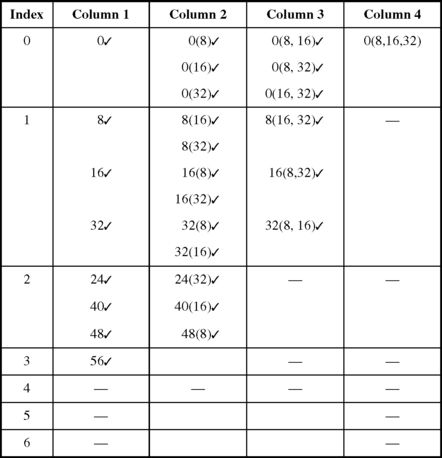
We require the simplification of the function G(F, E, D, C, B, A) = Σ 0, 8, 16, 24, 32, 40, 48, 56. The simplification is shown in Figure 2.17. The algorithm extends to four columns, and all minterms and implicants merge into the single prime implicant 0(8, 16, 32). The first three entries in Column 3 have been produced by detecting that 0(8) and 16(8) merge to form 0(8, 16). Also, 0(8) and 32(8) merge to form 0(8, 32). Also, 0(16) and 8(16) merge to form 0(16, 8), which is the same as the previously detected 0(8, 16). To form Column 4, 0(8, 16) and 32(8, 16) have been merged into 0(8, 16, 32), since these implicants have the same numbers in brackets and differ by a power of 2. Similarly, 0(8, 32) and 16(8, 32) merge into 0(8, 32, 16) which is the same as 0(8, 16, 32). Also, 0(16, 32) and 8(16, 32) merge into 0(16, 32, 8) which is the same as 0(8, 16, 32). The only prime implicant that is unmarked in the table is 0(8, 16, 32). This is ![]() ./C./B./A or /C./B./A6.
./C./B./A or /C./B./A6.
We require the simplification of the function H(E, D, C, B, A) = Σ 0,1, 2, 3, 10, 16, 17, 18, 19, 28, 29. The simplification is shown in Figure 2.18. The first few entries in Column 3 have been produced by detecting the following merges. Implicants 0(1) and 2(1) merge to form 0(1, 2). Implicants 0(1) and 16(1) merge to form 0(1, 16). Implicants 0(2) and 1(2) merge to form 0(1, 2). Implicants 0(2) and 16(2) merge to form 0(2, 16). Implicants 0(16) and 1(16) merge to form 0(1, 16), which has previously been detected.
To form Column 4, 0(1, 2) and 16(1, 2), merge into 0(1, 2, 16), since these implicants have the same numbers in brackets and differ by a power of 2. Similarly, 0(1, 16) and 2(1, 16) merge into 0(1, 2, 16). Also, 0(2, 16) merges with 1(2, 16) to form 0(1, 2, 16). The unmarked prime implicants are 2(8), 28(1) and 0(1, 2, 16).
Implicant 2(8) covers minterms 2 and 10, prime implicant 28(1) covers minterms 29 and 29, while implicant 0(1, 2, 16) covers the eight minterms 0, 1, 2, 3, 16, 17, 18, 19. The prime implicant selection table shows that all these are essential prime implicants. The simplified function is thus H = 2(8) + 28(1) + 0(1, 2, 16) = /E.![]() ./C.B./A + E.D.C./B.
./C.B./A + E.D.C./B.![]() +
+ ![]() ./D./C.
./D./C.![]() , that is, H = /E./C.B./A + E.D.C./B + /D./C.
, that is, H = /E./C.B./A + E.D.C./B + /D./C.
2.8 Problems
1. Given C = 1, B = 0, and A = 1, and F = /C.B./A + C./B.A + C.B./A + C.B.A, what is the value of F?
2. Given C = 1, B = 0, and A = 1, and G = /C./B./A + /C.B.A + C./B./A, what is the value of G?
3. Construct the truth table for F = /C.B./A + C./B.A + C.B./A + C.B.A.
4. Construct the truth table for G = /C./B./A + /C.B.A + C./B./A.
5. In Figure 2.6, in which squares are the orchestra members that play strings AND wind?
6. In Figure 2.6, in which squares are the orchestra members that play strings OR wind?
7. In Figure 2.6, in which squares are the orchestra members that do NOT play strings AND play wind?
8. In Figure 2.6, in which squares are the orchestra members that play strings OR percussion OR wind?
9. In Figure 2.6, in which squares are the orchestra members that do NOT play strings AND do NOT play percussion AND do NOT play wind?
10. In Figure 2.6, do the orchestra members in square 2 play strings?
11. In Figure 2.6, how can the members in squares 6, 7 be described?
12. Using a map, show that F = C./B.A + C.B.A. = C.A.
13. Using a map, show that F = BA + /C./B.A + C.B./A. = /C.A + C.B.
14. Using a map, show that F = BA + C.B + /B./A + /C./B = /C./B + B.A + C./A.
15. Using a map, show that F = BA + C.B + /B./A + /C./B = /B./A + /C.A + C.B.
17. Using a KV map, show that /D./C.B.A + /D.C./B.A + /D.C.B.A + D./C.B.A = /D.C.A + /C./B.A.
18. Using a KV map, show that /D./C./B./A + /D./C./B.A + D.C.B./A + D.C.B.A + /D.C = /D./B + C.B.
19. Solve Problem 12 using the Quine–McCluskey method.
20. Solve Problem 13 using the Quine–McCluskey method.
21. Solve Problem 14 using the Quine–McCluskey method.
22. Solve Problem 15 using the Quine–McCluskey method.
23. Solve Problem 16 using the Quine–McCluskey method.
24. Solve Problem 17 using the Quine–McCluskey method.
25. Solve Problem 18 using the Quine–McCluskey method.
26. Using the Quine–McCluskey method, simplify H(E, D, C, B, A) = Σ 0, 4, 9, 14, 25, 30.
1There are two possible answers to each of the three questions, so the number of possible answers to the three questions is 2 * 2 * 2 = 23 = 8.
2These are the basic rules of Boolean algebra, first demonstrated by George Boole in his book Mathematical Analysis of Logic, 1847.
3Incidentally, this indicates that Boolean functions may be factorized: S.P./W + S.P.W = S.P.(/W + W) = S.P.1 = S.P.
4This map method was originated by E. W. Veitch and modified by M. Karnaugh.
Veitch, E.W., ‘A Chart Method for Simplifying Truth Functions’, Proc. ACM, Pittsburgh, USA, pp. 127–133, May 1952.
Karnaugh, M., ‘The Map Method for Synthesis of Combinational Logic Circuits’, Trans. AIEE, Pt I, Vol. 72, No. 9, pp. 593–599, 1953.
5The Quine–McCluskey method was devised by W. V. Quine in 1952 and 1955 and modified by E. J. McCluskey in 1956.
6We might have written this result down immediately since the minterm list is all the multiples of 8 that can be accommodated in 6 bits. All multiples of 8 end in … 000.