
12 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
Problem 1.18 Demonstrate that if p.x/ is a polynomial, then we can compute
Z
p.x/
x
k
dx
with the techniques in this section.
Problem 1.19 Compute
Z
x
2
C 2
x
2
C 1
dx
Problem 1.20 Compute
Z
p
1 x
2
.1 x/.1 Cx/
dx
1.2 THE FUNDAMENTAL THEOREM
Before we can formally state the relationship between the integral and the derivative, we need
to define the definite integral.
Definition 1.4 Suppose that F .x/ D
Z
f .x/ dx. In other words, F .x/ is an anti-derivative of
f .x/. en the definite integral from x D a to x D b of f .x/ is defined to be:
Z
b
a
f .x/ dx D F .b/ F .a/
One nice thing about the definite integral is that it removes the unknown constant. If we write
F .x/
C
C
for the anti-derivative, then
.F .b/ CC / .F .a/ CC / D F .b/ F .a/ C C C D F .b/ F .a/
With the definite integral defined we can now state the first form of the fundamental theorem.

1.2. THE FUNDAMENTAL THEOREM 13
Knowledge Box 1.8
e First Fundamental eorem of Calculus
d
dx
Z
x
a
f .t/ dt D f .x/
for any constant a.
is form of the fundamental theorem tells us that the derivative of the integral of a function
is the same function, although the variable of integration (t in the above statement) may be
different from the variable appearing in the final expression.
Example 1.21
d
dx
Z
x
0
.t
2
C 1/ dt D x
2
C 1
˙
e integral of the derivative is also the same function – almost. e ubiquitous unknown
constant causes us to answer: except for the “+ C.” Later, we will see that this unknown constant
is where we place the starting point (position, velocity, etc.) into the formula when solving an
applied problem.
e second form of the fundamental theorem has more applications. It relates integrals to the
area under the graph of a function.
Knowledge Box 1.9
e Second Fundamental eorem of Calculus
Suppose that f .x/ 0 on the interval [a,b]. en, if A is the area under
the graph of f .x/ between a and b,
A D
Z
b
a
f .x/ dx

14 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
Example 1.22 Find the area A under the curve of y D x
2
between x D 0 and x D 3.
Solution:
A
4
-1
-1
9
Start with a picture:
Guided by the picture, compute the definite integral.
Z
3
0
x
2
dx D
1
3
x
3
ˇ
ˇ
ˇ
ˇ
3
0
D
1
3
3
3
1
3
0
3
D
1
3
27
1
3
0
D 9 0
D 9 units
2
˙
Notice the vertical bar notation, used to hold the limits until we plug them into the anti-
derivative.
At this point let’s check the intuition on this one. Why would the anti-derivative of a function
be the area under it? e first form of the fundamental theorem tells us that a function is the
derivative of its integral – but that means that a function is the rate of change of its integral.
e larger a function is, the faster the area under it is changing. e smaller a function is, the
slower the area under it is changing. So, a function is the rate of change of the area under the
function. If you’re unconvinced, wait for Section 1.4. We will use another approach to show
that the integral gives the area under the curve.
1.2. THE FUNDAMENTAL THEOREM 15
What meaning does the restriction f .x/ 0 in the second fundamental theorem have? e
short answer is: the area below the x axis, for which f .x/ 0, comes out negative. is actually
makes sense if we remember that the derivative is a rate of change. Positive derivatives represent
increases, negative ones represent decreases. Since there is no such thing as negative area, we
have to be careful when computing the total area between a graph and the x-axis.
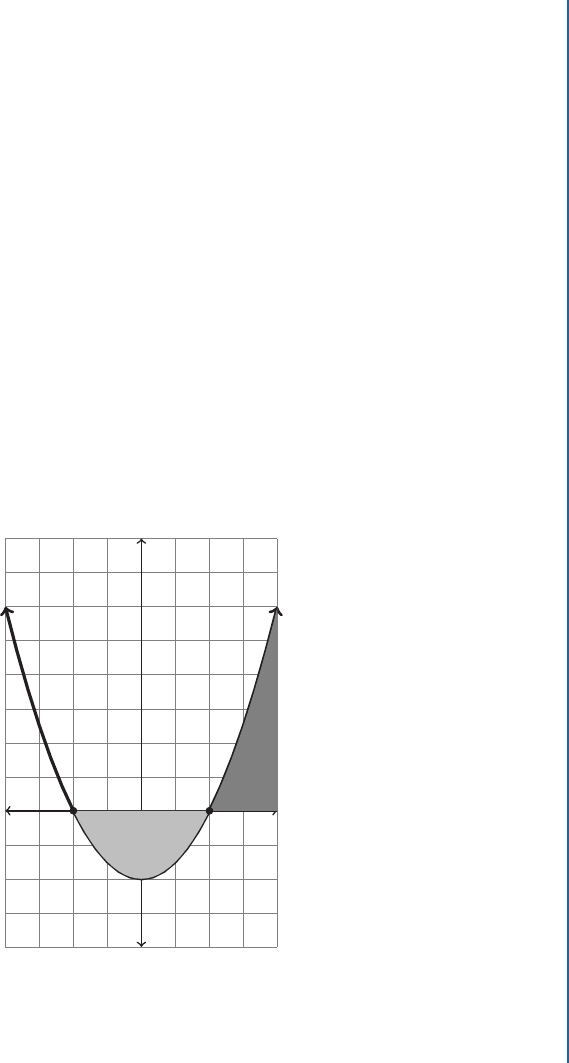
Example 1.23 Compare the definite integral and the area between the curve and the x-axis
for f .x/ D x
2
1 from x D 1 to x D 2.
Solution:
is picture shows the areas above and below the x-axis.
2-2
-2
4
+
-
Notice the points where f .x/ crosses the axis are x D ˙1.

16 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
First the integral:
Z
2
1
x
2
1
dx D
1
3
x
3
x
ˇ
ˇ
ˇ
ˇ
2
1
D
1
3
2
3
2
1
3
.1/
3
.1/
D
8
3
2 C
1
3
1
D
9
3
3
D 0
So, even though they are different shapes, the areas above and below the curve are equal. Now
we need to compute the areas separately and take the positive area minus the “negative” one:
Z
2
1
x
2
1
dx
Z
1
1
x
2
1
dx D
1
3
x
3
x
ˇ
ˇ
ˇ
ˇ
2
1
1
3
x
3
x
ˇ
ˇ
ˇ
ˇ
1
1
D
8
3
2
1
3
C 1
1
3
1 C
1
3
1
D
7
3
1
2
3
C 2
D
8
3
units
2
˙
Notice that the integral is a number and so has no units, while the area between the curve and
the x-axis has Cartesian units squared as its units. It is very important to keep clear in your mind
the context in which you are using an integral. e meaning of the result is different for different
procedures.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
