24 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
e sine function is non-negative on the entire interval so we may compute
A D
Z
0
sin.x/ dx
D cos.x/
ˇ
ˇ
ˇ
ˇ
0
D cos./ C cos.0/
D .1/ C1
D 2 units
2
˙
1.2.1 EVEN AND ODD FUNCTIONS
Even and odd functions have some useful properties, relative to integration. ese definitions
appear in the book on the differential calculus, but it is worth repeating them here.
Definition 1.5 A function is even if, for x where the function exists,
f .x/ D f .x/:
A good example of an even function is f .x/ D x
2
. Even functions forget signs.
Definition 1.6 A function is odd if, for x where the function exists,
f .x/ D f .x/:
A good example of an odd function is f .x/ D x
3
. Odd functions remember signs.
It turns out that we can save some effort when integrating these functions, sometimes, because
of special geometric properties of these functions.

1.2. THE FUNDAMENTAL THEOREM 25
Knowledge Box 1.11
Integrating an even function on a symmetric interval
If f .x/ is an even function, then
Z
a
a
f .x/ dx D 2
Z
a
0
f .x/ dx
Example 1.29 Find the integral of f .x/ D x
2
on Œ2; 2 .
Solution:
Remember that x
2
D .x/
2
. So f .x/ is an even function.
2-2
-1
4
f .x/ D x
2
e area on either side of the y-axis is the same so:
Z
2
2
x
2
dx D 2
Z
2
0
x
2
dx D 2
1
3
x
3
ˇ
ˇ
ˇ
ˇ
2
0
D
16
3
units
2
Not having to plug in the negative number avoids chances to make arithmetic mistakes.
˙
26 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
Knowledge Box 1.12
Integrating an odd function on a symmetric interval
If f .x/ is an odd function, then
Z
a
a
f .x/ dx D 0
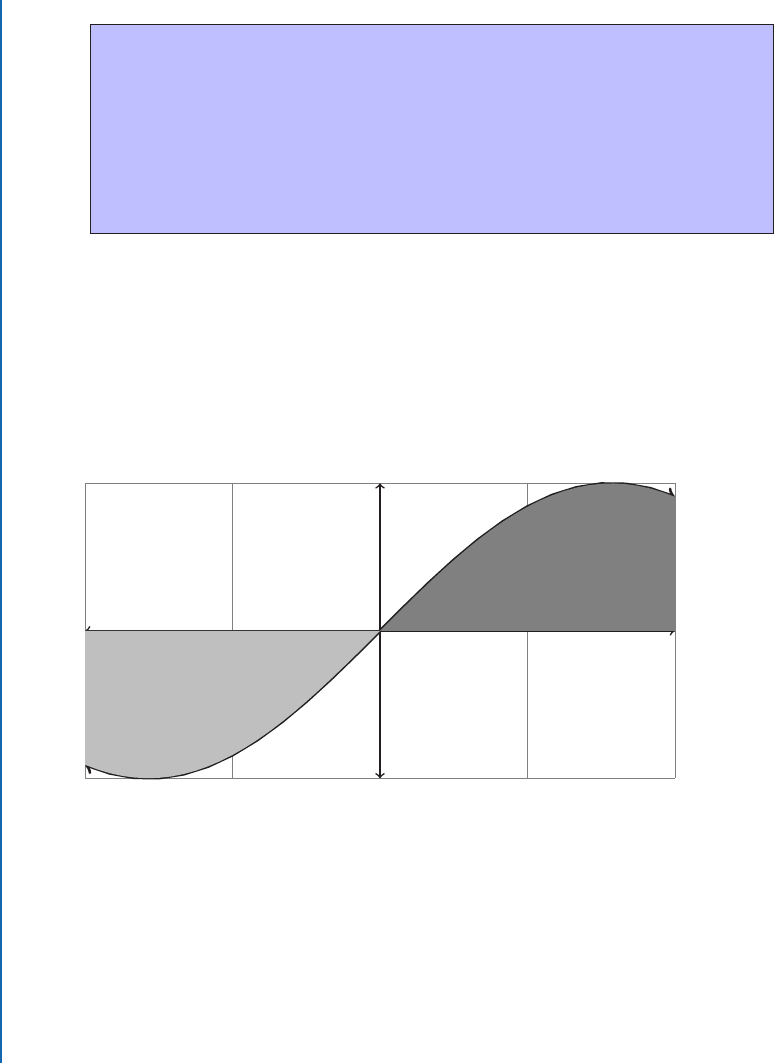
Example 1.30 Find the integral of g.x/ D sin.x/ on Œ2 ; 2 .
Solution:
Remember that sin.x/ D sin.x/. So g.x/ is an odd function.
2-2
-1
1
g.x/ D sin.x/
e area on either side of the y-axis is the same, but half is above the x axis, and half is below
the x-axis. So:
Z
2
2
sin.x/ dx D 0
Wow, is that easier than plugging in numbers.
˙

1.2. THE FUNDAMENTAL THEOREM 27
e odd and even function results are fairly special purpose. One of the big applications of odd
and even function is writing test questions that can be done much faster if the student notices
something is an odd function on a symmetric interval, for example. Symmetric intervals do also
show up in some application problems. If you’re good at shifting functions sideways, you can
also extend the application of these rules.
e set of even functions and the set of odd functions are closed under addition and also under
multiplication by a constant. is fact is occasionally useful. If you’re feeling ambitious, try and
prove it’s true. Also remember that you can break up an integral into a symmetric piece and
leftovers, to change a definite integral into a possibly simpler integral. Finally, if you see an
integral that you have no idea how to do, consider the possibility that the odd function shortcut
gives you a way of solving the problem without integrating.
PROBLEMS
Problem 1.31 Simplify each of the following. Assume Snerp.x/ has a domain of .1; 1/.
1.
d
dx
Z
x
1
t
t
2
C 1
dt
2.
d
dx
Z
x
cos.6t C 1/ dt
3.
d
dx
Z
x
0
te
t
2
dt
4.
d
dx
Z
x
6
e
s
C 1
e
s
1
ds
5.
d
dx
Z
x
2
e
y
ln.y/ C 4
dy
6.
d
dx
Z
x
0
Snerp.t C 2/ dt
Problem 1.32 Compute the following.
1.
Z
1
1
x
2
C x C1
dx
2.
Z
=2
=2
cos.x/ dx
3.
Z
3
1
1
x
x
2
C 1
dx
4.
Z
4
0
x
n
dx
5.
Z
1
0
.
x Ce
x
2
/
dx
6.
Z
p
3
0
dx
x
2
C 1

28 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
Problem 1.33 Compute
Z
5
5
x
5
C 3x
3
C 7x
2
x C1
dx
Problem 1.34 Compute the area between the following curves and the x axis on the stated
interval. Be careful, some of these have area above and below the x-axis. Pictures may help.
1. f .x/ D x
2
on Œ1; 1
2. g.x/ D x
3
on Œ1; 1
3. h.x/ D cos.x/ on Œ=2; 3=2
4. r.x/ D tan
1
.x/ on Œ1=
p
3; 1=
p
3
5. s.x/ D e
x
on Œ0; 5
6. q.x/ D 4 x
2
on Œ3; 3
Problem1.35 Compute the area bounded by the specified curves. You will need to know which
curve is higher. Again: pictures may help.
1. y D x
2
and y D x
3
2. y D x
2
and y D 6 x
3. y D sin.x/ and y D cos.x/ on Π0; 3=2
4. y D x
2
and y D 4x 3
5. y D x
2
and y D 9 x
2
6. y D x
3
and y D 4x
Problem 1.36 Find the area bounded by
y D x
n
and y D x
m
for all positive whole numbers m < n. ere will be different categories of answer based on
whether n and m are even or odd. at’s four categories: CC, C, C, and .
Problem 1.37 Compute the following definite integrals.
1.
Z
3
3
x
5
C x
3
C x C1
dx
2.
Z
2
0
.
cos.x/ C sin.x/
/
dx
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
