1.4. INDUCTION AND SUMS OF RECTANGLES 39
1.4 INDUCTION AND SUMS OF RECTANGLES
In this section we will study the theory of integration that was developed before the fundamental
theorem that doesn’t need the concept of the derivative. Let’s start with an example that could
be solved with calculus but need not be.
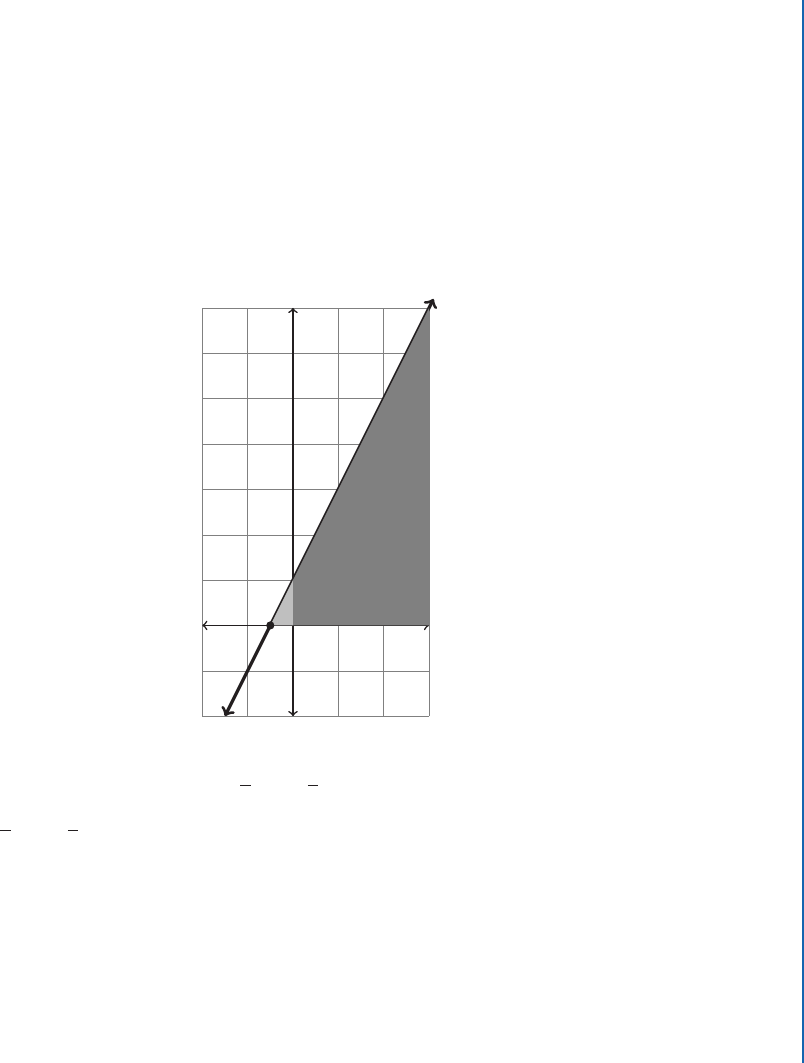
Example 1.64 Find, without using calculus, the area under f .x/ D 2x C 1 from x D 0 to
x D 3.
Solution:
A
-0.5
f .x/ D 2x C 1
3
-2
-2
7
e area of the large triangle is
1
2
bh D
1
2
3:5 7 D 12:25. e area of the light gray triangle is
also
1
2
bh D
1
2
0:5 1 D 0:25. e area we want, the dark gray, is thus 12:25 0:25 D 12 units
2
.
˙
e reason we don’t need calculus for this example is that the shape of the area is really simple.
As long as we remember that the area of a triangle is one-half base times height, we’re fine. As
soon as the integral is under a function that is curved, we will need calculus. Where does this
calculus come from? At this point we need a digression to create the mathematical machinery
that permits us to synthesize the calculus.

40 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
e symbol
X
means “add up the things following the symbol.” So
5
X
iD1
i
is a symbolic way of saying “add up the numbers i from i D 1 to i D 5. e name of the symbol
is uppercase sigma – not to be confused with which is called lowercase sigma. Applying
P
we get
5
X
iD1
i D 1 C 2 C 3 C 4 C 5 D 15
which isn’t too bad. e problem is when we get something like
200
X
iD1
i D 1 C 2 C C199 C 200 D 20; 100
e incomparable German mathematician Carl Friedrich Gauss found the following shortcut:
n
X
iD1
i D
1
2
n.n C1/
How do you prove a formula like that is correct?
e usual technique is called mathematical induction.
Knowledge Box 1.14
Mathematical induction
Suppose we wish to prove a proposition P .n/ is correct for all n c.
en the following steps suffice
• Verify that P .c/ is true.
• Assume that, for some n, P .n/ is true.
• Show that, if P .n/ is true, then so is P .n C 1/

1.4. INDUCTION AND SUMS OF RECTANGLES 41
e assumption in the second step is easy, because P .n/ is true when n D c, due to our work
on the first step. e key step is the third one. Once we’ve got it, P .c/ implies P.c C 1/ is true,
which in turn implies P .c C 2/ is true, and so on, until we hit any particular n c.
Example 1.65 Use mathematical induction to prove Gauss’ formula.
Solution:
e proposition is
P .n/ W
n
X
iD1
i D
1
2
n.n C1/
Let’s start with c D 1.
P .c/ D P.1/ W
1
X
iD1
i D 1 D
1
2
c.c C 1/ D
1
2
.1/.1 C1/ D 1
Since 1=1, this is true, and we have the first step of the induction. We now assume that P .n/ is
true (for some n) and look at P .n C 1/.
nC1
X
iD1
i D
n
X
iD1
i C .n C1/
D
1
2
n.n C1/ C .n C1/ Apply P.n/
D
n.n C1/ C 2.n C 1/
2
D
n
2
C 3n C 2
2
D
1
2
.n C1/.n C 2/
D
1
2
.n C1/..n C 1/ C1/ Which is P .n C 1/
So if P .n/ is true, we can show using algebra that P .n C1/ is true. is tells us, by mathematical
induction, that Gauss’ formula is true for all n 1.
˙

42 1. INTEGRATION, AREA, AND INITIAL VALUE PROBLEMS
Some other examples of proof with mathematical induction appear in the homework problems.
Now we know enough to calculate an integral or a curved function without using the funda-
mental theorem of calculus. Our goal is to approximate the area under the curve with shapes
we can compute.
Examine pictures of f .x/ D x
2
in Figure 1.1. e gray area is
Z
2
0
x
2
dx; the four rectangles
are a (bad) approximation of the area under the curve. How can we make the approximation
better? Use more rectangles! e more rectangles, the better the area is approximated.
2.5-2.5
-1
7
2.5-2.5
-1
7
2.5-2.5
-1
7
2.5-2.5
-1
7
Figure 1.1: Approximating an intgral with increasing number of rectangles.

1.4. INDUCTION AND SUMS OF RECTANGLES 43
It turns out that summing and integrating share two algebraic properties.
Knowledge Box 1.15
Algebraic properties of
P
b
X
iDa
f .i/ C g.i/ D
b
X
iDa
f .i/ C
b
X
iDa
g.i/
b
X
iDa
c f .i/ D c
b
X
iDa
f .i/
for any constant c
ere are an infinite number of summation formulas – but a few of them are especially useful.
All of these can be proved by induction (and you are asked to do so in the homework).
Knowledge Box 1.16
Useful sum formulas
•
n
X
iD1
1 D n
•
n
X
iD1
i D
n.n C 1/
2
•
n
X
iD1
i
2
D
n.n C 1/.2n C1/
6
•
n
X
iD1
i
3
D
n
2
.n C 1/
2
4
If we use n rectangles to approximate
Z
2
1
x
2
dx, then each rectangle has a width of w D
2
n
.
e right side of each rectangle (which determines its height) is x
i
D i w for i D 1; 2; : : : n.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
