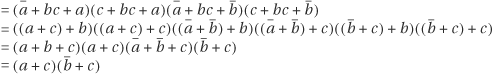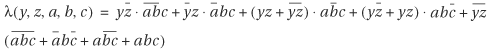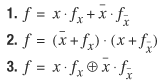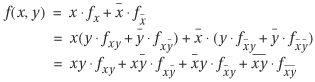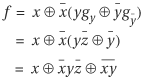Simulation-based verification relies much on one’s ability to generate vectors to explore corner cases. In reality, two major problems exist. First, it is almost impossible, especially in large designs, to consider all possible test scenarios and, as a result, bugs arise from scenarios that were never anticipated. Second, even if one could enumerate all the possible corner cases in a design, it must be done intelligently so that the computation time to verify them all is realistic. Formal verification is a systematic way to traverse exhaustively and implicitly a state space or subspace so that complete verification is achieved for designs or parts of designs. However, formal verification is not a panacea. As seen in later chapters, formal verification achieves complete verification only up to the accuracy of the design representation and the property description. A case in point, formal verification cannot prove that all properties of a design have been enumerated, although for a given property it can prove whether the property is satisfied.
Formal verification, in contrast to traditional simulation-based verification, requires a more rigorous mathematical background to understand and to apply effectively. Key concepts in formal verification can be stated in intuitive plain English, but mathematics makes the concepts more precise and concise. Therefore, the crux to being proficient with mathematical symbols and manipulations is to go beyond their complicated appearance and understand the ideas they represent. Once an intuitive understanding has been developed, the mathematics comes naturally. Complicated mathematical expressions may seem daunting at times. It is comforting to know that the great mathematician Godfrey H. Hardy once said, “There is no place for ugly mathematics.” (“A Mathemetician’s Apology,” G.H. Hardy, Cambridge University Press, Reprint Edition, 1992.) So, a complicated mathematical expression is more often than not a result of an ill-advised formulation, rather than a lack in the reader’s mathematical maturity. The message is: Do not get discouraged easily.
A set is a collection of distinct objects, and the objects, called the members of the set, are enclosed in a pair of curly braces. Set S, consisting of alphanumeric symbols x, 2, $, 3, %, and L2, can be written as S = {x, 2, $, 3, %, L2}. Inside the braces can be a qualification expression for the set members. For example, F = {p : p is a prime and p = 2i-1} represents the set of all prime numbers that can be expressed in the form 2i-1 for some integer i. The expression after the colon is the qualification expression. Sometimes a vertical bar is used in place of the colon: F = {pp is a prime and p = 2i-1}. Set U is often denoted as the universal set that consists of everything in the context. For example, in the context of integers, U consists of all integers. Set Z usually denotes the set of all nonnegative integers, whereas R represents the set of all real numbers. Z+ and R+ are positive integers and positive real numbers respectively. The number of elements in set S, called the cardinality of S, is denoted by |S|.
Membership in a set, such as x is a member of S, is denoted by x∉S. Similarly, y is not a member of S is denoted by y ∉ S. Using the previous definition of set F, we have 7 ∊ F and 11 ∉ F. Symbols ∀s and ∃s mean “for all variable s” and “for some variable s” respectively. Set V is a subset of set W, denoted as V⊆W, if ∀ s ∊ V⇒s ∊ W, which says, for every element s in set V, s is also in W. Symbol x ⇒ y means “x implies y”. If there is at least one element in W that is not in V,V is said to be a proper subset of W and is denoted as V ⊂ W. The equality sign is removed.
Compositions of sets can be defined in terms of the previous notations. If sets A and B are sets, then
This is called the intersection of A and B, which is the set of all elements common to A and B. Using sets S and F, we see that S ∩ F = {3}. If A and B do not have common element, the intersection is empty: A∩B = Ø. Two sets with an empty intersection are said to be disjoint.
The union of A and B is defined as
which is the set of all elements in A or B. Obviously, A⊆(A∪B), (A∩B)⊆A, and (A∩B)⊆(A∪B).
The Cartesian product A×B is defined as
The Cartesian product is a common method used to construct higher dimensional space from lower dimensional spaces. For example, the set of all positive rational numbers, K, can be constructed from positive integers and can be represented as K = {(a, b) | a and b are positive integers}, where a can be treated as the numerator and b, the denominator.
These set operations can be extended to a finite number of operands:

An element in a Cartesian product of k sets, denoted as (nl,...,nk), is called a k-tuple. It can be regarded as a point in the k-dimensional space.
The exclusion of B from A, or subtraction of B from A, is defined as
which is the set of all elements in A but not in B. As an example, the set of all positive integers Z+ is Z-{0}, and the set of all positive irrational numbers is R+–K. If U is the universal set, then U-B is called the complement of B, denoted by ![]() .
.
Mapping μ between two sets S1 and S2, denoted by μ(S1,S2), associates each element in S1 with an element or a subset in S2. An example of a mapping is the procedure that takes in a photograph and outputs all colors in the photograph. In this example, S1 is a set of photographs and S2 is a set of colors.
A mapping that associates an element in S1 with only one element in S2 is called a function. That is, a function maps one element S1 to exactly one element S2. However, a function can map several elements in S1 to the same element in S2. Set S1 is called the domain, and S2 is called the image or range of the function. A function or mapping that maps distinct elements in S1 to distinct elements in S2 is called a one-to-one function or one-to-one mapping.
The relation γ between S1 and S2 is the function γ(S1×S2, {0,1}). For x ∊ S1 and y ∊ S2, we say a relation exists between x and y if γ(x,y) = 1. An example of a relation is the less than relation, <, on real numbers. Relation < maps (2,3) to 1 because 2<3 exists. But it maps (5,1) to 0. For simplicity, we denote x related to y by γ(x,y). Furthermore, for γ(S×S, {0,1}), we say γ is a relation on S.
A partition of set S, λ = {Al,...,An}, is a collection of subsets of S, Al,...,An, such that
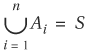
and
In words, a partition of set S is a division of S into disjoint subsets, which together make up S. Subsets A1,...,An are called the elements of the partition.
For notational convenience, let’s use overlines and semicolons to denote a partition. For the partition in the previous example, we have
A relation γ on S is an equivalence relation if it satisfies the following conditions:
Reflexive: γ(x,x) for all x ∊ S.
Symmetric: γ(x,y) ⇒ γ(y,x), for all x,y ∊ S.
Transitive: γ(x,y) and γ(y,z) implies γ(x,z).
An equivalence relation is denoted by ~; for example, x ~ y if x is equivalent to y. As an example, a nonequivalent relation is relation <, because it is not reflexive. For example, 2<2 does not exist. An example of an equivalence relation is the equality on real numbers, =. The main use of an equivalence relation is to partition a set to find all equivalent elements. When all equivalent elements are combined as a single element, the resulting set, called the quotient set, becomes smaller and easier to manipulate.
Given an equivalence relation ~, we would like to find a procedure to reduce a set based on the equivalence relation ~. Define Sx as the set {s : s ~ x where x ∊ S}. That is, Sx is a subset of S, whose elements are equivalent to x. Element x can be regarded as a representative element of Sx and Sx, as the equivalence neighborhood of x. If we find all representative elements in S, then S can be reduced to a set made of only representative elements. Theorem 7.1 guarantees this possibility.
Part 1 of this theorem says that any two equivalent elements must belong to the same subset. Part 2 says that any two nonequivalent elements must be in two different subsets. In other words, S is broken into equivalent subsets, each of which is the maximal equivalent subset. The subsets are maximal because of the definition of Sx. The pairwise nonequivalent elements in part 3 can be regarded as the representatives of the equivalent subsets, each representing all the elements to which it is equivalent. Therefore, λ is the equivalent partition with the minimum |λ|. That is, any other partition of S based on ~ has a greater or equal cardinality. λ is the coarsest partition.
This theorem states a method of maximally partitioning a set such that all elements of any subset are equivalent. To create the partition, take any element x, find all its equivalent elements, and make them into a subset Sx. Any elements not included in Sx must be not equivalent to x. Take any remaining elements and repeat this process. The partition ends when all elements have been included in a subset. This is summarized in the following list. Given an equivalence relation γ on set S, partition S according to γ.
Note that the relation must be an equivalence relation; otherwise, the subsets formed are not a partition, as seen in Example 7.2.
Of the three conditions for equivalent relation, if we replace the symmetric property with the asymmetric property, we have an ordering relation. An ordering relation is a generalization of the usual ≥ operator on real numbers. The meaning of an ordering relation extends beyond mere magnitude comparison; it is a more abstract concept of comparison. An ordering relation, x≥y, satisfies the following three conditions:
Reflexive: x≥x for all x ∊ S.
Asymmetric: (x≥y, y≥x) ⇒ x = y, for all x, y ∊ S.
Transitive: x≥y and y≥z implies x≥z.
The mathematical structure made of a set and an ordering relation is called a partially ordered set, or poset. The ordering relation operates on the elements of the set and arranges them according to the relation. It is called “partially ordered” because not all pairs of elements have a relation. Using the β(s, r) relation from Example 7.3, s ≥ r if r is a substring of s. In other words, s contains or subsumes r. However, no order exists for these two strings s = abc and r = xy, because we can write neither s ≥ r nor r ≥ s. That is, β cannot order s and r.
One way to visualize ordering of a poset is to use a Hasse diagram. For two elements, x and y, we say x covers minimally y if x≥y, and for all z ≥ y, z ≥ x. That is, x is the smaller element that is greater than y. If x covers minimally y, we draw a downward line from node x to node y. It may be clearer to draw an arrow from x to y, but a Hasse diagram traditionally does not rely on arrows but north-south direction.
Between two elements in a partially ordered set, we can define meet and join. A meet z between elements x and y is the greatest lower bound of x and y. That is, x ≥ z and y ≥ z. If there is an element w, such that x ≥ w and y ≥ w, then z ≥ w. We denote a meet between x and y by x · y. In Figure 7.1, the meet of
![]() and
and ![]() is
is ![]()
Note that there may not be a meet between any two elements. For instance,
![]() and
and ![]() do not have a meet.
do not have a meet.
Similarly, a join between two elements x and y, denoted as x + y, is the least upper bound of x and y. That is, join z of x and y is the smallest element such that z ≥ x and z ≥ y. In Figure 7.1, the join between ![]() and
and ![]() is
is ![]() . Note that
. Note that ![]() is not a join because
is not a join because ![]() is smaller than
is smaller than ![]() and is greater than both
and is greater than both ![]() and
and ![]() .
.
Understanding meet and join as the greatest low bound and the least upper bound, it is easy to see that Theorem 7.2 is intuitively reasonable.
As we have seen, not all pairs of elements have a meet or a join. However, when every pair of elements in a partially ordered set have a meet and a join, we call this mathematical structure (the set together with the meet and join operator) a lattice.
The set of partitions form a lattice if the meet and join are defined carefully. We define the meet of two partitions π1 · π2 to be a partition formed by the intersection of the elements in π1 and π2. That is, an element in the meet partition is an intersection of an element in π1 and an element in π2. We define the join, π1 + π2, to be a partition formed by the union of all chain-connected elements in π1 and π2. Two sets, S1 and Sn, are chain connected if there exists a sequence of sets, S2, ..., Sn - 1, such that Si and Si + 1 have a nonempty intersection for i = 1, ..., n - 1. It can be proved that with this definition of meet and join, the set of partitions constitutes a lattice.
Let B denote the set {0, 1}. A Boolean function of n variables is a mapping from Bn to B, written as ![]() . An example is
. An example is ![]() .
.
The set of variables in a Boolean function is called the support, denoted by supp(f). Thus, for the previous example function, supp(f) = {a,b,c}. Even when a variable is redundant in a function (that is, it does not affect the result of the function), the variable is still included in the support. For instance, variable r in ![]() is redundant, but supp(g) = {a, b, r}. If only nonredundant variables are required, the term minimum support is used to include only the nonredundant variables.
is redundant, but supp(g) = {a, b, r}. If only nonredundant variables are required, the term minimum support is used to include only the nonredundant variables.
A Boolean function can be represented in many ways. Let’s briefly review some common forms of representation. A sum of products representation is the ORing of all AND terms. An AND term, a product term, is also called a cube. A sum of products is written as
where xi, xj, ..., xn are literals. A literal is either a variable or the complement of the variable. Each product term or cube xixj...xn need not have all variables present. If a product term has all variables, it is called a minterm or vertex. The sum of products representation is also called disjunctive normal form (DNF).
For example, consider function ![]() . It is a sum of products representation. It has three cubes. There are six literals—namely, a,
. It is a sum of products representation. It has three cubes. There are six literals—namely, a, ![]() ,
, ![]() , c, b, and
, c, b, and ![]() . The last cube,
. The last cube, ![]() , is a minterm.
, is a minterm.
Similarly, a Boolean function can be represented as a product of sums, or conjunctive normal form (CNF), as written here:
where xi, xj, ..., xn are literals. Each sum term need not have all variables present. A sum term, the counterpart of a cube, is called a clause. If all variables are present in a clause, the term is called a maxterm.
Finally, a Boolean function can be written in a form mixed with sums of products and products of sums. This form is generically called multilevel representation. A sum of products can be implemented as a two-level circuit, with the first level being AND gates and the second, an OR gate. Similarly, a product of sums can be implemented as a circuit with a layer of ORs followed by an AND gate. Therefore, a mixed representation calls for multiple levels of gates to implement, hence the name. An example is ![]() .
.
Another way of obtaining DNF from CNF is to use the second form of the distributive laws of Boolean algebra stated here:
a · (b + c) = a · b + a · c
a + (b · c) = (a + b) · (a + c)
To many people, the first form is probably more familiar than the second. However, they are related through the duality principle of Boolean. The duality principle of Boolean Algebra states that by replacing AND with OR, OR with AND, 1 with 0, and 0 with 1 in a Boolean identity, we arrive at another Boolean identity. Suppose we start with identity
and apply the exchange operations of duality. We get
which is the second form of the distributive law.
As far as representation size is concerned, it is difficult to know when CNF or DNF is more compact. It is known that there are functions with a CNF that is of polynomial size in number of variables expands to a DNF of exponential size, and vice versa. A research result relating the size of CNF to DNF has the following bounds[1] . If function f has n variables and its CNF size is less than m, then its DNF size, ||f(n,m)||dnf, is bound by the following expression, where c1 and c2 are constants:

Given a function f in DNF, the problem of satisfying f is to determine whether there is an assignment of variables for which f evaluates to 0 (that is, whether f has a nonempty offset). Similarly, if f is in CNF, the satisfiability problem is to determine whether f can evaluate to 1 (in other words, f has a nonempty on set).
A brute-force method to solve the satisfiability problem is to expand the function into minterms or maxterms. This approach, in the worst case, encounters exponential numbers of terms and is practically infeasible, because the satisfiability problem is NP complete. We return to this topic in a later chapter.
Symmetric Boolean functions have some interesting properties and lend themselves to computational efficiency. A Boolean function can be regarded as a function of literals. For instance, ![]() is a function of literals a,
is a function of literals a, ![]() , and c, as opposed to a function of variables a, b, and c. With this clarification, we say that a Boolean function f(x1,...,xn) is symmetric with respect to a set of literals, x1,...,xn, if the function remains unchanged by any permutation of the literals. That is, f(x1,...,xn) = f(xσ(1),...,xσ(n)), where σ is a permutation map, which is a one-to-one mapping from {1,...,n} to {1,...,n}. An example of σ is the following: 1 maps to 2, 2 to 3, n to 1. In this case, f(xσ(1),...,xσ(n)) = f(x2,x3,...,xn,x1). It should be emphasized that xi is a literal, not a variable. In the previous example function, x1 =a,
, and c, as opposed to a function of variables a, b, and c. With this clarification, we say that a Boolean function f(x1,...,xn) is symmetric with respect to a set of literals, x1,...,xn, if the function remains unchanged by any permutation of the literals. That is, f(x1,...,xn) = f(xσ(1),...,xσ(n)), where σ is a permutation map, which is a one-to-one mapping from {1,...,n} to {1,...,n}. An example of σ is the following: 1 maps to 2, 2 to 3, n to 1. In this case, f(xσ(1),...,xσ(n)) = f(x2,x3,...,xn,x1). It should be emphasized that xi is a literal, not a variable. In the previous example function, x1 =a, ![]() , and x3 =c.
, and x3 =c.
It can be cumbersome to use this intuitive definition to determine whether a function is symmetric. Theorem 7.3 alleviates this task.
For example, ![]() takes the value of 1 if and only if zero or two of the literals a,
takes the value of 1 if and only if zero or two of the literals a, ![]() , or c have the value of 1, no matter which two. Therefore, this function is symmetric and I = {0, 2}. Consider function
, or c have the value of 1, no matter which two. Therefore, this function is symmetric and I = {0, 2}. Consider function ![]() . When a = 0, b = 1, and c = 1, the function evaluates to 1. However, when a = 1, b = 1, and c = 0, which also has two literals being 1, the function fails to evaluate to 1. Therefore, evaluation of this function does depend on which literals have the value of 1. Thus, we conclude, according to Theorem 7.3, that this function is not symmetric with respect to literals a, b, and c.
. When a = 0, b = 1, and c = 1, the function evaluates to 1. However, when a = 1, b = 1, and c = 0, which also has two literals being 1, the function fails to evaluate to 1. Therefore, evaluation of this function does depend on which literals have the value of 1. Thus, we conclude, according to Theorem 7.3, that this function is not symmetric with respect to literals a, b, and c.
Interestingly, if we rewrite the function as a function of literals a, b, and ![]() , and replace
, and replace ![]() with d, we have
with d, we have ![]() , which is symmetric with respect to a, b, and d. That is, the function is symmetric with respect to a, b,
, which is symmetric with respect to a, b, and d. That is, the function is symmetric with respect to a, b, ![]() , but not with respect to a, b, c. This example shows why we need to treat symmetric functions with respect to literals, instead of variables.
, but not with respect to a, b, c. This example shows why we need to treat symmetric functions with respect to literals, instead of variables.
Theorem 7.3 makes sense in that if a function is symmetric, then only the number of literals, not the specific literals, matters in determining the function’s output value, because a symmetric function cannot distinguish literals. Because the number of literals being 1 uniquely determines the function’s value, symmetric functions can be represented succinctly by the set I—in other words, SnI(x1,...,sn), where n denotes the number of variables in the function. For example, symmetric function ![]() is represented as S30.2(a,b,c), and
is represented as S30.2(a,b,c), and ![]() , by S31
, by S31 ![]() .
.
With these notations for symmetric functions, manipulation of symmetric functions becomes easy with Theorem 7.4. Logical operations become set operations on the indices.
Parts 1 and 2 state that ORing and ANDing of two symmetric functions amount to union and intersection of their respective index sets. The ORed result is 1 when at least one of its operands evaluates to 1. This means that the number of literals being 1 in the ORed result is in either or both index sets, giving rise to the union of the index sets. Similar reasoning applies to ANDing. In part 3, ⌝I denotes the complement of the index set I: ⌝I = {1,...,n}-I So, complementing a function amounts to complementing the index set. The complement of a function being 1 means the function itself is 0, meaning the number of literals being 1 is not in the index set. In part 4, n - I = {j : j = n - i, i ∊ I}, and it states that complementing the literals translates to complementing the individual indices.
A Boolean function can also be characterized by its on set, off set, and don’t-care set. An on set is the set of vertices that make the function 1; and an off set, 0. A don’t-care set is the set of vertices on which the function is not specified or a don’t-care. The union of on set, off set, and don’t-care set makes up the universe. If a Boolean function is completely specified, then the don’t-care set is empty; otherwise, the function is incompletely specified.
Representing incompletely specified Boolean functions becomes more complicated because a single incompletely specified Boolean function requires at least two Boolean expressions to represent: one for the on set and the other for the off set or don’t-care set. The matter becomes more so in multiple-output Boolean functions. An example of a multiple-output Boolean function is the next-state function of a finite-state machine with two D-type FFs. The next-state function has two components: f(v) = (f1(v), f2(v)), f1 for the first FF and f2 for the second. A multiple-output Boolean function is also called a vector Boolean function.
To deal with multiple-output Boolean functions, one may suggest treating each component as a function and representing each output function with its on set, off set, and don’t-care set. A difficulty arises when the output of a multiple-output Boolean function takes on more than one value at a given input value. For example, when v = 1011, f(v) can be either 11 or 00. It may be tempting to deduce that 1011 represents a don’t-care point in each of the output functions. The erroneous reasoning is that f1(1011) is either 1 or 0; thus, f1(1011) is a don’t-care. The same reasoning applies to f2(1011). Therefore, f(1011) = (*,*), where * represents a don’t-care. The fallacy is that by assuming that f1(1011) and f2(1011) are don’t-cares, the output don’t-care points include not just 11 and 00, but also 10 and 01, because (*,*) means either component can be any value. However, the problem states that for 1011, the output can be only 11 or 00. The root cause of this difficult is that in this case the multiple-output Boolean function is no longer a function but a relation, because it maps an input value to more than one output value. In the single-output situation, we simply use a don’t-care set to solve this multivalue output problem, but this technique no longer works for the multioutput situation.
To represent a Boolean relation, characteristic function plays a vital role. A characteristic function λ(S) representing set S is defined as follows:
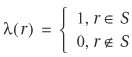
For a Boolean relation with input vector v and output vector w, the characteristic function is λ(v, w) and the set S is all I/O pairs describing the Boolean relation. In other words, λ(v, w) is 1 if w is an output for input v, and it is 0 otherwise.
In this section, we will study some common operators encountered in formal verification. Cofactor operation on function f with respect to a variable x has two phases—a positive and negative phase—denoted by fx and ![]() respectively. Cofactor fx is computed by setting variable x to 1, whereas
respectively. Cofactor fx is computed by setting variable x to 1, whereas ![]() is computed by setting x to 0. Therefore, fx and
is computed by setting x to 0. Therefore, fx and ![]() are functions without variable x. Functions fx and
are functions without variable x. Functions fx and ![]() can be further cofactored with respect to other variables. For example, cofactoring with respect to variable y gives (fx)y, which is written as fxy. It can be shown that fxy = fyx. Function f is related to its cofactors through the following Shannon theorem (Theorem 7.5).
can be further cofactored with respect to other variables. For example, cofactoring with respect to variable y gives (fx)y, which is written as fxy. It can be shown that fxy = fyx. Function f is related to its cofactors through the following Shannon theorem (Theorem 7.5).
This cofactor definition, sometimes called the classic cofactor, is based on a cube; that is, the c in cofactor fc is cube. The generalized cofactor function of a vector Boolean function f, fg, allows g to be any Boolean function and is defined as

where * denotes a don’t-care value. It is tempting to assume that fg is equal to fg, which gives f when g = 1. The following exercise shows that they are not the same.
The Boolean difference of function f with respect to variable x, ![]() , is defined to be
, is defined to be
If the Boolean difference of a function with respect to variable x is identically equal to 0, then the function is independent of x, because the cofactors with respect to x are equal, meaning the function remains the same whether x takes on the value of 1 or 0. Therefore, x is in the minimum support of a function if and only if its Boolean difference is not identically equal to 0.
The concept of Boolean difference is used widely in practice. For example, to determine whether a circuit can detect a stuck-at fault at node x, the decision procedure is equivalent to determining whether there is an input vector v such that
where f is the function of the circuit with the fault site x made as a primary input.
The problem of deciding whether a value v exists such that function f(v, w) evaluates to a specific function g(w) is called the existential problem, and is often denoted by the existential operation as ∃vf(v,w)≡g(w), To compute an existential problem, we simply enumerate all possible values of input v, evaluate the function on each of them, and OR together all outputs. If the result is equal to g(w), then such an input value exists. This procedure of computing existential operation in mathematical form is
where fm(v, w) is a cofactor with respect to minterm m. For instance, if the existential operator is on two variables, x and y, then all minterms are ![]() . This summation can be regarded as a Boolean operation for evaluating the existential operation. This operator, called the smooth operator, is
. This summation can be regarded as a Boolean operation for evaluating the existential operation. This operator, called the smooth operator, is
A special case is when the existential operator is on a single variable, say x. Then the equation becomes ![]()
The counteroperator of the existential operator is the universal operator. An example of an application of a universal operator is deciding whether function f(v, w) is always equal to some specific function g(w) for all values of v. This is denoted by ∀vf(v,w)≡g(w). To compute this universal operation, we can evaluate f(v, w) for each of possible values of v and AND the outputs. If the result is g(w), the answer is yes. Mathematically, the computation is
If the function has a single variable x, ![]()
In computer science literature, finite-state automata are used in the place of finite-state machines, with minor differences. A finite-state automaton accepts input symbols and transits just like a finite-state machine, but it does not produce any output as in a finite-state machine. By adding an output function to an automaton, we have a finite-state machine or a transducer. Furthermore, a finite-state automaton has a set of states designated as acceptance states that do not have a counterpart in finite-state machines.
A finite-state automaton is a mathematical object with five components, or a quintuple, (Q, Σ, δ, q0, F), where Q is the set of states, Σ is the set of input symbols, δ is the transition function with δ: Q×Σ → Q, q0 is an initial state, and F is a set of states designated as acceptance or final states. The transition function δ is based on the current state and an input symbol, and it produces the next state. Another way to represent δ is qi+1 = δ(qi, a), where qi is the present state at cycle i, qi+1 is the next state, and a ∊ Σ is an input symbol.
A transducer or finite-state machine is a 6-tupe (Q, Σ, Λ, δ, μ, q0), where Λ is the set of output symbols and μ is the output function with μ : Q×Σ → Λ. The output function here assumes the Mealy machine model in that the output is a function of both the current state and the input symbol. For a Moore machine, the output function is simply μ : Q → Λ.
A finite-state automaton can be depicted with a state diagram. A state diagram is a directed graph with nodes and directed edges connecting the nodes. A node is a state, and an edge is a transition. An input symbol that activates a transition is placed on an edge. An initial state is marked with a wedge, and an acceptance state is twice-circled node. In a finite-state machine, the output symbol is placed on a node if it depends only on the state (Moore machine); otherwise, it is placed over an edge (a Mealy machine).
So far, the automata and state machines discussed are deterministic, because their states over time can be predicted or determined. A nondeterministic finite-state automaton or finite-state machine, as an extension of the previous definitions, can have more than one initial state, or more than one next state on an input symbol, or a transition on no input symbol. It can be shown that nondeterministic finite-state automata can be transformed into a deterministic finite-state automaton with enlarged state spaces.
A finite-state automaton is completely specified if the next state is specified for every input symbol and every present state. Otherwise, it is incompletely specified. For finite-state machines, the additional requirement is that the output symbol is specified for every state in a Moore machine and for every state and input symbol in a Mealy machine.
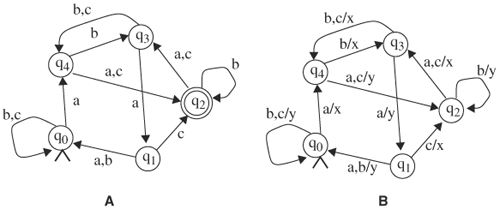
Figure 7.4 shows a nondeterministic finite-state automaton and an incompletely specified finite-state machine. In Figure 7.4A, the automaton has two initial states: q0 and q1. Furthermore, state q1 transits to states q0 and q2 on input symbol b. State q2 can nondeterministically transit to q3, even though no input symbol is present. In Figure 7.4B, ? denotes unspecified output. Furthermore, state q0 does not specify the next state on input symbol c.
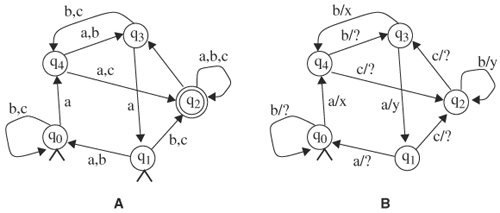
Figure 7.4. (A) A nondeterministic finite-state automaton. (B) An incompletely specified finite-state machine.
An input symbol makes an automaton transit from one state to another. Thus, a string of input symbols causes an automaton or a state machine to make a sequence of state transitions. A string of finite length is accepted if the automaton terminates at a final or acceptance state qf (in other words, qf ∊ F). The set of all accepted strings of an automaton is the language of the automaton.
Using ending states as a condition for acceptance is just one of many possible ways of defining string acceptance and hence the language of an automaton. In fact, different kinds of acceptance conditions give rise to different types of automata. The previous definition of acceptance will not work for defining acceptance of strings of infinite length. As an example of a different kind of acceptance condition, consider the following acceptance condition of infinite strings. An infinite string is accepted if the set of states visited infinitely often is a subset of the final state set F. A state is visited infinitely often if for every N, there is M > N such that the state is visited at cycle M. Automata with this acceptance condition are called Buchi automata. Symbolically, a Buchi automaton is a quintuple, (Q, Σ, δ, q0, F), with the acceptance condition that {q| q is visited infinitely often}⊆F.
Sometimes, one may be curious about situations when infinite strings may arise in practice. Indeed, all hardware machines are designed to function continuously over time, and therefore it is only realistic, although a bit counterintuitive, to assume that all input strings are of infinite length.
A system can consist of more than one finite-state machine that interact with each other. An example is a traffic light controller at a street intersection. There are four controllers required, one for each direction. These four controllers do not operate independently but take into consideration inputs from other controllers. Cars sensed waiting on the north–south-bound intersection prompt the east–west controller to move to red in the next cycle. Sometimes one must model a system of multiple interacting finite-state machines as one single finite-state machine. The resulting overall finite-state machine is called the product finite-state machine.
Given two finite-state machines, M1 = (Q1, Σ1, Λ1, δ1, μ1, q10) and M2 = (Q2, Σ2, Λ2, δ2, μ2, q20), the product machine M = M1×M2 is defined as (Q, Σ, Λ, δ, μ, q0), where

M1 and M2 are called the component machines of M. If Σ1 and Σ2 are identical, then Σ is either Σ1 or Σ2 instead of a Cartesian product of the two.
In a product machine, the size of the state space is the product of the component machines’ state spaces. If M = M1×...×Mn, then
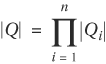
If the component machines have approximately the same state space size, say |Q1|, then |Q| = |Q1|n, which grows rather rapidly. This phenomenon is called state explosion.
In designing a finite-state machine, it is possible that there are equivalent states (in other words, that states are indistinguishable by an external observer who examines only the input strings fed to the machine and the output strings produced by it). These equivalent states can be combined to give a smaller, reachable state space. In this section we will study a method to identify all equivalent states and to produce minimal finite-state machines.
Two states in a finite-state machine are equivalent if for any input string the output strings produced starting from each of the two states are identical. If two states are not equivalent, there must be an input string that drives the machine to produce different output strings starting from either of the two states. For brevity, we say that the input string causes the two states to produce different output strings. Let’s look at an equivalent-state identification algorithm on Mealy machines. With minor modification, the algorithm can be applied to Moore machines.
The algorithm starts out by assuming all states are in one equivalent class, and then successively refines the equivalence class. Let’s use the state machine in Table 7.6 to illustrate the algorithm. The first column is the present state, and the second and third columns are the next states for input x equal to a and b respectively. The outputs are either 0 or 1 and are given after the next states. Initially, all states are assumed to be equivalent. Let’s group them into an equivalent class:
Table 7.6. State Machine for Equivalent-State Identification
PS | NS, x = a | NS, x = b |
|---|---|---|
S1 | S5/1 | S4/1 |
S2 | S5/0 | S4/0 |
S3 | S5/1 | S2/0 |
S4 | S5/0 | S2/0 |
S5 | S3/1 | S5/1 |
From the definition of state equivalence, two states that produce different outputs on the same input are not equivalent. From Table 7.6, we see that on input x = a, S1 and S2 produce different outputs, S1, giving and S2 giving 0. They must not be equivalent. Examining all states for x = a, states S1, S3, and S5 could still belong to the same group because they produce the same output. Similarly, S2 and S4 belong to the same group. Therefore, we can split the initial single group into two groups such that the states within the same group produce the same outputs. We then have
Now we examine the other input value, x = b. States S2, S3, and S4 produce output 0 whereas S1 and S5 produce 1. Thus, S3 and S1 are not equivalent. So, we can split the first group again:
If two states Si and Sj in the same group, on the same input symbol (say, y) transit to two states Ri and Rj that are in two different groups, then Si and Sj cannot be equivalent. The reasoning is as follows. Because Ri and Rj are not equivalent, there is an input string (say, z) that causes Ri and Rj to produce different output strings. The string yz (symbol y followed by string z) will cause Si and Sj to produce different output strings.
Examine the state transition table for the first group, (S1, S5). On input x = a, S1 goes to S5 and S5 goes to S3. Because S5 and S3 are in different groups, based on our reasoning we can conclude that S1 and S5 are not equivalent. So we can split the first group again:
The only group with more than one state is (S2, S4). On x = a, S2 and S4 both go to S5. On x = b, S2 goes to S4 whereas S4 goes to S2. The next states, S4 and S2, are in the same group; thus, no splitting is needed. Up to this point, all groups have been examined and we stop. Because S2 and S4 are in the same group, they are equivalent. Because there are no input strings that can distinguish between S2 and S4, we might as well represent both states with a single state, say S2. Therefore, we simplify the state transition table by replacing S4 with S2. The minimal-state machine is presented in Table 7.7.
Table 7.7. Minimized Finite-State Machine
PS | NS, x = a | NS, x = b |
|---|---|---|
S1 | S5/1 | S2/1 |
S2 | S5/0 | S2/0 |
S3 | S5/1 | S2/0 |
S5 | S3/1 | S5/1 |
The state equivalence identification and state minimization algorithm is summarized here:
We need to understand why states in the same group at the termination of the algorithm are equivalent. Suppose that states S and R are in the same group but are not equivalent. Then there must be an input string that causes S and R to produce different output strings. Let T be the first time the two output strings differ. Let ST be the present state at time T for the run of the machine starting from S. Similarly, let RT be the present state at time T for the run starting from R. Because ST and RT produce different outputs, the algorithm guarantees that they be in different groups. Step 2 of the algorithm also guarantees that the state pair one cycle before ST and RT belongs to different groups. Again, the state pair two cycles before ST and RT also belongs to different groups. Going backward, we will eventually arrive at S and R, and will conclude that S and R must belong to different groups, which is a contradiction.
A rigorous proof is based on mathematical induction on the length of the input string. When the length is 1, step 1 of the algorithm guarantees equivalence of states. Assume that the states produced by the algorithm are equivalent for any string of length less than n. For a string of length n, feed the first symbol to the machine. Two states in the same group will transit to the same group, as ensured by step 2 of the algorithm. Now we have an input string of length less than n. The induction hypothesis guarantees the two states be equivalent. I’ll leave the details of a proof based on mathematical induction to you to determine.
Furthermore, the algorithm finds all equivalent states. If two states are equivalent, then they must belong to the same group at the end of the algorithm. To see why this is so, we notice that initially all states are grouped by their outputs. So these two states must be grouped together in step 1. Because they are equivalent, they will not transit to two different groups; hence, step 2 will not split them. Therefore, they must remain in the same group at the termination of the algorithm.
This grouping of equivalent states can be regarded as a state partition. The state partition produced by the algorithm is unique. That is, if there is another partition of the states, then that partition must be identical to the one produced by the algorithm. Suppose this were not true. There must be two states, S and R, that belong to one group in one partition and belong to two different groups in the other partition. Belonging to two different groups means that they are not equivalent. However, on the other hand, they belong to the same group, meaning they are equivalent—a contradiction. Therefore, the state partition given by the algorithm is unique.
So far, the machine minimization algorithm has been applied only to finite-state machines. It can also be applied to finite-state automata. Because automata do not produce output, the meaning of state equivalence must be redefined. We define two states to be equivalent if the following condition is satisfied: whether the automaton accepts or rejects an input string is independent of which of the two states it starts at. In other words, an accepted (rejected) string by the machine starting at one state is also accepted (rejected) by the machine starting at the other state.
With this definition of state equivalence, the first step of the algorithm is to group final states as one group and the remaining states as another, because states in one group are accepted whereas the others are not. Thus, states in these two groups are not equivalent. Then we examine the next state of the states in each group, on each of the input symbols. Two states transiting to two different groups on the same input symbol are not equivalent, and thus the group must be split. This process continues until no group splitting exists. Just like the algorithm for finite-state machines, the reduced automata produced by combining the equivalent states indicated by this algorithm are minimal and unique.
During the course of a design project, it is sometimes required to determine whether two state machines are equivalent. Two finite-state machines are equivalent if their input and output behavior is identical. Comparing state machines ensures that a state machine, after undergoing a timing enhancement, is functionally equivalent to the original machine. For smaller, deterministic state machines, the following procedure can be used. First, minimize both machines using the previous algorithm. If these two reduced machines are indeed equivalent, there is a one-to-one correspondence between the states in the machines. That is, for every state in the first machine, there is a corresponding state in the second machine such that they play the same role in the machines except for possibly their names (in other words, they are isomorphic). To determine this one-to-one correspondence, assume their initial states correspond to each other. Then for each input symbol, make the next states from the respective initial state correspond to each other if they produce the same output.
When all next states of the initial state have been mapped, continue the same process on the next states of the respective mapped states. If, at the end, all states have been mapped, the two machines are equivalent; otherwise, they are not.
The state mapping step is difficult if the machines are nondeterministic, because there could be more than one initial state or next state, so that the correspondence between states is difficult to determine.
Because finite-state automata or machines can be represented by state diagrams, algorithms on automata and state machines often take the form of graph algorithms. For example, to inquire whether a state can be reached from the initial state, it is a question of whether the state vertex in the state diagram can be reached from the initial state vertex. In this section we will study several graph algorithms commonly encountered during formal verification procedures.
A directed graph or digraph consists of a set of vertices V and a set of directed edges E—in other words, G(V,E). An edge from vertex n to vertex m is represented by (n,m). In the context of a state diagram, the vertices represent states and the edges represent transitions. A vertex has a fanout if there is an edge from the vertex to another vertex, which is called the fanout vertex. A path from vertex n to vertex m is a sequence of alternating vertices and edges, with the first vertex being n and the last vertex m such that the ith edge goes from the ith node to the i + 1st node. Vertex n can be reached from vertex m if there is a path from m to n. Given a node n, the set of all nodes that can be reached from n is called the transitive closure of n.
A basic procedure on a graph is to visit, or traverse, the vertices in a systematic way so that all vertices are visited only once. Two popular traversal algorithms are DFS and breadth-first search (BFS). Let us study DFS first.
DFS starts from an arbitrary vertex, called the root of DFS, selects a fanout vertex, and visits all vertices that can be reached from the fanout vertex before repeating the traversal on the other fanout vertices. A DFS algorithm is shown here. The number N records when a vertex is visited. When a vertex is visited, N is stored in the entry time attribute of the vertex. When a vertex is done visiting, N is stored in the exit time attribute of the vertex. N is included for the sole purpose of showing the order in which the vertices are visited, and hence is not necessarily a part of the algorithm. In a DFS operation, unlike vertices, which are all traversed, not all edges have to be traversed. We will see that all traversed edges form a set of trees, or a forest. A tree is a graph with no loops. The set of traversed edges is called the DFS tree.
In a DFS tree, a vertex is called a parent of another vertex if there is an edge in the DFS tree that starts from the former and goes to the latter. The second vertex is called the child vertex. A vertex A is called a descendant of vertex B if A can be reached from B, following directed edges of the DFS tree. Vertex B is called an ancestor of A. Once a DFS tree or forest is determined, edges in the graph can be classified into the following four types: tree edges, back edges, forward edges, and cross edges. Tree edges are just edges of the DFS tree. Back edges connect descendants to ancestors. Forward edges connect ancestors to descendants. The remaining edges are cross edges.
One application of DFS is to find cycles or loops in a directed graph. Theorem 7.6 provides the necessary and sufficient condition.
Directed cycles are special instances of SCCs. An SCC of a directed graph is a maximal sub-graph such that every vertex can be reached from any other of its vertices. SCCs are an expanded notion of loop. A DAC is a tree or forest, and hence is free of SCCs. It is known that any directed graph can be decomposed into a DAC and SCCs. In other words, this decomposition breaks any directed graph into looping components and straight components. Once a graph is decomposed in such a way and the SCCs are encapsulated, the resulting graph is a DAC and is loop free. SCCs can be determined by applying DFS, as follows:
In step 2 of the algorithm, reversing an edge means making the head of the edge its tail, and vice versa. When applying DFS to this graph, in the while loop of the DFS algorithm, select the unvisited nodes in the order of decreasing exit numbers that were derived in step 1.
A BFS visits vertices level by level. First it selects a vertex, the root of the DFS, as the starting point of the search and visits all its fanout vertices before visiting other vertices. Then the fanout vertices of the recently visited fanout vertices are visited, and so on, until all vertices are visited. If we define the level number of a vertex with respect to the root to be the minimum number of edges from the root to the vertex, then vertices in a BFS are visited according to their level numbers from the root in increasing order, because the level numbers of fanout vertices of a vertex are one more than that of the vertex itself. Similar to DFS, all traversed edges form a BFS tree or forest. A BFS algorithm is as follows:
Input: G(V, E)
Output: a systematic traversal of vertices.
Initialization: N=1 // used to record entry time of a node
BFS (G) {
while (vertex v in V is not marked visited) VISIT(v);
}
VISIT(v) {
mark v visited;
place v in a queue Q.
while (Q is not empty) {
remove head of Q and call it u.
u.entry = N; N = N + 1; // record node entry time
for_each edge (u, r) where r is not yet marked {
mark r;
add (u, r) to the BFS tree;
place r in Q;
} // end of for_each
} // end of while
}
Theorem 7.7 shows two properties about BFS. Because BFS visits vertices in increasing order of level numbers, the first property, a direct result of the search procedure, says that for all edges (n, y) leading to y, the one closest to the root is selected first and thus belongs to a BFS tree. The second property is a consequence of successive manifestations of the first property. A path is made of a sequence of connecting edges. According to property 1, the edges on a BFS tree are the ones closest to the root; therefore, the shortest path from a root to a vertex is the one made of only tree edges in a BFS tree.
In this chapter we reviewed some of the basic mathematics encountered in formal verification. We started with set operations and then defined relations among sets. An especially interesting relation is the equivalence relation, based on which sets can be partitioned. Next we studied partially ordered sets along with meet and join, and introduced lattices.
We then moved to Boolean functions and their representations. We examined CNF, DNF, and multilevel representation. Symmetric Boolean functions have a concise way of representation, and we showed how operations on symmetric functions could be performed easily. For incompletely specified functions, we introduced representation using on set, off set, and don’t-care set. To represent Boolean relations, we used characteristic functions.
We went over several Boolean operators—namely, cofactor, which gives rise to Shannon expansion, generalized cofactor, Boolean difference, and existential and universal operators. In passing, we mentioned the generalized Reed–Muller form.
From the discussion of combinational domain we continued to sequential domain. First we defined finite-state automata, finite-state machines, completely specified, incompletely specified, deterministic, and nondeterministic. A language of an automaton is defined in terms of its acceptance condition. There are various forms of acceptance conditions, some for finite strings and some for infinite strings. Finally, we considered product machines and the state explosion phenomenon.
States may be equivalent in the sense that an external observer would not be able to distinguish the states. We provided an algorithm to determine all equivalent states and to reduce automata and machines to their minimal forms. We also looked at a procedure to determine the isomorphism of deterministic finite-state machines.
Lastly we studied some graph algorithms. We defined common graph terms, then looked at DFS and BFS in detail. We defined a DFS and BFS tree, applied DFS to finding directed cycles and SCCs, and showed how BFS levels nodes and produces the shortest path.
1. | The power set of set S, denoted by 2s, is defined to be the set of all subsets of S.
|
2. | Determine which of the following is an equivalence relation. If it is not an equivalence relation, explain why.
|
3. | Define two relations on the set of all regular polygons inscribed inside a unit cycle with a number of sides less than or equal to a constant N.
|
4. | Determine support, minimum support, and Boolean difference.
|
5. | Convert the following DNF to CNF. What is the ratio of the number of literals in DNF to that of CNF? |
6. | Prove or disprove |
7. | Determine whether the following function is symmetric. If it is symmetric, represent it using short-hand notation. Determine the complement of the function. |
8. | Represent the following Boolean functions/relations using characteristic functions.
|
9. | The output of a two-input combinational circuit, (f, g), is described by vector Boolean function |
10. | A finite-state machine’s next-state function is given by (f,g) = (as + br,b(r + as)), where a and b are inputs, and r and s are state bits.
|
11. | Derive a generalized Reed–Muller representation for the following function: |
12. | Review generalized cofactor calculation.
|
13. | Decide whether the following CNF can be satisfied (in other words, equal to 1). |
14. | Represent the finite-state machine’s transition function and output in Table 7.9 using characteristic functions. |
15. | Study product machines of nondeterministic and deterministic component machines.
|
16. | For the finite-state machine represented in Table 7.10, minimize the machine. |
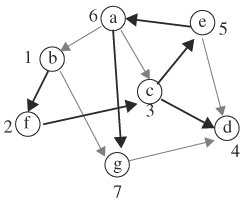
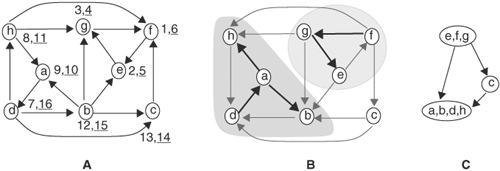
17. | Perform a DFS on the graph in Figure 7.15. Choose vertex a as the root of the DFS. Label the DFS tree. List the forward edges, back edges, and cross edges. |
18. | Find all SCCs in Figure 7.15. |
19. | Perform a BFS on Figure 7.15, with the BFS root being vertex a. Show the BFS tree and rearrange the vertices in levels according to the BFS. |
20. | Represent the graph in Figure 7.16 using a characteristic function. From the characteristic function, find a Boolean expression for all paths of length 2 between vertices x and y. Each edge is of length 1. |
[1] Miltersen, et al, “On Converging CNF to DNF,” Mathematical Foundations of Computer Science: 28th International Symposium, Bratislava, Slovakia, August 25–29, 2003, Lecture Notes in Computer Science 2747, 612–21.