1
COMPUTING CONCEPTS

Computers are everywhere now: in our homes, our schools, our offices—you might find a computer in your pocket, on your wrist, or even in your refrigerator. It’s easier than ever to find and use computers, but few people today really understand how computers work. This isn’t surprising, since learning the complexities of computing can be overwhelming. The goal of this book is to lay out the foundational principles of computing in a way that anyone with curiosity, and a bit of a technical bent, can follow. Before we dig into the nuts and bolts of how computers work, let’s take some time to get familiar with some major concepts of computing.
In this chapter we’ll begin by discussing the definition of a computer. From there, we’ll cover the differences between analog and digital data and then explore number systems and the terminology used to describe digital data.
Defining a Computer
Let’s start with a basic question: what is a computer? When people hear the word computer, most think of a laptop or desktop, sometimes referred to as a personal computer or PC. That is one class of device that this book covers, but let’s think a bit more broadly. Consider smartphones. Smartphones are certainly computers; they perform the same types of operations as PCs. In fact, for many people today, a smartphone is their primary computing device. Most computer users today also rely on the internet, which is powered by servers—another type of computer. Every time you visit a website or use an app that connects to the internet, you’re interacting with one or more servers connected to a global network. Video game consoles, fitness trackers, smart watches, smart televisions … all of these are computers!
A computer is any electronic device that can be programmed to carry out a set of logical instructions. With that definition in mind, it becomes clear that many modern devices are in fact computers!
Analog and Digital
You’ve probably heard a computer described as a digital device. This is in contrast to an analog device, such as a mechanical clock. But what do these two terms really mean? Understanding the differences between analog and digital is foundational to understanding computing, so let’s take a closer look at these two concepts.
The Analog Approach
Look around you. Pick an object. Ask yourself: What color is it? What size is it? How much does it weigh? By answering these questions, you’re describing the attributes, or data, of that object. Now, pick a different object and answer the same questions. If you repeat this process for even more objects, you’ll find that for each question, the potential answers are numerous. You might pick up a red object, a yellow object, or a blue object. Or the object could be a mix of the primary colors. This type of variation does not only apply to color. For a given property, the variations found across the objects in our world are potentially infinite.
It’s one thing to describe an object verbally, but let’s say you want to measure one of its attributes more precisely. If you wanted to measure an object’s weight, for example, you could put it on a scale. The scale, responding to the weight placed upon it, would move a needle along a numbered line, stopping when it reaches a position that corresponds to the weight. Read the number from the scale and you have the object’s weight.
This kind of measurement is common, but let’s think a little more about how we’re measuring this data. The position of the needle on the scale isn’t actually the weight; it’s a representation of the weight. The numbered line that the needle points to provides a means for us to easily convert between the needle’s position, representing a weight, and the numeric value of that weight. In other words, though the weight is an attribute of the object, here we can understand that attribute through something else: the position of the needle along the line. The needle’s position changes proportionally in response to the weight placed on the scale. Thus, the scale is working as an analogy where we understand the weight of the object through the needle’s position on the line. This is why we call this method of measuring the analog approach.
Another example of an analog measuring tool is a mercury thermometer. Mercury’s volume increases with temperature. Thermometer manufacturers utilize this property by placing mercury in a glass tube with markings that correspond to the expected volume of the mercury at various temperatures. Thus, the position of mercury in the tube serves as a representation of temperature. Notice that for both of these examples (a scale and a thermometer), when we make a measurement, we can use markings on the instrument to convert a position to a specific numeric value. But the value we read from the instrument is just an approximation. The true position of the needle or mercury can be anywhere within the range of the instrument, and we round up or down to the nearest marked value. So although it may seem that these tools can produce only a finite set of measurements, that’s a limitation imposed by the conversion to a number, not by the analogy itself.
Throughout most of human history, humans have measured things using an analog approach. But people don’t only use analog approaches for measurement. They’ve also devised clever ways to store data in an analog fashion. A phonograph record uses a modulated groove as an analog representation of audio that was recorded. The groove’s shape changes along its path in a way that corresponds to changes in the shape of the audio waveform over time. The groove isn’t the audio itself, but it’s an analogy of the original sound’s waveform. Film-based cameras do something similar by briefly exposing film to light from a camera lens, leading to a chemical change in the film. The chemical properties of the film are not the image itself, but a representation of the captured image, an analogy of the image.
Going Digital
What does all this have to do with computing? It turns out that all those analog representations of data are hard for computers to deal with. The types of analog systems used are so different and variable that creating a common computing device that can understand all of them is nearly impossible. For example, creating a machine that can measure the volume of mercury is a very different task than creating a machine that can read the grooves on a vinyl disc. Additionally, computers require highly reliable and accurate representations of certain types of data, such as numeric data sets and software programs. Analog representations of data can be difficult to measure precisely, tend to decay over time, and lose fidelity when copied. Computers need a way to represent all types of data in a format that can be accurately processed, stored, and copied.
If we don’t want to represent data as something with potentially infinitely varying analog values, what can we do? We can use a digital approach instead. A digital system represents data as a sequence of symbols, where each symbol is one of a limited set of values. Now, that description may sound a bit formal and a bit confusing, so rather than go deep on the theory of digital systems, I’ll explain what this means in practice. In almost all of today’s computers, data is represented with combinations of two symbols: 0 and 1. That’s it. Although a digital system could use more than two symbols, adding more symbols would increase the complexity and cost of the system. A set of only two symbols allows for simplified hardware and improved reliability. All data in most modern computing devices is represented as a sequence of 0s and 1s. From this point forward in this book, when I talk about digital computers, you can assume that I am talking about systems that only deal with 0s and 1s and not some other set of symbols. Nice and simple!
It’s a point worth repeating: everything on your computer is stored as 0s and 1s. The last photo you took on your smartphone? Your device stored the photo as a sequence of 0s and 1s. The song you streamed from the internet? 0s and 1s. The document you wrote on your computer? 0s and 1s. The app you installed? It was a bunch of 0s and 1s. The website you visited? 0s and 1s.
It may sound limiting to say that we can only use 0 and 1 to represent the infinite values found in nature. How can a musical recording or a detailed photograph be distilled down to 0s and 1s? Many find it counterintuitive that such a limited “vocabulary” can be used to express complex ideas. The key here is that digital systems use a sequence of 0s and 1s. A digital photograph, for example, usually consists of millions of 0s and 1s.
So what exactly are these 0s and 1s? You may see other terms used to describe these 0s and 1s: false and true, off and on, low and high, and so forth. This is because the computer doesn’t literally store the number 0 or 1. It stores a sequence of entries where each entry in the sequence can have only two possible states. Each entry is like a light switch that is either on or off. In practice, these sequences of 1s and 0s are stored in various ways. On a CD or DVD, the 0s and 1s are stored on the disc as bumps (0) or flat spaces (1). On a flash drive, the 1s and 0s are stored as electrical charges. A hard disk drive stores the 0s and 1s using magnetization. As you’ll see in Chapter 4, digital circuits represent 0s and 1s using voltage levels.
Before we move on, one final note on the term analog—it’s often used to simply mean “not digital.” For example, engineers may speak of an “analog signal,” meaning a signal that varies continuously and doesn’t align to digital values. In other words, it’s a non-digital signal but doesn’t necessarily represent an analogy of something else. So, when you see the term analog, consider that it might not always mean what you think.
Number Systems
So far, we’ve established that computers are digital machines that deal with 0s and 1s. For many people, this concept seems strange; they’re used to having 0 through 9 at their disposal when representing numbers. If we constrain ourselves to only two symbols, rather than ten, how should we represent large numbers? To answer that question, let’s back up and review an elementary school math topic: number systems.
Decimal Numbers
We typically write numbers using something called decimal place-value notation. Let’s break that down. Place-value notation (or positional notation) means that each position in a written number represents a different order of magnitude; decimal, or base 10, means that the orders of magnitude are factors of 10, and each place can have one of ten different symbols, 0 through 9. Look at the example of place-value notation in Figure 1-1.

Figure 1-1: Two hundred seventy-five represented in decimal place-value notation
In Figure 1-1, the number two hundred seventy-five is written in decimal notation as 275. The 5 is in the ones place, meaning its value is 5 × 1 = 5. The 7 is in the tens place, meaning its value is 7 × 10 = 70. The 2 is in the hundreds place, meaning its value is 2 × 100 = 200. The total value is the sum of all the places: 5 + 70 + 200 = 275.
Easy, right? You’ve probably understood this since first grade. But let’s examine this a bit closer. Why is the rightmost place the ones place? And why is the next place the tens place, and so on? It’s because we are working in decimal, or base 10, and therefore each place is a power of ten—in other words, 10 multiplied by itself a certain number of times. As seen in Figure 1-2, the rightmost place is 10 raised to 0, which is 1, because any number raised to 0 is 1. The next place is 10 raised to 1, which is 10, and the next place is 10 raised to 2 (10 × 10), which is 100.
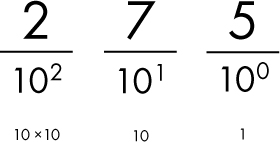
Figure 1-2: In decimal place-value notation, each place is a power of ten.
If we needed to represent a number larger than 999 in decimal, we’d add another place to the left, the thousands place, and its weight would be equal to 10 raised to 3 (10 × 10 × 10), which is 1,000. This pattern continues so that we can represent any large whole number by adding more places as needed.
We’ve established why the various places have certain weights, but let’s keep digging. Why does each place use the symbols 0 through 9? When working in decimal, we can only have ten symbols, because by definition each place can only represent ten different values. 0 through 9 are the symbols that are currently used, but really any set of ten unique symbols could be used, with each symbol corresponding to a certain numeric value.
Most humans prefer decimal, base 10, as a number system. Some say this is because we have ten fingers and ten toes, but whatever the reason, in the modern world most people read, write, and think of numbers in decimal. Of course, that’s just a convention we’ve collectively chosen to represent numbers. As we covered earlier, that convention doesn’t apply to computers, which instead use only two symbols. Let’s see how we can apply the principles of the place-value system while constraining ourselves to only two symbols.
Binary Numbers
The number system consisting of only two symbols is base 2, or binary. Binary is still a place-value system, so the fundamental mechanics are the same as decimal, but there are a couple of changes. First, each place represents a power of 2, rather than a power of 10. Second, each place can only have one of two symbols, rather than ten. Those two symbols are 0 and 1. Figure 1-3 has an example of how we’d represent a number using binary.

Figure 1-3: Five decimal represented in binary place-value notation
In Figure 1-3, we have a binary number: 101. That may look like one hundred and one to you, but when dealing in binary, this is actually a representation of five! If you wish to verbally say it, “one zero one binary” would be a good way to communicate what is written.
Just like in decimal, each place has a weight equal to the base raised to various powers. Since we are in base 2, the rightmost place is 2 raised to 0, which is 1. The next place is 2 raised to 1, which is 2, and the next place is 2 raised to 2 (2 × 2), which is 4. Also, just like in decimal, to get the total value, we multiply the symbol in each place by the place-value weight and sum the results. So, starting from the right, we have (1 × 1) + (0 × 2) + (1 × 4) = 5.
Now you can try converting from binary to decimal yourself.
You can check your answers in Appendix A. Did you get them right? The last one might have been a bit tricky, since it introduced another place to the left, the eights place. Now, try going the other way around, from decimal to binary.
I hope you got those correct too! Right away, you can see that dealing with both decimal and binary at the same time can be confusing, since a number like 10 represents ten in decimal or two in binary. From this point forward in the book, if there’s a chance of confusion, binary numbers will be written with a 0b prefix. I’ve chosen the 0b prefix because several programming languages use this approach. The leading 0 (zero) character indicates a numeric value and the b is short for binary. As an example, 0b10 represents two in binary, whereas 10, with no prefix, means ten in decimal.
Bits and Bytes
A single place or symbol in a decimal number is called a digit. A decimal number like 1,247 is a four-digit number. Similarly, a single place or symbol in a binary number is called a bit (a binary digit). Each bit can either be 0 or 1. A binary number like 0b110 is a 3-bit number.
A single bit cannot convey much information; it’s either off or on, 0 or 1. We need a sequence of bits to represent anything more complex. To make these sequences of bits easier to manage, computers group bits together in sets of eight, called bytes. Here are some examples of bits and bytes (leaving off the 0b prefix since they are all binary):
1 That’s a bit.
0 That is also a bit.
11001110 That’s a byte, or 8 bits.
00111000 That’s also a byte!
10100101 Yet another byte.
0011100010100101 That’s two bytes, or 16 bits.
NOTE
Fun fact: A 4-bit number, half a byte, is sometimes called a nibble (sometimes spelled nybble or nyble).
So how much data can we store in a byte? Another way to think about this question is how many unique combinations of 0s and 1s can we make with our 8 bits? Before we answer that question, let me illustrate with only 4 bits, as it’ll be easier to visualize.
In Table 1-1, I’ve listed all the possible combination of 0s and 1s in a 4-bit number. I’ve also included the corresponding decimal representation of that number.
Table 1-1: All Possible Values of a 4-bit Number
Binary |
Decimal |
|---|---|
0000 |
0 |
0001 |
1 |
0010 |
2 |
0011 |
3 |
0100 |
4 |
0101 |
5 |
0110 |
6 |
0111 |
7 |
1000 |
8 |
1001 |
9 |
1010 |
10 |
1011 |
11 |
1100 |
12 |
1101 |
13 |
1110 |
14 |
1111 |
15 |
As you can see in Table 1-1, we can represent 16 unique combinations of 0s and 1s in a 4-bit number, ranging in decimal value from 0 to 15. Seeing the list of combinations of bits helps to illustrate this, but we could have figured this out in a couple of ways without enumerating every possible combination.
We could determine the largest possible number that 4 bits can represent by setting all the bits to one, giving us 0b1111. That is 15 in decimal; if we add 1 to account for representing 0, then we come to our total of 16. Another shortcut is to raise 2 to the number of bits, 4 in this case, which gives us 24 = 2 × 2 × 2 × 2 = 16 total combinations of 0s and 1s.
Looking at 4 bits is a good start, but previously we were talking about bytes, which contain 8 bits. Using the preceding approach, we could list out all combinations of 0s and 1s, but let’s skip that step and go straight to a shortcut. Raise 2 to the power of 8 and you get 256, so that’s the number of unique combinations of bits in a byte.
Now we know that a 4-bit number allows for 16 combinations of 0s and 1s, and a byte allows for 256 combinations. What does that have to do with computing? Let’s say that a computer game has 12 levels; the game could easily store the current level number in only 4 bits. On the other hand, if the game has 99 levels, 4 bits won’t be enough … only 16 levels could be represented! A byte, on the other hand, would handle that 99-level requirement just fine. Computer engineers sometimes need to consider how many bits or bytes will be needed for storage of data.
Prefixes
Representing complex data types takes a large number of bits. Something as simple as the number 99 won’t require more than a byte; a video in a digital format, on the other hand, can require billions of bits. To more easily communicate the size of data, we use prefixes like giga- and mega-. The International System of Units (SI), also known as the metric system, defines a set of standard prefixes. These prefixes are used to describe anything that can be quantified, not just bits. We’ll see them again in upcoming chapters dealing with electrical circuits. Table 1-2 lists some of the common SI prefixes and their meanings.
Table 1-2: Common SI Prefixes
Prefix name |
Prefix symbol |
Value |
Base 10 |
English word |
|---|---|---|---|---|
tera |
T |
1,000,000,000,000 |
1012 |
trillion |
giga |
G |
1,000,000,000 |
109 |
billion |
mega |
M |
1,000,000 |
106 |
million |
kilo |
k |
1,000 |
103 |
thousand |
centi |
c |
0.01 |
10-2 |
hundredth |
milli |
m |
0.001 |
10-3 |
thousandth |
micro |
μ |
0.000001 |
10-6 |
millionth |
nano |
n |
0.000000001 |
10-9 |
billionth |
pico |
p |
0.000000000001 |
10-12 |
trillionth |
With these prefixes, if we want to say “3 billion bytes,” we can use the shorthand 3GB. Or if we want to represent 4 thousand bits, we can say 4kb. Note the uppercase B for byte and lowercase b for bit.
You’ll find that this convention is commonly used to represent quantities of bits and bytes. Unfortunately, it’s also often technically incorrect. Here’s why: when dealing with bytes, most software is actually working in base 2, not base 10. If your computer tells you that a file is 1MB in size, it is actually 1,048,576 bytes! That is approximately one million, but not quite. Seems like an odd number, doesn’t it? That’s because we are looking at it in decimal. In binary, that same number is expressed as 0b100000000000000000000. It’s a power of two, specifically 220. Table 1-3 shows how to interpret the SI prefixes when dealing with bytes.
Table 1-3: SI Prefix Meaning When Applied to Bytes
Prefix name |
Prefix symbol |
Value |
Base 2 |
|---|---|---|---|
tera |
T |
1,099,511,627,776 |
240 |
giga |
G |
1,073,741,824 |
230 |
mega |
M |
1,048,576 |
220 |
kilo |
k |
1,024 |
210 |
Another point of confusion with bits and bytes relates to network transfer rates. Internet service providers usually advertise in bits per second, base 10. So, if you get 50 megabits per second from your internet connection, that means you can only transfer about 6 megabytes per second. That is, 50,000,000 bits per second divided by 8 bits per byte gives us 6,250,000 bytes per second. Divide 6,250,000 by 220 and we get about 6 megabytes per second.
Hexadecimal
Before we leave the topic of thinking in binary, I’ll cover one more number system: hexadecimal. Quickly reviewing, our “normal” number system is decimal, or base 10. Computers use binary, or base 2. Hexadecimal is base 16! Given what you’ve already learned in this chapter, you probably know what that means. Hexadecimal, or just hex for short, is a place-value system where each place represents a power of 16, and each place can be one of 16 symbols.
As in all place-value systems, the rightmost place will still be the ones place. The next place to the left will be the sixteens place, then the 256s (16 × 16) place, then the 4,096s (16 × 16 × 16) place, and so on. Simple enough. But what about the other requirement that each place can be one of 16 symbols? We usually have ten symbols to use to represent numbers, 0 through 9. We need to add six more symbols to represent the other values. We could pick some random symbols like & @ #, but these symbols have no obvious order. Instead, the standard is to use A, B, C, D, E, and F (either uppercase or lowercase is fine!). In this scheme, A represents ten, B represents eleven, and so on, up to F, which represents fifteen. That makes sense; we need symbols that represent zero through one less than the base. So our extra symbols are A through F. It’s standard practice to use the prefix 0x to indicate hexadecimal, when needed for clarity. Table 1-5 lists each of the 16 hexadecimal symbols, along with their decimal and binary equivalents.
Table 1-5: Hexadecimal Symbols
Hexadecimal |
Decimal |
Binary (4-bit) |
|---|---|---|
0 |
0 |
0000 |
1 |
1 |
0001 |
2 |
2 |
0010 |
3 |
3 |
0011 |
4 |
4 |
0100 |
5 |
5 |
0101 |
6 |
6 |
0110 |
7 |
7 |
0111 |
8 |
8 |
1000 |
9 |
9 |
1001 |
A |
10 |
1010 |
B |
11 |
1011 |
C |
12 |
1100 |
D |
13 |
1101 |
E |
14 |
1110 |
F |
15 |
1111 |
What happens when you need to count higher than 15 decimal or 0xF? Just like in decimal, we add another place. After 0xF comes 0x10, which is 16 decimal. Then 0x11, 0x12, 0x13, and so on. Now take a look at Figure 1-4, where we see a larger hexadecimal number, 0x1A5.
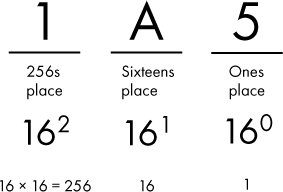
Figure 1-4: Hexadecimal number 0x1A5 broken out by place value
In Figure 1-4 we have the number 0x1A5 in hexadecimal. What’s the value of this number in decimal? The rightmost place is worth 5. The next place has a weight of 16, and there’s an A there, which is 10 in decimal, so the middle place is worth 16 × 10 = 160. The leftmost place has a weight of 256, and there’s a 1 in that place, so that place is worth 256. The total value then is 5 + 160 + 256 = 421 in decimal.
Just to reinforce the point, this example shows how the new symbols, like A, have a different value depending on the place in which they appear. 0xA is 10 decimal, but 0xA0 is 160 in decimal, because the A appears in the sixteens place.
At this point you may be saying to yourself “great, but what use is this?” I’m glad you asked. Computers don’t use hexadecimal, and neither do most people. And yet, hexadecimal is very useful for people who need to work in binary.
Using hexadecimal helps overcome two common difficulties with working in binary. First, most people are terrible at reading long sequences of 0s and 1s. After a while the bits all run together. Dealing with 16 or more bits is tedious and error-prone for humans. The second problem is that although people are good at working in decimal, converting between decimal and binary isn’t easy. It’s tough for most people to look at a decimal number and quickly tell which bits would be 1 or 0 if that number were represented in binary. But with hexadecimal, conversions to binary are much more straightforward. Table 1-6 provides a couple of examples of 16-bit binary numbers and their corresponding hexadecimal and decimal representations. Note that I’ve added spaces to the binary values for clarity.
Table 1-6: Examples of 16-bit Binary Numbers as Decimal and Hexadecimal
|
Example 1 |
Example 2 |
|---|---|---|
Binary |
1111 0000 0000 1111 |
1000 1000 1000 0001 |
Hexadecimal |
F00F |
8881 |
Decimal |
61,455 |
34,945 |
Consider Example 1 in Table 1-6. In binary, there’s a clear sequence: the first four bits are 1, the next eight bits are 0, and the last four bits are 1. In decimal, this sequence is obscured. It isn’t clear at all from looking at 61,455 which bits might be set to 0 or 1. Hexadecimal, on the other hand, mirrors the sequence in binary. The first hex symbol is F (which is 1111 in binary), the next two hex symbols are 0, and the final hex symbol is F.
Continuing to Example 2, the first three sets of four bits are all 1000 and the final set of four bits is 0001. That’s easy to see in binary, but rather hard to see in decimal. Hexadecimal provides a clearer picture, with the hexadecimal symbol of 8 corresponding to 1000 in binary and the hexadecimal symbol of 1 corresponding to, well, 1!
I hope you are seeing a pattern emerge: every four bits in binary correspond to one symbol in hexadecimal. If you remember, four bits is half a byte (or a nibble). Therefore, a byte can be easily represented with two hexadecimal symbols. A 16-bit number can be represented with four hex symbols, a 32-bit number with eight hex symbols, and so on. Let’s take the 32-bit number in Figure 1-5 as an example.

Figure 1-5: Each hexadecimal character maps to 4 bits
In Figure 1-5 we can digest this rather long number one half-byte at a time, something that isn’t possible using a decimal representation of the same number (2,320,695,040).
Because it’s relatively easy to move between binary and hex, many engineers will often use the two in tandem, converting to decimal numbers only when necessary. I’ll use hexadecimal later in this book where it makes sense.
Try converting from binary to hexadecimal without going through the intermediate step of converting to decimal.
Once you have the hang of binary to hexadecimal, try going the other way, from hex to binary.
Summary
In this chapter, we covered some of the foundational concepts of computing. You learned that a computer is any electronic device that can be programmed to carry out a set of logical instructions. You then saw that modern computers are digital devices rather than analog devices, and you learned the difference between the two: analog systems are those that use widely varying values to represent data, whereas digital systems represent data as a sequence of symbols. After that, we explored how modern digital computers rely on only two symbols, 0 and 1, and learned about a number system consisting of only two symbols, base 2, or binary. We covered bits, bytes, and the standard SI prefixes (giga-, mega-, kilo-, and so on) you can use to more easily describe the size of data. Lastly, you learned how hexadecimal is useful for people who need to work in binary.
In the next chapter we’ll look more closely at how binary is used in digital systems. We’ll take a look at how binary can be used to represent various types of data, and we’ll see how binary logic works.
