CHAPTER 7 Encryption Controls
Overview
Encryption is one of the core operational technologies used in information security. In its essential form, it helps provide confidentiality of information. Through innovative application, encryption can also confirm the integrity of information and the identity of the sender. Every commercial transaction performed over the Internet uses encryption to maintain information security. Encryption ensures that financial information such as credit card numbers sent over the Internet are not stolen during transit. In many cases, encryption is not only appropriate but also required by federal law. Encryption is therefore an essential part of the modern commercial infrastructure. In this chapter, we introduce the fundamentals of encryption technologies. We also discuss the operational challenges in implementing encryption and solutions that have been developed to address these challenges. At the end of this chapter, you should know:
- The three types of encryption commonly used and their most appropriate uses
- The standard, practical implementation of encryption technologies used in information exchange
- The alternate use of encryption technologies to verify identities in the form of certificates
- The infrastructure (PKI) that has been developed to make encryption convenient and practical
Introduction
What do we expect when we send information over the Internet? We certainly want the information to reach the receiver.1 However, is that enough? What if the message is – “I do not have money to pay the tuition bill this semester. Please transfer $1,000 into my checking account #0000101010 at the credit union, routing number 123456789. In case of any difficulty, the password is ‘hello123’.”
In the information security world, it is common to use the names Alice and Bob as the sender and receiver of messages when discussing secure communications.2 In our example above, say, Alice wants to send the message to Bob. What features would Alice desire in the communication? For one, she would like the message to reach Bob. Second, she probably would prefer that only Bob understand the message, even if her friends can see or hear the conversation. (After all, who wants their friends to know they have run out of money?) Upon receipt of the message, Bob is likely to want confirmation that the message came from Alice. Bob may also seek confirmation that the contents of the message are correct. Encryption cannot actually transmit the message, but encryption gives us all the other desired features in the communication between Alice and Bob. Adapting a well-known commercial, there are some things information security cannot do; for everything else, there is encryption.
At a high level of description, encryption converts the message into a form that only the receiver can decode, providing confidentiality. While decoding, the receiver can also detect if the message was modified during transit, providing integrity. Since encryption is so useful, it is used as the information security analog of a Swiss army knife. If information security is involved, chances are: encryption is being in some form or the other.
Encryption basics
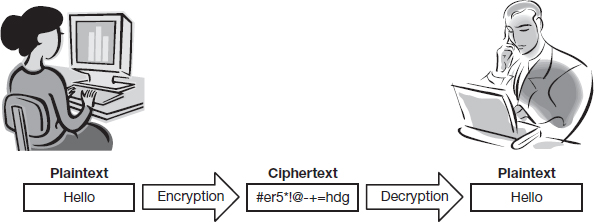
Encryption means to crypt and is accomplished through cryptography. Cryptography is a compound word created from the Greek words crypto (κρυπτo) and graphy (γραφη). “Crypto” means hidden and “graphy” means writing, and cryptography is the act of hidden writing. The ATIS telecom glossary, our standard source for definitions, defines encryption as the cryptographic transformation of data to produce ciphertext. This definition introduces two new terms – cryptography and ciphertext. We have already seen that cryptography is the act of hidden writing. More formally, based on the ATIS telecom glossary, we can define cryptography as the art or science of rendering plain information unintelligible, and for restoring encrypted information to intelligible form. Ciphertext is the encrypted text that is unintelligible to the reader. The etymology of ciphertext is based on the Arabic word cifr, meaning nothing. The word cifr was later also used to represent the number 0. At the receiving end, decryption is used to decipher3 the hidden message.
Figure 7.1 integrates these activities and shows the overall process of secure communication between Alice and Bob.
For all its utility, it is useful to remember that encryption can only do so much. A bolt cutter will break any lock, and a user who is willing to share his password will compromise any encryption scheme.
Origins
The first documented instance of encryption was used by Roman Emperor Julius Caesar (100 Bc –44 Bc). Figure 7.2 is an extract from the translated work where the encryption method is described;4 thus, “if there was occasion for secrecy, he used the alphabet in such a manner that not a single word could be made out. The way to decipher those epistles was to substitute d for a, and so of the other letters respectively.”
Thus, in the Caesar cipher, each letter was replaced by the letter three places to the right of the letter in the alphabet. Thus A → D; B → E, …, Q → T, …, W → Z, X → A, Y → B, Z → C. While Caesar always used a shift of three letters, we could just as easily use other shifts. For example, a shift of four characters to the right would give us an encryption scheme such as A → E; B → F.
This simple example illustrates an extremely important concept in encryption – keys. We will shortly have more to say about keys and their significance.
In fact, the method can be generalized even further. The letters do not need to be shifted by the same amount. Any mapping from one letter to another letter would work as an encryption scheme. For example, A → H; B → X, C → B … would be equally effective. In fact, this encryption scheme of replacing individual letters with other letters for the purpose of encryption is known in the security literature as mono-alphabetic substitution.
This example illustrates a very important building block of many encryption technologies – substitution. We will shortly illustrate how substitution is used in modern encryption technologies.
While encryption ensures the confidentiality of the data, this confidentiality is not always desired. There are currently malware in use that will encrypt data in a computer and keep it encrypted until a payment is made to the hacker. This type of malware is known as “ransomware.” Encryption poses a problem for security experts engaged in data forensics by obscuring the details of a security incident. It also hinders the use of firewalls and other network devices based on deep packet inspection in order to allow or block a specific data stream. If the data contained in a packet is encrypted, it cannot be inspected.
Encryption requirements analysis
What are the requirements that a good encryption technique should meet? Generally speaking, encryption techniques share many properties with locks and good encryption techniques are similar to good locks in many ways. What do we expect in good locks? First, we expect them to be easy to use for owners. Second, we expect them to be difficult to break for intruders. While most locks can eventually be broken, locks only need to either take long enough to break to draw the attention of onlookers or be too expensive to break to be worth the effort.
Good encryption techniques also share these properties. We expect a good encryption technique to be easy to use for authorized senders and receivers of the information. We also expect that unauthorized users will take so much time to break the encryption that they will either give up or their actions will be noticed before they succeed.
In information security, effort is measured in terms of computational requirements. A good encryption scheme will require minimal computations by authorized users to read and write data, but impossibly large number of computations from unauthorized users.
Creators of encryption techniques have to worry about the fact that intruders can be pretty smart about trying to break encryption schemes. The art of breaking ciphertext is called cryptanalysis. For example, if we use mono-alphabetic substitution with the English alphabet, we can use the fact that some letters are known to be more common than others (e.g., e > t > a > I > o > n > s > h > r > d > l > u) to guess the encryption scheme simply from a count of the letters and their relative frequencies. With this knowledge, it is estimated that a mono-alphabetic encryption scheme can be broken with a corpus of only approximately 600 encrypted characters. If we also guess probable words, only about 150 letters are needed. Attackers may even try to send selective plaintext and see how the encryption works. For example, sending “BAT” and “CAT” can indicate how a change in one letter in the plain text affects the encryption outcome, providing hints at breaking the encryption.
Keys
Just as it is not simple to come up with locking mechanisms that are easy and economical for authorized users, but difficult to break for unauthorized users, it is not easy to come up with encryption techniques with similar properties. Look around, how many different kinds of locks are there? There are key locks, combination locks, biometric locks, and perhaps some other types of locks. These few lock types secure all the gates and safes in the world. Similarly, just a few encryption techniques secure all the information in the world.
Returning to the lock analogy, if there are only a few good lock types, how do we use the same lock type to secure all homes in a neighborhood? After all, it wouldn't be very helpful if the method that opened one door also opened all other doors in the neighborhood. This brings us to keys – locks are made unique by keys. The key that opens any given lock is unique to the lock.
The encryption analog to a lock type is a cryptographic algorithm, algorithm for short. A cryptographic algorithm is a well-defined sequence of steps used to describe cryptographic processes. Generally, we just call them algorithms. A few good algorithms with all the desired properties have been discovered so far. Each instance of the chosen algorithm is made unique by a unique set of numbers, which are called a key. In the context of encryption, a key is a sequence of symbols that control the operations of encipherment and decipherment. Users with the correct key can easily exchange information with each other. Eavesdroppers will take a prohibitively long time guessing the correct key.
What are the properties of a good key? As we have repeatedly stated, a good key should be difficult to guess. In the encryption context, keys are broken by simply trying different keys until the correct one is found. If we use 1-digit keys, we have 10 possible keys (0, 1, …, 9). If an intruder takes about 1 second to try one key, he will require at most 10 seconds to guess the correct key. If the process were repeated many times, the average time would be half of this, or 5 seconds. This is because on some occasions the first guess would be right, on others it may be the sixth guess, and so on. To improve security, we could try 2-digit numbers. This increases the number of possible keys to 100 (0–99). At the same rate as before, the intruder would now take 100 seconds at most, and 50 seconds on average. Thus, longer keys improve security.
Since computers can compute and check many hundreds of thousands of keys a second, the keys used in practice are hundreds of digits long.
General algorithm properties
The encryption requirements in the previous paragraphs suggest some important properties of good crypto-algorithms. They may be seen as a process of randomizing input. Input (plaintext) typically has structure in the form of words, images, documents, etc. We have seen that if an intruder can guess any part of the internal structure of the plaintext, that information will be exploited to decode the ciphertext. Therefore, the encryption algorithm must make the ciphertext appear to be a completely random sequence of bits. However, the randomization must be recoverable to the user in possession of the correct key.
Not only should the actual characters in the message appear random, even the length of the ciphertext must appear to be random to an intruder. If not, in certain situations, the intruder might be able to guess the content of the message simply by looking at the length of the message and the context. For example, if you know that in a certain situation, the only two possible messages are “yes” and “no,” and you see an encrypted message that reads “!$#,” you do not need to decipher the message to know with certainty that the plaintext was “yes.”
Finally, another important property of algorithms is that a change in even 1 bit of the input should completely change the ciphertext, changing at least half the bits. This will prevent an intruder from trying to craft selective messages and try to guess the encryption scheme by looking at the ciphertext output.
At this point, we know that encryption involves an algorithm and a key. We also know that there are a few algorithms used universally to encrypt information, which are made unique for each instance by a key unique to that instance. We now turn to the kinds of algorithms in use and their applications.
Encryption types overview
All the known available encryption techniques can be categorized into three types. The categorization is done on the basis of the number of keys used to encrypt and decrypt information. A quick comparison of the three types of encryption is given in Table 7.1. The rest of the chapter discusses each of these three encryption types in detail.
A look at table, one might suggest that Hash functions might be the simplest encryption type to understand. That is probably true too. However, when people talk about encryption, they usually mean the use of secret key cryptography and public-key cryptography. In the sections that follow, therefore, we first discuss secret key cryptography, followed by public-key cryptography. We will talk about hash functions at the end because their use in encryption is less intuitive than the use of the other two encryption types.
Secret key cryptography
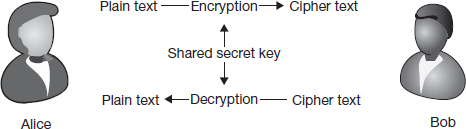
Secret key cryptography refers to encryption methods that use one key for both encryption and decryption. Figure 7.3 provides an overview of secret key cryptography.
As seen in the figure, the central feature of secret key cryptography is that the same key is used for both encryption and decryption. Due to this symmetry in the keys used for encryption and decryption, secret key cryptography is sometimes also called symmetric key cryptography, or symmetric key encryption.
The most common use of secret key cryptography is to transmit information securely. If Alice and Bob can both agree on the key, then Alice can encrypt her information with the key and Bob can decrypt the information using the same key. Similarly, Bob can encrypt his information with the shared key and Alice can decrypt the information using the shared key. The information is safe during transmission because only Alice and Bob know the key, and as we have agreed before, it is almost impossible to decrypt the transmitted information without knowledge of the key.
Secret key encryption can also be used to secure information stored in computers. If Bob wants to secure some information, he can select a key and encrypt information on his hard drive using the key. To retrieve the information, Bob simply has to enter his key and decrypt the information. Of course, if Bob forgets his key, he will never be able to retrieve the information on his computer.
The current standard for secret key cryptography is the Advanced Encryption Standard (AES). It was chosen by the National Institute for Standards and Technology (NIST) on November 26, 2001, after a selection process that lasted almost 5 years. The technology used in AES was developed by two Belgian cryptographers. Two technologies, the Data Encryption Standard (DES) and the International Data Encryption Algorithm (IDEA), were predecessor technologies to AES, and you may encounter these terms in the literature on information security. However, since AES is the current standard, we will not talk about DES and IDEA any further in this book. A brief overview of the technology behind AES is provided in the next section.
Public-key cryptography
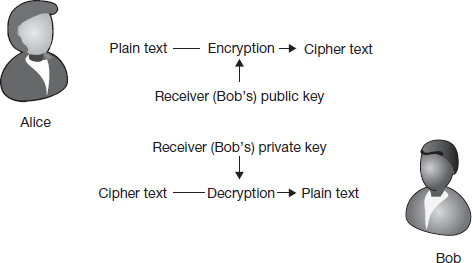
Public-key cryptography refers to encryption methods that use two keys, one for encryption and another for decryption. The technology is used for two different applications – data transmission and digital signatures. Figure 7.4 provides an overview of public-key cryptography for the purpose of data transmission.
A comparison of Figure 7.3 and 7.4 shows that the unique feature of public-key cryptography is that one key is used for encryption and a different key is used for decryption. Because of this asymmetry in the keys used, public-key cryptography is also called asymmetric key cryptography, or asymmetric key encryption.
As we will see in later sections, when we describe public-key cryptography in greater detail, the receiver's private key is kept confidential. For this reason, it is common to refer to the receiver's private key as the secret key. However, Kaufman et al5 recommend that the industry must standardize on calling this key the private key, and reserving the phrase “secret key” for the shared secret key used in secret key cryptography. In deference to that advice, we will also strive to avoid calling the private key the secret key.
What is public-key cryptography used for? As we will see, public-key cryptography can be seen as a supercharged version of secret key cryptography. As such, it can do anything that secret key cryptography can do, and some more. Why then do we even care about secret key cryptography?
It turns out that public-key cryptography is extremely demanding of computing resources, requiring many millions of times the processing capability required for secret key cryptography. Reckless use of public-key cryptography would bring even the fastest desktop computers to a grinding halt. In practice, therefore, we are extremely selective about when to use public-key cryptography, preferring to use secret key cryptography to the extent possible.
The primary use of public-key cryptography is to exchange keys. While going over the discussion of secret key cryptography in the previous section, did you give some thought on how Alice and Bob might agree on the same shared secret key? You may have noticed that we started with the assumption that Alice and Bob had a shared secret key. This might be possible if Bob and Alice had nearby offices. However, what if Bob was a service provider located in Washington, DC, and Alice was a customer located in Tampa, Florida? Could Alice and Bob possibly have a way of agreeing on a shared secret key that no one else would know? The answer is no. It can in fact be proven that there is no reliable way for Alice and Bob to exchange a secret key securely.6
Since there is no trivial way for Alice and Bob to exchange the secret key securely, public-key cryptography is used to do the job. When Alice and Bob are ready to communicate with each other, they first use public-key cryptography to exchange a secret key. Once the secret key has been agreed upon, Alice and Bob switch from using the computing intensive public-key cryptography to the much simpler secret key cryptography.
This is important to remember about public-key cryptography – the private key is known only to the owner of the key. It is not shared with anybody else.
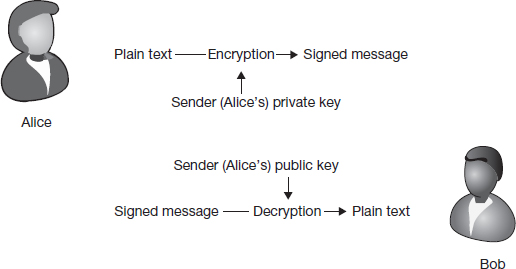
The second use of public-key cryptography comes from the unique relationship between a public key and its associated private key. It turns out that they exist in pairs. We have seen that information encrypted with the public key can be decrypted by the associated private key. This process also works in reverse. Information encrypted with the private key can be decrypted with the associated public key. This feature is used industrially to create digital signatures. Digital signatures are defined as cryptographic transformations of data that allow a recipient of the data to prove the source (non-repudiation) and integrity of the data.
When Alice sends a message to Bob, she can also send an encrypted version of the message, encrypted with her own private key. Bob can try decrypting this information. If the decrypted version matches the sent information, Bob knows not only that Alice sent the message, but also that the message was not modified en route. The process is shown in Figure 7.5.
Public-key encryption can be puzzling for the first time reader. It is also confusing to see two different uses of this puzzling technology. To facilitate learning, we use two approaches in this chapter. The first step is to compare Figures 7.4 and 7.5 and to isolate the differences between them. The second step will be in the next section, where we describe public-key encryption using an example.
Let's look at Figures 7.4 and 7.5.
What keys are used in each case? For data transmission, we used the receiver's keys. For digital signatures, we used the sender's keys. For data transmission, we used the public key for encryption. For digital signatures, we used the private key for encryption. This is summarized in Table 7.2.
What's going on here? Why the differences in the keys used. The critical thing to remember about public-key encryption is that a user only has access to one private key – his own. But everybody has access to everybody's public keys.
While transmitting data, we want to make sure the data cannot be read by others during transmission. The best way to accomplish that is to encrypt it in such a way that only the receiver can decrypt the information. How do you do that? What is unique to the receiver?
Well, we know that only the receiver has possession of his or her private key. We also know that if we encrypt some information with the receiver's public key, only the receiver will be able to decrypt the information using his private key. Fortunately, anybody in the world can get any user's public key. So, that is what we will do – encrypt the information with the receiver's public key and send it away. Only the receiver will be able to read the information.
When signing off on letters, privacy is not our concern. For example, Bob would like to be convinced that Alice did indeed send the letter.7 How can Alice do that? Well, both Alice and Bob know that only Alice is in possession of Alice's private key. If Alice can somehow convince Bob that she is indeed in possession of that key, Bob would be convinced. Fortunately, we have a way of doing that. If Alice encrypts some information with her private key, anybody in the world can decrypt it with her public key. Indeed, Bob does just that. If he succeeds, he is convinced that Alice has the private key she is supposed to have. And since no one else in the world ought to have Alice's private key, the letter must have come from Alice. The public key thus serves as a digital signature.
The way digital signatures are used in practice, we get a bonus feature as well. What message should Alice encrypt and send to Bob to convince him of her identity? We encrypt the message itself. This way, if Bob is able to decrypt successfully, not only is he convinced that the message came from Alice, he is also assured that the message was not modified during transmission.
The above has been simplified in one way compared to what actually happens. The simplification has been done for teaching purposes. In practice, we do not need to encrypt the entire message; we just need to encrypt a hash function of the message. Hash functions are discussed in the next section and we will revisit this issue at the end of the discussion of hash functions.
You may also be thinking – how can Alice keep the message confidential during data transmission if anybody can decrypt it using her public key? Great question. She cannot. Therefore, what we do is to send the message using the data transmission technique discussed above and also send a digital signature along with the message to confirm that the message did indeed come from Alice.
The current technology used to perform public-key cryptography is called RSA. It is named after the three creators of the technology – Ron Rivest, Adi Shamir, and Leonard Adleman. The technology was described in a paper published in 1977.8
Hash functions
Hash functions refer to encryption methods that use no keys. These functions are also called one-way transformations because there is no way to retrieve the message encrypted using a hash function. Now, that must really get you scratching your heads. Why would you care for an encrypt technology if you can never read the data back? As it turns out, this is actually very useful and, in fact, you have been using this property ever since you have used computers.
Hash functions take a message of any length and convert them to numbers of fixed length, usually 128 or 256 bits long. The length of the hash transform of the number “4” will be the same length as the hash transform of an entire DVD. Hash functions are used with passwords. We will shortly see how in the next paragraph, in the meanwhile, it may be a good exercise for you to think how hash functions may be useful with passwords.
Computers store passwords as the result of a hash transform instead of storing the actual value of the password. This way, the passwords can never be recovered even if the computer is stolen. When a user types in their password, the computer computes the hash of the password and compares the hash with the stored password hash. If the two matches, the computer accepts the provided password, otherwise not. This way, hash functions allow computers to verify passwords without storing a copy of the passwords themselves.
Hashed passwords are still vulnerable to brute-force and dictionary attacks, as we will see in Chapter 8. If a user selects a weak password, it could still be easily guessed. Hash functions can obscure passwords but cannot prevent them from being guessed.
The other use of passwords is to verify the integrity of information. If the sender sends a message as well as a hash of the message, the receiver can independently compute the hash of the message and compare it to the received hash. If the two hashes match, the receiver can be assured that the message was not modified during transmission. When hashes are used this way, they are called checksums. A checksum is a value computed on data to detect error or manipulation during transmission.
You see this commonly during data downloads. Software vendors often provide the checksums to their software downloads to help systems administrators verify that the software was downloaded without errors. Figure 7.6 shows an example from the download site for IBM Application Servers.
The most popular hash functions in use today are called MD5 and SHA-2. MD5 stands for version 5 of message digest algorithms. MD5 was universally used since its development by Ron Rivest (the same Ron Rivest who codeveloped RSA) in 1991. However, an array of flaws has been discovered in the algorithm and its use for cryptographic applications has been formally discouraged since December 31, 2008.9 However, MD5 continues to be popular for low-risk applications such as download verification.
SHA stands for secure hash algorithm and the suffix 2 stands for version 2 of the algorithm. The development of SHA has been facilitated by NIST, the National Institute of Standards and Technology. SHA-2 was published in 2001. Even though there are no known security vulnerabilities in SHA-2, the technology for the next version of SHA, SHA-3 was selected on October 2, 2012.10 The motivation for the development of the next generation of hash function before any apparent need was to be prepared in case an attack was developed against SHA-2. SHA-3 uses a completely different algorithm compared to SHA-2, so it is highly unlikely that an attack that compromises SHA-2 would also compromise SHA-3. Developers now have the choice of using SHA-2 or SHA-3 depending on their needs.
Encryption types details
The previous section provided an overview of the three types of encryption and their uses. In this section, we look at the primary technologies used in each encryption type in more detail.
Secret key cryptography
Secret key encryption is composed of two procedures – block encryption and cipher block chaining. Encrypting large messages of indefinite size requires enormous computing resources, beyond the capabilities of most end-user computers. Hence, user data is first broken into fixed-size blocks of manageable size. Breaking messages into reasonable-sized blocks offers the best combination of performance and security. Block encryption is the process of converting a plaintext block into an encrypted block. Most commercial encryption algorithms use 64- or 128-bit blocks. In particular, the current standard for secret key cryptography, AES, uses 128-bit blocks.
Block encryption
In general, block encryption uses a combination of two activities – substitution and permutation. We have already seen an example of substitution earlier in the chapter – the Caesar cipher and the more generic mono-alphabetic substitution. In the context of secret key cryptography, substitution specifies the k-bit output for each k-bit input. Permutation specifies the output position of each of the k input bits. Permutation is a special case of substitution because a specific bit of the input substitutes for a specific bit in the output. The generic operation of block encryption is shown in Figure 7.7.11
Figure 7.7, which is based on the DES technology standard, is representative of the operation of secret key encryption technologies. Within each block, the data is further broken into two parts. A substitution procedure mangles up all the bits in each part. The two mangled parts are then run through a permutation unit, which shuffles the bits in the block. The process is repeated until the input is satisfactorily encrypted.

FIGURE 7.7 Generic form of block encryption25
Why permutation?
An interested reader might ask – if permutation is just a special form of substitution, why use it at all? Why not just repeat the substitution operations.
The reason for using permutations is to further diffuse the impact of substitution. If you look at Figure 7.7 closely, you will find that if a bit in the left half of the input is changed, the substitution operation only affects the bits in the left half of the output. The same is true for a change in input bits in the right half – substitution only affects the bits in the right half. An adversary could use this property to craft special inputs and break the encryption algorithm. The permutation operation diffuses the impact of a change in a single bit of the input to the overall output of the block.
The substitution–permutation operation is repeated multiple times to ensure that changes in the input are distributed across all bits in the output. In Figure 7.7, a change in 1 bit in the input will impact 32 of the 64 bits in the output of the round (either the left half or the right half, followed by changes in the corresponding 32 bits of the final output of the round). This is not satisfactory. For good encryption, a change in 1 bit of the input should affect all 64 bits in the output equally. This is what will make the encryption difficult to break for an intruder. To accomplish this, the rounds are repeated until all output bits are affected by even the slightest change in the input. DES uses 16 rounds. AES uses 10–14 rounds, depending upon the size of the key.
Confusion–diffusion
The substitution–permutation sequence of block encryption algorithms implements Claude Shannon's ideas of confusion and diffusion. Shannon, widely considered the father of information theory, developed the idea that confusion and diffusion provided a good basis for secrecy systems.12 Confusion is making the relationship between the plaintext and ciphertext as complex as possible. Diffusion is spreading the impact of a change in 1 bit of the plaintext to all bits in the ciphertext.
In block encryption, substitution provides confusion and permutation provides diffusion.
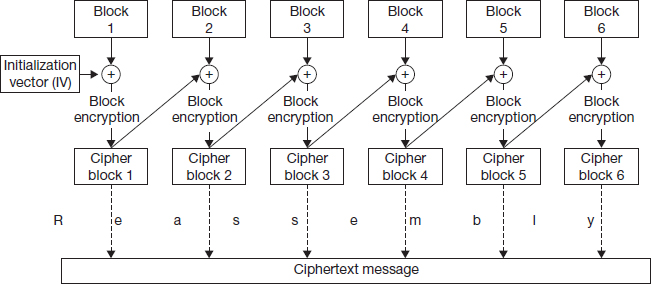
Cipher block chaining
Once the information in a block is encrypted, we need a way to use this mechanism to encrypt input of arbitrary size. The basic idea behind the methods used in practice to accomplish this goal is to collect all the encrypted blocks and aggregate them together suitably to get the encrypted version of the user's input. The simplest method to accomplish this might be to just collect all the blocks as shown in Figure 7.8. This method is very intuitive to understand; however, it is not used in practice for reasons discussed shortly. However, given its conceptual importance, the method is given a name – electronic code book (ECB). Electronic code book is the process of dividing a message into blocks and encrypting each block separately.
Why is ECB not used in practice? Figure 7.8 shows that there is insufficient diffusion of confusion in the method. If blocks 1 and 3 are identical, cipher blocks 1 and 3 will also be identical and this will be visible in the final encrypted output. This can potentially give an attacker some insight into the information being encrypted. Therefore, in practice, some complexity has to be introduced to diffuse the output adequately. Of these methods, one that is fairly intuitive to understand is called cipher block chaining (CBC). Cipher block chaining uses information from the previous cipher block while encrypting a cipher block. The mechanism is shown in Figure 7.9.
The difference between ECB and CBC is that before a block is encrypted, it is mangled with the output of the previous block. The diagonal arrows in the figure show the cipher output of the previous block being used to mangle the input of the next block. The operation commonly used to combine the two inputs is called “exclusive OR,” written as XOR, and represented in Figure 7.9 as +. XOR is a bitwise operation where the result is 0 if the 2 input bits are the same and 1 if the two input bits are different. As a result of the chaining of outputs, even if blocks 1 and 3 are the same, cipher blocks 1 and 3 will not be the same.
A randomly chosen initialization vector ensures that even if the same message is sent again, the output will be totally different. The final CBC output is obtained by simply collecting the cipher blocks together, as shown in the lower half of Figure 7.9.
As can be seen from this section, secret key cryptography relies on fairly simple operations. It is therefore computationally very conservative. However, as discussed earlier in the chapter, the challenge in using secret key encryption is key exchange. The sender and receiver have to be able to exchange the key before the encryption begins. Public-key cryptography, discussed in the next section, accomplishes this goal. Public-key cryptography is computationally very intensive, but its greatest virtue is that it allows secret communication over an insecure channel. It is therefore ideally suited for use in key exchange.
Public-key cryptography
Public-key cryptography uses two keys – one for encryption and another for decryption. The encryption key is widely distributed to allow users to send encrypted messages to the owner of the key. The decryption key is used to decrypt messages. Obviously, the owner guards the decryption key carefully. For this reason, a user's encryption key is called his public key and the decryption key, the private key.
To keep the discussion short and as simple as possible, in this section, we provide a simple example of the modular arithmetic that is behind most public-key cryptography algorithms. We then present RSA, the most popular public-key encryption algorithm.
Modular arithmetic used in public-key cryptography
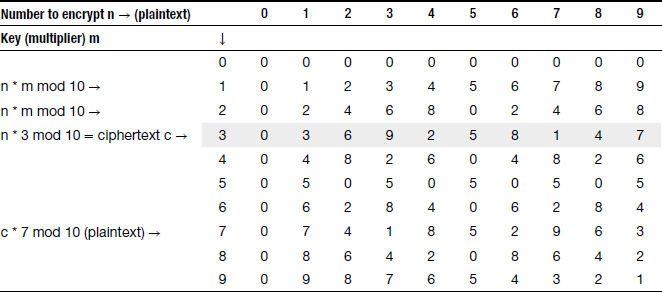
The modulus operation is sometimes also called the “remainder” operation. So, 17 mod 10 = 7, 94 mod 10 = 4, etc. The use of the modulo operation for public-key cryptography may be seen from Table 7.3.13 The table gives how decimal digits may be encrypted.
To use the table to encrypt data, multiply any number in the table header by 3 and take the modulus with respect to 10. For example, to encrypt 6, we use 6 * 3 mod 10 = 18 mod 10 = 8. Thus, 8 is the ciphertext for the number 6. The first highlighted row in the table shows the ciphertext computed this way for all possible single-digit numbers.
To decrypt, we multiply the ciphertext by 7 and take the modulus with respect to 10. For example, 8 * 7 mod 10 = 56 mod 10 = 6. Note that this gives us the plaintext 6, which had been encrypted to 8. The results for all other numbers are shown in the second highlighted row in the table.
In this example, we may write (3, 10) as the encryption (public) key and (7, 10) as the decryption (private) key. There are two interesting facts about the modulus operation used in this example.
First, data encrypted by the encryption key cannot be decrypted by the encryption key. For example, 8 * 3 mod 10 = 24 mod 10 = 4. But 4 ≠ 6, so an intruder cannot simply exploit his knowledge of the public key to decrypt data encrypted with the same key. Knowledge of the private key is required for decryption.
Second, either key can be used for encryption, and the other key will serve as the decryption key. For example, 6 * 7 mod 10 = 2 (encryption), and 2 * 3 mod 10 = 6 (decryption). This allows public-key cryptography to be used for digital signatures, as mentioned earlier in the chapter.
The example in Table 7.3 demonstrates the importance of key length in public-key cryptography. It would not take too long for an intruder to guess the private key (7, 10) given knowledge of the public key (3, 10). In practice, therefore, we use extremely large numbers to prevent intruders from guessing the private key in any reasonable amount of time.
RSA
The example in the earlier section uses a simple example to demonstrate the magical properties of public-key cryptography. RSA is the form of public-key cryptography used in practice. The RSA algorithm uses exponentiation instead of multiplication. The algorithm is described here in brief.14
- Start with two large prime numbers, called p and q. Typically these numbers are over 256 bits each (i.e., over 76 decimal digits each).
- Compute n = p * q.
- Compute φ = (p − 1) * (q − 1).
- Choose a number e that is relatively prime to ϕ, i.e., the two numbers do not share any common factors other than 1 (the letter e stands for encryption, and this number will be used for encryption).
- Choose a number d that is the multiplicative inverse of e mod ϕ, i.e., a number d such that d*e – 1 is divisible by ϕ (the letter d stands for decryption, and this number will be used for decryption).
- The pair <e, n> is the public key and is used for encryption
- The pair <d, n> is the private key and is used for decryption
- The keys are used as follows:
- To encrypt message m, compute ciphertext c = me mod n
- To decrypt ciphertext c, compute m = cd mod n.
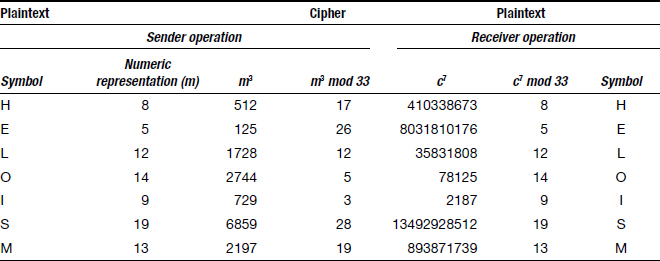
A simple example can demonstrate this. We have to be judicious in the numbers we choose since exponentiation very quickly leads to enormous numbers. However p = 3 and q = 11 work well.15 With this choice, we have
- n = 3 * 11 = 33·
- φ = (3 − 1) * (11 − 1) = 2 * 10 = 20·
- Say e = 3, since 3, does not share any factors with 20 other than 1.
- We can choose d = 7 since 3* 7 − 1 = 20 and 20 divides φ = 20·
- With these choices:
- c = m3 mod 33
- m = c7 mod 33.
Table 7.4 demonstrates the use of these choices in an RSA example. We start by converting plaintext to a numerical form. The example simply uses the position in the alphabet as the numerical representation, i.e., a = 1, b = 2, etc. The encryption and decryption operations may be verified from the table.
Since the public key includes the product n of the two numbers p, q chosen initially, if n could be factored, RSA could be broken. Therefore, the security of RSA depends critically upon the difficulty of factoring large numbers.
RSA also depends critically upon the availability of a large number of large prime numbers. If not, an intruder could simply create a table of all known prime numbers and try product combinations until n was obtained. Fortunately, prime numbers are abundant and it is impractical to store all known prime numbers. Therefore, if used with suitably large prime numbers, RSA is secure at least for now.
Prime number theorem
The probability that a number n is prime is approximately ![]() , where ln represents the natural logarithm. This is also equal to
, where ln represents the natural logarithm. This is also equal to ![]() , where log is the logarithm to the base 10. Say n is a 10-digit number. Since log (1010) = 10, the probability that the number is prime = 1/2.3 * 10 = 1/23. If n is a 100-digit number, the likelihood becomes 1 in 230.
, where log is the logarithm to the base 10. Say n is a 10-digit number. Since log (1010) = 10, the probability that the number is prime = 1/2.3 * 10 = 1/23. If n is a 100-digit number, the likelihood becomes 1 in 230.
In other words, if we randomly chose 230 100-digit numbers, we are very likely to find a prime number. Alternately, there are about 10100/230≈ 1097 100-digit prime numbers. All the computer storage in the world amounts to about 1020 bytes. It is therefore impractical to store all prime numbers to break RSA using guess-and-check procedures.
Hash functions
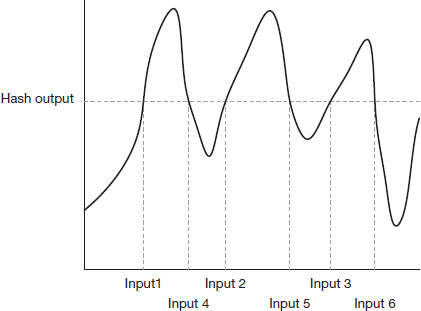
Hash functions are used to transform inputs into a fixed-length output. The transformation has two properties: (1) each input has a unique output and (2) it is impossible to guess an input from a given output. This is shown in Figure 7.10. It can be seen that all inputs have a unique output (which is why the transformation is called a function.16 But inputs 1–6 all transform to the same hash output. Therefore, given a hash output, it is impossible to determine which input led to the given output.
As discussed earlier, hash functions are used to store passwords. If passwords are saved as clear text, data theft could compromise the password. Saving passwords as hashes protects passwords from being stolen.
A good check to determine whether a website saves passwords in clear-text or as a hash is to ask for the password. If the site can send you your password, you know that the site kept the password in clear text, or it would not be able to send you the password.
Encryption in use
One remaining challenge in using encryption in practice is establishing trust in the public key sent by a user. We have seen that it is fairly simple to generate a public-key–private-key pair. What if an intruder sends you a public key and claims that it is the public key of the Bank of America. How would you detect that it is not? In the remaining sections of this chapter, we will see how public-key encryption is used in commercial technologies such as SSL/TLS and VPNs. We will then discuss the procedures used to establish trust in public keys.
SSL/TLS and VPN
The most common technologies used for encrypting information during network transfer are SSL/TLS (Security Sockets Layer and Transport Layer Security) and VPN (Virtual Private Network). In SSL/TLS, the transaction with a specific network server, such as a web or database server, is encrypted. In VPN, all communication from the computer is encrypted.
The salient feature of all such encryption technologies used in practice is that they combine the best features of secret key cryptography and public cryptography for a pleasant user experience. Secret key cryptography uses minimal computing power. However, it needs the shared key to be exchanged securely before secret communication can begin. Public key is prohibitively demanding of computing resources and therefore is not very appropriate to encrypt entire conversations particularly on small devices. However, even the simplest devices can use public-key cryptography briefly to exchange the secret key.
Therefore, in commercial practice, secure communication begins with the server providing its public key to the user. The user generates a secret key locally and encrypts the secret key with the server's public key. This ends the use of public-key cryptography for the communication. All subsequent transactions are encrypted with the shared secret key.
Certificates
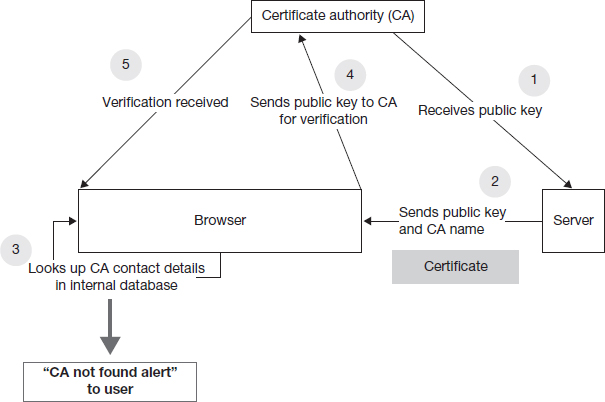
Real-world encryption critically depends upon the reliability of the public key sent by the server. This is quite analogous to the need for reliability of a driver's license produced as proof of identity in the physical world. In the physical world, we check for the reliability of the license by verifying whether the license was indeed issued by the state DMV. In the Internet world, there are companies called certificate authorities (CAs) that serve as the analogs of DMVs. CAs issue public keys to servers. The public-key exchange process works as shown in Figure 7.11.
Servers interested in participating in eCommerce transactions obtain a public key from one of the well-known public-key providers (certificate authorities). The CA encrypts the web server's public key and IP address with its own private key for use as a certificate. A certificate is a bundle of information containing the encrypted public key of the server and the identification of the key provider. Servers send their certificate to clients to identify themselves before starting a secure connection. The client (browser) comes preloaded with the public keys of all well-known certificate authorities. If the authority is known, the certificate is decrypted using the authority's known public key. The decrypted certificate contains the web server's public key.
To confirm that all is well, the browser also compares the web server's IP address with the IP address of the server it is connected to.17, 18
PKI
The last missing bit in this process is certificate authorities. What prevents an intruder from masquerading as a certificate authority?
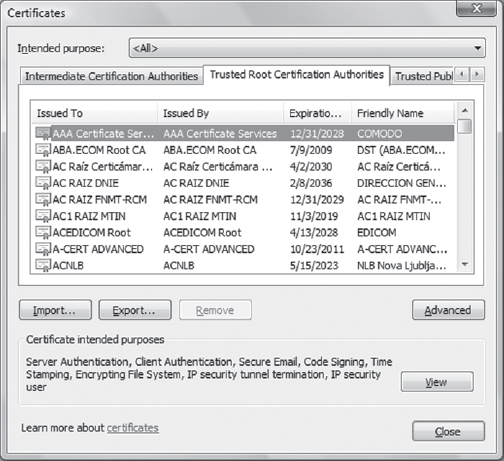
The way we deal with this issue is that browsers come with a preapproved list of certificate authorities. Figure 7.12 shows an example from the Chrome browser. If the certificate provided by the server is from one of these CAs, the browser uses its own information to contact the CA and confirm the correctness of the certificate. If the certificate is from some other organization (e.g., the university itself), the browser generally alerts the user about the issue to allow the user to use their personal judgment in trusting the certificate authority. One such alert is shown in Figure 7.13. The certificate in this case was generated on a local web server by Nessus. Since this web server is not one of the well-known CAs, the prudent route for the browser is to ask the user for advice on how to proceed.
The framework established to issue, maintain, and revoke public-key certificates is called the public-key infrastructure (PKI).
Example case–Nation technologies
We have seen in this chapter that the primary way we use encryption is by securing the channel of communication. Technologies such as VPN and SSL allow us to create an encrypted connection between computers, but the content itself remains unencrypted. Other commonly used encryption techniques encrypt the entire hard drive.
A common problem with all these encryption approaches is that though we really aim to encrypt information stored in files, these methods encrypt everything but the files themselves. Once a user is logged into their account, all files are visible. A phishing attack on the currently logged in user can successfully obtain all the files the user is privileged to access. Once a file is emailed, the sender has no control over how the receiver safeguards the information content in the file.
Would it not be convenient to encrypt just the files that need encryption? Better still, leave the files encrypted all the time, only unencrypting them for the duration of reading/editing, and only for designated users?
Such a technology is possible and has been developed by a company called Nation Technologies, founded by Stephen Nation, a former NYPD intelligence officer. The company's product and service allows customers to encrypt files individually. Encrypted files can be exchanged with any number of users. The person who encrypts the file can specify file access permissions for designated users, each identified by email address or other identifier. Receivers can save the file and open it for reading. When they close the file, it reverts back to its encrypted state.
A potential advantage to this approach is that organizations no longer have to worry about stolen secrets. Information is encrypted even when stored.
SUMMARY
In this chapter, we looked at encryption, in terms of applications, algorithms at a high level and the infrastructure that exists to enable seamless encryption. We looked at the three types of encryption – hash functions, secret key cryptography, and public-key cryptography. The encryption types differ in terms of the number of keys used for encryption.
Technologies used in practice such as SSL and VPN combine secret key cryptography with public-key cryptography. Public-key cryptography is used for the initial key exchange to avoid the computational overhead that would occur if public-key cryptography were used for the entire transaction.
The IT industry has established a set of procedures so that key verification and exchange proceeds smoothly. These procedures are collectively known as the public-key infrastructure. The success of these procedures may be gauged from the relative ignorance of most consumers about the activities taking place in the background to ensure that their eCommerce transactions are secure.
Recommendation
For a very engaging, humorous, and thorough treatment of encryption, the book by Kaufman, Perlman, and Speciner is highly recommended.19 All missing details in this chapter may be completed by referring to the book. Apart from being some of the most knowledgeable people on the subject, the experts are also extremely gifted writers and have put great effort to make this otherwise technical subject very accessible and personal. The authors have learned a lot about this subject from that resource.
CHAPTER REVIEW QUESTIONS
- What is encryption?
- What is encryption used for?
- Briefly describe the Caser cipher.
- What are the requirements of a good encryption algorithm?
- Why do modern encryption algorithms use keys?
- What is secret key cryptography?
- Provide a brief overview of the current standard for secret key cryptography. What are some of its applications?
- What is public-key cryptography?
- What are some applications of public-key cryptography?
- What are digital signatures?
- How is public-key cryptography used to provide digital signatures?
- What are hash functions? Provide a brief overview of some of the best-known hash functions.
- What are hash functions used for?
- What is block encryption? Why is data broken into blocks for secret key cryptography?
- What is substitution in the context of encryption?
- What is permutation in the context of encryption? Why is it needed?
- What is the confusion–diffusion paradigm of cryptography?
- What is cipher block chaining? Why is it necessary?
- Provide a brief overview of the RSA algorithm.
- What is SSL/TLS? What is it used for?
- What are some differences between SSL and VPNs?
- What are certificates?
- What are certificate authorities? What services do they provide?
- What is PKI?
- What is the need for PKI?
EXAMPLE CASE QUESTIONS
- Visit Nation Technology's website at www.nationtechnologies.com. What are some of the features of the company's product?
- Describe what in your opinion would be one useful way in which you might use the technology offered by Nation Technologies?
- Firms in which industry in your opinion would benefit the most from the technology offered by Nation Technologies? Why?
- What do you think are some of the most important business hazards faced by Nation Technologies?
HANDS-ON ACTIVITY–ENCRYPTION
These activities are included to demonstrate the use of encryption using the Linux virtual machine you configured in Chapter 2. You will perform encryption using hash functions (0 keys), secret key (1 key), and public key (2 keys). Ensure that you have Internet connectivity and open a terminal window to complete these activities.
Password hashes
As was mentioned during the chapter, operating systems store the result of a hashing function instead of storing the actual value of a password. In CentOS Linux, the default hashing function for passwords is now SHA-512 (in the past, DES and MD5 have been used as the default).
- Log in using the “alice” account (password: aisforapple) and open a terminal window
- CentOS includes a program grub_crypt which will allow us to see the result of different hashing functions without changing a user's password:
[alice@sunshine Desktop]$ grub-crypt --sha-512 Password: aisforapple Retype password: aisforapple $6$DqW2UfDcPZjKyQyc$fwQqIAxfEgEuy6 KFAKxEdKP1cWuy0d5vemqNRV2uNAPf1VNaX hpmZYOIZuW8iitC82MhQMaR2h8EY0DgQb5Z/1 [alice@sunshine Desktop]$ grub-crypt --sha-256 Password: aisforapple Retype password: aisforapple $5$omu31sk0zLzOVug1$2sbFJlcupATlu6Kw2iTf qXMMbbgYanXoNtEDjgVH876 [alice@sunshine Desktop]$ grub-crypt --md5 Password: aisforapple Retype password: aisforapple $1$S213Gc1H$sTKjWuHbrSrquDLzy4XT8/
The results contain three values separated by dollar signs. They are interpreted as ($id$salt$hash):
- Id – a numeric id that identifies which hashing algorithm was used (MD5, SHA-256, SHA-512).20
- Salt – random string of characters that is used to increase the length of the input to the function.
- Hash – result of the hashing algorithm on the user's password and the salt.
As you can see, the different algorithms yield vastly different results, even when using the same password as input.
Choose a strong password based on the rules mentioned in Chapter 8 and run grub-crypt with MD5, SHA-256, and SHA-512.
Run grub-crypt multiple times with the same password and encryption algorithm.
Questions
- Does the command yield the same results every time? Why or why not?
- Save the output from the previous commands into a text file /opt/book/encryption/results/ex1.txt
Deliverable: Submit the contents of ex1.txt to your instructor.
In addition to passwords, the other major use for hashing algorithms in Linux is for verifying the integrity of system files. The md5sum command provides an easy way to generate an MD5-based checksum21 of a file or compare a file to a known-good checksum. If the checksum of the file differs at all from the known-good value, the file has been modified and could mean the system has been compromised. To generate a checksum of a file:
[alice@sunshine ~]$ md5sum hello.txt 8ddd8be4b179a529afa5f2ffae4b9858 hello.txt
The MD5 checksum is based on the contents of the file, so the file can be copied or renamed without affecting the checksum value, but if the contents are modified in any way, md5sum will return a different value.
[alice@sunshine ~]$ cp hello.txt world.txt [alice@sunshine ~]$ md5sum world.txt 8ddd8be4b179a529afa5f2ffae4b9858 world. txt [alice@sunshine ~]$ echo '!' >> world.txt [alice@sunshine ~]$ md5sum hello.txt world .txt 8ddd8be4b179a529afa5f2ffae4b9858 hello.txt c231742ea29c9e53d4956d8fa4dd6d96 world.txt
The output from the md5sum command can also be stored as a text file; this is useful if you are generating the checksum for a large number of files. The text file can then be used as input for the –c switch of the md5sum command, which compares the checksums of all the files listed and reports on results.
[alice@sunshine ~]$ md5sum *.txt > check- sums.txt [alice@sunshine ~]$ cat checksums.txt 8ddd8be4b179a529afa5f2ffae4b9858 hello.txt c231742ea29c9e53d4956d8fa4dd6d96 world.txt [alice@sunshine ~]$ echo 'This has been modified' > hello.txt [alice@sunshine ~]$ md5sum -c checksums. txt hello.txt: FAILED world.txt: OK md5sum: WARNING: 1 of 2 computed check- sums did NOT match
Questions
The file /opt/book/encryption/checksum/checksums.txt contains a list of the MD5 checksums for the files in that directory, validate the integrity of the files.
- List any files that fail the checksum validation in /opt/book/encryption/results/failed.txt
- Create a text file that contains all of the checksums for the .png files in this directory and save it as /opt/book/encryption/results/checksum.txt
Deliverable: Submit the contents of failed.txt and checksum.txt to your instructor.
Secret key encryption
Secret key encryption is used extensively in Linux for file encryption. Most modern Linux distributions include support for one or more forms of encrypted filesystem, which encrypt all files as they are written to the disk. Configuring an encrypted filesystem is beyond the scope of this text, but the aescrypt command22 provides a way to protect individual files with the same form of secret key encryption. The list of command arguments is pretty simple, as given in Table 7.5.
We can use these commands to encrypt and decrypt the file hello.txt, as follows:
[alice@sunshine ~]$ cat hello.txt Hello World! [alice@sunshine ~]$ aescrypt -e hello.txt -p 1234qwer -o hello.txt.aes
[alice@sunshine ~]$ head -1 hello.txt.aes AES^B^@^@^XCREATED BY^@AESCRYPT 3.05^@^@^@^@^@^@^@^@^@^@^@^@^@^@^@^@^@^@^ @^@^@@^@ [alice@sunshine ~]$ aescrypt -d hello. txt.aes -p 1234qwer -o hello.decrypt.txt [alice@sunshine ~]$ cat hello.decrypt.txt Hello World!
Questions
For this exercise, change directories to /opt/book/encryption/secret-key
- Encrypt the plans.txt file using the password pinky and save the output to /opt/book/encryption/results/plans.aes
- Decrypt the encrypted.aes file using the password brain and save the output to /opt/book/encryption/results/plaintext.txt
Deliverable: Submit the contents of plans.aes and plaintext.txt to your instructor.
Public-key encryption using GPG23
GPG stands for GNU Privacy Guard. It is a free software alternative to PGP (Pretty Good Privacy) and is based on the OpenPGP standard. But that leaves the following question: “What is PGP?”
PGP was developed by Phillip Zimmerman in 1991. It was the first encryption software built upon public-key cryptography algorithms, including the RSA algorithm discussed in the chapter. Due to patenting issues, the OpenPGP standard was created, defining standard data formats for interoperability between encryption software. GPG is one of the most notable programs developed based on this standard. GPG allows you to encrypt data, “sign” it, and send it to others, who will use the public key you provide to them to decrypt the data.
To use public-key encryption, we generate a key pair, share the public key, and use the key pair for encryption and decryption.
Key generation
The first step in any public-key encryption system is to generate your public/private key pair. GPG provides the --gen-key switch that will walk you through the process:
[alice@sunshine ~]$ gpg --gen-key gpg (GnuPG) 2.0.14; Copyright (C) 2009 Free Software Foundation, Inc. This is free software: you are free to change and redistribute it. There is NO WARRANTY, to the extent per- mitted by law.
You will be prompted to choose which type of key you want for digital signatures and encryption. Select the default (RSA and RSA). You will then be asked for the key size. The default is 2048 bits. You can safely select this option. Then, you will choose the length of validity for the key. In real-world situations, this value would be between 1 and 5 years but for these assignments, keys do not need to expire.
Please select what kind of key you want:
(1) RSA and RSA (default)
(2) DSA and Elgamal
(3) DSA (sign only)
(4) RSA (sign only)
Your selection? 1
RSA keys may be between 1024 and 4096 bits
long.
What keysize do you want? (2048) 2048
Requested keysize is 2048 bits
Please specify how long the key should be
valid.
0 = key does not expire
<n> = key expires in n days
<n>w = key expires in n weeks
<n>m = key expires in n months
<n>y = key expires in n years
Key is valid for? (0) 0
Key does not expire at all
Is this correct? (y/N) y
Following this, you will be prompted to choose a name for the key, email address, and comment. Your real name and email address are both fine to use here. For the comment, you can put whatever company you'd like – e.g., “Sunshine State University.” GPG will use this information to create your keypair.
GnuPG needs to construct a user ID to identify your key. Real name: Alice Adams Email address: [email protected] Comment: Sunshine State University You selected this USER-ID: “Alice Adams (Sunshine State University) <[email protected]>” Change (N)ame, (C)omment, (E)mail or (O) kay/(Q)uit? O
Now, you will need a passphrase. You should see a dialog box similar to Figure 7.13. Enter something that is reasonably secure, but something that you will remember. Finally, the program will start generating your key. To increase the key's effectiveness, it's a good idea to move your mouse around in random directions or perform some other task on the computer, while the key generation is in progress. This could take seconds or minutes; it varies greatly depending on many factors.
Once this has been completed, then you will have just generated your first keypair.
We need to generate a lot of random bytes. It is a good idea to perform some other action (type on the keyboard, move the mouse, utilize the disks) during the prime generation; this gives the random number generator a better chance to gain enough entropy.
gpg: key 9ED0CE35 marked as ultimately
trusted
public and secret key created and signed.
gpg: checking the trustdb
gpg: 3 marginal(s) needed, 1 complete(s)
needed, PGP trust model
gpg: depth: 0 valid: 1 signed: 0 trust:
0-, 0q, 0n, 0m, 0f, 1u
pub 2048R/14382D17 2012-12-01
Key fingerprint = B317 3F83 705B
889D B414 7DF0 A3C1 B094 7E5B 6F3F
uid Alice Adams (Sunshine State
University) <[email protected]>
sub 2048R/C8761AAB 2012-12-01
What we have just done is created a keypair, which is located in a new hidden folder called .gnupg in your home directory. This folder, along with some other contents, includes pubring.gpg, and secring.gpg, which include your public and secret keys, respectively. The files are both stored in a binary format, so you can't read their contents, but GPG can interpret this file and display the information you need.
Key sharing
To list the public keys stored in GPG's “keyring,” type the following command:
[alice@sunshine ~]$ gpg --list-keys /home/alice/.gnupg/pubring.gpg ------------------------------ pub 2048R/14382D17 2012-12-01 uid Alice Adams (Sunshine State University) <[email protected]> sub 2048R/C8761AAB 2012-12-01
To list your private keys:
[alice@sunshine ~]$ gpg --list-secret-keys /home/alice/.gnupg/secring.gpg ------------------------------ sec 2048R/14382D17 2012-12-01 uid Alice Adams (Sunshine State University) <[email protected]> ssb 2048R/C8761AAB 2012-12-01
Before you can share encrypted data with others, you need to do two things: give them a copy of your public key and import a copy of their public key into GPG. To export your public key as a text file:
[alice@sunshine ~]$ gpg -a -o /tmp/alice_ adams.pub --export [alice@sunshine ~]$ head /tmp/alice_ adams.pub -----BEGIN PGP PUBLIC KEY BLOCK----- Version: GnuPG v2.0.14 (GNU/Linux)
mQENBFC6Q/MBCACjZH9O43XeK8TfDXVW084xmr2 lgiLsv7drbT9poQiuHmHrnbAm I/dm+nTIQn4qI8d+qTn0oWUsa9HD+N5sAsAHkYl5 kkmWgg/rtP8NtaH84/qqKSQN ktmd/zxfyNgJ4fTHhfqJA6RuHoKuFla+MMqKzR4u +ZSjxgmHl4tbSBph2+YgmMp8 fqLH18i4fSEoG5jZ6VciPw8KAyZvVIsC5TyOfX- W67UU8QJ7bEZaejxMtrhecF4F/
Now that if your key is exported, you will need to give it to the person you want to exchange information with. In the real world, the key would be emailed to the other party or, in extremely high security situations, hand-delivered to the recipient.
Note
If you have multiple keys, such as one for personal use and one for work use, you can specify which key you want to include using -u <user> where <user> is the email address of the key you want to use.
In our case, the key has already been transferred to another user at Sunshine State University ([email protected]) and he has imported the key to his GPG keyring. Bob has also generated his key pair and told us it can be found at /home/bob/public_html/bob_brown.pub or http://www.sunshine.edu/˜bob/bob_brown.pub so we have two options for importing Bob's public key. To import a file from the local filesystem:
[alice@sunshine ~]$ gpg --import /home/ bob/public_html/bob_brown.pub gpg: key 310C3E16: public key “Bob Brown (Sunshine State University) <[email protected]>” imported gpg: Total number processed: 1 gpg: imported: 1 (RSA: 1)
Or to import a file from a remote webserver:
[alice@sunshine ~]$ gpg --fetch-keys http://www.sunshine.edu/~bob/bob_brown. pub gpg: key 310C3E16: public key “Bob Brown (Sunshine State University) <[email protected]>” imported gpg: Total number processed: 1 gpg: imported: 1 (RSA: 1)
Either way, you will now have the public key to use.
Be careful when importing public keys from a remote host, either through the web or email. You must be sure that you are getting the correct public and that it has not been tampered with before using it for any secure communications.
If you run gpg -- list-keys again, you will now see the public key for Bob Brown in the list of available keys:
[alice@sunshine ~]$ gpg --list-keys /home/alice/.gnupg/pubring.gpg ------------------------------ pub 2048R/14382D17 2012-12-01 uid Alice Adams (Sunshine State University) <[email protected]> sub 2048R/C8761AAB 2012-12-01 pub 2048R/310C3E16 2012-12-01 uid Bob Brown (Sunshine State University) <[email protected]> sub 2048R/1EA93238 2012-12-01
Now that you have a public key, you will now be able to encrypt a message in such a way that it is designed for a particular recipient. To sign and encrypt a file, then save it as a text-based file (the default is a binary format). Use the -a and -e switches and specify whose public key should be used by using -r:
[alice@sunshine ~]$ gpg -s -a -r bob@sun- shine.edu -e hello.txt you need a passphrase to unlock the secret key for user: “Alice Adams (Sunshine State University) <[email protected]>” 2048-bit RSA key, ID 14382D17, created 2012-12-01
GPG then displays a dialog box for you to enter the password for Alice's private key. Once it is entered, it then checks its keyring for a public key belonging to [email protected]:
gpg: 1EA93238: There is no assurance this key belongs to the named user
pub 2048R/1EA93238 2012-12-01 Bob Brown (Sunshine State University) <bob@sun- shine.edu> Primary key fingerprint: 599F 4790 E781 ADBF 1850 F120 2B51 B871 310C 3E16 Subkey fingerprint: 26BF DCFC 0A62 7224 9D20 5DE5 9734 A6C4 1EA9 3238
It is NOT certain that the key belongs to the person named in the user ID. If you *really* know what you are doing, you may answer the next question with yes.
Use this key anyway? (y/N) y
GPG issues a warning that Bob's key may not be trustworthy because it has just been imported and there is no other data in the GPG keyring that can be used to verify the key's validity. You can safely ignore this message for this exercise, but if you plan on using GPG in a real-world situation, see the GNU Privacy Handbook24 for information on building a “Web of Trust” for key management.
[alice@sunshine ~]$ cat hello.txt.asc -----BEGIN PGP MESSAGE----- Version: GnuPG v2.0.14 (GNU/Linux)
hQEMA5c0psQeqTI4AQgAgpJ4Z4hiN93q+DdZ2ETg nm1ib+ciekRGmNtI4C5KMzPm b C W u s 0 c q m t L W E L 6 D j 4 o M 9 0 H B G 9 D i - iNKxrxKdjAneh9i/AYVf3/UleyW0Zb2dL/ dC v e C x l k N a G L C t K j V 0 9 6 7 e w / J s H B Q b V 1 2 j X R n q N 6 1 r m p / edFIQZ1tbXymXlcnfg3vm a R K n K S s X V a 0 q O H x P P n 0 +s k P 6 t F b M T / q / 5 F 1 D f p I f 9 N Y 1 m V L J D i M N Q G p y y 2 / ZZyKk 90PWxBsQC90CcWTfJqwjC1wPd4Ck2YOr+q6u36YR hz8cLwoM9I3MR2xVbtdElTGy Zd2ogWZImTRBxhKWYV7uVDre095Y4FNIzbzADZ1 KaNLAwgGGslcOrrCI4gpSkGIb DbvhuIr1r2rKeBRxR3dbQ+xb6Wm9S8v8440VSLDD D4f3TZFc6+/qUlAW7fU9Xu/1 4nqN4nu9NCQLgWmZyLtJr8RIry0tVxHQwhOQl- 2w6t34b0IZJvjLGzkmM589fwWNo ggE3krRiBvAE17z101Ncqn/zu5bfc6BUD2Okc- 36Qg56NUzvydGM3xgK2FRwgQfhr 7 T r s J p / 9 R +w X V 6 E G f T u o T o A / p1WY5311952l2Wrd7e2nwm6umeaKxgzgO4hrC9zS k576lCUi0cPyhwWBHQdK8UtssmBH1+tt2hEa6H+b Tf1OIOZptMU64NCG3rWgrI17 N W n t q 9 w w W Q T 5 a g q C a l t h L F M 4 7 n i / m K e 5 1 K a y 9 L c k N U m m 5PC8yA4oti5jnpIaW4Jw xRFvTSoRXH5ARlPc1INoNi+51X+jd8y9AB2096s2 x+BQFuCmG25K/z7E2BoJjsVV zf/qg6yQTbgPmvG83Jyvev71ykXd7TfKZGs4UlKq K+grJda8 =BxNI -----END PGP MESSAGE-----
Now that you have encrypted a message for Bob and signed it with your private key, it's time for him to decrypt it. We can switch users to Bob's account and decrypt the file to test it out.
[alice@sunshine ~]$ su - bob Password: [bob@sunshine ~]$ gpg -o hello.txt --decrypt ~alice/hello.txt.asc You need a passphrase to unlock the secret key for user: “Bob Brown (Sunshine State University) <[email protected]>” 2048-bit RSA key, ID 1EA93238, created 2012-12-01 (main key ID 310C3E16)
You should see the password entry dialog box at this point. Once you've entered the password for Bob's private key (bisforbanana), the file will be decrypted; however, you'll receive an error when verifying the signature:
gpg: encrypted with 2048-bit RSA key, ID 1EA93238, created 2012-12-01 “Bob Brown (Sunshine State University) <[email protected]>” gpg: Signature made Sun 02 Dec 2012 10:37:18 AM EST using RSA key ID 14382D17 gpg: Can't check signature: No public key
Bob must import Alice's public key before the signature on the file can be verified:
[alice@sunshine ~]$ gpg --import /tmp/ alice_adams.pub gpg: key 14382D17: public key “Alice Adams (Sunshine State University) <alice@ sunshine.edu>” imported gpg: Total number processed: 1 gpg: imported: 1 (RSA: 1)
Try the decrypt command again and this time the file will be decrypted and the contents saved to hello.txt. GPG will then verify the included signature:
gpg: Signature made Sun 02 Dec 2012 10:37:18 AM EST using RSA key ID 14382D17 gpg: Good signature from “Alice Adams (Sunshine State University) <alice@sun- shine.edu>” gpg: WARNING: This key is not certified with a trusted signature! gpg: There is no indication that the signature belongs to the owner. Primary key fingerprint: C42E 0E23 08A1 8116 019A AAB3 2D73 7113 1438 2D17
Again, GPG issues a warning because Bob's GPG keyring doesn't have enough information to validate the public key for [email protected]. Once the signature has been checked, you can verify that the contents of the decrypted file are correct:
[ bob@sunshine ~]$ cat hello.txt Hello World!
Questions
- Generate a new public/private key pair using your name, email address, and your school as the comment field.
- Export the public key and save it as /opt/book/encryption/results/key.pub
- Import the public key stored at /opt/book/encryption/public-key/eric_pierce.pub
- List the public and private keys stored in your GPG keyring and save the output as /opt/book/encryption/results/public-keyring.txt and /opt/book/encryption/results/private-keyring.txt respectively.
- Encrypt and sign /home/alice/hello.txt using the public key you just imported and save the output as /opt/book/encryption/results/encrypted.asc
Deliverable: Submit the contents of key.pub, public-keyring.txt, private-keyring.txt, and encrypted.asc to your instructor.
CRITICAL THINKING EXERCISE–ENCRYPTION KEYS EMBED BUSINESS MODELS
We haven't spent much time in this book discussing cloud computing and the risks specifically emanating from putting so much data on the cloud. Do you know where your Gmail data is? Or, where Microsoft saves the files you store on its SkyDrive service?
You probably don't care, and for most people it is the sensible thing to do. The companies have a lot to lose if they abuse the public trust. The current business model essentially seems to be that users trust free cloud service providers with their data with the understanding that the cloud service providers may peek into the contents of the files for limited purposes. Customizing online advertisements seems to be one such accepted purpose. So, the trade-off is free cloud storage service in return for advertising.
However, particularly since the revelations about the collaborations between cloud service providers and the NSA have emerged, some users may be concerned about the privacy of their information. What can they do if they still want to derive the convenience of cloud services?
From what we have read in this chapter, the solution is simple. Currently, the cloud service providers take care of encryption, i.e., the cloud service providers and not the data owners have the encryption keys to the data. This allows the cloud service providers to view your data on demand. Thus, the business model of advertising-for-storage is embedded in the service provider's ownership of the encryption keys.
If you wanted to prevent that, well, you could encrypt your data before you upload the data to the cloud service provider. You would then be responsible for key management because if you lost your decryption keys, you would not be able to read your own data.
REFERENCES
Falkenrath, R. “Op-ed: encryption, not restriction, is the key to safe cloud computing,” http://www.nextgov.com/cloud-computing/2012/10/op-ed-encryption-not-restriction-key-safe-cloud-computing/58608/ (accessed 07/18/2013)
Amazon Web Services, “Using client-side encryption,” http://docs.aws.amazon.com/AmazonS3/latest/dev/UsingClientSideEncryption.html (accessed 07/18/2013)
Schneier, B. Cryptogram, November 15, 2012
CRITICAL THINKING EXERCISE QUESTIONS
- Many popular cloud services such as Gmail are currently free because users allow advertisements in return for free service. How do you think the market will evolve if more and more data is encrypted where service providers can no longer monetize your data through advertising?
- What are some special concerns of regulated organizations such as government agencies when it comes to cloud computing? (The Nextgov op-ed has several examples.)
DESIGN CASE
Sunshine University's Admissions department is extremely active in terms of recruitment of students. It routinely visits local high schools in order to promote the university's programs, frequently gathering Personal Identifiable Information (PII) from high school students in order to help them apply for scholarships, financial aid, and other opportunities.
In order to record all this information, recruiters carry university-issued laptops to their visits. Recently, one of the recruiters' vehicle was broken into and the contents of the car stolen. Luckily, the perpetrator missed the laptop (containing 500 Social Security Numbers) in the trunk of the vehicle.
As an expert in security, the Provost reached out to you in order to ask for your opinion on what could be done to make these laptops safer. In reading your state's statutes you realize that, where whole disk encryption is employed on these laptops, the confidentiality of the information contained would be protected and there would be no need to report the incident.
Write a one-page recommendation to the Provost, covering the information in the previous paragraph and arguing for the purchase of a whole disk encryption solution for the university. In your report, include information on the following.
- Report on the legal requirements for such encryption in state universities in your state
- Outline your requirements for the product
- Do some research on popular product offerings and include a minimum of three vendors
- Explain the difference between file encryption and whole disk encryption
- When should one be used versus the other? Consider what each one protects against.
- Which operating systems are you covering?
- How will the decryption key be recovered if lost?
1For a brief primer on how information is sent and received on computer networks, see the appendix.
2Wikipedia states that these names were first used by Ron Rivest in his paper describing the encryption protocol that bears his name (the RSA protocol). We will have more to talk about RSA later in the chapter (http://en.wikipedia.org/wiki/Alice_and_Bob).
3Do you now see the etymology of this word? De-cipher is to de-zerofy the message, i.e., take an apparently meaningless message and find the meaning in it.
4Alexander Thomson, M.D. (M.DCC.XCVI (1796)). The lives of the first 12 Caesars, translated from the Latin of C. Suetonius Tranquillus: with annotations and a review of the government and literature of the different periods. London, U.K., G.G. and J. Robinson, Paternoster-Row.
5Kaufman, C., R. Perlman and M. Speciner (2002). Network Security: Private Communication in a Public World, Prentice-Hall ISBN 0130460192
6In the literature, this scenario is discussed as the two general problems. There is plenty of information available about this well-known problem on the Internet. See, for example, the Wikipedia article http://en.wikipedia.org/wiki/Two_Generals%27_Problem
7Say you receive an unsolicited job offer from the White House. How would you be convinced that the offer was for real?
8Rivest, R. Shamir, A. and Adleman, L. “A method for obtaining digital signatures and public-key cryptosystems.” Communications of the ACM, 1978, 21(2): 120–126. (The first few pages of the paper should be very interesting for an undergraduate student – the opening line talks about email in future tense.) The paper is also available at http://people.csail.mit.edu/rivest/Rsapaper.pdf (accessed: 10/19/2012).
9http://www.kb.cert.org/vuls/id/836068
10http://csrc.nist.gov/groups/ST/hash/sha-3/index.html
11The figure is adapted from FIPS PUB 46-3, Data Encryption Standard (DES), 10/25/99, http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf, (accessed 10/23/12).
25The figure is adapted from FIPS PUB 46-3, Data Encryption Standard (DES), 10/25/99, http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf, (accessed 10/23/12).
12Shannon, C. “Communication theory of secrecy systems,” 1946, http://netlab.cs.ucla.edu/wiki/files/shannon1949.pdf (accessed 10/23/12).
13This table is based on the example in Kaufman, C. Perlman, R. and Speciner, M. 2002. Network Security: Private Communication in a Public World, Prentice-Hall.
14A method for obtaining digital signatures and public-key cryptosystems, Rivest, R.L., Shamir, A. and Adleman, L. Communications of the ACM, 1978, 21(2): 120–126.
15These numbers were also chosen in the book, Tannenbaum, A.S. and Steen, M.v. Distributed Systems: Principles and Paradigms, 2002, Upper Saddle River, NJ, Prentice-Hall, Inc.
16Function: a rule of correspondence between two sets such that there is a unique element in the second set assigned to each element in the first set (Houghton-Mifflin Harcourt eReference).
17To see a more detailed explanation, visit http://www.moserware.com/2009/06/first-few-milliseconds-of-https.html (accessed 2/2/13).
18For a very interesting example of the encryption-certification process based on Hindu mythology, see the article “Alice and Bob can go on a holiday,” by S. Parthasarthy, http://profpartha.webs.com/publications/alicebob.pdf (accessed 07/18/2013). There may be other similar interesting and illustrative culture-specific analogies possible. We would love to hear about them for inclusion in future editions of the book (with attribution, of course).
19Kaufman, C., Perlman, R. and Speciner, M., 2002, Network Security: Private Communication in a Public World, Prentice-Hall.
20See the pam_unix man page (http://linux.die.net/man/8/pam_unix) for full list of supported algorithms.
21Commands for generating SHA-based checksums are also available, but MD5 is used more in practice.
22Not included in a standard CentOS install, but it is available at http://www.aescrypt.com
23Thanks to Clayton Whitelaw, a junior in Computer Science and member of the Whitehatters student club at USF for creating the first draft of this section