CHAPTER 3
Interest Rate Swaps in Practice
The previous chapter laid out the basic theory of pricing plain-vanilla interest rate swaps. As we saw, swap valuation boils down to extracting discount factors and using this discount factor curve to project and discount the cash flows. In this chapter, we consider the details of swap markets in practice using the USD market as our prime example.
In the United States, almost every major financial institution and corporation uses interest rate swaps. Like any other market instrument, swaps can be used for hedging or speculation. Commercial banks can use swaps to match the duration of their assets (long-term fixed rate loans) to their liabilities (short-rate deposits, CDs). Agencies use swaps and swap derivatives to fine-tune and hedge the duration of their mortgage portfolios in response to expected or realized prepayments, and for funding. Corporates typically follow a debt issuance (typically fixed-rate bonds) by swapping these to floating rates at opportune times (steep yield curves). Finally, speculators such as hedge funds and proprietary trading desks use swaps to express views or take advantage of level/slope/curvature of interest rate curves. Since swaps are over-the-counter (OTC) instruments, they are quite flexible and can be tailor-made to address one′s needs.
MARKET INSTRUMENTS
For the USD swap market, the benchmark floating index is the 3-month London Inter-Bank Offered Rate (LIBOR), which is the prevailing 3-month interest rate for dollar-deposits between London banks. The default settlement date, also known as the Spot Date, is 2 London business days after trade date, rolled forward if necessary to be a good New York and London business day.
In order to construct a Libor discount factor curve (Libor curve), a collection of the following input instruments are used.
Cash Deposit Rates, Libor Fixings
Every day, at 11:00 a.m. London time, the British Bankers Association (BBA) polls various dealers for cash deposit rates for various terms: Overnight (O/N), Tomorrow Next (T/N) (although no longer quoted), 1 week, 2 week, 1M, 2M, 3M, . . . , 12M, and publishes the resulting averages for various currencies. When USD swaps are traded during the day, these Libor fixings (rather than their live quoted values) are used to construct the front end of the Libor curve.
For USD, all these rates are quoted simple (no compounding) Act/360. The O/N rate is for a deposit starting on trade date to the next London business day, while T/N (use O/N if not available) is for an overnight forward deposit starting on the next London business day and ending 2 London business days from trade date. These 2 rates provide the discount factor for spot date.
The other deposit rates, 1wk, 2wk, 1m, . . . , 12m are for deposits starting on the spot date for the corresponding term.
The typical BBA fixings used are O/N, T/N, and 3m, and to a lesser degree 1m, 2m, 6m, rates. Other rates are rarely used.
FRAs
An n × m forward rate agreement (pronounced n-by-m FRA ′frä) is an agreement based on the economic value of a forward deposit starting n months from today, and maturing m months from today, with the payoff based on the difference between the actual ″m - n″-month rate versus the agreed-upon deposit rate K. So a 2 × 5 FRA is based on the 3m (forward) rate, starting in 2m. At inception, the rate K is chosen so that the FRA has zero value, that is, K is equated to the forward rate. A seasoned FRA has positive or negative value, depending on how the fixed rate K compares to the current market forward rate. The payoff of n × m FRA occurs at rate fixing date—n-months from now—and uses the actual rate for fixing and discounting (called ″FRA discounting″). For example, if one owns a 2 × 5 FRA struck at K, the payment in 2 months is: per unit of notional, where α ≈ 1/4 is the length (Act/360) of the [2m,5m] period.
per unit of notional, where α ≈ 1/4 is the length (Act/360) of the [2m,5m] period.
While not as liquid as ED futures, FRAs are quoted and can be used as input instruments to a Libor curve. One can think of FRAs as the basic building block for swaps. A swap is just a portfolio of FRAs, with the difference that floating payments are paid at the end of each calculation period, while FRAs pay the discounted value of this floating payment at the beginning: These would be economically equivalent as long as the floating index matches the funding cost. Another difference is that swaps typically have 1 fixed flow for each 2 floating flows, for example, USD swaps are semiannual/quarterly on fixed/floating legs. Modulo these differences, a swap is simply a portfolio of FRAs, or equivalently a FRA can be considered as a single-period/reset swap. The quote convention for FRAs is sometimes in reference to the floating index: buying, selling a FRA is same as paying/receiving in the single period swap.
Euro-Dollar Futures
Euro-dollar contracts are exchange-traded derivative contracts traded in the International Money Market (IMM) pit of the Chicago Mercantile Exchange (CME, or ″Merc″). Each contract settles on 2 London business days prior to the third Wednesday of the contract month based on that day′s BBA Libor fixing.
3m-Euro-dollar contracts settling on the last month of each quarter (March, June, September, December) are actively traded and fairly liquid for the first 3y of contracts (12 of them). Later contracts (up to 40, 10y out) can be traded, but have diminishing liquidity. There are also 6 monthly 3m-Euro-dollar contracts for the first 6 months, and also 12 monthly 1m-Euro-dollar contracts, but these are not as liquid as ″Quarterly 3m-Euro-dollar Futures Contracts″ (ED futures from now on).
Each ED is based on the interest payment of a hypothetical $1M 90-day deposit starting on the third Wednesday of quarter-end. A Euro-dollar ″tick″ is the change in value of the contract due to a 1 bp change in the implied interest rate:

ED futures trade based on price, and have an implied futures rate (100-Price). They are forward contracts and have 0 value at trade time. Other than opening a futures (margin) account and posting initial margin, and paying brokerage (about $1 per contract), no money is exchanged when trading them. So if ED1 is trading at 95.00 (implied futures rate 5%), and you buy 100 contracts, you pay no money (except $100 for brokerage). However, unlike true forward contracts (FRAs) which require no cash exchange until expiration, ED contracts are cash-settled daily.
At each day′s end, the Merc computes that day′s final settlement value based on the markets at the close, 2 p.m. Chicago time. Every open position will get cash-settled, akin to closing your ED position at settlement price, and immediately initiating an identical new position. For example, having bought 100 ED1 for 95.00, if that day′s settlement value is 95.10 (implied rate of 4.90%), you have made 10 ticks, or $25, 000 = 100 × 10 × $25, and this amount will be posted to your margin account. Until you close out the position (sell 100 ED1), each day an amount equal to the daily move (in ticks) times the number of contracts in your account is posted or taken from your futures account. When you close out the position (sell 100 ED1), the difference between the sale price and prior day′s settlement value is used and posted/taken from your futures account.
ED futures are also referred to in colors. The first 4 contracts are called whites, the next 4 reds, followed by 4 greens, 4 blues, 4 golds, 4 purples, 4 oranges, 4 pinks, 4 silvers, and 4 coppers. So ED5 is sometimes referred to as first red, ED6 as the second red, ED9 as the first green, and so on.
A common trade is to buy/sell an ED pack: 1 contract in each series of a specific color. Buying/selling 1 red pack means buying/selling 1 ED5, 1 ED6, 1 ED7, and 1 ED8. The PV01 of a pack is $100.
Trading an n-year ED bundle is the trading of the first 4 × n EDs. For example buying/selling 1 2y bundle is buying/selling of 1 ED1, 1 ED2, . . . , 1 ED8 contract. The PV01 of an n-year bundle has n × $100.
Packs and bundles are quoted based on change on day. For example, ″+3 (up 3) on day″ means each contract in the pack is priced at prior day′s close plus 3 ticks.
Future/Forward Convexity Adjustment
As stated, ED futures are not exactly forward rate contracts, as they have daily mark-to-market settlement, while true FRAs do not. For FRAs the P&L of the contract (the difference between the contracted value and the realized value) is only paid at the final settlement date, and hence its value today is the properly discounted value of this future settlement value. In contrast, the P&L of the future contract, while based on the same forward interest rate, is broken out into a series of daily P&Ls and paid daily without discounting. Since interest rates are highly correlated (overnight rates versus forward rates in our case), this daily settlement confers an advantage to a short position in the ED future contract, as he earns money and gets to reinvest it daily at overnight rates when interest rates are high, and loses money and hence has to borrow overnight money when interest rates are low. This systematic advantage for a short position does not go unnoticed by the market. The short is charged for this free lunch in the form of being required to sell the contract at a cheaper level than would have otherwise been if it was a true FRA. Therefore, the implied rate in the future contract (100 - price) is higher than the true forward rate, and this difference is known as the future-forward convexity adjustment. The size of convexity adjustment depends on the expected extra P&L of the short position over the life of the contract, which in turn depends on the volatility of the rates, and requires a model to calculate it. In general, it can be shown that the implied future rate is the expected rate at future′s settlement (see Appendix B). A commonly used formula based on the Ho-Lee model is as follows: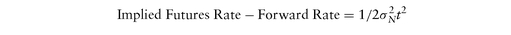 for a future contract that settles in t-years, and has Normalized volatility of σN. As can be seen, the effect of the convexity adjustment gets larger (t2 order) for later settlements, and this is one of the reasons that later contracts (3-years and out) are less liquid, as their value depends on the proper modeling of the convexity adjustment. Armed with a convexity adjustment model, one can construct a Libor curve purely based on a strip of ED futures, and calculate par-swap rate from this curve. The resulting par-swap rate is called the strip rate, and can be compared to quoted par-swap rates to potentially take advantage of differences.
for a future contract that settles in t-years, and has Normalized volatility of σN. As can be seen, the effect of the convexity adjustment gets larger (t2 order) for later settlements, and this is one of the reasons that later contracts (3-years and out) are less liquid, as their value depends on the proper modeling of the convexity adjustment. Armed with a convexity adjustment model, one can construct a Libor curve purely based on a strip of ED futures, and calculate par-swap rate from this curve. The resulting par-swap rate is called the strip rate, and can be compared to quoted par-swap rates to potentially take advantage of differences.
Stub Rate, Interpolated Libor
The first ED future′s settlement is rarely 1m or 3m away. One usually needs to obtain the discount factor for the ED1′s settlement, and some brokers quote a stub rate, which is for a deposit starting on Spot Date, and maturing on the ED1′s settlement date (2 London business days prior to the third Wed of the contract month).
An alternative is to interpolate BBA′s Libor fixings to come up with the stub rate. Assume that ED1 settles 45 days from Spot Date. In this case, we can linearly interpolate 1M Libor and 2M Libor to come up with a plausible stub rate.
Par-Swap Rates
Par-swap rates for various maturities are quoted and are used to construct a Libor curve. In USD, the following maturities are quoted: 2y-10y, 12y, 15y, 20y, 25y, 30y. Longer par-swap rates (40y, 50y, 60y) are quoted as spreads to 30y rates. Also, USD par-swap rates are typically quoted as (swap) spreads to current treasuries with similarly quoted maturity (CT2, CT3, CT5, CT10, CT30), or interpolated treasury yields for other maturities, though 12y spread is usually quoted as a spread to CT10. In most other currencies, the swap rates are directly quoted, and not as spreads to government yields. For 1y maturity, the swap rate is derived and calculated from the money market futures (ED for USD). As the 1y point is the cross over point between money market and capital markets, it is often quoted with a different frequency and/or day-count basis than other rates, so care needs to be taken when trading 1y swaps.
Regardless of the quote mechanics, one arrives at a series of par-swap rates.
SWAP TRADING—RATES OR SPREADS
USD par-swap rates are quoted as spreads to benchmark current (on-the-run) treasuries, and a typical broker swap screen is shown in Table 3.1, and the graph of the swap rates or spread versus maturity is known as the Swap and Spread curves, Figure 3.1. For example, a 2y spread market of 55-55.5 means that the dealer is willing to pay the yield of CT2 treasury, y2, plus 55 bp, and receive y2 plus 55.5 bp.
USD swaps can trade either as rates or spreads.
TABLE 3.1 A Typical USD Swap Broker Screen
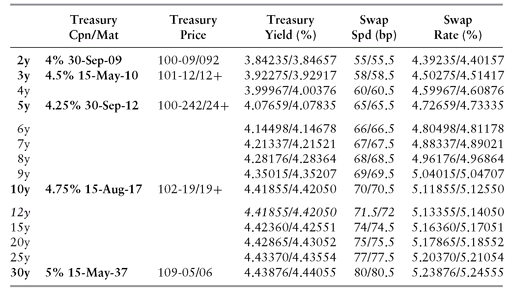
FIGURE 3.1 USD On-the-Run Treasury, Par-Swap, and Swap-Spread Curves
Trading in Rates
When one is trading rates, one is taking duration risk. For example, receiving in $100M 2y-swap has similar risk of buying $100M 2y treasuries. In this case, the inquiry should specify that swap rates are needed: ″My client wants to receive in $100M 2y swaps. Rates! Where will you pay?″ Dealer response: ″Spreads are 55-55.5. With 2y treasury trading at 100-09/100- 092 (3.84235%-3.84657%), I will pay 4.39235% (=3.84235% + 55 bp).″ The reason that the dealer is using the offered side of the treasury (100-092 price, 3.84235% yield) is that he is paying in the swap, so he has short duration risk. U.S. swap traders are not in the business of taking duration risk (that belongs to the cash/treasury desk), only spread risk. As soon as the trade is done, the trader will cover his short and buy treasuries, that is, lift the offer of 100-092. This will leave him with spread risk, where he is paying the bid side (55 bp) of the swap-spread market. With enough 2-way flows, he will try to pay the bid side of the swap-spread market, and receive the offered side, and make a living out of the bid-offer spread (of the swap-spread market).
Trading in Spreads
On the other hand, one can directly enter into a spread trade by entering into a swap and simultaneously providing the treasury hedge.
Buying a spread is the simultaneous purchase of treasuries (called cash), and paying in swaps. This is also called paying in spreads. Selling a spread is the simultaneous sale of treasuries, and receiving in swaps. This is called receiving in spreads. To remember it, always recall that in a spread trade, whatever you are doing to the treasury (buy/sell), you are doing to the spread (buy/sell).
The amount of treasuries is adjusted so that the PV01 of the treasury position (using the PV01 formula in Chapter 1) matches the PV01 of the swaps. For example, let the 2y treasury trade at 100-09/100-092, with PV01 of $185.10 per $1M face. Also assume that PV01 of 2y swap is $189 per $1M notional. A spread inquiry goes as follows: ″My client wants to receive in $100M 2y spreads. Where is your bid?″ Dealer response: ″2y spreads are 55-55.5, this is a good client, I′ll bid/pay 55.1!″ If the trade is done, one agrees on the price of the treasury, let′s say 100-08+, compute the yield (3.85501%) and compute the swap rate 4.40601 % (= 3.85501 % + 55.1 bp). One then calculates the PV01-equivalent amount of treasuries: $100M × 189/185.10 = $102.107M face. The trade ticket will state that the client sold $102.107M face of 2y treasury at the clean price of 100-08+, and simultaneously the client is receiving 4.40601% in $100M 2y swaps.
Note that since the dealer is being provided with the treasury hedge, he does not have duration risk, and the exact price of the passed-on treasuries is not as critical as when trading rates. However, he does have spread risk, expressed as Spread-PV01: $100M 2y-spread risk, or $18,900 (2y) Spread PV01.
Interpolated Spreads
For swap maturities where an equivalent-maturity Current Treasury does not exist, one uses an interpolated treasury yield, and quotes swap spread relative to this interpolated yield. For example, a quoted 7y swap-spread market of 67-67.5 bp is relative to 3/5 y5 + 2/5 y10 where y5, y10 are the yields of the current 5y, 10y treasuries (CT5, CT10).
Let′s assume that the CT5 is trading at 100-242/100-24+ (4.07835%- 4.07659%) with a PV01 of $444.90 per $1M face. Also, let CT10 trade at 102-19/102-19+ (4.42050%-4.41855%) with a PV01 of $801.30 per $1M face. Finally, let the PV01 of a 7y par swap be $589.70 per $1M notional.
A dealer will compute the 7y interpolated treasury yield market as 4.21337%-4.21521%. With 7y spreads trading at 67-67.5 bp, his market when trading rates would be 4.88337%-4.89021%. If receiving in $100M 7y rates, he will receive 4.89021% = 3/5 × 4.07835% + 2/5 × 4.42050% + 67.5 bp = 4.21521% + 67.5 bp. In order to hedge himself, he will then compute how much 5y and 10y treasuries he needs to sell: $79.528M = $100M × 2/5 × 589.70/444.90 of CT5 at 100-242, and $29.437M = $100M × 2/5 × 589.70/810.30 of CT10 at 102-19.
If receiving in spreads, the dealer will quote 67.5 bp as his offer. When the spread trade is done, one then fixes the 5y and 10y treasury prices that will be sold to the client as the hedge, and computes the interpolated yield from these prices. Let′s assume we use the offers: 100-24+ (4.07659% yield) for CT5, and 102-19+ (4.41855% yield) for CT10. The interpolated yield is then 4.21337% = 3/5 × 4.07659% + 2/5 × 4.41855%, and the dealer will be receiving in 4.88837% = 4.21337% + 67.5 bp in $100M 7y swaps. Simultaneously, he sells $79.528M CT5 at 100-24+ and $29.437M CT10 at 102-19+ to the client.
Swap Curve Trading
Similar to the treasury curve, one can express views or hedge exposure to the slope (longer rate - shorter rate) of the swap curve via curve trades. For 2 given swap maturities, one can put on a steepener by buying the curve, that is, receiving in the shorter-maturity swap and paying in the longer-maturity, with the notional of each swap chosen so that each swap has the same PV01. Similarly, one can put on a flattener by selling the curve: paying in the shorter-maturity and receiving in PV01-equivalent amount of the longer swap. For example, one can buy the 2′s/10′s swap curve by receiving in $100M 2y swap and paying in $24.54M (= $100M × 7.62/1.87) 10y swaps, where PV01 (2y) = 1.87, PV01 ( 10y) = 7.62 cents. In this trade, one is immune to parallel moves in the swap curve, but is carrying $18,700-per-01 2′s/10′s curve risk. For each 1 bp steepening/flattening of the 2′s/10′s curve, one makes/loses $18,700.
One can also trade curves forward. A forward swap curve steepener trade consists of receiving in shorter-maturity forward swap while paying in PV01-equivalent longer forward swap. For example a 1y-forward 2′s/10′s steepener consists of receiving in a 2y swap, 1y forward, while paying in a PV01-equivalent 10y swap, 1y forward.
SWAP SPREADS
In the USD swap market, swap traders are primarily trading swap spreads, and hedge most of their duration risk, either with other swaps or with U.S. treasuries. As such, they are mostly focused on swap spreads, and manage that risk. To understand swap spreads, one has to remember that they primarily represent the average credit spread of the Libor Panel—consisting of the banks polled by BBA to determine its estimate of Libor—generally thought to be equivalent to AA-, versus U.S. government credit. While many explanations have been offered as to what drives swap spreads, they all come back to relative supply/demand of bank versus government credit. For example, in the early 1990s government-sponsored agencies like Fannie-Mae, Freddie-Mac, would hedge the duration mismatch in their mortgage portfolios with U.S. treasuries, resulting in tightening swap spreads. When later in the decade, they switched to use swaps, swap spreads in general widened. Similarly, in a steep curve environment, corporates will swap their fixed-rate debt (either existing or new issue) by receiving in swaps to take advantage of lower short-term funding costs. This increased demand for receiving in swaps results in tightening swap spreads. Another supply/demand driver occurs when the government is running a deficit and issuing more debt via U.S. treasuries: this results in the tightening of swap spreads. On the flip side, during periods of economic turmoil and flight-to-safety, there is high demand for U.S. treasuries, resulting in widening swap spreads. As noted, all of these drivers boil down to relative supply/demand.
Another way to understand swap spreads is as the financing spread between U.S. treasuries versus swaps, that is, Libor versus repo. The 2y swap spread is the market′s expectation of the average UST repo versus Libor rates for the next 2 years. This is the basic understanding of quoted swap spreads, sometimes called headline spreads as they are the difference in the yields of the current treasuries versus par-swap rates. As a given current treasury, say CT10, is issued quarterly, it will remain current for 3 months, while the 10-year par-swap rate is for a swap that matures in exactly 10 years from trade date, headline swap spreads suffer from calendar roll-down and abrupt shift on auction dates.
Matched-Maturity Spread
A similar measure of swap spreads is the Matched-Maturity (sometimes called Yield-Yield) swap spreads, which measure the yield of a given treasury security to the par-swap rate of a swap maturing on the same date as the given treasury. When one buys/sells a matched-maturity spread, one buys/sell a given treasury and pays/receives in PV01-equivalent amount of a swap with the same maturity date. Therefore it is 2 trades, done as a package. When dealing with short-term treasuries, say treasury bills or treasuries less than 2 years remaining maturity, instead of swaps, one can buy/sell a strip of ED futures versus selling/buying the treasury. This yield spread is referred to as the Treasury-ED (TED) spread, expressed usually as the semi-annual yield of both (Treasury, ED) components.
Asset-Swap Spread
Another way of trading swap spreads is via asset-swaps where the swap fixed leg′s payment and dates are required to match exactly those of a given bond, and an asset-swap spread is added to the Libor leg of the swap, with either the notional of the floating leg matching the principal amount of the bond, par-par asset swap, or the initial dirty price of the bond, Market Value asset swap. In either case, the asset-swap spread is primarily the difference between the funding level for the treasury, that is, its repo rate, versus Libor until the maturity of swap/bond.
For example, if on trade date 2-Oct-2007, the U.S. CT2 with coupon rate C = 4%, maturity 30-Sep-2009 is trading at clean price of P = 100 - 02+, y = 3.95866%, with gross price of 100.11091% for settlement date 3-Oct- 2007, the cash flows of $100M CT2 on a asset swap are as follows:
1. On 3-Oct-2007, the buyer buys $100M CT2 from seller for either $100M in Par-Par, or $100,110,910 in Market-Value asset swap.
2. The buyer passes on all received payments of the bond. On every coupon date, 31-Mar-2008, 30-Sep-2008, 31-Mar-2009, 30-Sep-2009, the buyer pays the received coupon ($2M = $100M × 0.04/2) to the seller (receiver in swap), and also the principal $100M at maturity.
3. For each quarterly calculation period until maturity, the buyer receives ″3m-Libor minus Spread″ on $100M notional for par-par, or $100,110,910 notional for market-value, with Libor fixed at beginning of each calculation period and paid at end.
4. At maturity, the buyer receives the notional of the Libor leg: $100M for Par-Par, or $100,110,910 for Market-Value in exchange for passing the bond principal payment ($100M).
Note that in a par-par asset swap, the seller has to initially deliver the bond for par, so she is making a loan of $110,910 to the buyer, while in a market-value asset swap, the seller′s loan ($110,910) is shifted from upfront to the maturity date of the swap. In either case, the asset swap spread is solved for such that the PV of all these cash flows—including the up-front or back-end loan—is zero when discounted off the swap discount curve.
For the duration of the swap, a leveraged investor has to finance $100M CT2 at the prevailing overnight or term repo rate (plus variation margin) versus receiving Libor-Spread. Therefore, an asset swap′s ongoing payment are Libor-Spread versus repo. Said in another way, a leveraged buyer has locked in Libor-Repo spread at the asset swap level, and benefits if the realized spread payments turn out to be higher during the life of the swap.
Zero-Coupon Swap Spreads
The purest expression of swap spreads is the swap rate for a zero-coupon swap versus the yield of a similar-maturity zero-coupon treasury bond, as each instrument has a single cash flow, and hence their yield spread is just a measure of credit quality for the maturity point. A Zero-Coupon Swap consists of a fixed and a floating leg, with both legs having a single (net) payment at maturity. The floating leg is usually based on the benchmark swap index, Libor-3m for USD, and the final payment is based on the compounded interest of current and future Libor settings:
where T is the maturity of the swap, and N0 is the initial notional of the swap. Similarly, the fixed leg′s single payment is based on the compounded interest based on the quoted zero-coupon rate. For example, the fixed payment of an N-year swap with semi-annual zero-coupon rate of Z is
N0 × [(1 + L3m(0)/4) × (1 + L3m(3m)) × · · · × (1 + L3m(T - 3m)/4) - 1]
N0 × [(1 + Z/2)2N - 1]
In practice, one has to specify the initial notional (N0) or final notional (NFinal) of the swap, related by
N0 x (1 + Z/2)2N = NFinal
The fixed leg′s single payment is then NFinal—N0 and is called the fixed payment, paid at swap maturity (T).
Note that as long as our financing cost equals Libor-3m, then the present value of the floating leg is
N0—P V(N0 Paid at T)
In this case, since the par zero-Coupon rate is quoted so that the value of the swap at inception is zero, it is simply a way of expressing the Libor discount factor for T:

Z-Spread
Finally, another measure of swap spreads is the zero rate spread, most often called z-spread. The idea is to apply a parallel shift to the Libor discount curve so that the market (dirty) price of the bond is recovered if all the remaining cash flows are discounted using this shifted curve. The size of the required parallel shift applied to the zero rates is the z-spread. Note that to be precise, one has to pin down the quote convention of the zero rates (compounding frequency, if any, and treatment of fractional years), so there is no universal z-spread. Moreover, while popular with quants, z-spreads are not traded: they are merely a (and yet another) measure of swap spreads, and often provide pretty much the same information or cheap/rich signals as other (traded) spreads (matched-maturity, asset swap).
Swap Spread Curve
A graphical representation of any of the above spreads (headline, matched-maturity, asset swap, z, zero-coupon) versus maturity is referred to as the swap spread curve, or simply the spread curve. One can express views or hedge exposures to different points of the spread curve. When engaging in 2 simultaneous spread trades of different maturities, one is said to be trading spread of spreads or alternatively since each spread trade consists of two trades, one cash (treasury), and one swap, it is also referred to as a box trade. For example, when taking views on the slope of spread curve, say between 2y point and 5y point, buying a ″2′s-5′s spread of spreads″ means buying the 5y spreads (buying 5y cash, paying in 5y swaps), and selling the 2y spread (selling 2y cash, receiving in 2y swaps), thereby profiting from steepening of spread curve between the 2-year and 5-year maturities. The amount of treasuries (and hence swaps) on each leg is adjusted so that each will have the same spread PV01. In this way, the trade is immune to parallel moves in the spread curve.
Spread-Locks
A future headline swap spread can be locked via spread-lock trades, which come in 2 varieties: discrete-setting (also called European) spread-lock, or rolling spread-lock. In a discrete-setting spread-lock agreement for the N-year spread, the N-year headline swap spread is locked at a fixed level K for a future date, and at expiry, one enters into a N-year spread trade. If long a spread-lock, one pays in N-year swap with fixed rate set to expiry date′s par-swap rate S (as published by ISDAFIX 11:00 a.m. New York) and buying PV01-equivalent amount of US CT[N] at a yield of S—K , that is buying the headline spread at K. If one is short the spread-lock, then one receives in swaps at S and sells PV01-equivalent amount of CT[N] at S—K yield. Instead of physical settlement, one could instead opt for cash-settlement with cash value set to the difference between the N-year headline spread (as published by ISDAFIX 11:00 a.m. New York) versus the locked spread K , multiplied by PV01 of an N-year swap.
A rolling spread-lock is the periodic fixing and payments of the ISDAFIX headline spread versus the locked rate, accrued for the length of each calculation period. For example, in a 1-year quarterly rolling 10y spread-lock struck at K , there are 4 periodic payments of
per unit notional for each calculation period [Ti , Ti +1 ], where α(Ti , Ti +1 ) is the accrual fraction according to some day-count (typically 30/360) with payment at Ti+1.
(S(Ti )—K ) × α(Ti , Ti +1 )
Spread-locks are typically quoted as a spread to the current headline spread.
RISK, PV01, GAMMA LADDER
As opposed to bonds where we are dealing with a single yield-to-maturity, in swap-land we are dealing with a series of interest rates that are aggregated to construct a discount factor curve. This discount factor curve is then used to discount swap cash flows and calculate par-swap rates and forward rates. Therefore the value of a swap depends on all the input instruments used to construct the discount factor curve.
In order to compute the sensitivity of a swap-related instrument to changes in interest rates, 2 procedures are commonly used:
1. Parallel PV01: Bump up all input rates (cash, futures, par-swaps) by 1 bp, and revalue the instrument. The change in the value of the swap is called parallel PV01 (also called delta). A variation is to compensate for different input quote conventions (Act/360 for simple cash, futures rates; SA 30/360 for swaps), and either convert all quotes to a single convention, or reconstruct a new discount factor curve by bumping all the implied zero rates.
2. Partial PV01: For each input instrument, bump up its rate by 1 bp while holding all other inputs constant, and revalue the instrument. This gives rise to a series of sensitivities—one for each input—called bucket or partial PV01/Delta. The sum of partial PV01s should be close to parallel PV01, the difference due to instrument′s convexity and higher order effects.
Admittedly, interest rates do not move in either fashion: it is rare that only one rate changes while the others do not. Also, even when they move together, interest rates do not move by the same amount: short-term rates (say 2y) typically move more than longer (say 30y) rates. In order to hedge under a real-life rate movement scenario, we can compute the change in value due to a curve shift scenario. The assumed scenario is usually derived from a statistical analysis of historical curve movements using methods such principal component analysis (PCA).
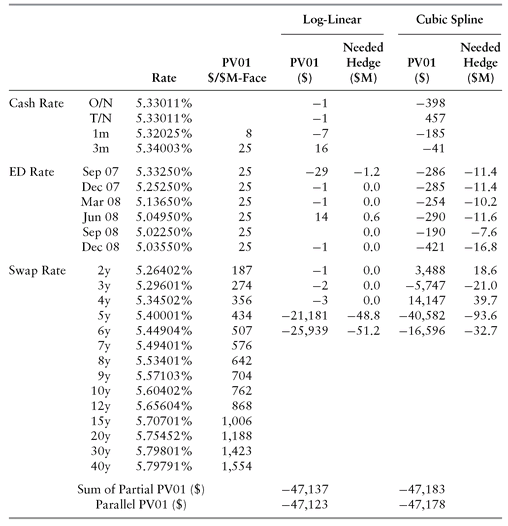
Armed with Partial PV01s, and the PV01 of each input instrument, we can then compute the amount of each input instrument needed to hedge. An example is shown in Table 3.2.
As alluded to before, the choice of curve build method greatly affects the prescribed hedge. For example, when hedging a $100M 5.5-year receiver swap, the log-linear interpolation method, while discontinuous in forward rates, prescribes paying in $48.8M 5y swaps, and $51.2M 6y swaps. This is intuitive, and close to what a trader expects. On the other hand, using cubic splines results in a smooth forward curve, but the prescribed hedge for a 5.5-year receiver swap is to receive in $18.6M 2y swap, pay in $21M 3y swap, receive in $39.7M 4y swap, pay in $93.6M 5y swap, and pay in $32.7M 6y swap! This tradeoff between smoothness in forward rates versus reasonable (local) hedge behavior affects any curve build method, and needs to be considered when choosing one.
Convexity, Gamma Ladder
Swap and option traders are not only interested in the parallel/partial deltas, but also how their deltas change when the market moves, that is, convexity which in swap-land is also referred to as gamma. When the market moves, a completely hedged book can gain/lose duration, and needs to be rebalanced. Often when there is a large market movement (market gap), there is not enough time to recompute partial deltas for a large book. In order to be prepared for such movements, traders precompute parallel and partial deltas for a variety of scenarios (typically a series of parallel shifts) to come up with a gamma ladder. This allows them to quickly rebalance their books under fast market conditions.
Reset Risk, IMM Swaps
Another risk that swap traders pay attention to is exposure of the floating leg to upcoming Libor fixings. Swap curves are usually constructed out of O/N, 1m, 2m, 3m, money-market futures, and par-swap quotes, and the bucketed risk to these rates are calculated. However, for the very front end, say the first 3 months, the difference between derived forward-3m rates versus their actual fixings, called reset risk, has to be monitored and hedged. The hedging is usually done via FRAs that start on the same date as the upcoming resets, and interdealer brokers routinely quote a strip of daily FRAs for, say, any day from today to 3 months from now.
TABLE 3.2 Parallel and Partial PV01s for a $100M 5.5y Swap
If the reset dates coincided with those of ED futures, loosely called IMM dates, then one could use ED futures to mitigate reset risk. Indeed, there is a variant of swaps, called IMM swaps, whose reset dates by design fall exactly on IMM dates. For IMM swaps, the fixed leg′s calculation periods are also required to fall on IMM dates. For example, 1-year USD IMM swap starting on March-2009 has 4 quarterly calculation periods book marked by [18-Mar-2009, 17-Jun-2009, 16-Sep-2009, 16-Dec-2009, 15-Mar-2010], and 2 semiannual calculation periods book marked by [18-Mar-2009, 16-Sep-2009, 15-Mar-2010]. Note that each calculation period starts/ends on 3rd Wednesday of each quarter end (IMM date), with reset date 2 London days prior to it.
CALENDAR RULES, DATE MINUTIAE
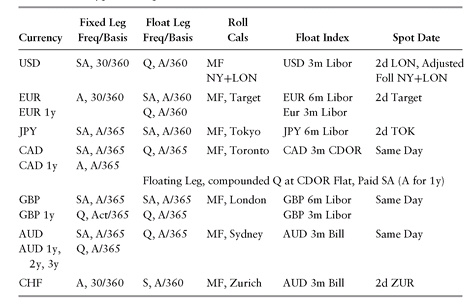
When trading swaps and their derivatives, they are generally quoted and traded based on terms, for example, a ″2-year″ swap, since the specification of all the relevant dates is cumbersome and time-consuming. Each swap market has a series of standard conventions used as default to generate most of the relevant dates (see Table 3.3). Therefore, only the most salient terms of a swap are communicated at trade time, and any remaining date ambiguity is generally resolved at the trade confirmation level, and if not captured at that stage, ultimately resolved (usually not amicably!) on payment dates. Note that each day of missed interest for a typical level of interest rates, say 5%, will cost 1.3889 cents, or $13,889.89 for a $100M swap, a typical size. A missed day here, and a missed day there, and pretty soon. . . .
Calculation Periods, Roll Conventions
Each swap leg is based on a series of contiguous calculation periods, book marked by the effective and the maturity dates. For each typical calculation period, there are 4 salient dates. Calculation start/end dates: the first/last day for the calculation period where interest accrues. These dates do not need to be, but often are, adjusted to be good business days; payment date: the date where the interest payment is made, which needs to be a good business day; index reset date: for floating payments, the date where the index, say 3m-Libor, is observed/reset.
All of the above dates are usually adjusted or rolled to be good business days according to some specified banking center(s), for example, New York and London for USD swaps. The two prevalent roll conventions are following and modified following. In the Following roll convention, if the date falls on a holiday, it is rolled to the next good (nonholiday) business day. In the modified following (MF) roll convention, a holiday date is adjusted to the next good business day, unless it rolls into the next month, in which case, the date is instead adjusted backwards to the last good business day. Similarly a previous and modified previous roll convention can be defined, but these are rarely used in practice.
TABLE 3.3 Typical Swap Conventions
To highlight the date issues, assume that it is Wednesday 27-Feb-2008, and we have just traded a standard 1-year USD swap. By standard, we mean the following default (see Table 3.3) attributes of USD swaps:
Fixed Leg: Semiannual, 30/360, Modified Following (MF), New York and London
Floating Leg: Quarterly reset and payment, Act/360, MF, New York and London, based on 3-month Libor (quoted Act/360, MF, London)
The above convention is sometimes abbreviated to Semi-Bond vs 3′s, which denotes semiannual, 30/360 (sometimes referred to as ″Bond″) convention for the fixed leg, versus 3-month Libor.
Effective, Maturity Dates
The first step is to resolve the effective and maturity dates of the swap, as these control the total number of interest-accrual days for each leg. Unless otherwise specified, swaps are spot-starting, so the Effective date is the same as the spot date. The spot date, or the default settlement date is market-specific: for USD market, it is 2 London business days after the trade date, adjusted forward if necessary to be a good NY+LON business day. In our example, the trade date is Wed 27-Feb-2008, and the spot date and hence the effective date is Fri, 29-Feb-2008 (2008 is a leap year). Maturity date is ″1-year″ after the effective date, which gets us to Sat, 28-Feb-2009. Since USD swaps are adjusted MFOL, this means that the adjusted maturity date is Fri, 27-Feb-2009. So we have a swap from 29-Feb-2008 to 27-Feb-2009.
Fixed Leg′s Calculation Dates
The fixed leg of USD swaps is paid semiannually, so we need to break the swap term into two calculation periods, [29-Feb-2008, X], [X, 27-Feb- 2009]. To determine the X, we have to first generate the date, and then adjust it according to the specified rule, MF—if ″unadjusted″ was specified, then we would leave it be even if it is a holiday.
The choice for the unadjusted intermediate date X can be:
Option 1. ″28-th rolls″ 6 months prior to unadjusted maturity date, Sat, 28-Feb-2009. This is the most common choice, where the intermediate unadjusted dates are generated backwards starting from unadjusted maturity date, and specified to fall on a particular day of the month (″roll day = 28th″, or ″28-th rolls″). In this case, the unadjusted intermediate date is Thu 28-Aug-2008, which is a good New York and London business day, so we do not need to adjust it.
Option 2. ″Month-end rolls″ 6 months prior to unadjusted maturity date, Sat, 28-Feb-2009. Since the unadjusted maturity date falls on the last day of the month, another option is to require X to also fall on the last day of the month, 6 months prior to it. In this case, the unadjusted intermediate date becomes Sun 31-Aug-2008, which gets adjusted (modified following) to Fri 29-Aug-2008.
Option 3. ″29-th rolls″ 6 months after the effective date, leading to Fri 29-Aug-2008, which is a good New York and London business day. This is rarely used in practice.
Option 4. 6 months prior to the adjusted Maturity Date, Fri, 27-Feb- 2009. This choice is rare, but if chosen it leads to Wed 27-Aug-2008, a good New York and London business day, and can be specified as ″27-th rolls.″
Floating Leg′s Calculation Dates
The floating leg of USD swaps is based on the 3-month Libor index, and is reset, accrued Act/360, and paid quarterly, so we need to generate 3 new quarterly intermediate dates between the effective and maturity dates: [29-Feb- 2008, X1], [X1, X2], [X2,X3],[X3, 27-Feb-2009]. A new wrinkle that arises is whether these dates are generated recursively, or with respect to the effective/maturity dates. For example, assume that we are generating the dates backwards starting from the maturity date. Having generated the intermediate date 3 months prior to the maturity date, X3, do we use X3 to generate a date 3 months prior to it, X2, or do we generate a date 6 months prior to the maturity date? The latter choice is the most common. A similar approach applies if generating dates forward from the effective date.
Similar to the preceding discussion for fixed leg, there are different choices on generating the calculation dates. We consider only Options 1 and 2, which are the most common:
Option 1. ″28-th rolls″ Generate dates backwards with reference to the unadjusted maturity date. The unadjusted intermediate dates following 28-th rolls are Wed 28-May-2008, Thu 28-Aug-2008, Fri 28-Nov-2008, which all happen to be good New York and London business days. If not, they would have to be adjusted MF, New York and London.
Option 2. ″Month-End rolls″ The unadjusted dates are required to fall on the last day of each month: Sat 31-May-2008, Sun 31-Aug-2008, Sun 30-Nov-2008, which are then adjusted MF to Fri 30-May-2008, Fri 29-Aug-2008, Fri 28-Nov-2008.
Payment Dates
Having generated the calculation periods, the next step is to generate the payment dates corresponding to each calculation period Since calculation dates are usually adjusted to be good business days, payment dates equate the calculation end date for each period (as long as the payment/calcuation periodicity and holiday calendars match), however for unadjusted calculation periods, the calculation end date (if a holiday) needs to be adjusted to be a good business day so that payments can actually be made and settled.
Index Dates: Reset, Start, End
Finally, for each calculation period of the floating leg, the rate reset date for the floating index needs to be generated. For USD swaps, the index is 3m-Libor and is observed/reset 2 London days prior to the beginning of each calculation period. On each calculation period′s index reset date, the market rate for a 3-month Libor deposit starting on the calculation start date, as published by BBA, is observed. These start/end dates of this underlying deposit are sometimes called rate effective/maturity dates or index start/end dates. While by construction, the rate effective date coincides with calculation start date, the rate end date does not necessarily coincide with the calculation end date, and these dates can be off by a few days. This is due to the way the swap calculation periods are generated (multiple months from the anchored unadjusted maturity date) and then rolled (MF, New York, and London) versus how the rate end date is generated (3 months after the calculation/rate start date) and rolled (MF, London only). Another way that this mismatch can arise is for IMM Swaps, where calculation periods are not 3 months apart, but cover inter-IMM intervals—sometimes called IMM gaps—that is, they run through 3rd Wednesdays of each quarter-end, and usually have 13 weeks (91 days), but occasionally 14 weeks (98 days). This date mismatch—while small, a few days for regular swaps, but as long as 6 days for IMM swaps—somewhat invalidates the perfect replication needed to establish the value of a floating leg as D(Effective Date) - D(Maturity Date), but is usually ignored in practice, or compensated for via a delay-of-payment convexity adjustment.
Day Count Basis
The actual cash flows of the swap for each calculation period consist of the interest rate—either fixed rate or the floating index—accrued for the length of the calculation period according to the specified day-count basis, and paid on the corresponding payment date. For a given calculation period, the day-count basis specifies the length of year for which the interest accrues. The most common type of bases are 30/360 (or any of its variants), Act/365, Act/360, and to a much lesser degree, Act/Act which is different and not to be confused with the Act/Act convention used to calculate accrued interest for bonds. The value of a swap is the PV of these cash flows, FV′ed to the settlement date—sometimes called the as-of date—which usually corresponds to the spot date.
Calculating the day-count fraction for Act/360 or Act/365 is simple. Count the actual number of calendar days in the calculation period, and divide by 360 or 365. The Act/Act ISDA method, while not common, is not the same as act/act method used to calculate the accrued interest for bonds. The latter is called Act/Act ISMA (now ICMA), or act/act bond convention, and is defined as the actual number of days for the partial coupon period divided by the ″number of days in the full calculation period multiplied by the number of coupons per year.″ The act/act ISDA method (also called act/act swap, or act/act historical) on the other hand, is calculated as the sum of the number of days falling in a non-leap-year divided by 365, plus number of accrual days falling in a leap-year divided by 366.
The 30/360 basis is based on each year having 12 30-day months, and is computed as 360(y2 - y1) + 12(m2 - m1) + (d2 - d1) divided by 360 for calculation period [y1/m1/d1, y2/m2/d2]. While this might seem a straightforward process, it turns out to introduce nuances when month-ends are considered, and has led to different variants to tackle them. All variants use the above formula, but require first adjusting the original dates as follows:
30/360 ISDA, bond basis, 30/360: If d2 = 31 and d1 = 30, 31, change d2 to 30. If d1 = 31, change d1 to 30.
30E/360 ICMA (formerly ISMA), Eurobond basis: If d1,2 = 31, change d1,2 to 30.
30E/360 ISDA: If d1 is last day of month, change d1 to 30. If d2 = 31, change d2 to 30. If d2 is not the maturity date and is last day of Feb, change d2 to 30.
There do exist other variants: SIA 30/360, SIFMA (formerly PSA, BMA) 30/360, 30E + 360, German 30/360, but these are not that common for swaps.
Worked-Out Example
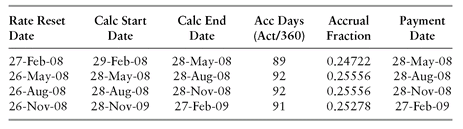
The cash flows for a standard 1y USD swap with 28-th rolls traded on Wed 27-Oct-2008 are presented in Tables 3.4 and 3.5. Note that if the fixed leg′s basis was 30E/360 ISDA instead of 30/360, the first calculation period (29-Feb-08 to 28-Aug-08) would have 178 days rather than 179, and would result in a different par-swap rate or swap value.
TABLE 3.4 Fixed Leg for 1y USD Swap
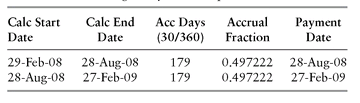
TABLE 3.5 Floating Leg of a 1y USD Swap
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
