CHAPTER 4
Separating Forward Curve from Discount Curve
The previous two chapters presented the standard treatment of building swap curves from traded instruments. Alongside plain-vanilla swaps, there is another class of floating-for-floating swaps, referred to as money-market basis swaps or simply basis swaps, where both legs of the swap are floating, but based on different short term (money-market) interest-rate indices.
Pricing and risk management of basis swaps is more nuanced than plain-vanillas. For one reason, the primary risk captured by them is the credit risk between the indices, say Government (Fed-Funds) versus Bank (Libor) credit. They also at times represent supply-demand dynamics of one index versus another one, independent of the inherent credit risk in each index. In order to provide a consistent framework to price them, one has to step back from the previous setup, where a single discount factor curve captured both discounting and calculation of forward rates, as basis swaps provide independent information about the forward/locking curve of an index, separate from the discount (funding) curve.
FORWARD CURVES FOR ASSETS
We have so far presented forward prices and rates in specialized instances. It will help to step back, and provide a generic definition of a forward contract. At a given time t, the value of an asset A for spot (cash) delivery is obviously A(t). However, if we need the asset only at some future time T > t, then we can enter into a forward contract. Such a forward contract for some specified delivery price, K , has a value today. From a buyer′s point of view, if K is too large, then the forward contract is an agreement to buy an asset in the future at an inflated price, and hence has negative value. Similarly, if K is too small, then one is buying an asset in the future on the cheap, and the value of the forward contract is positive. The delivery price K that would make the contract have zero value today is called the forward price of the asset, and is denoted by FA(t, T), T ≥ t.
Notice that there are two dates here: trading date t, and forward delivery date T > t. On any given trading date t, we can graph FA(t, ·) as a function of forward dates T, and come up with forward curve of the asset at t. Obviously, if T = t, then we have the spot/cash price of the asset: FA(t, t) = A(t). We can think of the forward curve as the indifference curve of the asset: Given all the information today, we are indifferent between paying A(t) for the asset today, or agreeing to pay FA(t, T) at some future delivery date T.
For a fixed forward delivery date T, the forward price at any trading day t ≤ T will fluctuate depending on market conditions. At the delivery date, of course, the forward price will coincide with the spot price: A(T) = F (T, T). Since the forward price fluctuates at any trading day, the value of a given (seasoned) forward contract with a fixed delivery price K will also fluctuate. For example, assume it is January 1, and an asset is trading at 100, and its forward value for delivery on March 31 is 101. We might enter into this contract at 101 with no exchange of money (just a handshake). For the next 3 months, the value of this contract will fluctuate, depending on each day′s market perception of the March-31 (forward) delivery price of the asset. At the maturity of the contract, if the spot price of the asset is higher than 101, then the contract has positive value, since it enables a long to gain the asset for lower than its market value. Similarly, if the spot price is lower than 101, then the contract has negative value, since it obligates the long to buy an asset for higher than its market value. Depending on the contract, one can either cash-settle, or take/make physical delivery of the asset at the agreed rather than the actual spot price.
One might think that determining the T-forward value would involve forecasting of the T-realized price of the asset. However, a simple cash-and-carry argument shows that we can determine the forward value of an asset without resorting to forecasting at the inception of the contract, t, he has to deliver the asset at time T in exchange for the (to be determined) forward value K = FA(t, T). He can conceptually buy that asset today t at A(t) by taking a loan—potentially collateralized by the asset—with maturity T and hold on to the asset till maturity. At maturity, he will deliver the asset, receive the K (agreed upon at time t and fixed thereafter), and repay the A(t) loan plus the interest. As long as K equals the loan and interest, he will have no risk. So the forward price, K, must equal loan plus its interest. If the asset can only be carried via an uncollateralized risk-free loan, then the forward prices can be related to risk-free interest rates or, equivalently, their implied discount factors:
FA(t, T) = A(t)/ D(t, T)
A similar expression can be derived for collateralized loans: for treasury bonds one should use their financing (repo) rate to arrive at the discount factor.
In general, the cash-and-carry argument shows that the forward value of an asset is the spot value plus the cost of carrying the asset minus any income that accrues to the holder of the asset, properly future valued to the forward date. For example, the forward gross value of a bond is its spot gross value plus the repo (carry cost) minus the future value of any intermediate coupon income. For dividend-paying stocks with known discrete dividends we need to subtract the future-value of the dividends from the carrying cost.
IMPLIED FORWARD RATES
When talking about forward rates, we need to distinguish between two ways that they can arise. If the underlying forward contract is an actual forward loan, requiring actual movement of cash, then the agreed-upon forward rate must express one′s indifference between spot and forward-start loans. The underlying asset, the loan, can be considered as a package of two simple cash flows: unit currency at inception and unit plus interest at maturity. As discount factors are today′s prices of future moneys, if available, they completely characterize each of these cash flows: To replicate a forward loan [T, T + ΔT] at a given loan lock rate K , one needs:
today, and the implied forward rate is the loan lock rate K that makes today′s value of this loan 0:
D(T) - (1 + K ΔT) D(T + ΔT)
K = f ([T, T + ΔT]) = [D(T)/D(T + ΔT) - 1]/ΔT
As such, it is just a derived (implied) rate from an already known discount factor curve.
The second way that forward rates arise is as a contract based on only the interest component of a hypothetical loan, with the future interest rate locked at some level K. For example, a USD FRA—equivalent to a single-period forward swap—is simply the interest component of a nominal loan at the future setting of the specified index, rΔT(T) (read Libor-3m), versus that of a locked (fixed) level K:
paid at T + ΔT, with K chosen so that this contract has zero value today. We previously argued that as long as we can invest future moneys at the same index, that is, our funding is based on rΔT, we can replicate the unknown future cash flow by owning/owing unit currency at start/end of the loan. Hence the value of floating payment paid at T + ΔT equals
which means that the rate K of a zero-cost FRA is the same as the implied forward rate. Therefore, if we already have our funding/discount curve, we can use it to calculate forward locking rates for the index. Alternatively, and more commonly, given a series of forward locking rates for our funding index, we can extract our funding/discount curve. For example, if we fund ourselves at some index X periodically, our funding/discount curve becomes: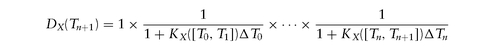 where K X([Ti , Ti +1 ]) is the locking (FRA) rate for the forward period [Ti, Ti+1] with 0 = T0 < T1 < . . . , and ΔTn = Tn+1—Tn.
where K X([Ti , Ti +1 ]) is the locking (FRA) rate for the forward period [Ti, Ti+1] with 0 = T0 < T1 < . . . , and ΔTn = Tn+1—Tn.
[rΔT(T) - K)] × ΔT
P V[rΔT (T) × ΔT paid at T + ΔT] = D(T) - D(T + ΔT)
= f ([T, T + ΔT]) × ΔT × D(T + ΔT)
= f ([T, T + ΔT]) × ΔT × D(T + ΔT)
FLOAT/FLOAT SWAPS
The above relationship between discount/funding curve, and forward lock rates is no longer valid for rate-lock agreements based on indexes different than our funding index. For example, if one funds at Libor-3m, and is asked to quote a rate-lock agreement where the floating index is another index X, say commercial paper (CP), then having money at the beginning of the hypothetical forward loan period is not sufficient to get to the desired final amount (initial + CP-based interest) as one cannot invest the funds at CP. As such, there is no arbitrage argument that will provide the fair locking level for X.
Still, one can focus on the expected difference between the index X(T) and the lockable funding index r (T). The payment of an FRA based on an index X is X(T) - KX properly accrued for the duration of the hypothetical loan, ΔT, and paid at T + ΔT. This can be reexpressed as:
where KX = KX-r + Kr . To determine the KX that will make the value of this rate-lock agreement zero, since we fund ourselves at r , we know how to calculate Kr so that the value of the second term becomes zero. Therefore, we just need to focus on selecting KX—r, that is, the locking level for our basis risk: the exposure to the difference between X and our funding index, r.
[X(T) - KX] × ΔT = [(X(T) - r (T)) - K X-r ] × ΔT + (r (T) - Kr ) × ΔT
Basis swaps are locking levels for forward basis risks, and their market quotes are based on expected future difference (spread) between the indexes. These market consensus levels are primarily based on market′s forecast of future credit spreads—usually projected forward from their historical levels—modulated by supply-demand dynamics. For example, the difference between Fed-Funds rate versus Libor is primarily U.S. Government credit versus banking credit. In times of good financial health for banking, this spread runs around 15 bp, and as such will be the expected spread as captured in Fed-Fund-Libor basis swaps. In times of turmoil, however, it can easily blow out.
USD Basis Swaps
The following are typical basis swaps traded in USD:
Fed-Funds versus 3M-Libor: Weighted arithmetic average of overnight Fed-Funds effective rate plus spread versus 3m-Libor, both legs paid Q, Act/360.
Prime versus 3M-Libor: Weighted average of daily resets of prime rates taken from the Fed statistical release H.15 minus spread versus 3m-Libor, both legs paid Q, Act/360.
Commercial-Paper (CP) versus 3M-Libor: Unweighted monthly average of daily resets of 1-month CP rate taken from the Fed statistical release H.15, converted from discount basis to Act/360, compounded monthly at CP flat, minus spread versus 3m-Libor, both legs paid Q, Act/360.
T-Bills versus 3M-Libor: Average of the bond-equivalent yield of the weekly auction average of the 3-month U.S. T-Bills taken from the Fed statistical release H.15 plus spread versus 3m-Libor, both legs paid Q, Act/360.
Basis swap based on constant-maturity-treasury (CMT) indexes published in H.15 used to be quoted, but these are now backed out from CMS swap level and spread-locks, although care has to be taken to adjust for the difference between a CMT index versus the U.S. current (CT) yields.
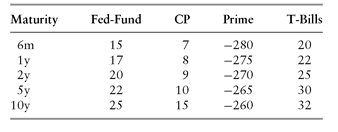
Table 4.1 shows sample quote sheets for a few of these swaps.
TABLE 4.1 Sample Mid-Market USD Basis Swap Quotes
Extracting Forward Rate Lock Curves
As seen from Table 4.1, each market quote for a basis swap refers to the average locking level for the basis risk for the relevant period. For example, the 1-year T-Bill/Libor basis swap quote of 22 bp refers to 4 quarterly resets of T-Bill index versus Libor-3m. In order to extract the individual locking level for each locking date (today, 3m, 6m, 9m), a de-averaging (bootstrap) method is needed. A simple way to proceed is to start from the spot level of the spread, say for Libor-3m versus T-Bills, and assume that the locking level for this spread is piecewise linear between quoted maturities. The end point of each linear segment is adjusted so that when we extract the locking spread level—and hence the locking level for the index—as the projected index, the basis swap for that maturity prices to zero at the quoted spread. The discounting of projected cash flows for both indices are off of our already extracted discount curve. This gives us a bootstrapped forward spread curve.
A consistent framework for capturing, pricing, and risk management of plain-vanilla and basis swaps emerges as follows:
1. Decide on our benchmark funding index L, say Libor-3m for a U.S. broker/dealer.
2. Using rate-lock instruments (FRAs, ED futures, par-swap rates) keyed to our funding index, via bootstrapping or other methods, simultaneously extract the locking curve for our index, fL(T), and our funding curve, DL(T).
3. For any other index X, extract its locking curve fX(T) so that the market basis swaps price to 0. To price the basis swap, we use fX(T) and fL(T) curves to replace future (unknown) floating resets with their locking rates, and discount the cash flows on both legs using our funding curve DL (T). Alternatively and equivalently, one can extract and use the forward spread curve, fX-L(T) = fX(T) - fL(T).
4. Having extracted the locking curve, fX(T), extract the funding/discount curve DX(T) for an X-funded entity.
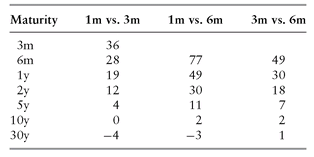
TABLE 4.2 Sample Mid-Market USD Libor/Libor Basis Swap Quotes
LIBOR/LIBOR BASIS SWAPS
In addition to basis swaps based on different indexes, there exist basis swaps between Libors of different maturities. For example, in USD, there is market for pairs of 1m, 3m, and 6m Libor, referred to as Libor/Libor basis swaps. A sample quote screen appears in Table 4.2.
It might seem strange that these swaps exist, since by prior arbitrage arguments, the compounded shorter-term rate must equal the longer rate, and the arbitrage-free spread should be zero. For example, the periodic payoff of a 3′s/6′s with a spread of s for each calculation period [T, T + 6m] is the net payment at T + 6m of
versus
or equivalently
[(1 + L3m(T)/4)(1 + L3m(T + 3m)/4) + s/2] - 1
(1 + L6m(T)/2) - 1
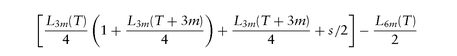
Prior arbitrage arguments suggest that the spread s above should be zero. However, we need to remember that our arbitrage arguments only hold for risk-free interest rates. If there is no potential for counterparty default, then any deviation of quoted forward rates from their arbitrage-free values can be arbitraged by entering into offsetting loans. For example, let us assume that there are risk-free interest rates quoted by default-free banks for 3m and 6m at r3m(0), r6m(0). What should the 3x6 FRA rate be? If there is no potential for the banks to default, then one can buy a 3x6 FRA struck at X, borrow at r3m(0) for the first 3 months, pay the principal and interest ((1 + r3m(0)/4)) in 3m, with the principal and interest financed by a new loan at the prevalent 3m rate, r3m(3m). In 6 months, one needs to pay
while one receives
as the reinvested payoff of the FRA, and also receives 1 + r6m(0)/2 as the 6m loan matures. Since it cost us nothing to enter these transactions, no-arbitrage requires the final moneys in 6m be the same and X to satisfy:
(1 + r3m(0)/4) × (1 + r3m(3m)/4)
(r3m(3m) - X)/4
(1 + r3m(0)/4) × (1 + X/4) = 1 + r6m/2
Since there is no net exchange of cash until maturity, the above relationship—being just a mathematical identity—must still hold even if all transactions were with a single risky bank. However, if we are borrowing, lending, and buying FRAs from different risky banks, it could happen that we lend money to a bank that subsequently defaults, while our other counterparties remain solvent, and we have to pay them. If we are dealing with counterparties of the same credit worthiness, the riskiest transaction is the longest loan as it has the longest default exposure window. Therefore, whoever is going to lend for 6m will quote/require a rate higher than what is implied by shorter-term (3m-rate, 3x6 FRA) rates.
(1 + r3m(0)/4) × (1 + X/4) = 1 + (r6m + Spread)/2
This is the main reason that two successive 3m FRAs do not equate to a 6m FRA even after adjusting for compounding, and why Libor-6m versus Libor-3m trades at a (usually) positive spread. In practice, this credit spread is further adjusted for liquidity of one tenor versus another tenor—which can make the spreads trade negative—and in consideration of particulars of Libor-fixing (BBA′s polling and averaging of bank′s estimate of what 3m interbank lending rates are).
To properly handle these basis swaps, we have to decide what our funding index is, say Libor-3m, and treat the other Libors (1m, 6m) just like other basis swaps, that is, extract a rate-lock curve for them so that the Libor-Libor basis swaps at market spreads price back to 0.
OVERNIGHT INDEXED SWAPS (OIS)
While most plain-vanilla swaps are indexed to unsecured interbank (Libor) rates with tenor of 3m or 6m, there is another variety of swaps indexed to overnight rates. The index is usually based on the policy rate of central banks for each currency, and are based on actual traded deposits. For example, in USD, the benchmark is daily Fed-Fund effective rate, which is a volume-weighted average of rates on Fed-Fund trades arranged by major brokers, and calculated and published next day by the Federal Reserve.
An overnight indexed swap (OIS) is a fixed-for-floating swap where the floating leg is based on an overnight index. The floating payment is typically the daily compounded interest at each overnight rate (weekends/holidays use previous business day′s fixing) over the calculation period,
where αi is the length of each compounding day according to some daycount basis (for example, αi = 1/360 or 3/360 for Fridays in USD), while the fixed payment is the fixed rate accrued for the same calculation period, resulting in a single net cash flow for each calculation period. OIS swaps of maturity less than 1-year have one calculation period, while longer-term swaps are broken into annual calculation periods. Below is a list of OIS swaps and their benchmark index for different currencies:
[1 + α1 × r1] × [1 + α2 × r2] × ··· × [1 + αN × rN] - 1
USD: FFER (Fed-Funds effective rate) as calculated by the New York Fed, Act/360.
EUR: EONIA (Euro overnight index average), the effective overnight rate computed as a weighted average of all overnight unsecured lending transactions in the interbank market, calculated by European Central Bank (ECB) and published by the European Bank Federation, Act/360.
GBP: SONIA (Sterling overnight index average), the weighted average rate of all unsecured overnight cash transactions brokered in London by the Wholesale Markets Brokers′ Association (WMBA). SONIA closely follows the Bank of England′s (BOE) policy rate, Act/365.
JPY: TONAR (Tokyo overnight average rate), based on uncollateralized overnight average call rates for lending among financial institutions, published by the Bank of Japan (BOJ). BOJ affects TONAR using open market operations to keep it in line with its policy rate (called Mutan), Act/365.
CAD: CORRA (Canadian overnight repo rate average) released by the Bank of Canada, Act/365.
OIS versus Libor Discounting
With the recent market turmoil affecting banks, and concern over reliability of Libor as a benchmark index, there has been an increased focus on OIS swaps, as these are keyed to actual traded effective policy rates by central banks. Another reason for renewed focus is that most swaps are traded under the Credit Support Annex (CSA) to the ISDA Master Agreement, which requires counterparties to post collateral as the mark-to-market value of the swap changes. Of special attention is the interest rate paid on posted collateral: Most CSAs specify overnight effective rates (for example, Fed-Funds effective rate for USD) to be paid on the posted collateral (cash or cash-equivalent like government securities). This means that the actual funding cost for a swap is not Libor, but the overnight effective rate. As such, one should use OIS swaps to extract the funding/discount curve for swaps and their derivatives, and use this OIS discount curve to extract rate lock (projection) curves for other indexes.
While this idea is gaining traction and acceptance among market participants, the market practice is to still use Libor rather than OIS discounting when creating projection curves out of quoted market swaps. At the same time—and inconsistently—when offering unwind prices for existing/ seasoned swaps with large mark-to-market value, the actual funding curve is conveniently remembered/invoked, usually (and not surprisingly) by the benefiting party!
As OIS swaps gain more liquidity and are traded for longer terms—there are currently liquid points for at most a few years—a more consistent framework for building Libor curves and pricing swaps should emerge. Until then, most at-market swaps would be priced and discounted off of the Libor curve, while off-market swaps with large mark-to-market value would use OIS or similar discount curves.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
