5
Lattice‐Based Cryptography and Internet of Things

Veronika Kuchta and Gaurav Sharma

5.1 Introduction

Post‐quantum cryptography is an essential research topic which became more popular since the start of research on quantum computing. Quantum computers are highly powerful machines which take advantage of subatomic particles which exist in more than one state at any time. Such machines are able to process information in an incomparably faster time than the fastest computers. IBM and Google are the leading companies in this race for the first quantum computer that will then be made publicly available and extremely useful. The main feature of such a powerful computer is that it will be able to perform calculations which are almost impossible to be simulated by a conventional computer. A computer with this feature will ewasily be able to break all of the current cryptographic constructions which have proven to be secure under number‐theoretical assumptions. A possible solution to this problem can be offered by the following research fields which are assumed to be resistant against quantum attacks:

  1. – Hash‐based Cryptography. A typical example for this field is given by the Merkle's hash‐tree public‐key signature scheme, which was introduced in 1979. While on the one side hash‐based cryptographic schemes offer an efficient solution to certain cryptographic problems, the main disadvantage of those schemes is the large size of signatures.
  2. – Code‐based Cryptography. McEliece's hidden Goppa‐code public‐key encryption represents a typical scheme of this research field. The scheme was introduced in 1979. The main idea of such cryptosystems, which are based on error‐correcting codes, is to construct a secure and efficient one‐way function.
  3. – Lattice‐based Cryptography. Another research topic of post‐quantum cryptography is given by the lattice‐based cryptography which also has the feature of conjectured quantum attacks resistance. Furthermore, lattice‐based cryptoschemes profit mostly from algorithmically simple and highly parallelizable constructions.
  4. – Multi‐variate quadratic equations Cryptography. Introduced in the 1980s, this type of scheme represents asymmetric cryptography where the public keys are defined as a set of multi‐variate polynomials and the security of such schemes is based on a problem of solving multi‐variate quadratic equations over finite fields.
  5. – Isogeny‐based Cryptography. This represents the newest direction in post‐quantum cryptography, where the cryptoschemes are based on supersingular elliptic curve isogenies. The security of those systems is based on the difficulty of constructing an isogeny between two supersingular curves having the same number of points as input.
  6. – Secret‐Key cryptography. The Rijndael cipher, developed in 1998, also known as the Advanced Encryption Standard (AES) is, nowadays, still the leading example for this type of cryptography.

We will focus here on one specific topic and its relation to the Internet of Things (IoT). We should consider the fact that we are at the very beginning of the application process of quantum‐resistant algorithms to IoT. Therefore, in this chapter we want to make the reader familiar with notions and the main constructions of lattice‐based cryptography and share our ideas on how to use these schemes in IoT.

5.1.1 Organization

In Section 2, we will have a closer look into the main definitions of lattice‐based cryptography and introduce the reader to the solutions of certain essential problems in this topic. In section 3, we discuss the main cryptographic primitives constructed from lattices. In section 4 we show the relation between lattice‐based cryptoschemes and IoT and provide some examples for these relations.

5.2 Lattice‐Based Cryptography

As we know, cryptography requires average‐case intractability, meaning that there are problems for which random instances are hard to solve. This intractability differs from the worst‐case notion of hardness, where a problem is considered to be hard if there exists some intractable instances. This latter notion of hardness is considered to be NP‐complete. A trivial conclusion follows that if there are problems which are hard in worst case, they often appear to be easier on the average.

A crucial contribution to this problem, according to lattice, has been made by Ajtai [3] who proved that certain problems are hard on the average if there are some lattice‐related problems which are hard in the worst case. Using this result, cryptographers can construct schemes which are note feasible to break, unless all instances of some certain lattice problems are easy to solve.

5.2.1 Notations

Let images denote the quotient ring modulo images, where images is a positive integer. Elements in images are given as images, with images. It holds that images is an additive group supporting scalar multiplication by integers, i.e. images for an integer images and images.

We use bold capital letters to denote matrices, such as images and bold lower‐case letters to denote column vectors, such as images. To indicate horizontal concatenation of vectors and matrices we use the following notation: images.

5.2.2 Preliminaries

5.2.2.1 Lattices

Let images be the basis of a lattice images which consists of images linearly independent vectors. The imagesdimensional lattice images is then defined as 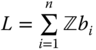images.

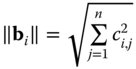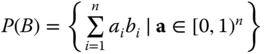The images‐th minimum of lattice images, denoted by images is the smallest radius images such that images contains images linearly independent vectors of norms images. (The norm of vector images is defined as images, where images are coefficients of vector images. We denote by images the minimum distance measured in the infinity norm, which is defined as images. Additionally, we recall images and its fundamental parallelepiped is given by images. Given a basis images for a lattice images and a vector images we define images as the unique vector in images such that images. If images is a lattice, its dual lattice is defined as

equation

5.2.2.2 Integer Lattices

The following specific lattices contain images as a sub‐lattice for a prime images. For images and images, define:

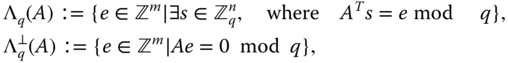
equation

Many lattice‐based works rely on Gaussian‐like distributions called Discrete Gaussians. In the following paragraph we recall the main notations of this distribution.

5.2.2.3 Discrete Gaussians

Let images be a subset of images. For a vector images and a positive images, define

equation

The discrete Gaussian distribution over images with center images and parameter images is given by images. The distribution images is usually defined over the lattice images for images. Ajtai [3] showed how to sample an uniform matrix images with a basis images of images with low Gram‐Schmidt norm. Gentry et al. [18] defined an algorithm for sampling from the introduced discrete Gaussian images for a given basis images of the images dimensional lattice images with a Gaussian parameter images, where images is the orthonormal basis of images, defined as follows:

The Gram‐Schmidt Norm of a Basis [1]

Let images be a set of images vectors images with the following functionalities:

  1. – images denotes the norm of the longest vector in 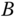images, i.e. images for images.
  2. – images is the Gram‐Schmidt orthogonalization of the vectors images.

The Gram‐Schmidt norm is denoted by images.

5.2.3 Computational Problems

In the next definitions we recall the most popular computational problems on lattices which can also be found in the report of Peikert [37]. The most well‐studied problem is the Shortest Vector Problem (SVP):

Apart from the main definition of the SVP problem, there are many approximation problems which are parameterized by an approximation factor images which is represented as a function in the lattice parameter images, i.e. images. The corresponding approximation problem for the SVP problem is defined as follows:

It is known that many cryptoschemes can be proved secure under the hardness of certain lattice problems in the worst case. But there is no known proof for the search version of images. But there are many proofs which are based on the following decision version of approximate‐SVP problem:

Another approximate version of SVP is recalled in the following definition:

Special case (presented in [13]) of short integer solution (SIS) problem introduced by Ajtai [3]. Another particularly important computational problem for cryptographic constructions is the Bounded‐Distance Decoding images problem.

The main difference between images and images is the uniqueness of the solution to the earlier problem, while the target of the latter can be an arbitrary point.

Most modern lattice‐based cryptographic schemes rely on the following average‐case problems, Short Integer Solution (SIS) and Learning with Errors (LWE) problems, their analogues defined over rings. They involve analytic techniques such as Gaussian probability distribution.

In matrix form, this problem looks as follows: collecting the vectors images into a matrix images and the error terms images and values images as the entries of the images‐dimensional vector images we obtain the input images.

5.2.4 State‐of‐the‐Art

In this chapter we want to briefly survey some of the previous significant works in lattice cryptography. The particularly ground‐breaking work of Ajtai [3] provided the first worst‐case to average‐case reductions for lattice problems. In that work, Ajtai introduced the average‐case short integer solution (SIS) and showed that solving it is at least as hard as approximating various lattice problems in the worst case. In a later work [4], Ajtai and Dwork presented a lattice‐based public‐key encryption scheme which became the basic template for all lattice‐based encryption schemes.

Almost at the same time, a concurrent work had been published by Hoffstein, Pipher, Silverman [25] introducing the NTRU public‐key encryption scheme. It was the first construction using polynomial rings. The advantages of that construction are the practical efficiency and particularly compact keys. The NTRU system is parameterized by a certain polynomial ring images, where images for a prime images, or images for images which is a power of two, with a sufficiently large modulus images, which defines the quotient ring images.

Around the same time, Goldreich, Goldwasser and Halevi [20] published a paper on public‐key encryption scheme and a digital‐signature scheme, both based on lattices. The main idea behind their constructions was that a public key is a “bad” basis of some basis consisting of long and non‐orthogonal lattice vectors, while the secret key is a “good” basis of the same lattice consisting of short lattice vectors.

Later on, Oded Regev [40] provided improvements to the results of Ajtai and Dwork's work by introducing Gaussian measures and harmonic analysis over lattices. The main consequences of these new techniques were simpler algorithms and tighter approximation factors for the underlying worst‐case lattice problems. In another important work, Regev [41] introduced the average‐case learning with error (LWE) problems, for which Oded Regev was awarded the Goedel Prize in 2018. In the same paper, the author introduced a new cryptosystem which can be proved secure under the new LWE assumption. This construction had the favourable feature of more efficient public keys, secret keys and ciphertexts, where the efficiency of the former was improved from images to images and the ciphertext efficiency improved from images to images.

5.3 Lattice‐Based Primitives

Some core constructions which were built upon (ring)‐SIS/LWE assumptions are listed below:

5.3.1 One‐Way and Collision‐Resistant Hash Functions

An example of this is the SWIFFT construction by Lyubashevsky et al. [34]. It is an instantiation of the ring‐SIS‐based hash function and is highly efficient in practice, as it uses the fast Fourier transform in images. Without going too deeply into details, we sketch the construction as follows: Let images be an invertible quadratic matrix over images. The SWIFFT hash function maps a key consisting of images vectors images and a vector images to the product images, where images is not an uniformly chosen matrix, but a block‐matrix generated using structured block as shown in [34]. The collision resistance property follows from the usage of worst case lattice problems on ideal lattices. A collision‐resistant hash function is a highly significant cryptographic tool, which plays the role of an important building block in many cryptoschemes. From a hash function, we move to more specific cryptographic constructions, discussed in the following sections.

5.3.2 Passively Secure Encryption

This topic contains all encryption schemes which are IND‐CPA secure. As the name already reveals, passively secure schemes involve a passive eavesdropper, who learns no more information about the messages, except seeing the public key and the ciphertext. The first such scheme has been introduced by Regev [41]. Gentry, Peikert and Vaikuntanathan [18] defined the dual version of Regev's encryption. The main feature of their construction is that public keys are uniformly random with many possible secret keys. But since Regev's encryption scheme [41] served as a basic building block for many successful schemes, we believe that it is useful to have this scheme recalled here. This scheme is based on LWE problem, where the size of the public keys is images bits and that of the ciphertext is images bits, where the ciphertext is an encryption of a single bit and images denotes the dimension of the underlying LWE problem. Let images be the number of samples and images denote an error distribution over images. The three algorithms images of Regev's LWE cryptoscheme are given as follows:

  1. – Since the construction is underlying an LWE problem, the secret key is a uniformly and random LWE secret 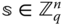images. The corresponding public key is a vector of 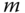images samples 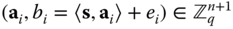images which are drawn from the LWE distribution images. The images samples are collected into a matrix
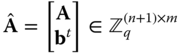
    equation

    It holds images, with images. The secret and public keys satisfy the relation images.

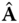  2. – Encryption algorithm takes as input, a message bit images and a public key images, chooses a uniformly random images and generates the ciphertext images.
  3. – Decryption algorithm uses the secret key 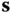images and computes 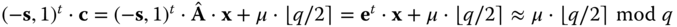images. The decryption is correct as long as the maximal size of 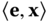images is q/4.

As mentioned before, the security of this scheme relies on the hardness of LWE assumption with parameters images.

Later on, Gentry et al. [18] constructed an LWE‐based encryption scheme which is dual to Regev's encryption [41]. The dualism is represented as follows: in [41] the public keys are generated corresponding to a non‐uniform LWE distribution with an unique secret key, while there are several options of ciphertext randomness which yield the same ciphertext. In the dual LWE [18], the public keys are uniformly and random, having many possible secret keys, while the encryption randomness is unique and outputs a certain ciphertext.

An enhancement of LWE cryptoscheme with smaller public and secret keys was provided by Lindner and Peikert [30], which uses a code‐based cryptosystem of Alekhnovich [5] and adapts it to LWE.

5.3.3 Actively Secure Encryption

This is represented by encryption schemes which are indistinguishable against chosen‐ciphertext attacks, in other words, they are IND‐CCA secure. Fujisaki and Okamoto showed a technique on how to convert any IND‐CPA cryptoscheme into an IND‐CCA secure public key encryption scheme. A lattice‐based instantiation of the Fujisaki‐Okamoto technique was introduced by Peikert [36]. The pioneer work of actively secure encryption over lattices (LWE assumption) defined in a standard model, was defined by Peikert and Waters [38]. Their construction was based on a concept called lossy trapdoor function family, where the public key images of a function images can either be generated along with a trapdoor images, and images is a function that can be inverted using images, or it can be generated without any trapdoor. Finally, the public keys generated in these two different ways are indistinguishable.

5.3.4 Trapdoor Functions

These are functions which are easy to evaluate but hard to invert. They can be generated with some trapdoor information. Gentry et al. [18] were the first to show that certain types of trapdoor functions can be constructed from lattice problems. These trapdoor functions can be used in many applications such as digital signature schemes, identity‐based and attribute‐based encryption. The basic idea of such constructions in [34] is to generate a collection of pre‐image sampleable functions which are collision resistant and one‐way trapdoor functions. To do so, let images be the public basis of lattice images. Then, in order to evaluate a function images from the collection of those preimage sampleable functions in a random lattice point images, we need to disturb it by a short error vector images, such that images. Inverting images means decoding the function to some lattice point images which is not necessarily equal to images, because of the disturbance there is more than one preimage of images.

5.3.5 Gadget Trapdoor

The core idea of gadget trapdoors is that they are represented by special matrices, called “gadget matrices” whose use makes solving LWE and SIS easy. This special primitive which is a favour of cryptographic trapdoors is significant for many constructions that have used gadget matrices as a building block. The easiest way to represent a gadget trapdoor images is a vector of powers of two, i.e. images, where images. For a given images, it is easy to find a solution to the equation

equation

by decomposing images into its binary representation in images. This SIS problem can be adapted to an LWE problem as follows: given any vector images with errors in the interval images, discover the most‐significant bit of images.

The one‐dimensional SIS and LWE problem as described above can be extended to images‐dimensional SIS and LWE using the block‐diagonal gadget matrix defined as

equation

The LWE problem is given by an approximate vector images, from which we have to recover vector images. The corresponding SIS problem is to find a short solution to the equation images, given a vector images, meaning that we have to find short solutions for images for each images. This procedure to find a SIS solution can be expressed using a decomposition function

equation

This gadget trapdoor is also useful to generate trapdoors for a parity‐check matrix images, where such a matrix is essential for several lattice‐based cryptoschemes and its trapdoor is a sufficiently short integer matrix. Let images be such a trapdoor of images, then the following equation holds: images, where images is an invertible matrix, normally called the tag of the trapdoor images. When the quality of a trapdoor is increasing, it's maximum norm is decreasing.

5.3.6 Digital Signatures without Trapdoors

The first paper in this topic was published by Lyubashevsky and Micciancio [33]. The authors developed a one‐time signature which is convertible to many‐time signature schemes using tree‐hashing techniques. The security of their scheme is based on hardness of Ring‐SIS assumption as defined in Def. 8. Because of the key size, signature size, message length and running time, the key generation, signature generation and verification procedure are all quasi‐linear in the security parameter, i.e. images. Due to the polylogarithmic factors used in the [33] scheme, that construction appears not to be practical in use. Therefore, the search for more efficient signatures lead to further contributions. Lyubashevsky [32] presented the first approach of a three‐move identification scheme which can be converted into a non‐interactive signature scheme applying Fiat‐Shamir characteristics, where the resulting scheme is defined in the Random Oracle Model (ROM). In the following paragraph, we sketch the main idea of the lattice‐based identification protocol from [32] as it represents a basic tool for several cryptographic constructions.

The prover's secret key is given by a short integer matrix images and the corresponding public key is images for a given public parameter images. The interactive protocol consists of the following steps:

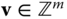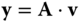  1. 1. The prover chooses a “somewhat short” vector images and sends images to the verifier.
  2. 2. The verifier chooses a random challenge images being a short vector and sends it to the prover.
  3. 3. The prover computes images
  4. 4. The prover decides whether to accept or to reject 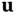images. This procedure is called rejection sampling and is better explained in the next paragraph.
  5. 5. If the prover accepts 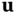images and sends it to the verifier, the latter checks 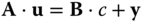images and that 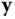images is sufficiently short.

5.3.6.1 Rejection Sampling

The goal of rejection sampling is to achieve independence from the distribution of images from the secret images. To do so, rejection sampling algorithm shifts the distribution of images to be a discrete Gaussian distribution with the center at zero instead of images. To avoid the problem when images gets rejected too often, we assume that images has a discrete Gaussian distribution with parameters which are proportional to images such that the two distributions, one centered at zero and another at images have sufficient overlap. In a later work, Ducas et al. [15] provided further refinement of that idea.

Applying Fiat‐Shamir heuristic to the interactive protocol yields a signature scheme with signature length of 60 kilobits making it practical for implementation.

5.3.7 Pseudorandom Functions (PRF)

This primitive was first introduced by Goldreich, Goldwasser, Micalli [21]. A pseudorandom function (PRF) with a secret seed images is a map from a certain domain to a certain range with the essential property that given a randomly chosen function from the family of such PRFs, it is infeasible to distinguish it from a uniformly random function given access to an oracle. The first PRF from lattice problems was constructed by Banerjee, Peikert, Rosen [8]. The authors first introduced the derandomized version of LWE, called learning with rounding (LWR). The main difference between this problem and LWE is that the error is deterministic. We shortly recall the LWR problem as follows: Let images be a secret and the LWR problem is to distinguish noisy and random inner products with images from a random value, i.e. for a given images and the rounding function images defined as images, the samples are given as follows:

equation

We recall the very first lattice‐based PRF from [8] based on LWE problem. This construction is particularly randomness‐efficient and practical. The function is given by a rounded subset product. Let images be a set of secret keys given as short Gaussian‐distributed matrices, an uniformly random vector images. Then, the lattice‐based PRF is given by the following function:

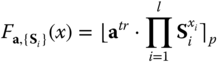
equation

An important feature of key homomorphism for lattice‐based PRFs has been introduced by Boneh et al. [10]. The authors provided the first standard‐model construction of key‐homomorphic PRF secure under LWE assumption. This additional property plays a significant role in distributing the function of key generation center, as it satisfies the following function images, for different secret keys images.

Furthermore, some other more advanced constructions have been developed in the last decade. These are:

5.3.8 Homomorphic Encryption

The first concept of fully homomorphic encryption (FHE) has been proposed by Rivest, Adleman and Dertouzos in 1978 [42]. The main idea of homomorphic encryption is to allow computation on encrypted data. In other words: given some data images, one can compute a ciphertext which encrypts an evaluated data images for any desired function images. The first FHE from lattices was introduced by Gentry [17], which is based on average‐case assumption about ideal lattices. Brakerski and Vaikuntanathan [12] introduced a new version of FHE from lattices, which is based on the standard LWE assumption. We shortly recall their scheme as it was used in many applications and served as a building block for several constructions.

The scheme in [12] supports addition and multiplication of multiple ciphertexts, while each ciphertext encrypts a single bit. Exploiting the homomorphic property of a scheme, we can evaluate any Boolean circuit. The secret key in this scheme is an LWE secret images. The encryption of a bit images is given by an LWE sample for an odd modulus q. The error term is an encoding of the message as its least‐significant bit. For the ciphertext images the following relations hold: images, with images being a small error, and images. To decrypt images, we simply compute images and lift the result to the unique representative of images. We output images.

As mentioned earlier, the scheme in [12] supports addition and multiplication, where the former operation is a straightforward computation in these schemes, while the latter represents a bigger challenge, to achieve the feature of multiplication of different ciphertexts. For reasons of simplicity, we observe two different ciphertexts which we want to evaluate, exploiting homomorphic property of the scheme. When we add two ciphertexts images, we get an encryption of the sum of the corresponding plaintexts images, as we can see:

equation

And as shown above for this error term holds images. The problem here is that the number of different ciphertexts cannot be unbounded as the error magnitude will exceed the limit of images.

To multiply two ciphertexts, we use the mathematical construct called tensor product images, which is an encryption of images, under the secret key images. Here also, the number of multiplication factors is bounded from the beginning. One of the main drawbacks of homomorphic encryption is that it always increases the error rate of a ciphertext. In the same paper [12], the authors introduced a technique to improve this issue, which is called ‘key switching technique’. This technique allows the conversion of a ciphertext that encrypts some message images into another ciphertext, that still encrypts the same message, but under some different secret key images and uses the previously introduced gadget trapdoor. For further details we refer to the original paper.

Another idea for the solution, called bootstrapping, was introduced by Gentry [17]. The idea involves a technique which reduces the error rate of a ciphertext and allows unbounded homomorphic computation. The technique is to homomorphically evaluate the decryption function on a low‐error encryption of the secret key, which represents a part of the public key.

An alternative scheme of homomorphic encryption was introduced by Gentry et al. [19] in 2013 which has some attractive properties. In order to perform homomorphic evaluations of the ciphertext, no key‐switching technique is required. The scheme [19] can also be adapted to an identity‐based‐encryption or an attribute‐based encryption. An extension of these schemes was proposed by [27], defining identity‐based encryption and attribute‐based encryption schemes in multi‐identity and multi‐authority settings, respectively.

5.3.9 Identity‐Based Encryption (IBE)

An Identity‐Based Encryption was first introduced by Shamir [44] and has the useful feature where any string can serve as a public key. The secret key is generated by an authority, called a key generation center (KGC), which has control over some master secret key. On input, this master secret key and some public string, the KGC derives a secret key for a user who can be identified by the mentioned public string. Every user can encrypt a certain message for a receiver, using the corresponding public string indicating the receiver's identity. The first lattice‐based IBE scheme was proposed by Gentry et al. [18] and is defined in the random oracle model. Since real random functions are not practical in use, it is still useful to assume that a hash function can behave like a truly random function and so provide a security proof. Even though such models would not be secure, when the pretended random function is replaced by a real hash function, it is still better to provide a construction in the random oracle model, as it will enable the understanding of some obvious attacks. The construction in [18] is, so far, most efficient IBE scheme which is secure against quantum attacks. The main idea behind the [18] construction is that the secret keys of each user are represented by a signature of the user's identity generated by the KGC. The corresponding public key is simply the hash value of the user's identity string. To gain a better understanding of the basic IBE scheme, we provide a short overview of it. An IBE scheme encompasses the following steps:

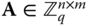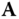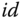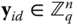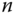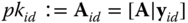  1. – The master public key is represented by a uniformly random parity‐check matrix images, while the corresponding master secret key is a trapdoor for this matrix images. There is a public hash function which takes as input an identity string images and maps it into a syndrome images, which is a images‐dimensional vector with coefficients reduced modulo images. This syndrome is used in combination with the public key images to represent a user‐specific public key images.
  2. – Next, to extract a secret key for the above‐mentioned identity string 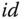images, we use a trapdoor to run the Gaussian sampling algorithm as defined in [18]. The algorithm samples from a discrete Gaussian over an 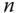images‐dimensional lattice 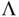images. Discrete Gaussians over lattices, are useful mathematical tools to study the complexity of lattice problems [35]. To sample from a discrete Gaussian the algorithm takes the parameters images, as input representing the standard deviation and the center of a distribution images. It also takes as input a trapdoor basis 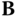images of the lattice 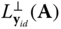images and outputs a lattice vector as long as the length of all the Gram‐Schmidt (see Definition of Gram‐Schmidt Norm in Section 2.2) vectors of basis images are exceeded by the standard deviation parameter. 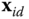The Gaussian‐distributed solution of key extraction is given by the vector images such that the following equation holds: 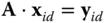images. The secret key 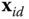images solves also the equation images.
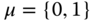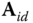  3. – To encrypt a message bit images using identity images as a public key, the encryptor uses the technique of dual LWE scheme, the given user‐specific public key images and computes the ciphertext as 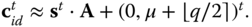images The corresponding decryption of this ciphertext is computed using the user's secret key images as follows: 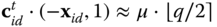images.

An IBE scheme which is defined in the standard model, was later defined by Cash et al. [14]. In the same work, the authors provided a construction of an hierarchical identity‐based encryption (HIBE) which allows any user to use their secret key in a secure way to delegate it to any subordinate user in hierarchy.

5.3.10 Attribute‐Based Encryption

The first construction of attribute‐based encryption (ABE) was introduced by Sahai and Waters [43]. It represents a generalization of identity‐based encryption. There are two flavours of ABE, ciphertext‐policy ABE (CP‐ABE) and key‐policy ABE (KP‐ABE). In the first case (CP‐ABE), the user's secret key is generated based on a certain set of attributes which satisfy a predicate formula. The ciphertext is computed by embedding that predicate formula, which is often called attribute policy. The user who is in possession of the attribute‐based secret key is able to decrypt the received ciphertext if and only if their secret key's attribute set satisfies the predicate formula. In the second case (KP‐ABE), the secret key is generated using an attribute predicate, while the attribute set is embedded into the ciphertext. The first lattice‐based construction of ABE has been provided by Agrawal et al. [2] which is inherited from the lattice‐based HIBE construction of [1]. An ABE for arbitrary predicates, expressed as circuits has been introduced by Gorbunov et al. [22]. The first lattice‐based ABE scheme was proposed by Agrawal et al. [2] and represents an adaptation of the lattice‐based HIBE scheme [1]. Here we recall this scheme.

First of all, we state that a finite field images is isomorphic to a matrix sub‐ring images, for a prime images and images. Then for an attribute vector images of length images the following holds:

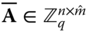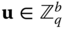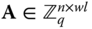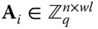  1. – The master public key is given by the matrix images which is generated using a trapdoor as shown in Section 3.5, where images. Further components of the public key is a syndrome images a uniformly random matrix images, which is a concatenation of images matrices, i.e.
    equation
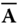    where each images. The corresponding master secret key is the trapdoor that was used to generate images.
  2. – As the scheme in [2] is a KP‐ABE construction, the secret key is generated based on a predicate vector 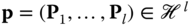images using the trapdoor for 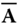images. A short integer matrix is defined using the Gadget trapdoor from Section 3.5:
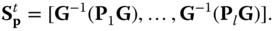
    equation

    Using this matrix we define images and sample a Gaussian‐distributed solution using a sampling algorithm described in the previous Section 3.9., i.e. images.

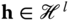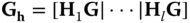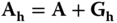  3. – The encryption is generated using a set of attributes images as defined above. Using the Gadget trapdoor images from Section 3.5, an attribute‐based trapdoor is defined as follows: images. Using this trapdoor images, define images. The attribute‐based public key is defined as a concatenation 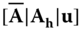images. Using this key, a message images is encrypted applying the dual LWE encryption with the corresponding LWE secret images. The ciphertext is given as follows: 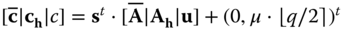images.
  4. – Decryption algorithm of this scheme by firstly multiplying the second component of the ciphertext by 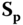images and secondly computing
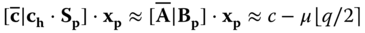
    equation

An ABE scheme arbitrary for any predicates represented as a priory bounded depth circuits based on a Lattice assumption was proposed by Gorbunov et al. [22]. The secret key in this scheme grows proportionally to the size of the circuit. An improvement of this scheme was later proposed by Boneh et al. [9].

5.4 Lattice‐Based Cryptography for IoT

Nowadays, we live in a world where more and more smart devices such as mobile phones, TV, smart household appliances, and cars are connected to the Internet. Most of such devices are equipped with wireless sensors which establish an information flow between the Internet and the device. For instance, many smart medical devices collect health information from customers and forward it to an Internet‐based database. Therefore, it is obvious that security and privacy of user's sensitive data, are the most significant challenges in such IoT systems. We know that next to symmetric cryptography, public key cryptography is one of the fundamental tools in IoT security. While the former provides security against quantum attacks, the latter is assumed to be vulnerable to these attacks. Lattice‐based cryptography as one promising topic of quantum‐based cryptography, offers solutions to IoT systems which one day may be exposed to quantum attacks.

IoT applications envision lattice‐based cryptography as a promising candidate for strong security primitives. The future smart IoT devices will be equally vulnerable to quantum threats and it would be extremely difficult to update their security settings from classical to quantum‐secure cryptography. Moreover, the computational and storage efficiency of lattice‐based primitives also motivates the adoption of it for lightweight devices. Existing implementations of R‐LWE on an 8‐bit microcontroller can finish faster than RSA‐1024 [31].

In [28], the authors reviewed the important role of attribute‐based and identity‐based authentication systems in IoT. They discussed the main opportunities and challenges which are faced in IoT by using attribute‐based authentication schemes. The authors also mention the significant meaning of attribute‐based signature (ABS) schemes in IoT, which represent an alternative to ABE schemes, where the signer generates a signature of a certain message using an attribute‐based secret key. The verification succeeds if and only if the signer can prove to the verifier, that they have the right key based on a set of attributes, which satisfy a certain predicate. The lattice‐based research on this area of cryptoscheme is not big; only few papers have been proposed in the recent years [16,26,45]. Therefore, because of the significant role of ABE and ABS schemes in IoT and the future perspective of quantum computers, the research topic of lattice‐based ABE and ABS is particularly interesting and a direct application of these schemes to IoT is useful.

In [39], an R‐LWE‐based signature scheme ‘BLISS’ is implemented to ascertain the feasibility of BLISS for lightweight devices. The authors provided a scalable implementation of BLISS on a Xilinx Spartan‐6 FPGA with optional 128‐bit, 160‐bit, or 192‐bit security. Other variants of BLISS are also available in literature in order to speed up the key generation process.

Homomorphic encryption is another cryptographic primitive which attracts more and more IoT developers because of its useful features which allow the evaluation of encrypted data. Often sensitive data in the IoT has to be processed in the cloud. In [29], the authors showed how confidentiality can be guaranteed in the cloud by using homomorphic encryption. They also proposed an acceleration mechanism to speed up the homomorphic evaluation.

Pseudorandom functions play a significant role in IoT too, as shown recently in [24]. As mentioned by the authors, remote software update procedures are becoming more useful in automative industry. Therefore, security of those procedures are considered to play a core role in that sector. Message authentication codes and pseudorandom functions (PRFs) are particularly helpful in the provision of security of the remote software updates. Thus, with the future move to quantum computers, quantum‐resistant constructions will be required, where lattice‐based schemes, in this particular case, the PRFs could offer an efficient and practical solution.

The post‐quantum key exchange is the most challenging phenomenon to address. The initial effort was made by Bos et al. [11] to transform classical TLS to the R‐LWE version of TLS considering post‐quantum requirements. With a small performance penalty their R‐LWE key exchange was successfully embedded in TLS and implemented on web servers. Alkim et al. [7] presented an efficient implementation of R‐LWE‐based key exchange protocol, namely New Hope [6]. Initially, their proposal was to implement it on large Intel processors however, their implementation is finally optimized for ARM Cortex‐M family of 32‐bit microcontrollers. Moreover, within Cortex‐M family, they choose Cortex‐M0 as low‐end and Cortex‐M4 as high‐end targets. The authors achieved 128‐bit security in a post‐quantum setting while implementing these embedded microcontrollers. Following the lattice‐based construction of NTRUEncrypt which is accepted as IEEE standard P1363.1, Guillen et al. [23] implemented NTRUEncrypt for Cortex‐M0 based microcontrollers. This ensures again the feasibility of lattice‐based encryption on IoT devices. Another implementation of R‐LWE‐based encryption scheme is presented by Liu et al. [31] which is computationally equivalent to NTRUEncrypt. The authors achieved 46‐bit security with encryption and decryption timings as 24.9 ms and 6.7 ms respectively, on an 8‐bit ATxmega128 microcontroller.

5.5 Conclusion

Our main target in this contribution was to provide a general overview of lattice‐based primitives and to summarize how these constructions can be applied to IoT. We first introduced the reader to the complex notions of lattice‐based cryptography, yet tried to avoid details which are too specific for the concept of this chapter. Then, using these notions, we provided a summary of lattice‐based constructions. Finally, in the last section, we reviewed the state‐of‐the‐art applications of cryptographic primitives to the IoT systems, where most of the existing applications are based on classical number‐theoretic assumptions, we want to catch the reader's attention to the importance of a switch to quantum‐resistant constructions, where lattice‐based constructions provide a powerful solution.

References

  1. 1 Agrawal, S., Boneh, D. and Boyen, X. (2010). Efficient lattice (H)IBE in the standard model. In: Advances in Cryptology –EUROCRYPT 2010. Lecture Notes in Computer Science, Vol. 6110 (ed. H. Gilbert), 553–572. Berlin, Heidelberg: Springer.
  2. 2 Agrawal, S., Freeman, D.M. and Vaikuntanathan, V. (2011). Functional encryption for inner product predicates from learning with errors. Advances in Cryptology ‐CRYPTO 2011, Proceedings. Santa Barbara, USA (14–18 August 2011). Springer.
  3. 3 Ajtai, M. (1996). Generating hard instances of lattice problems (extended abstract). STOC '96 Proceedings of the twenty‐eighth annual ACM symposium on Theory of Computing, Philadelphia, USA (22–24 May). ACM.
  4. 4 Ajtai, M. and Dwork, C. (1997). A public‐key cryptosystem with worst‐case/average‐case equivalence. STOC '97 Proceedings of the twenty‐ninth annual ACM symposium on Theory of computing, El Paso, USA, (04–06 May 2019). ACM.
  5. 5 Alekhnovich, M. (2003). More on average case vs approximation complexity. 44th Symposium on Foundations of Computer Science (FOCS 2003), Cambridge, USA (11–14 October 2003). IEEE Computer Society.
  6. 6 Alkim, E., Ducas, L., Pöppelmann, T. and Schwabe, P. (2016). Post‐quantum key exchange a new hope. USENIX Security Symposium. https://www.usenix.org/system/files/conference/usenixsecurity16/sec16_paper_alkim.pdf (accessed 25 June 2019).
  7. 7 Alkim, E., Jakubeit, P., and Schwabe, P. (2016). New hope on arm cortex‐m. International Conference on Security, Privacy, and Applied Cryptography Engineering, Hyderabad, India (14–18 December 2016). Springer.
  8. 8 Banerjee, A., Peikert, C. and Rosen, A. (2012). Pseudorandom functions and lattices. Advances in Cryptology. EUROCRYPT 2012. Proceedings, Cambridge, UK (15–19 April 2012). Springer.
  9. 9 Boneh, D., Gentry, C., Gorbunov, S. et al. (2014). Fully key‐homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. Advances in Cryptology ‐ EUROCRYPT 2014 ‐ Proceedings, volume 8441 of Lecture Notes in Computer Science, Copenhagen, Denmark (11–15 May 2014). Springer.
  10. 10 Boneh, D., Lewi, K., Montgomery, H.W. and Raghunathan, A. (2013). Key homomorphic prfs and their applications. Advances in Cryptology ‐ CRYPTO 2013. Proceedings, Part I, volume 8042 of Lecture Notes in Computer Science, Santa Barbara, USA (18–22 August 2013). Springer.
  11. 11 Bos, J.W., Costello, C., Naehrig, M. and Stebila, D. (2015). Post‐quantum key exchange for the tls protocol from the ring learning with errors problem. 2015 IEEE Symposium on Security and Privacy (SP), San Jose, USA (17–21 May 2015). IEEE.
  12. 12 Brakerski, Z. and Vaikuntanathan, V. (2011). E_cient fully homomorphic encryption from (standard) LWE. IEEE 52nd Annual Symposium on Foundations of Computer Science, Washington, USA (22–25 October 2011). IEEE Computer Society.
  13. 13 Brakerski, Z. and Vaikuntanathan, V. (2015). Constrained key‐homomorphic prfs from standard lattice assumptions ‐ or: How to secretly embed a circuit in your PRF. Theory of Cryptography ‐ Proceedings, Part II, volume 9015 of Lecture Notes in Computer Science, Warsaw, Poland (23–25 March 2015). Springer.
  14. 14 Cash, D., Hofheinz, D., Kiltz, E. and Peikert, C. (2010). Bonsai trees, or how to delegate a lattice basis. EUROCRYPT 2010, volume 6110 of LNCS, French Riviera, France (30 May–3 June 2010). Springer.
  15. 15 Ducas, L., Durmus, A., Lepoint, T. and Lyubashevsky, V. (2013). Lattice signatures and bimodal gaussians. Advances in Cryptology ‐ CRYPTO 2013 ‐ 33rd Annual Cryptology Conference, Santa Barbara, USA (18–22 August 2013). Springer.
  16. 16 El Kaafarani, A. and Katsumata, S. (2018). Attribute‐based signatures for unbounded circuits in the ROM and e_cient instantiations from lattices. Public‐Key Cryptography ‐ PKC 2018, Proceedings, Part II, Rio de Janeiro, Brazil (25–29 March 2018). Springer.
  17. 17 Gentry, C. (2009). Fully homomorphic encryption using ideal lattices. Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC, Bethesda, USA (31 May–2 June 2009). ACM.
  18. 18 Gentry, C., Peikert, C. and Vaikuntanathan, V. (2008). Trapdoors for hard lattices and new cryptographic constructions. STOC 08' Proceedings of the fortieth annual ACM symposium on Theory of computing, Victoria, Canada (17–20 May 2008). ACM.
  19. 19 Gentry, C., Sahai, A., and Waters, B. (2013). Homomorphic encryption from learning with errors: Conceptually simpler, asymptotically faster, attribute based. Advances in Cryptology –CRYPTO 2013, Santa Barbara, USA (18–22 August 2013). Springer.
  20. 20 Goldreich, O., Goldwasser, S, and Halevi, S. (1997). Public‐key cryptosystems from lattice reduction problems. Advances in Cryptology ‐ CRYPTO '97, 17th Annual International Cryptology Conference, Santa Barbara, USA (17–21 August 1997). Springer.
  21. 21 Goldreich, O., Goldwasser, S. and Micali, S. (1986). How to construct random functions. Journal of the ACM 33 (4): 792–807.
  22. 22 Gorbunov, S., Vaikuntanathan, V. and Wee, H. (2013). Attribute‐based encryption for circuits. Symposium on Theory of Computing Conference, STOC 2013, Palo Alto, USA (1–4 June 2013). ACM.
  23. 23 Guillen, O.M., Poppelmann, T., Mera, J.M.B. et al. (2017). Towards post‐quantum security for iot endpoints with ntru. Proceedings of the Conference on Design, Automation & Test in Europe, Lausanne, Switzerland (27–31 March 2017). European Design and Automation Association.
  24. 24 Hirose, S., Kuwakado, H. and Yoshida, H. (2018). A pseudorandom‐function mode based on lesamnta‐lw and the MDP domain extension and its applications. IEICE Transactions 101‐A (1):110–118.
  25. 25 Hoffstein, J., Pipher, J. and Silverman, J.H. (1998). NTRU: A ring‐based public key cryptosystem. Algorithmic Number Theory, Third International Symposium, ANTS‐III, Proceedings, Portland, USA (21–25 June 1998). Springer.
  26. 26 Kuchta, V., Sahu, R.A., Sharma, G. and Markowitch, O. (2017) On new zero‐knowledge arguments for attribute‐based group signatures from lattices. Information Security and Cryptology –ICISC 2017 –20th International Conference, Seoul, South Korea (29 November–1 December 2017). Springer.
  27. 27 Kuchta, V., Sharma, G., Sahu, R.A. and Markowitch, O. (2017). Multi‐party (leveled) homomorphic encryption on identity‐based and attribute‐based settings. Information Security and Cryptology ‐ ICISC 2017, Seoul, South Korea (29 November–1 December 2017). Springer.
  28. 28 Lam, K. and Chi, C. (2016). Identity in the internet‐of‐things (iot): New challenges and opportunities. Information and Communications Security ICICS 2016 –Proceedings, Singapore, Singapore (29 November–2 December 2016). Springer.
  29. 29 Leveugle, R., Mkhinini, A. and Maistri, P. (2018). Hardware support for security in the internet of things: From lightweight countermeasures to accelerated homomorphic encryption. Information 9 (5): 114.
  30. 30 Lindner, R. and Peikert, C. (2011). Better key sizes (and attacks) for lwe‐based encryption. Topics in Cryptology –CT‐RSA 2011 ‐ The Cryptographers Track at the RSA Conference 2011, San Francisco, USA (14–18 February 2011). Springer.
  31. 31 Liu, Z., Pöoppelmann, T., Oder, T. et al. (2017). High‐performance ideal lattice‐based cryptography on 8‐bit avr microcontrollers. ACM Transactions on Embedded Computing Systems (TECS) 16 (4): 117.
  32. 32 Lyubashevsky, V. (2008). Lattice‐based identification schemes secure under active attacks. Public Key Cryptography –PKC 2008, Proceedings, volume 4939 of Lecture Notes in Computer Science, Barcelona, Spain (9–12 March 2008). Springer.
  33. 33 Lyubashevsky, V. and Micciancio, D. (2008). Asymptotically efficient lattice‐based digital signatures. Theory of Cryptography, Fifth Theory of Cryptography Conference, New York, USA (19–21 March 2008). Springer.
  34. 34 Lyubashevsky, V., Micciancio, D., Peikert, C. and Rosen, A. (2008). SWIFFT: A modest proposal for FFT hashing. Fast Software Encryption, 15th International Workshop, FSE, Lausanne, Switzerland (10–13 February 2008). Springer.
  35. 35 Peikert, C. (2007). Limits on the hardness of lattice problems in l‐p norms. 22nd Annual IEEE Conference on Computational Complexity CCC 2007, San Diego, USA (13–16 June 2007). IEEE Computer Society.
  36. 36 Peikert, C. (2014). Lattice cryptography for the internet. Post‐Quantum Cryptography – 6th International Workshop, PQCrypto 2014, Waterloo, Canada, (1–3 October 2014). Springer.
  37. 37 C. Peikert. (2016). A decade of lattice cryptography. Foundations and Trends in Theoretical Computer Science 10 (4): 283–424.
  38. 38 Peikert, C. and Waters, B. (2008). Lossy trapdoor functions and their applications. Proceedings of the 40th Annual ACM Symposium on Theory of Computing, Victoria, Canada (17–20 May 2008). ACM.
  39. 39 Pöoppelmann, T., Ducas, L. and Guneysu, T. (2014). Enhanced lattice‐based signatures on reconfigurable hardware. International Workshop on Cryptographic Hardware and Embedded Systems, Busan, South Korea (23–26 September 2014). Springer.
  40. 40 Regev, O. (2003). New lattice based cryptographic constructions. STOC '03 Proceedings of the thirty‐fifth annual ACM symposium on Theory of computing, San Diego, USA (09–11 June 2003). ACM.
  41. 41 Regev, O. (2005). On lattices, learning with errors, random linear codes and cryptography. STOC '05 Proceedings of the thirty‐seventh annual ACM symposium on Theory of computing, Baltimore, USA (22–24 May 2005). ACM.
  42. 42 Rivest, R., Adleman, L. and Dertouzos, M. (1978). On data banks and privacy homomorphisms. Foundations of secure computation 4 (11): 169–180.
  43. 43 Sahai, A. and Waters, B. (2005). Fuzzy identity‐based encryption. EUROCRYPT 2005, Proceedings, Aarhus, Denmark (22–26 May 2005). Springer.
  44. 44 Shamir, A. (1984). Identity‐based cryptosystems and signature schemes. Advances in Cryptology, Proceedings of CRYPTO '84, Santa Barbara, USA (19–22 August 1984). Springer.
  45. 45 Wang, Q., Chen, S. and Ge, A. (2015). A new lattice‐based threshold attribute‐based signature scheme. Information Security Practice and Experience – 11th International Conference, ISPEC 2015, Beijing, China (5–8 May 2015). Springer.
..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.119.133.228