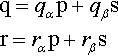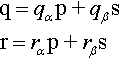The Cross Ratio
November-December 1998
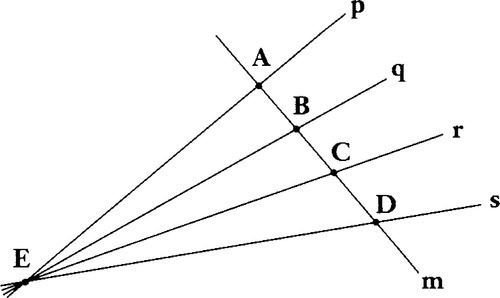
Geometry is the study of what properties of a figure stay the same as the figure undergoes some transformation. For example, in Euclidean geometry, the allowable transformations are rotations and translations. Properties that stay constant include distances and angles. For projective geometry, such as we use with homogeneous coordinates, the transformations include perspective projections. In this case, one thing that emphatically does not stay the same is geometric length. A property that does, however, is something called the cross ratio. Take a look at Figure 12.1 where lines p, q, r, and s all intersect at the same point; the cross ratio is the ratio of the ratios of the following distances:
χ=|AB|/|BD||AC|/|CD|
![]()
This value is constant no matter where line m is placed. It is also constant if the whole diagram undergoes a homogeneous transformation (possibly including perspective).
This has always puzzled me. If geometric distances aren't preserved, and ratios of geometric distances aren't preserved, then how come the ratio of ratios of geometric distances is preserved? Well, here's a quick demonstration.
The First Ratio
Let's begin by calculating the Euclidean distance between points A and B. I'll start with the 2D homogeneous coordinates of each point, which I will name as follows:
A=[AxAyAw]B=[BxByBw]
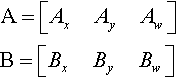
To calculate a Euclidean distance, we must turn these into the “real” coordinates by dividing out the homogeneous w coordinate giving the two 2D Euclidean points:
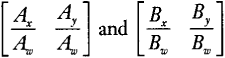
[AxAwAyAw]and[BxBwByBw]
Then subtract giving
[AxAw−BxBwAyAw−ByBw]
![]()
The desired distance is the length of this 2D vector. The fact that this quantity doesn't treat all three of the x, y, and w components symmetrically is a hint that Euclidean distance is not a meaningful concept in projective geometry.
Anyway, if we bash ahead to get the Euclidean length of the above vector, we would need to calculate the square root of the sum of the squares of these two components—wotta pain. Instead, let's pretend for a minute that the line m is horizontal and points A … D line up horizontally. In that case, the length of the vector is just the x component of the vector. In other words,
AxAw−BxBw=|AB|
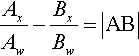
In general, though, the line will be at some angle θ. In this case, the x component will equal the length times the cosine of the tilt angle, or
AxAw−BxBw=|AB|cosθ
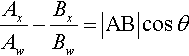
For the collinear segment BD, tipped by the same angle θ the x component would be
BxBw−DxDw=|BD|cosϑ
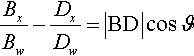
Here's where the first ratio will come in to simplify life. The top half of our desired cross ratio is the ratio between these segment AB and segment BD. And, by similarity, the ratio of the x components is the same as the ratio of the lengths. Taking the ratio of the above two equations, we find
AxAw−BxBwBxBw−DxDw=|AB|cosϑ|BD|cosϑ=|AB||BD|
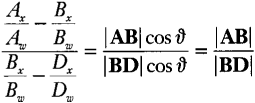
The angle dependency cancels. Yay! We can calculate the ratio of lengths without any squaring and square rooting.
The Second Ratio
Now let's look at the second ratio in the “ratio of ratios” game. Remember that what we are really interested in is
χ=|AB|/|BD||AC|/|CD|
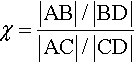
A little algebra on the AB/BD ratio turns it into
|AB||BD|=DwAw(AxBw−AwBxBxDw−BwDx)
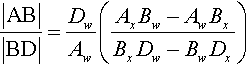
And by going through the same schtick, but everywhere changing B to C, we can see that the second of our two ratios is
|AC||CD|=DwAw(AxCw−AwCxCxDw−CwDx)
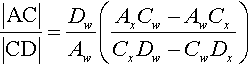
Now we can see why the ratio of ratios is something interesting homogeneously—it lets us cancel the ugly w component ratios. The whole cross ratio then boils down to
χ=|AB|/|BD||AC|/|CD|=AxBw−AwBxBxDw−BwDxCxDw−CwDxAxCw−AwCx
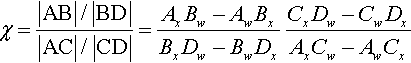
This is much more symmetric in x, y, and w, and closer to the sort of thing we expect we can make homogeneously constant.
Constancy with Changing m
Now we can ask why this ratio is independent of the position of the line m. The root cause must have something to do with the fact that we generate the points A, B, C, and D from the lines p, q, r, and s that have the special relationship of all intersecting at the same point E.
First, then, here's a brief reminder of the relationship between homogeneous points and lines. You can calculate the point at the intersection of two lines by taking the cross product of the line vectors. This means that the point at the intersection of the four lines is any of the six quantities:
E=c1(p×q)=c2(q×r)=c3(r×s)=c4(p×r)=c5(q×s)=c3(p×s)
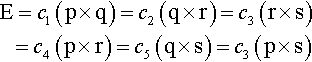
The inclusion of the constants ci recognizes the fact that the cross products can represent the same intersection point even though there might be a homogeneous scale factor applied to all three of the x, y, and w components.
After some fooling around, I have found that, for our purposes, the neatest algebraic way to use this relationship is to express the lines q and r in terms of p and s. I'll write this as
q=qαp+qβsr=rαp+rβs
You can think of the pairs [qαqβ]![]() and [rαrβ]
and [rαrβ]![]() as ID homogeneous coordinates for the collection of lines passing through E, the intersection of p and s. Any point passing through this intersection has an [αβ]
as ID homogeneous coordinates for the collection of lines passing through E, the intersection of p and s. Any point passing through this intersection has an [αβ]![]() pair that describes it. Any nonzero multiple of an [αβ]
pair that describes it. Any nonzero multiple of an [αβ]![]() pair represents the same line though.
pair represents the same line though.
Now, let's relate this to our points. Remember, the cross product is how we intersect lines, so we have
A=p×mB=q×mC=r×mD=s×m
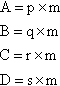
Write the interior point B in terms of the outside lines and points:
B=q×m=(qαp+qβs)×m=qα(p×m)+qβ(s×m)=qαA+qβD
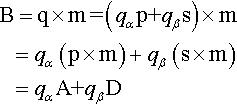
We can then write the top half of the cross ratio as
|AB|/|BD|=AwDwAxBw−AwBxBxDw−BwDx =AwDwAx(qαAw+qβDw)−Aw(qαAx+qβDx)(qαAx+qβDx)Dw−(qαAw+qβDw)Dx =AwDwqβAxDw−qβAwDxqαAxDw−qαAwDx =AwDwqβqα
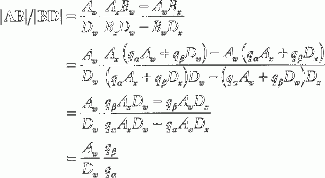
Again, run through this derivation with C instead of B, and you get
|AC|/|CD|=AwDwrβrα
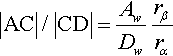
The net cross ratio is now
χ=|AB|/|BD||AC|/|CD|=qβ/qαrβ/rα
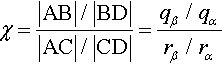
The interesting thing about this is that the whole dependence on the location of m has disappeared, as well as the dependence on which coordinate (here we used x) we chose to use as the measure of distance ratios. That is, it is only dependant on the orientations of the lines q and r relative to P and s. Any line m′![]() intersecting these will generate the same cross ratio. The cross ratio is thus a property of the locations of the four original lines, rather than the extra line m.
intersecting these will generate the same cross ratio. The cross ratio is thus a property of the locations of the four original lines, rather than the extra line m.
As another way of looking at this, start with the equations in (12.1) and cross them with P and s:
q×p=qαp×p+qβs×p=qβs×pq×s=qαp×s+qβs×s=qβp×sr×p=rαp×p+qβs×p=qβs×pr×s=rαp×s+qβs×s=qβp×s
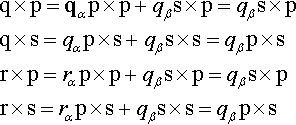
These are four vector equations. Turn them into scalars by dotting them with m:
m⋅q×p=qβm⋅s×pm⋅q×s=qβm⋅p×sm⋅r×p=qβm⋅s×pm⋅r×s=qβm⋅p×s
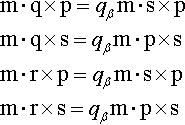
And now you can write the cross product in the following form:
x=qβrαqαrβ=(m⋅q×p)(m⋅r×s)(m⋅q×s)(m⋅r×p)
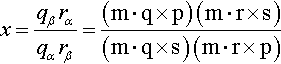
Here's another key fact: χ contains only the ratios of the alpha/beta pairs, so it is also independent of arbitrary homogeneous scalings of the vector for q and r. For example, if we replaced q with γ![]() q (geometrically the same line), it means that we are scaling both qα
q (geometrically the same line), it means that we are scaling both qα![]() and qβ
and qβ![]() by γ
by γ![]() , which will again cancel out in the formula for χ
, which will again cancel out in the formula for χ
Constancy under Perspective
Now let's see why the cross ratio is unchanged when we transform the four lines via an arbitrary transformation matrix. If we have a transformation T that changes our outer two lines as
p′=Tps′=Ts
![]()
the inner lines will be
q′=Tq=T(qαp+qβs)=qαTp+qβTs=qαp′+qβs′

And similarly
r′=rαp′+rβs′
![]()
Even if we try to disguise line q′![]() or r′
or r′![]() by multiplying by some homogeneous scale, we get the same value of cross ratio—the ratio of ratios:
by multiplying by some homogeneous scale, we get the same value of cross ratio—the ratio of ratios:
χ=qβ/qαrβ/rα
![]()
A particularly interesting special case of this occurs when we take the outside lines p and s as the x and y axes, and transform by a simple nonuniform scale factor. Numerically, this would be
p=[100],q=[qαqβ0],r=[rαrβ0]s=[010] T=[fx000fy0001]
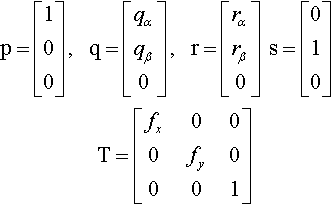
From this we get
p′=[fx00],q′=[fxqαfyqβ0],r′=[fxrαfyrβ0]s′=[0fy0]
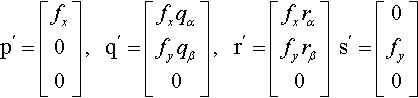
The alpha and beta components of q and r have changed to
q′α=fxqα,q′β=fyqβr′α=fxrα,r′β=fyrβ
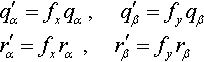
The lines p and s haven't moved, but the lines q and r both have. And the ratios of the [α,β]![]() values of the lines q and r are different:
values of the lines q and r are different:
q′β/q′α=fyfx(qβ/qα)r′β/r′α=fyfx(rβ/rα)
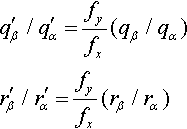
But sure enough, the ratio of ratios remains the same:
χ=q′β/q′αr′β/r′α=qβ/qαrβ/rα
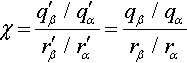
In other words, even though a transformation might not move the outside lines p and s, it will move the inside lines q and r in such a manner that the change in the ratio (qβ/qα)![]() is matched by the same change in the ratio (rβ/rα)
is matched by the same change in the ratio (rβ/rα)![]()
Summary
The cross ratio is as much a property of the four mutually intersecting lines p, q, r, and s as it is of the four collinear points A, B, C, and D. Any line m that you throw across the lines will generate four points with the same cross ratio.
You can, in turn, take any four collinear points A, B, C, and D, and throw various collections of four mutually intersecting lines through them. Each of these line collections will have the same cross ratio. Finally, you can project any of these figures perspectively and also get an unchanged cross ratio.
The true homogeneous nature of the cross ratio can best be seen by writing it as
χ=qβrαqαrβ
![]()
and reviewing the effect of an arbitrary homogeneous scaling on each of the four lines. Remember that
q=qαp +qβsr=rαp +rβs
■ Scaling only q will scale both qα and qβ but this cancels out.
χ=qβraqarβ
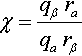
■ Scaling only r will scale rα and rβ, but these will cancel:
χ=qβraqarβ
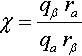
■ Scaling only p will require inversely scaling qaand ra to keep q and r the same in Equation (12.1). These again cancel:
χ=qβraqarβ
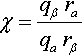
■ Scaling only s will require inversely scaling qβ and rβ. Same song, new verse:
χ=qβraqarβ
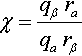
From this, we can see the necessity of this arrangement of ratio of ratios in constructing a quantity that remains homogeneously meaningful.
So, even though perspective transformations do not preserve distances, or ratios of distances, they do preserve these ratios of ratios of distances.