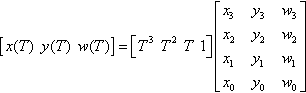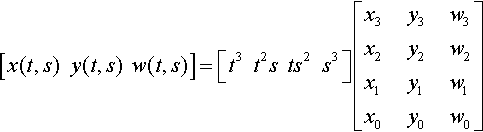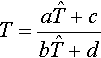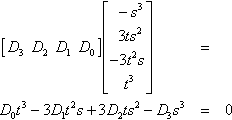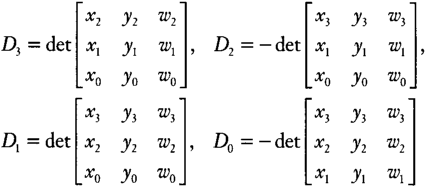How Many Different Rational Parametric Cubic Curves Are There? Part II, The “Same” Game
November-December 1999
RCM=˜C![]()
OK. Here's the deal. I've been playing with the question in the title on and off for over a year now. I'm interested in both the answer to the question and in finding the clearest possible derivation of that answer. My first efforts were very algebra intensive but had an aura of concreteness about them. As I played with the question and went through innumerable drafts of this column, I came up with more and more elegant ways to ward off the brute-force algebra and make the answer more intuitive without reams of calculation. In order for these elegant techniques to work, however, I needed to build up a collection of tools (or lemmas for the mathematically erudite) that themselves took a little time to explain.
The tool that I described in the previous chapter (the use of a particular matrix identity, which I will review here) popped up just before I started to write. I had to scrap my original idea for that chapter and rewrite it to describe this new tool. Using this tool to answer our big question has required major surgery to what you are now seeing in the current chapter.
I have already given you the answer to the big question: three. But deriving that answer in a clear and obvious manner is still a little ways away. But that's OK. The reason we are doing this is really not so much to answer the question as to build our intuition about the algebraic formulas and the geometry that they represent. Let's see, isn't there a phrase that encapsulates this idea? Oh yes: The journey is the reward.
Definition
So, let's reiterate what we are dealing with: parametric cubic curves defined by the formula
[x(T)y(T)w(T)]=[T3T2T1]?[x3y3w3x2y2w2x1y1w1x0y0w0]
We are interested in all points generated by this equation, for all values of T from − ∞ to + ∞. Infinite parameter values are easier to manipulate if we use a homogeneous parameterization, something like expressing the parameter in 1D homogeneous coordinates. I will denote the homogeneous parameter coordinates as [t,s], where T = t/s. In terms of the homogeneous parameterization, the curve equation is
[x(t,s)y(t,s)w(t,s)]=[t3t2sts2s3]?[x3y3w3x2y2w2x1y1w1x0y0w0]
I'll bounce back and forth between the more familiar nonhomogeneous parameter T and homogeneous parameter representation [t,s] as clarity dictates.
According to the homogeneous convention, any scalar multiple of a [t,s] coordinate represents the same parametric point, and will generate the same geometric point. To generate the whole curve, we must trace out a curve in [t,s] space that looks roughly semicircular around the origin. Why go only halfway around the origin? Well, if the curve starts at [t0,s0] and ends at [−t0,−s0], it will have returned to its geometric starting point. (If it started at [x0 y0 w0], it will now be at [−x0 −y0 −w0].) If you went around the parametric origin through a whole circle, you would trace out the curve twice.
The matrix of coefficients contains all the information about the curve, so I will give it a name:
[x3y3w3x2y2w2x1y1w1x0y0w0]≡C
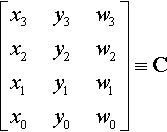
“Different” Means not the Same
Next, let's concretize what I mean by “different curves” by turning the question around and defining what makes two curves the “same.” We will then sort all the parametric cubic curves into groups of the same curves, and see how many groups we have.
The Same via Transformation
In projective geometry, we are interested in properties of shapes that remain constant even if the shape is subjected to a perspective transformation. The sorts of geometric properties that remain unchanged by such a transformation include intersections, tangency, and inflection points.
Algebraically, we typically express a perspective transformation as a homogeneous matrix multiplication:
[xyw]?M=[˜x˜y˜w]
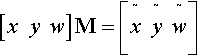
The coefficient matrix transforms in the same way:
CM=˜C
![]()
Accordingly, if we can find a nonsingular transformation matrix M that changes one coefficient matrix C into another one ˜C![]() , we will say that the curves generated by those matrices are the same.
, we will say that the curves generated by those matrices are the same.
The same via Reparametrization
There's another algebraic transformation we can perform on the curve equation that doesn't change the curve shape at all—we can change the parameterization. This change is possible because we're interested in the whole curve generated by the infinite parameter range − ∞ ≤ T ≤ + ∞. For example, if we define
T=aˆT+c
![]()
and run ˆT![]() from − ∞ to + ∞, we'll also generate all T's from − ∞ to + ∞. To see how this affects the algebra of the coefficient matrix, we calculate
from − ∞ to + ∞, we'll also generate all T's from − ∞ to + ∞. To see how this affects the algebra of the coefficient matrix, we calculate
T2=a2ˆT2+2acˆT+c2T3=a2ˆT3+3a2cˆT2+3ac2ˆT+c3
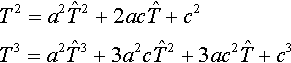
and write these equations in matrix form:
[T3T2T1]=[ˆT3ˆT2ˆT1]?[a30003a2ca2003ac22aca0c3c2c1]
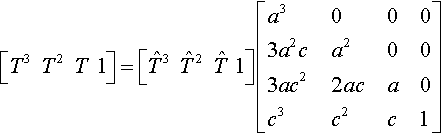
Plugging this into Equation (15.1), we can see that
[T3T2T1]?C=[ˆT3ˆT2ˆT1]?[a30003a2ca2003ac22aca0c3c2c1]?C

Evaluating each of these for all values of T and all values of ˆT![]() will generate exactly the same set of points. In other words, the coefficient matrices
will generate exactly the same set of points. In other words, the coefficient matrices
Cand[a30003a2ca2003ac22aca0c3c2c1]?C
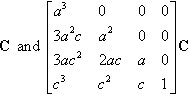
generate exactly the same curve without any geometric distortions.
When we go to the homogeneous parameterization, we can use an even more general transformation, a 1D perspective (rational linear) transform of the form
T=aˆT+cbˆT+d
A plot of this type of function looks like either a line or a hyperbola. Note that the function is still a one-to-one mapping of ˆT![]() to T (including infinite values) and that it's monotonic since the derivative dT/dˆT
to T (including infinite values) and that it's monotonic since the derivative dT/dˆT![]() has a constant sign.
has a constant sign.
Recasting this function in homogeneous parameter space, we get
ts=aˆtˆs+cbˆtˆs+d=aˆt+cˆsbˆt+dˆs

Writing this as a matrix gives
[ts]=[ˆtˆs]?[abcd]
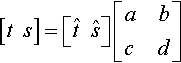
In other words, the reparametrization is a simple linear transformation of [t,s] space. This is OK as long as the transformation is nonsingular, which is as long as ad−bc≠0![]() .
.
To see how this reparametrization affects the form of the coefficient matrix, we calculate the following:
t3=(aˆt+cˆs)3t2s=(aˆt+cˆs)2?(bˆt+cˆs)ts2=(aˆt+cˆs)?(bˆt+cˆs)2S3=(bˆt+cˆs)3
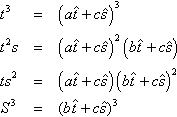
Expand this mess all out and write it as a matrix product, and we get
[t3t2sts2s3]=[ˆt3ˆt2ˆsˆtˆs2ˆs3]?R
where
R≡[a3a2bab2b33a2ca(2bc+ad)b(bc+2ad)3b2d3ac2c(bc+2ad)d(2bc+ad)−3bd2c3c2dcd2d3]
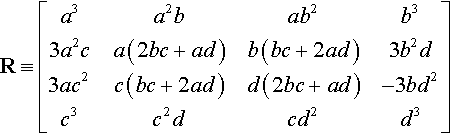
Now we combine Equations (15.2) and (15.4) to get
[xyw]=[ˆt3ˆt2ˆsˆtˆs2ˆs3]?RC
![]()
We say that any coefficient matrix C generates the same curve as the matrix RC for any R constructed with any values a,b,c,d such that ad ad−bc≠0![]() .
.
The Game
So here's what we're going to do. We're going to develop an algorithm that takes an arbitrary coefficient matrix C and transforms it via a (nonsingular) reparametrization matrix R and a (nonsingular) geometric transformation matrix M to turn it into a canonical form:
RCM=˜C
![]()
We'll devise this canonical form to be as simple as possible, with lots of zeros and ones as elements. It will turn out that there are six possible resulting types of ˜C![]() matrices, three that represent “true” cubics, and three that come from lower-order curves disguised as cubics.
matrices, three that represent “true” cubics, and three that come from lower-order curves disguised as cubics.
The Canonical Geometric Transform
As a warm-up exercise, let's start with an arbitrary second-order curve and simplify it via geometric transformations. We start with
[xyw]=[t2tss2]?[x2y2w2x1y1w1x0y0w0]
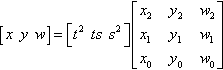
Transforming by the matrix M gives
[ˆxˆyˆz]=[t2tss2]?[x2y2w2x1y1w1x0y0w0]?M
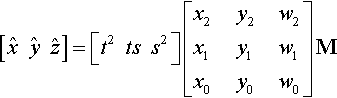
We want to find a matrix M that gives us as simple a product as possible with the coefficient matrix. Gee, what could that be? How about simply picking M as the inverse of the coefficient matrix. You would get
[ˆxˆyˆw]=[t2sts2]?[100010001]
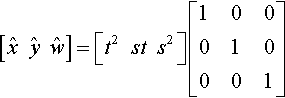
Any second-order curve with a nonsingular coefficient matrix is the “same” as this canonical curve, which happens to be a parabola. All conic sections are transformations of this canonical parabola. This means that, according to the rules of our game, there is exactly one second-order curve.
There is a bit of a gotcha though. We need to worry about the case where the coefficient matrix is singular. As it happens, this turns out to be linear curve (OK, a line) in disguise, not a true second-order curve. I'll deal with such cases in a separate column.
Now let's see what happens when we try to simplify a cubic in a similar manner. We want to find a transformation M that will simplify the coefficient matrix
[ˆxˆyˆw]=[t3t2sts2s3]?[x3y3w3x2y2w2x1y1w1x0y0w0]?M
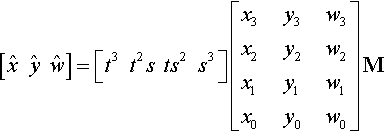
We could shave off the top three rows of the coefficient matrix and transform by the inverse of this 3 × 3 matrix. As long as this matrix is nonsingular, we'll get
[ˆxˆyˆw]=[t3t2sts2s3]?[100010001ˆx0ˆy0ˆw0]
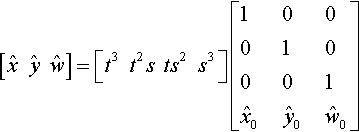
So we've boiled our cubic curve down to what, at first, looks like a three-parameter class of curves, depending on what we get for ˆx0,ˆy0,ˆw0![]() . To understand what to do next, we must remember our tool from the last chapter.
. To understand what to do next, we must remember our tool from the last chapter.
Inflection Points Revisited
In the previous chapter, we showed that the inflection points of a cubic curve are at parameter values that are the solutions to a homogeneous cubic polynomial:
?[D3D2D1D0]?[???−s3???3ts2−3t2s?????t3]=D0t3−3D1t2s+3D2ts2−D3s3=0
where the coefficients Di are the determinants of the various 3 × 3 submatrices of the coefficient matrix:
D3=det?[x2y2w2x1y1w1x0y0w0],D2=−det?[x3y3w3x1y1w1x0y0w0],D1=det?[x3y3w3x2y2w2x0y0w0],D0=−det?[x3y3w3x2y2w2x1y1w1]
Notice that the matrix defining D0 is the one we used for the canonical transform above.
Back to the Game
Now we can relate the values of ˆx0,?ˆy0?ˆw0![]() to the values of Di. We start by noting that each row of the coefficient matrix is a homogeneous point in the plane. I'll give names to these row vectors as follows (I include the ellipses to emphasize that the points are row vectors):
to the values of Di. We start by noting that each row of the coefficient matrix is a homogeneous point in the plane. I'll give names to these row vectors as follows (I include the ellipses to emphasize that the points are row vectors):
[x3y3w3x2y2w2x1y1w1x0y0w0]=[⋯p3⋯⋯p2⋯⋯p1⋯⋯p0⋯]
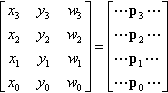
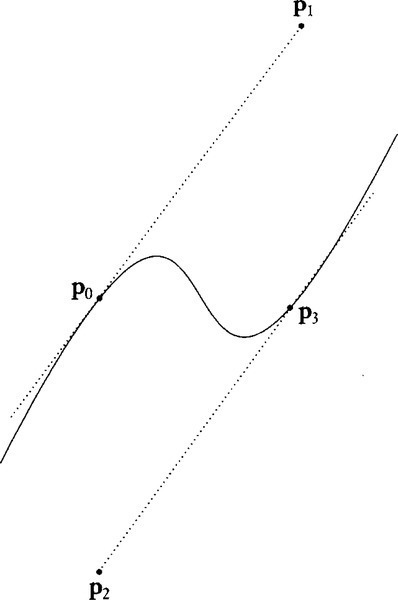
It's interesting to note that the top and bottom rows are points on the curve itself. p0 is the point at the homogeneous parameter value [0,1] (or at T = 0 in the nonhomogeneous formulation), and p3 is the point at the homogeneous parameter value [1,0] (or at T=∞![]() in the nonhomogeneous formulation). Furthermore, the line through p0 and p1 is tangent to the curve at p0. And the line through p2 and p3 is tangent to the curve at p3 (see Figure 15.1). Anyway, we can now rewrite the definition of the elements of the D vector from Equation (15.6) as
in the nonhomogeneous formulation). Furthermore, the line through p0 and p1 is tangent to the curve at p0. And the line through p2 and p3 is tangent to the curve at p3 (see Figure 15.1). Anyway, we can now rewrite the definition of the elements of the D vector from Equation (15.6) as
D3=???p2⋅p1×p0D2=−p3⋅p1×p0D1=???p3⋅p2×p0D0=−p3⋅p2×p1
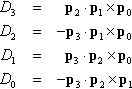
And the geometric transformation matrix we were using as our canonical transformation is simply
M=[⋯p3⋯⋯p2⋯⋯p1⋯]−1
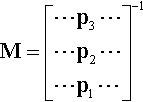
We can evaluate the matrix inverse from the cross products of the various row vectors. Each cross product gives a column vector, and the inverse is
[⋯p3⋯⋯p2⋯⋯p1⋯]−1=−1D0?[⋮⋮⋮p2×p1p1×p3p3×p2⋮⋮⋮]
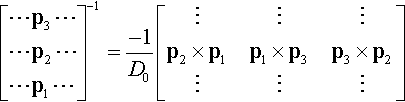
As long as this matrix is nonsingular (that is, the determinant, D0, is nonzero), we can see that our canonical transformation will generate
????[⋯p3⋯⋯p2⋯⋯p1⋯⋯p0⋯]?[⋯p3⋯⋯p2⋯⋯p1⋯]−1=[⋯p3⋯⋯p2⋯⋯p1⋯⋯p0⋯]−1D0[⋮⋮⋮p2×p1p1×p3p3×p2⋮⋮⋮]=[100010001−D3D0−D2D0−D1D0]
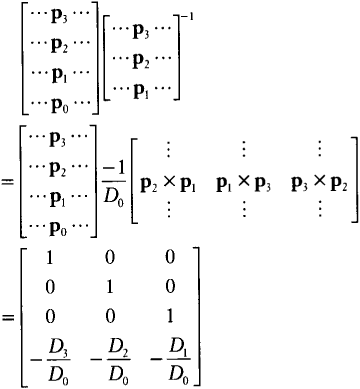
This, then, gives the meaning of the bottom row of the candidate canonical matrix. If, however, the original curve gave us a value of D0 = 0, this is not a good choice for a canonical transformation. All is not lost, however. We can pick a transformation matrix as the inverse of any of the other subsets of three of the four rows and get the following possibilities for canonical coefficient matrices:
[⋯p3⋯⋯p2⋯⋯p1⋯⋯p0⋯]?[⋯p3⋯⋯p2⋯⋯p0⋯]−1=[100010−D3D1−D2D1−D0D1001][⋯p3⋯⋯p2⋯⋯p1⋯⋯p0⋯]?[⋯p2⋯⋯p1⋯⋯p0⋯]−1=[100−D3D2−D1D2−D0D2010001][⋯p3⋯⋯p2⋯⋯p1⋯⋯p0⋯]?[⋯p2⋯⋯p1⋯⋯p0⋯]−1=[−D2D3−D1D3−D0D3100010001]
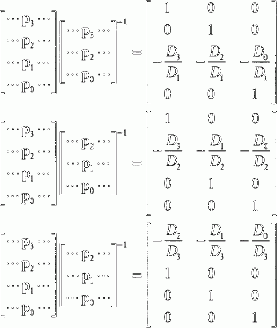
Which of these is best to choose will depend on what values we have for the Di's.
We have therefore been able to recast the question “How many different rational parametric cubic curves are there?” as “How many different homogeneous cubic polynomials are there?” We've gone from needing to understand the 12 numbers in the coefficient matrix to needing to understand the 4 coefficients in a homogeneous cubic polynomial.
How Does the Game Affect D?
The D vector determines where the inflection points are. The reason that inflection points are interesting is that the number of them will not change due to perspective transformations or due to reparametrization. How does this fact show up in the algebra of transformation that we just defined?
Geometric
When we transform C by a nonsingular geometric transformation M to the new matrix ˜C=CM![]() , what will be the elements of the D vector for this new coefficient matrix? Remember that the determinant of a product is the product of the determinants. So the determinant of any three rows of ˜C
, what will be the elements of the D vector for this new coefficient matrix? Remember that the determinant of a product is the product of the determinants. So the determinant of any three rows of ˜C![]() will equal the determinant of the same three rows of C times the determinant of M. Applying this to each 3 × 3 submatrix of C and ˜C
will equal the determinant of the same three rows of C times the determinant of M. Applying this to each 3 × 3 submatrix of C and ˜C![]() gives
gives
[˜D3˜D2˜D1˜D0]=(det??M)[D3D2D1D0]
![]()
In other words, a geometric transformation of the curve will just apply a uniform homogeneous scale of detM to the D vector. It will not change the location of the roots of the D polynomial, which are the parameter values at the inflection points. This pretty much makes sense.
Reparametrization
Reparametrization does not change the geometry of the curve at all, so inflection points stay put geometrically, while they may move around parametrically. To see where they move to, let's rewrite Equation (15.5) as
D0t3−3D1t2s+3D2ts2−D3s3=[t3t2sts2s3]?[D0−3D13D2−D3]=0
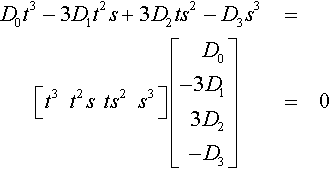
If we reparametrize this using Equation (15.4), we get
[ˆt3ˆt2sˆtˆs2ˆs3]?R?[D0−3D13D2−D3]=0
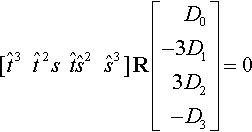
In other words, the coefficients of the reparametrized D are
R?[D0−3D13D2−D3]=[ˆD0−3ˆD13ˆD2−ˆD3]
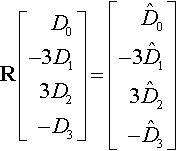
If you plot the function
f(t,s)=D0t3−3D1t2s+3D2ts2−D3s3
![]()
and consider what reparametrization does to it, you can see that it is just a rotation and shear of the function in parameter space. It mangles the shape, but one thing it does not do is to change the number and multiplicity of roots of the polynomial.
Winning the Game
The next order of business is to immerse ourselves in what types of homogeneous cubic polynomials exist under reparametrization. Our goal will be to pick a reparametrization matrix that makes the new values ˆDi![]() as simple as possible. We'll tackle that in the next millennium. (This was written just before New Year's Day 2000…. Oh, I really crack myself up.)
as simple as possible. We'll tackle that in the next millennium. (This was written just before New Year's Day 2000…. Oh, I really crack myself up.)