APPENDIX A
Deductive Reasoning and Proofs
“Education is the lighting of the fire, not the filling of a bucket.
—WILLIAM BUTLER YEATS (1865–1939, Nobel Prize in Literature, 1923)
A mind is a fire to be kindled, not a vessel to be filled.”
—PLUTARCH (AD 45–125, Priest of the Delphic Oracle)
A.1 Introduction
One of your objectives in studying this book should be to improve your skill in deductive reasoning. This activity ought to be enjoyable, as it involves real thinking of an analytic nature. Finding a convincing justification for a suspected truth after a long search is very good for your ego! It is creative activity akin to solving a puzzle. But it is better than that, because in some cases you may have established a fact for the first time in history, and thus have actually added to civilization’s store of knowledge.
Strings of logical arguments are essential in mathematics. They can put a stamp of validity on a conjecture that was only guessed at the start. Or they can lay to rest as incorrect some other conjecture. As you probably know, there are many conjectures in mathematics that have impressive evidence for their validity, yet have no complete justification. For example: Is it true that there are infinitely many prime numbers, n, such that n + 2 is also prime? These pairs are called twin primes. Examples are (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), and so on. Nobody knows whether this string of examples comes to a halt or continues forever.
There are many opportunities to practice the art of deductive reasoning in the subject of linear algebra. However, at the beginning, we can discuss some aspects of deduction in other more familiar contexts, such as in calculus, geometry, or algebra.
A.2 Deductive Reasoning and Direct Verification
One method of establishing the validity of some result is the use of direct verification. Usually this means that the proving process has a natural starting place with something known, and proceeds from there on a straight logical path to the desired conclusion. Often in such a procedure, there is no inventiveness required—only a calculation. Let us give an example.
THEOREM 1
If x and y are real numbers, and if a = y2 − x2, b = 2xy, and c = x2 + y2, then a2 + b2 = c2.
PROOF With a, b, c as given we have
 |
|
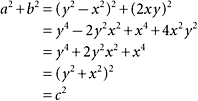In the previous demonstration, a small black box has been printed to signify the end of the proof. This notation is used throughout this book to indicate the end of proofs or examples.
In Theorem 1, if x and y are integers satisfying the inequality 0 < x < y, then a and b are the integer sides of a right triangle and c is the hypotenuse. For example, (3, 4, 5) is such a triple, obtained by taking x = 1 and y = 2. If a, b, and c are positive integers such that a2 + b2 = c2, then we call (a, b, c) a Pythagorean1 triple.
1 The Greek mathematician and savant Pythagoras flourished around 500 BC. He was born on the island of Samos, but emigrated to Croton in southern Italy around 531 BC. He is credited with discovery of the ratios among pleasing musical intervals. In Croton, he drew about him disciples in a new religion open to both men and women, which was unusual for the time. His group seems to have grasped the notion that the earth is spherical. He or his group discovered irrational numbers and the so-called Pythagorean Theorem about right triangles. In ancient times these matters were of practical importance in building, because they made it easy to construct right angles.
Why don’t you try an example (unless you are already skilled in this art)? Here is one to test yourself on.
THEOREM 2
Every integer that can be expressed in the form 14n − 3 can be expressed in the form 7k + 4, where n and k are integers.
A.3 Implications
In mathematics, we are often trying to establish implications. This means proving that one assertion implies another. These implications have the form ‘‘If P then Q,’’ where P and Q are assertions. A typical example of an implication (one that happens to be true) is
‘‘If x is a real number, then x2 is greater than or equal to 0.’’
The symbol ⇒ is often used to mean implies. Thus, the preceding example can be abbreviated by writing
 |
|
An assertion P ⇒ Q can be read as (P implies Q) or (if P is true, then Q is true). There are several other variations in the phraseology:
‘‘P is sufficient for Q,’’ or ‘‘Q is necessary for P,’’ or ‘‘Q if P,’’
‘‘P only if Q,’’ or ‘‘if Q is false, then so is P,’’ or
‘‘if P is true, then so is Q.’’
Consider a statement of the form P ⇒ Q. The contrapositive of this statement is ¬ Q ⇒ ¬ P. The symbol ¬ means negation. The contrapositive is logically equivalent to the original statement. In other words, if one is true then so is the other.
The converse of P ⇒ Q is Q ⇒ P. The converse is not equivalent to the original statement, P ⇒ Q.
The symbol ⇔ means if and only if. In this case, there are two implications, going in opposite directions. As an example, let P stand for ‘‘x2 − 3x + 2 = 0,’’ and let Q stand for ‘‘either x = 1 or x = 2.’’ In this case, we have P ⇔ Q. The terminology is that P and Q are logically equivalent to each other. We also say, ‘‘P is true if and only if Q is true.’’ Another similar expression is ‘‘P is a necessary and sufficient condition for Q.’’ Because the relationship is reciprocal, we can also say ‘‘Q is necessary and sufficient for P, or Q is true if and only if P is true.’’
Despite the great difference between the two implications P ⇒ Q and Q ⇒ P, we often begin a search for a proof of P ⇒ Q by asking, What follows from assuming Q? Thus, we might start with Q and draw conclusions from it. If we can arrive at P in a logical manner, then we can try to reverse all the implications, to get a proof of P ⇒ Q. Here is an illustration of this modus operandi.
EXAMPLE 1
Find the solutions of the equation 
.
SOLUTION This sort of problem arises in many guises, and most mathematicians would start the search by stating the equation in the form 
. In other words, we begin by assuming the validity of the equation, and we will see what might follow from that premise. By elementary algebra, these consequences follow:
 |
|
Thus, we obtain x = 7 or x = 3. So far we have proved that if x satisfies the given equation, then x is either 7 or 3. It is not legitimate to conclude that 7 and 3 are solutions, because one of the implications in the chain is not reversible. It is the step where we have put x = 3 and want to get back to the equation 
with that value. Testing 3 as a possible solution reveals that 3 is not a solution of the original equation.
Do not make the mistake of thinking that P ⇒ Q is the same as Q ⇒ P. Each of these implications is the converse of the other. For example, the converse of
‘‘If n is divisible by 2, then n is divisible by 6’’
is the statement
‘‘If n is divisible by 6, then n is divisible by 2’’
The first statement is false, whereas the second (the converse of the first) is true. For another example, consider this proposition:
‘‘If a and b are the legs of a right triangle and the hypotenuse is c, then a2 + b2 = c2.’’
The converse of this assertion is
‘‘If a2 + b2 = c2, then the triangle having sides |a|, |b|, |c| is a right triangle.’’
A.4 Method of Contradiction
Suppose that we want to prove a theorem of the form P ⇒ Q. We can assume that P is true and Q is false and see whether that leads to an obvious contradiction. If it does, then the hypothesis P and not Q is not tenable. In other words, if P is true then so is Q.
EXAMPLE 2
Use the method of contradiction to prove that for real numbers x and y we always have |x + y| ≤ |x| + |y|.
SOLUTION Suppose that for some pair of numbers x and y we have
 |
|
We seek some consequence of that assumption that is immediately seen to be false. Let σ = 1 if x + y ≥ 0 and σ = −1 if x + y < 0. Then |x| ≥ σx and |y| ≥ σy. Hence, we have
 |
|
This is plainly false, as no number can be greater than itself. This contradiction establishes the desired inequality.
A.5 Mathematical Induction
An important technique in establishing theorems is called mathematical induction. This is often used when a proposition depends on a positive integer n. Call it P(n). We want to establish P(n) for all values of n. That is, n = 1, n = 2, n = 3, n = 4, and so on.
THEOREM 3 Mathematical Induction
For each natural number n, let P(n) be a mathematical statement. If P(1) is true and if the implication P(n) ⇒ P(n + 1) is true for n = 1, 2, 3, …, then P(n) is true for all natural numbers n.
PROOF We use the method of contradiction. Thus, we assume the hypotheses are true while the conclusion is false. We then expect to arrive at a contradiction. Suppose that P(n) is sometimes false. Let m be the first integer for which P(m) is false. Thus, P(1), P(2), …, P(m − 1) are true but P(m) is false. Here, we must invoke another principle of logic: It asserts that every nonempty set of positive integers must contain a least element. Note that m > 1 because P(1) is true. Note also that P(m − 1) is true. But P(m − 1) implies P(m). So by our second hypothesis P(m) must be true, contradicting our choice of m.
SOLUTION Use P(n) to stand for this equation. First, we verify that P(1) is true. This is easy, as P(1) simply states that 
. Now we establish the implication P(n) ⇒ P(n + 1). In this part of our work, P(n) becomes our hypothesis, and n is fixed. Hence, we can write
 |
|
This last expression is exactly the formula we want for P(n + 1).
Induction can be defined in two different forms: weak induction and strong induction.
Definition of Weak Induction
If P(1) is true (base case) and P(n) ⇒ P(n + 1) for n = 1, 2, …, (inductive step), then P(n) is true for all positive integers n.
Definition of Strong Induction
If P(1) is true (base case) and whenever P(1), P(2), …, P(n) are all true ⇒ P(n + 1) is true (inductive step), then P(n) is true for all positive integers n.
Obviously, the difference is in the inductive step. In ordinary or weak induction, we proceed from one step to the next step as on rungs of a ladder. In strong induction, one must know that all the rungs below the current step are true before concluding that the current case is true. From a practical point of view, they are logically the same. Nevertheless, strong induction may make the inductive step easier to prove.
Induction can be generalized by taking P(k) as the first step (assumed to be true). Then we establish that when P(n) is true P(n + 1) is also true (inductive step). Here n = k, k + 1,…. The conclusion is that P(n) is true for all positive integers n greater than or equal to k.
A.6 Truth Tables
Sometimes, in complicated arguments, one needs truth tables. The simplest example of a truth table is the one for logical not:
(Here the notation ¬P is used for not-P.) This table is interpreted as follows: If P is true then not-P is false, and if P is false then not-P is true.
The truth table for implication is especially important:
Notice that the only circumstance in which the implication (P ⇒ Q) is false is that P is true while Q is false. For example, the following statement is false: ‘‘If 52 = 25, then Caesar wrote The Merchant of Venice.’’
Here is the truth table for P and Q (denoted by P ∧ Q).
A.7 Subsets and de Morgan Laws
A common occurrence in proofs is the need to establish that two sets, say S and T, are equal. This task can be broken into two parts: First, we show that every member of S is a member of T, and second we show that every member of T is a member of S. A moment’s thought should convince you that with these two facts established, the sets must be identical. Both assertions are needed, however. Using the symbol ⊆, we say that we must prove S ⊆ T and T ⊆ S. (The symbol ⊆ is rendered in English as ‘‘is a subset of’’ or ‘‘is contained in.’’) We are using this principle of logic:
 |
|
SOLUTION We have
 |
|
Recall the definitions of union, intersection, and difference of sets:
 |
|
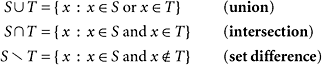FIGURE A.1 de Morgan laws and Venn diagrams. The diagrams illustrate (A B)∪(B A)∪(A∩B) = A∪B.
PROOF We prove the first and leave the second to the reader. We have this string of equivalences:
 |
|
In Figure A.1 there are illustrations of the de Morgan laws.
A.8 Quantifiers
Many mathematical assertions have quantifiers in them. There are two types of quantifier: ‘‘For all x, …’’ and ‘‘For some x, …’’ The first is called a universal quantifier and the second is called an existential quantifier. Typical examples are these two (true) statements:
1. For all integers n, n3 − n is divisible by 3.
2. There exists a real number x such that x2 + 3x − 7 = 0.
Often a shorthand is used for these two quantifiers. The symbol ∀ means for all, and ∃ means there exists. These are particularly useful for homework and informal proofs. However, neither of these should be used in formal mathematical exposition unless absolutely necessary for clarity. When there are several quantifiers in one statement, it sometimes helps to use these symbols. Consider an example where we are working with real numbers and integers (n, m).
 |
|
In words, it says: For every positive number ε there exists a positive integer m with the property that for any integer n greater than m, we have 
. This is the mathematically exact way of stating that
 |
|
A.9 Denial of a Quantified Assertion
To create the denial of a statement involving quantifiers, follow these patterns, where the symbol ¬ means not, and P(x) is some statement involving x:
 |
|
These symbolic statements have simple verbalizations. The first is:
‘‘Asserting that P(x) is not always true is logically equivalent to asserting that for some x, P(x) is false.’’
The second is:
‘‘Asserting that no x satisfies P(x) is equivalent to asserting that for all x, P(x) is false.’’
For example, if we wish to deny the statement about limits above, we write
 |
|
A.10 Some More Questionable ‘‘Proofs’’
In the remainder of Appendix A, we shall examine some proofs and pseudoproofs. We shall use the term pseudoproof to designate a line of reasoning that falls short of being a genuine proof because of some lapse in logic.
One very common mistake is to attempt a proof that P ⇒ Q by an argument that in fact establishes Q ⇒ P. In such a case, if the logical steps can be reversed, a proof of P ⇒ Q emerges. But this last step of reversing the argument is essential. Here are two illustrations.
EXAMPLE 5
We want to prove that 5 = 7.
SOLUTION It is natural to start with 5 = 7. Then add −6 to both sides, getting −1 = 1. Upon squaring both terms in the last equation, we get 1 = 1. What does this short argument actually prove? It proves that if 5 = 7, then 1 = 1. That is a true statement, but not of any value. (Refer to the truth table for implication to see that a false statement implies any other statement, true or false.) What we really should have proved is the argument in reverse: If 1 = 1, then 5 = 7. (That’s much harder, isn’t it?)
EXAMPLE 6
Here is another such pseudoproof. We want to prove that π is really 0.
SOLUTION Start with the equation π = 0. Take the sine function of both sides of the equation, getting sin π = sin 0 = 0.
EXAMPLE 7
We want to prove that if x and y are positive integers, then so is (x5 + y5)/(x + y). Because of that division, this assertion is certainly suspicious.
SOLUTION We note that
 |
|
It follows that
 |
|
Can you find a flaw in this argument?
SUMMARY APPENDIX A
• Pythagorean triple (a, b, c): a2 + b2 = c2, where a, b, and c are positive integers.
• If a = y2 − x2, b = 2xy, and c = x2 + y2, where x, y ∈ 
, then a2 + b2 = c2.
• Mathematical Induction: For n ∈ 
, let P(n) be a mathematical statement. If P(1) is true and if the implication P(n) ⇒ P(n + 1) is true for all n ∈ , then P(n) is true for all n ∈ .
• Union: S ∪ T = { x : x ∈ S or x ∈ T}
Intersection: S ∩T = { x : x ∈ S and x ∈ T}
Difference: S T = { x : x ∈ S and x ∉ T}
• de Morgan Laws: For sets A and B in the universal set U, we have
 |
|
• Function: If f maps X into Y, then X is the domain of f, and Y is the codomain of f. If y is the image of x by the mapping f, then y = f(x). The range of f is the set {f(x) : x ∈ X}.
• The composition of two mappings f and g is defined by the equation (f 
g)(x) = f(g(x)).
KEY CONCEPTS APPENDIX A
Twin primes, deductive reasoning, direct verification, Pythagorean triples, pseudoproofs, implication, contrapositive, converse, inverse, method of contradiction, logical equivalence, weak and strong induction, hypothesis, conclusion, algebra of sets, truth tables, de Morgan’s Laws, union, difference, and intersection of sets, functions, mappings, domain, codomain, range, composition of mappings, universal and existential quantifiers, denial of a quantified assertion, more pseudoproofs
GENERAL EXERCISES APPENDIX A
1. Establish this factorization:
 |
|
Begin by writing in detail the first three cases: n = 2, 3, and 4, and verifying that they are correct. Then you should see how to verify the general case. Mathematical induction is not recommended; the problem requires only elementary algebra.
2. (Continuation.) Establish that for every positive integer n, 7n − 4n is an integer multiple of 3. (Hint: Use General Exercise 1.)
3. Compute the first few partial sums in the expression 13 + 23 + 33 + 43 + ··· and observe that the results are perfect squares. Establish that this is true for all partial sums. Try to find a formula for the partial sums in question.
4. Justify the claim that for positive real numbers x and y we have the arithmetic–geometric mean property: 
5. Although an easier method is available, use induction to establish the formula 
.
6. Pythagorean triples (a, b, c) are three integers that satisfy a2 + b2 = c2, which was known to Euclid and used by Diophantus. A way to generate these triples is to let n and m be integers n > m and define a = n2 − m2, b = 2nm, and c = m2 + n2. Can you establish that the resulting three numbers a, b, and c always form a Pythagorean triple?
7. (Continuation.) Find all the Pythagorean triples (a, b, c) in which b = a + 1. Here, a theorem should be formulated and justified with a suitable argument.
8.
a. Establish the assertion that if a prime number greater than 3 is divided by 6, then the remainder is either 1 or 5.
b. If you succeed with this, go on to establish that if p is a prime number greater than 3, then either p + 1 or p − 1 is amultiple of 6.
c. If you succeed with this, justify the assertion that if p is a prime greater than 3 such that p + 2 is also prime, then p = 6 n − 1 for some integer n.
d. Finally, take the giant step of establishing that there are infinitely many integers n having the property that 6n − 1 and 6n + 1 are prime.
9. Establish that for arbitrary sets Ai contained in a set X, the de Morgan Laws are valid:
 |
|
Note that ∪i Ai is the set of all x that belong to at least one of the sets Ai. The expression ∩i Ai is similar. It is the set of all entities that belong to each Ai.
10. Find the relationship between f(∩i Ai) and ∩i f(Ai). Establish your answer with suitable deductions and give examples to convince one that no stronger relationship is valid in general.
11. Establish that for arbitrary sets, if A ⊆ B and B ⊆ C, then A ⊆ C.
12. Establish the famous theorem from elementary geometry that the altitudes of a triangle meet at a point. (A line segment is an altitude of a triangle if it starts at a vertex and ends at the side opposite that vertex, meeting that side in a right angle. The side in question may have to be extended to the point of intersection mentioned.)
13. Assume that x is not 0 or a negative integer. Find a formula for
 |
|
Let n → ∞ in your formula and find the limit of the preceding expression. A partial fraction decomposition familiar from calculus can be used.
14. Discover and justify this formula: (1)(2) + (2)(3) + (3)(4) + ··· + (n)(n + 1). Perhaps there is a formula of the type a + bn + cn2 + dn3 + en4 + ··· .
15. Here is the technical definition of continuity of a function f at every point: (∀x)(∀ ε > 0)(∃δ > 0)(∀y)[|x −y| < δ ⇒ |f(x) − f(y)| < ε]. What is the denial of this assertion in symbols?
16. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. Verify that the three medians of any triangle meet at a point.
17. What is the negation (denial) of the assertion that for every nonzero real number x, x4 is positive?
18. Establish that for every positive integer, n3 − n is divisible by 3.
19. Show that if (a, b, c) is a Pythagorean triangle‡ and if the three integers a, b, and c have no common factor, then a and b have opposite polarity; that is, one is odd and the other is even.
‡Olga Taussky-Todd (1906–1995) gave her International Linear Algebra Society’s Noether Lecture, which honors women who have made fundamental and sustained contributions to the mathematical sciences, on ‘‘The many aspects of Pythagorean triangles.’’ See Taussky-Todd [1982], which was coauthored with her husband John Todd. She wrote ‘‘… both in the work of others and in my own work I look for beauty, and not only for achievement.’’
20. Discover and justify a formula for the sum: 1 + 3 + 5 + 7 + ··· + (2n − 1)
21. Affirm that the two roots of a quadratic equation, ax2 + bx + c = 0, add up to −b/a. Is there a similar result for the roots of a cubic equation, ax3 + bx2 + cx + d = 0? What generalization can you establish?
22. Establish that for any two sets A and B, we have A = B if and only if A ⊆ B and B ⊆ A.
23. Show that for three sets, C, D, and E, if C ⊆ D and D ⊆ E, then C ⊆ E.
24. Explain why if B = A∩B, then B ⊆ A, and conversely.
25. Argue that if B = A∪B, then A ⊆ B, and conversely.
26. Show that real numbers obey this rule: |x + y| ≤ |x| + |y|. This is the triangle inequality. (Do not copy the proof used in illustrating the Method of Contradiction.)
27. Explain why or give a counterexample to the assertion that |x| ≤ |y| if and only if −y ≤ x ≤ y.
28. The triangular numbers are the integers generated by the partial sums of the series 1 + 2 + 3 + 4 + 5 + 6 + ···. The first few are therefore 1, 3, 6, 10, …. Sometimes a triangular number is a perfect square. For example, 1 and 36 are triangular and perfect squares. Are there any others? Can you find a way of getting all of them? (See Silverman [2001].)
29. The result of General Exercise 4 has a generalization: If the average of n positive numbers is raised to the nth power, the result is not less than the product of those numbers. Establish this. (See Hall and Knight [1948].)
30. We write a sequence of real numbers in the following way: x = [x0, x1, x2, …]. If all the differences x1 − x0, x2 − x1, x3 − x2 … are equal, the sequence is called an arithmetic progression. Show that, for any arithmetic progression, there is a formula xn = a + bn, where a and b are two constants, and n is a positive integer.
31. (Continuation.) Given an arithmetic progression, as described in the preceding exercise, find a formula for the sum of the first n terms.
32. (Continuation.) Let x0, x1, x2, … be an arithmetic progression. If the sum of the first seven terms is 49 and the sum of the first 17 terms is 289, what is the formula for the sequence?
33. (Continuation.) If the sum of the first n terms in an arithmetic progression is n(5n − 3), what is the formula for the progression?
34. A sequence x = [x0, x1, x2,…] called a geometric progression if the ratios x1/x0, x2/x1 … are all the same. Affirm that such a sequence must obey a rule of the form xn = arn, for n = 0, 1, 2,….
35. (Continuation.) Find and prove a rule for the sum of n terms in a geometric progression. Use it to find the sums of the geometric progression whose first two terms are 
and −2.
36. Confirm that:
 |
|
37. Use induction to establish the Binomial Theorem: 
, for n ≥ 1 and x ∈ 
. The binomial coefficients are defined by 
.
38. Verify that for every integer n greater than 2, the number n4 + 2n3 − n2 − 2n is divisible by 24.
39. Consider this assertion: (∀x ∈ )(x2 ≥ 0). Is its denial (∀x ∈ )(x2 < 0)?
40. Critique this ‘‘solution’’ of 
+ x = 12: = 12 − x ⇒ x = 144 − 24x + x2 ⇒ x2 − 25x + 144 = 0 ⇒ (x − 9)(x − 16) = 0 ⇒ x = 9 or 16.
41. If xi ≥ 1 for i = 1, 2, …, n, how large can 
be? Answer the same question for 
.
42. Establish the formula 
.
43. Critique this ‘‘proof’’: For n = 0, 1, 2, …, define fn by the equation fn(x) = xn. We shall prove by induction that these functions are all constant. The assertion is obviously correct for n = 0 because f0(x) = 1. If the assertion is correct for n = 0, 1, 2, …, k, then it is true for n = k + 1 by the following reasoning. First, fk+1 = f1fk. Second, 
, since f1 is constant (by the induction hypothesis). Third, 
because the induction hypothesis tells us that fk is constant. Then 
. (See Barbeau [2000].)
44. Under what circumstances is this implication not true? [(P or Q) and (P or R)] ⇒ (Q or R).
45. Is this a theorem about propositions? {(P or Q) and (P or R) and [not (Q or R)]} ⇒ P
46. Examine the accompanying triangular figure. It shows how some right triangles can be dissected and arranged in two different ways and produce two answers for the total area. Explain the fallacy.
47. Find the truth table for [P or (Q and R)].
48. The harmonic mean of n numbers 
. Show that the harmonic mean of n positive numbers is not greater than their arithmetic mean (average).
49. Some integers can be represented as a sum of an even number of consecutive integers. For example, 3=1+2, 10=1+2+3+4, 14=2+3+4+5. Find some examples of integers that are not representable in this way. Can you prove a theorem about those integers that are not representable in the way described? (See Halmos [1991].)
50. If P ⇒ Q, does it follow that P is true whenever Q is true? Provide the truth table for (P ⇒ Q) ⇒ (Q ⇒ P).
51. If P implies Q, does it follow that not-Q implies not-P? Give the truth table for the latter.
52. Critique this ‘‘proof’’ that 1 is the largest positive integer. Let n be the largest positive integer. We want to prove that n = 1. Since n2 is a positive integer, and n is the largest positive integer, n2 ≤ n. Divide this inequality by n to get n ≤ 1. This says that the largest positive integer is less than or equal to 1. (See the book by Barbeau [2000].)
53. (Continuation.) Critique this ‘‘proof’’ by induction, that every positive integer n satisfies the equation (n − 2)2 = n2. First, we note that the formula is correct for n = 1. Assuming the formula to be true for n, we prove it for n + 1. That is the assertion ((n + 1) − 2)2 = (n + 1)2. Equivalently, (n − 1)2 = (n + 1)2. Further equivalent equations then are n2 − 2n + 1 = n2 + 2n + 1, and −4n2 = 0. Next, we have −4n = 0. Multiply this equation by 1 − 1/n to get −4n + 4 = 0. Add n2 to get n2 − 4n + 4 = n2, or (n − 2)2 = n2. Since this is the induction hypothesis, it is true by assumption. Hence the case n + 1 is established. (Here again we refer to Barbeau [2000].)
54. Write down a number of true assertions using these symbols correctly:
 |
|
55. Refer to General Exercise 30. If all the successive differences in a sequence [xn] obey the formula xn + 1 − xn = cn, what is the closed formula for xn?
56. Establish this formula, known as summation by parts:
 |
|
where Si = a1 + a2 + ··· + ai, So = 0, and 1 ≤ n. This formula is the discrete analog of integration-by-parts in calculus.
57. For real numbers, we have (a + b) − a = b. The corresponding assertions for sets would be (A∪B) A = B. Is it true?
58. An arithmetic progression is a sequence a, a + b, a + 2b, …, a + nb. Find and prove a formula for the sum of these terms.
59. Critique this ‘‘proof’’ that a symmetric transitive relation is an equivalence relation: Let x ≡ y. Then y ≡ x by symmetry and x ≡ x by transitivity. (See Birkhoff and MacLane [1941].)
60. Define an equivalence relation as follows: [a, b, c, d] ≡ [a′, b′, c′, d′] means that |c| + |d| > 0, |c′| + |d′| > 0, [c′, d′] is a multiple of [c, d], and [a′ − a, b′ − b] is a multiple of [c, d]. Establish that this is an equivalence relation and explain its connection to lines in 
.
61. A real number is said to be rational if it can be expressed as the quotient of two integers. In the contrary case, the number is said to be irrational. Substantiate the correct statements and give suitable counterexamples for the incorrect ones:
a. The sum of any two rational numbers is rational.
b. The sum of any two irrational numbers is irrational.
c. The product of any two rational numbers is rational.
d. The product of any two irrational numbers is irrational.
e. The sum of a rational number and an irrational number is irrational.
f. The product of a rational number and an irrational number is irrational.
62. Establish the items that are true and find counterexamples to those that are false:
a. x > 7 ⇒ x > 6
b. x2 = 9 ⇒ x = 3
c. sin x = 0 ⇒ x = 0
d. ex = 0 ⇒ x > 0
e. x > e ⇒ x > π
63. Define a function 
by these two equations: f(1) = 1 and f(n + 1) = f(n) + n + 1 for n = 1, 2, 3,…. (This is an example of a recurrence relation.) Find a closed formula for f(n) and prove its correctness.
64. (Continuation, but a more challenging problem.) Define a function by these two equations: f(1) = 3 and f(n + 1) = n + 1 + f(n) for n = 1, 2, 3,…. Find a closed formula for f. Establish, by induction, that your formula is correct.
65. Show that, for every positive integer n, the number n(n + 1)(n + 2) is divisible by 6. Is there any better conclusion of that type?
66. If an integer n is divisible by two different integers, k and m, does it follow that n is divisible by km? Give examples and formulate theorems about this question. You may assume the theorem that every positive integer n is the product p1p2 … pk, where each pk is a prime number. (The prime numbers in the product can be repeated.) For example, 18 = 2 · 3 · 3.
67. Explain this puzzle: We let 
and 
. Then we have 
so that y = x. But each term in the series x − y is positive, and therefore x > y. (This example is from the book by Maxwell [1959].)
68. Critique a student’s ‘‘solution’’ of the equation (x + 3)(2 − x) = 4 that goes like this: Since the equation is in factored form, either x + 3 = 4 or 2 − x = 4. Thus, we get the solutions x = 1 or x = −2. To verify the work we first substitute x = 1 in the original equation, getting (1 + 3)(2 − 1) = 4. Then we substitute x = −2 in the equation, getting (−2 + 3)(2 − ( −2)) = 4. The method used is correct because we checked the answers. (This example is due to Edwin A. Maxwell [1959].)
69. Show that 3200 > 2300. Avoid using a calculator or the use of logarithms, if possible.
70. Affirm that if x > 0 then x + (1/x) > 2.
71. Show that, for any three numbers, x, y, z, we have x2 + y2 + z2 ≥ xy + yz + zx. Can you generalize this to any number of variables? Under what conditions do we get the strict inequality (>) instead of the weak version?
72. Critique this sequence of logical deductions: From the well-known equation cos2 x + sin2 x = 1, we obtain 
. Hence, we have 
. Let x = π, so that cos x = −1 and sin x = 0. The result is 0 = 2. (This example is from Maxwell [1959].)
73. In proving the principle of mathematical induction, we invoked the more basic theorem that every nonempty set of positive integers contains a smallest member. What other sets of real numbers have this property? Theorems and examples are needed.
74. Solve the equation 
, and check your work in an independent manner. Explain any unexpected results.
75. Invent a proposition P(n) that involves the positive integers and that is true for n = 1, 2, 3, …, 50, but fails for n = 51.
76. Establish that the square of every odd integer is odd. Is the same true for the cubes of odd integers? What can you say about other powers, n = 4, 5,…?
77. Substantiate this case of the Cauchy– Schwarz inequality. For arbitrary real numbers a, b, x, y, we have (ax + by)2 ≤ (a2 + b2)(x2 + y2).
78. Show that if r is a real number such that rx + x2 ≥ 0 for all real values of x, then r = 0.
79. The triangular numbers are the integers generated by the recursive formulas x0 = 0 and xn+1 = xn + n. Find a formula for xn. (This should be easy.)
80. Use induction to prove that n2 − n is even for all n ∈ 
. What can you discover about negative values of n?