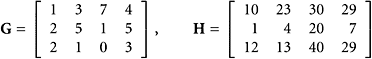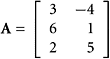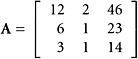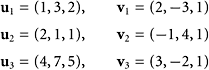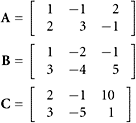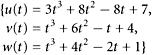CHAPTER FIVE
Vector Subspaces
5.1 COLUMN, ROW, AND NULL SPACES
The essence of mathematics is not to make simple things compli cated, but to make complicated things simple.
—S. GUDDEN
Everything should be made as simple as possible, but not simpler.
—ALBERT EINSTEIN (1879–1955)
KISS Principle: Keep It Simple, Stupid!
Introduction
In Example 5 of Section 2.4, we encountered avector space that was contained in a larger vector space and sharedwith the larger space its definitions of vector addition and scalar multiplication. This is a common phenomenon, deserving our special study.
DEFINITION
A subset in a vector space is a subspace if it is nonempty and closed under the operations of adding vectors and multipling vectors by scalars.
A subspace is nonempty by the definition of the term ‘‘subspace.’’ If an element x is in the subspace, then 0 is in the subspace because 0 = 0 · x. Thus, a subspace must contain the zero element of the larger space. We can state these requirements for a subspace U as follows:
1. If x and y are in U, then x + y is in U. (U is closed under vector addition.)
2. If x is in U and c is a scalar, then cx is in U. (U is closed under scalar multiplication.)
3. U is nonempty.
One sees immediately that under those circumstances, U is a vector space, too. All the axioms listed in Section 2.4 will be true for U. Most of these axioms are true automatically because U is a subset of V, and V obeys the axioms. The closure axioms are different in nature, however. Furthermore, we want to be sure that U is nonempty. The element that must be there is, of course, 0.
We notice that two extreme cases of subspaces occur in any vector space V: namely, the subspace 0 and V itself. Any other subspace, U, must lie between these extremes: 0 ⊆ U ⊆ V. The subspace of V that contains only the zero vector is denoted by 0 or {0}. We summarize all this in a formal statement:
THEOREM 1
Let U be a subset of a vector space V. Suppose that U contains the zero element and is closed under vector addition and multiplication by scalars. Then U is a subspace of V.
THEOREM 2
The span of a nonempty set in a vector space is a subspace of that vector space.
PROOF Let the vector space be V and let S be a nonempty subset of V. If x and y are two elements of Span(S), then each is a linear combination of elements of S. Simple algebra shows that the vector αx + βy will also be a linear combination of elements in S. This verifies the two closure axioms for Span(S).
There are many examples of linear subspaces, such as subspaces of polynomials, subspaces of trigonometric polynomials, subspaces of matrices ![]() m×n, subspaces of upper or lower triangular matrices, and subspaces of the image or the kernel of some linear operators such as differentiation and integration.
m×n, subspaces of upper or lower triangular matrices, and subspaces of the image or the kernel of some linear operators such as differentiation and integration.
EXAMPLE 1
In the vector space ![]() consisting of all polynomials (of any degree), consider the four monomials p0, p1, p2, and p3, where pi(t) = ti. What is the span of the set {p0, p1, p2, p3}?
consisting of all polynomials (of any degree), consider the four monomials p0, p1, p2, and p3, where pi(t) = ti. What is the span of the set {p0, p1, p2, p3}?
SOLUTION This is the vector space ![]() . It is a subspace of
. It is a subspace of ![]() . (The zero-polynomial has no degree.)
. (The zero-polynomial has no degree.)
EXAMPLE 2
Illustrate Theorem 2.
SOLUTION The set of polynomials of the form t ![]() at + bt2 + ct5 + dt7 is a subspace of
at + bt2 + ct5 + dt7 is a subspace of ![]() . (
. (![]() is defined in Example 1.)
is defined in Example 1.)
EXAMPLE 3
Let s and t be variables that range independently over ![]() . Consider the vectors of the form
. Consider the vectors of the form
|
Is the set of all vectors of that form a subspace of ![]() ?
?
SOLUTION We have no theorem that directly addresses such a problem. However, we may be able to see that the set in question is the linear span of asetof vectors. If so, Theorem 1 will apply. Observe that
 |
|
Hence, the set of vectors considered at the beginning is identical to the span of a pair of vectors:
|
This pair isobviously linearly independent, and,therefore, generates a two-dimensional subspace of ![]() . (The concept of dimension is taken up in Section 5.2.)
. (The concept of dimension is taken up in Section 5.2.)
From two subspaces X and Y in a vector space, we can construct two more subspaces, X + Y and X ∩ Y. (These arise in General Exercises 13–14.) The vector sum, X + Y, and the intersection, X ∩ Y, are defined as follows:
|
The union of two subspaces is usually not a subspace! (See General Exercises 15–16.)
THEOREM 3
The vector sum of two subspaces in a vector space is also a subspace.
PROOF Let X and Y be two subspaces of a vector space V. Then X and Y contain the zero element of V. Therefore, X + Y contains the zero element of V. Is X + Y closed under addition? Let v and ![]() be two points in X + Y. Then v = x + y and
be two points in X + Y. Then v = x + y and ![]() for suitable points x, y,
for suitable points x, y, ![]() , and
, and ![]() . Thus, we obtain
. Thus, we obtain ![]() . A similar equation shows that X + Y is closed under scalar multiplication.
. A similar equation shows that X + Y is closed under scalar multiplication.
EXAMPLE 4
In ![]() , let U be the subspace consisting of all scalar multiples of the vector u = (1, 3, −4).Let V be the subspace consisting of all scalar multiples of thevector v = (5, −1, 2). What is U + V?
, let U be the subspace consisting of all scalar multiples of the vector u = (1, 3, −4).Let V be the subspace consisting of all scalar multiples of thevector v = (5, −1, 2). What is U + V?
SOLUTION The vector sum U + V consists of all vectors expressible as αu + βv. In other words, this is the span of the pair {u, v}.
THEOREM 4
The intersection of two subspaces in a vector space is also a subspace of that vector space.
The proofis left as General Exercise 14.
EXAMPLE 5
Let U be the set of all vectors u = (u1, u2, u3) in ![]() such that u1 + 3u2 − 4u3 = 0. Let V be the set of all vectors v = (v1, v2, v3) such that 2v1 + 3v3 = 0. What is U ∩ V?
such that u1 + 3u2 − 4u3 = 0. Let V be the set of all vectors v = (v1, v2, v3) such that 2v1 + 3v3 = 0. What is U ∩ V?
SOLUTION U ∩ V is the set of all x such that x1 +3x2 − 4x3 = 0 and 2x1 +3x2 = 0. Geometrically, we are considering two planes in ![]() and their intersection, which in this case is a line in
and their intersection, which in this case is a line in ![]() through the origin.
through the origin.
Images and inverse images of subspaces by linear transformations are also subspaces.
DEFINITION
If f is a mapping of a set X to a set Y, then for any set U in X, f[U] is defined to be the set of images of points in U. In symbols, we have
|
THEOREM 5
If f is a linear transformation from a vector space X to a vector space Y, then for any subspace U in X, f[U] is a subspace of Y.
PROOF Since U is a subspace, it contains 0.Since f is linear, f(0) = 0. Thus, 0 is in f[U]. If x and y are in U, then so are αx + βy. Hence, we have f(αx + βy) ![]() f[U]. Since f is linear, αf(x) + βf(y)
f[U]. Since f is linear, αf(x) + βf(y) ![]() f[U]. Thus, f[U] is closed under addition and scalar multiplication.
f[U]. Thus, f[U] is closed under addition and scalar multiplication.
EXAMPLE 6
This example illustrates Theorem 5 with specific vectors and subspaces. Define a linear transformation f from ![]() to
to ![]() by the equation
by the equation
|
Let W be the span of a set of two vectors in ![]() :
:
|
Thus, f maps ![]() into
into ![]() . Find a simple description of f[W].
. Find a simple description of f[W].
SOLUTION Using the formula for f we obtain
|
It follows that
|
DEFINITION
If f is a mapping from one set X to another set Y, then for any subset S in Y, f−1[S] is defined to be the set of all points in X that are mapped by f into S. This set is the inverse image of S in X. In symbols, we have
|
See Figure 5.1 for an illustration of f[U] and f−1[S]. The notation f−1[S] involves a set S. Its use here does not imply that f is an invertible mapping.
THEOREM 6
If f is a linear transformation from a vector space X to a vector space Y, then for any subspace V in Y, f−1[V] is a subspace in X.
PROOF Since V is a subspace in Y, the zero vectoris in V. Since f is a linear transformation and X is a vector space, 0 ![]() X and f(0) = 0. Hence, we have 0
X and f(0) = 0. Hence, we have 0 ![]() f−1[V]. If x and y are in f−1[V], then x = f(z) and y
f−1[V]. If x and y are in f−1[V], then x = f(z) and y ![]() f(w), for some z and w in V. Thus, we obtain
f(w), for some z and w in V. Thus, we obtain
 |
|
This proves that αx + βy ![]() f−1[V] and that f−1[V] is closed under vector addition and scalar multiplication. Hence, f−1[V] is a subspace of X.
f−1[V] and that f−1[V] is closed under vector addition and scalar multiplication. Hence, f−1[V] is a subspace of X.

FIGURE 5.1 Sketch of (a) f[U] and (b) f−1[V].
EXAMPLE 7
Continuing the previous example, let V = Span{z, w}, where z = (1, 1, 0) and w =(0, 1, 1). Describe the set f−1[V] in simple terms.
SOLUTION Letting (3x1, 2x2 − x1, x4) = (1, 1, 0), we obtain ![]() ,
, ![]() , and x4 = 0. Hence, we have
, and x4 = 0. Hence, we have ![]() . Similarly, letting (3x1, 2x2 − x1, x4) = (0, 1, 1), we have x1 = 0,
. Similarly, letting (3x1, 2x2 − x1, x4) = (0, 1, 1), we have x1 = 0, ![]() , and x4 = 1 and
, and x4 = 1 and ![]() . Consequently, we obtain
. Consequently, we obtain
|
for any s ![]()
![]()
Linear Transformations
Recall the notion of null space (or kernel) of a linear transformation. It consists of all vectors that are mapped into 0 by the transformation.
THEOREM 7
The kernel of a linear transformation is a subspace in the domain of that transformation.
PROOF Let T be a linear transformation from one vector space V to another vector space W. The kernel or null space of T is the set
|
It is obviously a subset of V. It is a subspace of V because first, 0 ∈ Ker(T). Second, if x and y belong to the kernel of T, then αx + βy also belong to the kernel because
|
EXAMPLE 8
Let (c1, c2, …, cn) be any fixed vector in ![]() . Define a linear transformation T:
. Define a linear transformation T: ![]() →
→ ![]() by the following equation, in which x = (x1, x2, …, xn):
by the following equation, in which x = (x1, x2, …, xn):
|
Describe the kernel of T.
SOLUTION It is the set of all vectors x that satisfy the equation
|
If n = 3, we can visualize this set as a plane through the origin in ![]() . This is true if the vector c is not 0. If c is zero, the subspace here is all of
. This is true if the vector c is not 0. If c is zero, the subspace here is all of ![]() . If n = 2, the set in question is a line through 0 if c ≠ 0. If c = 0, the set is all of
. If n = 2, the set in question is a line through 0 if c ≠ 0. If c = 0, the set is all of ![]() .
.
EXAMPLE 9
Draw asketch of the kernel of this linear map:
For x = (x1, x2), define T(x) = 3x1 − 2x2.
SOLUTION The kernel of T consists of all vectors in ![]() for which 3x1 − 2x2 = 0. Thus, we have
for which 3x1 − 2x2 = 0. Thus, we have ![]() . The graph of this equation is the straight line through the origin with slope
. The graph of this equation is the straight line through the origin with slope ![]() . The two points (0, 0) and (2, 3) determine this line. See Figure 5.2.
. The two points (0, 0) and (2, 3) determine this line. See Figure 5.2.
EXAMPLE 10
We can obtain a subspace by this description:
Take all the vectors x = (x1, x2, x3, x4) in ![]() that are linear combinations of (3, 7, 4, 2) and (2, 0, 1, 3), and in addition obey the equation
that are linear combinations of (3, 7, 4, 2) and (2, 0, 1, 3), and in addition obey the equation
|
Here we are taking the intersection of two subspaces to get a third subspace.
SOLUTION We have
|

FIGURE 5.2 Kernel of T(x) = 3x1 − 2x2.
We also set
|
Thus, we obtain ![]() . In the first preceding equation, replace b by this multiple of a, and arrive at
. In the first preceding equation, replace b by this multiple of a, and arrive at
|
The solution is that the points described are all the scalar multiples of the vector (11, 35, 18, 4).
EXAMPLE 11
In ![]() , let U be the span of the single vector u = (3, 2, 4, 0). Let V be the kernel of the matrix
, let U be the span of the single vector u = (3, 2, 4, 0). Let V be the kernel of the matrix
|
Find a simple description of the subspace U + V in ![]() .
.
SOLUTION To understand the kernel of A, we use the standard row-reduction process to get
|
The general solution of the associated homogeneous system is given by
|
As usual, we write this as
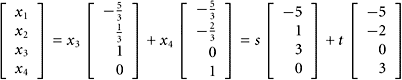 |
|
where s and t are free parameters. Thus, the subspace in question is the span of a set of three vectors; namely,
|
THEOREM 8
The range of a linear transformation is a subspace of its co-domain.
PROOF If T is a linear transformation, say from U to V, then its range is
|
The vector 0 of V is in Range(T) because 0 = T(0). Thus, V is nonempty. If x and y are in Range(T), then x = T(u) and y = T(w), for suitable u and w in U. It follows that
|
This shows that Range(T) is closed under vector addition and scalar multiplication. Notice that we used the linearity of T and the hypotheses that U and V are vector spaces.
EXAMPLE 12
Let  , and define T by the equation T(x) = Ax. Describe the range of T in simpler terms.
, and define T by the equation T(x) = Ax. Describe the range of T in simpler terms.
SOLUTION Every point in the range of T is of the form Ax for some x. Thus, the range of T is the span of the columns of A. If the columns of A form a linearly dependent set, then some columns are not needed in describing the range of T. A row reduction shows that
 |
|
Because the systems Ax = 0 and Bx = 0 have the same solutions, we can use columns 1 and 2 in A to span the range of T:
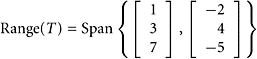 |
|
Notice that we cannot use the columns of B to describe the range of A in this problem. Each of those columns has 0 as its last entry, whereas the range of A obviously contains some vectors that do not have that property.
Revisiting Kernels and Null Spaces
Recall from your study of elementary algebra the important topic of solving equations. For example, you learned how to find the ‘‘roots’’ of an equation such as 7x2 + 3x − 15 = 0. In linear algebra, the corresponding topic is the finding of solutions of an equation of the form L(x) = v, where L is a linear transformation. Even the simple case, L(x) = 0, requires some study. Several of the preceding chapters have dealt with the matrix version of that topic.
Recall that the terms null space and kernel are interchangable. They both refer to
|
The first case is more general as it does not require a matrix, but only a linear mapping. We define the null space of a matrix A as the set
|
which we can find by solving Ax = 0.
EXAMPLE 13
Let
|
Are the two vectors, u = [3, 7, −8, 9]T and v = [7, 1, 4, −5]T, in the null space of C? Are these vectors w = [5, −3] and z = [0, 0] in the left null space of CT?
SOLUTION The question is answered by computing Cu =[10, 38]T and Cv =[0, 0]T. Thus, we obtain v ![]() Null(C), but u ∉ Null(C). Also, we find that w is not in the null space of CT, but z is because CT w ≠ 0 and CTz = 0.
Null(C), but u ∉ Null(C). Also, we find that w is not in the null space of CT, but z is because CT w ≠ 0 and CTz = 0.
EXAMPLE 14
Use the matrix C in the preceding example, and find simple descriptions of the null spaces of C and CT.
SOLUTION The null space of C consists of all solutions to the equation Cx = 0. One can use row reduction on the augmented matrix:
|
For the associated homogeneous system, the general solution is
|
This can be written as
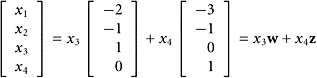 |
|
where x3 and x4 are free variables. Thus, the null space is the span of a pair of vectors; namely, w = [−2, −1, 1, 0]T and z = [−3, −1, 0, 1]T.
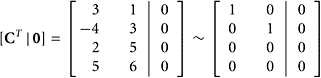
With regard to the null space of CT, we obtain
 |
|
Thus the null space of CT is {0}.
The Row Space and Column Space of a Matrix
Two important vector subspaces associated with a given matrix are its row space andits column space.
DEFINITION
The row space of a matrix A is the span of the set of rows in A. This is denoted by Row(A).
The column space of A is the span of the set of columns in A. This is denoted by Col(A).
Translating these definitions into alternative terminology, we can say that
|
Here we have assumed that A is an m × n matrix whose rows are ri and whose columns are aj.
THEOREM 9
If two matrices are row equivalent to each other, then they have the same row space.
PROOF Let A be any matrix. We will prove that any single row operation performed on A to produce a new matrix à has no effect on the row space of A. Once this has been established, it will follow that a sequence of row operations performed on A will also have no effect on the row space. In carrying out this proof, it suffices to consider just the two row operations labeled as Types 1 and 2 in Section 1.1. Consider first the operation of adding to one row a multiple of another (replacement). There is no loss of generality in considering the operation r1 ← r1 + αr2. This notation means replace the first row by row 1 plus α times row 2. Any element in the row space of à has the form
|
This i sclearly a linear combination of rows r1, r2, … rn. Hence, we have Row(Ã) ⊆ Row(A). The reverse inclusion is also true because the row operation in question is reversible by another row operation of the same type (explicitly, use r1 ← r1 − αr2). A similar analysis handles any row operation of Type 2 (scale, multiplying a row by a nonzero scalar).
SOLUTION Because row operations generally simplify a matrix and the row space is not affected, we carry out a row reduction, arriving at
 |
|
The row space of A is the row space of B, and it is spanned by the first three rowsof B. We can write
|
the latter being a more elegant description. The rows of an augmented matrix correspond to equations in a linear system. In the row-reduction process, each system has the same solution. Consequently, once the pivot positions are determined, we can use the corresponding rows in any of these coefficient matrices to span the row space! Conversely, the column space of A is given only by the span of the columns from A corresponding to the pivot positions. In this example, we obtain:
 |
|
Think about why this is so!
SOLUTION We examine the reduced row echelon form of each matrix.
Calling upon mathematical software and changing some numbers into simple fractions, we arrive at
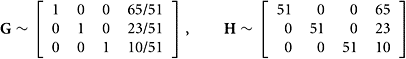 |
|
The answer is yes! The row spaces are the same, and the three rows of this last matrix form a simple set of three vectors that spans the common row space. The first three columns of G form a linearly independent set that spans Col(G) = ![]() . Similarly, the first three columns of H span Col(H) =
. Similarly, the first three columns of H span Col(H) = ![]() .
.
THEOREM 10
The column space of an m × n matrix A is the set {Ax : x ![]()
![]() }.
}.
PROOF Recall that the product Ax is defined to be a linear combination of the columns of A, in which the coefficients are the components of the vector x. Thus, with the notation of the preceding paragraphs, we have
|
(We suppose that A has n columns, aj.) Because x runs over all possible vectors in ![]() , we get all the linear combinations of columns of A. In other words, we get the span of the set of columns in A.
, we get all the linear combinations of columns of A. In other words, we get the span of the set of columns in A.
SOLUTION We are asking whether some vector x exists for which Ax = b. This question is answered by attempting to solve that equation. The appropriate augmented matrix is
 |
|
Yes, the system is consistent and has the solution x = [3, 2]T. Checking with an independent verification, we have 3[3, 6, 2]T + 2[−4, 1, 5]T = [1, 20, 16]T.
To describethe row space of a matrix inasimilar manner, weobserve that the row space of an m × n matrix A isthecolumn space of the n × m matrix AT . One may object that vectors inthe row space should be row vectors, whereas vectors in the column space should be column vectors. However, these distinctions come into play only when we insist on a vector being treated as a matrix. Then a column vector and a row vector must be interpreted differently. But we can take transposes to get rows from columns, and vice versa. Thus, we have
|
THEOREM 11
The row space of a matrix A is the column space of AT.
SOLUTION Because elementary row operations do not change the row space (Theorem 7), weare free to carry out the row-reduction process, obtaining
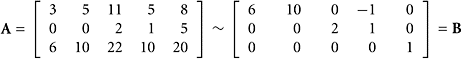 |
|
The row space is the span of the set consisting of the row vectors in matrix B:
|
The column space is spanned by columns 1, 3, and 5 of matrix A:
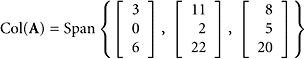 |
|
EXAMPLE 19
Let
|
Also, set v =[3, 12]T and w = [−4, 15, 22, 11]. Is v in the column space of F? Is w in the row space of F?
SOLUTION We see that thevector v is inthecolumn space of F because
|
So we have −3[1, −2]T + 2[3, 3]T = [3, 12]T.
To determine whether thevector w is in the row space of F, we take the transpose of the matrix and vector.
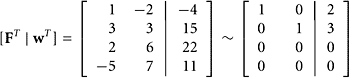 |
|
The row reduction shows that column three is a linear combination of columns one and two. Checking, we find the relationship 2[1, 3, 2, −5] + 3[−2, 3, 6, 7] = [−4, 15, 22, 11].
Here is another way to answer the question in Example 19 about a row space. The two rows of the matrix F form a linearly independent pair because neither row is a scalar multiple of the other. If we insert the vector w as a third row in this matrix, we can call the resulting matrix G. In going from F to G, the row space will either grow or remain unchanged. In the first case, the vector w is not inthe row space of F, but in the second case it is. We leave the details as General Exercise 38.
Caution
If A ~ B and the matrix B is in reducedrow echelon form, then Col(A) is thespan of the set of pivot columns in A, whereas Row(A) is the span of the set of pivot rows in B.
SUMMARY 5.1
•Asubset in a vector space V is a subspace of V if it is nonempty and closed under the operations of vector addition and scalar multiplication.
•Let U be a subset of a vector space V. Suppose that the zero element of V is in U, that U is closed under vector addition, and that U is closed under multiplication by scalars. Then U is a vector space—indeed,asubspace of V .
•The span of a nonempty set in a vector space is a subspace of that vector space.
•The kernel of a linear transformation is a subspace of the domain of that transformation.
•The vector sum of two subspaces in a vector space is also a subspace.
•The intersection of two subspaces in a vector space is also a subspace of that vector space.
•For any mapping f : X → Y, we define f[Q] = {f(x) : x ∈ Q} for any Q ⊆ X. We define f−1[S] = {x ∈ X : f(x) ∈ S} for any S ⊆ Y.
•The range of a linear transformation is a subspace of its co-domain.
•The null space of a matrix A is defined to be Null(A) = {x : Ax = 0}.
•The row space of amatrix A is defined to be the span of the set of rows in A. This is denoted by Row(A). The column space of A, denoted by Col(A), is the span of the set of columns in A.
•If two matrices are row equivalent to each other then they have the same row space.
•The column space of an m × n matrix A is the same as the set {Ax : x ∈ ![]() n}.
n}.
•Different ways in which a subspace U can be created:
•As the span of a given set of vectors: U = Span(S)
•As the kernel of a linear transformation: U = Ker(T)
•As the range of a linear transformation: U = T(V )
•As the vector sum of two subspaces: U = V + W
•As the intersection of two subspaces: U = V ∩ W
•As the image of a subspace via a linear transformation: U = T(V)
•As the inverse image of a linear subspace by a linear transformation: U = T−1(V)
KEY CONCEPTS 5.1
Subspaces, kernel, vector sum, vector intersection, images, inverse image, range, row space, column space, null space, creating subspaces, row equivalent
GENERAL EXERCISES 5.1
1. Determine whether the set of matrices having the form ![]() is a subspace of
is a subspace of ![]() 2×2.
2×2.
2. All invertible n × n matrices have the same row space. What is it?
3. Verify that the set {p ∈ ![]() : p′(3) = 2p(5)} is a subspace of the space
: p′(3) = 2p(5)} is a subspace of the space ![]() of all polynomials.
of all polynomials.
4. In ![]() , consider the set of all vectors that have the form (3α −2β, α + β + 2, −2β + α, 5α − πβ, α + β. Is this set a subspace of
, consider the set of all vectors that have the form (3α −2β, α + β + 2, −2β + α, 5α − πβ, α + β. Is this set a subspace of ![]() ?
?
5. Is the set of all vectorsof the form (s3 − t, 5s3 + 2t, 0) a subspace of ![]() ? Here s and t run over
? Here s and t run over ![]() .
.
6. Determine whether the set of all 2 × 2 matrices of the form ![]() is a subspace
is a subspace ![]() 2×2.
2×2.
7. In Example 1, we noted that ![]() is a subspace of
is a subspace of ![]() . Explain why we do not say that
. Explain why we do not say that ![]() is a subspace of
is a subspace of ![]() .
.
8. Do these two matrices have the same row space?
 |
|
9. Define T : ![]() →
→ ![]() by T(x1, x2, x3) = (3x1 − 2x2 +5x3, 2x1 + x2 − x3). Define U = {x ∈
by T(x1, x2, x3) = (3x1 − 2x2 +5x3, 2x1 + x2 − x3). Define U = {x ∈ ![]() : x1 + x2 − 2x3 = 0}. Find a simple description of T[U].
: x1 + x2 − 2x3 = 0}. Find a simple description of T[U].
10. Describe in simple terms the row and column spaces of 
11. What is the simplest example of two matrices that are row equivalent to each other yet have different column spaces?
12. The trace of a square matrix is the sum of its diagonal elements. Thus, if A is n × n, then ![]() . In the vector space
. In the vector space ![]() , consisting of all n × n matrices, is the set of matrices with zero trace a subspace?
, consisting of all n × n matrices, is the set of matrices with zero trace a subspace?
13. Give an example and a geometric interpretation of two subspaces U and W of the vector space ![]() . Note that their sum is also a subspace of
. Note that their sum is also a subspace of ![]() . The sum is defined by U + W = {u + w : u ∈ U and w ∈ W}. This illustrates Theorem 3.
. The sum is defined by U + W = {u + w : u ∈ U and w ∈ W}. This illustrates Theorem 3.
14. Establish that if U and W are subspaces of a vector space V, then their intersection is also a subspace of V. The intersection is defined by U ∩ W = {x : x ∈ U and x ∈ W}. This is Theorem 4.
15. Is the union of two subspaces in a vector space always a subspace? Explain why or find a counterexample. The union is defined by U ∪ W = {x : x ∈ U or x ∈ W}. (In mathematics, we always use the inclusive or. Thus, p or q is true when either p is true or q is true orboth are true.)
16. (Continuation.) Find the exact conditions on subspaces U and W in a vector space V in order that their union be a subspace.
17. Let ![]() be the vector space of all polynomials and let
be the vector space of all polynomials and let ![]() be the vector space of all polynomials of degree at most n. Explain why
be the vector space of all polynomials of degree at most n. Explain why ![]() may be viewed as a subspace of
may be viewed as a subspace of ![]() . Let
. Let ![]() be the collection of polynomials with only even powers of t. Is
be the collection of polynomials with only even powers of t. Is ![]() a subspace of
a subspace of ![]() ? (Assume that a constant polynomial c
? (Assume that a constant polynomial c ![]() ct0 is an even power of t.)
ct0 is an even power of t.)
18. Fix a set of vectors {u1, u2, …, un} in some vector space. Explain why the set of n-tuples (c1, c2, …, cn) such that ![]() is a subspace of
is a subspace of ![]() .
.
19. Argue that if A ~ B, then each row of B is a linear combination of rows in A.
20. Give a proof of Theorem 1.
21. Show why the set of all non invertible 2 × 2 matrices (with the usual operations) is not a vector space.
22. Explain why if T : U → V is a linear transformation, the inverse image of a subspace W in V via the transformation T is a subspace of U. The inverse image is defined by T−1[W] = {x ∈ U : T(x) ∈ W}.
Caution: The notation T−1[W] does not insinuate that T has an inverse. Every map (invertible or not) has inverse images as defined in the preceding equation.
23. Establish that if T is a linear transformation, then the image of a subspace in the domain of T is a subspace in the co-domain of T.
24. Establish that the span of a set in a vector space is the smallest subspace containing that set.
25. In a vector space, suppose that w = u + v and z = u − v. Explain why the spans of {u, v} and {w, z} are the same.
26. What conclusion can be drawn about a set S in a vector space if it satisfies the equation Span(S) = S?
27. Use the standard polynomials p0, p1, …, where pi(t) = ti. Then we write ![]() = Span{p0, p1, … pn}. Let D denote the differentiation operator. Establish that
= Span{p0, p1, … pn}. Let D denote the differentiation operator. Establish that ![]() . Also, show that Span{p1, p2, … pn} is the same as the set {p ∈
. Also, show that Span{p1, p2, … pn} is the same as the set {p ∈ ![]() : p(0) = 0}.
: p(0) = 0}.
28. Explain why two matrices cannot have the same column space if one matrix has a row of zeros and the other does not.
29. If A and B are row equivalent to each other, does it follow that A and B have the same column space? (A proof or counterexample is needed.)
30. Explain why the ith row of AB is xTB, where xT is the ith row of A.
31. Establish that if ui is the ith column of A and if ![]() is the ith row of B, then AB =
is the ith row of B, then AB = ![]() . (Notice that if A is m × n and if B is n × p, then each ui is m × 1 and each
. (Notice that if A is m × n and if B is n × p, then each ui is m × 1 and each ![]() is 1× p. Hence each
is 1× p. Hence each ![]() is m × p.)
is m × p.)
32. If f : X → Y and if U ⊆ X, then we can create a new function g by the equation g(x) = f(x) for all x in U. If U is a proper subset of X, then g ≠ f because they have different domains. The function g is called the restriction of f to U. The notation g = f|U is often used. Suppose now that X and Y are linear spaces and L is a linear map from X to Y. Let U be a subspace of X. Is L|U linear? What is its domain? Do L and L|U have the same range? (Arguments and examples are needed.)
33. Can this be used as the definition of a subspace? A subspace in a vector space is a subset that is closed under the operations of vector addition and multiplication of a vector by an arbitrary scalar.
34. Let A and B be arbitrary matrices subject only to the condition that the product AB exist. Use the notation Col to indicate the column space of a matrix. Consider these two inclusion relations: Col(AB) ⊆ Col(A) and Col(AB) ⊆ Col(B). Select the one of these that is always correct and prove it.
35. Give an example in which Col(AB) = Col(A). Give another example in which Col(AB) ≠ Col(A). Finally, give an example in which Col(AB) = Col(B).
36. Establish that each row of AB is a linear combination of the rows of B, and thus establish that Row(AB) ⊆ Row(B).
37. Let ![]() ∞ be the space of all infinite sequences of the form [x1, x2, …], where the xi are arbitrary real numbers. Let X be the subset of
∞ be the space of all infinite sequences of the form [x1, x2, …], where the xi are arbitrary real numbers. Let X be the subset of ![]() ∞ consisting of all sequences that have only finitely many nonzero terms. Is X a subspace of
∞ consisting of all sequences that have only finitely many nonzero terms. Is X a subspace of ![]() ∞?
∞?
38. In the last part of Example 19, use row reduction on the matrix G to show that w is inthe row space of F.
39. Use ![]() in this exercise.
in this exercise.
a. Find a set of vectors that spans the column space.
b. Is [−1, 1]T in the column space?
c. Find a set of vectors that spans the row space.
d. Is [−1, 1, 1, 4] in the row space?
e. Find a set of vectors that spans the null space.
f. Is [−2, 1, −6, 1]T in the null space?
40. Is the set of all vectors x =[x1, x2, x3, x4]T that are linear combinations of vectors[4, 2, 0, 1]T and [6, 3, −1, 2]T, and in addition satisfy the equation x1 = 2x2 a subspace of ![]() ? Explain why or why not.
? Explain why or why not.
41. Write out the details in the solution to Example 2.
42. Write out the details in the alternative solution to Example 19.
43. Explain why f[Span(W)] = Span(f[W]) when f is linear. Hint: This is needed in Example 6.
44. Let p0, p1, p2, …, pn be polynomials such that the degree of pk is k, for 0 ≤ k ≤ n. Explain why {p0, p1, p2…., pn} is a basis for ![]() .
.
45. Let 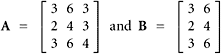 Find the null space of each of these matrices as well as for AT and BT.
Find the null space of each of these matrices as well as for AT and BT.
46. Let U consist of all vectors in ![]() whose entries are equal. Explain why U is a subspace of
whose entries are equal. Explain why U is a subspace of ![]() and describe U geometrically.
and describe U geometrically.
47. Let U consist of the span of all 2 × 2 matrices whose second row is zero. Let V be the span of those whose second column is zero. Explain why U + W and U ∩ W are vector subspaces of ![]() 2×2, which is the vector space of all 2 × 2 matrices.
2×2, which is the vector space of all 2 × 2 matrices.
48. Let W be the subspace of ![]() spanned by these vectors: u1 = (1, 2, 1, 3, 2), u2 = (1, 3, 3, 5, 3), u3 = (3, 8, 7, 13, 8), u4 = (1, 4, 6, 9, 7), and u5 = (5, 13, 13, 25, 19). Find a basis for W.
spanned by these vectors: u1 = (1, 2, 1, 3, 2), u2 = (1, 3, 3, 5, 3), u3 = (3, 8, 7, 13, 8), u4 = (1, 4, 6, 9, 7), and u5 = (5, 13, 13, 25, 19). Find a basis for W.
49. Consider
 |
|
Find bases for the row space and the column space of A.
50. Explain and discuss the following.
a. Span{v1, v2, v3, v4} is a subspace of ![]() , where in the vector vi the first i entries are one and all others are zero.
, where in the vector vi the first i entries are one and all others are zero.
b. Let Span{1, p1(x), p2(x), …, pn(x)} be a subspace of Pn, where pi(x) = (x − 1)i. Here ![]() is the vector space of all polynomials of degree less than or equal to n.
is the vector space of all polynomials of degree less than or equal to n.
c. ![]() is a subspace of
is a subspace of ![]() 2×3, where
2×3, where ![]() are 2 × 3 matrices with one in entry (i, j) and zero elsewhere. Here
are 2 × 3 matrices with one in entry (i, j) and zero elsewhere. Here ![]() m×n is the vector space of all m × n matrices for fixed m and n.
m×n is the vector space of all m × n matrices for fixed m and n.
COMPUTER EXERCISES 5.1
a. null space
b. column space
c. row space
a. kernel of T
b. range of T
a. null space
b. column space
c. row space
5.2 BASES AND DIMENSION
A thing is obvious mathematically after you see it.
—IN ROSE (ED.), MATHEMATICAL MAXIMS AND MINIMS [1988]
“Obvious” is the most dangerous word in mathematics.
—ERIC TEMPLE BELL (1883–1960)
Mathematics consists in proving the most obvious thing in the least obvious way.
—GEORGE POLYÁ (1889–1988)
Basis for a Vector Space
In this section, we explore the different ways in which the elements of a vector space can be represented by using various coordinate systems. The unifying concept is that of a basis for a vector space.
DEFINITION
In a vector space V, a linearly independent set that spans V is called a basis for V .
EXAMPLE 1
In ![]() , the set of standard unit vectors e1, e2, …, en have components given by (ei)j = δij. (Recall the Kronecker δij, which is 1 if i = j and 0 otherwise.) These vectors ej are the column vectors in the n × n identity matrix In. Is this set of vectors a basis for
, the set of standard unit vectors e1, e2, …, en have components given by (ei)j = δij. (Recall the Kronecker δij, which is 1 if i = j and 0 otherwise.) These vectors ej are the column vectors in the n × n identity matrix In. Is this set of vectors a basis for ![]() ?
?
SOLUTION Yes! This set spans ![]() and is linearly independent. Thus, it is a basis. It is often referred to as the standard basis for
and is linearly independent. Thus, it is a basis. It is often referred to as the standard basis for ![]() .
.
EXAMPLE 2
Consider 
Is the set of columns in this matrix a basis for ![]() ?
?
SOLUTION We ask: “Can we solve any equation Ax = b, when b is an arbitrary vector in ![]() ?” Yes; we start with the fourth equation, which gives x1 = b4 (and there is no other choice!). Then go to the third equation. It can be solved for x2 because x1 is known. Again, there is no other possible value for x2. Continue upward through the set offour equations, noting that there are no choices to be made. The solution is uniquely determined by the vector b. Consequently, if b = 0, then x = 0 necessarily follows. We have proved that the columns formal in early independent set of vectors that spans
?” Yes; we start with the fourth equation, which gives x1 = b4 (and there is no other choice!). Then go to the third equation. It can be solved for x2 because x1 is known. Again, there is no other possible value for x2. Continue upward through the set offour equations, noting that there are no choices to be made. The solution is uniquely determined by the vector b. Consequently, if b = 0, then x = 0 necessarily follows. We have proved that the columns formal in early independent set of vectors that spans ![]() .
.
EXAMPLE 3
Let u = (3, 2, −4), v = (6, 7, 3), w = (2, 1, 0).
Do these vectors constitute a basis for ![]() ?
?
SOLUTION Put the vectors into a matrix A as columns. We ask first whether the equation Ax = 0 has any nontrivial solutions. Row reduction leads to
 |
|
(Here we omit the righthand-side zero-vector.) This shows that the equation Ax = 0 can be true only if x = 0. Hence, the set of columns is linearly independent. The row reduction also shows that the equation Ax = b can be solved for any b in ![]() . Therefore, the setof columns spans
. Therefore, the setof columns spans ![]() and provides a basis for
and provides a basis for ![]() .
.
EXAMPLE 4
Let 
Do the columns of this matrix form a basis for ![]() ?
?
SOLUTION We happen to notice that column three in this matrix is equal to column two minus column one. The set of columns is, therefore, a linearly dependent set. Hence, it is not a basis for anything. Of course, this set of columns spans a two-dimensional subspace in ![]() , but it is not a basis for that subspace because of its linear dependence. Columns one and two in this matrix, taken together, provide a basis for the column space of A. That is a two-dimensional subspace in
, but it is not a basis for that subspace because of its linear dependence. Columns one and two in this matrix, taken together, provide a basis for the column space of A. That is a two-dimensional subspace in ![]() . In otherwords, a plane in three-space passing through 0. (In this discussion, the term dimension is being used in an informal way. Precise definitions are forthcoming.)
. In otherwords, a plane in three-space passing through 0. (In this discussion, the term dimension is being used in an informal way. Precise definitions are forthcoming.)
The preceding four examples suggest that a general theorem can be proved.
THEOREM 1
The set of columns of any n × n invertible matrix is a basis for ![]() .
.
PROOF Let A be such a matrix. Do its columns span ![]() ? Can we solve the system of equations Ax = b for any b in
? Can we solve the system of equations Ax = b for any b in ![]() ? Yes, because A−1b solves the system. Thus, thecolumns of A span
? Yes, because A−1b solves the system. Thus, thecolumns of A span ![]() . What about the linear independence of the set of columns? Is there a non zero solution to the equation Ax = 0? No, because if Ax = 0, then x = 0, as is seen by multiplying by A−1. So the columns constitute a linearly independent set that spans
. What about the linear independence of the set of columns? Is there a non zero solution to the equation Ax = 0? No, because if Ax = 0, then x = 0, as is seen by multiplying by A−1. So the columns constitute a linearly independent set that spans ![]() .
.
SOLUTION Let us investigate the spanning property first. Given any polynomial q in ![]() , say q(t) = a0 + a1t + a2t2 + a3t3, can we express it in terms of Legendre polynomials? In otherwords, can we solve this equation for c0, c1, c2, c3?
, say q(t) = a0 + a1t + a2t2 + a3t3, can we express it in terms of Legendre polynomials? In otherwords, can we solve this equation for c0, c1, c2, c3?
|
Putting inmore detail, we have
|
Collecting similar terms on the left brings us to
|
From elementary algebra, we recall that two polynomials are the same if and only if the coefficients of each power of t are the same. Thus, we must have 2c0 − c2 = 2a0, 2c1 − 3c3 = 2a1, 3c2 = 2a2, and 5c3 = 2a3. We can indeed solve for the coefficients ci using these equations in reverse order. We arrive at ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . This proves that the span of the first four Legendre polynomials is
. This proves that the span of the first four Legendre polynomials is ![]() . For the linear independence question, just substitute p = 0 in the preceding calculation to see that all cj must be zero(because a0 = a1 = a2 = a3 = 0).
. For the linear independence question, just substitute p = 0 in the preceding calculation to see that all cj must be zero(because a0 = a1 = a2 = a3 = 0).
THEOREM 2
If a basis is given for a vector space, then each vector in the space has a unique expression as a linear combination of elements in that basis.
PROOF This is established by Theorem 6 in Section 2.4. The reader can probably supply a proof without referring to Section 2.4. The proof relies on the concepts of basis, spanning, and linear independence.
Let’s look at a more provocative example, where the vectors involved are again polynomials.
SOLUTION The correspondence between these polynomials and their terms can be displayed as follows:

The four column vectors headed by p1, p2, p3, and p4, in this table need to be analyzed to uncover any linear dependencies. A row reduction is called for:
 |
|
(There is no need to keep the zero row.) The row-reduced form shows that column four is a linear combination of the first three columns. This is true of the beginning matrixaswell as the final matrix. (The row-reduction process does not disturb linear dependencies among the columns of a matrix.) Hence, a basis is {p1, p2, p3}. (We do not need p4.)
Another question for the same example: What non trivial linear relationship exists among p1, p2, p3, p4? We continue the reduction process on the preceding matrix, ending at the reduced echelon form:
 |
|
We obtain ![]() ,
, ![]() , and x3 = −3.2x4. Leting x4 = 5, we have x = (8, 6, −16, 5). Therefore, we have 8p1 + 6p2 − 16p3 + 5p4 = 0. This verifies that p4 can be expressed in terms of the basis.
, and x3 = −3.2x4. Leting x4 = 5, we have x = (8, 6, −16, 5). Therefore, we have 8p1 + 6p2 − 16p3 + 5p4 = 0. This verifies that p4 can be expressed in terms of the basis.
Coordinate Vector
We almost always restrict our attention to ordered bases, so that we can refer to their elements by subscript notation. For example, we might write
|
If this is a basis for a vector space V, then each vector x in V can be written in one and only one way as ![]() . The n-tuple (c1, c2, …, cn) that arises in this way is called the coordinate vector of x associated with the (ordered) basis
. The n-tuple (c1, c2, …, cn) that arises in this way is called the coordinate vector of x associated with the (ordered) basis ![]() . It is denoted by
. It is denoted by ![]() .
.
EXAMPLE 7
What is the coordinate vector of x if x = (−15, 35, 2) and if the basis used is ![]() = {u1, u2, u3} where u1 = (1, 3, 2), u2 = (−2, 4, −1), and u3 = (2, −2, 0)?
= {u1, u2, u3} where u1 = (1, 3, 2), u2 = (−2, 4, −1), and u3 = (2, −2, 0)?
SOLUTION This problem can be turned into a system of linear equations that must be solved:
 |
|
Row reduction of the augmented matrix leads to c = (3, 4, −5), as shown next:
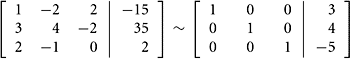 |
|
An independent verification consists in computing
 |
|
THEOREM 3
If ![]() is a basis, then the mapping of x to its coordinate vector
is a basis, then the mapping of x to its coordinate vector ![]() is linear.
is linear.
PROOF There are two aspects of linearity, which we can combine and address as follows:
|
where α and β are scalars. To see that this equation is true, let ![]() and
and ![]() . Then these three equations follow:
. Then these three equations follow:
|
Hence, we obtain
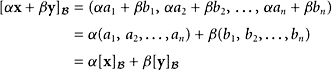 |
|
THEOREM 4
The mapping of a vector x to its coordinate vector ![]() (with respect to a given basis
(with respect to a given basis ![]() ) is surjective (onto) and injective (one-to-one).
) is surjective (onto) and injective (one-to-one).
PROOF Is this map surjective (onto)? Is every vector in ![]() an image of some x in V? Let c be any vector in
an image of some x in V? Let c be any vector in ![]() , and write c = (c1, c2, …, cn). Is c equal to
, and write c = (c1, c2, …, cn). Is c equal to ![]() for some x in V? Of course: it is the image of the vector
for some x in V? Of course: it is the image of the vector ![]() . (Refer to Section 2.3, Theorem 4.)
. (Refer to Section 2.3, Theorem 4.)
Is our mapping injective (one-to-one)? Because we know it to be linear, it suffices to verify that only the element 0 in V maps into the vector 0 of ![]() . But this is easy, because if
. But this is easy, because if ![]() , then
, then ![]() . (Refer to Section 2.3, Theorem 5.)
. (Refer to Section 2.3, Theorem 5.)
Isomorphism and Equivalence Relations
In Theorem 4, we have observed a pair of vector spaces, V and ![]() , that are related by a linear, injective, and surjective map. Such a map is called an isomorphism, and the spaces are said to be isomorphic to each other. The relationship of two spaces being isomorphic to each other is an example of an equivalence relation.
, that are related by a linear, injective, and surjective map. Such a map is called an isomorphism, and the spaces are said to be isomorphic to each other. The relationship of two spaces being isomorphic to each other is an example of an equivalence relation.
DEFINITION
A relation (written as ≡) is an equivalence relation on a set X if it has these three properties for all x, y, and z in X:
THEOREM 5
The relation of isomorphism between two vector spaces is an equivalence relation.
PROOF There are three properties to verify.
1. Is a vector space, V, isomorphic to itself? Yes, because the identity map I : V → V can serve as the isomorphism.
2. If V is isomorphic to W, does it follow that W is isomorphic to V? Yes, because if T : V → W is an isomorphism, then so is T−1 : W → V.
3. If V is isomorphic to W and if W is isomorphic to U, is V isomorphic to U? Yes: Suppose that we are given the isomorphisms T : V → W and S : W → U. To get from V to U, we use the composite mapping S ![]() T, which has the desired properties. The reader should recall that S
T, which has the desired properties. The reader should recall that S ![]() T is linear, injective, and surjective.
T is linear, injective, and surjective.
We discuss equivalence relations briefly in Section 1.1 and will return to them again in Section 5.3.
EXAMPLE 8
Are the spaces ![]() and
and ![]() isomorphic to each other?
isomorphic to each other?
SOLUTION If we think that these spaces are isomorphic to each other, we must invent an isomorphism, and prove that it is one. Given a polynomial in ![]() , write it in detail—for example, in the standard form
, write it in detail—for example, in the standard form
|
With the polynomial p, we can now associate the vectorin ![]()
|
This is another example of selecting a basis for a space and then identifying each element in the space with its coordinate vector relative to the basis. In this example, we associate ![]() with p, and the isomorphism is the map
with p, and the isomorphism is the map ![]() . Theorems 3 and 4 indicate that we have an isomorphism. What basis for
. Theorems 3 and 4 indicate that we have an isomorphism. What basis for ![]() are we using? It is the (ordered) set of functions t
are we using? It is the (ordered) set of functions t ![]() 1, t, t2, …, tn.
1, t, t2, …, tn.
EXAMPLE 9
Is ![]() isomorphic to
isomorphic to ![]() ?
?
SOLUTION Consider the map  .
.
We get all of ![]() , and L is surjective. If
, and L is surjective. If  , then
, then ![]() . Hence, L is injective. Thus, L is one-to-one and maps
. Hence, L is injective. Thus, L is one-to-one and maps ![]() onto
onto ![]() . The mapping L is linear. Hence, it is an isomorphism.
. The mapping L is linear. Hence, it is an isomorphism.
EXAMPLE 10
Is ![]() isomorphic to
isomorphic to ![]() ?
?
SOLUTION Let p(t) = a0 + a1t + a2t2 + a3t3 + a4t4 + a5t5, so that p is a generic element of ![]() . The vector of coefficients [a0, a1, a2, a3, a4, a5]T is in
. The vector of coefficients [a0, a1, a2, a3, a4, a5]T is in ![]() , and the matrix
, and the matrix ![]() is in
is in ![]() . The mapping from p to the 2 × 3 matrix is linear, injective, and surjective.
. The mapping from p to the 2 × 3 matrix is linear, injective, and surjective.
THEOREM 6
If a vector space has a finite basis, then all of its bases have the same number of elements.
PROOF I. Let ![]() be a finite basis for the vector space being considered. Let
be a finite basis for the vector space being considered. Let ![]() be another basis for the same space. Since
be another basis for the same space. Since ![]() is linearly independent and
is linearly independent and ![]() spans the space, the number of elements in
spans the space, the number of elements in ![]() is not greater than the number of elements in
is not greater than the number of elements in ![]() , by Theorem 10 in Section 2.4. Conversely, since
, by Theorem 10 in Section 2.4. Conversely, since ![]() is linearly independent and
is linearly independent and ![]() spans the space, the number of elements in
spans the space, the number of elements in ![]() is no greater than the number of elements in
is no greater than the number of elements in ![]() .
.
We give another, slightly different, proof. This is by the method of contradiction, and it uses coordinate vectors.
PROOF II. Let n denote the number of elements in ![]() , and suppose that
, and suppose that ![]() has more than n elements. Select v1, v2, …, vm in
has more than n elements. Select v1, v2, …, vm in ![]() , where m > n. We intend to show that
, where m > n. We intend to show that ![]() is linearly dependent, hence not a basis. Consider the equation
is linearly dependent, hence not a basis. Consider the equation
|
Each ![]() is a column vector having n components, because n is the number of elements in
is a column vector having n components, because n is the number of elements in ![]() . Thus, the preceding vector equation has n equations and m unknowns. By Corollary 2 in Section 1.3, this system has a nontrivial solution. By the linearity of the map
. Thus, the preceding vector equation has n equations and m unknowns. By Corollary 2 in Section 1.3, this system has a nontrivial solution. By the linearity of the map ![]() , we have
, we have
|
nontrivially. Thus, ![]() is linearly dependent.
is linearly dependent.
Finite-Dimensional and Infinite-Dimensional Vector Spaces
A vector space having a finite basis is said to be finite dimensional. The number of elements in any basis for that space is called the dimension of the space. Thus, we can now say that ![]() is n-dimensional, and
is n-dimensional, and ![]() has dimension n + 1. In both cases, it suffices to exhibit a basis of the space and count thenumber of elements in it. In the same way, we find that the dimension of
has dimension n + 1. In both cases, it suffices to exhibit a basis of the space and count thenumber of elements in it. In the same way, we find that the dimension of ![]() is mn. If V is a finite-dimensional vector space, we use Dim(V) for its dimension. Thus, for example, we have
is mn. If V is a finite-dimensional vector space, we use Dim(V) for its dimension. Thus, for example, we have
|
The space ![]() , defined in Section 2.4, Example 3, is not finite dimensional. This fact is most easily established by noting that the vectors en defined by (en)i = δni are infinite in number yet form a linearly independent set. By Theorem 6 in Section 2.4, this vector space cannot have a finite spanning set. Naturally, we call such vector spaces infinite dimensional. Many such spaces are needed in applied mathematics and they have been assiduously studied for more than a century. Hilbert spaces and Banach spaces are examples. So are Sobolev spaces. (These topics are beyond the scope of this book.)
, defined in Section 2.4, Example 3, is not finite dimensional. This fact is most easily established by noting that the vectors en defined by (en)i = δni are infinite in number yet form a linearly independent set. By Theorem 6 in Section 2.4, this vector space cannot have a finite spanning set. Naturally, we call such vector spaces infinite dimensional. Many such spaces are needed in applied mathematics and they have been assiduously studied for more than a century. Hilbert spaces and Banach spaces are examples. So are Sobolev spaces. (These topics are beyond the scope of this book.)
The linear space of all continuous real-valued functions on the interval [0, 1] is infinite dimensional. To be convinced of this, it suffices to exhibit an infinite linearly independent family of continuous functions on [0, 1]. The set of monomials, pn(t) = tn, where n = 0, 1, 2, …, serves this purpose.
DEFINITION
A vector space is finite dimensional if it has a finite basis; in that event, its dimension is the number of elements in any basis.
THEOREM 7
Two finite-dimensional vector spaces are isomorphic to each other if and only if their dimensions are the same.
PROOF First, suppose that the twospaces U and V are finite dimensional and have the same dimension. Select bases {u1, u2, …, un} for U and {v1, v2, …, vn} for V. Define a linear transformation T by writing T(ui) = vi, for i = 1, 2, …, n. Thus, the effect of T on any point
|
in U is like this:
|
Is T injective? Suppose T(u) = 0. Thus, we have
|
Yes, T is one-to-one by Theorem 5 in Section 2.3 because it follows that ![]() . Is T surjective? For any v in V, write
. Is T surjective? For any v in V, write
|
Yes, T is onto by Theorem 4 in Section 2.3.
For the other half of the proof, let T be an isomorphism from U onto V. Let {u1, u2, …, un} be a basis for U. Then {T(ui) : 1 ≤ i ≤ n} is a basis for V. This assertion has two parts, each requiring proof. First, is that set linearly independent? If
|
then
|
But, since T is an isomorphism, it is injective, and so ![]() and
and ![]() by the linear independence of {ui : 1 ≤ i ≤ n}. Second, does thesetin question span V ? If v ∈ V, then v = T(u) for some u ∈ U, because T is surjective. Then it follows that
by the linear independence of {ui : 1 ≤ i ≤ n}. Second, does thesetin question span V ? If v ∈ V, then v = T(u) for some u ∈ U, because T is surjective. Then it follows that
|
EXAMPLE 11
Are the spaces of matrices ![]() and
and ![]() isomorphic to one another? Are the spaces
isomorphic to one another? Are the spaces ![]() and
and ![]() isomorphic to each other?
isomorphic to each other?
SOLUTION The two matrix spaces have dimension mn, and those two spaces are therefore isomorphic to each other by Theorem 7. The other pair of spaces is isomorphic for the same reason: they have the same dimension, namely 21.
SOLUTION Notice that v = 2u −3w; namely, (13, 3, 4) = 2(2, 3, −1) − 3(−3, 1, −2). Thus, if we have a generic element of the span, we can do some simplifying, like this:
|
This equation shows that
|
The vector v, which was a linear combination of u and w, is not needed in describing the span. This calculation can be done in greater generality, as shown in the next result.
THEOREM 8
The span of a set is not affected by removing from the set one element that is a linear combination of other elements of that set.
PROOF Let S be the set, and suppose that
|
where the vectors v0, v1, …, vn are distinct members of S. Let w be any vector in the span of S. Write
|
We may require that m ≥ n, and we permit some coefficients ai to be zero. Then rewrite
|
where, if necessary, we have inserted some zero coefficients. Now we have
|
This shows that w is representable as a linear combination of elements in S, but without using v0.
THEOREM 9
If a set of n vectors spans an n-dimensional vector space, then the set is a basis for that vector space.
PROOF If S is the set and its span is V, we have only to prove that S is linearly independent. Suppose S is linearly dependent. Then some element of S is a linear combination of the other elements of S. Removing that element does not affect the span of the set, by Theorem 8. By Theorem 6 in Section 2.4, every linearly independent set in V can have at most n − 1 elements. Hence, we have Dim(V) ≤ n − 1, a contradiction.
THEOREM 10
In an n-dimensional vector space, every linearly independent set of n vectors is a basis.
PROOF If S is the given set and fails to be a basis, it must fail to span the vector space. Therefore, some point x in the vector space is not in the span of S. Now the set S ∪ {x} is linearly independent, and the dimension of the space must be greater than n.
SOLUTION Again, we use the principle that row-equivalent matrices have the same row space. The row-reduction process yields this reduced echelon matrix:
 |
|
The dimension of the row space is three, and the first three rows of the matrix B provide a basis for the row space of A. It may or may not be true that the first three rows in A give a basis for the row space. Do not assume that this is true. (The next example illustrates this.)
SOLUTION A row reduction leads to
 |
|
The first two rows of B give a simple basis for the row space of A, but the first two rowsof A do not span the row space. (Why?)
THEOREM 11
If a set of n vectors spans a vector space, then the dimension of that space is at most n.
PROOF According to Theorem 6 in Section 2.4, a linearly independent set in a vector space can have no more elements than a spanning set. Hence, a basis can have no more elements than a spanning set.
THEOREM 12
If a set of n vectors is linearly independent in a vector space, then the dimension of the space is at least n.
PROOF Let {v1, v2, …, vn} be a linearly independent set in a vector space V. By Theorem 6 in Section 2.4, any spanning set in V must have at least n elements. Hence, any basis for V must have at least n elements, and Dim(V) ≥ n.
THEOREM 13
The pivot columns of a matrix form a basis for its column space.
PROOF Let A be any matrix, and denote by B its reduced echelon form. The pivot columns in B form a linearly independent set because no pivot column in B is a linear combination of columns that precede it. (Look at Example 15, which shows a typical case.) Because A is row equivalent to B, the pivot columns of A form a linearly independent set. In this situation, remember that the vectors x that satisfy the equation Ax = 0 are the same as the vectors that satisfy Bx = 0. Each nonpivot column in A is a linear combination of the pivot columns of A. The set of pivot columns in A spans Col(A) and is linearly independent. Hence, it is a basis for the column space of A.
SOLUTION The row-reduction process on A yields a matrix B:
 |
|
Notice that in B, columns three and four are linear combinations of columns one and two. Hence, the same is true for the columns of A. We conclude that columns one, two, and five in A constitute a basis for Col(A). Observe that columns one, two, and five in B certainly do not constitute a basis for Col(A). (Why?)
EXAMPLE 16
Let f(t) = 5t3 + 7t2 − 8t + 9.
Is the set {f, f′, f″, f![]() } a basis for
} a basis for ![]() ?
?
SOLUTION From f(t) = 5t3 + 7t2 − 8t + 9, we find
|
Suppose ![]() ; that is,
; that is,
|
or
|
Using the coefficients in these equations, we obtain this linear system
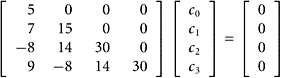 |
|
From forward substitution, we find that c0 = 0, c1 = 0, c2 = 0, and c3 = 0. The set is linearly independent. Therefore, the set is a basis for ![]() .
.
SOLUTION We create this matrix and transform it to reduced echelon form
 |
|
Use columns one, two, four, and five in A as a basis. Notice that a linear combination of the first two columns gives the third column in A. The columns of B do not solve the stated problem because B does not contain the two given vectors.
Linear Transformation of a Set
The next theorem asserts that the application of a linear transformation to a set cannot increase its dimension. Stated in other terms, the dimension of the range of a linear transformation cannot be greater than the dimension of its domain.
THEOREM 14
For any finite-dimensional vector space U, for any vector space V, and for any linear transformation L from U to V, we have
|
PROOF Select a basis {u1, u2, …, un} for U. If x ∈ U, then ![]() for suitable ci. Consequently, we have
for suitable ci. Consequently, we have
|
Since x was arbitrary in U, we have
|
Hence, we obtain Dim(L[U]) ≤ n = Dim(U).
THEOREM 15
Let {u1, u2, …, un} be a basis for a vector space U. Let V be any vector space. A linear transformation T : U → V is completely determined by specifying the values of vi = T(ui) for i = 1, 2, …, n. These values, in turn, can be any vectors whatsoever in V.
PROOF If x is any point in U, its coordinates (a1, a2, …, an) with respect to the basis {u1, u2, …, un} are uniquely determined. Then
|
Since T is linear,
|
A common pitfall is to assume that a linear transformation can be defined by specifying T(wi) = yi for i = 1, 2, …, n for any vectors wi and yi. Theorem 15 does not say that, does it?
SOLUTION We are tempted to use Theorem 15. But the set {u1, u2, u3} is linearly dependent, in as much as
|
If T is a linear transformation, then
|
Putting in the details, we eventually get a contradiction:
 |
|
Thus there is no such linear transformation.
THEOREM 16
In a finite-dimensional vector space, any linearly independent set can be expanded to create a basis.
PROOF Let {u1, u2, …, uk} be linearly independent. If {u1, u2, …, uk} spans the given vector space V, then it is a basis (because it is linearly independent and spans V). If{u1, u2, …, uk} does not span V, find uk+1 that is in V but not in Span{u1, u2, …, uk}. Then {u1, u2, …, uk, uk+1} is linearly independent. Repeat this process. See Theorem 11 in Section 2.4.
Dimensions of Various Subspaces
If T is a linear transformation defined on one vector space U and taking values in another vector space V, we already have two spaces related to T: its domain (U) and its co-domain (V). Then we can go on to define the kernel of T by writing
|
This is also called the null space of T and is denoted by Null(T). The nullity of a linear transformation T is the dimension of its null space. The kernel of T consists of all the vectors in U that are mapped by T into 0. Next, we can define the range of T,
|
This is the set of all images created by T when it acts on all the vectors in U. The kernel of T is a subspace of U, and the range of T is a subspace of V. These assertions have been proved in Section 5.1. (See Theorems 7 and 8 in Section 5.1.) The preceding definitions are valid without restricting U or V to be finite dimensional. However, if U is finite dimensional, we can establish some relations among the dimensions of these spaces. (All of these dimension numbers are non negative integers.) Begin by observing that if U is of dimension n, then the range of T cannot be of dimension greater than n. (Recall Theorem 14, which asserts that one cannot increase the dimension of a set by applying a linear transformation to it.)
The theorem we will prove can be illustrated in a simple case where the dimensions are easily discerned.
EXAMPLE 19
Consider a linear transformation T : ![]() →
→ ![]() defined by the following matrix A. Recall that this terminology means T(x) = Ax. We show also the reduced row echelon form of A as the matrix Ã.
defined by the following matrix A. Recall that this terminology means T(x) = Ax. We show also the reduced row echelon form of A as the matrix Ã.
 |
|
What are the dimensions of the various subspaces associated with A?
SOLUTION The dimension of the kernel of A will be two because there are two free variables in Ã. Columns one, three, and five in à form a linearly independent set because they are pivot columns. Therefore, columns one, three, and five in A form a linearly independent set. These columns in A, (not in Ã) give a basis for the range of T. Hence, the dimension of the range of T is 3. The sum of the dimensions of the range and kernel is 5, which is also the dimension of the domain of T.
The preceding calculation should generalize to any matrix. Here is the general case, for an arbitrary matrix.
EXAMPLE 20
Let A be an m × n matrix. Let à be its reduced echelon form. Suppose there are k pivots in à or A. How are the dimensions of the column space and null space related?
SOLUTION There will be k columns having pivots and n − k columns without pivots. Each column without a pivot adds to the dimension of the null space because those columns correspond to free variables. Hence, we have
|
The columns of A that have pivot positions form a basis for the range of A. Hence, the equation (n − k) + k = n allows us to conclude that
|
This theoretical result can be formulated without referring to matrices as follows.
PROOF Select a basis {y1, y2, …, ym} for the range of T. Select a basis {x1, x2, …, xk} for the kernel of T. Select vectors ui so that T(ui) = yi for i = 1, 2, …, m. Define
|
It is to be proved that ![]() is a basis for the domain of T. Let the domain of T be the space U. First, we will prove that
is a basis for the domain of T. Let the domain of T be the space U. First, we will prove that ![]() spans U. Let v ∈ U. Then T(v) is in the range of T. Therefore, we obtain
spans U. Let v ∈ U. Then T(v) is in the range of T. Therefore, we obtain
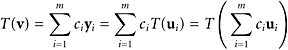 |
|
This shows that
 |
|
and that ![]() is in the kernel of T. From this it follows that
is in the kernel of T. From this it follows that ![]() , whence
, whence ![]() . Next, we prove that
. Next, we prove that ![]() is linearly independent. Suppose that
is linearly independent. Suppose that ![]() . Then
. Then
 |
|
Hence, all bj are zero. Then ![]() and all ai are zero. Conclusion:
and all ai are zero. Conclusion:
|
The purely matrix form of Theorem 17 can be stated as follows.
THEOREM 18 Rank–Nullity Theorem
For any matrix, the number of columns equals the dimension of the column space plus the dimension of the null space.
Think of this theorem as stating that each column of a matrix contributes either to the dimension of the null space or the dimension of the column space. Ultimately, this depends on the very simple observation that each column either has a pivot position orit does not. The columns with pivots add to the dimension of the column space, whereas thecolumns without pivots add to the dimension of the null space (because they correspond to free variables in solving the homogeneous problem Ax = 0). In otherwords, for an m × n matrix, we have
|
The next theorem is an important one in linear algebra. It may even be surprising, because it draws a connection between the row space and the column space of a matrix. In general, these are subspaces in completely different vector spaces, ![]() and
and ![]() , if the matrix in question is m × n.
, if the matrix in question is m × n.
PROOF Let A be an m × n matrix of rank r. Let à denote its reduced row echelon form. Then r is the number of nonzero rows in Ã, by the definition of the term rank. Each nonzero row in à must have a pivot element, and these rows form a linearly independent set. Hence, they constitute a basis for the row space of A. Thus, r is the dimension of the row space of A. Because r rows have pivots, r columns have pivots. The remaining n − r columns do not have pivots. Each of these columns gives rise to a free variable, and the dimension of the null space of A equals this number n − r. The column space of A has dimension r, because the pivotal columns (of A) constitute a basis for the column space.
Another way to see that the column space has dimension r is to use Theorem 17. The dimension of the domain of A (interpreted as a linear transformation in the usual fashion x ![]() Ax) is n. The kernel of A has dimension n − r. Therefore, the range of A is of dimension r. The range of A is its column space.
Ax) is n. The kernel of A has dimension n − r. Therefore, the range of A is of dimension r. The range of A is its column space.
In some books and technical papers, you will encounter the terminology row rank and column rank of a matrix. These are the dimension of the row space and the dimension of the column space, respectively. Thus, Theorem 18 can be stated in the form ‘‘The row rank and column rank of a matrix are equal.’’
EXAMPLE 21
Is there an example of a linear transformation T from ![]() to
to ![]() whose range has dimension seven and whose kernel has dimension nine?
whose range has dimension seven and whose kernel has dimension nine?
SOLUTION Before attempting to construct such an example, we test the equation
|
The information given would lead to 9 + 7 = 17, which is incorrect. No such linear transformation exists.
EXAMPLE 22
Use Theorem 17 to prove that Dim (T[U]) ≤ Dim(U). Here T is a linear transformation defined on a vector space U.
SOLUTION In this inequality, let U be the domain of T. The notation T[U] represents the image of the vector space U under the linear transformation T. Hence, it is the range of T. By Theorem 17, the inequality follows at once, because the kernel of T cannot have a negative dimension.
EXAMPLE 23
Let 
Find bases for each of the spaces Null(A), Col(A), and Row(A).
SOLUTION We find this row equivalence:
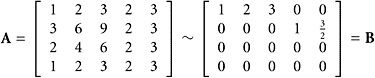 |
|
The reduced echelon form revealsthat insolving theequation Ax = 0 we obtain x1 + 2x2 + 3x3 = 0 and ![]() , or
, or
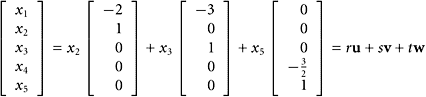 |
|
A basis for the null space is {u, v, w}. Therefore, we obtain Dim(Null(A)) = 3. A basis for the column space of A is given by columns one and four of A or
|
Consequently, we obtain Dim(Col(A)) = 2. A basis for the row space of A is given by rows one and two of B or
|
Finally, as a check, we have Dim Col(A)) + Dim (Null(A)) = 2 + 3 = 5 = n, where A is m × n = 4 × 5.
Caution
If A ~ B, where B is the reduced echelon form of A, then select pivot columns from A for the basis of Col(A), but select pivot rows from B for Row(A). Remember that row operations preserve the linear dependence among the columns but not among the rows!
SUMMARY 5.2
• In a vector space V, a linearly independent set that spans V is a basis for V.
• The set of columns of any n × n invertible matrix is a basis for ![]() .
.
• If a basis is given for a vector space, then each vector in the space has a unique expression as a linear combination of elements in that basis.
• The mapping of x to its coordinate vector ![]() (as described previously) is linear.
(as described previously) is linear.
• The mapping ![]() defined previously is injective (one-to-one) and surjective (onto) from V to
defined previously is injective (one-to-one) and surjective (onto) from V to ![]() .
.
• The relation of isomorphism between two vector spaces is an equivalence relation.
• If a vector space has a finite basis, then all of its bases have the same number of elements.
• A vector space is finite dimensional if it has a finite basis; in that event, its dimension is the number of elements in any basis.
• Two finite-dimensional vector spaces are isomorphic to each other if and only if their dimensions are the same.
• The span of a set is not affected by removing from the set one element that is a linear combination of other elements of that set.
• If a set of n vectors spans an n-dimensional vector space, then the set is a basis for that vector space.
• In an n-dimensional vector space every linearly independent set of n vectors is a basis.
• If a set of n vectors spans a vector space, then the dimension of that space is at most n.
• If a set of n vectors is linearly independent in a vector space V, then the dimension of V is at least n.
• The pivot columns of a matrix form a basis for its column space.
• For any finite-dimensional vector space U and any linear transformation L : U → V, we have Dim (L[U]) ≤ Dim(U).
• Let {u1, u2, …, un} be a basis for a vector space U. Let V be any vector space. A linear transformation T : U → V is completely determined by specifying the values of T(ui) for i = 1, 2, …, n. These values, in turn, can be any vectors whatsoever in V.
• In a finite-dimensional vector space, any linearly independent set can be expanded to get a basis.
• If T is a linear transformation whose domain is an n-dimensional vector space, then Dim (Ker(T)) + Dim (Range(T)) = n
• (Rank–Nullity Theorem.) For any matrix, the number of columns, n, equals the dimension of the column space plus the dimension of the null space:
Dim (Col(A)) + Dim (Null(A)) = n
• The row space and column space of a matrix have the same dimension:
Dim (Row(A)) = Dim (Col(A))
• Caution: If A ~ B, (the latter being the reduced echelon form) then select pivot columns from A as the basis vectors of Col(A) but select pivot rows from B for Row(A).
KEY CONCEPTS 5.2
Basis for avector space, standard basis, coordinate vector of an element in a vector space ![]() , isomorphism, isomorphic, equivalence relations, dimension of a vector space, finite dimensional and infinite dimensional, kernel, domain, range, co-domain, dimensions of various subspaces, column space, row space, null space, rank, nullity
, isomorphism, isomorphic, equivalence relations, dimension of a vector space, finite dimensional and infinite dimensional, kernel, domain, range, co-domain, dimensions of various subspaces, column space, row space, null space, rank, nullity
GENERAL EXERCISES 5.2
1. Consider 
Do the rows of this matrix form a basis for a subspace in ![]() ?
?
2. Let ![]() and x = (3, 2, −1). What is
and x = (3, 2, −1). What is ![]() ?
?
3. Express the polynomial p defined by p(t) = 3(t − 2) + 4(3 − 5t)2 − t3 in terms of Legendre polynomials.
4. Express the polynomial defined by p = 3P0 − 4P1 + 2P2 − P3 in standard form. (Here, Pk is the kth degree Legendre polynomial defined in Example 5.)
5. Find the coordinates of x = (−5, 1, 2) with respect to the basis consisting of u1 = (1, 3, 2), u2 = (2, 1, 4), and u3 = (1, 0, 6).
6. Find the dimension of the span of four polynomials whose definitions are p1(t) = 4 + 3t + 2t2 + t3, p2(t) = 5 + 4t + 3t2 + 2t3, p3(t) = 6 + 5t + 4t2 + 3t3, p4(t) = 7 + 6t + 5t2 + 4t3.
7. Let 
Find a basis for the null space of A. Check your work by an independent calculation.
8. Determine whether (1, 5, 6) is in the row space of this matrix 
9. Explain why the map ![]() defined by the equation L(p) = p + p′ is an isomorphism. You may assume that L is linear. (Here p′ is the derivative of p.)
defined by the equation L(p) = p + p′ is an isomorphism. You may assume that L is linear. (Here p′ is the derivative of p.)
10. Define polynomials p1(t) = 1 − 2t − t2, p2(t) = t + t2 + t3, p3(t) = 1 − t + t3, and p4(t) = 3 + 4t + t2 + 4t3. Let S be the set of these four functions. Find a subset of S that is a basis for the span of S.
11. Suppose A is 5 × 6 and all solutions of Ax = 0 are multiples of one nonzero vector. Will the equation Ax = b be solvable for all b?
12. Consider S = {1, 3, 2, 0]T, [−2, 0, 6, 7]T, [0, 6, 10, 7]T, [2, 10, −3, 1]T}. Find a basis for Span(S).
13. Suppose that A is a 6 × 8 matrix, and the system Ax = b has a solution with two free variables. Are there in consistent cases?
14. Let p be a polynomial of degree n, ![]() with
with ![]() . Is the set {p, p′, p″, …, p(n)} necessarily a basis for
. Is the set {p, p′, p″, …, p(n)} necessarily a basis for ![]() ? Explain why or give a counterexample. (Related to Example 16.)
? Explain why or give a counterexample. (Related to Example 16.)
15. Define four polynomials as follows: p1(t) = t3 − 2t2 + 1, p2(t) = 2t2 + t, p3(t) = 2t3 + 3t + 2, p4(t) = 4t2 + 4t. Find a subset of {p1, p2, p3, p4} that is a basis for the span of this set of four polynomials. Explain.
16. Consider the four vectors u = (1, 1, 1, 1), v = (1, 1, 1, −1), w = (1, 1, −1, −1), and x = (1, −1, −1, −1). Verify that {u, v, w, x} is a basis for ![]() . Explain what you are doing.
. Explain what you are doing.
17. Determine whether ![]() is in the row space of this matrix:
is in the row space of this matrix: 
18. Let ![]() be defined by L(p) = p″. What are Ker(L), Range(L), and Dim (Domain(L))?
be defined by L(p) = p″. What are Ker(L), Range(L), and Dim (Domain(L))?
19. Let u = (1, 1), v = (3, −2), w = (4, 3), and y = (−3, 4). Let L be a linear map from ![]() to
to ![]() such that L(u) = w and L(v) = y. If z = (7, 5), what is L(z)?
such that L(u) = w and L(v) = y. If z = (7, 5), what is L(z)?
20. Let 
Find a basis for the row space of A.
21. Establish that the Chebyshev polynomials p0(t) = 1, p1(t) = t, p2(t) = 2t2 − 1, p3(t) = 4t3 − 3t form a basis for ![]() .
.
22. Let 
Find a simple basis for the column space of A. Explain why {x : Ax = 0} is a subspace of ![]() , and compute its dimension.
, and compute its dimension.
23. Use determinants to show that each of these is a basis for ![]() :
:
a. [1, 0, 0]T, [0, 1, 0]T, [0, 0, 1]T
b. [1, 1, 1]T, [1, 1, 0]T, [1, 0, 0]T
c. [2, 1, 3]T, [5, 2, 1]T, [3, 7, 2]T
24. (Continuation.) Consider [1, 3, 2]T, [4, 2, 3]T, [−1, 1, 0]T, [3, 0, 1]. Find a basis for ![]() from among these vectors. Use determinants to verify your results.
from among these vectors. Use determinants to verify your results.
25. Consider {[−1, 1, 0]T, [4, 2, 3]T, [1, 3, 2]T, [4, 6, 5]T}. What is a basis for the space spanned by this set?
26. Extend this set {[1, 2, 3]T, [0, 2, 3]T} to a basis for ![]() .
.
27. Let 
Find asimple basis for the row space of A.
28. Construct a simple basis for the span of the set of four vectors given here: (1, 0, 3, 0), (3, 1, 11, 0), (5, 1, 17, 1), and (9, 2, 31, 1).
29. Let 
Find bases for the range and the kernel of A. Find values for Dim (Ker(A)), Dim (Range(A)), Dim (Domain(A)).
30. Explain why a line through the origin in avector space is a subspace of dimension one. Recall the representation of a line as discussed in Sections 2.1–2.2.
31. Establish that if S is a linearly independent set of n elements in a vector space, then Dim (Span(S)) = n. Every linearly independent set is a basis for something.
32. Affirm that the rank of a matrix equals the dimension of its row space. (The term rank was defined in Section 1.3.)
33. Establish that if T is a linearly independent set in an n-dimensional vector space, and if S spans that vector space, then #(T) ≤ n ≤ #(S). The notation #(T) denotes the number of elements in the set T.
34. Verify that the dimension of ![]() is mn. What is the dimension of the subspace of
is mn. What is the dimension of the subspace of ![]() consisting of symmetric matrices? An argument is required.
consisting of symmetric matrices? An argument is required.
35. What is the dimension of the space of n × n matrices having zero trace? (The trace of an n × n matrix A is ![]() .) Justify your answer.
.) Justify your answer.
36. What is the dimension of the space of polynomials having degree at most n and taking the value 0 at the point 0? An argument is required. Also explain why this space really is a vector subspace.
37. Let B be an n × n noninvertible matrix. Let V be the set of all n × n matrices A such that BA = 0. Is V a vector space? If so, what is its dimension?
38. Apropos Theorem 12: Give an example of a map from ![]() onto
onto ![]() . Thus, if we admit nonlinear maps, the dimension of the range can be greater than the dimension of the domain.
. Thus, if we admit nonlinear maps, the dimension of the range can be greater than the dimension of the domain.
39. Explain why the composition of two isomorphisms is an isomorphism.
40. Select a nonzerovector v in ![]() , and define a subspace by the equation
, and define a subspace by the equation ![]() . (Here we interpret vT as a matrix with one row and x as a matrix with one column, so that the matrix product vTx makes sense.) What is the dimension of U?
. (Here we interpret vT as a matrix with one row and x as a matrix with one column, so that the matrix product vTx makes sense.) What is the dimension of U?
41. What is the dimension of the set of all polynomials that can be written in the form p(t) = at9 + bt17 + ct7?
42. Criticize this argument: We have three vectors, u1 = (1, 3, 2), u2 = (−2, 4, 5), and u3 = (−1, 7, 7). We notice that u3 is a linear combination of u1 and u2. Furthermore, u2 is a linear combination of u1 and u3. Using Theorem 8 twice, we conclude that both u2 and u3 can be removed from the set {u1, u2, u3} without affecting the span of that set.
43. Establish that the vector space of all sequences of real numbers having only a finite number of nonzero terms has the basis {u1, u2, …, uk,…}, where u1 = (1, 0, 0,…), u2 = (0, 1, 0,…), and so on. (There are infinitely many vectors uk.)
44. In Theorem 14, why do we not prove that Dim (L(V )) = Dim(V)?
45. Establish that if the rows of an n × n matrix span ![]() , then the same is true of the columns.
, then the same is true of the columns.
46. Is the row space of a matrix isomorphic to its column space?
47. Argue that if the rows of an n × n matrix form a linearly independent set, then the columns span ![]() .
.
48. Finish the proof of Theorem 3.
49. Justify that ![]() if
if ![]() is a basis.
is a basis.
50. In the set ![]() consisting of all integers, define n ≡ m to signify that n − m is divisible by 7. Explain why this defines an equivalence relation.
consisting of all integers, define n ≡ m to signify that n − m is divisible by 7. Explain why this defines an equivalence relation.
51. Substantiate that if a vector space V contains a linearly independent set of k vectors and if another set of k vectors spans V, then Dim(V) = k.
52. An isomorphism preserves dimensions. More precisely, if there is an isomorphism between two finite dimensional vector spaces, then the spaces have the same dimension. Justify this result.
53. An isomorphism maps every linearly independent set into a linearly independent set. It also maps a linearly dependent set into a linearly dependent set. Justify these assertions.
54. Explain why every subset of a linearly independent set is linearly independent.
55. Establish that a basis for a finite-dimensional vector space is any maximal linearly independent set. (Such a set is linearly independent and is not a proper subset of another linearly independent set.)
56. Explain why a basis for a finite-dimensional vector space is any minimal spanning set. (Such a set spans the given vector space but it contains no smaller spanning set. A spanning set is any set that spans the given vector space.)
57. Verify that if the columns of an m × n matrix form a basis for ![]() , then n = m.
, then n = m.
58. Is there a linear map from ![]() onto
onto ![]() ? Why or why not?
? Why or why not?
59. Confirm that ![]() is isomorphic to
is isomorphic to ![]() if and only if the product nm equals the product pq.
if and only if the product nm equals the product pq.
60. Verify that if V and W are finite-dimensional vector spaces that are not isomorphic to each other, then their dimensions are not the same.
61. Let pj(t) = tj for j = 0, 1, 2,…. Explain why any set of such functions is linearly independent.
62. Let U be a subspace of a vector space X. Define x ≡ y to mean x − y ∈ U. Is this an equivalence relation on X?
63. Use the notation #S to signify the number of elements of a set S. Explain why a finite set S in a vector space must obey the inequality Dim (Span(S)) ≤ #S.
64. Let A be an m × n matrix, and B be an n × k matrix. Establish that if k > m, then the columns of AB form a linearly dependent set.
65. Consider the vector space consisting of all real-valued sequences, (…, x−2, x−1, x0, x1, x2,…). The algebraic operations are the standard ones. This space is infinite-dimensional, and we see at once that it is the same as the set of all real-valued functions defined on ![]() (the set of all integers, positive, negative, and zero). Find the dimension of the subspace consisting of all sequences that obey the rule xn = 3xn−1 − xn−2 for all n.
(the set of all integers, positive, negative, and zero). Find the dimension of the subspace consisting of all sequences that obey the rule xn = 3xn−1 − xn−2 for all n.
66. Let S be a subset of a vector space, V. Suppose that S spans V, and that there is at least one vector in V that has a unique expression as a linear combination of the vectors in S. Is S necessarily a basis for V?
67. Let Q be a set of vectors that spans a vector space X. If some vector in X can be expressed in two different ways as a linear combination of vectors in Q, does it follow that every vector in X has this property?
68. Let A be an m × n matrix. Let B be an n × k matrix. Let k > n. Is it a justifiable conclusion that the columns of AB form a linearly dependent set?
69. Let A be a 10 × 7 matrix of rank five. What are the dimensions of the domain of A, the kernel of A, the row space of A, the column space of A, and the range of A? Explain how you arrive at each answer, demonstrating along the way that you know the definitions of the terms and some applicable theorems.
70. Explain why the rows of an n × n invertible matrix provide a basis for ![]() .
.
71. Establish that the columns of an n × n invertible matrix form a basis for ![]() . Your proof should use directly the definitions of basis and invertible. It should demonstrate that you know the meanings of these terms. (Do not simply quote part of the Invertible Matrix Theorem.)
. Your proof should use directly the definitions of basis and invertible. It should demonstrate that you know the meanings of these terms. (Do not simply quote part of the Invertible Matrix Theorem.)
72. In a certain vector space W, we have two sets of vectors V = {v1, v2, …,v7}, and U = {u1, u2, …,u8}. One of these sets spans W and the other is linearly independent. Which set has which property? What is the dimension of W? Explain fully.
73. State the theorem that relates the dimensions of certain vector spaces connected with a linear transformation. This theorem concerns an arbitrary linear transformation from a finite-dimensional vector space into another vector space (which need not be finite dimensional). Illustrate the theorem by using the polynomials pi(t) = ti and a linear transformation L defined by L(ap4 + bp3 + cp2 + dp1 + ep0) = cp2 + dp1 + ep0. Find the dimensions of the three important subspaces connected with such a transformation.You should compute the dimensions of those three linear spaces. The transformation L maps ![]() to
to ![]() .
.
74. Let {y1, y2, …, yn} be a basis for the range of a linear transformation T. Let xi be points in the domain of T such that T(xi) = yi for 1 ≤ i ≤ n. Establish that {x1, x2, …, xn} is linearly independent. If possible, improve this result by weakening the hypothesis on {y1, y2, …, yn}.
75. We call a linear transformation robust if it maps no nonzero vectors to zero. Explain why the domain and range of a robust transformation have equal dimensions.
76. Establish that for any m × n matrix A, the rank of A is n minus the dimension of the kernel of A.
77. Let T be the operator T(f) = f + f′ + f″, being applied in the polynomial space ![]() . What are the dimensions of the domain, the range, and the null space of T? What polynomials are in the kernel?
. What are the dimensions of the domain, the range, and the null space of T? What polynomials are in the kernel?
78. Let A be a 12 × 15 matrix. Suppose that the equation Ax = b has a solution for every b ∈ ![]() . What are the dimensions of the domain, the range, and the kernel of A?
. What are the dimensions of the domain, the range, and the kernel of A?
79. Explain why a matrix and its transpose have the same rank.
80. In detail, explain the last questions in Examples 14 and 15. Verify them. Find other examples to illustrate this concept.
81. Give an example of a matrix in reduced row echelon form for which the co-domain, domain, range, and kernel have dimensions 8, 7, 4, and 3, respectively.
82. Let A be an 9 × 6 matrix whose kernel is two dimensional. What are the dimensions of the row space, the column space, and the range?
83. Confirm that the rank of an m × n matrix cannot be greater than the lesser of m and n. In symbols, Rank(A) ≤ min{m, n}.
84. Let A be any matrix and à its reduced row echelon form. Explain why Ax = 0 is true if and only if Ãx = 0.
85. Is there a 2 × 2 matrix whose powers span ![]() ?
?
86. Confirm, for an arbitrary m × n matrix A, that the rank of A is n if and only if the kernel of A contains only the vector 0.
87. Establish that the kernel of amatrix and the column space of its transpose can have only 0 in common.
88. (Continuation.) Let A bean m × n matrix. Explain the logical equivalence of these two conditions:
a. The equation Ax = b is consistent for all b in ![]() .
.
b. The kernel of AT contains only 0.
89. Verify that if integers k, n, m satisfy the inequality 0 ≤ k ≤ n ≤ m, then there is an m × n matrix A such that Dim (Ker(A)) = n − k and Dim (Range(A)) = k.
90. Explain why the following inequality holds for any linear transformation T: Dim (Range(T)) ≤ Dim (Domain(T)).
COMPUTER EXERCISES 5.2
a. Null space
b. Column space
c. Row space
2. Consider this n × n matrix
 |
|
Determine numerically for what values of m this matrix is noninvertible.
3. Consider this matrix
 |
|
Numerically compute the following:
a. Null space
b. Column space
c. Row space
a. Determine numerically the general solution.
b. Find the basis for the column space of A and its dimension.
c. Is the righthand vector b in the column space?
5.3 COORDINATE SYSTEMS
The more you know, the less sure you are.
—VOLTAIRE (1694–1778)
You know that I write slowly. This is chiefly because I am never satisfied until I have said as much as possible in a few words, and writing briefly takes far more time than writing at length.
—KARL FRIEDRICH GAUSS (1777–1855)
Coordinate Vectors
In Section 5.2, we considered an arbitrary n-dimensional vector space V and a prescribed ordered basis for V: ![]() = {u1, u2, …, un}. Every vector x in V has a uniquely determined set of coefficients (a1, a2, …, an) such that
= {u1, u2, …, un}. Every vector x in V has a uniquely determined set of coefficients (a1, a2, …, an) such that ![]() . This set of coefficients is denoted by
. This set of coefficients is denoted by ![]() and is called the coordinate vector of x relative to the basis
and is called the coordinate vector of x relative to the basis ![]() , or the coordinatization of x associated with
, or the coordinatization of x associated with ![]() . It is a vector in
. It is a vector in ![]() . Thus, the equation
. Thus, the equation ![]() = a is true if and only if
= a is true if and only if
|
Here, of course, we have written a = (a1, a2, …, an). One must think of ![]() as an ordered set {u1, u2, …, un} so that the coefficients ai will match with the vectors ui.
as an ordered set {u1, u2, …, un} so that the coefficients ai will match with the vectors ui.
EXAMPLE 1
Let 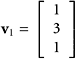 ,
,  ,
, 
What is the coordinate vector of  with respect to the basis
with respect to the basis ![]() = {v1, v2, v3}?
= {v1, v2, v3}?
SOLUTION We place the vectors in an augmented matrix and find its reduced echelon form:
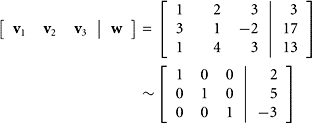 |
|
The result is  , and one can verify it by computing 2v1 + 5v2 − 3v3 = w.
, and one can verify it by computing 2v1 + 5v2 − 3v3 = w.
Changing Coordinates
Now there is the question of how to change coordinates from one basis to another. Thus, two bases will be active in a single vector space, and we shall seek a method to go back and forth between the two types of coordinatization. Suppose, then, that the vector space V is finite-dimensional, and that two bases, ![]() and
and ![]() , have been prescribed. How can
, have been prescribed. How can ![]() be computed from
be computed from ![]() ? Here is the appropriate analysis.
? Here is the appropriate analysis.
First, we must name the elements in the first basis. ![]() = {u1, u2, …, un}. Let x be any element of V, and let
= {u1, u2, …, un}. Let x be any element of V, and let ![]() = (a1, a2, …, an). Then
= (a1, a2, …, an). Then ![]() and
and
|
This equation used crucially the linear property of coordinatization (Theorem 3 in Section 5.2). Now recall that a linear combination of vectors can be written as a matrix times a column vector. The columns of the matrix are the vectors figuring in the linear combination, whereas the entries of the single additional column vector are the coefficients in this linear combination. Accordingly, we construct a matrix P whose columns are ![]() , and write
, and write
 |
|
where
|
The matrix P is called the transition matrix that goes from basis ![]() to basis
to basis ![]() . This discussion has proved the following theorem.
. This discussion has proved the following theorem.
THEOREM 1
Let V be a finite-dimensional vector space in which two ordered bases ![]() and
and ![]() have been prescribed. Let P be the matrix whose columns are the
have been prescribed. Let P be the matrix whose columns are the ![]() -coordinates of the basis vectors in
-coordinates of the basis vectors in ![]() . Then we have
. Then we have ![]() for all x in V.
for all x in V.
This theorem can be illustrated with the following diagram
|
in which the transition matrix P goes from basis ![]() to basis
to basis ![]() .
.
EXAMPLE 2
Let two bases for ![]() be prescribed as follows:
be prescribed as follows:
![]()
where
![]()
Find the transition matrix P that is needed for converting ![]() -coordinates to
-coordinates to ![]() -coordinates.
-coordinates.
SOLUTION By Theorem 1, the columns of P should be ![]() and
and ![]() . Concentrating on the first column of P, we ask for the coefficients x1 and x2 such that
. Concentrating on the first column of P, we ask for the coefficients x1 and x2 such that
|
The augmented matrix for this problem is ![]() . The solution is x1 = 1 and x2 = −1. Hence, column one in P is
. The solution is x1 = 1 and x2 = −1. Hence, column one in P is ![]() .
.
Going on to column two in P, we must find the coefficients y1 and y2 such that
|
The augmented matrix for this system of equations is ![]() .
.
The solution is y1 = −2 and y2 = 3. Hence, column two in P is ![]() . It follows that the P-matrix is
. It follows that the P-matrix is ![]() .
.
A more efficient approach is to note that there are two systems of equations to solve and that they share a coefficient matrix, A. The two systems of equations are Ax = u1 and Ay = u2. One should think of this problem as
|
For the augmented matrix, the steps in row reduction are like this:
 |
|
One obtains the same P as found previously.
EXAMPLE 3
For ![]() , let us use two bases, where the first consists of Chebyshev1 polynomials:
, let us use two bases, where the first consists of Chebyshev1 polynomials:
|
For the second basis, the simple monomials are used. This basis is called the natural basis or the standard basis:
|
What is the matrix needed for transforming ![]() coordinates to
coordinates to ![]() coordinates?
coordinates?
SOLUTION Call this matrix P. The columns of P should be ![]() , where 0 ≤ i ≤ 3. We observe that
, where 0 ≤ i ≤ 3. We observe that
|
1 Pafnuty Lvovich Chebyshev (1821–1894) founded a strong school of mathematics in St.Petersburg, Russia. In number theory, his name is attached to the theorem that asserts the existence of at least one prime number between n and 2n − 2, for n = 4, 5,…. He made outstanding contributions to approximation theory and statistics.
Hence, we obtain
 |
|
EXAMPLE 4
In the same situation as Example 3, what is the transition matrix for coordinates ![]() to coordinates
to coordinates ![]() ?
?
SOLUTION Let’s not call it P because that will confuse the two examples. Use instead Q. The columns of Q should be ![]() , and
, and ![]() . Consider first p0. How can it be expressed as a linear combination of T0, T1, T2, T3? Call the unknown coefficients z0, z1, z2, z3. We want z0T0 + z1T1 + z2T2 + z3T3 = p0. Representing the polynomials just by their coefficients, we must have
. Consider first p0. How can it be expressed as a linear combination of T0, T1, T2, T3? Call the unknown coefficients z0, z1, z2, z3. We want z0T0 + z1T1 + z2T2 + z3T3 = p0. Representing the polynomials just by their coefficients, we must have
 |
|
This is a system of equations that can be solved by row reduction. Each Ti must be treated in the same way, and the coefficient matrix remains the same for each. Hence, we should solve the system whose augmented matrix is
 |
|
It is clear that we are finding the inverse of P by this calculation! But now it is obvious from Theorem 1 that the inverse of P is indeed what is wanted: From ![]() , we have immediately
, we have immediately ![]() . Thus, we obtain Q = P−1. For the record, the answer is
. Thus, we obtain Q = P−1. For the record, the answer is
 |
|
Examples 3 and 4 can be illustrated with the following diagram:
 |
|
Here the transition matrix P goes from basis ![]() to basis
to basis ![]() , and its inverse P−1 goes from basis
, and its inverse P−1 goes from basis ![]() back to basis
back to basis ![]() .
.
Linear Transformations
Theorem 3 in Section 2.3 asserted that a linear transformation from ![]() to
to ![]() is completely determined by the images of the standard basis elements ei in
is completely determined by the images of the standard basis elements ei in ![]() . A more general result along these lines is possible; it is the same as Theorem 15 in Section 5.2 except that there the basis is finite.
. A more general result along these lines is possible; it is the same as Theorem 15 in Section 5.2 except that there the basis is finite.
THEOREM 2
A linear transformation from one vector space to another is completely determined by the images of any basis in the domain. These images can, in turn, be completely arbitrary.
PROOF We employ the usual notation, L : X → Y, to name the map, the domain, and the co-domain. Let ![]() be a basis for the domain. (It need not be finite.) If x is any point in X, then for a suitable finite set of elements ui in
be a basis for the domain. (It need not be finite.) If x is any point in X, then for a suitable finite set of elements ui in ![]() and accompanying scalars ai, we have
and accompanying scalars ai, we have ![]() . By linearity, it follows that
. By linearity, it follows that
|
EXAMPLE 5
Is there a linear transformation that maps these vectors u1 = (2, 3) to v1 = (−1, 5) and u2 = (4, 1) to v2 = (3, 0)?
SOLUTION We only have to be sure that the two vectors u1 and u2 form a linearly independent set. That they do so is obvious because neither is a multiple of the other. These two vectors forma basis for their span. Notice that AU = V where
|
EXAMPLE 6
Find a linear transformation that maps (1, 3, −7) to (2, 0, 2) and (3, 2, 1) to (−1, 1, 5) and (−3, 5, −23) to (8, −2, 5).
SOLUTION If the linear transformation is given by a 3 × 3 matrix X, then we want
 |
|
The equation XB = C is not the sort of problem we have become skilled at solving. Ta ketransposes to get a familiar problem, BTXT = CT. The accompanying augmented matrix is
 |
|
The system is obviously inconsistent. There is a linear relation among the columns of B, and any linear transformation must preserve that. In other words, the third vector is not free. The following theorem is pertinent.
THEOREM 3
If ![]() and if L is linear, then
and if L is linear, then ![]() .
.
PROOF We have at once
|
A linear transformation mapping a finite-dimensional vector space into another vector space (not necessarily finite-dimensional) can be described by a matrix, after bases have been chosen for the domain and range of the transformation. Suppose that the transformation is L : X → Y and that bases have been chosen: ![]() = {u1, u2, …, un} for X, and
= {u1, u2, …, un} for X, and ![]() = {v1, v2, …, vm} for the range of L. By Theorem 11 (in Section 5.2), we know that m ≤ n.
= {v1, v2, …, vm} for the range of L. By Theorem 11 (in Section 5.2), we know that m ≤ n.
For any x in X, we can write ![]() . The scalars αi are the coordinates of x with respect to the basis
. The scalars αi are the coordinates of x with respect to the basis ![]() . Because L is linear, we can proceed to the equation
. Because L is linear, we can proceed to the equation ![]() . Now take the
. Now take the ![]() -coordinates of both sides, using the fact that this process is also linear (Theorem 3 of Section 5.2). The result is
-coordinates of both sides, using the fact that this process is also linear (Theorem 3 of Section 5.2). The result is ![]() . Form a matrix A by putting
. Form a matrix A by putting ![]() as the columns of A. The preceding equation is then
as the columns of A. The preceding equation is then
|
because the αi are the entries in the coordinate vector for x. We have established the following result.
THEOREM 4
Let L be a linear transformation from a finite-dimensional vector space X into a vector space Y. Let ![]() and
and ![]() be ordered bases for X and L(X), respectively. Let A be the matrix whose columns are the vectors
be ordered bases for X and L(X), respectively. Let A be the matrix whose columns are the vectors ![]() , where ui are the ordered elements of
, where ui are the ordered elements of ![]() . Then for all x in X, the equation
. Then for all x in X, the equation ![]() is valid.
is valid.
EXAMPLE 7
Let X = ![]() , and use the basis of Chebyshev polynomials: T0(x) = 1, T1(x) = x, T2(x) = 2x2 − 1, T3(x) = 4x3 − 3x, and T4(x) = 8x4 − 8x2 + 1. Let L be the differentiation operator that maps
, and use the basis of Chebyshev polynomials: T0(x) = 1, T1(x) = x, T2(x) = 2x2 − 1, T3(x) = 4x3 − 3x, and T4(x) = 8x4 − 8x2 + 1. Let L be the differentiation operator that maps ![]() onto
onto ![]() . Just for variety, let us use the standard basis for
. Just for variety, let us use the standard basis for ![]() , pi(x) = xi. What is the matrix A in this case?
, pi(x) = xi. What is the matrix A in this case?
SOLUTION To answer this, we must find L(pi) and ![]() . We have L(p0) = 0, L(p1) = 1, L(p2) = 4x, L(p3) = 12x2 − 3, L(p4) = 32x3 − 16x. Therefore, the matrix sought is
. We have L(p0) = 0, L(p1) = 1, L(p2) = 4x, L(p3) = 12x2 − 3, L(p4) = 32x3 − 16x. Therefore, the matrix sought is
 |
|
If we desire to know the effect of applying L to a typical random polynomial x = 3T0 − 2T1 + 7T2 − 4T3 + 6T4, the answer is ![]() , which is computed from the matrix A:
, which is computed from the matrix A:
 |
|
In other words, the resulting polynomial is x ![]() 10 − 68x − 48x2 + 192x3. Checking with an independent verification:
10 − 68x − 48x2 + 192x3. Checking with an independent verification:
 |
|
The derivative is 10 − 68x − 48x2 + 192x3.
EXAMPLE 8
Consider the linear transformation ![]() defined by
defined by
 |
|
Suppose that the basis for ![]() is chosen to be
is chosen to be
|
where
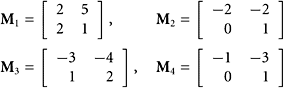 |
|
and the basis for ![]() is
is
|
where
 |
|
Find the matrix A such that ![]() .
.
SOLUTION The transformation is
 |
|
Associate with each matrix ![]() in the basis
in the basis ![]() the vector
the vector 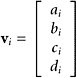 ; namely,
; namely,
 |
|
We seek the matrix A such that ![]() . Matrix A has columns
. Matrix A has columns ![]() for i = 1, 2, 3, 4. We find
for i = 1, 2, 3, 4. We find
 |
|
The matrix A is therefore
 |
|
Mapping a Vector Space into Itself
The final question that we want to address pertains to the case of a linear transformation mapping a vector space into itself. We want to understand the various matrices that can represent our mapping when the bases are changed. Let L : X → X be a linear map, where X is an n-dimensional vector space. Let X be given two bases, ![]() and
and ![]() . We already know how to get the matrix for L when we restrict our attention to
. We already know how to get the matrix for L when we restrict our attention to ![]() , using it twice, once for the domain and once for the co-domain. Specifically, we form the matrix A whose columns are
, using it twice, once for the domain and once for the co-domain. Specifically, we form the matrix A whose columns are ![]() , where ui are the vectors in
, where ui are the vectors in ![]() . Having done so, we have, by Theorem 4,
. Having done so, we have, by Theorem 4,
|
In the same way, there is a matrix B such that for all x,
|
Finally, another matrix P enters as the transition matrix in Theorem 1. Thus, P does the following task:
|
for all x. Putting this all together, we have
|
Because ![]() can be any vector in
can be any vector in ![]() , we conclude that B = PAP−1. This is the relationship we sought to uncover. The result is the following theorem.
, we conclude that B = PAP−1. This is the relationship we sought to uncover. The result is the following theorem.
THEOREM 5
If n × n matrices A and B represent the same linear transformation, but with respect to two bases, then for an appropriate invertible matrix P, we have B = PAP−1.
Similar Matrices
The relationship between A and B in Theorem 5 is called similarity. Thus, as often happens, a common English word receives a highly technical meaning in mathematics.
DEFINITION
Let A and B be two n × n matrices. We say that A is similar to B if there is an invertible matrix P such that A = PBP−1.
Similarity is an equivalence relation, as discussed in Section 5.2. Thus, if we express ‘‘A is similar to B’’ by A ![]() B, we have these properties:
B, we have these properties:
EXAMPLE 9
Do these two matrices represent the same linear transformation with respect to different bases? In otherwords, are these two matrices similar to each other?
 |
|
SOLUTION The answer is Yes, because the matrices
 |
|
have the property A = PBP−1. How did we find P? See the next example.
EXAMPLE 10
Let 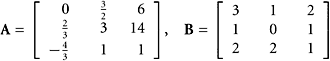
Are these matrices similar to each other?
SOLUTION Given n × n matrices A and B, finding a matrix P such that
|
can be a complicated problem. We would need to solve the homogeneous system
|
involving n2 equations in n2 unknowns. Letting
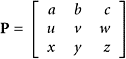 |
|
and using the particular matrices A and B given previously, we find that the equation AP − PB = 0 leads to these nine linear equations: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Setting up the augmented matrix and transforming it to reduced echelon form, we have
. Setting up the augmented matrix and transforming it to reduced echelon form, we have
 |
|
So we obtain the general solution ![]() ,
, ![]() ,
, ![]() , u = 4x + 6z, v = 13/3x + 2z, w = 16/3x, and y = 0. Yes, A and B are similar! For example, letting x = 0 and z = 1, we obtain
, u = 4x + 6z, v = 13/3x + 2z, w = 16/3x, and y = 0. Yes, A and B are similar! For example, letting x = 0 and z = 1, we obtain
 |
|
Checking by simple matrix multiplication verifies that A = PBP−1.
THEOREM 6
If A = PQP−1 and if the columns of P are taken as the basis ![]() , then
, then ![]() . In other words, Q is the matrix for x
. In other words, Q is the matrix for x ![]() Ax when the chosen basis is
Ax when the chosen basis is ![]() .
.
PROOF Observe that for all x, ![]() . It follows that
. It follows that ![]() and that
and that ![]() . From A = PQP−1, we obtain P−1A = QP−1 and finally we obtain
. From A = PQP−1, we obtain P−1A = QP−1 and finally we obtain ![]() .
.
More on Equivalence Relations
This is a topic that arises naturally in many diverse situations. The basic idea is very simple: We divide a set of elements into disjoint subclasses, and think of the entities of each subclass as being related in some way. You have seen many examples of this, such as dividing people into the two classes, male and female, or dividing the set of all polynomials into distinct classes depending on their degree. A division of the set of all integers into even or odd integers is another familiar example. A generalization of this idea is as follows. We divide each integer by a fixed number n and classify the integers by the remainder that results in this division. It must be 0 or 1 or 2 or … or (n − 1). This is call modulo(n) arithmetic.
Now, having divided a given set X into mutually disjoint subclasses, let us concentrate on the relationship between elements of the same subclass. We say that two elements, x and y, of the same subclass are equivalent to each other, and write x ≡ y. Then we can prove these properties of the ≡ relation:
Any relation that has these three properties is called an equivalence relation. Some equivalence relations have special names. For example, in plane geometry, we speak of similar triangles and congruent triangles. These concepts involve equivalence relations.
The tables can be turned. Suppose that an equivalence relation ≡ on a set X is given. With each element x in X, we associate an equivalence class {y : y ≡ x}. These equivalence classes are mutually disjoint. To prove this, let E(x) denote the equivalence class containing x, as just defined. Consider a different equivalence class, say E(u). Can they have an element in common? Suppose y belongs to both. Then y ≡ x and y ≡ u. By the preceding axioms, it follows that x ≡ u, and so E(x) =E(u). The last equation is demonstrated by taking an arbitrary element z in E(x). Then it follows that z ≡ x, z ≡ u, and z ![]() E(u). Hence, we have E(x) ⊆ E(u). By symmetry intheargument, E(u) ⊆ E(x).Because E(u) =E(x), we have contradicted the choice of E(u) as an equivalence class different from E(x). The reader is urged to go over this argument carefully to reach a thorough understanding of the concepts involved. We do not claim that it is easy.
E(u). Hence, we have E(x) ⊆ E(u). By symmetry intheargument, E(u) ⊆ E(x).Because E(u) =E(x), we have contradicted the choice of E(u) as an equivalence class different from E(x). The reader is urged to go over this argument carefully to reach a thorough understanding of the concepts involved. We do not claim that it is easy.
Among matrices there are several useful equivalence relations. For example one can define the row equivalence of two matrices to mean that they have the same reduced row echelon form. This special equivalence relation is denoted in this book by ~. For example, we have
 |
|
because both of these matrices are row equivalent to I3.
As mentioned previously, another equivalence relation discussed here is that of similarity, written A ![]() B. These two equivalence relations, ~ and
B. These two equivalence relations, ~ and ![]() , are completely different from each other!
, are completely different from each other!
Further Examples
The following five examples illustrate thenew concepts introducedinthis section.
EXAMPLE 11
Let g1(t) = 3t2+t−1, g2(t)=t2−t+2, g3(t)=2t2+3t+1. Do these polynomials provide a basis for ![]() ? If so, what is the coordinate vector for the polynomial p defined by p(t) = 11t2 + 17t − 4?
? If so, what is the coordinate vector for the polynomial p defined by p(t) = 11t2 + 17t − 4?
SOLUTION We put the coefficients of the polynomials in an augmented matrix and find its reduced echelon form:
 |
|
Yes, ![]() = {g1, g2, g3} is a basis for
= {g1, g2, g3} is a basis for ![]() . Furthermore,
. Furthermore,  .
.
We can verify these results with aseparate calculation: 2g1 − 3g2 + 4g3 = 2(3t2 + t − 1) − 3(t2 − t + 2) + 4(2t2 + 3t + 1) = 11t2 + 17t − 4.
EXAMPLE 12
Use the transition matrix of Example 3 to express the polynomial p = 3T0 −7T1 + 5T2 + 4T3 in terms of the natural (standard) basis for ![]() . Here T0, T1, T2, T3 are Chebyshev polynomials as in Example 7.
. Here T0, T1, T2, T3 are Chebyshev polynomials as in Example 7.
SOLUTION The polynomial p has coordinate vector ![]() . Hence, we have
. Hence, we have
 |
|
The result is p(t) = −2 − 19t + 10t2 + 16t3. An independent calculation will verify the results:
|
EXAMPLE 13
First, define matrices
|
Then use coordinate mappings to determine whether the set {A1, A2, A3} is linearly independent.
SOLUTION One basis for ![]() is
is
 |
|
It is easy to express the A matrices in terms of the B matrices:
|
The question is whether there is a linear dependence of the form
|
Therefore, we want to find the solutions of the equation
 |
|
The row-reduction process applied to the coefficient matrix yields
 |
|
This proves that the homogeneous problem has no solution other than the zero vector, and {A1, A2, A3} is linearly independent.
EXAMPLE 14
Two bases for ![]() are given:
are given:
|
where
 |
|
and
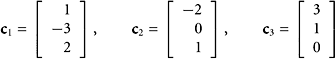 |
|
What is the P-matrix that enables us to convert from the ![]() -coordinates to the
-coordinates to the ![]() -coordinates?
-coordinates?
SOLUTION The P-matrix should have this property:
|
for all x ![]()
![]() . Our theory tells us that the columns of P should be
. Our theory tells us that the columns of P should be ![]() ,
, ![]() ,
, ![]() . To start, we must represent b1 in terms of the
. To start, we must represent b1 in terms of the ![]() -basis. Thus, we need to solve the equation x1c1 + x2c2 + x3c3 = b1 or
-basis. Thus, we need to solve the equation x1c1 + x2c2 + x3c3 = b1 or
 |
|
The vector x = [x1, x2, x3]T (when it has been computed) will be the first column in the matrix P. Similar remarks pertain to the vectors b2 and b3. The computations can be done simultaneously:
 |
|
Row reduction leads to
 |
|
One can test the equation
|
For example let x = [5, −1, 3]T. It is known that x = 1b1 + 0b2 + 0b3. Therefore, we have ![]() . We obtain
. We obtain ![]() . Further testing obtains 1c1 + 1c2 + 2c3 = [1, −3, 2]T + [−2, 0, 1]T +2[3, 1, 0]T = [5, −1, 3]T.
. Further testing obtains 1c1 + 1c2 + 2c3 = [1, −3, 2]T + [−2, 0, 1]T +2[3, 1, 0]T = [5, −1, 3]T.
In the solution to Example 14, we follow this path of reasoning: [C | B] ~ [EC | EB] = [I | P] by row reduction. Thus, we have EC = I, EB = P, E = C−1, and P = EB = C−1B.
EXAMPLE 15
The first few Chebyshev polynomials are defined by the equations T0(t) = 1, T1(t) = t, T2(t) = 2t2 − 1, T3(t) = 4t3 − 3t.
Express the polynomial p(x) = 5x3 − 2x2 + 3x − 1 as a linear combination of these Chebyshev polynomials.
SOLUTION We want to find the coefficients in the equation
|
The correct coefficients will solve this linear system:
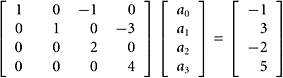 |
|
The augmented matrix and its row-reduced form are
 |
|
Verifying independently, we find
|
SUMMARY 5.3
• Every vector x in an n-dimensional vector space V, with an ordered basis ![]() = {u1, u2, …, un}, can be written
= {u1, u2, …, un}, can be written ![]() , where the coefficients (a1, a2, …, an) are uniquely determined. Here
, where the coefficients (a1, a2, …, an) are uniquely determined. Here ![]() is the coordinate vector of x relative to the basis
is the coordinate vector of x relative to the basis ![]() .
.
• The transition matrix P from a basis ![]() = u1, u2, …, un} to a basis
= u1, u2, …, un} to a basis ![]() = {v1, v2, …, vn} {has the form
= {v1, v2, …, vn} {has the form ![]() , where
, where ![]() ,
, ![]() .
.
• The transition matrix P−1 from a basis ![]() = {v1, v2, …, vn} to a basis
= {v1, v2, …, vn} to a basis ![]() = {u1, u2, …, un} has the form
= {u1, u2, …, un} has the form ![]() .
.
• An equivalence relationship ≡ on any set has these properties:
• For each x in X, x ≡ x. (reflexive).
• If x ≡ y, then y ≡ x. (symmetric).
• If x ≡ y and y ≡ z, then x ≡ z. (transitive).
• A is similar to B if B = PAP−1 for some invertible matrix P.
• Similarity is an equivalence relationship.
• Theorems:
• Let V be a finite-dimensional vector space in which two ordered bases ![]() and
and ![]() have been prescribed. Let P be the matrix whose columns arethe
have been prescribed. Let P be the matrix whose columns arethe ![]() -coordinates of the basis vectors in
-coordinates of the basis vectors in ![]() . Then for all x in V, we have
. Then for all x in V, we have ![]() .
.
• A linear transformation from one vector space to another is completely determined by the images of any basis for the domain. These images can, in turn, be completely arbitrary.
• If ![]() and if L is linear, then
and if L is linear, then ![]() .
.
• Let L be a linear transformation from a finite-dimensional vector space X into a vector space Y. Let ![]() and
and ![]() be ordered bases for X and L(X), respectively. Let A be the matrix whose columns are the vectors
be ordered bases for X and L(X), respectively. Let A be the matrix whose columns are the vectors ![]() , where ui are the ordered elements of
, where ui are the ordered elements of ![]() . Then for all x in X, we obtain
. Then for all x in X, we obtain ![]() .
.
• If n × n matrices A and B represent the same linear transformation, but with respect to two bases, then for an appropriate invertible matrix P, we have B = PAP−1.
• If A = PQP−1 and if the columns of P are taken as the basis ![]() , then
, then ![]() . Here, Q is the matrix for x
. Here, Q is the matrix for x ![]() Ax when the chosen basis is
Ax when the chosen basis is ![]() .
.
KEY CONCEPTS 5.3
Coordinate vector, coordination, bases, changing coordinates, transition matrix, Chebyshev polynomials, natural/standard basis, linear transformation, finite/infinite dimensional vector spaces, mapping a vector space into itself, similar matrices, similarity, equivalence relation, reflexive, symmetric, transition
GENERAL EXERCISES 5.3
1. Find the transition matrix from basis ![]() to basis
to basis ![]() when
when ![]() has elements u1 = (−2, −2) and u2 = (−3, −2) and
has elements u1 = (−2, −2) and u2 = (−3, −2) and ![]() has v1 = (1, 2) and v2 = (3, 4). Use the matrix to compute
has v1 = (1, 2) and v2 = (3, 4). Use the matrix to compute ![]() when
when ![]() . What is x in its usual form, that is, as an element of
. What is x in its usual form, that is, as an element of ![]() ?
?
2. Let {e1, e2} be the standard basis for ![]() . Form a new basis by selecting a positive angle θ and rotating e1 and e2 counterclockwise through the angle θ. Find the explicit form of the new basis elements by using trigonometry.
. Form a new basis by selecting a positive angle θ and rotating e1 and e2 counterclockwise through the angle θ. Find the explicit form of the new basis elements by using trigonometry.
3. (Continuation.) Find the transition matrix for converting standard coordinates to coordinates in the rotated system.
4. The first four Chebyshev polynomials are given in Example 3. You will need also the fifth: T4(t) = 9t4 − 7t2 + 1. The first five Legendre2 polynomials are P0, P1 , …, P4, where P0(t) = 1, P1(t) = t, P2(t) = (3t2 − 1)/2, P3(t) = (5t3 − 3t)/2, and P4(t) = (35t4 − 30t2 + 3)/8. Find the transition matrix for converting polynomials in ![]() from combinations of Chebyshev polynomials to combinations of Legendre polynomials.
from combinations of Chebyshev polynomials to combinations of Legendre polynomials.
5. The Chebyshev polynomials (discussed in Example 3) obey the following relations: T0(x) = 1, T1(x) = x, and, in general, Tk+1(x) = 2xTk(x) − Tk−1(x). Here, k = 1, 2, 3,…. (We say that these polynomials are defined recursively.) Find the transition matrix that converts a linear combination of T0, T1, …, T5 into a polynomial in standard form.
6. Define these six vectors: u1 = (1, 4, 7, 2), u2 = (3, 1, 1, 5), u3 = (−3, 10, 19, −4), v1 = (7, 1, 6, 5), v2 = (−2, 1, 3, 1), and v3 = (11, 3, 2, 9). Find a linear transformation L such that L(ui) = vi for 1 ≤ i ≤ 3.
7. Let one basis, ![]() , for
, for ![]() have the vectors (2, 1, 7), (3, 2, 1), and (−2, 0, 1). Let another basis,
have the vectors (2, 1, 7), (3, 2, 1), and (−2, 0, 1). Let another basis, ![]() , have vectors (1, 3, 2), (−4, 0, 5), and (2, −1, 3). Find the transition matrix P that allows us to calculate
, have vectors (1, 3, 2), (−4, 0, 5), and (2, −1, 3). Find the transition matrix P that allows us to calculate ![]() from
from ![]() .
.
2 Adrien Marie Legendre (1752–1833) worked on number theory and differential equations, one of which is named after him: (1 − x2)f″(x) − 2f′ + n(n − 1)f(x) = 0. The Legendre polynomials satisfy this differential equation. Legendre published a popular geometry textbook in 1794.
8. Let ![]() = {u1, u2}, u1 = [3, 1]T, u2 = [2, 5]T, and x = [−8, −33]T. Compute
= {u1, u2}, u1 = [3, 1]T, u2 = [2, 5]T, and x = [−8, −33]T. Compute ![]() .
.
9. The matrices ![]() and
and ![]() are similar. Solve for P in the equation A = P−1BP.
are similar. Solve for P in the equation A = P−1BP.
10. In ![]() , consider the bases
, consider the bases
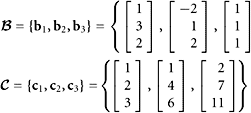 |
|
What is the Matrix P needed to change ![]() -coordinates to
-coordinates to ![]() -coordinates?
-coordinates?
11. Let ![]() = {d1, d2, d3} and
= {d1, d2, d3} and ![]() = {f1, f2, f3} be bases for V. Suppose f1 = 2d1 − d2 + d3, f2 = 3d2 + d3, and f3 = −3d1 + 2d3. Find the matrix for changing
= {f1, f2, f3} be bases for V. Suppose f1 = 2d1 − d2 + d3, f2 = 3d2 + d3, and f3 = −3d1 + 2d3. Find the matrix for changing ![]() coordinates to
coordinates to ![]() coordinates. Find
coordinates. Find ![]() if x = f1 − 2f2 + 2f3.
if x = f1 − 2f2 + 2f3.
12. Let T : V → W, where V has basis ![]() = {b1, b2}, W has basis
= {b1, b2}, W has basis ![]() = {c1, c2, c3}, T(b1) = 3c1 + 5c2 − 7c3, and T(b2) = 2c1 − c2 + 4c3. Find M so that
= {c1, c2, c3}, T(b1) = 3c1 + 5c2 − 7c3, and T(b2) = 2c1 − c2 + 4c3. Find M so that ![]() . If
. If ![]() , then what is
, then what is ![]() ?
?
13. Let u1(t) = 1, u2(t) = sin t, and u3(t) = cos t. These constitute a basis for a three-dimensional vector space. If T(u1) = 0, T(u2) = u3, and T(u3) = −u2, what is the matrix for T? If x = 3u1 − 2u2 + 7u3, then what is T(x)? Use the matrix to find this.
14. Let L : ![]() be defined by
be defined by ![]()
Use for ![]() the standard basis in
the standard basis in ![]() and for
and for ![]() the standard basis in
the standard basis in ![]() . What is the matrix that does this task?
. What is the matrix that does this task?
15. Define a linear transformation L from ![]() to
to ![]() as follows: If p(t) = a3t2 + a2t + a1, then L(p) = (a3 + a2, 2a1 − a3). Let the standard bases be prescribed:
as follows: If p(t) = a3t2 + a2t + a1, then L(p) = (a3 + a2, 2a1 − a3). Let the standard bases be prescribed: ![]() for
for ![]() : q2(t) = t2, q1(t) = t, q0(t) = 1;
: q2(t) = t2, q1(t) = t, q0(t) = 1; ![]() for
for ![]() : v1 = (1, 0), v2 = (0, 1). What is the matrix for L with respect to these two ordered bases? In other words, what is
: v1 = (1, 0), v2 = (0, 1). What is the matrix for L with respect to these two ordered bases? In other words, what is ![]() ? Use the matrix found to compute L(p) when p(t) = 4t2 −t + 1. Also verify your result by a direct calculation using the definition of L.
? Use the matrix found to compute L(p) when p(t) = 4t2 −t + 1. Also verify your result by a direct calculation using the definition of L.
16. Let V be a vector space with ordered basis ![]() = {d1, d2}, and let W be a vector space with ordered basis
= {d1, d2}, and let W be a vector space with ordered basis ![]() = {b1, b2}. Let T be a linear transformation from V to W such that T(d1) = −3b2 + 2b1 and T(d2) = 5b2 − 4b1. What is the matrix for T relative to these two ordered bases?
= {b1, b2}. Let T be a linear transformation from V to W such that T(d1) = −3b2 + 2b1 and T(d2) = 5b2 − 4b1. What is the matrix for T relative to these two ordered bases?
17. Let ![]() = {u1, u2}, where u1 = (1, 3), u2 = (−2, 1). Let
= {u1, u2}, where u1 = (1, 3), u2 = (−2, 1). Let ![]() = {v1, v2}, where v1 = (2, 7), v2 = (1, 2). Define a linear transformation T such that T(u1) = 2v1 − 3v2 and T(u2) = v1 + 4v2. Find the matrix A such that
= {v1, v2}, where v1 = (2, 7), v2 = (1, 2). Define a linear transformation T such that T(u1) = 2v1 − 3v2 and T(u2) = v1 + 4v2. Find the matrix A such that ![]() .
.
18. Let ![]() = {u1, u2}, where u1 = (3, 1), u2 = (2, 5), and x = (−8, −33). Compute
= {u1, u2}, where u1 = (3, 1), u2 = (2, 5), and x = (−8, −33). Compute ![]() .
.
19. Verify that ![]() if α ≠ 0. (Here
if α ≠ 0. (Here ![]() is the similarity equivalence relation.)
is the similarity equivalence relation.)
20. Establish that if P is the transition matrix for changing ![]() -coordinates to
-coordinates to ![]() -coordinates, and if Q does the same for
-coordinates, and if Q does the same for ![]() to
to ![]() , then QP is the transition matrix for
, then QP is the transition matrix for ![]() to
to ![]() .
.
21. Give an argument for this assertion. If ![]() is a basis for some vector space and
is a basis for some vector space and ![]() = {u1, u2, …, un}, then for each i, the coordinate vector for ui is ei (the ith standard unit vector in
= {u1, u2, …, un}, then for each i, the coordinate vector for ui is ei (the ith standard unit vector in ![]() ). Thus, in symbols,
). Thus, in symbols, ![]() .
.
22. Let ![]() be a basis for a finite-dimensional vector space, V. Establish that if S is a linearly dependent set in V then the set
be a basis for a finite-dimensional vector space, V. Establish that if S is a linearly dependent set in V then the set ![]() is also linearly dependent. Establish a stronger result, if you can.
is also linearly dependent. Establish a stronger result, if you can.
23. Let {u1, u2, …, un} be a basis for ![]() . Interpret these vectors as columns of a matrix A, and call this basis
. Interpret these vectors as columns of a matrix A, and call this basis ![]() . In terms of A, what are the transition matrices for converting standard coordinates to
. In terms of A, what are the transition matrices for converting standard coordinates to ![]() -coordinates and vice versa?
-coordinates and vice versa?
24. Substantiate that two similar matrices have the same determinant. Is the converse true?
25. Affirm that ![]() is an equivalence relation. (Recall that
is an equivalence relation. (Recall that ![]() means similarity.)
means similarity.)
26. Find a basis for the set of all 2 × 2 matrices that commute with the matrix ![]()
27. Explain that if one of A and B is invertible, then AB ![]() BA. Is the invertibility hypothesis necessary? (An example or theorem is needed.)
BA. Is the invertibility hypothesis necessary? (An example or theorem is needed.)
28. If two matrices are similar (in the technical meaning of this word), does it follow that they are row equivalent?
29. Show that every 2 × 2 matrix is similar to its transpose.
30. Verify by an independent calculation the correctness of the final assertion in Example 5.
31. Does the matrix equation AP = PB imply that A is similar to B?
32. Explain why transition matrices are always invertible.
33. Explain why Px = 0 implies that x = 0. Here, P is a transition matrix,
34. Give an example of matrices such that AP = PB but P ≠ 0 and A is not similar to B.
35. Find necessary and sufficient conditions on general 2 × 2 matrices A and B so that they are similar.
36. For this exercise only, we say that two sets of vectors in a vector space are equivalent to each other if each is in the span of the other. Is this an equivalence relation?
37. The Fibonacci sequence is F = (1, 1, 2, 3, 5, 8, 13, 21,…). Its definition is x1 = 1, x2 = 1, and (for n ≥ 3) xn = xn−1 + xn−2. Its name is from a mathematician Fibonacci (born around 1175, died around 1250), who needed it in his study of the breeding of rabbits. Explain why any sequence that satisfies the recurrence relation xn = xn−1 + xn−2 is a linear combination of F and G = (0, 1, 2, 3, 5, 8, 13, 21,…).
38. Derive P and P−1 in Example 9. Verify in both of these examples that A = PBP−1.
39. Are these equivalence relations? Explain.
40. Find the coordinate vector for the given vector relative to the basis shown.
a. ![]()
b. 
c. 
41. Find the transition matrix Q for transforming the ![]() -coordinates to the
-coordinates to the ![]() -coordinates.
-coordinates.
a. 
b. 
42. (Continuation.) Using the previous results, find the transition matrix P used in converting from the ![]() -coordinates back to the
-coordinates back to the ![]() -coordinates.
-coordinates.
43. In ![]() , are these equivalence relations? Explain.
, are these equivalence relations? Explain.
a. aRb means lines a and b have a point in common.
b. aSb means lines a and b are parallel or coincident.
44. Find the transition matrix Q used in converting from the ![]() -coordinates to the
-coordinates to the ![]() coordinates,
coordinates,
a. ![]()
b. ![]()
c. 
45. (Continuation.) Using the previous results, find the transition matrix P used in converting from the ![]() -coordinates back to the
-coordinates back to the ![]() -coordinates.
-coordinates.
46. Find the matrix representation for the linear mapping given by T(A) = AX where ![]() with regard to the standard basis
with regard to the standard basis
|
where Eij is the 2 × 2 matrix with 1 in the (i, j) location and 0’s elsewhere.
47. Find the coordinate vector for the given vector relative to the basis.
a. 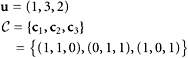
b. 
48. Find the coordinate vectors for the given vector relative to these bases.
a. ![]()
b. ![]()
a. ![]()
b. ![]()
c. 
50. Establish the following.
a. If D is an invertible diagonal matrix, then D is similar to itself.
b. If A is similar to B, then B is similar to A, and B−1 is similar to A−1.
c. If A is similar to B, then Ak is similar to Bk.
51. Are these linear mappings? Explain.
a. F(x, y) = (x, x + y)
b. G(x, y) = |x − y|
c. H(x, y, z) = (y, x + 1, y + z)
d. L(x, y, z) = (2x, −3y, 4z)
52. Let F(x, y) = (3x + y, 2x − 5y) be a linear mapping from ![]() to
to ![]() relative to the basis
relative to the basis ![]() = {u1, u2} = {(1, −2), (3, −4)}.
= {u1, u2} = {(1, −2), (3, −4)}.
a. For an arbitrary vector (a, b), find the coordinate vector ![]() .
.
b. Write F(u1) and F(u2) as a linear combination of the basis vectors.
c. Find F, which is the matrix representation of F in the basis.
53.
a. Let (a, b) ![]()
![]() be an arbitrary vector. Find the coordinate vector
be an arbitrary vector. Find the coordinate vector ![]() with respect to the basis
with respect to the basis
|
b. Write the basis vectors of ![]() = {v1, v2} = {(1, −2), (3, −4)} as a linear combination of the basis vectors of
= {v1, v2} = {(1, −2), (3, −4)} as a linear combination of the basis vectors of ![]() .
.
c. Find the change of basis matrix P from basis ![]() to
to ![]() .
.
d. Find the change of basis matrix Q from basis ![]() to
to ![]() .
.
e. Show that PQ = I.
54. Let T(v) = Av where ![]() Find the matrix representation relative to these bases.
Find the matrix representation relative to these bases.
a. ![]()
b. ![]()
55. Determine if these aresimilar matrices.
a. ![]()
b. ![]()
Hint: eiθ = cos θ + i sin θ
COMPUTER EXERCISES 5.3
Use mathematical software such as Maple to solve these problems numerically.