This recipe will use a simple maze environment to find a path starting at the start point and ending at the exit point. You can either prepare one by yourself or let the computer create one for you. A map will be represented by a 2D-map structure where each cell will consist of a cell type and cell connections. The cell type values are as follows:

Cell connections will use a bitmask value to get information about which cells are connected to the current cell. The following diagram contains cell connection bitmask values with their respective positions:

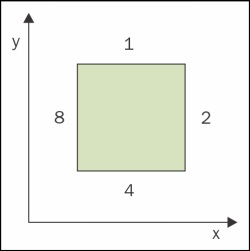
Now, the quite common problem in programming is how to implement an efficient data structure for 2D maps. Usually, this is done either with a relatively large one-dimensional array or with an array of arrays. All these arrays have a specified static size, so map dimensions are fixed. The problem arises when you use a simple 1D array and you need to change the map size during gameplay or the map size should be unlimited. This is where map cell indexing comes into place. Often you can use this formula to compute the cell index from 2D map coordinates:

local index = x + y * map_width
map[index] = value

There's nothing wrong with this approach when the map size is definite. However, changing the map size would invalidate the whole data structure as the map_width variable would change its value. A solution to this is to use indexing that's independent from the map size. This way you can ensure consistent access to all elements even if you resize the 2D map.

You can use some kind of hashing algorithm that packs map cell coordinates into one value that can be used as a unique key. Another way to accomplish this is to use the Cantor pairing function, which is defined for two input coordinates:

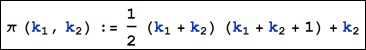
Index value distribution is shown in the following diagram:

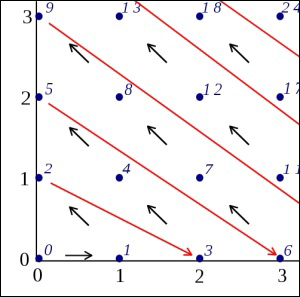
The Cantor pairing function ensures that there are no key collisions no matter what coordinates you use. What's more, it can be trivially extended to support three or more input coordinates. To illustrate the usage of the Cantor pairing function for more dimensions, its primitive form will be defined as a function cantor(k1, k2), where k1 and k2 are input coordinates. The pairing function for three dimensions will look like this:

local function cantor3D(k1, k2, k3)
  return cantor(cantor(k1, k2), k3)
end

Keep in mind that the Cantor pairing function always returns one integer value. With higher number of dimensions, you'll soon get very large values in the results. This may pose a problem because the Lua language can offer 52 bits for integer values. For example, for 2D coordinates (83114015, 11792250) you'll get a value 0x000FFFFFFFFFFFFF that still can fit into 52-bit integer values without rounding errors. The larger coordinates will return inaccurate values and subsequently you'd get key collisions. Value overflow can be avoided by dividing large maps into smaller ones, where each one uses the full address space that Lua numbers can offer. You can use another coordinate to identify submaps.

This recipe will use specialized data structures for a 2D map with the Cantor pairing function for internal cell indexing. You can use the following code to prepare this type of data structure:

function map2D(defaultValue)
  local t = {}
  -- Cantor pair function
  local function cantorPair(k1, k2)
    return 0.5 * (k1 + k2) * ((k1 + k2) + 1) + k2
  end
  setmetatable(t, {
    __index = function(_, k)
      if type(k)=="table" then
        local i = rawget(t, cantorPair(k[1] or 1, k[2] or 1))
        return i or defaultValue
      end
    end,
    __newindex = function(_, k, v)
      if type(k)=="table" then
        rawset(t, cantorPair(k[1] or 1, k[2] or 1), v)
      else
        rawset(t, k, v)
      end
    end,
  })
  return t
end

The maze generator as well as the pathfinding algorithm will need a stack data structure. For more information, refer to the Making a stack recipe from Chapter 1, Basics of the Game Engine.

This section is divided into two parts, where each one solves very similar problems from the perspective of the maze generator and the maze solver.

git clone https://github.com/soulik/maze_generator

local mazeGenerator = require 'maze'
local maze = mazeGenerator {
  width = 50,
  height = 25,
  entry = {x = 2, y = 2},
  exit = {x = 30, y = 4},
  finishOnExit = false,
}

for i=1,12500 do
  local result = maze.generate()
  if result == 1 then
    break
  end
end

local cell = maze.map[{x, y}]
local cellType = cell.type
local cellConnections = cell.connections

local currentPosition = {maze.entry.x, maze.entry.y}
local visistedCells = map2D(false)
local path = stack()

-- A placeholder for neighbours function that will be defined later
local neighbours

-- testing function for passable cells
local cellTestFn = function(cell, position)
  return (cell.type >= 1) and (not visitedCells[position])
end

-- include starting point into path
visitedCells[currentPosition] = true
path.push(currentPosition)

while true do
  local currentCell = maze.map[currentPosition]
  -- is current cell an exit point?
  if currentCell and
    (currentCell.type == 3 or currentCell.type == 4) then
    break
  else
    -- have a look around and find viable cells
    local possibleCells = neighbours(currentPosition, cellTestFn)
    if #possibleCells > 0 then
      -- let's try the first available cell
      currentPosition = possibleCells[1]
      visitedCells[currentPosition] = true
      path.push(currentPosition)
    elseif not path.empty() then
      -- get back one step
      currentPosition = path.pop()
    else
      -- there's no solution
      break
    end
  end
end

-- A shorthand for direction coordinates
local neighbourLocations = {
  [0] = {0, 1},
  [1] = {1, 0},
  [2] = {0, -1},
  [3] = {-1, 0},
}

local function neighbours(position0, fn)
  local neighbours = {}
  local currentCell = map[position0]
  if type(currentCell)=='table' then
    local connections = currentCell.connections
    for i=0,3 do
      -- is this cell connected?
      if bit.band(connections, 2^i) >= 1 then
        local neighbourLocation = neighbourLocations[i]
        local position1 = {position0[1] + neighbourLocation[1], position0[2] + neighbourLocation[2]}
        if (position1[1]>=1 and position1[1] <= maze.width and position1[2]>=1 and position1[2] <= maze.height) then
          if type(fn)=="function" then
            if fn(map[position1], position1) then
              table.insert(neighbours, position1)
            end
          else
            table.insert(neighbours, position1)
          end
        end
      end
    end
  end
  return neighbours
end

This pathfinding algorithm uses two main steps. First, it looks around the current maze cell to find cells that are connected to the current maze cell with a passage. This will result in a list of possible cells that haven't been visited yet. In this case, the algorithm will always use the first available cell from this list. Each step is recorded in the stack structure, so in the end, you can reconstruct the whole path from the exit point to the entry point. If there are no maze cells to go, it will head back to the previous cell from the stack.

The most important is the neighbours function, which determines where to go from the current point. It uses two input parameters: current position and a cell testing function. It looks around the current cell in four directions in clockwise order: up, right, down, and left. There must be a passage from the current cell to each surrounding cell; otherwise, it'll just skip to the next cell. Another step determines whether the cell is within the rectangular maze region. Finally, the cell is passed into the user-defined testing function, which will determine whether to include the current cell in a list of usable cells.

The maze cell testing function consists of a simple Boolean expression. It returns true if the cell has a correct cell type (not a wall) and hasn't been visited yet. A positive result will lead to inclusion of this cell to a list of usable cells.

Note that even if this pathfinding algorithm finds a path to the exit point, it doesn't guarantee that this path is the shortest possible.