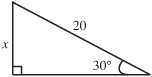
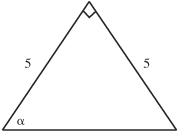
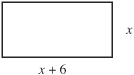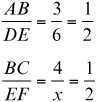In this chapter you will find an introduction to the basics of plane and solid geometry, trigonometry, and analytic geometry; that is, the world of angles and triangles, rectangles, squares, circles, cubes, and cylinders. We will not have to become involved with proofs, but only with word problems that ask for numerical answers.
In plane geometry, we will calculate areas of triangles and other planar figures and their perimeters, circumferences, diameters, and radii of circles, and, later on, the volumes of cubes and cylinders.
You will learn about the Pythagorean Theorem and how to apply it. You will become acquainted with similar triangles and how they are used for various calculations.
Then we will move onto problems involving figures with more than three sides, such as quadrilaterals, polygons (for example, the Pentagon in Washington, D.C, with five angles and five sides, is a polygon), and also circles.
In solid geometry you will calculate areas and volumes of different solid figures, such as cubes and cylinders. In the section on trigonometry there will be problems involving the three important functions sine, cosine, and tangent and how to find their values using a calculator. Finally, in the section on analytic geometry (also called coordinate geometry), you will learn how to represent points and equations by their coordinates in a graph and how to calculate distances between points or areas of triangles and rectangles formed by these points.
This chapter deals with the basics of geometry. There are no proofs, only calculations. In plane geometry we deal with lines, rays, and line segments.
A straight line has no beginning, no end, and no size, only direction. It is represented by a line with arrows. A ray is a part of a line with a beginning but no end. A line segment is a part of a line with a beginning and an end.

Angles are formed by two rays with the same endpoint (vertex). They are measured in degrees. If the rays coincide, the angle measure is 0°. When the rays form a straight line, the angle measure is 180°: This is a straight angle. When the angles are perpendicular, the angle measure is 90°: This is a right angle. A right angle looks like the corner of a book or any other rectangular object. Symbol for angle: ∠
An angle between 0° and 90° is acute and an angle between 90° and 180° is obtuse. When two angles’ measurements add up to 180°, they are supplementary, and two angles whose measurements add up to 90° are complementary.
Example:
Find the supplementary angle to 135°.
Two supplementary angles add up to 180°, so 180 – 135 = 45. The angle is 45°.
Practice Problem:
The perimeter of a plane figure is the total length around it. Think of measuring it with a tape measure.
Example:
A rectangle has a perimeter of 72 inches. If the length is 6 inches more than the width, find the length and width.
Call the width x. Then the length is x + 6 and the perimeter is
x + x + 6 + x + x + 6
= 72
4x + 12
= 72
4x
= 60
x
= 15
x + 6
= 21
The width is 15 inches and the length is 21 inches.
Check: 15 + 21 + 15 + 21 = 72
Example:
The base of an isosceles triangle is 7 inches and the perimeter is 29 inches. Find the other sides.
An isosceles triangle has two equal sides. The third side is called the base.
Call each of the equal sides x.
The perimeter is
x + x + 7
= 29.
2x + 7
= 29
2x
= 22
x
= 11
The sides are each 11 inches.
Practice Problems:
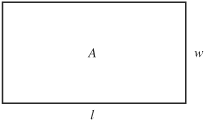
The area of a rectangle is length × width.
Example:
A rectangle has a length of 10 cm and a width of 6 cm. Find the area.
l × w = 10 cm × 6 cm = 60 cm2 (square centimeters).
Note that all areas are expressed in square units.
Example:
A square has a perimeter of 24 inches. Find the area.
A square is a rectangle with all sides equal. The side is usually called s, so the area is s × s, or s2.
4s = 24
s = 6
A = 6 × 6 = 36 in.2
The area is 36 square inches.
The area of a triangle is A = 1/2bh where b is the base and h is the height (or altitude), which is a line segment from the vertex (corner) opposite the base and perpendicular (under right angles) to the base.
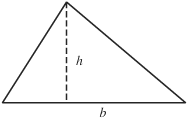
Any side of the triangle can be considered the base. Each base has an altitude connected to it.
Example:
Find the area of a triangle with a base of 4 inches and the height of 3 inches.
Formula: ![]()
The area is 6 square inches.
Example:
The legs (the sides that form the right angle) of a right triangle are 5 cm and 8 cm. Find the area.
If one leg of the right triangle is taken as the base, the other leg is the height.
Area: ![]()
The area is 20 cm2.
Practice Problems:
If the legs of a right triangle are a and b, we have the relationship a2 + b2 = c2, where c is the hypotenuse (the longest side).

Example:
Find the hypotenuse if the legs are 3 inches and 4 inches.
32 + 42 = 9 + 16 = 25 = 52
Answer: The hypotenuse is 5 inches.
Example:
Find the other leg, if one leg is 5 cm and the hypotenuse is 13 cm.
Call the missing side x.
x2 + 52 = 132
x2 + 25 = 169
x2 = 144
x = 12
The leg is 12 cm.
Practice Problems:
The sum of the angles in any triangle is 180°.
Example:
If the angles in a triangle are x, 2x, and 3x, find x.
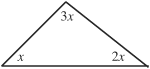
x + 2x + 3x
= 180
6x
= 180
x
= 30
The angle marked x is 30°.
The other angles are 60° and 90°.
Practice Problems:

If one side of a triangle is extended, the angle formed between the extended side and the other side is called exterior.
An exterior angle is equal to the sum of the two non-adjacentangles. In other words,
x = α + β
Example:
How many exterior angles does a triangle have?
Each vertex (corner) can create two exterior angles, and they are always equal; therefore, there are at most three different exterior angles.
Example:
Find the exterior angles in a triangle where the angles are 37°, 42°, and 101°.
37° + 42°
= 79°
37° + 101°
= 138°
42° + 101°
= 143°
The exterior angles are 79°, 138°, and 143°.
What is the sum of the three exterior angles in the previous example? Is that true for all triangles?
Example:
Find the angles of the following triangle: One exterior angle is 14x – 6° and the two non-adjacent interior angles are 7x and 5x + 10°.
14x – 6
= 7x + 5x + 10
14x – 6
= 12x + 10
2x
= 16
x
= 8
Exterior: 14(8°) – 6° = 106°
Non-adjacent interior: 7(8°) = 56°
Non-adjacent interior: 5(8°) + 10° = 40° + 10° = 50°
Third interior: 180° – 106° = 74°
The angles are 74°, 56°, and 50°.
Practice Problems:
If two triangles are equal in both shape and size, they are congruent. If one triangle were cut out and moved, it would fit exactly over the other. Symbol: ≅.
The concept of congruence is used mainly in proofs. The concept of similarity is more useful for word problems. Similar figures have the same shape but not the same size. Symbol: ˜.
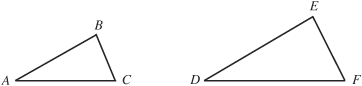
Similar triangles have the corresponding angles equal and corresponding sides proportional.
For example, if triangle ABC ˜ triangle DEF, then
∠A ≅ ∠D ∠B ≅ ∠E ∠C ≅ ∠F
Example:
In the previous example, if AB = 3, BC = 4, AC = 5, DE = 6, what are EF and DF?
Practice Problems:
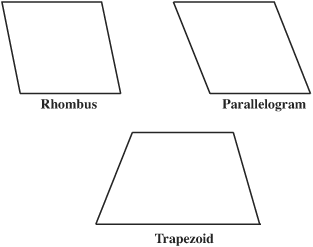
The word polygon means many angles. But it also used to mean many sides. The simplest polygons are triangles and then quadrilaterals (four-sided). Here belong the square, the rectangle, the rhombus, the parallelogram, and the trapezoid.
If a polygon is enlarged, all sides are enlarged in the same proportion. What happens to the area?
As an example, take a 2 × 3 rectangle. Its area is 2 times 3 = 6 square units.
Multiply each side by 2. The new rectangle has a width of 4 units and a length of 6 units. Its area is 24 square units, that is, 4 times the original rectangle.
Example:
The ratio of the perimeters in two polygons is 2:3. If the area of the small polygon is 5 in.2, find the area of the large polygon.
The ratio of the areas is the square of 2:3 or 4:9.
Cross multiply:
4x
= 45
x
= 11.25
The area is 11.25 in.2.
The circle’s perimeter is called the circumference. C = 2πr, where C is the circumference, π is approximately 3.14, and r is the radius of the circle. The formula can also be written as C = πd, where d is the diameter of the circle.

The area of the circle is A = πr2.
Example:
Find the circumference and the area of a circle with a radius of 2 inches.
C = 2πr = 2 × 3.14 × 2 in. = 12.56 in.
A = πr2 = 3.14 × (2)2 in.2 = 12.56 in.2
Practice Problems:
A rectangular solid looks like a box. It has 6 rectangular faces, 12 edges, and 8 vertices (corners). The figure on the left shows the box and the figure on the right shows the box flattened out.
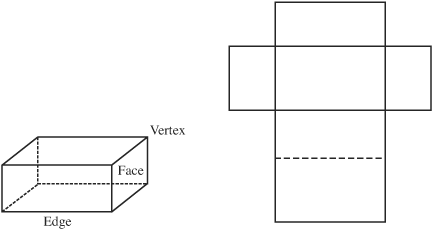
A cylinder looks like a can. Sometimes it has a top and a bottom like a can but sometimes it does not.

The area of a rectangular solid equals the sum of the areas of the 6 faces.
Example:
A rectangular solid has the edges 3 in., 4 in., and 5 in. Find the total surface area.
There are 2 (3 × 4) rectangles, 2 (3 × 5) rectangles, and 2 (4 × 5) rectangles.
Total area:
2 × 3 × 4 in.2
= 24 in.2
2 × 3 × 5 in.2
= 30 in.2
2 × 4 × 5 in.2
= 40 in.2
The surface area is (24 + 30 + 40) in.2 = 94 in.2
Practice Problems:
The surface area of a cylinder is as follows. If it has a top and a bottom, pretend that you remove both with a can opener. You now have two circles and a top/bottomless cylinder. Slit this cylinder vertically and flatten it. You have now obtained a rectangle with a width equal to the height of the cylinder and a length of 2πr, where r is the radius of the circles that have been cut out. Refer to the figure on page 127.
Example:
Find the surface area of a cylinder that has a height of 8 in. and two base areas with diameters of 4 in.
The base areas have each an area of π(4/2)2 inches = π(4) inches = 4π inches.
The area of the remaining rectangle is π(4)(8) inches = 32π inches. Total area: 4π inches + 4π inches + 32π inches = 40π inches.
Practice Problem:
The volume of a rectanglular solid is width × length × height.
Example:
A rectangular solid has the edges 3 in., 4 in., and 5 in. Find the volume.
The width is 3 in., the length is 4 in., and the height is 5 in.
The volume is 3 × 4 × 5 cubic inches (in.3) = 60 in.3.
Example:
Find the volume of a cylinder that has a height of 8 in. and two base areas with a diameter of 4 in.
The volume of a cylinder is base × height = πr2 × h.
r = 4/2 inches = 2 inches. The radius is half of the diameter.
h = 8 inches
V = π22 × 8 in.2 = 32π in.2 or approximately 32 × 3.14 which is 100 in.2 (rounded).
Practice Problems:
Trigonometry, the study of triangles, has become a major branch of mathematics. Here we are only looking at the very basic area of trigonometry, namely the trigonometry of right angles.
In the figure on the next page, we have a right triangle with two angles equal to 45°. You can make your own 45° by folding the corner of a sheet of writing paper so that the sides (length and width) come together at a straight edge. With a ruler make two lines parallel to the side marked Leg, as shown in the figure on the next page.

The leg next to the 45° angle is adjacent, the leg opposite the 45° angle is opposite, and the longest side is the hypotenuse. Measure the legs and the hypotenuses in all three triangles and fill in the following table.
Make a table:
Name | Adjacent | Opposite | Hypotenuse | o/h | a/h | o/a |
Triangle 1 | ||||||
Triangle 2 | ||||||
Triangle 3 |
Then, using your calculator, determine a/h, o/h, and o/a.
If you have a scientific calculator, find sin(e) 45°, cos(ine) 45°, and tan(gent) 45°. You usually have to key in the angle first: 45, cos. These are the trigonometric functions and you probably got very similar answers when you got them from the triangles.
In all 45° triangles these ratios are the same. All other angles have the same properties, so you can find the trigonometric functions by using a calculator or a table.
It is common to write SOHCAHTOA to help you to remember which legs in a right triangle give you which identity.
SOH means sine = opposite over hypotenuse
CAH means cosine = adjacent over hypotenuse
TOA means tangent = opposite over adjacent.
If you know the value of a certain trigonometric function, say tangent, you enter the value into your calculator and then press the shift key.
For example, if the value of cosine is 0.5, find the angle. 0.5, shift, cos gives you 60. Is it true that cos 60° equals 0.5?
Example:
Find sine, cosine, and tangent of ∠A and ∠B.

Determine a rule for the trigonometric functions of the non-right angles in right triangles.
sin A = 3/5 = 0.6
sin B = 4/5 = 0.8
cos A = 4/5 = 0.8
cos B = 3/5 = 0.6
tan A = 3/4
tan B = 4/3
Answer: The sine of one angle is equal to the cosine of the other angle. The tangents are reciprocals.
Practice Problems:
Use a calculator for these problems.
This branch of mathematics is also called coordinate geometry, because points and equations are represented graphically in a coordinate plane.
The coordinate plane:
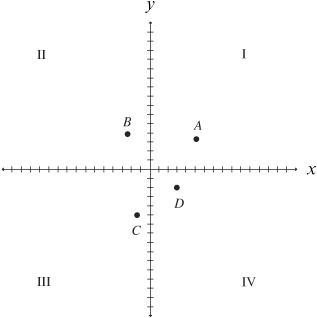
Two perpendicular number lines divide the plane into four parts, quadrants I, II, III, and IV. The horizontal number line is called the x –axis and the vertical number line is called the y-axis. Points are represented in the plane with two numbers (x, y) and are also called ordered pairs.
Example:
Plot the following points:
A: (5,3)
B:(–2,4)
C:(–1,–5)
D: (3,–2)
Use the figure on the preceding page to make your own graph. Start at the point of intersection of the number lines, the origin, and move. A positive x tells you to move to the right and a positive y tells you to move up. A negative x goes to the left and a negative y goes down. If either x or y is zero, you get the message: “Stand still.” You don’t move in the zero direction.
Practice Problems:
Example:
Go back to the figure on page 133 or your own graph and find the distance between the points in 8.47 a and between the points in 8.47 b. You can find these distances simply by counting the squares between in a the y-numbers and in b the x-numbers.
Practice Problems:
Find the distance between a) points (5,9) and (5,5); b) points (5,5) and (3,5). | |
Find the distance between a) points (3,–2) and (3,–7); b) points (–4,–6) and (2,–6). |
If we have two points in a coordinate system and want to find the distance between them, we can create a right triangle and use the Pythagorean Theorem. For example, the points in practice problem 8.49 form a right triangle with the sides 4 and 2 units. The distance between the points, that is, the hypotenuse in the right triangle, is
Example:
Find the distance between the points (4,–3) and (–2,5).
Make a right triangle on paper or in your mind:
The horizontal leg is 5 – (–3) = 5 + 3 = 8.
The vertical leg is 4 – (–2) = 4 + 2 = 6.
The distance is
The distance is 10 units.
Practice Problems:
Find the distance between the points (0,–4) and (3,0). | |
Find the distance between the points (–2,6) and (4,3). |
You can calculate the areas or perimeters of geometric figures by placing them in a coordinate system. There are many more things you can investigate with analytic geometry but here we are limited to a few.
Find the area of a triangle with the vertices (–5,0), (3,0), and (0,4).
The base of the triangle is 3 – (–5) = 8 and the corresponding height is 4. Draw a figure to check if this is right. The area is 8(4)/2 square units = 16 square units.
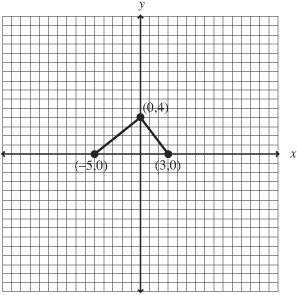
Practice Problems:
Find the area of a triangle with vertices (0,0), (10,0), and (5,3). | |
Find the area of a rectangle with vertices (5,6), (13,6), (5,2), and (13,2). |
Example:
Find the area of a quadrilateral whose vertices are (2,3), (3,6), (10,4), and (4,2).
Mark the vertices on a coordinate system:
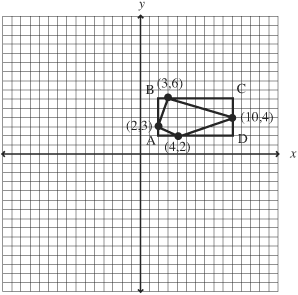
Draw horizontal lines through (4,2) and (3,6). Draw vertical lines through (2,3) and (10,4). Now we have one rectangle from which we can subtract the areas of four right triangles. The rectangle ABCD has vertices (2,2), (2,6), (10,6), and (10,2). The area of the rectangle is:
(10 – 2)(6 – 2) = 8(4) = 32 square units
The areas of the right triangles are:
Vertex A: 2(1)/2 = 1 square unit
Vertex B: 1(3)/2 = 1.5 square units
Vertex C: 7(2)/2 = 7 square units
Vertex D: 6(2)/2 = 6 square units
Total:15.5 square units
The area of the quadrilateral is:
(32 – 15.5) square units = 16.5 square units
Practice Problem: