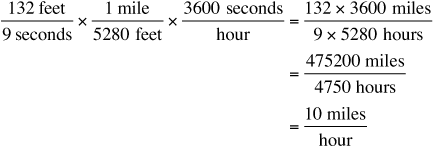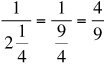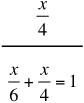The word rate is frequently used in word problems. It is usually accompanied by another word, such as per, for, or in. For example: miles per hour, interest per year, price per pound or price for a certain weight, work done per hour or work done in so many hours.
In this chapter there will be examples of motion problems. When a car or person moves at a known speed (miles per hour) we can calculate the distance they will cover if we know the time it will take. Or knowing the distance and the time it takes, we can calculate the rate (speed) at which they travel. Or knowing the rate and time, we can calculate the distance.
We will also encounter problems where different objects (cars, boats, people) move at different rates and in different directions and where we want to calculate how far apart they will be in a given time or how long it will take them to cover a given distance. Or what happens when you row with the current of the river or against it.
In this chapter you will also learn how to solve work problems: how long it will take you to complete a certain task when you know how much you can do in an hour. For example, if you know that in one hour you can paint half the wall of your living room (that’s your rate), how long will it take you to paint all four walls? Or if your friend agrees to help you and he paints twice as fast as you do, how long will it take?
Finally, there are the filling and emptying problems; such as, how long it takes to fill the bathtub when you forget to close the drain.
This category includes anything that moves; such as cars, boats, river currents, and airplanes.
Example:
Beth walked 2 miles in 40 minutes. What was her rate in miles per hour (mph)?
Here we are given the time in minutes, so we have to convert that into hours.
There are 60 minutes in 1 hour, so 40 minutes is 40/60 = 2/3 hour.
To get speed per hour we divide 2 miles ÷ 2/3 hour:
Beth’s rate was 3 mph.
Example:
Sheldon drove his car at an average of 55 mph. How far did he drive in 4 hours?
The formula we can use is: distance = rate× time.
d = 55 × 4 = 220 miles
With help of dimensional analysis (see Chapter 5), we can check if our units are correct.
(We reduce, or cancel, the unit hours.)
Example:
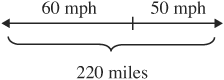
A car travels east at a speed of 50 mph and a motorcycle travels west at a speed of 60 mph. If they start at the same time and place, how long will it take them to be 220 miles apart?
Often with these types of problems it is useful to draw a picture.
Make a table and recall that distance traveled equals time × rate:
Miles per hour is abbreviated as mph and
Rate (speed) (mph)
Time (hours)
Distance (miles)
Car
50
x
50x
Motorcycle
60
x
60x
Total
220
The total distance traveled is 50x + 60x = 220.
Solve the equation: 110x = 220 or x = 2
It took them 2 hours to be 220 miles apart.
Example:
Use dimensional analysis (Chapter 5) to convert 132 feet per 9 seconds to miles per hour.
Feet must be converted to miles and seconds to hours.
132 feet in 9 seconds equals 10 miles per hour.
Example:
Anne drove to her friend’s house at a speed of 55 mph. During the trip back home, she could only drive 35 mph. It took her 2 hours longer to get home. How many miles is between Anne’s home and her friend’s?
Make a table:
Rate (mph)
Time (hours)
Distance (miles)
To the friend
55
x
55x
Back
35
(x +2)
35(x +2)
Note that the distance is the same going there as going home.
55x
= 35(x + 2)
55x
= 35x + 70
20x
= 70
x
= 3.5
Because it took her 3.5 hours to drive at a speed of 55 mph, the distance was:
3.5 × 55 miles = 192.5
Check: 35(3.5 + 2) miles = 35(5.5) miles = 192.5 miles
Practice Problems:
Example:
A bicyclist was training for a race. The training route was 75 miles. If the racer could increase his speed by 5 mph, he could complete the same course in 3/4 of the time he did earlier. Find his average rate of speed.
Table:
Rate (mph)
Time (hours)
Distance (miles)
Case 1
x
y
xy = 75
Case 2
(x + 5)
3/4y
(x + 5)3/4y = 75
We have two equations:
xy = 75
(x + 5)3/4y = 75 → 3/4xy + 5(3/4)y = 75 → 3xy + 15y = 300 (Multiply both sides by 4.)
Substitute xy = 75 in the previous equation:
3(75) + 15y
= 300
225 + 15 y
= 300
15 y
= 75
y
= 5
It took 5 hours to bicycle 75 miles, so his speed was 15 mph.
Practice Problems:
Example:
It takes Jim 3 hours to row 12 miles with the current downstream and it takes him 6 hours to row the same distance against the current upstream. How fast can Jim row in still water? What is the speed of the current?
Think of what happens when he rows with the current: The current pushes him along so he will go faster. On the other hand, when he rows against the current, he is hindered by the current and goes slower. If Jim’s speed is x mph and the current’s y mph, then the speed with the current is x + y and against the current x – y. (Don’t write y – x, because then he would be going backwards!)
Make a table:
Rate (mph)
Time (hours)
Distance (miles)
With
x + y mph
3 hours
(x + y)3 miles = 12 miles
Against
x – y mph
6 hours
(x – y)6 miles = 12 miles
Recall that parentheses followed or preceded by a number means multiplication.
We now have two unknowns and two equations:
(x + y)3 = 12 and (x – y)6 = 12
Solve this system of equations by dividing the first by 3 and the second by 6:
Jim rows 3 mph in still water and the speed of the current is 1 mph.
Practice Problems:
Work problems are another type of rate problem. If we know how long it takes a worker to complete a certain task, we know the rate or which part of the job he can do per hour.
Example:
Lou can stamp 600 envelopes in two hours. What is his rate?
The total job takes 2 hours. Every hour he does 1/2 of the job. His rate is 1/2 of the total, or he can stamp
· 600 = 300 envelopes per hour.
Example:
It takes Edwin 2 1/4 hours to paint a wall. What is his rate?
The total job takes 2 1/4 hours.
The rate per hour is:
He completes 4/9 of the job every hour.
Check: In 2 hours he completes 8/9 of the job and in 1/4 of an hour he completes the last 1/9 of the job.
Most work word problems deal with two people working together. Other problems deal with bathtubs that can be filled in a certain amount of time. Sometimes we leave the outlet plug open by mistake and then, how long does it take to fill the tub?
Example:
Anna can paint a room in 6 hours while Barbara can paint the same room in 4 hours. How long does it take if they work together?
Make a table:
Name
Rate/Hour
Time (hours)
Total Work
Anna
x
Barbara
Total
x
The total job is 1.
LCD = 12 (The least common denominator).
Multiply both sides by 12:
2 x + 3 x = 12
5 x= 12
hours = 2 hr. +
× 60 min. = 2 hr. 24 min.
The total work time is 2 hours and 24 minutes.
Example:
Steven can wallpaper a room in 4 hours and Evie can wallpaper the same room in 6 hours. If Steven works alone for 1 hour and then both Steven and Evie work together to finish the room, how long will it take them assuming they keep their usual speed?
Make a table:
Name
Rate
Time
Total Work
Steven
1/4
1 + x
(1 + x)1/4
Evie
1/6
x
1/6(x)
Equation:
(1+ x)3 + 2x
= 12
3 + 3x + 2x
= 12
5x
= 9
x
= 9/5
9/5 hours = 1 + 4/5 hour = 108 minutes
Practice Problems:
Example:
If 3 men can paint 4 houses in 5 days, how many days does it take for 7 men to paint 14 houses?
We have to suppose that all the men work at the same speed. Three men can paint 4/5 houses per day and one man can paint
per day. At this rate it takes 7 men x days to paint 14 houses. That means that one man can paint
per day.
These two expressions are equal:
.
Reduce the right side of the equation and we get
.
Cross multiply: 4x = 30, so x = 7.5
It takes 7 1/2 days to paint these houses.
Practice Problem:
Robots are used to assemble automobiles in a factory. Three robots assemble 17 cars in 10 minutes. If all robots assemble cars at the same speed, how many cars can 14 robots assemble in 45 minutes?
Example:
It takes the hot water tap 30 minutes to fill the bathtub, while the cold water tap takes 20 minutes. How long would it take to fill the bathtub if both taps were open? Assume it takes x minutes.
Make a table:
Rate
Time (minutes)
Part of bathtub filled
Hot water
1/30
x
x/30
Cold water
1/20
x
x/20
Equation: The bathtub is now filled, so we get the equation: x/30 + x/20 = 1
Multiply both sides by 60(LCD), simplify, and solve.
2 x + 3 x
= 60
5 x
= 60
x
= 12
Answer: It takes 12 minutes to fill the bathtub when both taps are open.
Example:
In the previous bathtub example, if the drain had been left open by mistake, how long will it take to fill the bathtub if the drain can empty the bathtub in 15 minutes?
As before, call the time x and make a table. Note that the rate when the bathtub is emptied is negative.
Make a table:
Rate
Time (minutes)
Part of bathtub filled
Hot water
1/30
x
x/30
Cold water
1/20
x
x/20
Drain
-1/15
x
-x/15
Equation:
Multiply both sides by 60 (LCD), simplify, and solve.
2x + 3x – 4x
= 60
x
= 60
Answer: With the drain open, it takes 60 minutes to fill the bathtub.
Practice Problems: