In this chapter we will continue to analyze and solve age-related word problems, but the ones in the following pages are more complicated than the ones we solved previously. Therefore, we will have to spend more time to analyze and understand what the question is and how we can set up the equation, or sometimes two equations, that will help us to come up with an answer.

As before, these problems involve age differences between one child and another, between a child and an adult, or more than two persons, and we will have to read the problems carefully in order to calculate the ages of these persons now, or in a given number of years.

By setting up tables that list the facts and then generating equations from these tables, we will be able to solve the problems and come up with the correct answers. At the end of this chapter we will learn how to set up quadratic equations needed to solve certain kinds of problems.

Example:

Alan is 5 years older than Bert. If, in 3 years, Alan’s age will be twice Bert’s, how old are Alan and Bert now?

If Bert’s age is x, then Alan’s age is x + 5. Set up a table:

Alan’s age is twice (2 times) Bert’s.

Bert’s age is 2 and Alan’s age is 2 + 5 = 7

This problem could also have been solved with Alan’s age as x, but keep in mind that if Alan is older than Bert, then Bert is younger than Alan. Therefore:

Alan is 7 and Bert is 7 – 5 = 2.

Example:

Elsa is 7 years younger than Thor. The sum of their ages is 35. How old are they?

Practice Problems:

Example:

The sum of Tom’s and Lou’s age is 41 and the difference is 31. How old are they?

Here we work with both x and y. Let x stand for Tom’s age and y stand for Lou’s age.

Tom is 36 years old and Lou is 41 – 36 = 5 years old.

Now, if the problem were stated differently: The sum of Lou’s age and his father’s is 41 and the difference is 31, we must realize that the father is older. If we call Lou’s age x and the father’s age y, we get:

The father is 36 years old and Lou is 5 years old.

Practice Problems:

Use two variables for practice.

Example:

The ratio of John’s age to David’s age is 6:5. In 7 years the ratio will be 7:6. What are their ages now?

A ratio is a comparison of two numbers by division. 6:5 is the same ratio as 12:10,18:15, etc. Since the ratio is 6:5, we can call the ages 6x and 5x. (See also the Ratio problems in Chapter 5.)

Set up a table:

The ratio of the ages is then 7:6 and we can set up an equation:

This is a proportion (two equal ratios), so we can cross multiply:

John is 6(7) = 42 years old and David is 5(7) = 35 years old.

Check: In 7 years John will be 49 years old and David 42.

Ratio: 49:42 = 7:6

Alternate Solution:

Equations: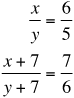

Cross multiply both equations:

We now have two equations:

Practice Problems:

Example:

Twice Lydia’s age plus 1 equals 3 times her age less 4. How old is Lydia now?

Practice Problems:

Example:

When Ralph asked his math teacher how old she was, she answered: “Ten years ago, my age was equal to the square of my daughter’s age. In 14 years, I will be twice as old as my daughter.”

Call the teacher’s age x and her daughter’s age y.

Make a table:

Equations: x – 10 = (y – 10)²→x – 10 = y² – 20y + 100

x + 14 = 2(y +14) → x + 14 = 2y + 28 → x = 2y + 14

Substitute x in the top equation with the expression for x in the second equation:

We must reject y = 6 because 10 years ago, the daughter would be -4.

We find the teacher’s age by substituting in one of the original equations.

The teacher is 46 years old.

Check: In 14 years the teacher will be 60 years old and her daughter 30 years old.

Practice Problems: